2. 哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001;
3. 上海中船船舶设计技术国家工程研究中心有限公司,上海 200083
2. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China;
3. Shanghai Zhongchuan Ship Design Technology National Engineering Research Center Co., Ltd, Shanghai 200083, China
效能评估对装备系统的设计、研制、采购及使用都十分重要,对装备系统的论证更是必不可少[1-2]。输转作业是指作业中与作业实体位置变化相关的所有作业,包括货物装卸、升降机运输、叉车转运等复杂环节,涉及车辆、升降机、保障装备等多种设备。输转作业效能评估就是对执行输转任务中输转系统的可靠性、可信性和能力等因素的综合评价,是对整个输转作业所涉及的主要因素进行的综合计算,并用量化的数据来衡量该系统完成输转任务的优劣程度。
国内在效能评估领域的研究多集中在某一武器装备或某一武器系统的效能评估,多属于对ADC效能评估模型的简单应用[3-5]。有一些文献虽然涉及到多个子系统效能问题,但只是把这些子系统的效能进行了相加,并没有分析这些子系统效能之间的串并联关系[6-7],存在无法分析流程内的瓶颈环节和流程优化等难题。
针对输转作业系统的作业环节多、设备类型复杂和影响参数多的特点,提出将复杂系统划分为若干具有一定串并联关系的子系统,先求解子系统效能,然后再求解总系统效能的处理方法。具体处理方法如下:将总系统按照不同功能或用途进行划分,得到若干个子系统。划分后的子系统称作节点,子系统的效能称为节点效能。根据子系统间的串并联关系,对节点效能进行集成,求解系统的总效能。这种处理方法不仅可以简化求解过程,降低求解难度,并且能够根据不同节点的特性选用不同的效能度量模型,使效能度量结果符合系统特性。传统的计算方法只能发现整个系统效能的优劣,而不能准确确定到装备系统细节中。与传统效能评估方法相比,本文的求解方法将评估目标划分若干个子节点,逐一求解,避免了整体内权重分配的困难,且子节点间是相互独立又相对联系的个体,便于单独评估某个子节点效能,同时每个子节点指标变化又会影响到系统的综合效能值,符合系统评估的需要。
1 系统效能求解方法研究依据串并联效能层次结构图的组成,对系统效能的求解方法进行改进。首先,根据任务或者功能设备将系统划分为若干个子系统,然后用串并联概念来定义子系统之间的组织结构。最后采用先求解子系统效能再求解总系统效能的方法解决输转作业效能问题。
串并联求解效能的方法可以避免将所有数据运用到一个系统效能求解的数学模型中。采用先对子系统效能求解,然后对子系统效能进行有机合并实现求解系统效能的方法,从而降低了数据处理难度,便于查找影响系统效能的瓶颈部分。
为了能够在效能计算过程中体现效能层中子系统间真实的串并联结构关系并且简化效能计算过程,分步计算各节点效能,然后按照一定运算关系集成得到系统效能。
如图1所示某系统串并联效能层次结构图,节点效能
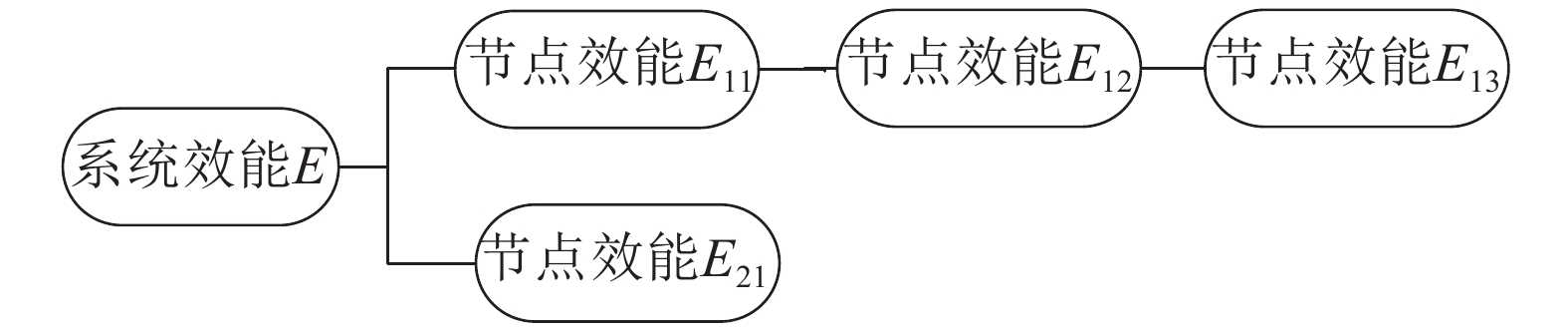
|
Download:
|
| 图 1 串并联效能层次结构简图 | |
根据上述系统结构图,系统节点是串联关系的效能计算模型的一般表达式为
| ${E_{\text{串联}}} = \prod\limits_j^{} {{E_{ij}}} \left( {2 \leqslant j \leqslant n} \right)$ |
即系统效能为各串联节点效能相乘。
1.2 并联节点计算模型系统节点是并联关系的效能计算模型的一般表达式为
| ${E_{\text{并联}}} = \sum\limits_i^{} {{\lambda _i}{E_{ij}}} \left( {2 \leqslant i \leqslant n} \right)$ |
即系统效能为各并联节点效能相加。其中
对应图2、3的2种典型节点串并联混合方式,其效能计算模型的一般表达式如式(1)、(2)所示。

|
Download:
|
| 图 2 串并联混合方式一 | |

|
Download:
|
| 图 3 串并联混合方式二 | |
| ${E_{\text{串并联}}} = \sum\limits_i^{} {{\lambda _i}\left( {\prod\limits_j^{} {{E_{ij}}} } \right)} \left( {2 \leqslant i,j \leqslant n} \right)$ | (1) |
| ${E_{\text{串并联}}} = \prod\limits_j^{} {\left( {\sum\limits_i^{} {{\lambda _i}{E_{ij}}} } \right)} \left( {2 \leqslant i,j \leqslant n} \right)$ | (2) |
根据上述思想,提出输转作业效能的求解步骤如下:
1)划分子系统,确定系统节点;
2)建立效能层次结构图;
3)求解系统节点效能;
4)求解输转作业系统的效能。
2 节点效能计算方法研究ADC模型是由美国工业界武器系统效能咨询委员会WSEIAC(Weapons System Effectiveness Industry Advisory Committee)提出,它被广泛应用于系统效能的评估[10-11]。该方法以装备系统的总体构成为对象,以所完成的任务为前提对装备效能进行评估。ADC模型的含义:系统效能是预期一个系统满足一组特定任务要求程度的量度,是系统可用性A、可信性D与固有能力C的函数。可用度是在开始执行任务时系统状态的度量;可信性是在已知系统开始执行任务时所处状态的条件下,在执行任务过程中某个瞬间或多个瞬间的系统状态的度量;固有能力是在己知系统执行任务过程中所处状态条件下,系统达到任务目标的能力的度量。由于输转作业的效能受工作时间长短影响,是动态的数据,因此输转作业中各节点效能的计算选择ADC模型。
ADC模型的计算公式为
| ${ E} = { A} \cdot { D} \cdot { C}$ |
以系统包含两种状态计算为例,介绍ADC求解公式[12]。
| $\left\{ \begin{gathered} {A} = \left( {\begin{array}{*{20}{c}} {\displaystyle\frac{{{T_{{{MTBF}}}}}}{{{T_{{{MTBF}}}} + {T_{{{MTTR}}}}}}}&{\displaystyle\frac{{{T_{{{MTTR}}}}}}{{{T_{{{MTBF}}}} + {T_{{{MTTR}}}}}}} \end{array}} \right) \hfill \\ {D} = \left( {\begin{array}{*{20}{c}} {{{{e}}^{ - \textstyle\frac{t}{{{T_{{{MTBF}}}}}}}}}&{1 - {{{e}}^{ - \frac{t}{{{T_{{{MTBF}}}}}}}}} \\ {1 - {{{e}}^{ - \frac{t}{{{T_{{{MTTR}}}}}}}}}&{{{{e}}^{ - \frac{t}{{{T_{{{MTTR}}}}}}}}} \end{array}} \right) \hfill \\ {C} = \sum\limits_{k = 1}^2 {{w_k}{\mu _k}} \hfill \\ \end{gathered} \right.$ |
式中:
某货船有输转作业任务,货物存储在下层甲板仓库中,现要将货物通过吊车、叉车、升降机运输到上层甲板指定位置。从空间利用率角度考虑设计输转系统,现有2个输转系统方案,2种输转系统结构、货物布置方案分别如图4、5所示。
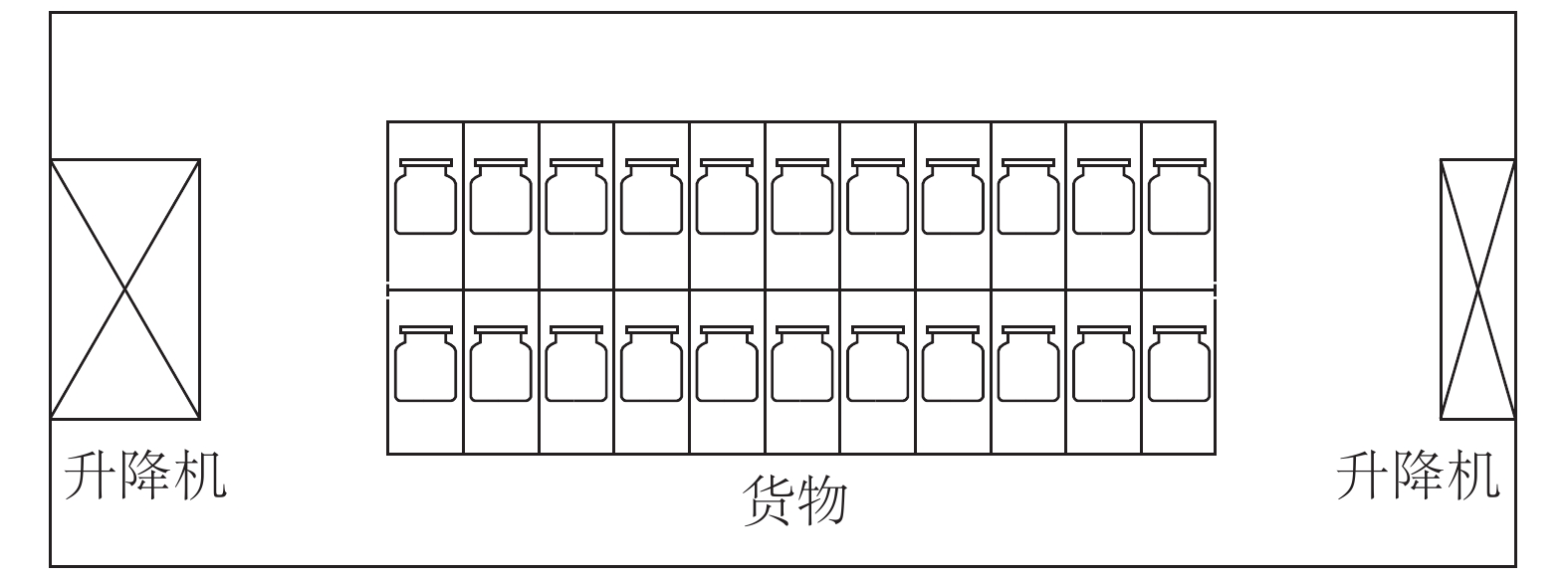
|
Download:
|
| 图 4 方案1结构简图 | |

|
Download:
|
| 图 5 方案2结构简图 | |
方案1有两架升降机共同工作,一架升降机一次运输两箱货物,另一架升降机一次运输一箱货物;方案2只有一架升降机工作,该升降机一次能运输两箱货物。从空间利用角度考虑,方案2比方案1节省舱室空间,利于货物转运操作;从输转效率角度考虑,方案1比方案2节省时间。为了保证输转任务顺利完成,并且使设备使用年限最大,需要通过效能评估,来选择其中较优的输转系统方案。
3.1 系统结构图建立梳理输转作业任务,建立方案1和方案2的系统结构图,如图6、7所示。
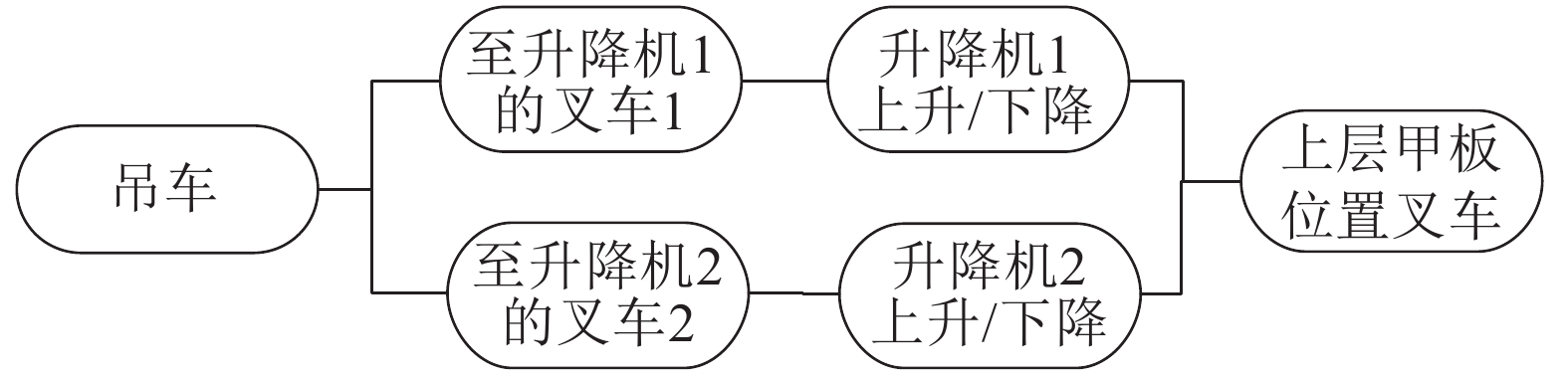
|
Download:
|
| 图 6 方案1系统结构 | |
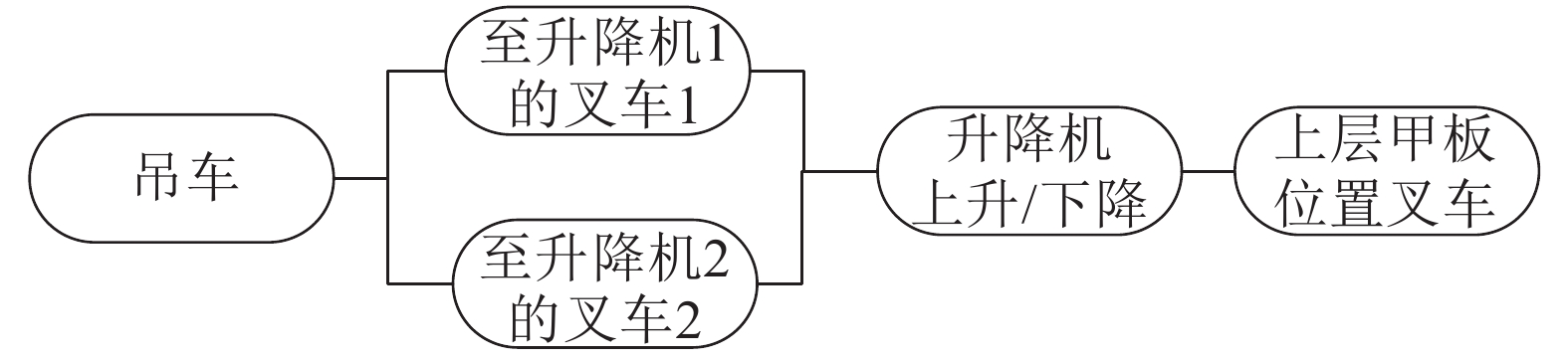
|
Download:
|
| 图 7 方案2系统结构 | |
输转系统中各设备的能力主要受以下指标决定:
1)叉车包括动力装置指标、传动装置指标、执行装置指标、装载量指标;
2)升降机包括动力装置指标、传动装置指标、控制装置指标、执行装置指标、装载量指标;
3)吊车包括动力装置指标、传动装置指标、控制装置指标、执行装置指标、装载量指标。
以吊车为例,建立如图8所示效能指标体系。

|
Download:
|
| 图 8 升降机效能评估指标体系 | |
|
|
表 1 装备数据 |
|
|
表 2 设备的指标能力值 |
方案1的输转系统结构完成输转任务需15 h,求解输转作业中各节点效能。根据计算方法求解吊车的节点效能
可用性:
| ${{A}_1} = \left( {\begin{array}{*{20}{c}} {{{0}}{{.990\,\,4}}}&{{{0}}{{.009\,\,6}}} \end{array}} \right)$ | (3) |
可信性:
| ${{D}_1} = \left( {\begin{array}{*{20}{c}} {0.985\,\,6}&{0.014\,\,4} \\ {0.776\,\,9}&{0.223\,\,1} \end{array}} \right)$ | (4) |
能力矩阵如表3所示。
|
|
表 3 各装置间重要性比较矩阵 |
一致性检验计算如式(5)所示。
| $\left\{ \begin{gathered} {\lambda _{\max }} = 5.013 \,\,3 \hfill \\ {\omega} = \left( {\begin{array}{*{20}{c}} {0.313 \,\,3}&{0.098 \,\,6}&{0.098\,\, 6}&{0.176 \,\,2}&{0.313 \,\,3} \end{array}} \right) \hfill \\ C_I = \frac{{{\lambda _{\max }} - n}}{{n - 1}} = 0.003 \,\,3 \hfill \\ \end{gathered} \right.$ | (5) |
式中:
用模糊关系合成原理计算吊车的能力矩阵值:
| $\begin{array}{l}{{ C}_1} = \left( {\begin{array}{*{20}{c}}{0.313\,\,3} & {0.098\,\,6} & {0.098\,\,6} & {0.176\,\,2} & {0.313\,\,3}\end{array}} \right) \cdot \\\quad \quad \quad \left( {\begin{array}{*{20}{c}}{0.95}\\{0.87}\\{0.92}\\{0.91}\\{0.95}\end{array}} \right) = 0.932\end{array}$ |
即
| ${{C}_1} = {\left( {\begin{array}{*{20}{c}} {0.932}&0 \end{array}} \right)^{{T}}}$ | (6) |
根据式(3)、(4)和(6),得到吊车的节点效能:
| ${E_1} = {{A}_1} \cdot {{D}_1} \cdot {{C}_1} = 0.916 \; 7$ |
同理得:
| $\left\{ \begin{gathered} {E_2} = 0.888\,\,9 \hfill \\ {E_3} = 0.888\,\,9 \hfill \\ {E_4} = 0.923\,\,8 \hfill \\ {E_5} = 0.803\,\,9 \hfill \\ {E_6} = 0.924\,\,8 \hfill \\ \end{gathered} \right.$ | (7) |
用层次分析法求解方案1并联线路权重,得到如表4所示的权重关系,故可表示为式(8)。
| ${{M}_3} = \left( {\begin{array}{*{20}{c}} 1&3 \\ {1/3}&1 \end{array}} \right)$ | (8) |
|
|
表 4 两线路间重要性比较矩阵 |
| $\left\{ \begin{gathered} {\lambda _{\max }} = 2 \hfill \\ {\omega} = \left( {\begin{array}{*{20}{c}} {0.75}&{0.25} \end{array}} \right) \hfill \\ CI = \frac{{{\lambda _{\max }} - n}}{{n - 1}} = 0 \hfill \\ \end{gathered} \right.$ |
故输转作业方案1的总效能:
| ${E_{\text{方案}{{1}}}}{{ = }}{E_1} \cdot \left[ {{\omega _1}\left( {{E_2} \cdot {E_4}} \right) + {\omega _2}\left( {{E_3} \cdot {E_5}} \right)} \right] \cdot {E_6} = 0.674$ | (9) |
方案2的输转系统结构完成输转作业任务需25 h,求解输转作业中各节点效能步骤同方案1。
得方案2输转作业的节点效能:
| $\left\{ \begin{gathered} {E_{{1}}} = {{0}}{{.909}}\,\, {{3}} \hfill \\ {E_2} = 0.8{{75}} \,\,{{1}} \hfill \\ {E_3} = 0.8{{75}} \,\,{{1}} \hfill \\ {E_4} = 0.9{{10}} \,\,{{9}} \hfill \\ {E_5} = 0.{{909}} \,\,{{1}} \hfill \\ \end{gathered} \right.$ | (10) |
两支路的权重:
| ${\omega} = \left( {\begin{array}{*{20}{c}} {0.5}&{0.5} \end{array}} \right)$ |
| ${E_{\text{方案}{{2}}}}{{ = }}{E_1} \cdot \left( {{\omega _{{1}}} \cdot {E_2} + {\omega _2} \cdot {E_3}} \right) \cdot {E_4} \cdot {E_5} = 0.6{{59}}$ | (11) |
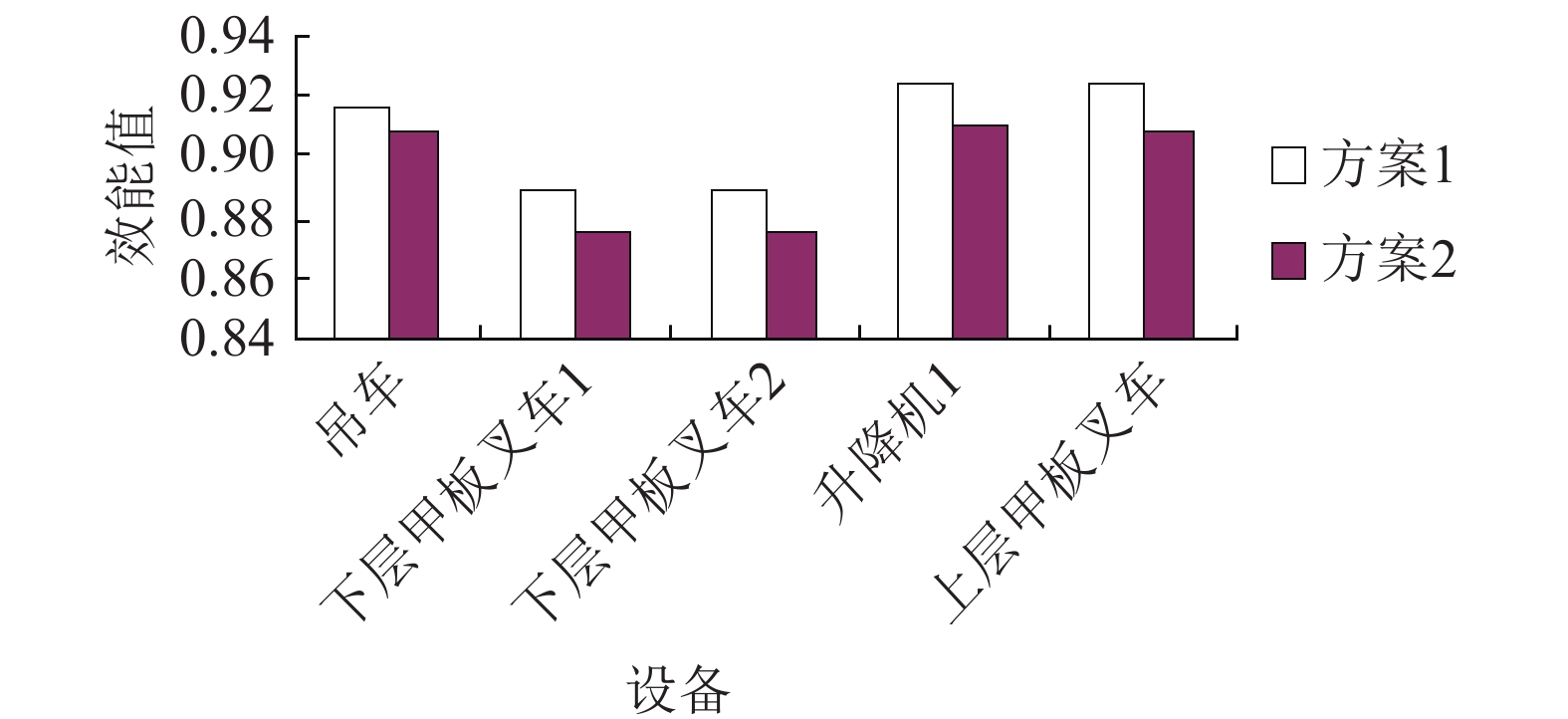
方案1、2的节点效能对比如图9所示,可知方案各节点效能值均在0.8以上,因此评估指标的量化和预处理操作合理,建立的效能评估数学模型可行。方案1对应节点的效能较优,且两个方案间效能值的主要差异在下层甲板叉车2和上层甲板叉车处。由式(9)和(11)可知,方案1的综合效能值较大,因此两个方案中方案1的输转方案设计更优。可通过优化下层甲板叉车2和上层甲板叉车及其关联流程节点来提高效能值,例如改变下层甲板货物布置,缩短叉车运输路径长度,降低叉车操作难度,即提高叉车执行装置能力。
由式(7)、(9)~(11)可知,综合效能值在多个子节点串联即节点效能相乘后趋近0.5,随着子节点数目增加,综合效能值将趋近0,从而无法完成设计方案的效能评估,因此在划分子节点时,应合理控制子节点数量。
|
Download:
|
| 图 9 两方案间节点效能对比 | |
根据输转作业流程复杂、装备多等特点,本文提出了一种基于ADC法划分子系统、建立子系统间串并联关系的效能计算方法,经过实例计算证明该方法可行。
1)能有效降低求解难度,各子系统可以根据各自属性采用不同的效能求解方法,这样使得求解结果更加合理;
2)能够体现系统中设备间的真实关系,且能够清晰的知道哪一任务阶段中哪一装备作业对效能结果影响较大。
当ADC法矩阵阶数较大或子节点数量较多时,会存在计算量很大的情况,因此下一阶段将开展效能评估系统软件设计开发工作,缩短方案评估时间。
| [1] |
谭乐祖, 杨明军, 向迎春, 等. 武器系统效能评估方法研究[J]. 兵工自动化, 2010, 29(8): 13-15, 22. ( 0) 0)
|
| [2] |
张廷良, 陈立新. 军用直升机作战效能评估与运筹分析方法[M]. 北京: 国防工业出版社, 2013.
( 0) 0)
|
| [3] |
孟庆德, 张俊, 魏军辉, 等. 基于ADC法的舰炮武器系统作战效能评估模型[J]. 火炮发射与控制学报, 2015, 36(1): 73-76, 85. ( 0) 0)
|
| [4] |
王君, 赵杰, 邵雷, 等. 基于ADC方法的地空导弹系统效能评估模型[J]. 现代防御技术, 2015, 43(6): 13-20. ( 0) 0)
|
| [5] |
黄炎焱. 武器装备作战效能稳健评估方法及其支撑技术研究[D]. 长沙: 国防科学技术大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-90002-2007141169.htm
( 0) 0)
|
| [6] |
苏琛, 张珂. 后方仓库综合保障效能评估[J]. 物流技术, 2007, 26(5): 119-122. ( 0) 0)
|
| [7] |
陈明, 荀烨, 秦超. 基于ADC法的军事物流基地物资保障效能评估模型[J]. 军事交通学院学报, 2015, 17(10): 46-50. DOI:10.3969/j.issn.1674-2192.2015.10.012 ( 0) 0)
|
| [8] |
杨小彬, 李和明, 尹忠东, 等. 基于层次分析法的配电网能效指标体系[J]. 电力系统自动化, 2013, 37(21): 146-150. DOI:10.7500/AEPS201212085 ( 0) 0)
|
| [9] |
曾建权. 层次分析法在确定企业家评价指标权重中的应用[J]. 南京理工大学学报, 2004, 28(1): 99-104. ( 0) 0)
|
| [10] |
郭齐胜, 罗小明, 潘高田, 等. 武器装备试验理论与检验方法[M]. 北京: 国防工业出版社, 2013.
( 0) 0)
|
| [11] |
尤扬. 系统效能评估及经典方法研究[J]. 科技信息, 2008(29): 217-219. ( 0) 0)
|
| [12] |
李彤岩, 王培国, 张婷. 基于ADC模型的通信网络效能评估方法研究[J]. 电子技术应用, 2015, 14(9): 18-20, 28. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


