2. 武汉武高电气技术有限责任公司,湖北 武汉 430074
2. Wuhan Wugao Electricity Co., Ltd., Wuhan 430074, China
智能电网和“互联网+电力”新模式的蓬勃发展,使得大规模的电力电子器件引入到电力网络中,深刻地改变着电网结构和电力负荷。电能波动、冲击与非线性等质量异常扰动,严重影响供电可靠性,造成了电力用户的经济损失[1]。
电能质量检测是从电压和电流的物理和应用维度,准确、实时地检测电力运行特征和参数指标[2],能够及时反映电能传输与承载线路之间的匹配关系,因此成为了保障电力网络可靠运行的有力手段。但是电能质量检测通常采取在变电站10 kV母线上提取电能特征和参数,其存在铁磁谐振过电压现象以及接地端匹配模糊,导致电能质量检测误差大[3]。在对实际运行的南方电网某110 kV新投运GIS (gas insulated substation)变电站进行电能质量检测时,在10 kV母线上检测到电压谐波含有率为7.3%,而在该变电站110 kV侧检测到的电压谐波含有率仅为0.7%。根据谐波的传播特性,低电压等级的系统谐波应按容量比向高电压等级系统传递。因此仅有站用负荷的新投运站测量到的7.3%谐波含有率带有明显的误差。
数学理论的发展以及电力技术进步,推动世界各国对于电能质量检测的研究。基于电谐波特征变换[4-5]和人工智能特征推理[6-7]是当前电能质量检测的两种主流方法。基于特征变换的电能质量检测方法主要对电谐波特征进行傅里叶变换、小波变换、正交变换等异域特征转化,为了解决频谱泄露以及分辨率受限等缺点,将加窗插值、锁相电路、线性调频Z变换等方法引入,能够有效修正傅里叶变换方法带来的检测误差。小波变换能够提供对电力信号多尺度的特征观测,但是稳定的连续小波变换需要消耗更大的计算资源。正交变换可以将电流分解成相互垂直的分量,但是无法检测出瞬时的多阶谐波电流。为了强化利用电力网络特别是智能电网的学习推理能力,在谐波检测以及谐波源定位中,融合神经网络和支持向量机[8],能够提升电能质量检测的推理能力和误差分析能力。但是复杂的电网结构和不确定的电能运行状态,使得构建预测先验样本需要建立复杂的数学模型。
导致电能质量测量误差的原因,除了现有的测量方式无法解决铁磁谐振过电压以及接地端匹配模糊问题,还存在电压互感器(potential transformer,PT)二次回路的电位差异[9]。常规测量方法将分析仪的N端子接到屏柜的接地端,而PT二次回路的N回路与柜体接地点距离较远,造成2个接地点之间并非绝对的等电位,造成10 kVI段母线零序电压测量值较大,尤其是3次谐波电压[10]。由于铁芯磁化曲线的非线性,励磁电流有不同程度的畸变,使不接地系统的中性点电压产生偏移,不能实现准确测量。这些不稳定的干扰通过PT的传递,影响了仪器对母线电压谐波特性的准确测量。目前测试仪的设计多数针对中性点直接接地系统,面对中性点不接地系统时就会出现难以适应的问题。
1 电压谐波测量误差机理和模型以某110 kV变电站为例,该站为单主变,联接组别为YN, d11,低压侧采用单相PT监测对地相电压,测量电路如图1所示。
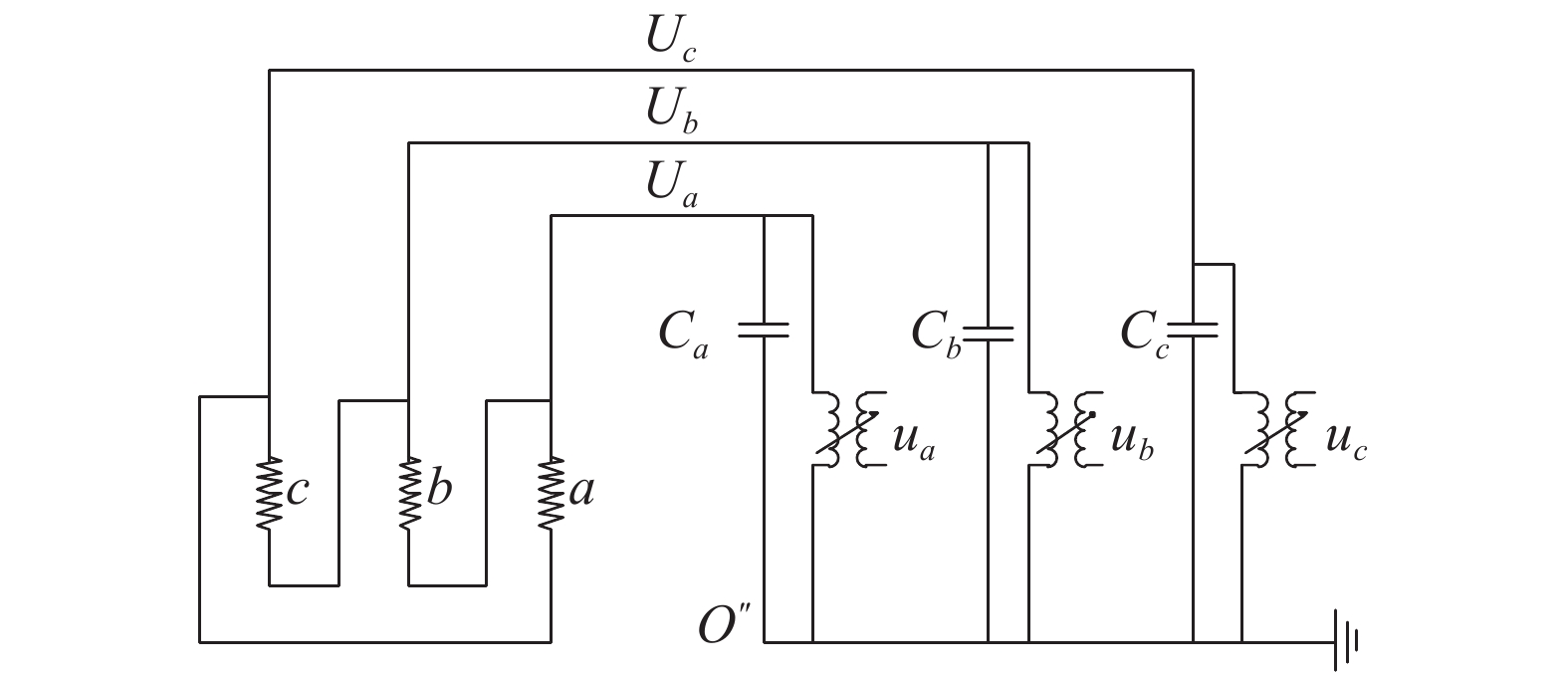
|
图 1 三角形接线系统相电压测量电路 |
其中,Ua、Ub、Uc为三相母线电压,O″为电压互感器尾端公共点,Ca、Cb、Cc为系统对地O的分布电容,ua、ub、uc为电压互感器二次侧电压。
结合变压器结构以及测量电路得出单相测量等值电路,如图2所示。
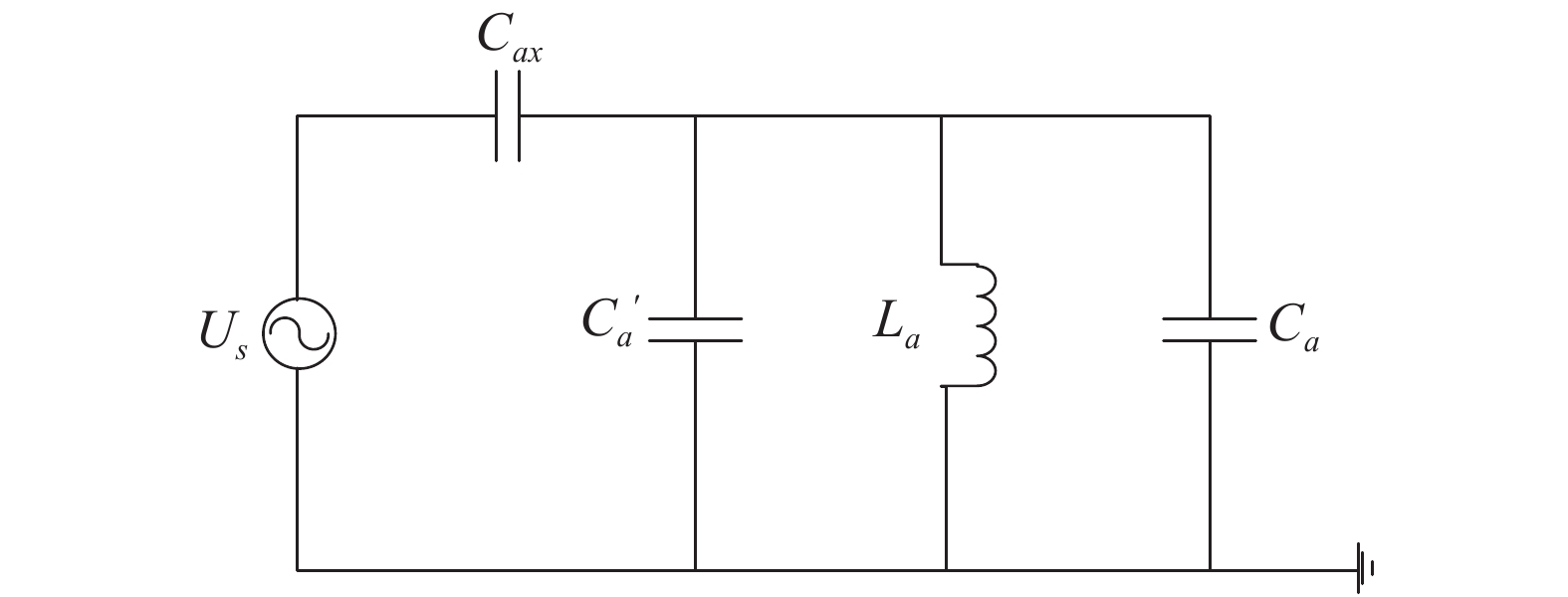
|
图 2 相电压测量单相等值电路 |
图中Us为主变高压绕组与低压绕组之间的电场形成的等值电压激励源,Cax为高、低压绕组间的耦合电容,
在激励源Us的作用下,由储能元件Ca、
| $f = \frac{1}{{2{\rm{\pi }}\sqrt {\left( {{C_a} + C_a^\prime} \right){L_a}} }}$ | (1) |
谐振的存在相当于在由电压互感器尾端构成的测量中性点O″与系统真实零电位点O′之间存在一个干扰源T(t)。T(t)并不是固定的,它随着各相对地电容及电压互感器励磁电抗参数变化而改变,它的存在使得O″相对O′发生不规则的偏移,如图3所示。

|
图 3 中性点偏移矢量 |
此时电压互感器二次侧电压为
| $\left\{ {\begin{aligned}& {\mathop {{U_a}}\limits^{\displaystyle\cdot} = k\left[ {{U_m}\sin \left( {\omega t} \right) + T\left( t \right)} \right]}\\& {\mathop {{U_b}}\limits^{\displaystyle\cdot} = k\left[ {{U_m}\sin \left( {\omega t - 120{\rm{^\circ }}} \right) + T\left( t \right)} \right]}\\& {\mathop {{U_c}}\limits^{\displaystyle\cdot} = k\left[ {{U_m}\sin \left( {\omega t - 240{\rm{^\circ }}} \right) + T\left( t \right)} \right]}\end{aligned}} \right.$ | (2) |
式中k为PT变比。
目前,在变电站10 kV侧进行电压质量测试,基本都是从电压互感器二次侧直接测量各相对地电压。根据式(2),直接测量的电压包含了参数谐振形成的干扰成分,当测量结果用于电压谐波及谐波潮流分析时会产生较大的误差。
构建变压器结构的单相测量等值电路,确保电能质量各项指标检测的准确性,从而为消除参数谐振影响提供基础。
2 三同阻并行接入电压谐波误差检测 2.1 三同阻并行接入积分相电压对运行系统的测量,在无法改变系统运行方式的情况下,可通过对测量仪器的改造,让其适应运行系统,实现电压的准确测量[11]。
文中提出的具体改造方案为在仪器的输入端Y接3个阻值完全相同的纯电阻,通过测量流过电阻的电流与电阻R的乘积即可得到实际的相电压,如图4所示。

|
图 4 仪器输入端Y接电阻示意图 |
对式(2)的电压互感器二次侧电压做差分运算,得到线电压:
| $\left\{ {\begin{aligned}& {\mathop {{U_{ab}}}\limits^ {\displaystyle\cdot} = \mathop {{U_a}}\limits^ {\displaystyle\cdot} - \mathop {{U_b}}\limits^ {\displaystyle\cdot} = k{U_m}\sin \left( {\omega t + 30{\rm{^\circ }}} \right)}\\& {\mathop {{U_{bc}}}\limits^ {\displaystyle\cdot} = \mathop {{U_b}}\limits^ {\displaystyle\cdot} - \mathop {{U_c}}\limits^ {\displaystyle\cdot} = k{U_m}\sin \left( {\omega t - 90{\rm{^\circ }}} \right)}\\& {\mathop {{U_{ca}}}\limits^ {\displaystyle\cdot} = \mathop {{U_c}}\limits^ {\displaystyle\cdot} - \mathop {{U_a}}\limits^ {\displaystyle\cdot} = k{U_m}\sin \left( {\omega t - 210{\rm{^\circ }}} \right)}\end{aligned}} \right.$ | (3) |
由式(3)可知,通过三同阻并行接入积分相电压转化,线电压并不包含干扰源T(t)。因此利用线电压来进行检测,则能从原理上排除参数谐振形成的干扰源T(t)。
2.2 星网变换谐振电压消除
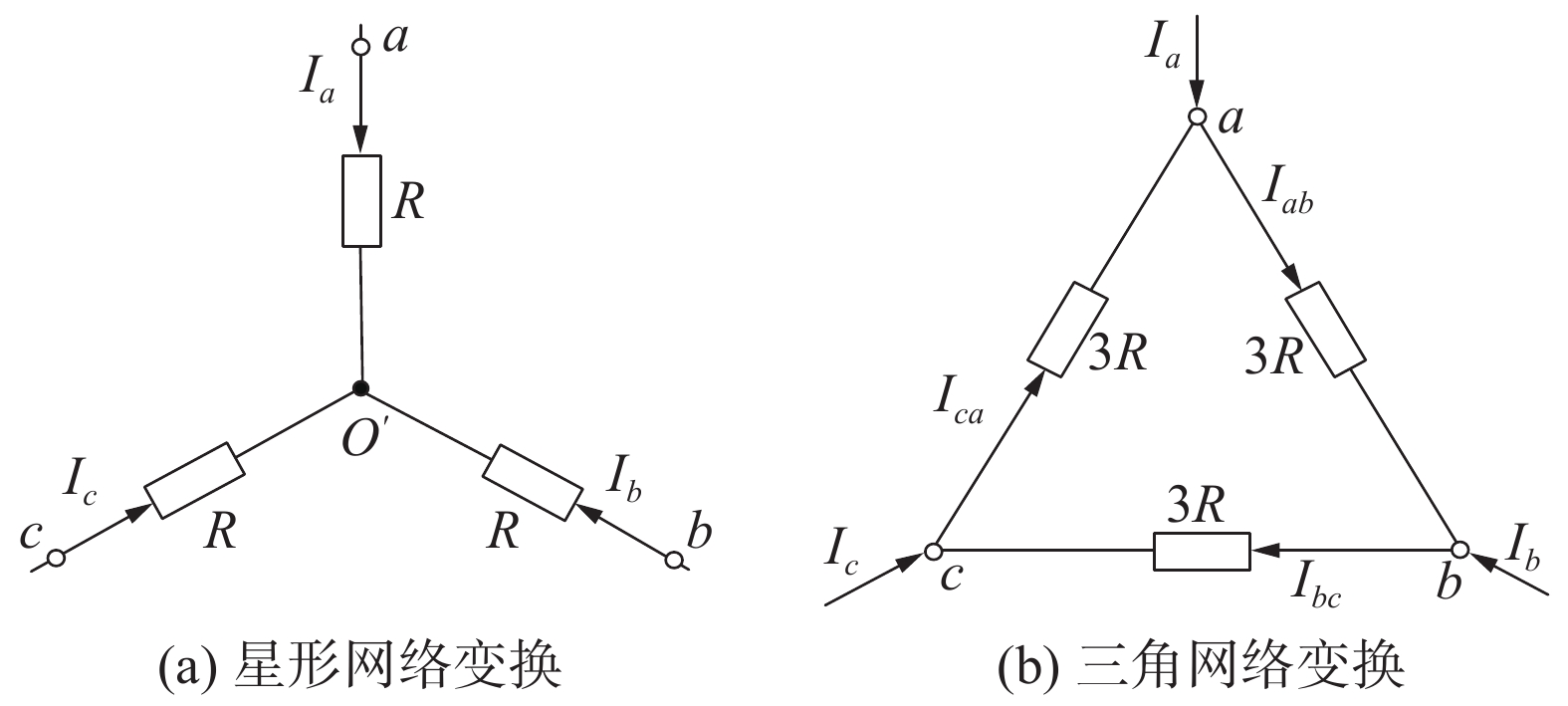
|
图 5 星网变换示意图 |
根据图5(b)可得
| $\left\{ {\begin{array}{*{20}{c}}{\mathop {{I_a}}\limits^ {\displaystyle\cdot} = \mathop {{I_{ab}}}\limits^ {\displaystyle\cdot} - \mathop {{I_{ca}}}\limits^ {\displaystyle\cdot} }\\{\mathop {{I_b}}\limits^ {\displaystyle\cdot} = \mathop {{I_{bc}}}\limits^ {\displaystyle\cdot} - \mathop {{I_{ab}}}\limits^ {\displaystyle\cdot} }\\{\mathop {{I_c}}\limits^ {\displaystyle\cdot} = \mathop {{I_{ca}}}\limits^ {\displaystyle\cdot} - \mathop {{I_{bc}}}\limits^ {\displaystyle\cdot} }\end{array}} \right.$ | (4) |
式中:
| $\left\{ {\begin{array}{*{20}{c}}{\mathop {{I_{ab}}}\limits^ {\displaystyle\cdot} = \mathop {{U_{ab}}}\limits^ {\displaystyle\cdot} /3R}\\{\mathop {{I_{bc}}}\limits^ {\displaystyle\cdot} = \mathop {{U_{bc}}}\limits^ {\displaystyle\cdot} /3R}\\{\mathop {{I_{ca}}}\limits^ {\displaystyle\cdot} = \mathop {{U_{ca}}}\limits^ {\displaystyle\cdot} /3R}\end{array}} \right.$ | (5) |
根据式(4)、(5)及图5(a)可得到消除谐振电压干扰后的相电压
| $\left\{ {\begin{aligned}& {{{\mathop {{U_a}}\limits^ {{\displaystyle\cdot}} }\!'} = R\mathop {{I_a}}\limits^ {\displaystyle\cdot} = \left( {{U_{ab}} - \mathop {{U_{ca}}}\limits^ {\displaystyle\cdot} } \right)/3R}\\& {{{\mathop {{U_b}}\limits^ {\displaystyle\cdot} }\!'} = R\mathop {{I_b}}\limits^ {\displaystyle\cdot} = \left( {\mathop {{U_{bc}}}\limits^ {\displaystyle\cdot} - {U_{ab}}} \right)/3R}\\& {{{\mathop {{U_c}}\limits^ {\displaystyle\cdot} }\!'} = R\mathop {{I_c}}\limits^ {\displaystyle\cdot} = \left( {\mathop {{U_{ca}}}\limits^ {\displaystyle\cdot} - \mathop {{U_{bc}}}\limits^ {\displaystyle\cdot} } \right)/3R}\end{aligned}} \right.$ | (6) |
式(6)中各相电压包含了线电压上由其他电压等级传递过来所有分量,即经过变换之后的测量值,既包含了系统固有的谐波分量,又可排除因参数谐振引入的干扰分量T(t)。
2.3 谐波传递的理论约束条件由于三角形接线的特殊性[12],在三角形接线系统内,除了可能产生的干扰外,其电压和电流还存在着以下约束条件。
约束A:3个线电压的各次谐波电压之和均等于零。
约束B:因为没有地线的存在,除了由分布电容漏出的少量容性电流外,系统中各相电流及其谐波之和也均等于零。
根据傅里叶变换,电压和电流信号可以分解为基波与各次谐波之和,三相系统中各次谐波分量又可分解为正序、负序和零序分量。
根据式(3),经傅里叶变换分解后三相线电压可表示为
| $\left\{ {\begin{aligned}& {\mathop {{U_{ab}}}\limits^ {\displaystyle\cdot} = \mathop {{U_a}}\limits^ {\displaystyle\cdot} - \mathop {{U_b}}\limits^ {\displaystyle\cdot} = k{U_{1m}}\sin \left( {\omega t + 30{\rm{^\circ }}} \right) + g\left( t \right)}\\& {\mathop {{U_{bc}}}\limits^ {\displaystyle\cdot} = \mathop {{U_b}}\limits^ {\displaystyle\cdot} - \mathop {{U_c}}\limits^ {\displaystyle\cdot} = k{U_{1m}}\sin \left( {\omega t - 90{\rm{^\circ }}} \right) + h\left( t \right)}\\& {\mathop {{U_{ca}}}\limits^ {\displaystyle\cdot} = \mathop {{U_c}}\limits^ {\displaystyle\cdot} - \mathop {{U_a}}\limits^ {\displaystyle\cdot} = k{U_{1m}}\sin \left( {\omega t - 210{\rm{^\circ }}} \right) + j\left( t \right)}\end{aligned}} \right.$ | (7) |
式中:g(t)、h(t)、j(t)分别为三相线电压上的非基波分量之和,U1m为基波峰值。
由约束A,
| $g\left( t \right) + h\left( t \right) + j\left( t \right) = 0$ | (8) |
将各次谐波分量在三相系统中分解为正序分量、负序分量、零序分量,正序和负序均满足式(8),由于零序相位相同,只有零序分量的幅值为零才能够满足式(8)。所以在三角形接线系统中,各次谐波均不存在零序分量,正序和负序则可以在中性点不接地系统中存在,并向其他YN结线的电压等级传递。
结合式(6)、(7)可得:
| $\left\{ {\begin{aligned}& {{{\mathop {{U_a}}\limits^ {\displaystyle\cdot} }\!'} = \frac{{\sqrt 3 }}{3}{U_{1m}}\sin \left( {\omega t} \right) + \frac{1}{3}\left[ {g\left( t \right) - j\left( t \right)} \right]}\\& {{{\mathop {{U_b}}\limits^ {\displaystyle\cdot} }\!'} = \frac{{\sqrt 3 }}{3}{U_{1m}}\sin \left( {\omega t - 120{\rm{^\circ }}} \right) + \frac{1}{3}\left[ {g\left( t \right) - j\left( t \right)} \right]}\\& {{{\mathop {{U_c}}\limits^ {\displaystyle\cdot} }\!'} = \frac{{\sqrt 3 }}{3}{U_{1m}}\sin \left( {\omega t - 240{\rm{^\circ }}} \right) + \frac{1}{3}\left[ {g\left( t \right) - j\left( t \right)} \right]}\end{aligned}} \right.$ | (9) |
根据图4的三同阻并行接入积分相电压输入端改造方案,测得的相电压
为检验新方案的准确性,使用MATLAB软件进行电压谐波误差检测仿真计算,验证测量性能和特征。
3.1 仿真计算步骤仿真过程包括3个步骤:
1)模拟在YN,D11连接的变压器高压侧输入含有谐波的原始波形;
2)设变压器变比为1:1,得到经过变压器传递的三角形侧的线电压波形,并分析波形中的谐波含有情况;
3)经仪器输入端网星连接电阻的变换,计算得到变换后的波形及谐波含有情况,并将其与输入波形的各次谐波含有率进行对比。
3.2 仿真过程及结果输入原始波形,基波幅值为1 000,3次谐波的正序含量为5%,负序含量1%,零序含量1%;4次谐波为5%零序;5次谐波含正序5%,负序1%。模拟输入波形各次谐波序含量如表1所示。
|
|
表 1 输入波形各次谐波序含量 |
输入波形经变比为1:1的变压器传递至三角形侧各次谐波序含量如表2所示。
|
|
表 2 经变压器传递后的各次谐波序含量 |
仪器输入端改造后测量波形各次谐波序含量如表3所示。
|
|
表 3 测量波形各次谐波序含量 |
变压器高压侧的输入波形在传递至低压侧时,由于电路的特殊性,其零序分量无法传递。各次谐波的正序、负序含有率没有变化,仅存在与对应相位相同的相位移动。采用图4所示改造方案的仪器,其测量的相电压包含了线电压的各序分量,应测得的各次分量均得到准确传递。
4 实验测试分析在试验室使用模拟谐波信号发生器建立一个中性点不接地系统的干扰模拟运行电路,进行测试,如图6所示。
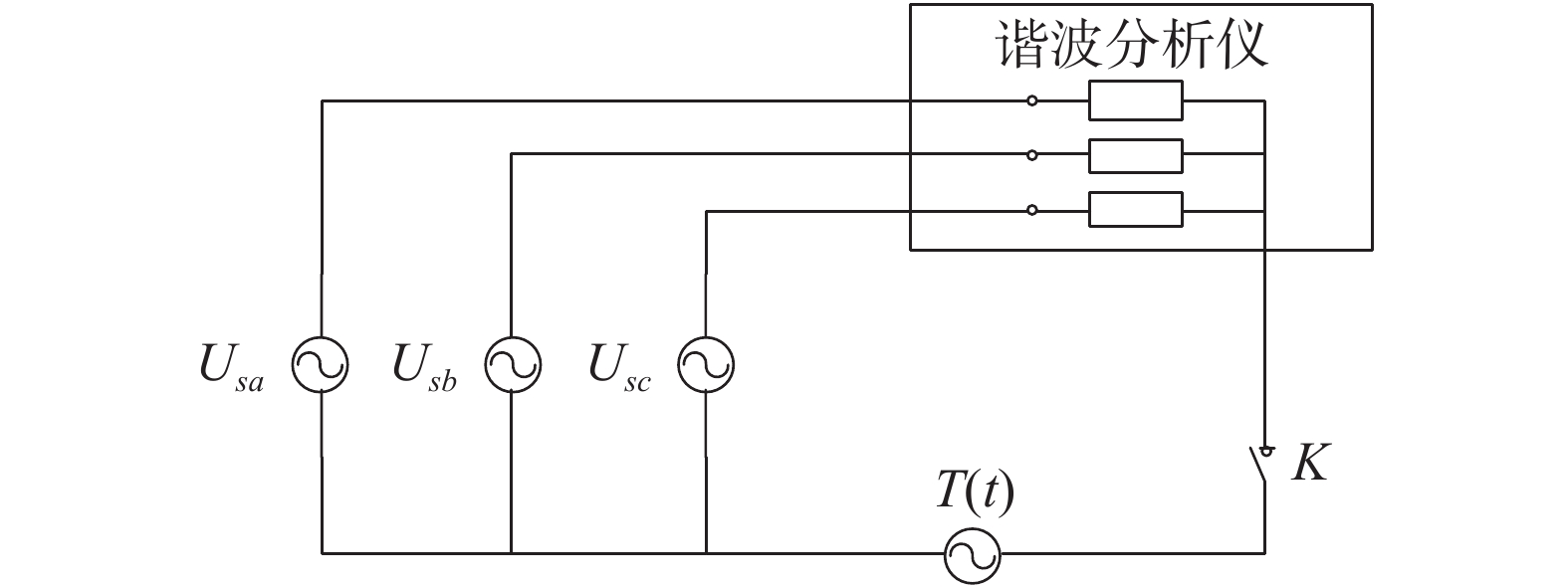
|
图 6 模拟试验系统示意图 |
图中Usa、Usb、Usc为三相电压信号源,可附带谐波分量。干扰源T(t)串接在中性点回路。测试仪器为专用的电能质量测试设备,内部附带可控制的接地开关K,使仪器的测试回路呈现Y或Y0工作模式。
试验1 输入信号1为100 V基波电压,无谐波分量,理论总谐波畸变率(total harmonics distortion,THD)为0;输入信号2为100 V基波电压附带1%的5次谐波,理论THD为1%。干扰信号T(t)有效值为5.6 V、频率为540 Hz。分别在Y及Y0模式下对2组信号进行分析,电压测试波形及测试结果如图7与表4所示。
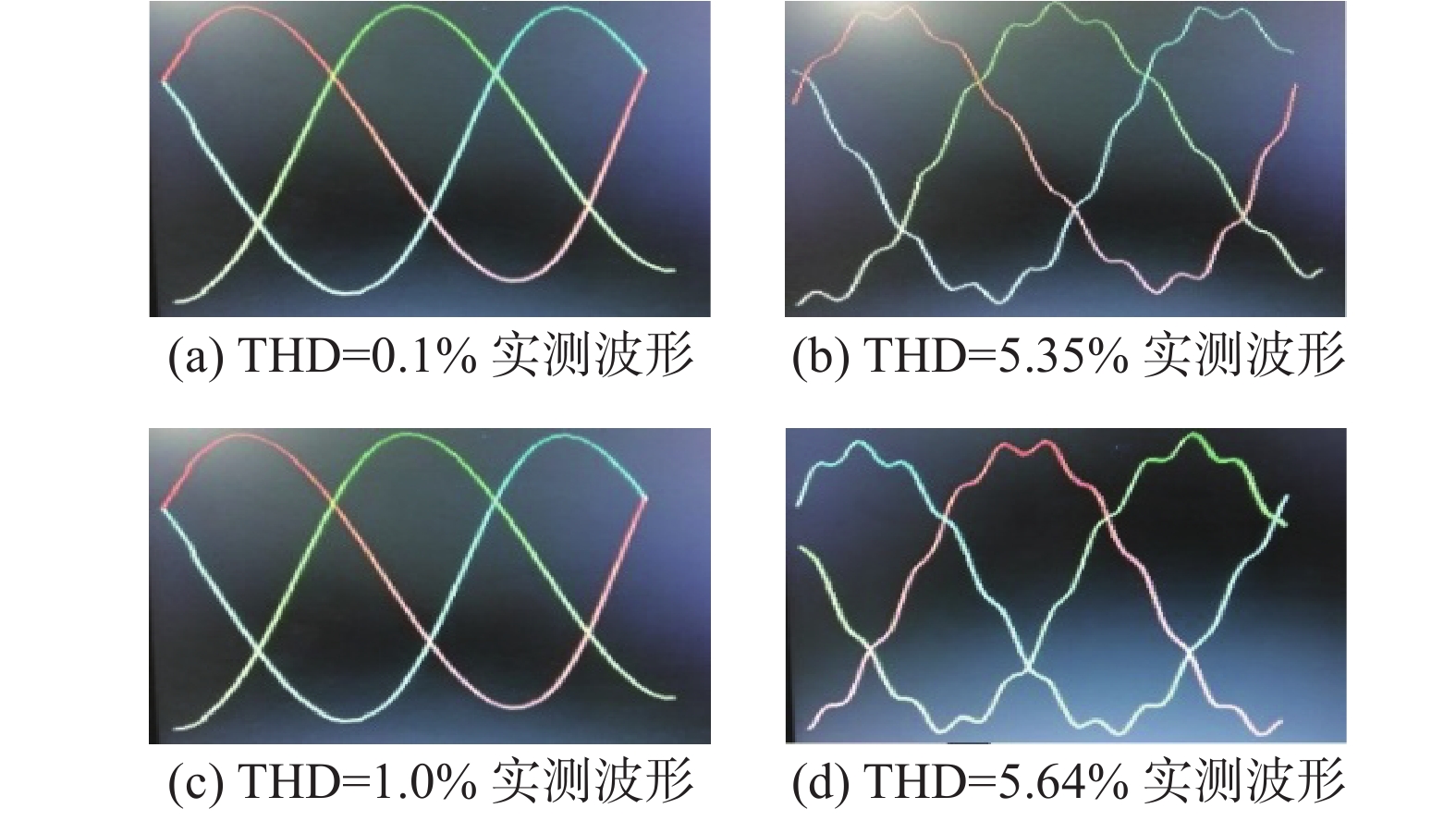
|
图 7 不同信号源在Y和Y0接线方式下的试验波形 |
试验1的基波含有率测试结果如表4所示。
|
|
表 4 不同信号源在Y和Y0接线方式下的试验结果 |
试验2 输入信号1为100 V基波电压附带1%的7、11和19次谐波,理论总谐波畸变率(THD)为1.732%;输入信号2为100 V基波电压附带3%的7、11和19次谐波,理论总谐波畸变率为5.19%。干扰信号T(t)有效值为6.2 V,频率313 Hz。分别在Y及Y0模式下对两组信号进行分析,测试结果如表5所示。
|
|
表 5 含不同高次谐波信号源在Y和Y0接线方式下的试验结果 |
由表4、5可以看出,在仪器输入端的Y接线模式下,测量结果基本与输入信号基本一致,在Y0接线模式下,测量结果则引入了干扰信号T(t),出现了比较大的测量误差。
5 结论本文分析指出了系统参数谐振是引起在不接地系统电压互感器二次侧进行电能质量检测误差的主要原因,构建变压器结构的单相测量等值电路,从而为消除参数谐振影响提供基础。提出了三同阻并行接入积分相电压的测量方案,并通过仿真与实验进行了验证,结论如下:
1)由于受到参数谐振的影响,在变电站10 kV母线电压互感器二次侧直接测量时,测量结果包含了系统的参数谐振谐波,误差较大,不能反应系统的真实情况。
2)系统线电压中不包含参数谐振信号,通过测量线电压从原理上过滤掉参数谐振信号,降低测量误差。
3)通过改造仪器的电压输入回路,实现三相系统从线电压到相电压的转换,实现相电压准确测量。
4)现有电能质量检测设备在中性点不直接接地系统中使用有其局限性。由于受到电路变换引起的电压幅值和相位的影响,该方案不能简单前置应用于现有测量仪器。
| [1] |
GB/T 14549-1993. 电能质量—公用电网谐波[S]. 北京: 中国标准出版社, 1994: 1-2.
( 0) 0)
|
| [2] |
李薇, 张文, 郑妍. 基于改进的小波阈值的电能质量信号去噪[J]. 应用科技, 2012, 39(2): 15-18. ( 0) 0)
|
| [3] |
谢志文. 变电站三次电压谐波测试及抑制[D]. 广州: 华南理工大学, 2012: 54-55.
( 0) 0)
|
| [4] |
王春萌. 一种解决中性点不接地系统铁磁谐振问题的新技术[J]. 电气技术, 2014(9): 94-96. ( 0) 0)
|
| [5] |
周默, 孙岩洲. 电网中性点不同接地方式下铁磁谐振的消谐研究[J]. 高压电器, 2015, 51(1): 81-85. ( 0) 0)
|
| [6] |
WU L. A tighter piecewise linear approximation of quadratic cost curves for unit commitment problems[J]. IEEE transactions on power systems, 2011, 26(4): 2581-2583. ( 0) 0)
|
| [7] |
RESTREPO J F, GALIANA F D. Assessing the yearly impact of wind power through a new hybrid deterministic/ stochastic unit commitment[J]. IEEE transactions on power systems, 2011, 26(1): 401-410. ( 0) 0)
|
| [8] |
戎骏, 胡海涛, 邵洋, 等. 基于敏感度分析的海上风电场谐波谐振研究[J]. 电网技术, 2016, 40(8): 2510-2517. ( 0) 0)
|
| [9] |
周文, 潘朝霞, 刘英. 220 kV变电站 10 kV母线零序电压测量值异常情况分析[J]. 电力系统及其自动化, 2014(2): 66-68, 83. ( 0) 0)
|
| [10] |
张晶晶, 宋传盼. 电压不平衡分析及解决方案[J]. 贵州电力技术, 2014, 17(12): 30-31, 88. ( 0) 0)
|
| [11] |
陈立伟, 刘欢, 冯驰, 等. Kaiser窗三谱线插值电力谐波分析[J]. 应用科技, 2014, 41(2): 5-11. ( 0) 0)
|
| [12] |
乔立慧, 孔红, 李佳琦. 基于傅立叶方法的铁磁谐振谐波分析[J]. 测控自动化, 2010, 26(25): 230-233. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


