三峡工程的全面完成，不仅标志着三峡大坝工程的防洪、发电、航运、补水等综合效益开始全面发挥，也标志着三峡移民任务的全面完成，三峡库区正在由搬得出、稳得住逐步向实现安稳致富的战略目标转变，三峡库区整体进入了后三峡时代。

后三峡时代是指三峡工程建成后对下游生态、生产、生活等方方面面的综合影响^[1]。为了减小该影响，中国政府计划投资1 700亿用于三峡工程后期的规划工作。我们在关注三峡工程给我国带来巨大的经济和社会效益的同时，也要重视三峡库区的环境问题。环境问题影响人们的生活，给人们带来诸多不便。如果不能有效解决这个问题，不但将危害三峡库区及周边地区人们的生命财产安全，而且将阻碍长江中下游地区甚至全国的可持续发展。

二氧化碳过度排放会造成温室效应^[2]，但是如果全面减少二氧化碳的排放就会阻碍经济的发展。就重庆三峡库区(包括万州区、涪陵区、巫溪县等22个区、县，占整个三峡库区面积的85%)而言，碳的排放主要来源于2个部分，其中一部分是来自人们的日常活动，另一部分来源于工业生产。若是为减少二氧化碳的排放而关停一些大型的工业企业，将会阻碍经济的平稳快速增长。因此，寻求一种对能源需求不高的经济增长路径是非常有必要的，需要各行各业专家、学者的共同努力。

本文主要研究三峡库区的二氧化碳排放预测问题，将利用庞特里亚金最大值原理和马尔可夫过程建立三峡库区的二氧化碳排放模型，将碳排放问题转化为一阶偏微分方程，然后利用四阶变步长龙格-库塔方法计算出2015~2021年三峡库区的整体二氧化碳排放量^[3]，对三峡库区的碳排放情况进行预测，为三峡库区环境治理提供数据支持。

1 数学模型

模型主要采用类似于文献[4]的处理方法，选取效用函数：

$u({c_t}) = \frac{{{{({c_t} - \bar c)}^{1 - \sigma }}}}{{1 - \sigma }}$

式中：c_t为每个社会个体在时间t的消费量， $\bar c$ 为最低消费水平，σ为风险厌恶系数， $u({c_t})$ 称为Stone-Geary效用函数。这一效用函数表明人们的消费只有达到了最低消费 $\bar c$ ，即保证了生存下去的条件以后，自己的需求、欲望才会得到满足，效用值才会为正。

1.1 能源和经济之间动态关系的模型

在最优经济增长模型中^[4-5]，全社会是由许许多多的个体组成的，这些社会个体可以是单个成年人或是家庭。每个社会个体在一段的时间内消费，都会得到一定的效用值。全社会的效用值就是社会中每一个社会个体效用值的总和。社会计划者的目标，就是使未来无穷时间段内，全社会效用值贴现到当前值的最大，即

${\rm{max }}U = \int_0^\infty {u({c_t})} {N_t}\exp ( - \rho t){\rm{d}}t$

(1)

式中：t为时间，N_t为t时刻社会个体数量， $u( \cdot )$ 为每个社会个体的效用函数，c_t为t时刻的每个个体的消费，ρ为贴现率。将 $u({c_t}) = \displaystyle\frac{{{{({c_t} - \bar c)}^{1 - \sigma }}}}{{1 - \sigma }}$ 带入式(1)中得

${\rm{max }}U = \int_{{\rm{ }}0}^{{\rm{ }}\infty } {N_0^\sigma } \exp \left( {(n\sigma - \rho )t} \right){\displaystyle{{{{({c_t} - \bar c)}^{1 - \sigma }}} \over {1 - \sigma }}}{\rm{d}}t$

(2)

式中：C_t为整个社会全体的消费，n为人口增长率，N₀为初始年份的人口数。

每一个社会个体拥有一定量的资本以及一单位的劳动力。本文的生产函数采用柯布−道格拉斯生产函数的形式^[6]，社会产出不仅与资本以及劳动力有关，还与所消耗的能源有关。具体的生产函数形式如下

$\begin{array}{*{20}{c}}{{Y_t} = {A_0}\exp (vt)K_t^\alpha E_t^{1 - \alpha }L_t^\gamma ,}&{0 < \alpha < }\end{array}1$

(3)

式中：A₀为总要素生产率，其增长速度为v，K_t为物质资本投入，E_t为能源投入，L_t为劳动力投入，α为资本产出的弹性系数，γ为劳动力产出的弹性系数。其中各要素的弹性系数的和 $\alpha + (1 - \alpha ) + \gamma > 1$ ，这表明该生产函数的类型为递增报酬型，即按现有技术水平，用扩大生产规模的方式来增加总产出，是非常可行的。

考虑到能源投入来自两个方面：一是从国外进口，另一个是本国生产。能源上的消费采用如下形式^[7-8]：

${\theta _t} = {p_{d,t}}{s_t} + {p_{a,t}}(1 - {s_t})$

式中：θ_t为能源的平均价格，s_t为本国生产的能源的份额， ${P_{d,t}}$ 为本国能源价格， ${P_{d,t}}$ 为外国能源的价格。

能源强度是指一个国家或地区、部门或行业单位产值一定时间内消耗的能源量。根据定义可以给出能源强度的表达式：

$\tau = \frac{E}{Y}$

(4)

将式(4)带入式（3）中，得到

$\begin{array}{*{20}{c}}{{Y_t} = {{\left( {{A_0}\exp (vt)} \right)}^{{\textstyle{1 \over \alpha }}}}{K_t}{\tau _t}^{{\textstyle{{1 - \alpha } \over \alpha }}}{L_t}^{{\textstyle{\gamma \over \alpha }}}},&{0 < \alpha < 1}\end{array}$

资本存量积累满足如下关系：

$\begin{split}{K_t} \!=\! & {Y_t} \!-\! \delta {K_t} \!-\! {\theta _t}{E_t} \!-\! {C_t} = ({Y_t} \!-\! {\theta _t}{\tau _t}{Y_t}) \!-\! \delta {K_t} \!-\! {C_t} = \\& (1\! -\! {\theta _t}{\tau _t}){\left( {{A_0}\exp (vt)} \right)^{{\textstyle{1 \over \alpha }}}}{K_t}{\tau _t}^{{\textstyle{{1 \!-\! \alpha } \over \alpha }}}{L_t}^{{\textstyle{\gamma \over \alpha }}}\! -\! \delta {K_t} \!-\! {C_t}\end{split}$

(5)

结合式(5)和式(2)的目标函数，得到如下最优控制问题的模型：

${\rm{max }}U = \int_{{\rm{ }}0}^{{\rm{ }}\infty } {N_0^\sigma } \exp \left( {(n\sigma - \rho )t} \right){\displaystyle{{{{({c_t} - \bar c)}^{1 - \sigma }}} \over {1 - \sigma }}}{\rm{d}}t$

相应的约束条件为

${\dot K_t} = (1 - {\theta _t}{\tau _t}){\left( {{A_0}\exp (vt)} \right)^{{\textstyle{1 \over \alpha }}}}{K_t}{\tau _t}^{{\textstyle{{1 - \alpha } \over \alpha }}}{L_t}^{{\textstyle{\gamma \over \alpha }}} - \delta {K_t} - {C_t}$

其中消费C_t为控制变量，K_t为状态变量。

下面求解此最优控制问题，将采用传统的庞特里亚金最大值原理。首先，定义哈密顿函数：

$H = N_0^\sigma \exp \left( {(n\sigma - \rho )t} \right){\displaystyle{{{{({c_t} - \bar c)}^{1 - \sigma }}} \over {1 - \sigma }}} + \lambda {\dot K_t}$

式中λ为资本的影子价格。其经济意义为求解资源最优利用时，即在解决如何使有限资源的总产出最大的过程中，得出相应的极小值，其解就是对偶解，极小值作为对资源的经济评价，表现为影子价格。然后，将哈密顿函数H对控制变量C_t求偏导，并令其等于零：

$\frac{{\partial {H_t}}}{{\partial {C_t}}} = N_0^\sigma \exp \left( {(n\sigma - \rho )t} \right){({C_t} - \bar C)^{ - \sigma }} - \lambda = 0$

(6)

最后，将哈密顿函数H对状态变量K_t求偏导，并令它等于影子价格λ对时间的导数的相反数，得

$\dot \lambda \!=\! - \frac{{\partial H}}{{\partial {K_t}}} \!=\! - \lambda [(1 \!-\! {\theta _t}{\tau _t}){({A_0}\exp (vt))^{{\textstyle{1 \over \alpha }}}}{\tau _t}^{{\textstyle{{1 - \alpha } \over \alpha }}}{L_t}^{{\textstyle{\gamma \over \alpha }}} \!-\! \delta ]$

(7)

在式(6)两边对t求偏导得

$\begin{aligned}& (n\sigma - \rho )N_0^\sigma \exp \left( {(n\sigma - \rho )t} \right){({C_t} - \bar C)^{ - \sigma }} + \\& N_0^\sigma \exp \left( {(n\sigma - \rho )t} \right)( - \sigma ){({C_t} - \bar C)^{ - \sigma - 1}}{{\dot C}_t} - \dot \lambda = 0\end{aligned}$

(8)

将式(6)和(7)分别代入式(8)，经过化简得

$\begin{split} {{\dot C}_t} = & \frac{1}{\sigma }[(n\sigma - \rho - \delta ) + \\& (1 - {\theta _t}{\tau _t}){({A_0}\exp (vt))^{\textstyle\frac{1}{\alpha }}}{\tau _t}^{\textstyle\frac{{1 - \alpha }}{\alpha }}{L_t}^{\textstyle\frac{\gamma }{\alpha }}] \times ({C_t} - \bar C)\end{split}$

(9)

从而得到消费增长率的表达式：

$\begin{aligned}& {g_c} = \\& \frac{{\displaystyle\frac{1}{\sigma }[(n\sigma \! - \! \rho \!- \!\delta ) \!+\! (1 \!-\! {\theta _t}{\tau _t}){{({A_0}\exp (vt))}^{\textstyle\frac{1}{\alpha }}}{\tau _t}^{\textstyle\frac{{1 - \alpha }}{\alpha }}{L_t}^{\textstyle\frac{\gamma }{\alpha }}]({C_t} \!-\! \bar C)}}{{{C_t}}}\end{aligned}$

在这里，为了更加符合实际，选取了形式复杂一些的效用函数以后，导致了经济增长率 $g = \displaystyle\frac{{{{\dot C}_t}}}{{{C_t}}}$ 中含有了未知函数C_t，这就使得不能根据能源强度τ的数据来直接得出经济增长率的值。所以，采用数值方法求解上述常微分方程(9)，得出未知函数C_t在具体节点上的值，再根据实际经济意义，得到经济增长率的值为

${g_t} = \frac{{{C_t} - {C_{t - 1}}}}{{{C_{t - 1}}}}$

1.2 马尔可夫模型

马尔可夫过程是在给定当前知识或信息的情况下，只有当前的状态用来预测将来，过去（即当前以前的历史状态）对于预测将来（即当前以后的未来状态）是无关的。即：未来的状态只与当前状态有关，而与过去无关^[9]。所以，马尔可夫模型中关键的2个要素为初始状态向量与转移概率矩阵。

定义初始状态向量为 ${\mathit{\boldsymbol{s}}^{(0)}} = \left( {\mathit{\boldsymbol{s}}_1^{(0)},\mathit{\boldsymbol{s}}_2^{(0)}, \cdots ,\mathit{\boldsymbol{s}}_n^{(0)}} \right)$ ，当n=3时为产业结构预测模型，n=1,2,3分别代表第一、第二、第三产业；当n=4时为能源混合预测模型，n=1,2,3,4分别代表煤、石油、天然气、沼气等化石燃料。

定义转移概率矩阵为

$\mathit{\boldsymbol{P}} = \left( {\begin{array}{*{20}{c}}{{P_{11}}}&{{P_{12}}}& \ldots &{{P_{1n}}}\\[6pt]{{P_{21}}}&{{P_{22}}}& \ldots &{{P_{2n}}}\\[6pt] \ldots & \ldots & \ldots & \ldots \\[6pt]{{P_{n1}}}&{{P_{n2}}}& \ldots &{{P_{nn}}}\end{array}} \right)$

式中P_ij从状态i到状态j的一步转移概率，且P_ij满足： $\begin{array}{*{20}{c}}{0 \!\!\leqslant \!\!{P_{ij}} \!\!\leqslant 1} \!\!\!\! & \!\! {(i,j \! = \! 1,2, \cdots ,n)}\end{array}$ ， $\begin{array}{*{20}{c}}{\displaystyle\sum\limits_{j \!\!=\!\! 1}^n {{P_{ij}} \!\!=\!\! 1} }& \!\!\!\! {(i \!\!=\!\! 1,2, \cdots ,n)}\end{array}$

根据马尔可夫链的理论，在k时刻的状态向量应满足：

${\mathit{\boldsymbol{s}}^{(k)}} = {\mathit{\boldsymbol{s}}^{(0)}} \cdot {\mathit{\boldsymbol{P}}^k}$

2 模型中参数的估计 2.1 经济系统中的参数

对于生产函数

${Y_t} = {A_0}\exp (vt)K_t^\alpha E_t^{1 - \alpha }L_t^\gamma ,$

先在两边同时取对数，得到

$Y' = {a_0} + vt + \alpha K' + \gamma L' + \zeta $

式中： $Y' \!\!=\!\! \ln (Y/E)$ ， ${a_0} \!\!=\!\! \ln ({A_0})$ ， $K' \!\!=\!\! \ln (K/E)$ ， $L' \!\!=\!\! \ln (L)$ , $\zeta $ 为残差项。

再由《中国统计年鉴2010》以及《新中国50年统计资料汇编》中的数据，通过线性回归的方法得到相应参数的具体数据：总要素生产率的初始值A₀=0.017 4，总要素生产率增长速率v=0.001 44，资本产出弹性系数α=0.781 5，劳动力产出的弹性系数γ=0.390 2。

2.2 其他参数

效用函数中最低消费水平常数 $\bar C$ ，本文采用重庆民政局2014年颁布的最低生活保障作为数据来源，具体数字为每人每月400元。初值 $C(0)$ 根据《重庆统计年鉴2015》农场和城镇居民消费加权平均得到^[10]，数值为13 604.616元。

有关其他参数的估计详见参考文献[4]，具体结果为资本折旧率δ=9.6%，贴现率ρ=0.065，风险厌恶系数σ= 2.5，能源的不变平均价格θ=1 751元/吨油当量。

人口增长率是根据联合国人口展望的数据以及利用Lagrange插值方法，通过MATLAB软件计算而来^[11]，劳动力数据是用人口数据乘以劳动参与率得到^[12]，具体数据见表1。

2.3 转移概率矩阵

根据国家统计局的数据，可以得出能源混合转移概率矩阵为

${\mathit{\boldsymbol{P}}_1} = \left( {\begin{array}{*{20}{c}}{0.987}&{0.016}&{0.000}&{0.000}\\[6pt]{0.000}&{0.811}&{0.029}&{0.160}\\[6pt]{0.253}&{0.000}&{0.725}&{0.021}\\[6pt]{0.000}&{0.496}&{0.000}&{0.504}\end{array}} \right)$

产业结构的转移概率矩阵为

${\mathit{\boldsymbol{P}}_2} = \left( {\begin{array}{*{20}{c}}{0.977}&{0.008}&{0.015}\\[6pt]{0.000}&{0.977}&{0.023}\\[6pt]{0.000}&{0.023}&{0.977}\end{array}} \right)$

3 三峡库区的碳排放预测

根据《重庆统计年鉴2015》的数据显示，2014年，三峡库区第一、第二、第三产业的份额g分别为9.2%、50.1%、40.7%。各产业能源强度的值τ分别为27.658 7、165.924 6、51.768 3吨油当量/百万元，再根据历史数据，各产业能源强度下降的速率分别为2.1%、5.2%、4.1%。因此，计算出三峡库区分产业的能源强度变化情况分别为

$ {{\tau _1} = 27.658 \,\,7{{\rm{e}}^{ - 0.021{\rm{ }}t}}}\times 10^{-6} \ {\rm t\cdot Yuan} $

${{\tau _2} = 165.924 6{{\rm{e}}^{ - 0.052{\rm{ }}t}}}\times 10^{-6} \ {\rm t \cdot Yuan}$

${{\tau _3} = 51.768 3{{\rm{e}}^{ - 0.041{\rm{ t}}}}}\times 10^{-6} \ {\rm t \cdot Yuan}$

于是可以得到从2014年算起的第t年的能源强度为

$\begin{split}& \tau \!=\! {g_1}^t{\tau _1} \!+\! {g_2}^t{\tau _2} \!+\! {g_3}^t{\tau _3} \!=\! \left( {\begin{array}{*{20}{c}}{{g_1}^t}&{{g_2}^t}&{{g_3}^t}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{\tau _1}}\\[6pt]{{\tau _2}}\\[6pt]{{\tau _3}}\end{array}} \right) = \\& \quad \quad \left( {\begin{array}{*{20}{c}}{{g_{\rm{1}}}^0}&{{g_{\rm{2}}}^0}&{{g_{\rm{3}}}^0}\end{array}} \right){\rm{ }}{\mathit{\boldsymbol{P}}_2}^t\left( {\begin{array}{*{20}{c}}{{\tau _1}}\\[6pt]{{\tau _2}}\\[6pt]{{\tau _3}}\end{array}} \right)\end{split}$

(10)

式中g₁、g₂、g₃分别为第一产业、第二产业、第三产业的份额。

首先，将P₂对角化得

$\begin{array}{*{20}{l}}{{P_2} = V\Lambda {V^{ - 1}} = \left( {\begin{array}{*{20}{c}}1 & {0.577\,\,4} & { - 0.210\,\,4}\\[6pt]0 & {0.577\,\,4} & { - 0.691\,\,3}\\[6pt]0 & {0.577\,\,4} & {0.691\,\,3}\end{array}} \right) \times }\\[24pt]\begin{array}{l}\quad \quad \left( {\begin{array}{*{20}{c}}{0.977} & {0} & {0}\\[6pt]0 & {1} & {0}\\[6pt]0 & {0} & {0.954}\end{array}} \right) \times \\[24pt]\quad \quad {\left( {\begin{array}{*{20}{c}}1 & {0.577\,\,4} & { - 0.210\,\,4}\\[6pt]0 & {0.577\,\,4} & { - 0.691\,\,3}\\[6pt]0 & {0.577\,\,4} & {0.691\,\,3}\end{array}} \right)^{ - 1}}\end{array}\end{array}$

于是

$\begin{array}{l}P_2^t = \left( {\begin{array}{*{20}{c}}1 & {0.577\,\,4} & { - 0.210\,\,4}\\[6pt]0 & {0.577\,\,4} & { - 0.691\,\,3}\\[6pt]0 & {0.577\,\,4} & {0.691\,\,3}\end{array}} \right) \times \\[24pt]\quad \quad {\left( {\begin{array}{*{20}{c}}{0.977} & 0 & 0\\[6pt]0 & 1 & 0\\[6pt]0 & 0 & {0.954}\end{array}} \right)^t} \times \\[24pt]\quad \quad {\left( {\begin{array}{*{20}{c}}1 & {0.577\,\,4} & { - 0.210\,\,4}\\[6pt]0 & {0.577\,\,4} & { - 0.691\,\,3}\\[6pt]0 & {0.577\,\,4} & {0.691\,\,3}\end{array}} \right)^{ - 1}}\end{array}$

这样，矩阵的乘法就转化为多项式运算。第t年的能源强度τ_t可以写成

$\begin{split}{\tau _t} = & 0.092 \times {0.977^t} \times 27.6587{\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - 0.021t}} + \\[7pt] & ( - 0.06 \times {0.977^t} + 0.5 + 0.061 \times {0.954^t}) \times \\[7pt] & 165.9246{\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - 0.052t}} + ( - 0.032 \times {0.977^t} + 0.5 - \\[7pt] & 0.061 \times {0.954^t}) \times 51.7683{\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - 0.041t}}\end{split}$

(11)

将式(11)以及前面得到的各参数代入式(9)中，得初值问题：

$\left\{ {\begin{aligned}& {{{\dot C}_t} = \frac{1}{\sigma }[(n\sigma - \rho - \delta ) + }\\[7pt]& \quad \quad {(1 - {\theta _t}{\tau _t}){{({A_0}\exp (vt))}^{\textstyle\frac{1}{\alpha }}}{\tau _t}^{\textstyle\frac{{1 - \alpha }}{\alpha }}{L_t}^{\textstyle\frac{\gamma }{\alpha }}]({C_t} - \bar C)}\\[7pt]& {C\left( 0 \right) = 2 \,\,\,\, 112.7}\end{aligned}} \right.$

(12)

由于人口增长率以及劳动参与率的数据不是常数，所以在求解初值问题式(12)的时候，采用分段的方法。由于表达式的形式复杂，不能给出问题的解析解，因此考虑求该问题的数值近似解。本文利用MATLAB软件编写四阶龙格-库塔方法的程序来求解问题(12)的数值解。

龙格-库塔法是一种在工程上应用广泛的高精度单步算法。理论基础来源于泰勒公式和使用斜率近似表达微分，它在积分区间多预计算出几个点的斜率，然后进行加权平均，用做下一点计算的依据，从而构造出精度更高的数值计算方法。

对于常微分方程初值问题：

$\left\{ {\begin{aligned}& {y' = f(x,y)}\\[6pt]& {y({x_0}) = {y_0}}\end{aligned}} \right.$

其对应的四阶变步长龙格-库塔公式为^[13]

$\left\{ \begin{aligned}& {y_{n + 1}} = {y_n} + {\displaystyle{h \over 6}}({K_1} + 2{K_2} + 2{K_3} + {K_4})\\[7pt]& {K_1} = f({x_n},{y_n})\\[7pt]& {K_2} = f({x_n} + {\displaystyle{h \over 2}},{y_n} + {\displaystyle{h \over 2}}{K_1})\\[7pt]& {K_3} = f({x_n} + {\displaystyle{h \over 2}},{y_n} + {\displaystyle{h \over 2}}{K_2})\\[7pt]& {K_4} = f({x_n} + h,{y_n} + h{K_3})\end{aligned} \right.$

为了求解人口增长率和劳动参与率，采用分段的方法，其数值结果表2。

根据表2中的消费增长率以及消费增长率和经济增长率相一致的假设，结合《重庆统计年鉴2015》中三峡库区的GDP数据，推算出2014~2021年三峡库区的社会总产出的数据如表3。

接下来考虑能源强度，根据式(11)同样算出2014~2021年的能源强度数据及其下降速率，结果如表4。

再由式(4)得到

$E = \tau \cdot Y$

于是根据表3、4的数据，得出了2014~2021年的能源使用量E，数据如表5。

最后，根据能源使用量，求出碳排放的值。假定碳排放系数均为恒定，其中煤、石油、天然气、非化石能源的排放系数分别为1.005 2，0.753，0.617 3，0。同时，根据《重庆统计年鉴2015》，煤、石油、天然气、非化石能源的份额g_i分别为0.586，0.134，0.014 1，0.139。且份额的转化过程由转移概率矩阵g_i给出，于是，得到下面碳排放量P₁的计算公式：

$\begin{split}e = E(\begin{array}{*{20}{c}}{{g_1}^{(t)}}&{{g_2}^{(t)}}&{{g_3}^{(t)}}&{{g_4}^{(t)}}\end{array})\left( {\begin{array}{*{20}{c}}{1.005\,\,2}\\[6pt]{0.753}\\[6pt]{0.617\,\,3}\\[6pt]0\end{array}} \right) = \\[20pt]E(\begin{array}{*{20}{c}}{{g_1}^{(0)}}&{{g_2}^{(0)}}&{{g_3}^{(0)}}&{{g_4}^{(0)}}\end{array})\mathit{\boldsymbol{P}}_1^t\left( {\begin{array}{*{20}{c}}{1.005\,\,2}\\[6pt]{0.753}\\[6pt]{0.617\,\,3}\\[6pt]0\end{array}} \right)\end{split}$

(13)

根据式(13)以及表5，得出碳排放量的结果如表6所示。

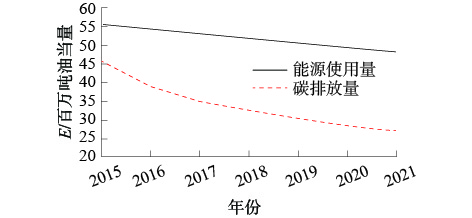
根据表5、6中的数据，可以绘制出能源使用量和碳排放量曲线，如图1所示。

从图1可以看到，三峡库区的能源使用量和碳排放量的走势大体上一致，都呈现减少的趋势，但是能源使用量减少趋势比较平缓，碳排放量在2016年之前的减少相对比较剧烈，2016年之后比较平缓，总体来说三峡库区能源使用量和碳排放量在今后几年都会持续减少。

4 结论

1)应用庞特里亚金最大值原理和马尔可夫过程研究三峡库区的碳排放问题，建立了污染问题的最优控制问题模型。

2)利用经典的龙格-库塔方法求解实际的三峡库区污染问题，将对三峡库区的环境保护研究发挥越来越重要的作用。

3)根据数值结果，得出能源使用量与碳的排放量有着直接关系，如果大量排放二氧化碳很可能导致全球的温室效应，然而刻意减少能源使用量就会影响三峡库区经济的增长。

本文计算出的2015～2021年的碳排放量，可以用来预测三峡库区未来几年的碳排放的趋势，合理调整各种能源的使用量，这将对三峡库区的环境治理起到非常重要的作用。