矩量法由于积分方程自动满足辐射条件,不但适用于任何形状的复杂目标,而且数值计算精度与效率高,同时避免了色散误差传播积累和网格截断误差等影响,目前已经在天线辐射、复杂散射体的电磁散射和电磁兼容等实际工程领域获得了广泛的应用。但是,在运用该方法求解开域问题,如散射和辐射问题时,将积分方程离散后,得到的阻抗矩阵是满秩的,所消耗的计算机内存和计算复杂度分别为
另一类是基于代数意义的快速算法被称为基于矩阵压缩的算法,如多层矩阵分解方法(multilevel matrix decomposition algorithm,MLMDA)、多层QR分解、多层UV分解、快速双多层正交化(multilevel Gram Schmidt,MGS)分解、自适应交叉算法(adaptive cross approximation,ACA)算法等[4-5]。这类算法只依赖于对矩阵的数学操作,不涉及积分核函数和网格的投影操作。但大多数的算法分解需要知道完整的子矩阵信息,这样就导致计算量的增大。例如,多层QR分解需要
对于三维理想导体目标电磁散射问题,在入射场Ei的照射下,根据等效原理,满足理想导体表面切向电场为零的边界条件,可得到:
| $- {E^s}(r){|_{\tan }} = {E^i}(r){|_{\tan }}$ | (1) |
式中r为表面S上的场向量,当平面波照射到理想导体上时,导体表面会产生感应电流,感应电流可用RWG基函数
| $\mathit{\boldsymbol{ZI}} = \mathit{\boldsymbol{V}}$ |
式中:Z表示阻抗矩阵,I是待求电流向量,V是激励矢量。
文中以矩量法为基础,运用文献[8]所述的方法,得到阻抗矩阵元素
| $\begin{aligned}{\mathit{\boldsymbol{Z}}_{mn}} = & {l_m}[{\rm{j}}w(A_{mn}^ + \cdot \frac{{\rho _m^{c + }}}{2} + A_{mn}^ - \cdot \frac{{\rho _m^{c - }}}{2}) + \varPhi _{mn}^ - - \varPhi _{mn}^ + ]\\{{V}_m} = & {l_m}(E_m^ + \cdot \frac{{\rho _m^{c + }}}{2} + E_m^ - \cdot \frac{{\rho _m^{c - }}}{2})\\{A}_{mn}^ \pm = & \frac{\mu }{{4{\rm{\pi }}}}\int_S {{f_n}(r')\frac{{{{\rm{e}}^{ - {\rm{j}}kR}}{m^ \pm }}}{{R_m^ \pm }})} {\rm{d}}S'\\\varPhi _{mn}^ \pm = & - \frac{\mu }{{4{\rm{\pi j}}w\varepsilon }}\int_S {{\nabla _S}^\prime \cdot {f_n}(r')} \frac{{{{\rm{e}}^{ - jkR}}{m^ \pm }}}{{R_m^ \pm }}{\rm d}S'\end{aligned}$ |
式中:lm表示第m对三角面元的公共边长度;
由于矩量法通过基函数和权函数来表达场点和源点间的相互作用,从而形成阻抗矩阵。根据格林函数表达式,两点距离越近,其相互作用所对应的元素值就相对越大;两点距离越远,其相互作用所对应的元素值就相对越小[9]。自适应交叉近似算法就是利用远场组所形成的阻抗矩阵具有低秩的特点,对阻抗矩阵元素进行分解,如式(2)[10]:
| ${\tilde{Z}^{m \times n}}{\rm{ = }}{\mathit{\boldsymbol{U}}^{m \times k}}{\mathit{\boldsymbol{V}}^{k \times n}}{\rm{ = }}\sum\limits_{i = 1}^k {u_i^{m \times 1}v_i^{1 \times n}} $ | (2) |
式中:k为矩阵
ACA算法选取的秩由式(3)所示:
| $\parallel {\mathit{\boldsymbol{R}}^{m \times n}}\parallel = \parallel {\mathit{\boldsymbol{Z}}^{m \times n}} - {\tilde{Z}^{m \times n}}\parallel \leqslant \varepsilon \parallel {\mathit{\boldsymbol{Z}}^{m \times n}}\parallel $ | (3) |
式中:ε为误差迭代门限,R为误差矩阵,
ACA算法流程分为初始化部分和第k次的迭代[7]。
初始化部分:
1) 初始化第一个行索引I1=1,初始化
2) 初始化误差矩阵的第一行:
3) 在第一行搜索最大值确定第一个列标号J1:
4) V矩阵第一行表示为
5) 初始化误差矩阵第一列
6) U的第一列为
7)
8) 搜索第1列最大值确定第2个行标号I2:
第k次迭代:
1) 更新误差矩阵的
2) 搜索第Ik行中最大值,确定第k列的标号Jk。使得:
3) V矩阵第k行
4) 更新误差矩阵第Jk列
5) 更新U矩阵的每一列
6)
7) 检查收敛性:如果
8) 寻找下一个行标号
在上述迭代过程中,步骤7)的终止条件是根据秩r的选取由式(3)所得。
1.2.2 再压缩技术由于经过ACA算法得到的2个酉矩阵
首先需要对经过ACA算法得到的
| $\begin{aligned}& {\mathit{\boldsymbol{U}}^{m \times k}} = \mathit{\boldsymbol{Q}}_U^{m \times k}\mathit{\boldsymbol{R}}_U^{k \times k}\\& {\mathit{\boldsymbol{V}}^{n \times k}} = \mathit{\boldsymbol{Q}}_V^{n \times k}\mathit{\boldsymbol{R}}_V^{k \times k}\end{aligned}$ |
然后对经过QR分解后得到的2个上三角阵的乘积进行SVD分解:
| $\mathit{\boldsymbol{R}}_U^{k \times k}{(\mathit{\boldsymbol{R}}_V^{k \times k})^{\rm{T}}} = {\hat{U}^{k \times r}}\hat{S}{\hat{V}^{r \times k}}$ |
这个部分采用的是压缩的SVD分解算法,在所有的特征值中满足
算法的流程图如图1所示。
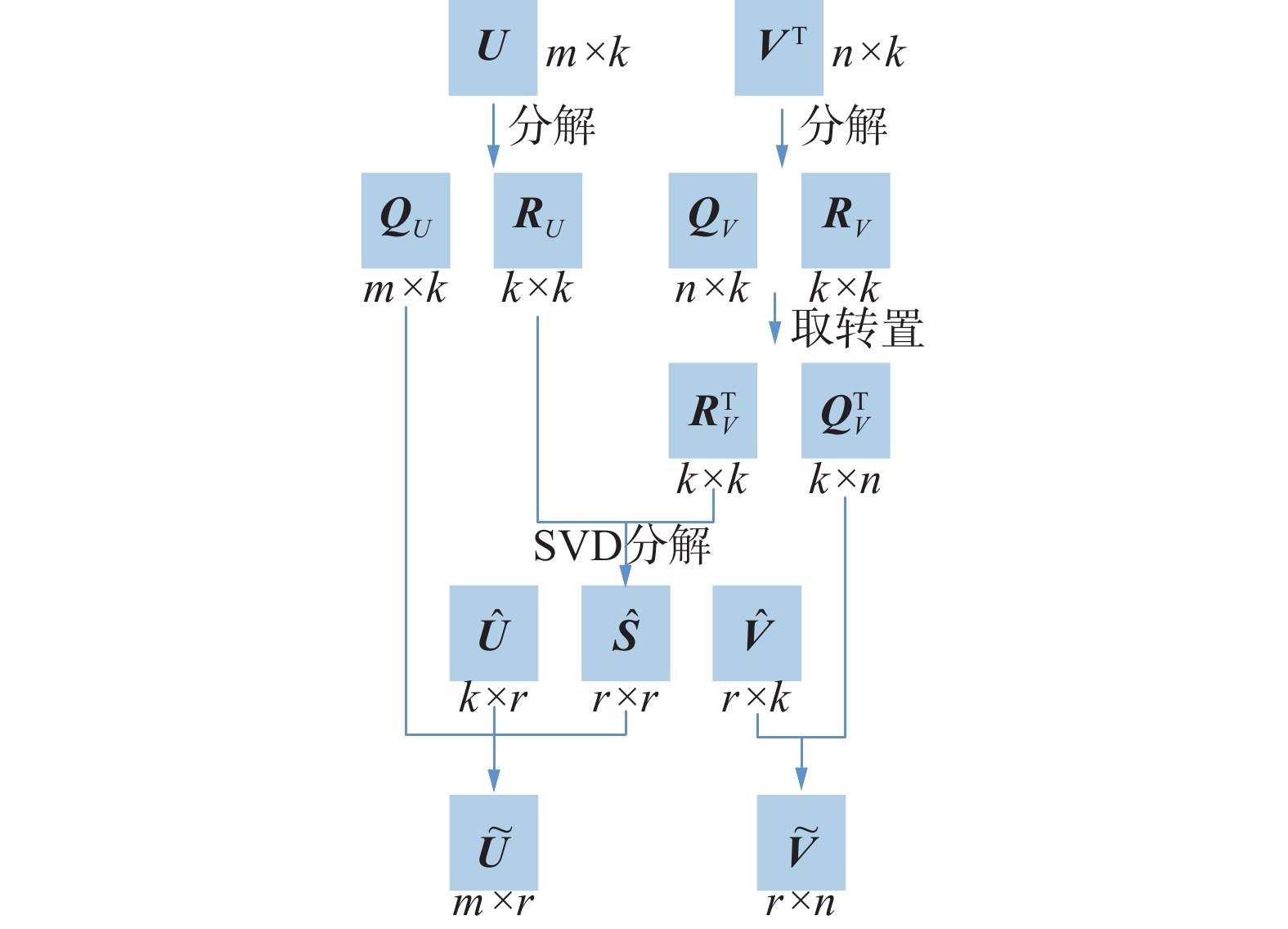
|
图 1 ACA-SVD算法流程 |
对于式(2)阻抗矩阵元素Zmn的计算,采用MATLAB和C语言的混合编程来实现。MATLAB具有强大的数值计算功能,但运行速度较慢。而C语言可对操作系统和应用程序以及硬件进行直接操作,优于其他解释型高级语言。因此,将MATLAB与C语言混合编程可以提高阻抗矩阵的计算效率。在完成阻抗矩阵填充之后,求解矩阵方程时采用广义最小余量法(generalized minimal residual,GMRES),这是一种动态迭代解法,也称为Krylov子空间迭代解法,求解时可将计算量降为
本文算例程序均基于MATLAB2010b仿真平台,应用具有良好稳定性的GMRES算法进行迭代求解,收敛精度设置为10–3,所有算例在Intel Pentium G2020 2.9 GHz CPU、1.95 GB内存的台式计算机上运行。
算例1 分析在平面波入射频率f=300 MHz,入射角度为(θ, ϕ) = (0°, 0°),双站RCS散射波的观察角度为(θs,ϕs) = (0°~180°, 0°)。球体表面按照λ/10标准剖分,剖分得到的未知量个数为3 072,其中λ为自由空间的波长的条件下。分别采用传统矩量法、结合ACA的矩量法以及结合ACA-SVD的矩量法进行求解,得到的GMRES迭代求解球体的迭代次数和迭代误差曲线如图2所示。根据计算结果,比较ACA阈值和SVD阈值选取不同值时内存的压缩效果。
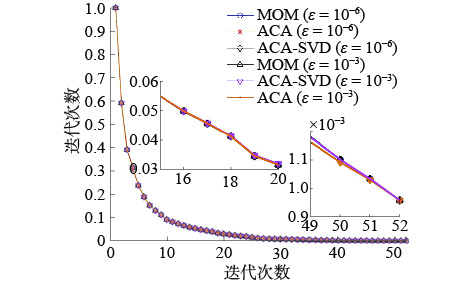
|
图 2 半径1 m的PEC球体采用GMRES求解迭代次数与迭代误差 |
通过图2可以看出,ACA算法迭代误差门限选用ε=10–3或是ε=10–6,求解过程均在51次时到达收敛。下面给出了2个算例的内存消耗,如表1所示。
|
|
表 1 两种算例的内存消耗比较 |
通过表1可以看出,ACA算法迭代误差门限并不是越小越好。这是因为门限越小,所需要的内存越多,算得越慢。
表2给出了ACA阈值和SVD阈值选取不同阈值时内存压缩效果的比较。
|
|
表 2 球体不同阈值时消耗内存比较 |
表2中的相对误差是指
算例2 分析理想导体球的双站RCS,平面波入射频率f=300 MHz,入射角度为(θ, ϕ) = (0°, 0°),双站RCS散射波的观察角度为(θs, ϕs)=(0°∼180°, 0°)。球体表面按照λ/10标准剖分,剖分得到的未知量个数为3 072,其中λ为自由空间的波长。分别采用传统矩量法、结合ACA的矩量法以及结合ACA-SVD的矩量法进行求解,其中,ACA算法迭代误差门限分别为ε=10–3和ε=10–6的条件下。SVD分解所选取的误差分别为ε=10–2和ε=10–5,求解得到的RCS对比曲线如图3所示。从图中可以看出2种方法结果吻合的良好。

|
图 3 半径1 m的PEC球在300 MHz的平面波照射下的VV极化双站RCS |
由图3可见,分别采用结合了ACA压缩算法的矩量法以及结合了ACA-SVD压缩算法的矩量法求解双站RCS,结果与Mie级数解吻合良好,说明ACA和ACA-SVD算法在对矩阵进行压缩的同时并未损失矩量法的计算精度。
图4显示了PEC球体的剖分细度不一样时,产生不同未知量的未知数,此时运算过程所占内存的变化趋势。

|
图 4 球体存储量变化曲线 |
通过图4可以看出,矩量法的存储量的增加趋势为
通过以上算例可以得知,ACA和ACA-SVD算法的运用,在不影响MOM计算精度的前提下,可以大大减少计算的存储空间,提高计算速度。例如,对于PEC球体,在ε=10-3的条件下,相比于传统矩量法,ACA和ACA-SVD算法的引入,分别可以减少59.25%的存储空间和78.10%的存储空间,从而可以加速后续的矩阵向量乘的计算。
3 结论文中应用ACA和ACA-SVD算法求解导体目标双站RCS。在远场组作用区,利用该方法压缩阻抗矩阵,减少矩阵填充时间、节省内存;在近场作用区,采用传统矩量法精确填充阻抗矩阵元素来提高计算效率。通过数值计算结果可以看出:
1) ACA算法可以有效地压缩阻抗矩阵,加速矩阵填充和矩阵向量乘。在保证一定计算精度的前提下,相比于传统的ACA算法,ACA-SVD的方法可以更快速地进行阻抗矩阵的填充,压缩效率更高,并通过仿真结果发现矩阵的规模越大,剖分的未知量数目越多,压缩效果越明显。
2) 验证了ACA-SVD算法的优越性。在基于RWG基函数的矩量法中加入ACA-SVD算法,大大降低计算的存储量和复杂度,提升矩量法的计算效率。
3) 下一步可以尝试将ACA-SVD算法与其他阻抗矩阵填充算法混合,进一步提高算法的性能,节省计算机内存和计算时间。该方法对研究复杂目标电磁散射特型有一定的参考价值。
| [1] |
张爱奎. 应用ACA-SVD算法快速求解导体目标RCS[J]. 中国科技论文, 2015, 10(14): 1656-1659. ( 0) 0)
|
| [2] |
BEBENDORF M, KUNIS S. Recompression techniques for adaptive cross approximation[J]. Journal of integral equations & applications, 2009, 21(3): 331-357. ( 0) 0)
|
| [3] |
马佳佳. 电磁场积分方程的快速直接解法[D]. 南京: 南京理工大学, 2014: 10-13.
( 0) 0)
|
| [4] |
张博. 等效原理算法及其结合快速算法分析目标的电磁散射[D]. 西安: 西安电子科技大学, 2013: 24-26.
( 0) 0)
|
| [5] |
聂文艳, 王仲根. 应用ACA算法快速分析导体目标电磁散射特性[J]. 计算机工程与应用, 2015, 51(4): 232-234. ( 0) 0)
|
| [6] |
BEBENDORF M. Approximation of boundary elements matrices[J]. Numerische mathematik, 2000, 86(4): 565-589. ( 0) 0)
|
| [7] |
ZHAO K Z, VOUVAKIS M N, LEE J F. The adaptive cross approximation algorithm for accelerate method of moments computations of EMC problems[J]. IEEE transactions on electromagnetic compatibility, 2005, 45(4): 763-773. ( 0) 0)
|
| [8] |
RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary Shape[J]. IEEE transactions on antennas and propagation, 1982, 30(3): 409-418. ( 0) 0)
|
| [9] |
吴君辉, 梁昌宏, 袁浩波, 等. 自适应交叉近似算法的核外计算方法[J]. 西安电子科技大学学报: 自然科学版, 2014, 41(5): 161-165. ( 0) 0)
|
| [10] |
吴君辉, 曹祥玉, 袁浩波, 等. 自适应交叉近似算法在矩量法中的应用[J]. 空军工程大学学报, 2013, 14(4): 76-79. ( 0) 0)
|
| [11] |
姚雨帆, 孙语法, 王仲根, 等. 应用EDM和ACA算法快速计算电大开缝导体RCS[J]. 合肥工业大学学报: 自然科学版, 2014, 37(4): 440-443. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


