现代电子战场中愈发复杂的电磁环境要求接收机要具有大的带宽,并且能对同时到达的多个信号全概率截获。瞬时带宽达到1 GHz的数字接收机才能较好的满足要求,同时也是国内外研究的重点。
关于数字信道化方面的研究,国外较为早于国内,J ames B Y Tsui等[1-2]研究了基于快速傅里叶变换和离散傅里叶变换的数字信道化接收机。虽然在国内从20世纪90年代初期才开始系统地进行数字信道化的相关研究,但是这项技术在初期即受到了国家的重视,在二十几年的时间里已有越来越多的知名高校和科研单位着手研究这个方向的问题,并且已取得了相当大的成果,对于数字信道化的研究已经逐渐趋向于成熟阶段。李冰等[3]研究了软件无线电中的信道化技术,与此同时朱晓等[4]则进行了一种高效的动态数字信道化方法的研究。
传统意义上的信道化接收机巨大的数据计算量一直是一个急需解决的问题,而多相滤波信道化接收机则提供了一种实时且高效的处理算法,但由于可实现的滤波器都是非理想的,信道间不可避免地会存在漏警及混叠[5]。因此,设计出一种无漏警无混叠的数字接收机有着重要的意义。本文通过重叠部分滤波器组的方法来解决此问题,最后通过MATLAB仿真实验验证了此方法的可行性。
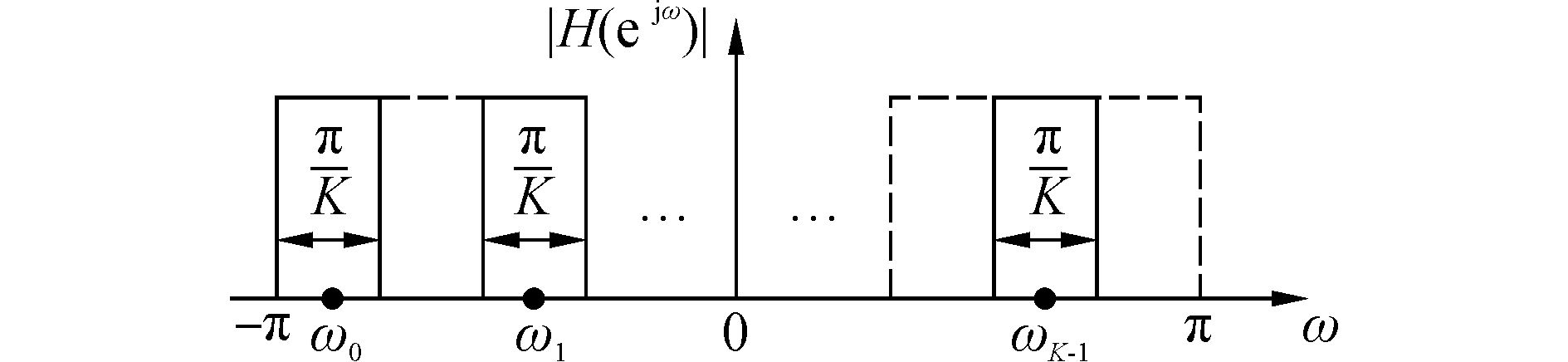
1 多相滤波信道化数字接收机 1.1 实信号信道划分为了推导实信号信道化接收机模型,先对实信号进行频带划分,如图 1所示。
|
图 1 实信号信道划分 |
虚线频带为对应的镜像,ωk为第k个信道的中心频率,K为数据抽取率,此时的ωk为
| ${\omega _k} = \left( {k - \frac{{2K - 1}}{4}} \right) \cdot \frac{{2{\rm{\pi }}}}{K},k = 0,1, \cdots ,K - 1$ | (1) |
频率信道化的基本结构是把每个子频段通过下变频搬移到零中频,然后经过一个带宽为信道宽度的低通滤波器,最后再经过K倍抽取[6]。这种信道化的实现方法被称为信道化的低通实现,如图 2所示。

|
图 2 信道化的低通实现 |
假设输入信号为s(n),所采用的低通滤波器响应函数为h(n), 由图 2所得第k路信道的输出为
| $\begin{array}{l} {y_k}\left( m \right) = \left\{ {\left[ {s\left( n \right) \cdot {{\rm{e}}^{{\rm{j}}{\omega _k}n}}} \right]h\left( n \right)} \right\}{|_{n = mD}} = \\ \quad \quad \sum\limits_{i = 0}^{N - 1} {s\left( {n - i} \right){{\rm{e}}^{{\rm{j}}{\omega _k}(n - i)}}h\left( i \right){|_{n = mD}}} = \\ \quad \quad \sum\limits_{i = 0}^{N - 1} {s\left( {mD - i} \right){{\rm{e}}^{{\rm{j}}{\omega _k}(mD - i)}} \cdot h\left( i \right)} \end{array}$ | (2) |
其中信号经过D倍抽取后的多相结构的表达式以及滤波器的多相分量的表达式分别为[7]
| ${s_p}\left( m \right) = s\left( {mD - p} \right),{h_p}\left( m \right) = h\left( {mK + p} \right)$ | (3) |
将i=iK+p代入式(2),可得
| $\begin{array}{l} {y_k}\left( m \right) = \sum\limits_{p = 0}^{K - 1} {\sum\limits_{i = 0}^{L - 1} {s\left( {mD - iK - p} \right){{\rm{e}}^{{\rm{j}}{\omega _k}(mD - iK - p)}}} } \cdot h\left( {iK + p} \right) = \\ \sum\limits_{p = 0}^{K - 1} {\sum\limits_{i = 0}^{L - 1} {s\left[ {\left( {m - iF} \right)D - p} \right]{{\rm{e}}^{{\rm{j}}{\omega _k}[\left( {m - iF} \right)D]}} \cdot {h_p}\left( i \right){{\rm{e}}^{ - {\rm{j}}{\omega _k}p}}} } \end{array}$ | (4) |
令s=iF, 则
| ${{y}_{k}}\left( m \right)=\sum\limits_{p=0}^{K-1}{\sum\limits_{s=0}^{\left( s-1 \right)F}{s\left[ \left( m-s \right)D-p \right]{{\text{e}}^{\text{j}{{\omega }_{k}}[\left( m-s \right)D]}}}}\cdot {{h}_{p}}\left( \frac{s}{F} \right){{\text{e}}^{-\text{j}{{\omega }_{k}}p}}$ | (5) |
定义
| $\begin{align} & {{y}_{k}}\left( m \right)=\sum\limits_{p=0}^{K-1}{\sum\limits_{s=0}^{\left( s-1 \right)F}{{{s}_{p}}\left( m-s \right){{\text{e}}^{\text{j}{{\omega }_{k}}[\left( m-s \right)D]}}}}~\cdot h_{p}^{'}\left( s \right){{\text{e}}^{-\text{j}{{\omega }_{k}}p}}= \\ & \quad \quad \sum\limits_{p=0}^{K-1}{\{[{{s}_{p}}\left( m \right)~\cdot {{\text{e}}^{\text{j}{{\omega }_{k}}mD}}]h_{p}^{'}\left( m \right)\}{{\text{e}}^{-\text{j}{{\omega }_{k}}p}}} \\ \end{align}$ | (6) |
根据1.1节中实信号的频带划分,将第k信道的中心频率ωk代入式(6) 中,即可推导出实信号的多相滤波信道化结构模型。
令s′p(m)=[sp(m)·ejωkmD]h′p(m),则
| ${{y}_{k}}\left( m \right)=\sum\limits_{p=0}^{K-1}{s_{p}^{'}\left( m \right){{\text{e}}^{-\text{j}{{\omega }_{k}}p}}}$ | (7) |
将
| $\begin{align} & \quad \quad \quad \quad {{y}_{k}}\left( m \right)=\sum\limits_{p=0}^{K-1}{s_{p}^{'}\left( m \right){{\rm{e}}^{-\rm{j}\left( \mathit{k}-\frac{2\mathit{K}-1}{4} \right)\cdot \frac{2\ \rm{ }\!\!\pi\!\!\rm{ }}{\mathit{K}}\mathit{p}}}=} \\ & \sum\limits_{p=0}^{K-1}{{{{{s}'}}_{p}}\left( m \right){{\rm{e}}^{-\rm{j}\frac{2\mathit{k}\ \rm{ }\!\!\pi\!\!\rm{ }}{\mathit{K}}\mathit{p}}}\cdot {{\rm{e}}^{\rm{j}\frac{\left( 2\mathit{K}-1 \right)\,\ \rm{ }\!\!\pi\!\!\rm{ }}{2\mathit{K}}\,\mathit{p}}}}=\rm{DFT}[{{{{\mathit{s}}'}}_{\mathit{p}}}\left( \mathit{m} \right)\cdot {{\rm{e}}^{\rm{j}\frac{\left( 2\mathit{K}-1 \right)\,\ \rm{ }\!\!\pi\!\!\rm{ }}{2\mathit{K}}\mathit{p}}}] \\ \end{align}$ | (8) |
式中:
| $\begin{align} & \quad \quad \quad s_{p}^{'}\left( m \right)=[{{s}_{p}}\left( m \right)\cdot {{\rm{e}}^{\rm{j}{{\mathit{w}}_{\mathit{k}}}\mathit{mD}}}]h_{p}^{'}\left( m \right)= \\ & [{{s}_{p}}\left( m \right)\cdot {{\rm{e}}^{\rm{j}\left( \mathit{k}-\frac{2\mathit{K}-1}{4} \right)\frac{2\,\rm{ }\!\!\pi\!\!\rm{ }}{\mathit{K}}\mathit{mD}}}]{{h}_{p}}\left( m \right)=[{{s}_{p}}\left( m \right)\cdot {{\rm{e}}^{\rm{j}\frac{4\mathit{k}+1}{2\mathit{F}}\rm{ }\!\!\pi\!\!\rm{ }\,\mathit{m}}}]{{h}_{p}}\left( \frac{m}{F} \right) \\ \end{align}$ | (9) |
基于上述推导过程,得出实信号的多相滤波信道化结构,如图 3所示。

|
图 3 实信号非最大抽取多相滤波信道化结构 |
现对图 3所示结构进行简要分析,这种实信号非最大抽取多相滤波信道化结构的实现方法是通过对一个低通原型滤波器乘以一个复因子进行调制然后将其转换为滤波器的多相结构[8]。此结构把整个频带分割成若干个并行的输出,从而使处于任意一个信道的信号都能够被接收到。此外,多相滤波器的使用,使计算量降低到原有的1/D,提高了信道化接收机的实时处理能力。在这整个设计过程中,低通滤波器组的设计是整个系统能否实现的关键。而现实中滤波器不可能达到理想状态,故总会出现一定程度的漏警[9]。
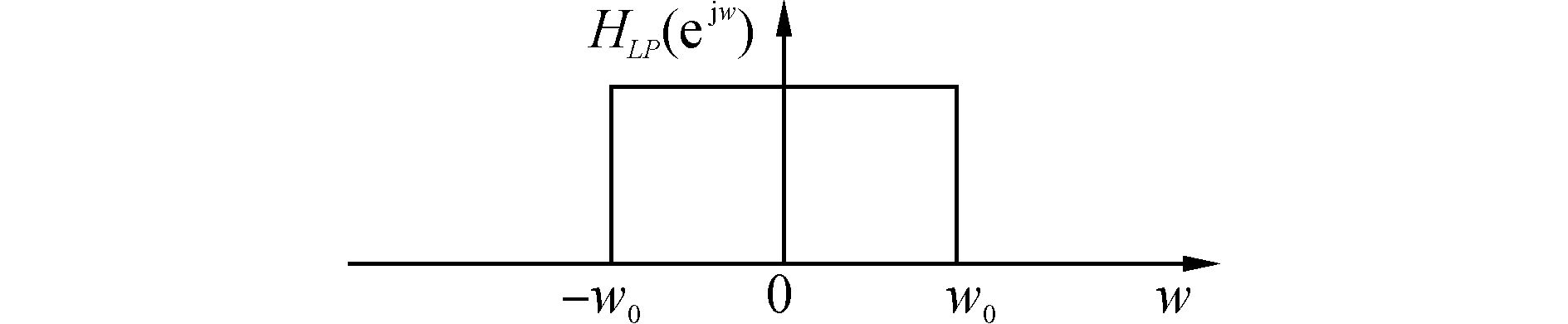
2 无漏警无混叠信道化数字接收机 2.1 漏警及混叠的产生理想状态下的滤波器的矩形系数应是1,如图 4所示。
|
图 4 理想低通滤波器示意图 |
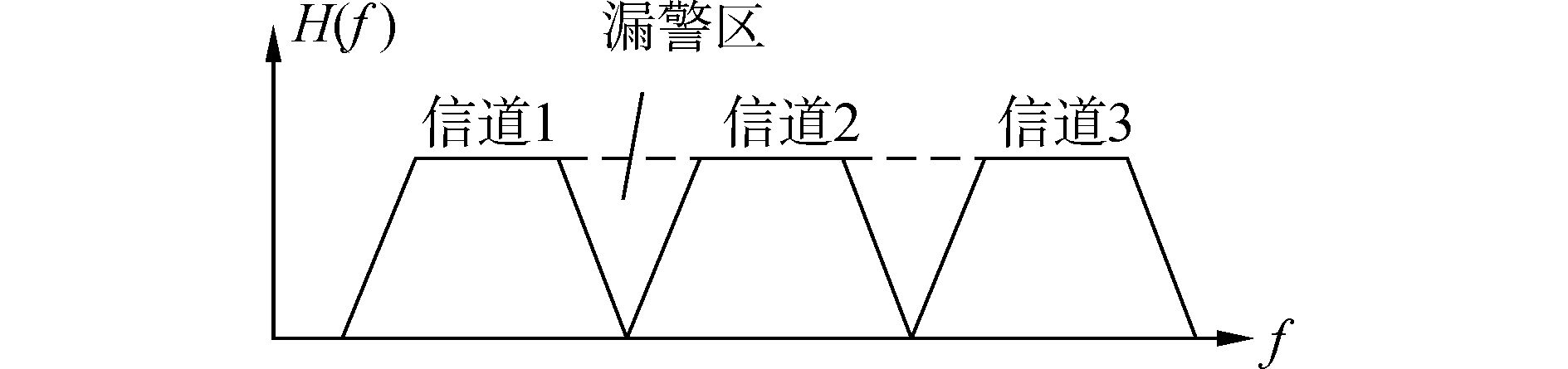
由于实际的原型滤波器设计过程中是梯形的,有着过渡带的存在[10],若过渡带没有重叠(如图 5所示),这样就会出现漏警的现象,即当信号落入漏警区时无法被检测到。
|
图 5 无混叠划分方式 |
分析上述情况,改善的方法大致有以下两种:
1) 改善滤波器的设计要求,获得一个过渡带更窄的滤波器。但这种方法势必会增加滤波器的阶数,从而增加硬件复杂度和增大运算量,难以实现[11]。
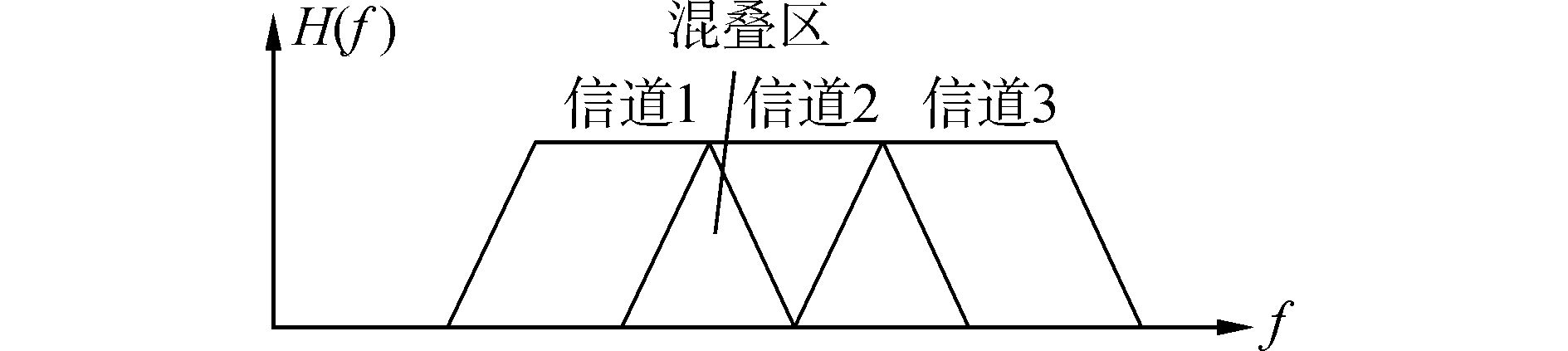
2) 对图 5所示的滤波器组的通带带宽进行延伸。基于此,将会获得一个漏警区相对小的的结构,当延伸到一定的长度时,漏警区就会消失,如图 6所示。
|
图 6 无漏警划分方式 |
但此划分方式将会导致混叠的出现。即落入混叠区的信号会被多个信道检测出。
2.2 无漏警无混叠信道化数字接收机模型推导为了解决相邻2个信道之间的漏警及混叠问题,本文提出了延伸其处理带宽的方法予以解决。如图 7所示,信道间重叠了1/3,处理带宽也随之增长。

|
图 7 无漏警无混叠划分方式 |
对上文中实信号非最大抽取多相滤波信道化结构进行改造后,可以得到一种非最大抽取无漏警无混叠的多相滤波信道化结构,如图 8所示。经过延长后的处理带宽不仅提高了输出的数据率,也解决了实信号非最大抽取多相滤波信道化结构中所存在的漏警以及混叠的问题[12-13]。采用此划分方式,对于原型滤波器的过渡带要求不再严苛,相应的降低了滤波器的阶数,更易于实现。而且当信道数为2的整数次幂时,此结构中并行离散傅里叶模块(DFT)可由快速傅里叶模块(FFT)取代,将极大地提升运算速度和效率,同时降低了系统设计的复杂度,更易于实现[14]。

|
图 8 无漏警无混叠非最大抽取多相滤波信道化结构 |
由于信号经过分析滤波器组后,各子带信号会有噪声的干扰,有时需要根据信号的输出瞬时频率来对信号进行判断处理[15]。
信号经过多相滤波信道化结构之后输出的信号为复数值信号,设为yk=Ik(m)+jQk(m),则可得到信号的瞬时相位为
| $\varphi \left( m \right)=\arctan \frac{{{Q}_{k}}\left( m \right)}{{{I}_{k}}\left( m \right)}$ | (10) |
则信号的瞬时频率为
| $f\left( m \right)=\frac{\varphi \left( m \right)-\varphi \left( m-1 \right)}{{{T}_{s}}}$ | (11) |
式中Ts为信号的采样时间间隔。
为避免相位超过2π测量时会发生的模糊现象,本文采用差分获得瞬时频率之前先对信号的瞬时相位进行解卷绕去除模糊[16]。整个瞬时测频过程如图 9所示。

|
图 9 瞬时测频测量过程 |
对2.2节中所示无漏警无混叠非最大抽取多相滤波信道化结构进行仿真。
仿真条件:取F=1,滤波器组划分子带数目为8,系统采样频率为960 MHz,每个子带的带宽均为60 MHz,原型低通FIR滤波器的通带设置为30 MHz,阻带设置为40 MHz,阻带衰减设置为120 dB;3个输入信号中输入信号1为起始频率20 MHz,终止频率80 MHz,脉宽5 μs的线性调频信号;输入信号2为载波频率260 MHz的正弦信号;输入信号3为起始频率310 MHz,终止频率340 MHz,带宽30 MHz,脉宽5 μs,调频斜率为6×1012 Hz/s的线性调频信号。
设计的原型低通滤波器的阶数为N=423,幅频响应仿真结果如图 10所示。

|
图 10 原型低通FIR滤波器的幅频响应 |
所设计的3个输入信号的频谱分析以及数字滤波器组的各子带频谱分布特征的仿真结果如图 11所示。

|
图 11 输入信号以及各子带滤波器频谱分布特征 |
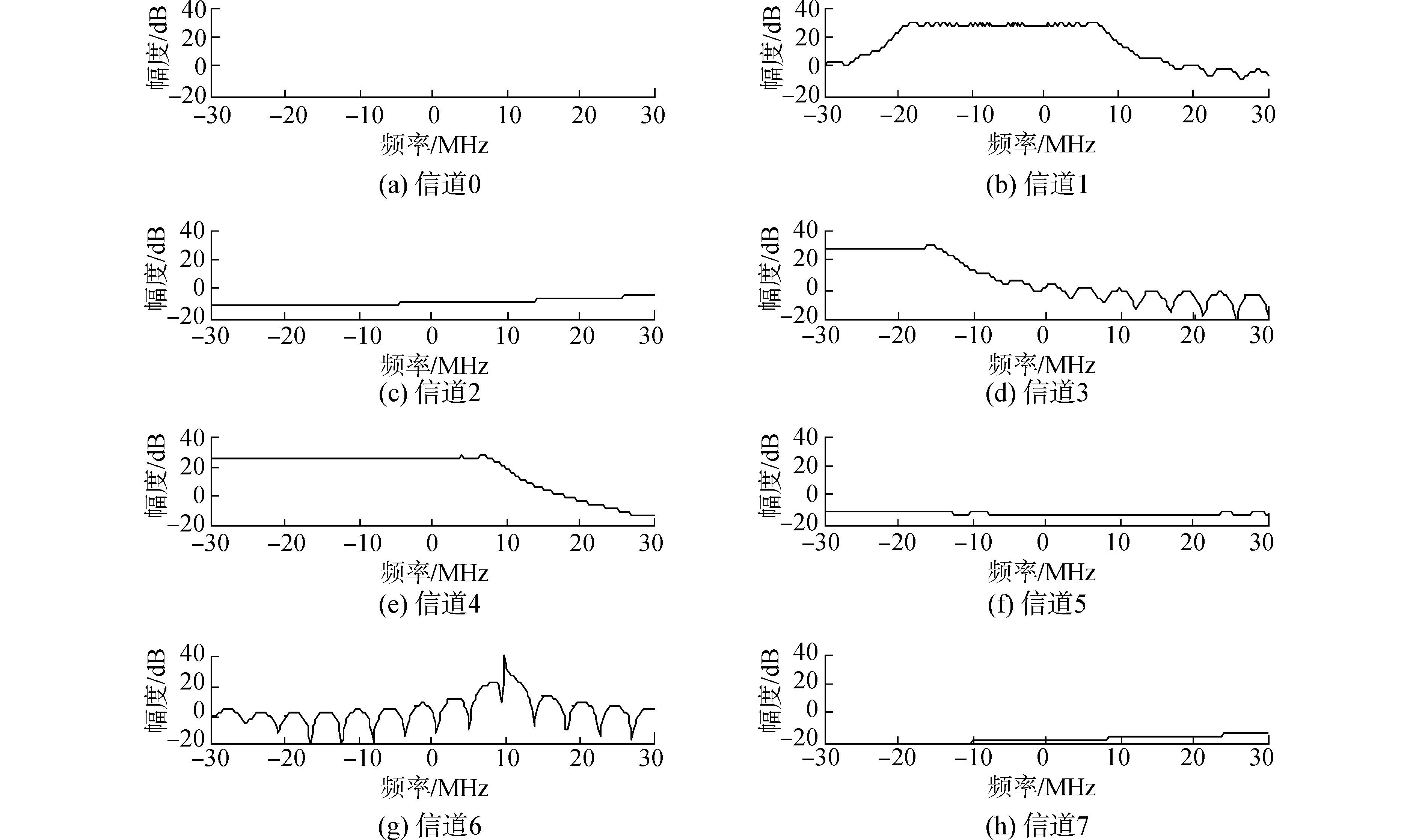
输入信号在经过此无漏警无混叠非最大抽取多相滤波信道化结构后,各个子带输出的基带信号时域情况如图 12所示,相对应的频谱分析情况如图 13所示。

|
图 12 各子带输出信号时域特征 |
|
图 13 各子带输出信号频域输出 |
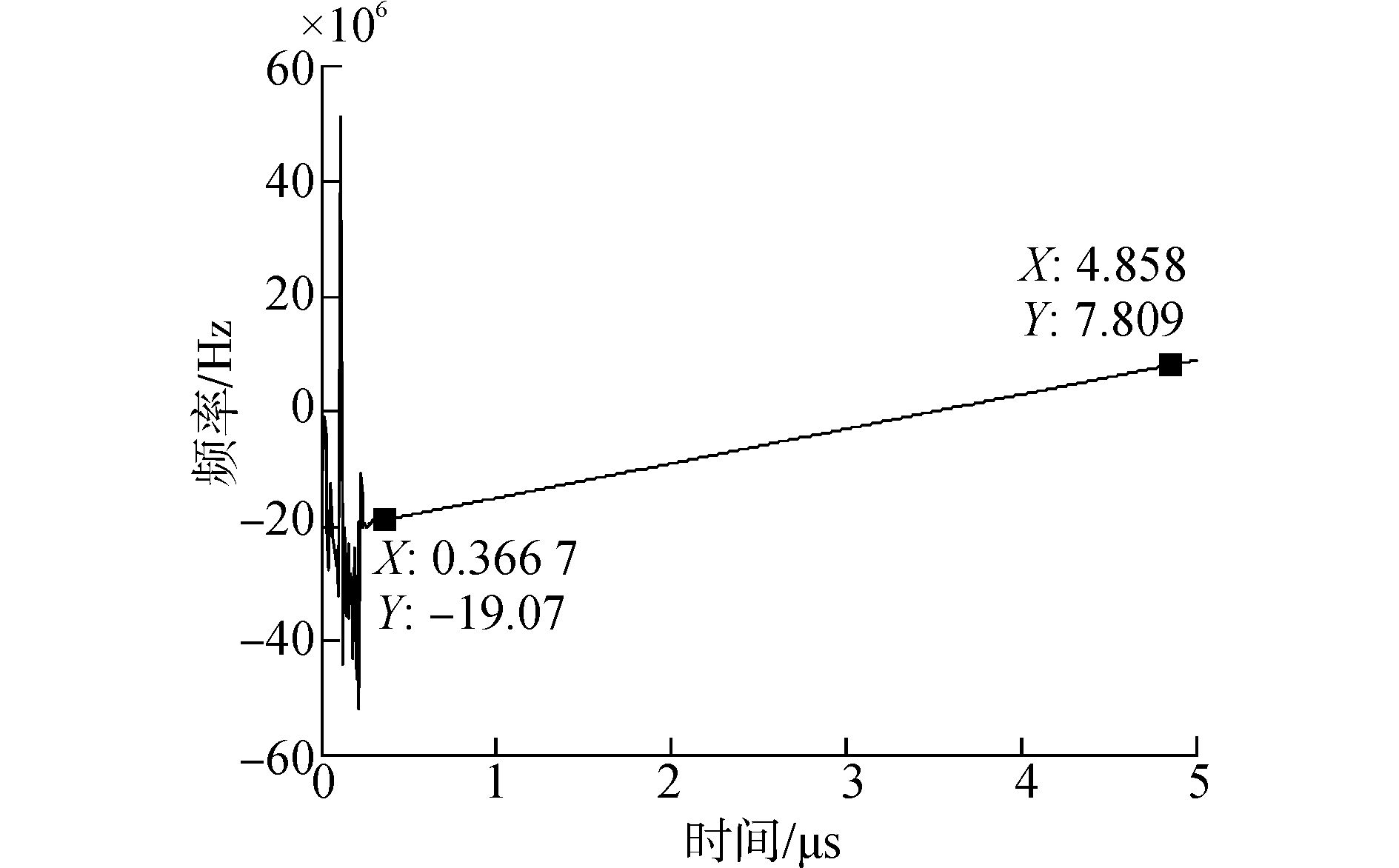
利用文中介绍的关于信号瞬时频率测量的算法,测得子带1输出的基带信号的瞬时频率如图 14所示。
|
图 14 子带1输出基带信号的瞬时频率测量 |
根据输入信号以及滤波器组各子带频谱性质,输入信号1经过分析滤波器组后,信号主要信息分布在子带3以及4中;输入信号2主要信息分布在子带6中;输入信号3主要信息分布在子带1中,图 12以及图 13所示仿真结果与理论分析相符。并且信号在与子带1中心频率330 MHz混频得到低频子带信号后,起止频率变为-20 MHz和10 MHz,带宽30 MHz,调频斜6×1012Hz/s。由图 14的仿真结果可得到子带1输出信号的调频斜率为5.98×1012Hz/s,在误差允许范围内与理论分析相符合,可验证此低复杂度的滤波器组结构设计是正确的。
在此无漏警无混叠非最大抽取多相滤波信道化结构设计仿真过程中,主要存在3种失真误差。第1种是主要是由于原型低通滤波器不可能实现完全理想滤波,在设计中存在一定宽度的过渡带,阻带衰减特性非理想,这将引起滤波后各子带之间的混叠误差[17];第2种是在由原型滤波器系数进行多相抽取后形成各子带滤波器时也将引入一定的设计误差[18];第3种是整个分析滤波系统中的幅度失真误差。
4 结论本文针对多相滤波信道化结构中存在的问题进行了分析, 完成无漏警无混叠非最大抽取多相滤波信道化结构的推导与仿真。
1) 多相滤波信道化模型结构固定,适用性较低,本文推导的结构内部因子灵活可变,适用于不同情况,具有广泛的适用性。
2) 在多相滤波信道化模型中,当信号落在相邻信道的交界处时,将会产生漏警现象。本文推导的漏警无混叠非最大抽取多相滤波信道化结构仿真结果中,位于漏警区与混叠区的信号均被准确清晰的检测了出来,与理论分析相符。
3) 采用差分获得瞬时频率之前先对信号的瞬时相位进行解卷绕去除模糊的方法得到了子带输出信号的调频斜率,在误差允许范围内与理论分析一致。
现代复杂电磁环境下接收机高带宽高截获率的要求之下,本文提出的无漏警无混叠非最大抽取多相滤波信道化结构极大的提升了接收机截获信号的概率和准确性,具有广泛的适用性,仿真实验的结果验证了此改进模型的正确性。本文研究内容对电子侦察领域改善接收机性能有着一定的指导意义。
| [1] |
TSUI J B Y, STEPHENS J P. Digital microwave receiver technology[J]. IEEE transactions on microwave theory and techniques, 2002, 50(3): 699-705. DOI:10.1109/22.989955 ( 0) 0)
|
| [2] |
MAHESH R, VINOD A P, LAI M K, et al. Filter bank channelizers for multi-standard software defined radio receivers[J]. Journal of signal processing systems, 2011, 62(2): 157-171. DOI:10.1007/s11265-008-0327-y ( 0) 0)
|
| [3] |
李冰. 软件无线电中的信道化技术研究[D]. 南京: 中国人民解放军信息工程大学. 2007.
( 0) 0)
|
| [4] |
朱晓. 新型宽带数字接收机及脉冲压缩雷达信号参数估计算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
( 0) 0)
|
| [5] |
MICHAEL N, VINOD A P, MOY C, et al. Design of multistandard channelization accelerators for software defined radio handsets[J]. IEEE Transactions on signal processing, 2011, 59(10): 4767-4780. DOI:10.1109/TSP.2011.2161301 ( 0) 0)
|
| [6] |
LIN M, VINOD A P, SEE C M. A new flexible filter bank for low complexity spectrum sensing in cognitive radios[J]. Journal of signal processing systems, 2011, 62(2): 205-215. DOI:10.1007/s11265-008-0329-9 ( 0) 0)
|
| [7] |
李坡. 宽带数字侦察接收系统关键技术研究与实现[D]. 长沙: 国防科学技术大学, 2010.
( 0) 0)
|
| [8] |
陈涛, 岳玮, 刘颜琼, 等. 宽带数字信道化接收机部分信道重构技术[J]. 哈尔滨工程大学学报, 2011, 32(13): 1610-1616. ( 0) 0)
|
| [9] |
刘旭波. 基于数字信道化接收机LPI雷达信号参数估计与分选[D]. 哈尔滨: 哈尔滨工程大学, 2011: 11-22.
( 0) 0)
|
| [10] |
王海生, 黄振, 葛宁. 基于多相滤波结构的高效动态数字信道化接收机设计[J]. 电路与系统学报, 2013, 18(2): 1-5. ( 0) 0)
|
| [11] |
NARENDAR M, VINOD A P, MACHUKUMAR A S, et al. A tree-structured DFT filter bank based on spectrum sensor for estimation of radio channel edge frequencies in military wideband receivers[C]//10th International Conference on Information Sciences Signal Processing and their Applications. Kuala Lumpur:Malaysia, 2010:534-537.
( 0) 0)
|
| [12] |
杨君, 袁嗣杰, 吕镜清. 一种非均匀信道化滤波方法[J]. 现代雷达, 2010, 32(9): 59-62. ( 0) 0)
|
| [13] |
唐鹏飞, 林钱强, 袁斌, 等. 一种新的动态信道化接收机设计方法[J]. 国防科技大学学报, 2013, 35(3): 164-169. ( 0) 0)
|
| [14] |
王杨, 凌万胜. 基于信道化的测频方法研究[J]. 无线电工程, 2007(4): 48-50. ( 0) 0)
|
| [15] |
司伟建, 米胜男, 曲志昱, 等. 数字信道化的调制信号测频方法[J]. 应用科技, 2016, 43(3): 28-33. ( 0) 0)
|
| [16] |
罗义军, 陆冬冬, 李勤. 信道化接收机的结构优化和实现[J]. 电子技术应用, 2016, 42(1): 72-74. ( 0) 0)
|
| [17] |
陈涛, 王莹, 刘勇. 基于频率响应屏蔽的窄过渡带信道化接收机[J]. 吉林大学学报, 2015, 45(1): 335-340. ( 0) 0)
|
| [18] |
HARRIS F, VENOSA E, CHEN X, et al. An efficient channelizer tree for portable software defined radios[J]. Annals of telecommunications, 2014, 69(1): 99-110. ( 0) 0)
|
 2017, Vol. 44
2017, Vol. 44


