近年来,网络的迅速发展推动了世界经济与社会的进步,同时也带来了泛滥的网络入侵与攻击事件,网络入侵检测作为一种主动防御技术成为当今网络安全防护的有效手段。入侵检测即通过实时监控网络数据包,收集与分析网络连接数据的特征属性,从而及时发现入侵行为,避免恶意攻击[1]。检测率、误报率、检测速度是衡量入侵检测优劣的重要参数,准确性与实时性是入侵检测要解决的关键问题。由于网络入侵检测所处理的数据特征维数高、数据量大,导致入侵检测系统负荷大、检测速度慢、实时性差,针对此问题,可行的解决办法之一就是对网络数据进行特征选择,通过约简系统要处理数据的维度间接减少系统要计算的数据量,从而提高系统实时性。
在特征选择算法中,遗传算法[2-4]因其强大的空间搜索能力得到了众多研究学者的关注,陈果等[5]针对遗传算法的适应度函数提出了4种构造方法,在不降低分类能力的基础上对数据特征进行了有效约简;遗传算法也常常与其他方法相结合构成混合算法的特征选择方法,这些算法包括混沌免疫算法[6]、量子计算[7]、互信息[8]等,同时量子进化算法[9]、回溯搜索算法[10]等也被应用到特征选择中。
本文提出了一种将自适应遗传算法与信息增益相结合的特征选择方法(adaptive genetic algorithm with information gain,IG-GA),采用基于支持向量机(SVM)的分类器作为自适应遗传算法中适应度函数计算以及特征选择结果性能评价,该算法具有更优的解空间寻优能力与特征约简能力,有利于解决入侵检测系统的实时性问题。
1 特征选择特征选择的过程是在特征子集空间中搜索具有最优性能的特征子集,这一过程涉及到两个关键问题:一是确定特征子集的搜索策略;二是确定特征子集性能的评价标准。特征子集的搜索策略决定了如何搜索特征子集空间,影响着特征选择算法的收敛性及收敛速度,而评价标准的不同会产生不同的优化结果。算法设计的关键就是寻找适合的搜索策略与评价标准。
特征选择的搜索策略主要穷举搜索、启发式搜索和不确定搜索[11]。不确定搜索作为前两类策略的综合方法,减小了穷举搜索的时间复杂性,弥补了启发式搜索的搜索空间局限性,遗传算法即属于不确定搜索算法。评价标准又根据其是否与分类器有关分为封装器模式和过滤器模式[12]两类,封装器模式以分类器的检测率作为评价函数的一环,因而基于这种模式选择的特征子集的入侵检测准确性高,然而由于分类器的引入,相对于过滤式模式会耗费更多的计算资源,降低了特征选择过程的速率,过滤器模式则相反。基于此再结合遗传算法的空间搜索特性,IG-GA算法首先采用信息增益这一过滤器模式对41维特征空间进行约简,将得到的特征属性输入到自适应遗传算法中,在遗传算法中采用封装器模式的评价函数,构成半混合器模式,并选用基于SVM的分类器的检测率作为个体的适应度函数计算,基于IG-GA的特征选择流程如图 1所示。

|
| 图 1 基于IG-GA的特征选择流程 |
熵是在信息论中广泛使用的一个度量标准,它刻画了任意样本集的纯度,给定包含正反样例的样本集S,则S的熵为
 |
(1) |
由式(1)可知,样本集中的正反例分布越均匀,样本集的熵越大。
信息增益是属性分类训练数据的度量标准,给定特征属性fi,则该属性相对于样本集S的信息增益为
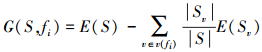 |
(2) |
式中:v(fi)是特征属性fi的所有可能取值的集合,Sv是S中属性fi的值为v的子集。信息增益越大,说明由于属性fi的已知,使得样本集的熵越小,样本集的正反例分类越明确,表明属性fi对样本的分类能力越强,因此通过信息增益算法,可以初步选择那些对样本分类能力强的特征属性,删除对样本分类能力弱的特征属性。
例如,在KDDCUP9910%数据集的494 021条连接数据中,第20列特征属性名称为num_outbound_cmds,代表文件传输协议会话中带外命令的数量,这个特征属性的所有取值均为0,则对于特征属性f20,v(f20)=[0],Sv=S,特征属性f20的信息增益为
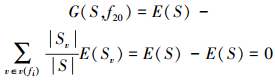 |
(3) |
由式(3)可知,特征属性f20对样本不具备分类能力,故应将其进行删除,信息增益算法的目的就是删除这一类对样本分类能力弱的特征属性。
2.2 IG-GA算法设计 2.2.1 种群个体编码及种群初始化自适应遗传算法的种群个体采用二进制编码,一个染色体表示一个特征子集,则染色体可以表示为x={g1, g2, …, gn}。其中gi=0或1:0表示删除该属性,1表示选择该属性。
2.2.2 适应度函数计算采用封装器模式的评价函数,评价函数与入侵检测的检测率直接相关,即将基于SVM的入侵检测分类器的检测率作为特征子集评价函数的因子,同时由于特征选择的定义,在不降低分类器精度的条件下希望获得更小维度的特征子集,所以将特征子集的维数加入到评价函数中,得到适应度函数定义如下:
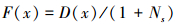 |
(4) |
式中:D(x)为x染色体的SVM分类器的检测率,Ns为染色体中gi取值为1的个数,也即特征子集的维数。
2.2.3 遗传操作遗传操作分为选择、交叉和变异3个步骤。选择的目的是确定交叉群体,我们采用轮盘赌选择策略,同时采取基于排序的适应度分配,在这种分配下,每个个体的选择概率仅仅取决于个体适应度在种群中的序位,而与实际的个体适应度无等值对应关系。排序方法将单纯基于适应度的选择进行修正,可以避免在选择压力过小的情况下,搜索带迅速变窄而产生的过早收敛。选择概率计算公式为:pi=c(1-c)i-1,i为个体排序序号,c为排序第1的个体的选择概率。交叉与选择的目的是产生新的个体,使个体以一定的概率或步长发生变化,保证了算法的全局搜索能力,IG-GA算法采用单点交叉与单点变异策略。交叉概率Pc与变异概率Pm直接影响算法的收敛性,Pc越大,新个体产生速度越快,但Pc过大则会导致高适应度的个体很快被破坏,算法难以收敛;Pc过小则会造成搜索过程缓慢,算法停滞不前;Pm与之类似。自适应遗传算法相对于传统算法进行了改进,针对每个个体单独计算合适的交叉概率Pc与变异概率Pm,Pc和Pm的计算公式为
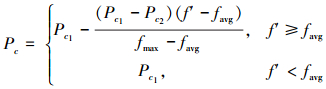 |
(5) |
 |
(6) |
式中:fmax为每代群体中最大的适应度值,favg为每代群体的平均适应度值,f′为交叉的2个个体中较大的适应度值,f为变异个体的适应度值。自适应遗传算法可以在保证搜索速度的同时,保证算法的收敛性。
2.2.4 算法终止条件传统遗传算法常以最大迭代代数作为算法终止条件,在此基础上,当相邻种群的平均适应度连续5次小于指定阈值时,IG-GA算法将提前终止迭代。
3 实验及结果分析 3.1 实验数据实验使用KDDCUP9910%数据集,每条连接数据具有41个特征属性[13],训练样本与测试样本分别提取自训练数据集kddcup.data_10_percent_corrected.gz和测试数据集corrected.gz,在其中随机选取2组5 000条训练数据和6组3 000条测试数据,共同构成本次实验数据,为全面衡量算法性能,将测试样本2、3的异常类型设置为单一的网络高发攻击类型smurf与neptune,其余样本的异常类型为混合类型。训练样本1及测试样本1用于IG-GA算法特征选择过程中适应度的计算,训练样本2及测试样本2~7用于测试特征子集的性能。样本构成原则为正常数据连接与异常数据连接数目比为1 ∶4,与原样本中的数据分布保持一致。
3.2 实验设置实验的硬件环境是Intel i3-2120 3.30 GHz、4 GB内存、操作系统为Windows XP 32 位SP3,编程环境为Microsoft Visual Studio 2008,MATLAB R2010a。表 1给出了算法的参数设置。
| 参数名称 | 参数符号 | 参数取值 |
| 种群大小 | pop_size | 20 |
| 染色体基因数 | chromo_size | 41 |
| 最大进化代数 | generation_size | 50 |
| 交叉率参数 | Pc1, Pc2 | 0.9,0.6 |
| 变异率参数 | Pm1, Pm2 | 0.1,0.001 |
3.3 算法结果及性能评估 3.3.1 IG-GA算法与GA算法的寻优性能对比
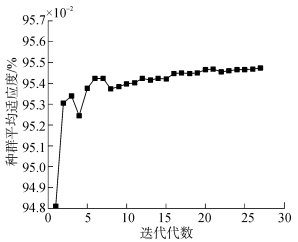
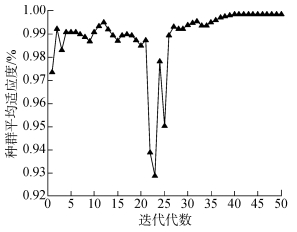
为验证IG-GA算法的特征选择性能,将其与GA算法进行比较,实验选用训练样本1及测试样本1作为输入数据,分别用IG-GA算法、GA算法进行了30次特征选择实验,算法的参数设置均相同。图 2、3分别给出了其中一次特征选择实验中IG-GA算法和GA算法的每代种群平均适应度favg随进化代数的变化趋势,其余实验的变化趋势与本次实验基本相同。
|
| 图 2 IG-GA算法平均适应度随代数的变化 |
|
| 图 3 GA算法平均适应度随代数的变化 |
实验结果说明:IG-GA算法的种群平均适应度favg随进化代数g增加而增大,在第27代时提前结束特征选择过程,GA算法的种群平均适应度favg随进化代数变化振荡较大,达到最大迭代代数50时算法结束。表明IG-GA算法是有效的且收敛速度较快,一定程度上解决了GA算法收敛速度慢的问题。同时,IG-GA全局空间搜索能力也优于GA算法。
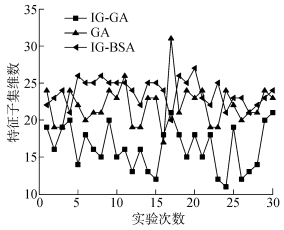
3.3.2 IG-GA、GA、IG-BSA选择结果对比为了验证IG-GA算法特征选择结果的入侵检测性能,将IG-GA算法与GA、IG-BSA算法进行比较。首先以训练样本1、测试样本1作为输入数据,用IG-GA算法、GA算法、IG-BSA算法进行特征选择实验,将得到的特征选择结果予以保存。为避免单次特征选择结果的偶然性,每个算法进行30次实验。然后以训练样本2、测试样本2为输入数据,以基于SVM分类器的检测率与误报率作为性能衡量参数。图 4给出了IG-GA算法、GA算法、IG-BSA算法的30次特征选择结果的特征子集维度变化,图 5、6分别给出了3种算法的30次特征选择结果的检测率与误报率。
|
| 图 4 特征选择结果的维度变化 |

|
| 图 5 特征选择结果的检测率变化 |

|
| 图 6 特征选择结果的误报率变化 |
从图 4可以看出,IG-GA算法特征选择结果的维数总体低于其他2种算法,在特征维度的约简上明显好于其他2种算法,从整体上看,IG-BSA算法在特征维度的优化上最差,但GA在个别次实验中获得了更差的特征维度约简结果。
从图 5、6可以看出,在30次实验中,IG-GA算法特征选择结果的检测率要好于IG-BSA算法,但误报率高于IG-BSA算法,GA算法特征选择结果的检测率最高、相应的误报率也最高,由上文分析可知,这是由于GA算法的输入维数过大,空间搜索能力易陷入局部最优值造成的。而采用信息增益对GA算法与BSA算法进行优化后,搜索能力明显增强。但IG-GA与IG-BSA在均以SVM分类器的检测率作为适应度函数计算的情况下,IG-GA更易获得检测率高的特征子集,IG-BSA则更易获得误报率低的特征子集。
表 2给出了3种算法特征选择结果的主要性能参数,总体来说,IG-GA算法降维能力强,且特征选择结果具有较高的检测率与较低的误报率,适用于检测率参数优先,同时对维数要求高的情况;IG-BSA的降维能力最弱,误报率低于IG-GA算法,适应于误报率参数优先,同时对维数要求不高的情况;未经改进的GA算法在降维与检测率、误报率参数上均无明显的优势。
| 算法名称 | 平均检测率 | 平均误报率 | 平均维数 | 最小维数 |
| IG-GA | 0.9 843 | 0.0 478 | 16 | 11 |
| GA | 0.9 982 | 0.0 581 | 22 | 17 |
| IG-BSA | 0.9 066 | 0.0 143 | 24 | 20 |
3.3.3 特征选择结果及性能对比
在入侵检测中,检测率与误报率是负相关的2个参数,高检测率往往对应高误报率,不能单纯追求检测率最大化,否则过高的误报率会造成用户对入侵检测系统结果的麻木。因此在上述3个算法的30次特征选择结果中综合考虑检测率与误报率,然后考虑维数优化,由此得到的特征选择结果由表 3给出。为全面验证特征选择结果的优劣,以训练样本2作为SVM的训练数据、以测试样本2~7作为测试数据,采用基于SVM的入侵检测分类器,对3个特征选择子集进行性能测试。
| 算法 | 特征序号 |
| IG-GA | 2,4,5,10,25,26,28,19,30,32,33,35,38 |
| GA | 1,4,5,6,9,12,14,19,20,25,27,28,29,32,35,36,40,41 |
| IG-BSA | 1,2,6,10,12,13,16,19,22,26,28,29,31,32,34,35,37,39,40,41 |
图 7、8分别给出了针对不同测试集3个特征选择结果的检测率与误报率。由图 7、8可知,相对于GA、IG-BSA算法,由IG-GA算法得到的特征子集在单一异常类型smurf和neptune样本与混合样本中均具有较好的检测率与误报率。3种算法对于单一异常类型的误报率均明显高于混合类型,说明用于入侵检测算法性能测试的SVM算法还应进一步优化。同时,IG-GA算法得到的特征子集维数为13维,特征约简效果明显优于GA算法的18维与IGABSA算法的20维。

|
| 图 7 6组测试样本的检测率 |

|
| 图 8 6组测试样本的误报率 |
本文将信息增益与自适应遗传算法相结合,提出了一种新的半混合器模式的特征选择算法,该方法具有更强的特征约简能力与解空间寻优能力。
1)探索性地将回溯算法与信息增益相结合。该算法更易于获得误报率低的特征子集,适用于对误报率性能要求高的情况。
2)最终获得了13维的特征子集,并且检测率与误报率综合性能优于其他特征子集结果。
因此,本文提出的IG-GA算法具有较好的特征约简能力与解空间寻优能力,在不降低检测性能甚至优化了检测性能的基础上,能够对数据特征进行有效约简,一定程度上解决了入侵检测的实时性问题。
| [1] | ANDERSON J P. Computer security threat monitoring and surveillance[R]. Fort Washington, Pennsylvania:James Pennsylvania Anderson Company, 1980. |
| [2] | ROSTAMI M, MORADI P. A clustering based genetic algorithm for feature selection[C]//Proceedings of the 6th Conference on Information and Knowledge Technology (IKT). Shahrood, 2014:112-116. |
| [3] | YANG Wenzhu, LI Daoliang, ZHU Liang. An improved genetic algorithm for optimal feature subset selection from multi-character feature set[J]. Expert systems with applications,2011, 38 (3) : 2733 –2740. |
| [4] | SAROJ, JYOTI. Multi-objective genetic algorithm approach to feature subset optimization[C]//Proceedings of IEEE International Advance Computing Conference (IACC). Gurgaon, 2014:544-548. |
| [5] | 陈果, 邓堰. 遗传算法特征选取中的几种适应度函数构造新方法及其应用[J]. 机械科学与技术,2011, 30 (1) : 124 –128. |
| [6] | 贾花萍, 李尧龙. 混沌免疫遗传算法的网络入侵检测模型[J]. 计算机工程与应用,2014, 50 (21) : 96 –99. |
| [7] | 刘晙, 狄文辉. 基于改进量子遗传算法的入侵检测特征选择[J]. 计算机测量与控制,2011, 19 (4) : 813 –815. |
| [8] | GE Hong, HU Tianliang. Genetic algorithm for feature selection with mutual information[C]//Proceedings of the Seventh International Symposium on Computational Intelligence and Design. Hangzhou, China, 2014:116-119. |
| [9] | 张宗飞. 基于量子进化算法的网络入侵检测特征选择[J]. 计算机应用,2013, 33 (5) : 1357 –1361. |
| [10] | CIVICIOGLU P. Backtracking search optimization algorithm for numerical optimization problems[J]. Applied mathematics and computation,2013, 219 (15) : 8121 –8144. |
| [11] | 陈友, 程学旗, 李洋, 等. 基于特征选择的轻量级入侵检测系统[J]. 软件学报,2007, 18 (7) : 1639 –1651. |
| [12] | KOHAVI R, JOHN G H. Wrappers for feature subset selection[J]. Artificial intelligence,1997, 97 (1/2) : 273 –324. |
| [13] | HETTICH S, BAY S D. KDD cup 1999 data[EB/OL].[2015-06-03]. http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html. |



