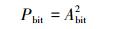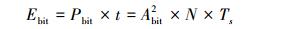2. College of Information And Communication Engineering, Harbin Engineering University, Harbin 150001, China
水声发射机是主动声纳设备的重要组成部分,它通过匹配电路与换能器进行连接,负责实现功率放大[1]。D类功放因其功耗小、效率高的特点,在水声领域有广泛的应用。它要求输入两路反相的数字信号使两个功放管交替导通,从而实现功率的传输[2-5]。对于任意一个宽带信号,要实现开关工作,需要采用可行的调制方式,使调制输出为1位比特流形式,且功放输出端应能够进行有效地解调。
传统的PWM调制技术将模拟信号与特定频率的三角波进行比较,得到正负脉冲交替的输出信号,其低频特性与待调制宽带信号的原始信息一致,但含有丰富的谐波分量。ΣΔ调制技术是通过反馈回路与反馈值进行比较,得到正负脉冲交替的输出信号,其输出信号的瞬时平均值随原始信号变化,低频特性与待调制宽带信号的原始信息也一致,但几乎不存在谐波分量。这2种调制方式都能够对信号的幅度信息进行很好的调制,对于正交频分复用调制 (orthogonal frequency division multiplexing, OFDM) 等时域波形不规则的水声信号,这2种方式能够在驱动发射机的同时严格保存原始波形信息。
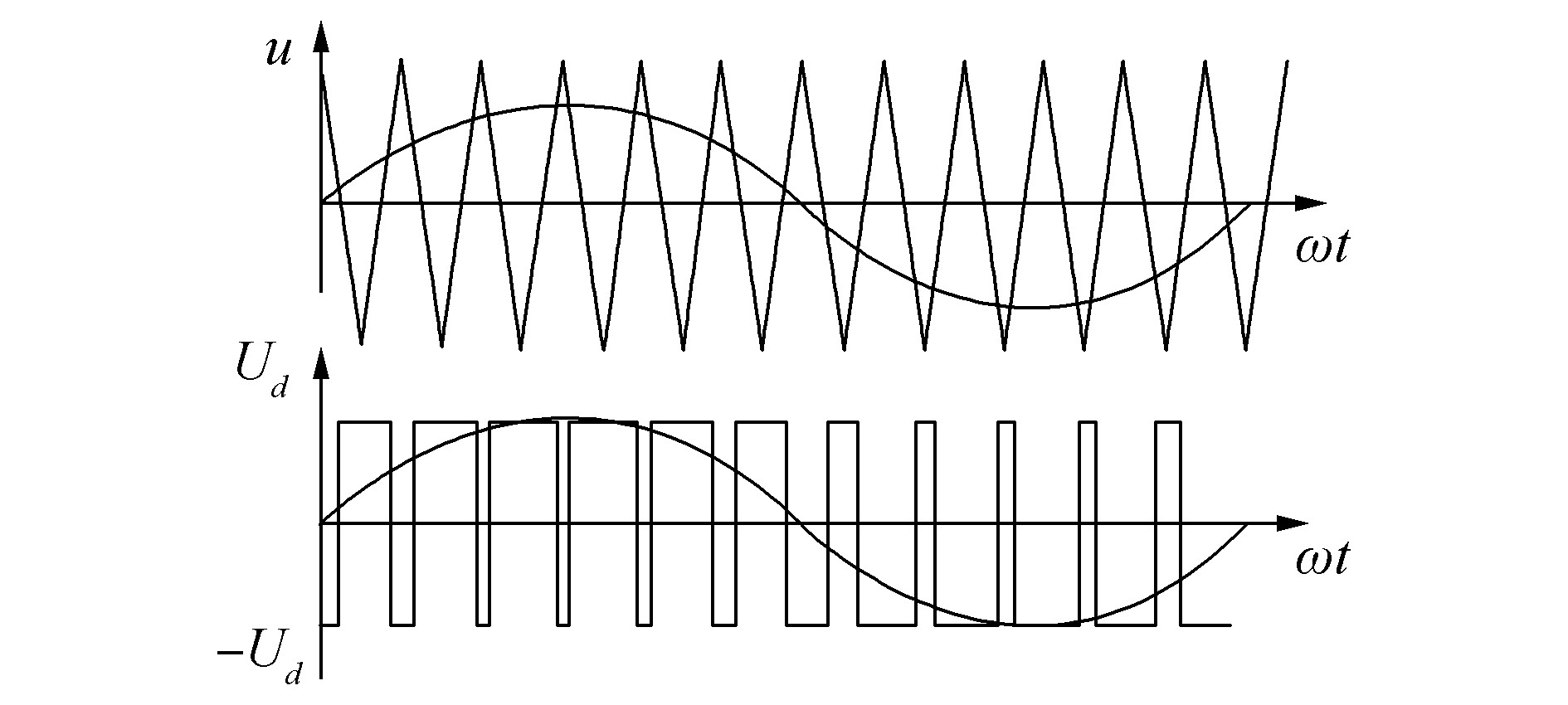
1 基本调制原理 1.1 PWM调制原理双极性PWM调制形成原理如图 1所示,根据三角载波与正弦调制波幅值的比较结果,相应的将输出结果赋值正负电压最大值。双极性控制方法在载波的两个极性范围内变化,得到的SPWM波形,也在两个极性范围内变化。
|
| 图 1 PWM调制原理 |
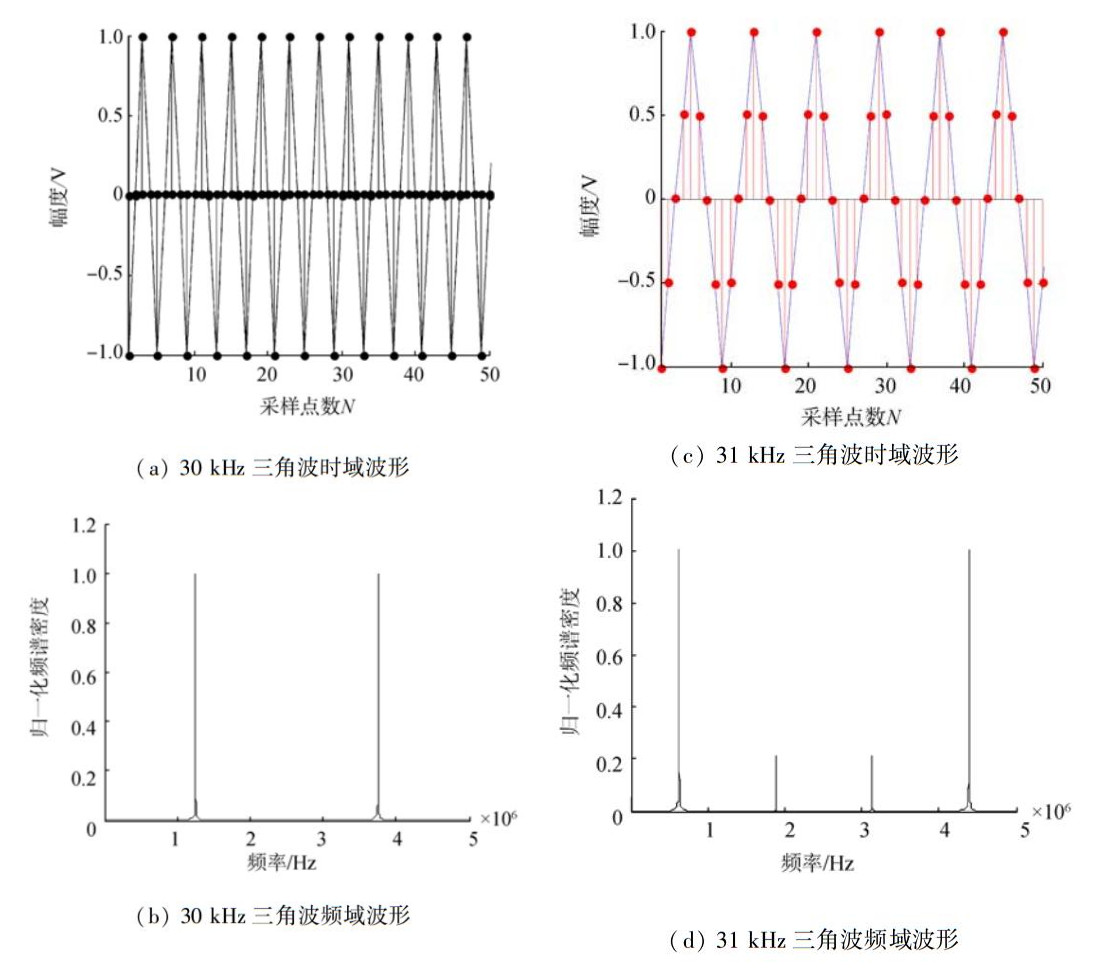
三角波在离散过程中,若保证采样率不变,则可以通过改变三角波的频率控制离散点的位置。图 2表示三角波的不同离散位置及其对应的频域波形,其中,图 2(a)三角波的频率分别为30 kHz,采样点只取到峰谷值以及零值位置;图 2(b)中三角波的频率分别为31 kHz,采样点取到峰谷零值的同时还取到了中间值。这样做是为了保证三角波携带的频率干扰成分尽可能的少,但是不利于保留输入信号的幅度信息。若要求精确恢复原始信号信息,则需将三角波进行更多级量化。
|
| 图 2 PWM调制三角波频率 |
文中未进行讨论时的默认参数取值如表 1所示。
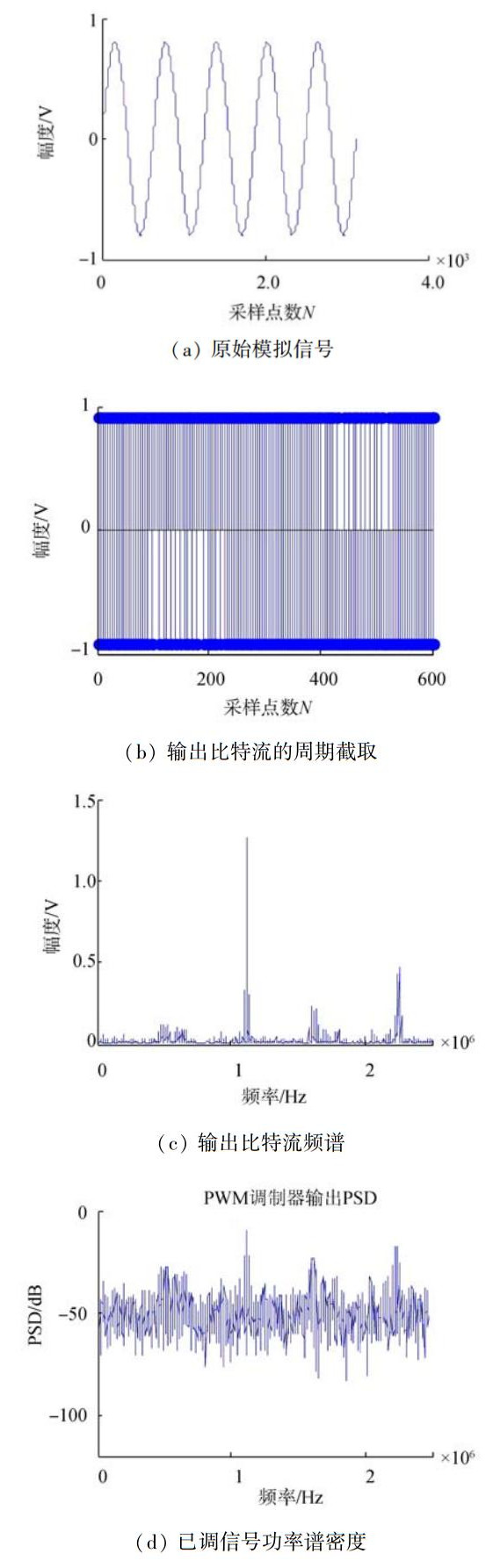
PWM调制效果如图 3所示。PWM调制与D类功放结合时,将引入谐波和非谐波失真,使得带内噪声很大[6]。
|
| 图 3 PWM调制仿真 |
ΣΔ调制利用过采样和噪声整形技术,实现了速度与精度的最优折中[7]。它的基本原理就是通过合理设计系统的传递函数,使信号全通,而噪声被整形为低频衰减、高频放大的形式。其调制框图如图 4所示[8],它在增量调制的基础上通过添加一个离散时间积分器 (传递函数

|
| 图 4 ΣΔ调制系统框图 |
文中的仿真采用基于Boser-wooley模型[9]的二阶调制模型,主要原因:1) 二阶调制模型噪声整形能力提升,能够增加输出信噪比;2) 二阶调制模型能够有效抑制输出频谱中的噪声频谱杂波[10];3) 在不使用级联结构的情况下,二阶调制系统具有较好的稳定性;4) 噪声整形会将高频噪声进行放大,且阶数越大,放大效果越大,过大的调制器阶数会加大能量损失。
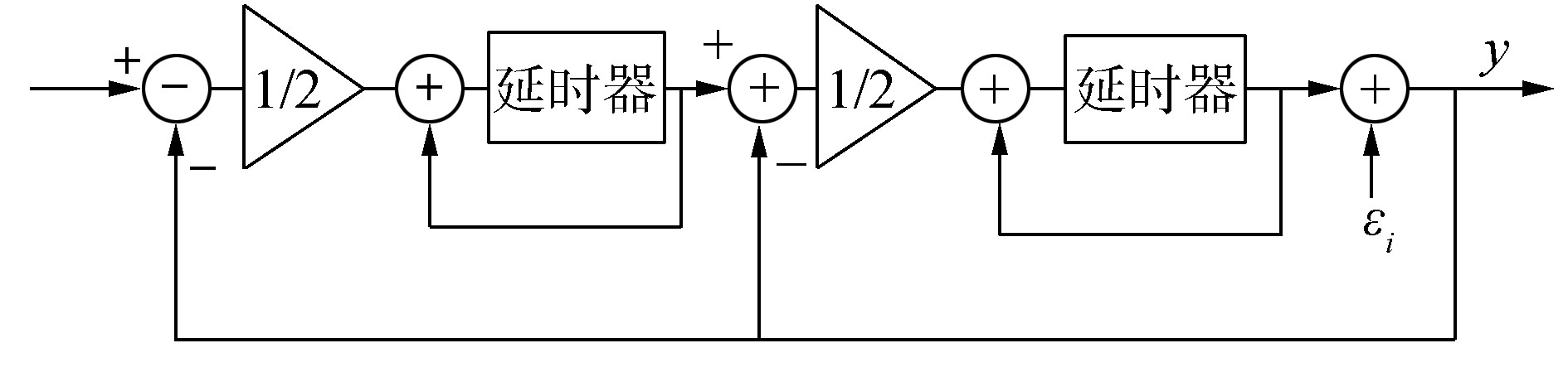
图 5为Boser-wooley模型的等效框图,此时,信号传递函数STF=z-1,噪声传递函数NTF=(1-z-1)2。按此模型对ΣΔ调制原理进行仿真,仿真结果如图 6所示。
|
| 图 5 Boser-wooley模型 |
通过图 3与图 6的对比可以看出PWM调制和ΣΔ调制输出频谱的各自特点。PWM调制输出频谱中含有较丰富的谐波分量,且比较三角波的引入会在固定频率处引入比较明显的频率干扰。而ΣΔ调制的输出频谱中的噪声都被搬移至较高频率处,远离信号频带,但高频处的干扰造成的能量损失也是不容忽视的。与传统PWM调制方式相比,ΣΔ调制的最大优势就是对量化噪声的整形,使我们可以通过比较简单的滤波器设计就能滤除大部分量化噪声,增大输出信噪比[11]。

|
| 图 6 ΣΔ调制仿真 |
调制有效性定义为调制算法对待调制信号能够进行正确调制的能力,衡量标准为能够正确进行调制与解调的归一化输入信号幅度。为方便进行对比,文中信号幅度均包含如下假设条件:ΣΔ调制的反馈回路电压与PWM调制比较三角波幅值电压相同,且输入输出信号均经过此值归一化。
图 7为模拟信号调制和解调的过程图。由模拟输入信号产生1位比特流的过程中,定义输入信号最大幅度Amax为能够正确进行调制和解调的归一化输入信号幅度Asin。

|
| 图 7 调制和解调过程波形图 |
在理论上,矩形信号的能量是同幅度信号的最大值,因此上述2种方法的调制过程都是一个将信号能量最大化的过程。在仿真中,通过理论赋值就能做到这种放大;而在实际电路实现中,增加的能量来自于供电电路。又因为输出比特流为正负电压交替的形式,我们可以认为对于相同长度的离散输入信号,PWM调制和ΣΔ调制的输出比特流含有相同的能量。
定义调制过程中功率增益的概念为调制输出比特流的功率值与原始输入信号的功率之比。对于PWM调制和ΣΔ调制均有如下计算:
正弦波模拟输入信号的功率:
采样后的时域能量表示为
输出比特流功率:
输出比特流能量:
功率增益:
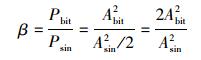 |
(1) |
式中:Asin为输入信号幅值;Abit为输出比特流幅值,本文中默认取值为1 V;N为采样点数;Ts为采样时间。由式 (1) 可以看出,该定义方式的功率增益仅与输入信号幅度和输出信号幅度有关,输入信号的幅值越小,输出比特流幅值越大,则在实现过程中需要外界提供的能量就越大。
2.3 滤波效率与传输有效性按照声呐发射机的工作原理[12],上述调制信号用来驱动D类功放,经功率放大之后的信号仍为正负幅值电压交替形式,只是根据变压器的不同变比和D类功放MOS管管压降的不同,该幅值电压不同。如图 8的功放电路,仍取U′0的归一化的幅度对各信号的滤波效率进行讨论。此脉冲信号与水声换能器相连接,水声换能器和匹配回路可视为天然的低通滤波器,通过匹配电路的硬件设计总能找到合适的电容、电感、电阻组合值使信号在换能器的发送端为不失真的正弦信号。上述调制信号都可通过此低通滤波器后完成信号的发射。传输有效性定义为已调信号放大后能够驱动换能器完成发射的能力,衡量标准为放大后的信号经过匹配网络最终加在换能器两端的功率。

|
| 图 8 功率放大放电路 |
定义滤波效率的概念为调制信号经过滤波网络后获得的有效功率与平均功率的比,即对已调信号进行滤波之后保留下的能量 (功率) 与归一化比特流能量 (功率) 的比值。
通过时域计算:
 |
(2) |
通过频域计算:
 |
(3) |
上述2种调制方式在调制过程中均包含功率放大的过程,在滤波解调的过程中又都包含能量损失的过程。谐波失真度是指输出信号比输入信号多出的谐波成分。它既能作为衡量调制过程线性度的衡量标准,也从另一方面解释了滤波过程中的能量损失的方式。故在对这2种非线性调制过程的性能评估中引入谐波失真指标。谐波失真度的常用计算公式为
 |
(4) |
式中:H为谐波限值,文中取至10次谐波;GH和G1分别为谐波和基波的有效值。文中的调制性能分析更关心的是谐波中能量的分布,故谐波失真度的计算采用频域计算能量的方法。
2.5 线性度与调制精度本设计中定义线性度的概念,表示该调制算法对于输入信号幅度信息的调制精度。输入信号经调制后转化为数字信号,由于PWM调制和ΣΔ调制的输出为1为比特流,且输出信号幅度由比较的结果赋值而得 (在实际电路设计时,有电路的供电电源决定)。采用CIC抽取滤波器[13]转化为多量化信号。将此多位量化信号的归一化幅度值与原始输入信号的幅度值的线性关系作为2种调制方法的线性度衡量标准。
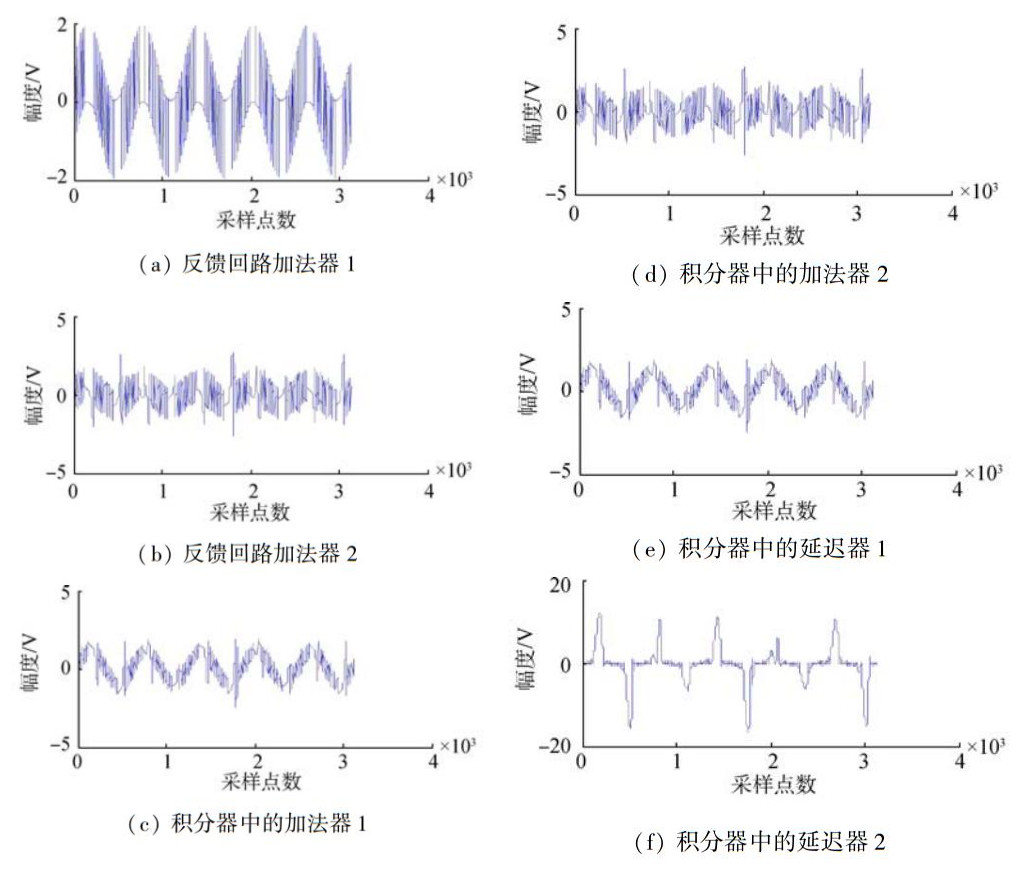
3 仿真结果 3.1 输入信号幅度ΣΔ调制对输入信号幅度存在要求,当输入信号幅度过大时,会导致整个调制系统的不稳定。具体表现为:1) 输出比特流中存在大量的连续1或-1;2) 系统内各个寄存器数据溢出,如图 9所示,横坐标对应采样点数,纵坐标对应幅值;3) 噪声整形效果变差或消失,如图 10所示。对于PWM调制:输入信号归一化幅度为1时,也能够进行正确调制输出。
|
| 图 9 寄存器数据溢出 |

|
| 图 10 输入信号幅度对噪声整形效果的影响 |
对于ΣΔ调制和PWM调制,采用的滤波器设计主要包括两部分,首先是窗函数法设计的FIR数字滤波器,然后是根据实际模拟电路等效模型建立的低通滤波网络, 巴特沃斯滤波器的设计方法见文献[14],换能器等效模型见文献[15]。
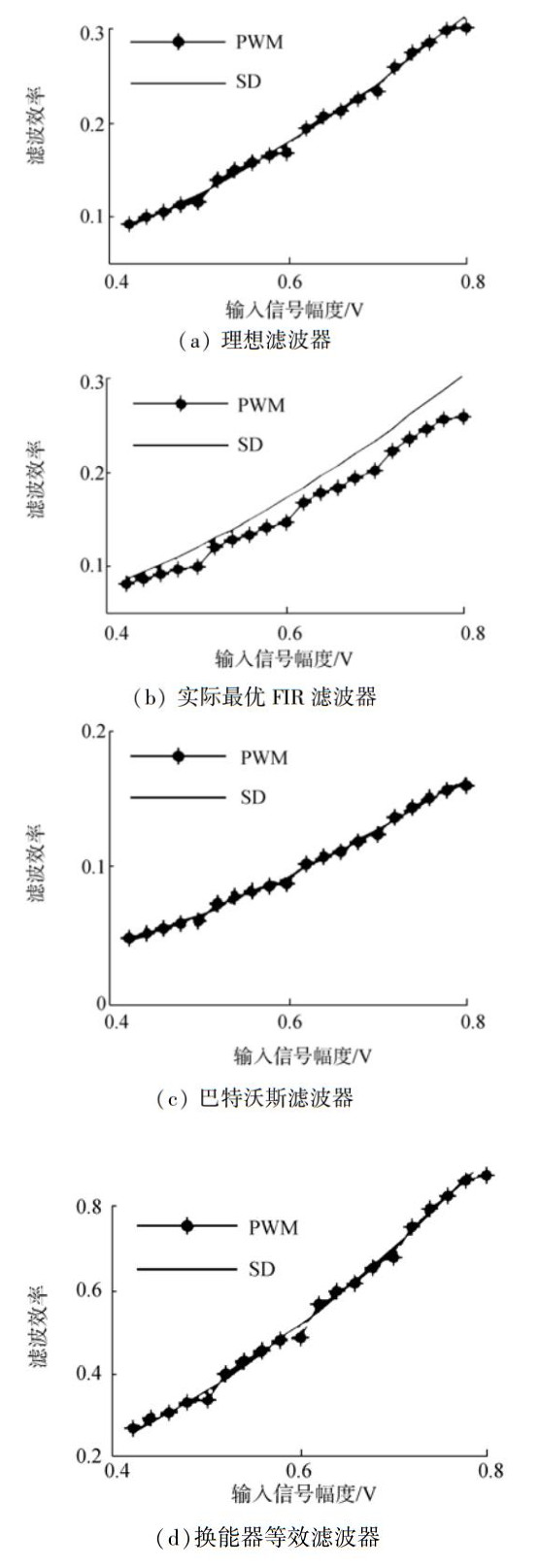
图 11对应2种调制方式在不同滤波器解调过程中的滤波效率。其中图例中的SD调制表示ΣΔ调制。
|
| 图 11 滤波效率仿真结果 |
1) 2种调制方式在滤波解调的过程中都有大量的能量损失掉了,PWM调制能量的损失主要来自于比较三角波引入的固定频率以及调制过程中的谐波分量,而ΣΔ调制的能量损失是来自于噪声整形过程中被推向高频并成倍数放大了的量化噪声。
2) 在理想情况下,PWM与ΣΔ调制的滤波效率基本相同。这是因为同幅度信号经两者调制后信号谱峰所携带的能量相同,理想滤波器滤除信号谱峰外的所有干扰,根据能量守恒定律,两者的滤波效率几乎相同。
3) 使用换能器等效的方法进行的滤波效率仿真结果中,两种调制方式的滤波效率均有增加,这是因为换能器构成的滤波网络引入了谐振回路,相比于FIR滤波器能够将能力更集中于谐振频率处。
4) 在巴特沃斯等效和换能器等效情况下,PWM与ΣΔ调制的效率相差不大,这是因为两者都能通过等效的传递函数实现无用信息的滤除,ΣΔ调制在噪声整形方面存在的优势在实际D类功放结合时并不明显,因为对于信号的大功率输出来说,量化噪声太小了。
5) 效率只是从能量的角度分析了滤波前后的能量损耗,不能作为衡量调制性能的唯一标准。ΣΔ与PWM调制相比,即使在相同效率情况下,信号与噪声的分布也是有差别的。ΣΔ中包含的是相对纯净的信号,而PWM中含有不能完全滤除的谐波分量和量化噪声。
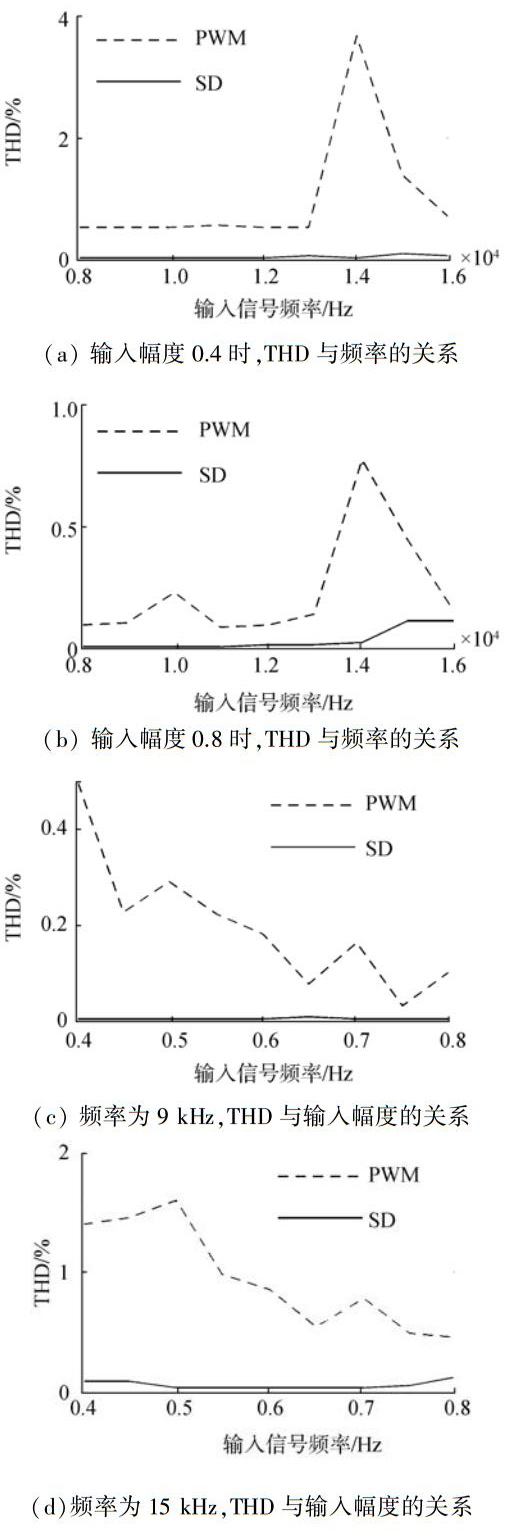
3.3 谐波失真度图 12为PWM与ΣΔ调制谐波失真度 (total harmonic distortion, THD) 的仿真结果,讨论的参数有输入信号的归一化幅度以及输入信号频率。图 12(a)、12(b)为输入信号幅度固定时,THD与频率的关系;图 12(c)、12(d)为频率固定时,THD与输入信号幅度的关系。
|
| 图 12 THD仿真结果 |
由图 12得出以下结论:
1) 输入信号幅度对PWM调制影响较大,而对于ΣΔ调制几乎没有;
2) 输入信号频率对PWM调制存在影响,而对于ΣΔ调制几乎没有;
3) 对于任意能够保证正确调制的输入信号,ΣΔ调制抑制谐波的能力都远远优于PWM调制。
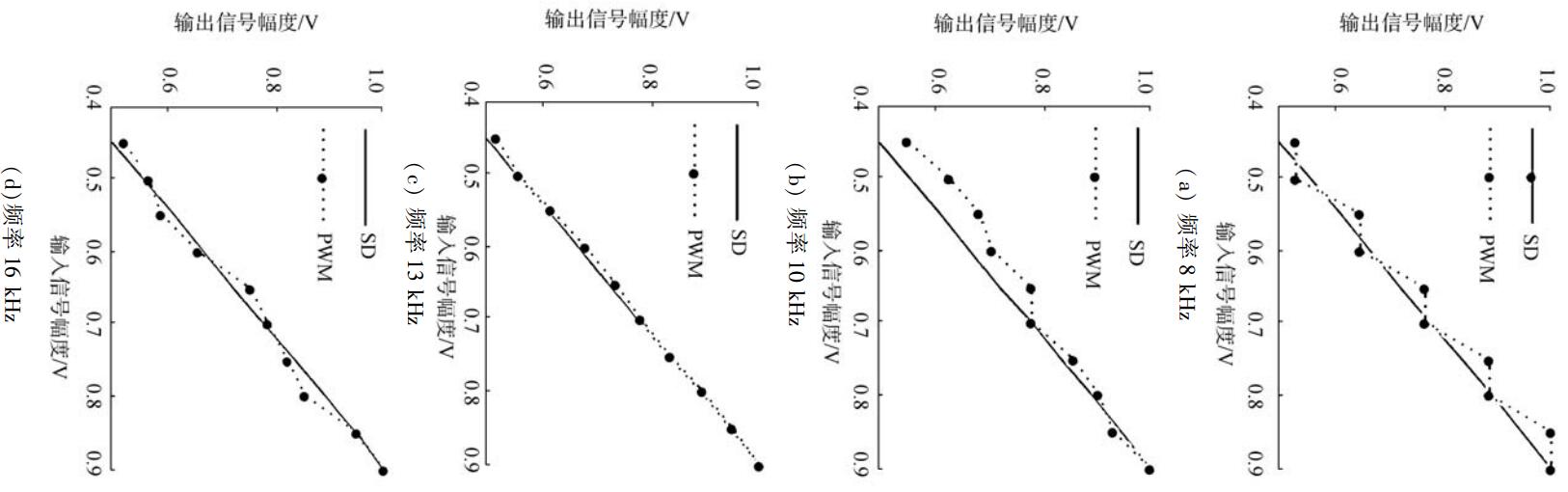
3.4 线性度图 13为输入信号取不同频率时,PWM调制与ΣΔ调制线性度结果仿真图。
|
| 图 13 线性度仿真结果 |
由图 13得出以下结论:
1) PWM调制的线性度与输入信号的频率有关,更确切的说,是与输入信号频率,三角波频率和采样率之间的关系有关;
2)ΣΔ调制在各频率下均有很高的线性度,基于此调制算法的D类功放,可以弥补传统D类功放线性度不高的问题。
4 结论文中从PWM调制和ΣΔ调制的原理出发,通过MATLAB软件仿真,在给出两者的输出比特流及其频谱特性的同时,通过5种衡量调制性能的指标及其计算方法的结果对比,得出结论如下:
1) 对于完成匹配的换能器网络,PWM与ΣΔ调制的具有基本相同的调制电效率;
2) 相比于PWM调制,ΣΔ调制输出比特流的谐波失真度较小,即在输出功率相同的条件下,能够使能量更集中于信号频率;
3)ΣΔ调制的线性度较高,即在保持信号幅度信息上更有优势,与D类功放相结合,更够在保证线性度的同时提高线性度要求;
4) 在对原始信息需要精确恢复的地方要优先考虑ΣΔ调制;
5) 在对精度要求不高的情况下,也可以考虑PWM调制中较少采样点的方式设计发射机。
在实际应用中,应根据系统指标要求,更加理性的选择调制方式,并同硬件电路设计技术相结合,最终实现特定需求的声纳发射系统设计。
| [1] | 田坦, 刘国枝, 孙大军. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000: 5-10. |
| [2] | 陈新国, 程耕国. D类功放输出功率与效率的分析[J]. 声学技术, 2005, 24(4): 265-267 |
| [3] | 宋张, 许建平, 贺明智. Σ-Δ调制在D类放大器中的应用[J]. 自动化信息, 2006(10): 45-46 |
| [4] | 吕泽政. 超短基线定位系统接收与信号处理电路的硬件设计实现[D]. 哈尔滨: 哈尔滨工程大学, 2011: 26-44. |
| [5] | 王永恒. 成像声纳接收和发射单元的设计与实现[D]. 哈尔滨: 哈尔滨工程大学, 2012: 35-39. |
| [6] | FENG Hui, YU Zeqi, HAN Zhigang, et al. System level design of a digital audio class D power amplifier[C]//Proceedings of 2010 Internalional Conference on Multimdia Technology, Ningbo: IEEE, 2010: 1-5. |
| [7] | MALOBERTI F. Data Converters[M]. Dordrecht Netherlands: Springer, 2007: 258-302. |
| [8] | NORSWORTHY S R, SCHREIER R, TEMES G C. Delta-sigma Data Converters[M]. New York: Wiley-IEEE Press, 1996: 6-9. |
| [9] | BOSER B E, WOOLEY B A. The design of sigma-delta modulation analog-to-digital converters[J]. IEEE journal of solid-state circuits, 1988, 23(6): 1298-1308 DOI:10.1109/4.90025 |
| [10] | 马绍宇. 高性能、低功耗ΣΔ模数转换器的研究与实现[D]. 杭州: 浙江大学, 2008: 23-27. |
| [11] | FUJIMOTO Y, RE P L, MIYAMOTO M. A delta sigma modulator for a 1-bit digital switching amplifier[J]. IEEE journal of solid-state circuits, 2005, 40(9): 1865-1871 DOI:10.1109/JSSC.2005.848145 |
| [12] | 徐威. 水声通信发射机设计与实现[D]. 哈尔滨: 哈尔滨工程大学, 2011: 37-60. |
| [13] | 朱国军, 张浩, 张志军. 基于FPGA的CIC滤波器实现[J]. 电子科技, 2006(11): 19-22 DOI:10.3969/j.issn.1009-6108.2006.11.002 |
| [14] | 森荣二. LC滤波器的设计与制作[M]. 薛培鼎, 译. 北京: 科学出版社, 2006: 9-15. |
| [15] | 闵祥国. 一种宽带水声换能器匹配方法的研究[J]. 枣庄学院学报, 2007, 24(5): 31-33 |