并联机构运动学问题包括正解问题与反解问题,运动学问题是并联机构研究的基础,运动学计算在并联机构的工作空间优化、误差分析、速度加速度分析、实时运动控制等方面均有重要作用[1]。由于并联机构结构的复杂性,位置正解过程中需要对多元非线性方程进行求解,因此正解比较复杂。
目前运动学正解求解可分为解析法与数值法两大类。解析解法是对方程式进行降维处理,即利用约束方程消去未知数,使方程成为只含有一个未知数的高次多项式。此方法的具体实现方式有矢量代数法、几何法、矩阵法、对偶矩阵法、螺旋代数法、四元数法等[2]。解析解法优点在于能够得到正解的全部解;缺点在于难度大、通用性差。
目前六自由度并联结构正解多用数值解法完成,方法可分为智能算法求解、基于几何结构或拓扑结构求解、迭代法求解[3]。智能算法求解包括神经网络算法、遗传算法、粒子群算法等,此类方法存在算法复杂、计算精度较低等缺点[4, 5, 6, 7, 8]。利用几何结构或拓扑结构求解的研究相对较少,主要有几何迭代法、拓扑结构分析法等。迭代法求解是应用较广泛的一种数值解法,该方法利用牛顿-拉松迭代对正解问题中的非线性方程组进行求解。该方法通过迭代可以获得较高的求解精度,但是该方法依赖迭代初值的选取。若初值选取不当,则求解的迭代步数会急剧增加,甚至可能导致算法不收敛。董彦良等[9]使用附加位移传感器法与牛顿-拉松迭代法结合的正解方法,能够获得实时正解,并减少了计算量。米士彬等[1]提出了一种新型的雅克比矩阵法,该方法将初始杆长与目标杆长的差值离散化,按照离散化后的杆长值进行迭代计算,该方法的精度取决于离散化的精度。刘玉梅等[10]提出了一种基于齐次变换矩阵数值解的正解算法,该方法利用空间姿态旋转矩阵的正交特性及杆长约束,得到了雅克比矩阵解析总表达式,然后采用牛顿拉松迭代法求解齐次变换矩阵的数值解。 1 并联机构运动学分析
六自由度并联平台结构如图 1所示。平台主要由活动平台、固定底座、伸缩杆及铰链组成。伸缩杆通过铰链分别与活动平台及固定底座连接。铰链多为虎克铰,伸缩杆按动力源划分有电动缸式伸缩杆、液压缸式伸缩杆。平台工作时,通过调整各伸缩杆长度实现对活动平台位置姿态的控制。
 |
| 图 1 六自由度并联平台结构示意 |
为进行并联机构运动学分析,分别建立如图 2所示的2个笛卡尔坐标系。固定底座共有6个铰链,分别编号为S1~S6。现建立与固定底座固连的静坐标系O′-X′Y′Z′,其原点位于静平台铰点外接圆的圆心处,铰点S1与S6位于X′轴正半侧,且沿X′轴对称。活动平台共有6个铰链,分别编号为M1~M6。现建立与活动平台固连的动坐标系O-XYZ,其原点位于活动平台铰点外接圆的圆心处,铰点M1与M6位于X轴正半侧,且沿X轴对称。
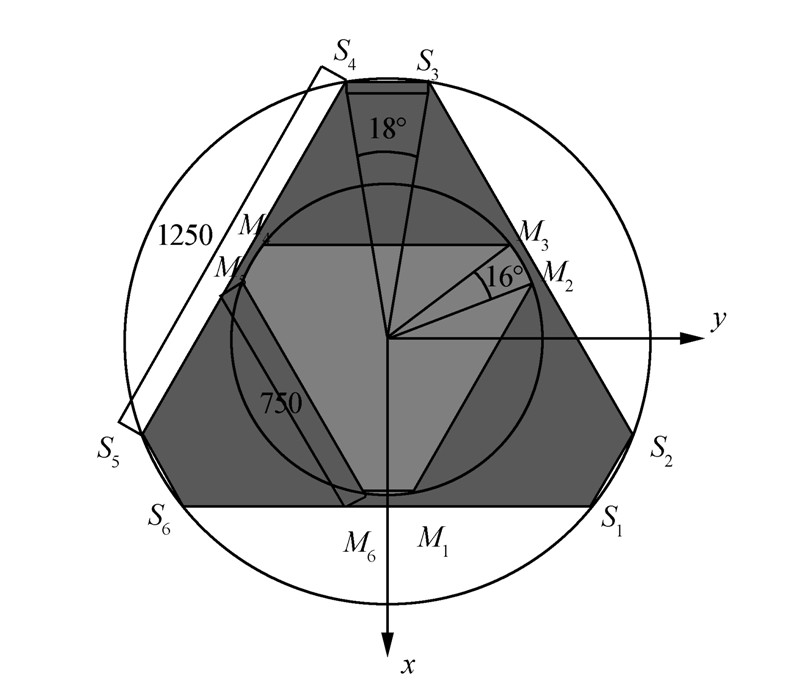 |
| 图 2 坐标系示意图 |
平台位于初始状态下时,各伸缩杆长度相等。动坐标系O-XYZ各坐标轴方向分别与静坐标系O′-X′Y′Z′对应坐标轴方向一致。Z轴与Z′轴重合,均垂直于动平台平面向上。
并联机构运动学反解即根据已知的活动平台的位置姿态,求解各伸缩杆长度。根据杆长条件,可以得到各支杆长度Li为
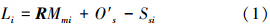
为避免欧拉角旋转矩阵引起的旋转矩阵奇异问题,旋转矩阵R使用RPY角进行描述,其表达式为

牛顿-拉松迭代法是一种常用的非线性方程求解方法,其原理简单,计算过程清晰,因此在六自由度并联机构运动学数值正解中应用较多。牛顿-拉松迭代法求解运动学正解的思路是利用反解得到的杆长逼近目标杆长,最终得到正确的位置正解。其计算流程如图 3所示。
 |
| 图 3 牛顿-拉松迭代法计算流程 |
首先给定目标杆长L,位置姿态搜索原点P0及P0所对应的杆长L0。然后计算得到杆长差ΔL=L-L0以及位置姿态差ΔP=J0ΔL。根据位置姿态差ΔL可求得第一次修正后的位置姿态P1=P0+ΔP。重复上述过程,直至满足迭代完成的条件,则可认为此时求得的第k+1次修正后的位置姿态值Pk+1为目标杆长L所对应的位置姿态值。
牛顿-拉松迭代法尽管有精度高等优点,其缺点也比较明显,如计算量较大、依赖搜索初值的选取等。初值选取不合适时,会导致迭代步数过多,甚至计算不收敛。 2 变搜索原点牛顿-拉松迭代实时正解
并联平台运动时,其末端位置姿态及各个电动缸杆长的变化均是连续的。尽管并联机构正解在其完整的工作空间内存在多解,但是根据运动连续性可知,在一小段连续轨迹所处的较小的工作空间区域内正解只有唯一解。同时,根据牛顿-拉松迭代法的原理可知,若搜索原点与实际解比较接近,则通过较少的迭代步数即可完成求解过程。
在并联平台实际的运动控制中,平台开始工作之前需要完成归零动作,即回到工作空间零位或中位等特殊位置姿态点上,然后以此为起始点完成后续运动。因此,平台运动的起始位置姿态及该姿态所对应的驱动杆长度已知。当平台连续动作时,驱动杆长度可以通过测量或计算得到,而动平台的位置姿态可以通过正解算法计算得到。由于平台的运动控制多为离散控制系统,系统最小时间刻度为伺服周期,该参数多为毫秒级。由于平台自身运动速度限制,当伺服周期足够小时,上一伺服周期平台位置姿态及杆长参数与当前伺服周期内平台的位置姿态及杆长参数很接近,这为变搜索原点迭代法实现运动学正解提供了实现的基础。
变搜索原点迭代法求解原理如下。在tk+1时刻,运动学正解任务是根据当前驱动杆长度Lk+1计算位置姿态Pk+1。在传统牛顿迭代法正解中,以平台零位位置姿态为搜索原点进行正解计算。但在实际应用中,tk+1时刻可以得到上一时刻tk的位置姿态Pk以及对应的驱动杆长度Lk,同时还可知tk+1时刻预期的位置姿态P′k+1以及预期的驱动杆长度L′k+1。若以Pk或P′k+1作为搜索原点进行迭代求解均可减少迭代次数。为了使迭代搜索原点更接近目标解,Lk、Lk+1及L′k+1对位置姿态进行线性插值处理,得到新的搜索原点Pk+1new,并以此为搜索原点进行正解计算。Pk+1new求解表达式为
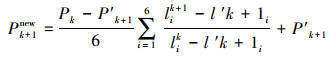
变原点迭代法正解的搜索原点从工作空间零点变为平台运动时上一时刻的位置姿态值,减少了迭代步数,也就是减少了正解计算量,提高了计算效率。当两次计算之间的时间差Δt越小时,则搜索原点位置姿态值与目标杆长对应位置姿态值越接近,计算效率、稳定性及可靠性越高。
迭代法求解需设定收敛条件,文中使用的收敛条件为
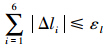
当相邻两次迭代过程中,各驱动杆长度差值绝对值的和小于允许误差时,即判定迭代计算完成。变搜索原点迭代法求正解流程如图 4所示。
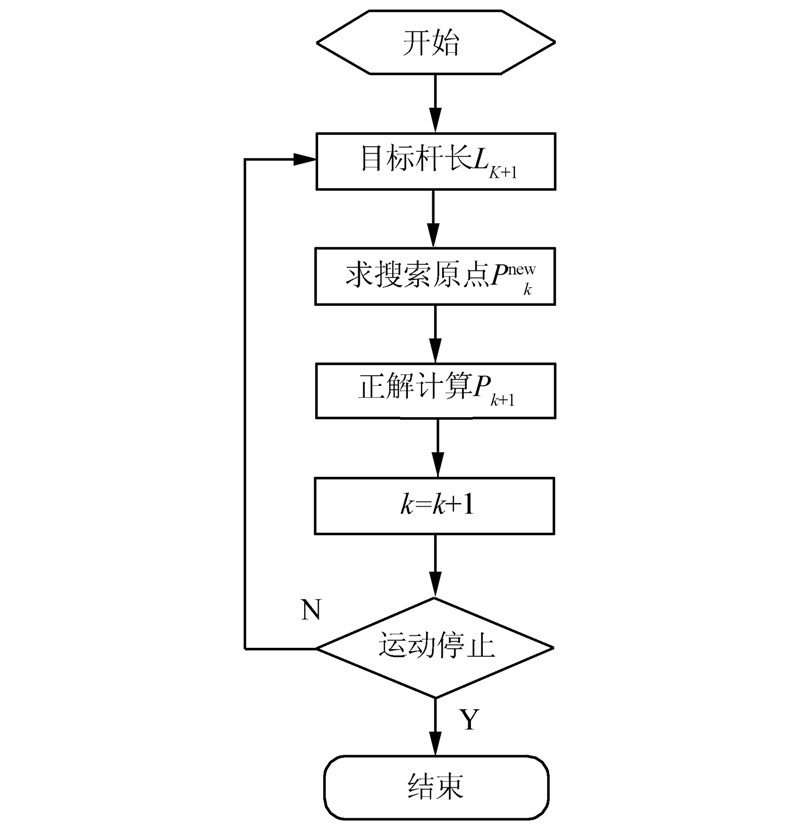 |
| 图 4 变搜索原点迭代法求解流程 |
为验证变搜索原点迭代正解方法的计算效果,从计算精度与计算时间两方面与牛顿-拉松迭代正解方法进行对比。程序使用C语言编写,在Windows XP SP3操作系统下使用Visual Studio2010编译,仿真计算硬件平台为Pentium 4 CPU,内存2 GB。计算时间的测量使用Windows系统自带的高解析度计数器实现。
运动学正解仿真计算按照下面的方式进行。
1)给定动平台位置姿态,通过运动学反解得到电动缸长度。
2)根据电动缸长度,分别使用牛顿-拉松迭代法与变搜索原点迭代法进行正解仿真计算。
3)求正解计算时间及计算误差。计算时间通过软件计时的方式得到。
由于无法通过直接测量的形式获得平台末端位置姿态坐标,因此仿真中将正解计算得到的位置姿态值与给定的位置姿态值进行对比,计算得到正解算法实际误差值。通过比较正解结果与给定的位置姿态值,对计算精度进行评价;通过多次计算后得到的平均计算时间,对计算速度进行评价。
假设动平台自零位启动,绕Z轴做幅值为20°、频率为0.2 Hz转动正弦运动。在所得到的理论轨迹上每隔10 ms取一次位置姿态值进行反解计算得到电动缸长度,然后根据所得电动缸长度数据进行正解计算测试。计算结果如图 5~7所示。
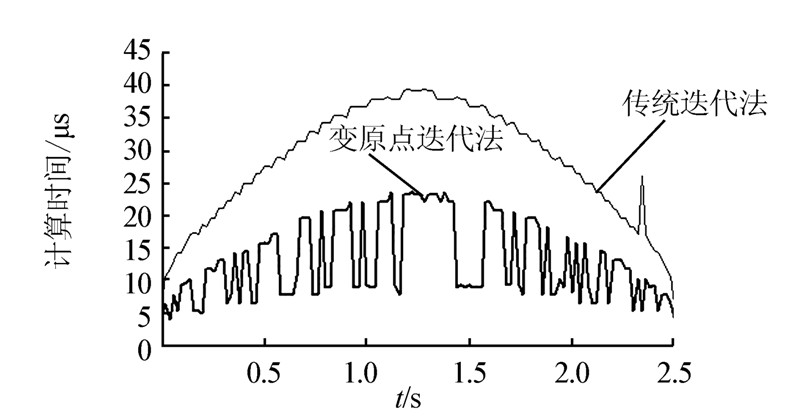 |
| 图 5 正解计算时间 |
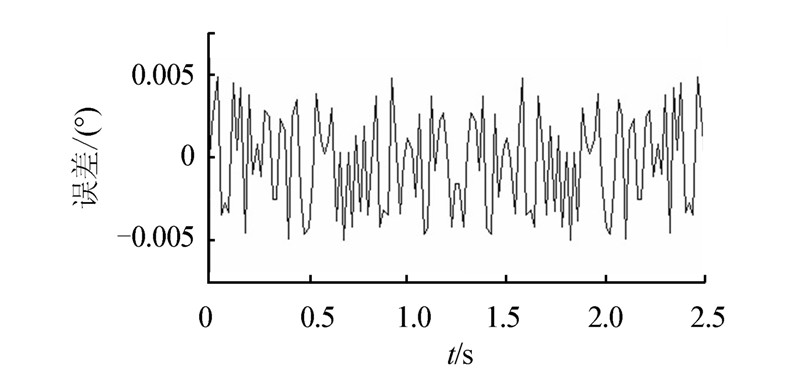 |
| 图 6 牛顿-拉松迭代法正解误差 |
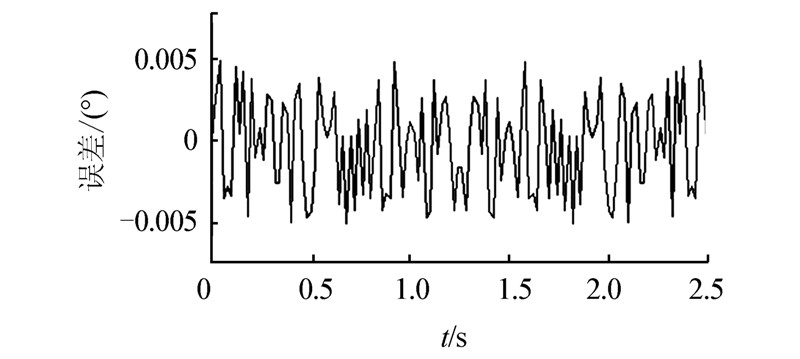 |
| 图 7 变搜索原点正解误差 |
两种计算方法的计算误差基本一致,绕Z轴角度计算误差在±0.05°以内,而其他5个自由度的计算误差在10-5量级内。两种方法的计算时间均有随角度增大而增大的趋势。
但传统方法中,计算时间最长约42 μs,最短约8 μs,而对应的变搜索原点正解方法中,最长计算时间约24 μs,最短计算时间约4 μs。相同的位置姿态点上,变搜索原点位置正解方法的计算时间比传统牛顿-拉松迭代法的计算时间减少约40%。
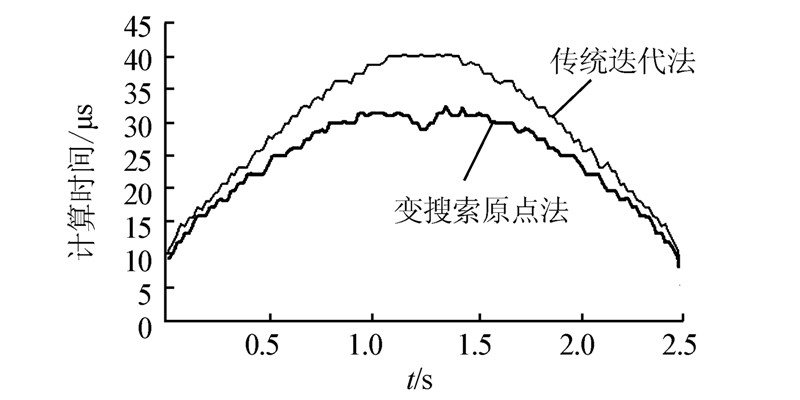
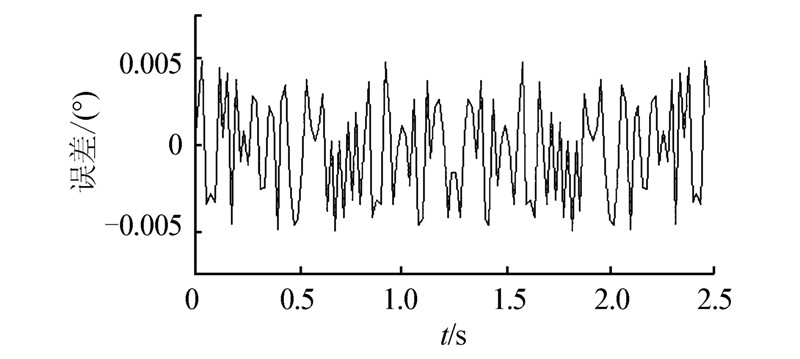
假设动平台自零位启动,绕X、Y、Z轴同时做幅值为10°、频率为0.2 Hz转动正弦运动,沿X、Y、Z同时做幅值为10 mm、频率为0.2 Hz平动正弦运动。在所得到的理论轨迹上每隔10 ms取一次位置姿态值进行反解计算得到电动缸长度,然后根据所得电动缸长度数据进行正解计算测试。计算结果如图 8~10所示。
 |
| 图 8 正解计算时间 |
 |
| 图 9 牛顿-拉松迭代法正解误差 |
 |
| 图 10 变搜索原点正解误差 |
两种方法的求解精度基本一致。其中,3个转动自由度误差曲线重合且均在±0.005°以内;3个平动自由度误差曲线重合且均在±0.005 mm以内。2种方法的计算时间均随运动幅度的增大而增加。牛顿-拉松迭代法正解最长计算时间约42 μs,变搜索原点迭代法正解对应位置姿态点计算时间约为27 μs;牛顿-拉松迭代法正解最短计算时间约8 μs,变搜索原点迭代法正解对应位置姿态点计算时间约为4 μs。变搜索原点迭代法正解计算时间比牛顿-拉松迭代法正解计算时间减少了约30%~40%。 4 结束语
文中对并联平台的运动学正解进行了分析,在已有的牛顿-拉松迭代求正解的基础上,根据平台多为离散控制的实际情况,将变搜索原点的迭代方法用于实时正解。仿真结果表明,求解精度一致的条件下,变搜索原点迭代正解方法较牛顿-拉松迭代方法计算时间减少了约40%。
| [1] | 米士彬, 金振林. 基于雅克比矩阵求解并联机器人位置正解方法[J]. 燕山大学学报, 2011, 35(5):391-395. |
| [2] | 韩方元. 并联机器人运动学正解新算法及工作空间本体研究[D]. 长春:吉林大学, 2011:15-17. |
| [3] | 沈惠平, 尹洪波, 王振, 等. 基于拓扑结构分析的求解6-SPS并联机构位置正解的研究[J]. 机械工程学报, 2013, 49(21):70-80. |
| [4] | AKCALI I D, MUTLU H. A novel approach in the direct kinematics of Stewart platform mechanisms with planar platforms[J]. Journal of mechanical design, 2006, 128(1):252-263. |
| [5] | 郝轶宁, 王军政, 汪首坤, 等. 基于神经网络的六自由度摇摆台位置正解[J]. 北京理工大学学报, 2004, 23(6):736-739. |
| [6] | 谢志江, 冯超, 王成飞. 基于BP神经网络的6-PSS并联机器人运动学正解[J]. 机械设计, 2014, 31(10):36-39. |
| [7] | 车林仙, 何兵, 易建, 等. 对称结构Stewart机构位置正解的改进粒子群算法[J]. 农业机械学报, 2008, 39(10):158-163. |
| [8] | 郑春红, 焦李成. 基于遗传算法的Stewart并联机器人位置正解分析[J]. 西安电子科技大学学报:自然科学版, 2003, 30(2):165-168, 173. |
| [9] | 董彦良, 吴盛林. 一种实用的6-6 Stewart平台的实时位置正解法[J]. 哈尔滨工业大学学报, 2002, 34(1):116-119. |
| [10] | 刘玉梅, 曹晓宁, 王秀刚, 等. 基于齐次变换矩阵数值解的6自由度并联机构位姿正解解算[J]. 哈尔滨工程大学学报, 2013, 34(7):894-898. |



