目前,弹跳机器人领域的研究主要分为2个方向:一是面向实际应用型的弹跳机器人,这类机器人起源于星际探索,在低重力空间中,传统轮式小车摩擦力减小、运动受到限制,而弹跳机器人的性能却得到提高,典型的应用型弹跳机器人如美国密歇根州立大学研制的小型自扶正弹跳机器人[1]和韩国首尔大学研制的跳蚤弹跳机器人[2]等;二是将重点集中于仿生跳跃理论探索的研究,这类机器人多是将自然界的生物运动简化降维至平面运动,利用机构模拟动物身体结构建立有效的数学模型,研究生物连续跳跃运动模式和深入了解平稳跳跃机理。两类研究虽然内容和目标不同,却存在着相似的问题,即跳跃运动具有爆发性和灵活性的优点的同时,也存在驱动功率要求高和自身负载小等技术难点。以往的研究中机器人的驱动方式主要有:1)电机驱动。如美国俄勒冈州立大学Jesse A.G等[3]以人为原型设计和制造了包含弹簧腿的机器人ATRIAS1.0,但由于受制于电机功率,机器人自身重量、负载和能源供给都成为机器人实用化的障碍;2)液压驱动。如日本Tohoku大学研制的Kenken[4]模仿狗腿关节,利用2个液压驱动器实现肌肉功能,液压驱动能够很好地满足跳跃高驱动功率的要求,但需要外接液压源;3)气动人工肌肉。如日本东京大学研制的双足机器人Mowgli[5],气动人工肌肉同液压驱动相似,机器人自身负载难以满足将动力源安装在机器人本体上。
为了提高机器人弹跳爆发力,同时减小驱动系统自重、提高机器人负载能力,一些研究机构采用了电机加弹性元件通过蓄能方式驱动系统的方案,此类研究大多集中在多连杆闭链的机构中,如西北工业大学研究的闭链式六杆机器人[6]和哈尔滨工业大学研究的仿青蛙跳跃机器人[7]。闭链弹跳机器人一般采用单自由度机构,能够完成稳定的跳跃;而青蛙腿部的开链式多连杆结构动作幅度更大,跳跃性能更好。本文以弹簧被动驱动的多连杆仿蛙跳跃机器人为研究对象,建立起跳阶段的多刚体动力学模型,得到了弹簧驱动下机器人的运动规律。
1 仿蛙机器人机构组成与运动原理本文的研究对象是一种含有弹性储能机构的仿蛙跳跃机器人,仿蛙机器人采用弹性储能驱动方案具有驱动功率高、爆发性好的优点,同时模仿青蛙的腿部生理结构及以青蛙起跳过程关节角度轨迹为灵感,利用仿生四连杆和同步带传动机构设计了铰接的多连杆弹跳后腿,如图 1所示。仿蛙机器人弹跳后腿是由脚掌、小腿、大腿和躯干4部分组成,传动连杆、大腿、小腿和躯干组成的四连杆机构使髋关节和膝关节联动,膝关节和踝关节间利用同步带传动。
 |
| 图 1 仿蛙机器人结构模型 |
机器人采用电机带动弹簧储能的方式实现小功率电机驱动的目的,起跳前,机器人首先进行储能:在大腿与躯干间和大腿与小腿间均安装有储能弹簧,电机安装在躯干上,并通过齿轮传动系统带动曲柄回转,回转曲柄与传动轴间装有单向轴承,当单向轴承正向受力时能够通过储能拉索拉动大腿向前摆动为弹簧储能,当曲柄回转到最前点时,弹簧拉伸达到最大位置,完成储能。回转曲柄转动到最前点是单向轴承受力方向转变的临界点,当曲柄继续回转时,单向轴承将工作在分离状态,曲柄与传动轴间约束解除,储蓄的弹簧能量触发释放完成起跳。
2 机器人起跳阶段运动学分析 2.1 仿蛙机器人的运动学模型仿蛙机器人的运动学模型如图 2所示,图中mi(i=1,2,3,4)表示各连杆质量,各连杆均铰接,假设起跳过程中脚掌与地面间不产生滑动,将后肢趾尖与地面间视为铰接的欠驱动关节,前肢主要作用为起跳阶段支撑相支撑和落地减震,起跳瞬间已经离地,因此可以将前腿、电机和传动机构等的质量及转动惯量叠加到躯干当中,忽略轻质连杆E1E2质量。
 |
| 图 2 仿蛙机器人机构模型 |
建立以地面上的一点O为原点,水平方向为X轴,垂直方向为Y轴的笛卡尔基坐标系。起跳过程中,机器人绕脚趾尖端A点转动,用D-H方法建立下关节设置的坐标系,如图 2所示。记坐标原点O与A点距离为lA,连杆i的长度为li、质量为mi、转动惯量为Ii(i=1,2,3,4),各连杆质心位置为lCi,相邻两连杆关节夹角为θi,连杆与地面间夹角坐标为qi,以逆时针为正。
qi和θi存在如下关系:
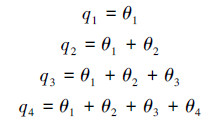
定义方向余弦矩阵[8]:
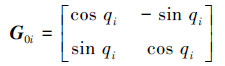
根据机器人机构学[9]坐标变化方法,可以得到各连杆质心绝对位置矢量rCi,质心矢量构成的向量可表示为
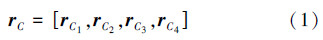

机器人各连杆质量之和为m,则总质心位置可表示为
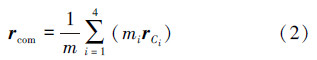
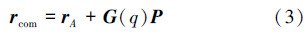
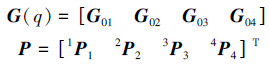
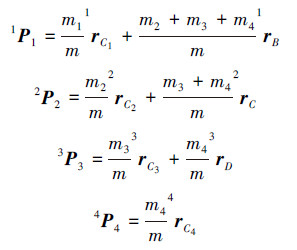
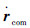 :
:
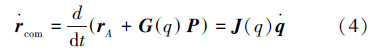
式中质心速度雅可比矩阵
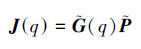
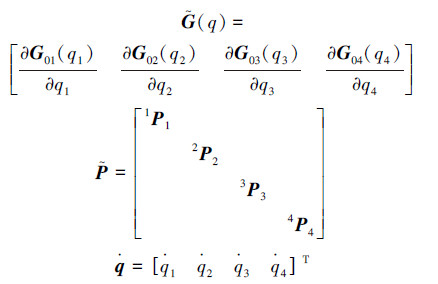
总质心速度 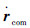 是广义变量q和
是广义变量q和 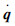 的函数,将式(4)对时间t求导,可以得到总质心加速度矢量:
的函数,将式(4)对时间t求导,可以得到总质心加速度矢量:

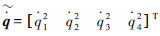 。
3 起跳阶段动力学分析
。
3 起跳阶段动力学分析
前文中建立了机器人起跳的运动学模型,得出了关节角度和质心轨迹间的函数关系;为了求解机器人在弹性元件驱动下的质心运动轨迹,一般采用拉格朗日方法来处理此类动力学正问题。
3.1 建立拉格朗日方程根据动力学普遍方程,系统的动力学方程可以用拉格朗日函数表示成:
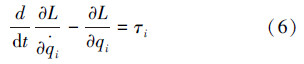
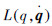 定义为系统的总动能K与总势能V之差,即
定义为系统的总动能K与总势能V之差,即 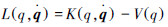 ;τi为关节输入力矩。
;τi为关节输入力矩。
由于弹簧驱动的弹跳机器人起跳过程中没有主动输入力矩,所以拉格朗日方程右边关节力矩τi为零向量,求解拉格朗日方程关键是求解系统动能与势能。
3.2 机器人系统动能机器人系统动能是由各连杆平移动能和旋转动能组成的,机器人机构模型的总自由度为2,取脚掌与地面间的夹角θ1和踝关节角度θ2为广义坐标,求解机器人系统总动能K:
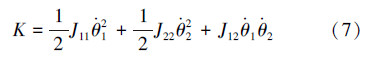
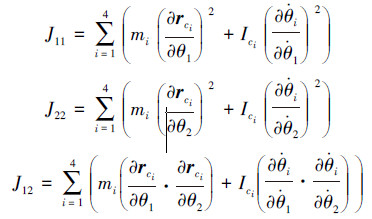
机器人机构如图 2所示,膝关节与踝关节用一组同步带相连,两关节具有如下关系:
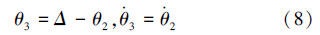
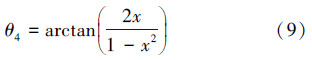
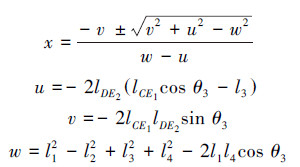
为了简化计算过程,节省求解时间,用三次曲线拟合θ3与θ4的关系式,得到的方程为
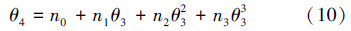
机器人起跳过程中,系统势能包括2部分:一是系统的重力势能VG;二是蓄能弹簧的弹性势能VP。
取地平面为重力势能零点,系统重力势能为

储能弹簧安装在关节轴上,系统的弹性势能只与广义坐标θ2有关,弹性势能的表达式为
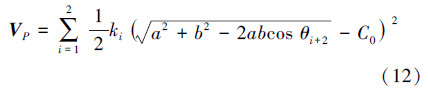
机器人完成起跳瞬时,脚掌与地面间作用力为0,所以机器人完成起跳的时间判断条件可以表达为

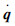 >0。
>0。
将式(13)代入式(5)得关节空间起跳判断条件:
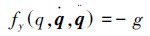
将式(8)~(12)代入式(7)中,并根据文献[8]中的化简方法,将拉格朗日方程化简成如下形式:
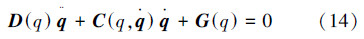
 :
C为科氏矩阵:
:
C为科氏矩阵:

G为势能向量,包括重力势能VG和弹性势能VP:
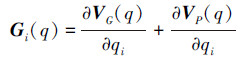
利用MATLAB中的ODE45函数对式(14)进行求解[11, 12],计算过程中使用的机器人结构参数和机器人储能结束后准备起跳的初始位姿如表 1所示,当数值迭代达到起跳完成判断条件时停止计算。
| 连杆序号 | 质量mi/kg | 杆长li/mm | 初始角度θi/(°) | 转动惯量ICi/(kg·mm2) |
| 1 | 0.119 | 90 | 155 | 123 |
| 2 | 0.102 | 90 | 215 | 100 |
| 3 | 0.157 | 90 | 145 | 396 |
| 4 | 1.161 | 220 | 210 | 3 667 |
| 注:g=9.8 m/s2,C0=24 mm,k1=k2=7 N/mm。 | ||||
求解得出的关节转角坐标θ1,θ2, 的变化规律曲线如图 3所示。
的变化规律曲线如图 3所示。
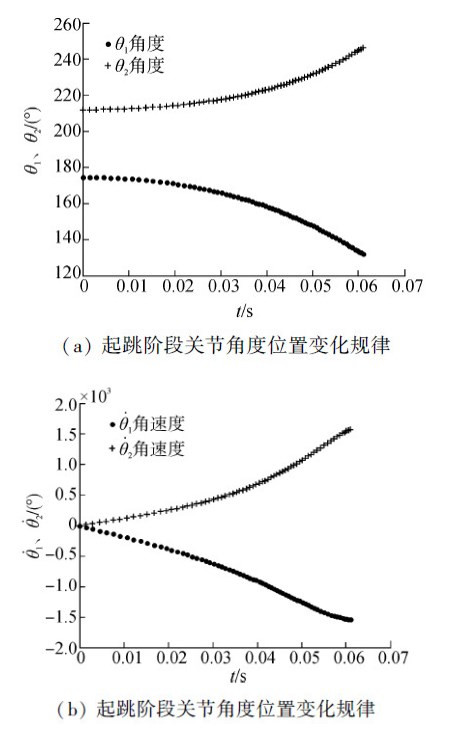 |
| 图 3 变化规律曲线 |
将求解出的广义坐标变量数值矩阵代入到式(1)~(5)中,可以得到机器人起跳阶段的质心运动轨迹和质心速度,如图 4所示。
 |
| 图 4 MATLAB数值求解结果曲线 |
为检验理论建模及数值求解的合理性和有效性,将机器人系统的三维模型导入ADAMS中进行动力学仿真,图 5为机器人仿真起跳步态。最后将ADAMS仿真得出的起跳质心轨迹提取出来,输入MATLAB与理论求解得出的质心轨迹进行比较,如图 6所示。通过曲线对比,可以看出动力学求解得出质心轨迹与仿真得出的质心轨迹相近,由于理论计算中未考虑系统关节摩擦等因素,产生少量误差是合理的,从而可以证明动力学分析的有效性。
 |
| 图 5 ADAMS仿真起跳步态 |
 |
| 图 6 ADAMS仿真与MATLAB数值计算质心轨迹对比 |
仿蛙机器人是一种储能弹簧驱动的间歇式跳跃机器人,具有起跳爆发力强、自身质量小和不受电机功率限制等优点,能够实现稳定跳跃运动的仿蛙机器人在侦察、探测和抢险救灾等领域有着广阔的应用前景。然而,仿蛙机器人起跳阶段属于被动弹跳的机械装置,其多关节动力学耦合和趾尖欠驱动的特性使得起跳运动分析变得更加复杂。
本文利用D-H方法建立了仿蛙机器人起跳阶段的运动学模型,在运动学模型基础上分析了固定机构参数和初始姿态下的仿蛙机器人起跳阶段的动能和势能,根据多刚体动力学理论建立了拉格朗日方程,并利用MATLAB中ODE45函数进行了数值求解,得出了起跳阶段的关节轨迹、质心轨迹和质心速度,并ADAMS动力学仿真验证了求解结果的正确性。
文中建立的动力学模型能够求解任意初始位姿下的起跳速度和质心位置,反之当预期起跳目标确定时可以定量的设置初始位姿及机构参数。另外,本文中得到的起跳速度参数为仿蛙机器人腾空跳跃轨迹规划提供了研究基础。
| [1] | ZHAO Jianguo,XU Jing,GAO Bingtuan,et al.MSU jumper:A single-motor-actuated miniature steerable jumping robot[J].IEEE transactions on robotics,2013,29(3):602-614. |
| [2] | KOH J S,JUNG S P,NOH M,et al.Flea inspired catapult mechanism with active energy storage and release for small scale jumping robot[C]//Proceedings of IEEE International Conference on Robotics and Automation(ICRA).Karlsruhe,Germany,2013:26-31. |
| [3] | GRIMES J A,HURST J W.The design of ATRIAS 1.0:a unique monopod,hopping robot[C]//Proceedings of the 15th International Conference on Climbing and Walking Robots and the Support Technologies for Mobile Machines.Baltimore,USA,2012:548-554. |
| [4] | HYON S H,EMURA T,MITA T.Dynamics-based control of a one-legged hopping robot[J].Proceedings of the institution of mechanical engineers,part I:journal of systems and control engineering,2004,217(2):83-98. |
| [5] | NⅡYAMA R,NAGAKUBO A,KUNIYOSHI Y.Mowgli:a bipedal jumping and landing robot with an artificial musculoskeletal system[C]//Proceedings of IEEE International Conference on Robotics and Automation.Roma,Italy,2007:10-14. |
| [6] | 柴辉,葛文杰,杨方,等.闭链式弹跳机器人起跳阶段动力学分析[J].华中科技大学学报:自然科学版,2012,40(11):17-21. |
| [7] | 王猛.仿青蛙跳跃机器人的研制[D].哈尔滨:哈尔滨工业大学,2009:37-49. |
| [8] | 陈恳,付成龙.仿人机器人理论与技术[M].北京:清华大学出版社,2010:23-41. |
| [9] | 熊有伦,唐立新,丁汉,等.机器人技术基础[M].武昌:华中科技大学出版社,1996. |
| [10] | 张纪元.机构分析与综合的解[M].北京:人民交通出版社,2007:59-60. |
| [11] | BOGDANOV A.Optimal control of a double inverted pendulum on a cart.Technical Report CSE-04-006[R].Department of Computer Science and Electrical Engineering,OGI School of Science and Engineering,OHSU,2004. |
| [12] | 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].2版.北京:清华大学出版社,2008:230-242. |



