做为大型高精密仪器,太空可展开天线具有反射面精度、收纳率、展开刚度等一系列特有的工作性能指标。只有在这些性能指标均满足指定要求的情况下,天线才能在太空正常工作[1, 2, 3, 4],而通过优化设计来合理地给定天线的结构参数是实现上述目标最为行之有效的方法。
文中所研究的可展开天线整体结构形式如图 1所示。其中,天线的索网体系由48片结构形式相同并且呈辐射状分布的索网结构组成,它主要用于形成天线的反射面系统,并且两端分别与周边桁架和中央圆筒相连。该索网体系的具体结构形式如图 2所示。
 |
| 图 1 可展开天线整体结构 |
 |
| 图 2 天线索网体系 |
当索网结构中所有上弦索节点的初始坐标位置均处于理想抛物线上时,在对结构施加初始预张力后,上弦索节点在张力的作用下将偏离其原来的理想位置而导致结构表面精度下降。因此,若希望在初始预张力已经确定的情况下进一步提高结构的表面精度性能,则可以通过形状优化的方法来给出更为合理的上弦索节点初始坐标位置,从而使平衡态时的上弦索形状更接近理想抛物线,以达到提高表面精度的目的。同时,由索单元切线刚度矩阵表达式可知,索单元节点的坐标位置也是影响单元切线刚度矩阵的因素之一。因此,基于以上考虑,文中将上弦索节点的初始坐标位置作为索网结构优化计算中的设计变量来研究它对结构性能的影响规律。
1 优化参数的设定由于可展开天线索网体系是带有几何非线性特征的柔性结构,而且其结构形式复杂,单元数目众多,难于整体优化分析和设计,因此,为了便于研究,文中将具有相同结构形式的单片辐射索网结构作为子结构先行分离出来进行分析,以实现由简到繁、由局部到整体的优化设计思路。
提取出的单片辐射索网结构的有限元模型如图 3所示。该模型采用两节点直杆索单元建立,图中标号1~36为节点号,θ1和θ2分别为上弦索单元K1、K2与水平方向所成夹角。结构中的上、下弦索沿中轴线对称分布,它们均由17个索单元平滑连接组成;而中间纵向索则是由在对称节点位置连接上、下弦索的16个竖直方向的索单元组成;整个单片索网结构共包含50个索单元。
 |
| 图 3 单片辐射索网结构 |
可展开天线能够正常工作的首要前提是确保其电性能达到预定要求。由天线设计理论中的Ruze公式可知,当天线反射面为理想设计曲面时,反射后的电磁波在其口面上会处于等相位状态,而在这种理想情况下天线增益将不会有所损失。但实际上,天线反射面在外界载荷或结构内力的影响下必然会产生变形,这一变形将会使天线口面不再是等相位面从而引起电磁波的路程差(或称光程差),并导致天线增益下降[5, 6, 7]。考虑到天线反射面变形程度对其工作性能的重要影响,文中将上弦索的表面精度作为单片辐射索网结构的优化设计性能指标之一,该指标能够较好地反映上弦索实际形状与理想抛物线的变形偏差情况。
另外,由于天线在太空展开和工作时都必然会遇到振动的情况,故需要尽量提高结构基频,使其远离激励(卫星姿态调整或变轨)频率,从而避免谐振现象对天线的破坏,确保天线结构的动力性能。因此,文中以单片辐射索网结构的基频作为优化设计的另一个性能指标。
在优化设计变量方面,如前文所述,将上弦索节点的初始坐标位置作为索网结构形状优化中的设计变量。需要指出的是,如果从索网结构的生产制造实际情况出发,则优化上弦索节点初始坐标位置实质上就是对上弦索单元和中间纵向索单元原始索段长度的优化调整。
由于单片辐射索网结构的表面精度是根据上弦索单元节点平衡态时的纵坐标值与其在理想抛物线上的纵坐标值之间的偏差计算得出的,因此,为避免过多的设计变量数目给优化计算带来不利影响,文中仅将上弦索节点初始纵坐标值相对于理想位置的变化量作为优化时的设计变量;在优化迭代计算时只需将这一变化量与节点在原来理想位置时的纵坐标值相加得到新的节点初始纵坐标值。另外,因为索网结构上弦索单元共包含18个节点,而左右两端的2个节点又为固结点,故此处节点纵坐标变化量的数目共有16个。
2 以表面精度为目标函数时的优化计算分析以表面精度最小为目标函数,以16个上弦索节点纵坐标变化量为设计变量,可以建立如下优化数学模型:

图 3所示的单片辐射索网结构为优化对象进行优化计算时,索网结构的索材料设为芳纶纤维材料,其单元弹性模量和密度分别取为1.24e11 N/m2和1.45e3 kg/m3;优化计算时将索单元初始预张力值均取为50 N,索单元半径值均取为1 mm。在确定设计变量取值范围方面,由于索网结构需具有反向双曲结构形式,这样就要求节点纵坐标的变化范围不能设的太大而使上弦索出现直线或与原方向相反的弯曲结构形式。为此,在进行了一些试算的基础上,文中将上弦索节点纵坐标变化量取值的上、下限分别设为1 mm和-1 mm,优化计算时16个设计变量的初始值均取为0 mm,此时上弦索的初始位置将正好处于理想抛物线上。
采用序列二次规划法[9, 10, 11, 12]对优化模型进行求解,得到的优化结果如图 4所示。其中,表面精度最优值为0.011 53 mm,它与计算初始值0.086 18 mm相比下降了86.62%;另外,此时的基频值为4.303 25 Hz。表 1列出了在最优解处设计变量的具体取值情况。
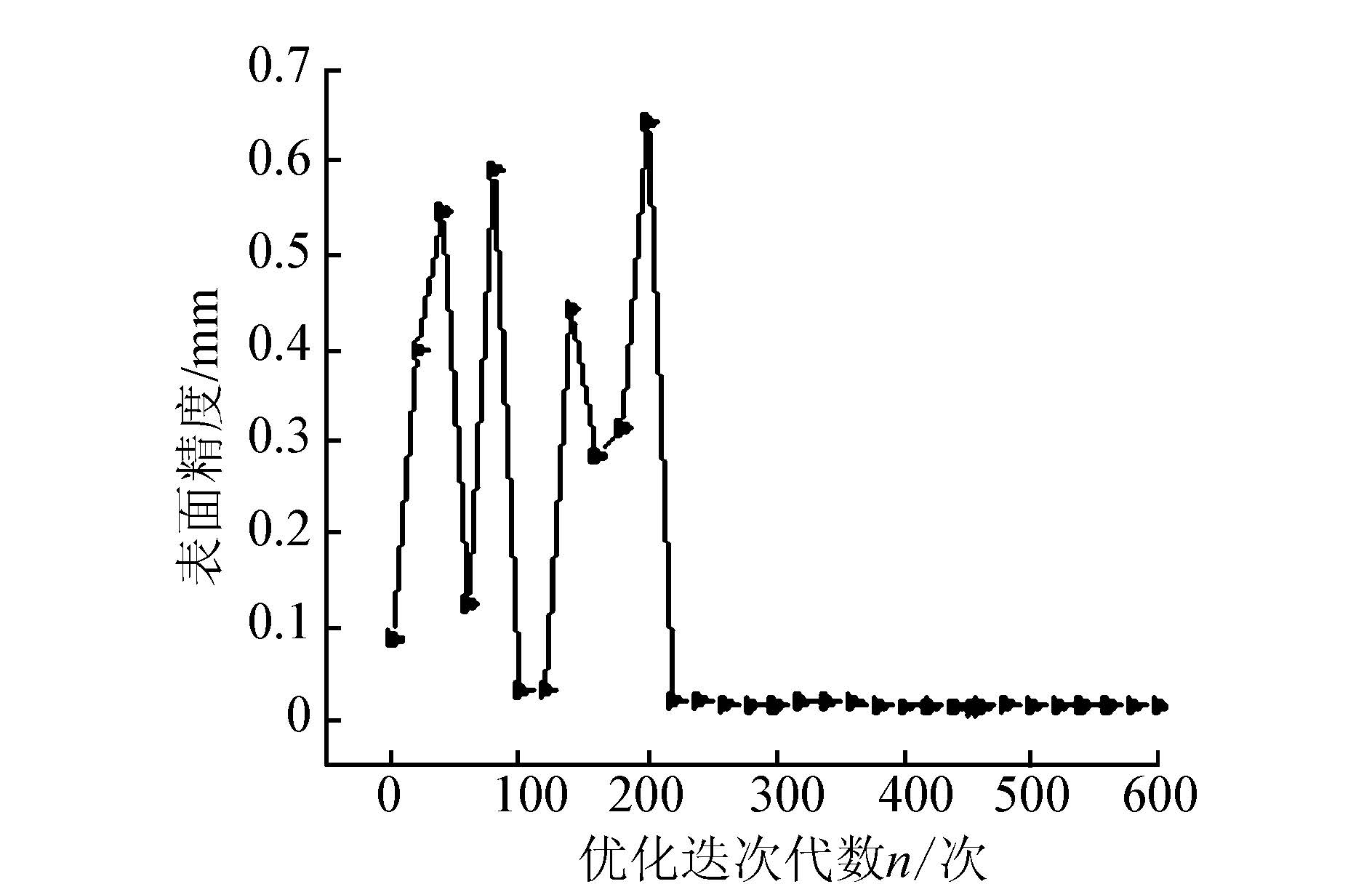 |
| 图 4 表面精度在优化迭代计算中的变化情况图 |
| 上弦索节点号 | 纵坐标变化量Δz/mm | 上弦索节点号 | 纵坐标变化量Δz/mm |
| 2 | -0.004 258 | 10 | 0.021 160 |
| 3 | -0.015 370 | 11 | 0.033 460 |
| 4 | -0.042 490 | 12 | 0.088 490 |
| 5 | -0.036 420 | 13 | 0.108 500 |
| 6 | 0.042 900 | 14 | 0.168 100 |
| 7 | -0.035 840 | 15 | 0.219 600 |
| 8 | -0.007 770 | 16 | 0.278 400 |
| 9 | 0.014 440 | 17 | 0.307 900 |
由表 1可知,在最优解处上弦索节点纵坐标变化量的大小与其所在的索单元同水平方向夹角的大小有关,与水平方向夹角大的单元节点的纵坐标变化量也相应较大。这是因为当以表面精度为优化目标时,优化计算的作用实质上就是相对于理想位置预先给上弦节点一个变形量,以使变形后的上弦索形状能够尽量与理想抛物线重合,因此,优化得到的节点纵坐标变化量实际上反映的是各节点受力后偏离其原位置的程度。因为在初始预张力的作用下,与水平方向夹角大的索单元在竖直方向获得的分力相应较大,故该单元上的节点在纵坐标方向上的变形量也较大,因此最优解处得到的节点纵坐标变化量会随着节点所在单元与水平方向夹角的增大而增大。
另一方面,在整个优化计算过程中结构基频值的变化很小,由此可知,当以节点坐标位置为设计变量时,可以实现在不影响结构的动力性能的前提下对表面精度进行优化设计。
国内相关研究机构已对可展开天线中的索网结构进行了较长时间的研究,在已有的较为成熟全面的研究中,文献[8]以可展开天线中索网单元的预张力为设计变量进行了天线结构的优化设计,取得的优化结果中索网表面精度值为2 mm左右,且优化计算中基频值受设计变量的影响非常大,这导致优化目标受基频变化的影响难以得到更理想的最优解;文献[13]以可展开天线中纵向索单元的长度为设计变量对天线索网结构进行了优化设计,取得的优化结果中索网表面精度值也为毫米量级,且基频值受设计变量的影响同样很大。与这些研究相比,文中取得的优化结果中,索网结构表面精度值为0.011 53 mm,且以文中提出的形状优化方法进行优化计算时,结构基频变化很小,这将能为可展开天线整体性能优化计算提供更有利的优化手段。
3 以基频为目标函数时的优化计算分析以结构的基频最大为优化目标,以16个上弦索节点纵坐标变化量为设计变量,可以建立以下优化数学模型:
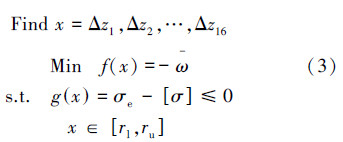
采用与上一节相同的参数设置以及计算方法来求解上面的优化模型,得到的优化结果如图 5所示。其中,最大结构基频值为4.304 22 Hz,它与计算初始值4.303 29 Hz相比提高了0.021 61%;另外,此时的表面精度值为0.857 2 mm。表 2列出了在最优解处设计变量的具体取值情况。
 |
| 图 5 基频在优化迭代计算中的变化情况 |
由表 2可知,最优解处上弦索最右端节点的纵坐标上移至取值范围的上限,而中间13个节点的纵坐标则下移至取值范围的下限。这样的取值使得上弦索具有更大的弯曲程度,从而令结构内的应力水平达到最大,并相应地使结构基频在此处也得到了它的最大值。
| 上弦索节点号 | 纵坐标变化量Δz/mm | 上弦索节点号 | 纵坐标变化量Δz/mm |
| 2 | 0 | 10 | -1 |
| 3 | -1 | 11 | -1 |
| 4 | -1 | 12 | -1 |
| 5 | -1 | 13 | -1 |
| 6 | -1 | 14 | -1 |
| 7 | -1 | 15 | -1 |
| 8 | -1 | 16 | 0 |
| 9 | -1 | 17 | 1 |
另外,在整个优化计算过程中结构基频值的变化很小,这与上一节得到的计算效果相同。因此,可以进一步证实:上弦索节点纵坐标初始位置在较小范围内的变化对结构的动力性能将不会产生很大的影响。因此,在可展开天线刚性结构部分设计给定的情况下,采用文中方法对索网结构进行优化设计,将不会降低天线的整体动力性能,这一点将有利于可展开天线整体结构的优化设计。
4 结论1)算例表明,以索单元节点坐标值为优化设计变量,应用序列二次规划法,可以较好地解决包含精度、频率等复杂优化目标的可展开天线几何非线性索网结构的形状优化问题,得到的优化结果对于工程实践具有一定的指导意义。
2)通过以索网表面精度为目标的优化计算可知,最优解处上弦索节点纵坐标变化量的大小与其所在的索单元同水平方向夹角的大小有关,节点纵坐标变化量会随着节点所在单元与水平方向夹角的增大而增大。由此可知,与水平方向夹角大的上弦索单元的节点纵坐标值在优化过程中对优化目标具有较大的影响。
3)由上面两类优化计算可知,上弦索节点纵坐标初始位置在较小范围内的变化对结构的动力性能将不会产生很大的影响。这表明,以节点坐标位置为设计变量的天线索网结构形状优化设计,不会在优化的同时降低索网结构的动力性能。
| [1] | 刘明治, 高桂芳. 空间可展开天线结构研究进展[J]. 宇航学报, 2003, 24(1): 82-87. |
| [2] | TIBERT G. Deployment tensegrity structure for space applications[D]. Stockholm, Sweden: Royal Institute of Technology Department of Mechanics, 2002: 16-32. |
| [3] | 陈建军, 曹鸿钧, 张建国, 等. 论大型星载展开天线结构系统的可靠性[J]. 工程力学, 2014, 31(2): 25-34. |
| [4] | 范叶森, 李团结, 马小飞, 等. 非对称环形桁架索网天线预张力设计解析算法[J]. 哈尔滨工业大学学报, 2015, 47(1): 124-128. |
| [5] | 李明, 李迎松, 杨晓冬, 等. 小型化陷波超宽带天线的研究与设计[J]. 应用科技, 2011, 38(9): 28-31. |
| [6] | 宗亚雳, 王伟, 王从思, 等. 型面周期性误差对环形桁架可展开天线电性能的影响及其消除方法[J]. 电子学报, 2014, 42(5): 963-970. |
| [7] | 范叶森, 李团结, 马小飞, 等. 一种等张力空间索网结构找形方法[J]. 西安电子科技大学学报:自然科学版, 2015, 42(1): 49-55. |
| [8] | 罗鹰. 大型星载可展开天线的动力优化设计与工程结构的系统优化设[D]. 西安: 西安电子科技大学, 2004: 45-56. |
| [9] | 陶海, 沈祥福. 斜拉桥索力优化的强次可行序列二次规划法[J]. 力学学报, 2006, 38(3): 381-384. |
| [10] | 陈晓, 王新民, 周健. 基于序列二次规划法优化无人机飞行性能[J]. 计算机仿真, 2012, 29(12): 99-102, 161. |
| [11] | 张鼎逆, 刘毅. 基于改进遗传算法和序列二次规划的再入轨迹优化[J]. 浙江大学学报:工学版, 2014, 48(1): 161-167. |
| [12] | 汪凤月, 汪芳宗, 胡佳怡. 基于序列二次规划法的分布式电源优化配置研究[J]. 计算技术与自动化, 2012, 31(3): 76-79. |
| [13] | 狄杰建. 索网式可展开天线结构的反射面精度优化调整技术研究[D]. 西安: 西安电子科技大学, 2005: 59-73. |



