直线特征具有平移、旋转和尺度不变等良好特性。正确有效地提取图像中的直线特征,对于提高感兴趣目标的识别率和算法的鲁棒性有重要的意义。作为一个比较基本的图像处理任务,直线检测广泛用于目标物体的识别、形状检测、道路/航线检测等方面[1, 2, 3, 4]。
众所周知,Hough变换的一个重要应用是直线检测[5, 6, 7]。但是Hough变换存在一些不足。首先,在进行Hough变换之前需进行边缘检测,Hough变换的结果对边缘检测的结果高度敏感[7];第二,Hough变换花费的大量时间对一些实时应用来说是不可接受的,比如说车辆自动驾驶系统中的道路边线检测,以及航道检测等[4]。
从数学定义上讲,Radon变换与Hough变换是等效的[8]。但是从实现方式上看,Radon变换更优于Hough变换。这是因为中心切片定理从理论上保证了可以使用快速傅里叶变换(fast Fourier transform,FFT)方法来实现Radon变换,从而使其具有更高的计算效率。然而实际应用表明:这种快速变换方法的结果直接受到笛卡尔-直角坐标变换过程中插值误差的影响。插值误差导致图像的 Radon变换中存在较多的虚假峰值点,从而影响直线检测的精度[9, 10, 11, 12]。
Pan等[11]在图像配准中提出了一种可修改的多层分数傅里叶方法,Shi等[9]在Pan的基础上提出了一种傅里叶变换和Hough蝶形区域联合起来,在峰值检测之前加了个一个带通滤波器起到峰值增强作用,从而可以得出更为精确的直线检测结果。通过中心切片定理[13, 14],Radon变换可以用快速傅里叶变换来实现,而多层分数傅里叶变换则被用来解决传统快速傅里叶变换的插值误差问题。Zheng等[12]提出了一种广义插值傅里叶变换(generalized interpolated Fourier transform,GIFT)的方法。通过在X和Y轴分别使用不同的参数使插值更加灵活。GIFT方法中,参数L和C =(α1 ,α2)的选择是至关重要的,这里L和C分别是GIFT中分数傅里叶变换的层数和X-Y轴的阶数。Pan等的方法中,参数C中(α1 ,α2)的值是相等的,且参数L和C的选择只定义了某一种插值情况下的插值误差,计算时只选择了部分点来参与计算[11]。文中介绍了一种最优选择合适的参数L和(α1 ,α2)的方法,使得插值误差尽可能小,从而达到提高直线检测精度的目的。但是,无论Pan等[11]的方法,还是Shi[9]和Zheng等[12]的方法,都需要计算从笛卡尔坐标到极坐标的转换操作。从笛卡尔坐标到极坐标的转换包含了大量的乘法和正余弦操作,因此这一转换过程需要花费大量时间。考虑到从笛卡尔坐标到极坐标的转换是一对一映射,这种映射关系与图像的具体内容无关,只与像素点的位置信息有关,文中在介绍完GIFT参数选择方法之后又提出了一种快速转换方法。首先,对于大小固定的图像来说,用位置映射文件存储笛卡尔到极坐标的映射信息;然后,通过查找这个映射文件来实现从笛卡尔到极坐标的转换。相对于计算的方法来说,这种查表法大大节省了计算时间。
1 基于GIFT的Radon变换
Radon变换在角度θ的线积分公式如下:
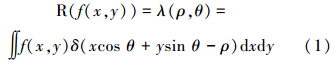
在执行方面,Sθ表示切片(投影)操作,其中

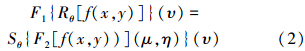
式(2)描述的中心切片定理可表述如下:函数的Radon变换在角度θ的投影的一维傅里叶变换等于函数的二维傅里叶变换在同样角度的投影。因此,通过执行函数(图像)的二维傅里叶变换,插值实现笛卡尔到极坐标的转换,对结果的每一行执行一维傅里叶逆变换来实现其Radon变换是完全可行的。但是FFT会增加混淆问题,容易产生虚假峰值点(如图 1所示),使得直线检测的精确度下降。
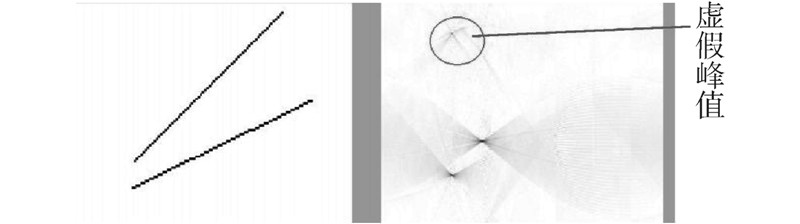 |
| 图 1 快速Radon变换中的虚假峰值 |
为了解决混淆问题,Zheng等[12]提出了一种广义插值傅里叶变换(GIFT)的方法,N×N图像f(n1,n2)的GIFT被定义如下:

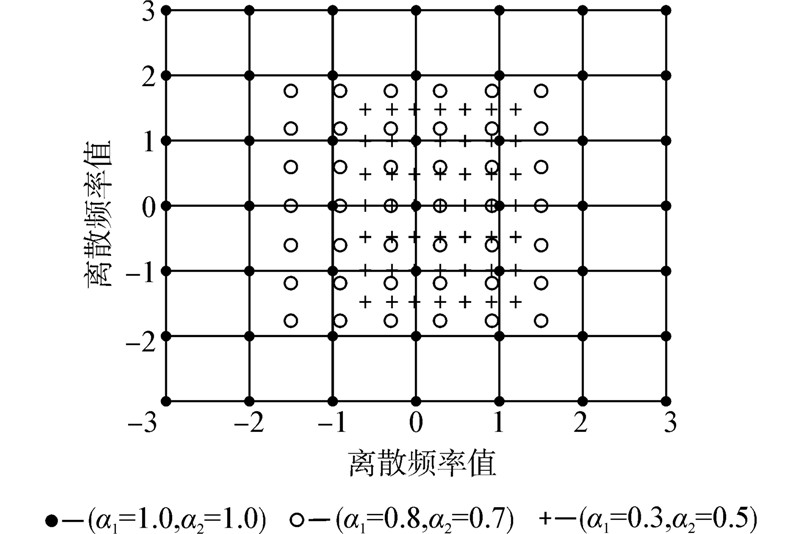 |
| 图 2 GIFT的频率分布 |
图 2中横轴纵轴分别表示笛卡尔坐标的XY轴,即图像的长和宽,单位为像素。随着阶数(α1,α2)取不同的值,所得到的频率插值网格会具有不同的形状,其中水平方向频率的范围为(-πα1,πα1),而垂直方向的范围为(-πα2,πα2)。多层联合起来形成一个完整的傅里叶频谱。这样形成的频率域比传统的单层傅里叶变换包含更多的采样点,从而使得混淆效果最小。
GIFT网格的分辨率依赖于2个参数,分别是层数L和近似的分数阶数C,其定义为
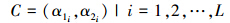
频率域的插值网格被定于如下:
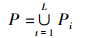
 α2i)∈C}
α2i)∈C}
从笛卡尔到极坐标的转换方面,传统的方法是通过(x=υcos φ,y=υsinφ)计算每一个对应点。由于二维傅里叶谱是关于原点对称的,因此只需计算出其上半部分的傅里叶谱,其下半部分可以通过共轭映射来得到。其上半部分笛卡尔坐标x-y到极坐标υ-φ的转换用了一种线性插值方法:
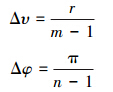
2 GIFT参数的选取方法
对于插值误差来说,层数L和参数C = (α1,α2)的选择是至关重要的。层数L依赖于实际应用的类型。一般来讲,层数越大,插值误差越小。综合考虑到插值误差及其时间消耗,在大多数情况下推荐L取3或者4。实际上,正确的方法应该是如果精确度没有达到要求的话就应该适当的增加层数L,同时,应该综合考虑时间方面的花费[11]。
一旦层数L确定了,对C的选择就是非常苛刻的。Pan等[11]提出的关于阶数C的选择方法,其(α1,α2)取值一样,而且只定义了一种最近邻插值法下的插值误差,由于在计算插值误差时候这个过程比较慢,采用了只计算部分点的插值误差来估计全局插值误差。这样计算出来的插值误差可能会不太精确。而文中提出的方法,定义了不同插值方法下的插值误差,并且在笛卡尔到极坐标转换中文中采用查表法,对于固定大小的图像,只需计算一次C,因此在计算插值误差时可以不用考虑时间方面的花费,通过计算全局插值误差来求得是插值误差最小的参数,从而使得结果更加精确。
考虑到从笛卡尔到极坐标的转换过程中,极坐标远离原点的部分将会变得稀疏,而这部分正好对应于高频区域。在直线检测中,高频区域包含更多有用的信息,所以要考虑高频区域中的插值问题。因此,将每一层的C=(α1,α2)范围限定在0.5~1。
对于不同的插值方法,插值误差的定义是不同的。文中讨论了2种不同的插值方法及其相应的参数选择方法。
假定通过(x=υcos φ,y=υsin φ)计算得出的笛卡尔坐标中对应的点为(Xreal,Yreal)。
1)最近邻插值法:将L层频率谱叠加在一起,找出(Xreal,Yreal)点周围最近邻的4个点,即左上、左下、右上、右下4个方向距离(Xreal,Yreal)最近的4个点。计算出这4个点中距离(Xreal,Yreal)最近的点作为其插值点。此种插值法下插值误差被定义为

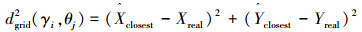
2)均值插值法:将L层频率谱叠加在一起,找出(Xreal,Yreal)点周围最近邻的4个点(同1)中的4个点),将这4个点的平均频率值作为点(Xreal,Yreal)的值。此种插值法下插值误差被定义为

C在0.5~1近似的取(0.5,0.6,0.7,0.8,0.9,1)中的一个。使C遍历从0.5~1,得到其使得插值误差最小的值作为C的最优解。如果C已经达到最优,但是插值误差还没有达到实际需要的状态,应该再继续增加层数L然后接着再继续重新优化C。当图像大小确定,插值方法确定,计算出一个使得插值误差最小的C值之后,以后对于同样大小的图像,都可以用这个计算出来的参数来达到最佳的插值效果。
3 基于查表技术的笛卡尔到极坐标的快速转换方法
从笛卡尔到极坐标的转换,每个点需要4次计算(x=υcos φ,y=υsin φ),分别是2次正余弦计算和2次乘法计算。由于二维傅里叶谱是关于原点对称的,只需计算出其上半部分的频率分布,下半部分可以通过共轭映射得到。对于大小为N×N的图像,则其时间复杂度为O (N/2×N×4)=O(2N2)。
对于大小固定的图像I,由于笛卡尔坐标中的一点对应于极坐标中唯一的一点,因此建立了一个文件,用来存储笛卡尔坐标到极坐标对应位置之间的映射信息,对于固定大小的N×N图像,只需第一次计算其笛卡尔坐标和极坐标对应位置(x=υcos φ,y=υsin φ),然后将其映射关系存储到的文件中。后续在对同样大小的图像进行笛卡尔到极坐标的转换时不用计算只需查文件即可知道笛卡尔到极坐标的对应位置信息。文件中存储的映射关系按极坐标中的顺序存储(从上到下,从左到右),因此查找 时候也按顺序查找,每个元素查找的时间复杂度为O(1),根据二维傅里叶谱的对称性,只需找到上面一半即可,剩下一半共轭映射即可得到。因此查文件法的时间复杂度为O(N/2×N)=O(N2/2),速度比原来的线性插值方法有了明显的提高。其查表映射模型如图 3所示。对于每一个(υ,φ)初始计算其在笛卡尔坐标的对应坐标,并将其极坐标和笛卡尔坐标对应的位置信息存入查找表中,后续对于同样大小的图像只需读取此查找表即可。对极坐标从左到右,从上到下(类似于矩阵的顺序存储)依次在查找表中找到其对应于笛卡尔坐标中的位置(此位置为第3部分插值完成后的对应位置信息),从而得到其极坐标频谱。
 |
| 图 3 笛卡尔x-y到极坐标 |
综合以上,图像中的直线检测可分为以下几个步骤(如图 4所示):
 |
| 图 4 基于改进的GIFT实现Radon变换进行的直线检测 |
1)用第2节所述的方法选择合适的参数L和C;
2)用步骤1)中得出的参数计算输入图像I的GIFT;
3)通过步骤2)获得L层的频谱图;
4)用第3节所述的方法将笛卡尔坐标转换到极坐标,并通过共轭映射得到完整的极坐标频谱;
5)通过对极坐标谱做一维IFFT得到输入图像的Radon变换;
6)在蝶形区域中检测极大峰值点,其对应于输入图像中的直线。
4 仿真结果与分析
本节通过仿真实验分别分析了所提出的GIFT参数选取方法和笛卡尔到极坐标的快速转换方法的性能。
4.1 GIFT参数选取方法的仿真结果及分析
综合时间花费和精确度方面的考虑,取L=3。将C中前2层的4个值分别从0.5取到1,间隔为0.1,第3层参数都取1,共有1 296种取值。
1)最近邻插值法。通过第2节1)中插值方法定义的插值误差公式,C不同的取值对应的插值误差如图 5所示。
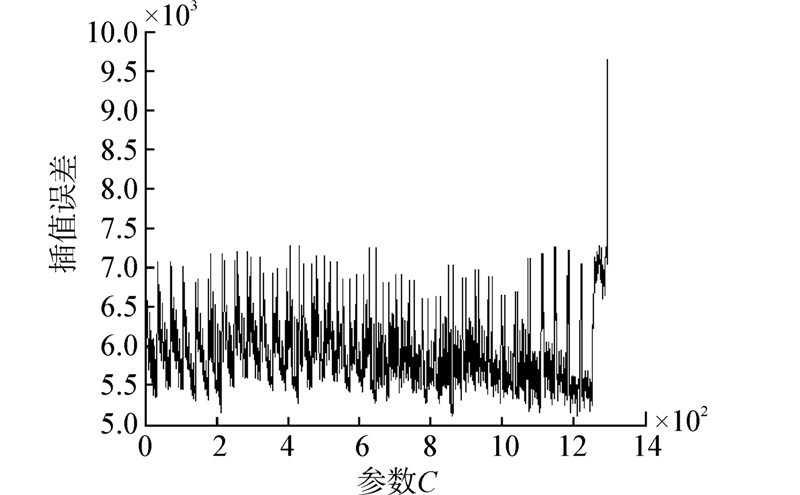 |
| 图 5 最近邻插值法L=3,C取不同值时的插值误差 |
在第862个点,即C取(0.8,1)(1,0.8)(1,1)时插值误差最小为5 136.352。在最后一个点,即C取(1,1)(1,1)(1,1)时插值误差最大为9 665.285。相应的Radon变换结果如图 6所示。
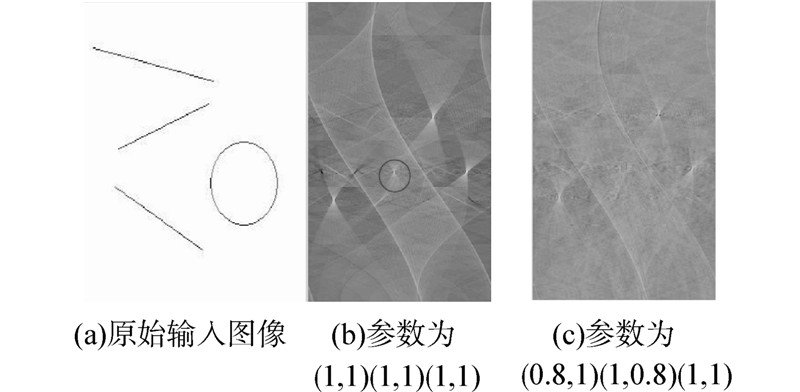 |
| 图 6 最近邻插值法不同参数下得到的Radon变换图像 |
从图 6可以看出,当参数C取(1,1)(1,1)(1,1)时,有明显的虚假峰值点;而当参数C取(0.8,1)(1,0.8)(1,1)时不仅虚假峰值点消失,而且峰值点看起来更加细小锋锐,这样检测出的直线将更加精确。
2)均值插值法:通过第2节2)中定义的均值插值法的插值误差公式,C不同的取值对应的插值误差如图 7所示,在第645个点,即C取(0.7,1)(1,0.7)(1,1)时插值误差最小为29 300.95 。在最后一个点,即C取(1,1)(1,1)(1,1)时插值误差最大为41 023.8。相应的Radon变换结果如图 8所示。
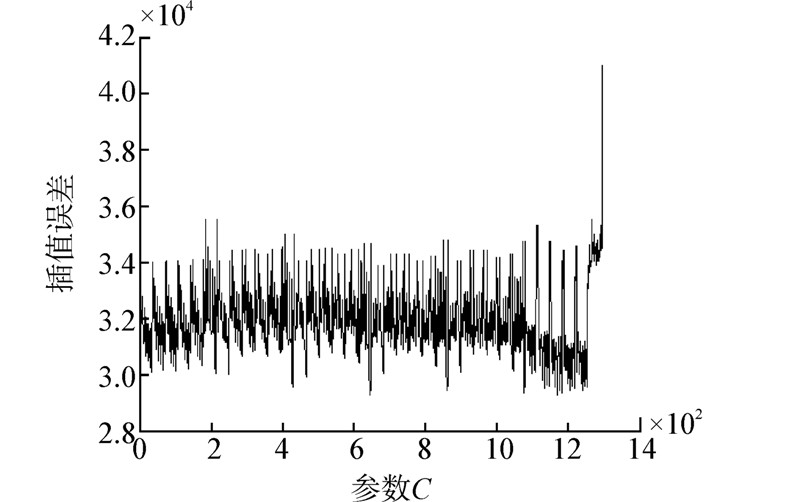 |
| 图 7 均值插值法法L=3,C取不同值时的插值误差 |
 |
| 图 8 均值插值法不同参数下得到的Radon变换图像 |
从图 8可以看出,当参数C取(1,1)(1,1)(1,1)时,虚假峰值点仍然存在,且峰值点比较粗,不易于其参数的获取。而当参数C取(0.7,1)(1,0.7)(1,1)时虚假峰值点明显消失,而且峰值点更加细小锋锐,这样检测出的直线将更加精确。
对于这2种不同的插值方法,由于均值插值法具有平滑作用,可以使不规则的峰值点变得相对平滑、规则,更加适用于宽直线的检测;而最近邻插值法,则适合于细直线的检测。
4.2 笛卡尔到极坐标的转换仿真与分析
对不同大小的图像做了验证,2种方法的时间花费如表 1所示。结果显示计算法的时间花费大约是查表法的4倍,这进一步验证了本文对时间复杂度的分析。
| 图像大小 | 查表法/s | 计算法/s |
| 256×256 | 0.009 936 | 0.039 49 |
| 512×512 | 0.066 702 | 0.266 82 |
| 1024×1024 | 0.199 045 | 0.796 13 |
5 结束语
在现有GIFT的基础上,定义了不同插值方法下的插值误差,给出了一种其参数确定的方法,缩小了插值误差,使得检测结果更加精确。同时在图像频谱从笛卡尔坐标到极坐标转换的过程中,给出了一种基于查表的快速实现方法,用查表代替了原算法的正余弦和乘法操作,减少了基于GIFT的Radon的直线检测的时间开销。对于其他有关笛卡尔到极坐标的转换的应用都有借鉴意义。文中方法对基于GIFT的直线检测的精度和时间复杂度有了一定的提高,对于宽直线、线段及共线线段的检测还需进一步深入研究。
| [1] | 刘进, 闫利, 李德仁. 利用点对分析法检测线段[J]. 武汉大学学报: 信息科学版, 2008, 33(3): 314-317. |
| [2] | HILLEL A B, LERNER R, LEVI D, et al, Recent progress in road and lane detection: a surey[J]. Machine Vision and Applications, 2014, 25(3): 727-745. |
| [3] | HAN J, KIM D, LEE M, et al. Enhanced road boundary and obstacle detection using a downward-looking lidar sensor[J]. IEEE Transactions on Vehicular Technology, 2012, 61(3): 971-985. |
| [4] | MAGLI E, OLMO G. On high resolution positioning of straight patterns via multiscale matched filtering of the Hough transform[J]. Pattern Recognition Letters, 2001, 22: 705-713. |
| [5] | HOUGH P V C. Method and means for recognizing complex patterns: USA, 3069654[P]. 1962-12-18. |
| [6] | DUDA R O, HART P E. Use of Hough transform to detect lines and curves in pictures[J]. Commun ACM, 1972, 15(1): 11-15. |
| [7] | MOCHIZUKI Y, TORII A, IMIYA A. N-point Hough transform for line detection[J]. Journal of Visual Communication and Image Representation, 2009, 20(4): 242-253. |
| [8] | DEANS S R. Hough transform from the Radon transform [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1981(2): 185-188. |
| [9] | SHI D, ZHENG L, LIU J. Advanced Hough transform using a multilayer fractional Fourier method [J]. IEEE Transactions on Image Processing, 2010, 19(6): 1558-1566. |
| [10] | HO C G, YOUNG R C D, BRADFIELD C D, et al. A fast Hough transform for the parametrisation of straight lines using Fourier methods[J]. Real Time Imaging, 2000, 6(2): 113-127. |
| [11] | PAN W, QIN H K, CHEN Y. An adaptable-multilayer fractional Fourier transform approach for image registration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(3): 400-414. |
| [12] | ZHENG L, SHI D. Advanced Radon transform using generalized interpolated Fourier method for straight line detection[J]. Computer Vision and Image Understanding, 2011, 115: 152-160. |
| [13] | MERSEREAU R M, OPPENHEIM A V. Digital reconstruction of multidimensional signals from their projections [J]. Proceedings of the IEEE, 1974, 62(10): 1319-1338. |
| [14] | Jr EASTON R L, BARRETT H H. Tomographic transformations in optical signal processing[M]. New York: Academic Press, 1987: 335-386. |



