药品检验/检测方法,尤其需收载到药典等的法定方法[1-2],必须经过充分验证(validation),以保证方法能达到其预期用途。检测方法的总变异直接影响药品检验结果的正确性,同时也能反映此检测方法能否满足产品检测的需求。
如何确立方法满足预期用途的标准?如,对于一个质量属性的限度标准为90.0%~110.0%时,检测方法的最大变异不能超过多少算满足预期要求?如何在出现不合格检测时,快速判断是生产过程导致了质量问题,还是方法自身的变异导致了假阳性结果?一个确认过的方法,正常产生不合格(out-of- specification,OOS)结果的概率是多少?一个法定方法,应该具有多大的变异比较合适?这些问题,在药品检测实验室越来越受到关注,然而,至今未有系统的阐述和讨论。
本文采用六西格玛(six Sigma,6σ)理论,通过过程能力指数(process capability index,PCI)计算的方式,对理化分析中定量测定方法[1-2]满足其预期用途的标准进行探讨。这些定量测定方法按照药典分类包括Ⅰ类方法(原料药中主要成分或成药中活性成分(包括防腐剂)进行定量测定的方法)和Ⅱa类方法(原料药中杂质或成药中降解物质进行定量测定的方法)。为简化表述,下文中统一使用定量理化分析方法进行表述。至于理化分析中有关物质的限度分析方法(Ⅱb类限度分析方法)和溶出度/药品释放度测定分析方法(Ⅲ类分析方法)的评价标准,将另文论述。
1 过程能力指数和方法能力指数过程能力(process capabllity)[3]被定义为过程满足客户期望的能力。过程能力分析是指通过比较过程输出数据的分布与产品特性量值上下限,来判定产品质量是否具有一致性的技术方法,其中“过程”是ISO 9000中定义的“将输入转化为输出的相互关联或相互作用的一组活动”。过程能力分析技术不仅可用于生产工艺过程的分析,同时也可用于检测方法的评价[4]。过程能力分析通过PCI和控制图(control chart)来反映过程能力满足产品某一技术要求的程度。PCI以6σ理论为基础[5],根据不同条件和要求,选用不同的PCI,其中应用最广泛的为Cp(Cpl、Cpu)、Cpk、Cpm[4]。
本文所采用的PCI是以Cp为例进行介绍。使用Cp时,需要满足[4-5]:(1)过程处于稳态,没有异常因素出现,也没有发生漂移和震荡;(2)过程观测产品的特性量值服从正态分布(本文采用不涉及非正态分布情形的理想模式,实际应用中如果数据不满足正态分布,则应进行数据的转换,使其满足正态分布的要求再进行计算);(3)样本具有代表性而且相互独立;(4)产品特性量值限度(上下限)能够准确反映产品要求;(5)质量标准中的目标值T与数据的均值μ重合。计算公式如下:
| $ {C_{\rm{P}}} = \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6{\rm{ \mathsf{ σ} }}}} \approx \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6{\rm{SD}}}} $ | (1) |
公式中,USL:特性量值(检测指标)限度标准的上限;LSL:特性量值限度标准的下限;σ:过程的总体标准差(过程总体变异);SD:过程的样本标准差(代替总体标准差)。
对于某一产品,一般其变异(σ or SD)包括检测方法的变异和产品变异(包括稳定性和生产工艺导致的变异),故PCI公式可表达为:
| $ {C_{\rm{P}}} = \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6\sigma }} = \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6\sqrt {\sigma _{{\rm{product}}}^2 + \sigma _{{\rm{method}}}^2} }} \approx \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6\sqrt {{\rm{SD}}_{{\rm{product}}}^2 + {\rm{SD}}_{{\rm{method}}}^2} }} $ | (2) |
其中σproduct、σmethod分别代表产品总变异和方法总变异,SDproduct、SDmethod分别代表各自的样本变异。
公式2是对一个产品从生产到检测的总体过程评价;进行方法建立和确认研究时,均需采用同一批样品或对照品在短期内进行评价,故,这时其σproduct为0。可将公式2中PCI简化为专门对方法进行评价的方法能力指数(method capability index,MCI):
| $ {\rm{MCI}} = \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6{\sigma _{{\rm{product}}}}}} \approx \frac{{{\rm{USL}} - {\rm{LSL}}}}{{{\rm{S}}{{\rm{D}}_{{\rm{method}}}}}} $ | (3) |
由此,可以按照PCI指数的所有理论和计算要求,对MCI进行解释和理解,如前面提到的计算所需前提条件,不同MCI所对应的方法分级和OOS发生率等。
2 最小方法能力指数的选择对一个过程的能力评价,按照6σ理论,可将PCI分为5个级别[4-6]:PCI < 0.67时为Ⅴ级,过程能力被认为严重不足,一般不使用;0.67≤PCI < 1.00时为Ⅳ级,过程能力被认为仍有不足,但在某些特定情况下,如不造成危害的特性量值(或叫指标),则基本可接受;1.00≤PCI < 1.33时为Ⅲ级,过程能力被认为尚可;对于一些可造成危害的指标,能力仍显不足,需Ⅱ以上的过程能力,对产生严重危害的特性量值(指标),其过程能力指数一般要求其超过Ⅱ,即1.33≤PCI < 1.67;当PCI≥1.67时为Ⅰ级。
PCI越大越好,一般最低要求PCI≥0.67 [7]。选取不同PCI,当方法变异占(产品)过程总变异的比例不同时计算MCI值,确定其可接受的最小值,结果见表 1。
|
|
表 1 不同过程能力指数(Cp)下方法变异所占过程总变异不同比例所对应的MCI Tab.1 MCI values corresponding to different proportions of method variability in total process variability under different process capability index (Cp) |
表 1中,Cp水平的选取主要依据过程能力各分级的界限(值);而方法变异占过程总变异的比例水平选取,主要依据:1)当Cp很大时,说明过程稳定,这时假定工艺非常稳定,则方法变异可以采用相对大的水平,采用8/9倍的过程总变异进行计算;2)方法变异占总变异的最小值,选择1/3倍的过程总变异,主要依据ISO13528[8]和不确定度合成理论[9],认为该情形下,方法的变异在总变异中所占比例小于10%,可以忽略。
从表 1中可见,方法变异占产品总变异的比例越大时,计算出的MCI就越小。例如Cp为0.67,如果方法的变异完全占据了产品总过程变异,即产品生产不同批次之间没有任何差异的理想状态,这时MCI值即为0.67。然而,这种理想状态不具有任何实际意义,因为产品在每次生产中,总会有一定的变异发生,即各批产品间的变异不可能等于0。因此假定选用方法变异达到总体变异的8/9作为计算依据,这时,MCI=0.75,将此值作为MCI的最小值似乎具有可行性,但这仍然是在假定数据是标准正态分布状态下的最小值,而产品实际生产的工艺数据不可能完全处于正态分布(通常在小数据样本下,以t分布描述更准确)。
关于方法MCI的最小取值问题,需要从实际出发,综合考虑方法所检测指标的危害性大小、方法的经济性和方法是否还有改进空间等因素。对于一个新建立的检测方法,MCI最好不低于0.90,这样可更好地保证所检测结果的可靠性[10]。随着方法的应用,再进一步优化和提高。
根据文献[3, 6, 10],Cp和MCI的大小与过程/方法产生OOS的概率,即误判率,可用下列公式进行计算:
| $ \begin{array}{l} {\rm{Prob}}\left( {{\rm{OOS}}} \right) = 2\left( {1 - \Phi \left( {3 \times {\rm{PCI}}} \right)} \right) = 2 \times \left( {1 - {\rm{Normsdist}}} \right.\\ \left. {\left( {3 \times {\rm{PCI}}} \right)} \right) = 2 \times \left( {1 - {\rm{Norm}}{\rm{.s}}{\rm{.dist}}\left( {3 \times {\rm{PCI}}, {\rm{true}}} \right)} \right) \end{array} $ | (4) |
或
| $ \begin{array}{l} {\rm{Prob}}\left( {{\rm{OOS}}} \right) = 2\left( {1 - \Phi \left( {3 \times {\rm{MCI}}} \right)} \right) = 2 \times \left( {1 - {\rm{Normsdist}}} \right.\\ \left. {\left( {3 \times {\rm{MCI}}} \right)} \right) = 2 \times \left( {1 - {\rm{Norm}}{\rm{.s}}{\rm{.dist}}\left( {3 \times {\rm{MCI}}, {\rm{true}}} \right)} \right) \end{array} $ | (5) |
Prob(OOS)指OOS发生的概率;Φ代表标准正态分布(平均值为0,标准差为1)下累积分布函数;Normsdist与Norm.s.dist均为在Excel内,计算标准正态分布下累积分布函数值的函数。
根据公式5,当MCI=0.75时,因该方法变异导致误判产品不合格的概率,即Prob(OOS)为2.4%。当MCI=1,因方法变异导致的OOS仅为0.27%,基本可以判断,检测的产品出现不合格时,主要是生产工艺的变异所导致的,即产品本身不合格。表 2对一些特定方法能力指数所产生的OOS概率值进行了计算汇总。
|
|
表 2 不同MCI所对应的方法所致OOS发生概率 Tab.2 Probability of OOS occurrence from the method under different levels of MCI |
在药典常见品种的质量标准中,其含量测定指标(特性量值)的限度水平有:原料药的98.0%~102.0%,制剂的95.0%~105.0%、90.0%~ 110.0%和80.0%~120.0%4个限度标准范围。根据公式3,选择不同的MCI,可获得检测方法的最大变异值,见表 3。
|
|
表 3 理化特性量值限度标准、所对应方法最大允许变异及OOS发生率 Tab.3 Physicochemical property value limit criteria, the maximum allowable variability of the corresponding method and the incidence of OOS |
表 3给出了方法在不同能力指数(第1列)和特性量值的限度标准(第2列)下,方法允许的最大变异值(第3列)和该方法在实际应用时,导致OOS的概率。应该注意的是,表 3中不同MCI下所得方法最大允许变异,是在数据完全处于无偏倚的理想状态下所得。结合前面的分析,作为一个可用的新建方法,建议选择MCI不小于0.90进行方法确认的评价为宜,然后逐步优化提高。如:当MCI=1.00,对于原料药的限度标准在98.0%~102.0%时,检测方法满足其预期用途的评价中,其方法的总变异(RSD)应不超过0.67%;对于产品限度标准为90.0%~110.0%的检测方法进行评价时,其方法总变异应不超过3.33%。当方法变异满足这些标准时,则由于方法导致检验结果误判的概率仅为0.27%。
4 方法总变异中精密度与准确度的关系在新方法确认中,都要求计算方法的准确度和精密度;一般准确度用偏倚(bias)或相对偏倚(relative bias,RB)表示,精密度(重复性/中间精密度/再现性)用标准差或相对标准差表示(σr /σIP /σR)。准确度和精密度是确定方法总变异的基础。其关系如下:
| $ {\sigma _{{\rm{method}}}} = \sqrt {{\rm{R}}{{\rm{B}}^2} + \sigma _{\rm{r}}^2} \;\;\;\;\;\;\;\;{\rm{或}}\;\;\;\;\;\;\;{\sigma _{{\rm{method}}}} = \sqrt {{\rm{R}}{{\rm{B}}^2} + \sigma _{{\rm{IP}}}^2} $ | (6) |
公式中RB为相对偏倚,σr、σIP分别代表方法的重复性精密度和中间精密度。
公式6主要用于方法确认的早期,即方法主研发实验室阶段,这时只能获得的重复性精密度σr或中间精密度σIP。当一个方法被药典等法规收载时,需经过多个实验室验证后,获得再现性精密度(σR),这时可将公式6中的精密度值用σR替代。
这时的公式3,可进一步表达为
| $ {\rm{MCI}} = \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6{\sigma _{{\rm{method}}}}}} = \frac{{{\rm{USL}} - {\rm{LSL}}}}{{6\sqrt {{\rm{R}}{{\rm{B}}^2} + \sigma _{\rm{r}}^2} }}{\rm{or}}\frac{{{\rm{USL}} - {\rm{LSL}}}}{{6\sqrt {{\rm{R}}{{\rm{B}}^2} + \sigma _{{\rm{IP}}}^2} }} $ | (7) |
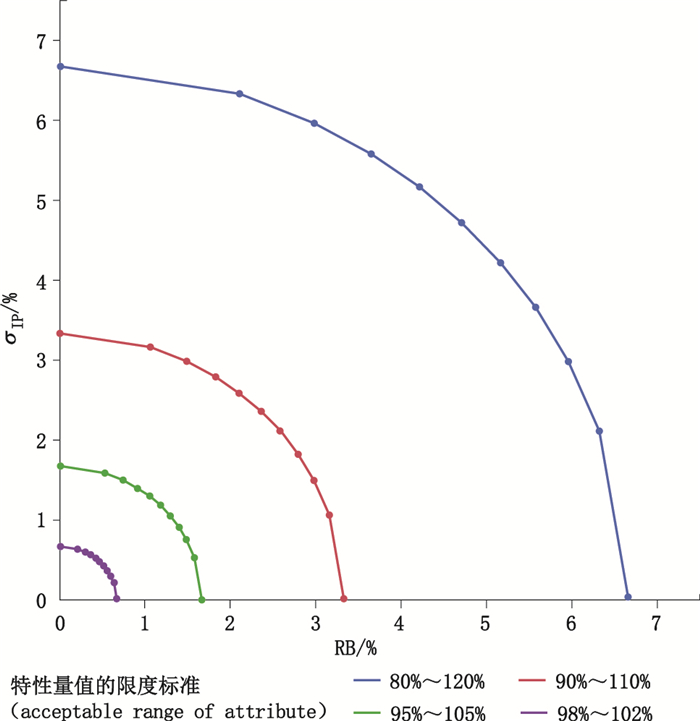
由公式6可见,当方法总变异已确定(见表 3),如果偏倚增大,则方法的精密度需相应的减小。两者在限度标准下的关系如图 1所示。
|
图 1 检测方法在MCI=1时不同方法总变异下的精密度与准确度变化图 Fig.1 Precision and accuracy changes for the total variability of different methods at MCI=1 |
从图 1可见,当产品的限度标准在90.0%~ 110.0%时,其方法的总变异RSD=3.33%,如果精密度为3.33%,则RB=0方可满足方法的预定用途;当方法有1.50σ偏移时,则其精密度不能超过2.97%。因此,在实际判断检测方法是否适用于产品的检验时,需要同时考虑准确度和精密度,而不是单方面地仅计算其精密度或准确度,这正是在文献[7, 11]中将准确度和精密度进行联合验证的理论基础。
5 讨论和结论 5.1 关于方法是否满足其预期用途问题要评价方法是否满足其预期用途,需要2个条件:方法基本稳定(A)和对方法拟检测指标的限度标准有基本预判(B)。关于条件A,将在本专栏中《方法验证性能参数的获取和评价新方式探讨》一文详细讨论,这里主要讨论条件B。
有关方法与检测指标限度标准的关系,应从2个方面考虑:(1)对于一个全新产品,即还没有完全确定该类产品的质量标准时,应根据方法确认所求得的偏倚和中间精密度,求出方法的最大变异,以便判断该方法能适于哪类质量限度标准的产品所用,或者为该产品质量的标准制定提供相应的依据。(2)对于已建立质量限度标准的产品,可根据限度标准和方法变异度来判断该方法的分析能力和使用该方法会产生误判的概率。
5.2 关于最小MCI值选择问题关于MCI最小值的问题,学界和行业内没有完全统一的观点。由于MCI与方法误判率(即方法OOS发生概率)直接相关,故在选择时,应充分考虑方法误判导致的危害性(最大能承受的风险)、检测支出成本等;如果所检测的指标(质量属性)会造成严重危害,则必须采用较高的过程控制能力,即MCI必须足够大,如采用Ⅱ级方法(MCI≥1.33)甚至是Ⅰ级方法(MCI≥1.67),以便保证所放行产品不会因方法误判而产生严重损失。当所检测的指标(质量属性)危害性较小时,可将MCI适当减小,如使用0.75。
目前,《中华人民共和国药典》(以下简称《中国药典》)2015年版指导原则[1]中给出的精密度限度标准,是按照Horwitz方程得出的,这与美国药典论坛[7]上引用的一致。但该方式已经被否定[12]。欧洲官方实验室(OMCL)一般采用MCI=0.67,即把方法误判率设置在4.5%左右作为方法满足要求的标准[13],采用该标准的缺点除在“4”项中讨论的问题外,还有一个问题是当样品为边缘产品时,会出现更多的误判概率。如对一个质量标准为98.0%~102.0%的产品,若其实际含量为98.5%,采用一个变异为1%的方法进行检测,会有大于32%的误判率,即10次实验,将有3.2次判定该产品不合格。
在推荐最小MCI时,作者建议以MCI不小于0.90为宜。主要基于以下考虑:(1)方法确认或预确认阶段是方法刚建立不久的初级阶段,实验人员的熟练程度、操作程序还需进一步提高,故开始要求过高的MCI值,不现实;待方法经过长期优化后,再逐步提高为宜。(2)有些文献,如美国药典论坛[7],要求精密度准确度联合变异的测定结果用t分布求得不小于0.95,该种方式从日常使用该方法角度进行评价,因为这时的样本量较小,通过比较,可看出该要求与正态分布下MCI在0.90左右相当。(3)正文中谈到MCI最小为0.75,是基于产品总过程能力指数不小于0.67,产生OOS概率不超过4.55%,且总过程中的变异主要来源于方法变异所致。这时,方法变异占总变异的89%(0.89σ),留给产品变异的空间约为过程总变异的44%(0.44σ)。但是,在实际使用中,考虑到所测结果非正态分布等因素,建议MCI取值以不小于0.90为宜。(4)使用Horwitz方程计算的变异作为方法总变异进行评价已经被否定。在2018年新版USP[14]中,也间接否定了该方式。(5)为了便于不熟悉统计计算的分析人员在方法确认中更好地评价其所确认的方法,因地制宜地选择所需的MCI,作者特地构建了表 3,以方便分析人员查阅。
5.3 方法的RB和σIP的预设标准《中国药典》[1]和欧洲官方实验室[13]都对方法在确认时的RB和σIP变动范围大小进行了规定,这种规定在过去一段时间发挥了积极作用,但该方式割裂了两者的关系。通过本文“4”项的阐述和“3”项的判断标准,可见使用方法的变异度更有优势,且能更准确地描述方法的检测能力。
本文采用生产质量管理中的6σ理论和过程能力指数工具,探讨了判断定量理化分析类方法满足预定用途的标准,并将分析方法在不同限度标准下的最大变异以表格方式(表 3)提供给读者,为今后读者对定量理化分析类方法在进行确认时,快速判断所建方法是否满足其预期用途提供了依据。
| [1] |
中华人民共和国药典2015年版.四部[S]. 2015: 附录9101 ChP 2015. Vol Ⅳ[S]. 2015: Appendices 9101 |
| [2] |
USP 40-NF 35.[S]. 2015: 1780(< 1225> Validation of Compendial Procedures)
|
| [3] |
陶靖轩. 关于过程能力指数和不合格品率之间的关系研究[J]. 中国计量学院学报, 2012, 23(3): 315. TAO JX. Relationship of process capability index and nonconforming rate[J]. J China Jiliang Univ, 2012, 23(3): 315. DOI:10.3969/j.issn.1004-1540.2012.03.020 |
| [4] |
谭德讲, 赵嘉, 曹秀堂. 过程能力指数及在药品质量控制中的应用探讨[J]. 中国药事, 2014, 28(11): 1213. TAN DJ, ZHAO J, CAO XT. Process capability indexes and their applications in pharmaceutical quality control[J]. Chin Pharm Aff, 2014, 28(11): 1213. |
| [5] |
张根保, 刘英. 质量管理与可靠性[M]. 北京: 中国科学技术出版社, 2001. ZHANG GB, LIU Y. Quality Management and Reliability[M]. Beijing: China Science and Technology Press, 2001. |
| [6] |
王斌会, 胡志萍. 过程能力指数与不合格率的关系模型[J]. 数理统计与管理, 2007, 26(1): 57. WANG BH, HU ZP. The relation model between process capability index and nonconforming rate[J]. App1 Stat Manage, 2007, 26(1): 57. DOI:10.3969/j.issn.1002-1566.2007.01.011 |
| [7] |
< 1200> Requirements for Compendial Validation[J/OL].USP Pharmacopeial Forum, 2015, 41(5)[2017-08-07].http://www.usppf.com/pf/pub/index.html
|
| [8] |
GB/T 28043-2011/ISO 13528: 2005利用实验室间比对进行能力验证的统计方法[S]. 2011 GB/T 28043-2011/ISO 13528: 2005 Statistical Methods for Proficiency Testing Using Interlaboratory Comparisons[S]. 2011 |
| [9] |
JCGM 100: 2008 Evalution of Measurement Data-Guide to the Expression of Uncertainty in Measurement (GUM)[S]. 2008
|
| [10] |
USP 40-NF 35[S]. 2015: 935(< 1033> Biological Assay Validation)
|
| [11] |
< 1210> Statistical Tools for Procedure Validation[J/OL].2014, 40(5)[2017-07-29].http://www.usppf.com/pf/pub/index.html
|
| [12] |
DESIMONI E, BRUNETTI B. Uncertainty of measurement and conformity assessment:a review[J]. Anal Bioanal Chem, 2011, 400: 1729. DOI:10.1007/s00216-011-4776-y |
| [13] |
OMCL Network of the Council of Europe. PA/PH/OMCL(14)89R. Evaluation and Reporting of Results Annex 2A[EB/OL].(2015)[2018-06-28]. https://www.edqm.eu/en/quality-management-guidelines-86.html
|
| [14] |
USP 41-NF 36[S]. 2018: 7623(< 1210> Statistical Tools for Procedure Validation)
|
 2019, Vol. 39
2019, Vol. 39 
