2. 大连理工大学 经济管理学院, 辽宁 大连 116024
近年来,深圳、青岛、郑州等相对缺乏"双一流"高校或科研机构的地区,不断出台包括建设用地、资金支持和人才激励等方面的优惠政策措施,加大对高等教育机构/科研院所的吸引力度。那么,通过高等教育机构加强研究生教育是否且如何促进其所在区域经济增长,影响机制是什么?相关问题引起了学者们高度关注[1]。
目前,国内外学者在现代人力资本理论和新增长理论基础上,对高等教育与经济增长关系进行了系统研究。首先,我国高等教育对经济增长具有显著的积极影响。尽管采用不同的度量指标和方法测算了高等教育对经济增长的贡献率/产出弹性系数,但大都认为与物质资本投资的贡献相比,高等教育对经济增长的贡献相对较小。例如崔玉平(2000)[2]、樊星和马树才(2017)[3]、李锋亮和王瑜琪(2020)[4]等的实证研究。其次,高等教育投入(包含经费投入和人力投入)对经济增长具有积极的长期影响,并且这一积极影响在东部发达地区的作用较大,在中、西部等欠发达地区的作用相对较小。例如叶茂林等(2003)[5]、Zhou和Luo(2018)[6]、吴东姣和马永红(2019)[7]等的研究。最后,关于我国高等教育与经济增长间关系的研究,主要是在柯布-道格拉斯(Cobb-Douglas)生产函数基础上,分别采用面板数据非线性回归模型[8]、双重差分法[9]、脉冲响应函数模型[3]、误差修正模型[10]等不同研究方法展开的。此外,还有少数学者探讨了我国研究生教育对经济增长的贡献,例如黄海军和李立国(2012)[11]、李锋亮和袁本涛(2013)[12]分别测算了我国研究生教育对经济增长的积极贡献率。
综上所述,尽管现有关于高等教育对经济增长的影响研究已取得了丰硕成果,但鲜有研究探讨高等教育的金字塔顶端——研究生教育对经济增长的影响机制。事实上,研究生教育不仅能够为经济、社会发展培养大批的高素质人才,增加高素质人力资本存量,直接参与生产活动,加速经济发展;而且还能够创造新知识、申请新技术专利,提高经济社会发展质量。因此,研究生教育对我国经济增长至关重要,需要进一步探讨研究生教育如何影响区域经济增长,以及如何通过技术创新对经济增长产生影响。这一问题的解决不仅从理论上有助于打开研究生教育对区域经济增长作用的"黑箱",而且从实践上还有助于正确引导各地区出台相关政策,加大对高校与科研院所的吸引力度和建设力度。
二、理论基础与分析框架 (一) 研究生教育与经济增长目前,教育经济学领域的研究大都集中关注于高等教育对经济增长的影响研究,并达成了较为一致的结论:高等教育不仅对经济增长具有直接的关键作用[13],而且还可以通过增强技术吸收能力和提高R & D水平对经济增长产生间接的积极作用[7, 14]。此外,对我国高等教育与经济增长的研究表明,由于我国存在人均受教育年限低、高等教育投资不足、市场意识不强、科技成果转化缺乏中介途径、地区教育不均衡等问题[15-16],我国高等教育对经济增长的贡献相对较小,并未充分发挥应有的潜力。
然而,关于研究生教育与经济增长关系的研究相对较少,研究生教育如何通过技术创新促进经济增长的研究更少。李锋亮和袁本涛(2013)[12]通过采用宏观明瑟收入模型对2003—2009年我国研究生教育与经济增长的关系分析发现,我国研究生教育对经济增长具有积极的影响,并且东部地区研究生教育的作用最大。方超和罗英姿(2017)[17]采用空间计量经济学模型测算了1996—2014年我国研究生教育对经济增长的正向效应在0.8%~1.9%之间,并且研究生教育存在积极的空间溢出效应。事实上,研究生教育为地区经济发展提供了大量的高质量人力资本和丰硕的科研成果。因此,其对经济增长可能具有积极影响。
(二) 技术创新与经济增长基于Romer内生经济增长理论和Schumpeter创新经济学,已有大量理论和实证研究探讨了技术创新与经济增长的关系,并已达成较为一致共识:技术创新是经济增长的核心驱动力[18]。这些研究认为技术创新不仅对经济增长具有直接促进作用,而且还能够通过有效提高生产率、促进产业转型升级或产生诸如新产品/服务、新技术所形成的技术领先优势来间接促进经济增长。例如李苗苗等(2015)[19]、李成刚等(2019)[20]分别使用有向无环图分析方法和动态空间杜宾模型验证了技术创新是促进区域经济增长的直接原因。2018年诺贝尔经济学奖获得者罗默和诺德豪斯将知识尤其是与技术创新相关的知识、自然与市场经济相结合,进一步强调了技术创新不仅是引领绿色发展、可持续发展的新动力,而且也是缩小"南北"差距的重要途径[21]。
纵观国内外关于技术创新与经济增长关系的研究发现,技术创新是经济持续增长的关键驱动力。关于教育与经济增长的相关研究发现,高等教育尤其是研究生教育不仅是技术创新的重要来源,而且还能增强技术吸收能力和提高R & D水平,从而促进经济高质量发展。作为高等教育金字塔顶端,研究生教育除了直接为技术创新提供优秀的高端人才外,还可直接进行自主创新。因此,它对技术创新至关重要,而技术创新是经济增长的关键驱动力,研究生教育对经济增长也应很重要,即技术创新有可能是研究生教育与经济增长间关系的中介变量。
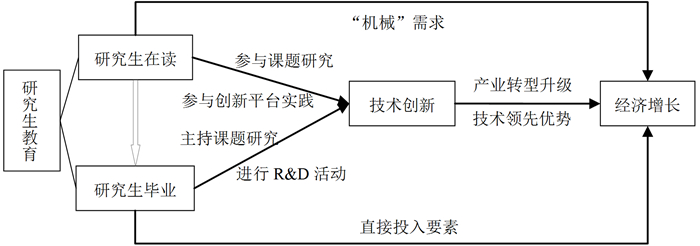
(三) 研究生教育、技术创新与经济增长的关系在借鉴国内外研究成果基础上,本文认为研究生教育、技术创新和经济增长之间的关系如图 1所示。研究生教育不仅能够通过"机械"需求和高级教育人力资本投入直接促进区域经济增长,而且还可通过技术创新来促进区域经济增长。
|
图 1 研究生教育与技术创新、经济增长的关系 |
研究生在读期间,通过直接参与科学技术创新研究的工作和实践,能够直接创造技术创新产出的同时,还能够积累各类技术创新知识、了解和掌握技术前沿,因此,不仅增强科研机构或高校所在区域的技术创新能力,而且促进该区域高质量发展。(1)通过参与导师主持的国家级、省部级等各类基础性或应用性科技创新研究项目,能够创造新思想、新知识、新技术、新材料,申请各类专利等,从而在不断积累技术创新元知识的同时,直接促进技术创新产出,提高所在区域的自主创新能力。(2)通过以助研或助岗的身份进入基础型和应用型创新平台工作,直接参与实践并了解和掌握技术前沿,不断提升自身科研实践能力。为了加快促进产学研融合发展,大学、科研机构往往与企业联合建立各类实验室、技术研究中心或工程技术研究中心等创新平台。大部分研究生在校期间能够以助研或助岗的身份进入上述创新平台工作,直接参与技术应用研究开发的实践,及时了解和掌握技术前沿,为毕业后参与R & D工作奠定良好基础。(3)还可以通过更加"机械"的需求渠道直接影响所在区域的经济增长。在校研究生通过生活、学习等方面的消费,增加了对当地产品和服务的购买,从而直接对当地的经济增长产生积极的影响。尤其是当一所新研究机构、新大学校区入驻某一区域时,或者当研究生教育机构的运营经费主要来自国家政府部门(或其它地区政府部门)提供的资金时,研究生教育与该地区的经济增长之间关系更强[1]。
研究生毕业之后,成为高质量的人力资本,不仅可以直接作为生产投入要素直接参与生产部门的生产活动,而且还可以直接补充、壮大科研队伍,增加所在区域的高质量人力资本存量、提升该区域技术创新能力,进而促进该区域高质量发展。依据教育部统计数据显示,自1999年我国扩大研究生招生规模以来,我国大学和科研机构培养研究生毕业生(含博士研究生和硕士研究生)人数由1999年的54670人迅速猛增至2018年的578045人,累计超过664.7万人,年均增长率约13.22%。这些研究生毕业后,有一部分选择去高校、科研机构工作,剩下的大部分则进入企业工作。(1)毕业后在高校、科研机构工作的研究生,通过短短几年的成长往往能够成为科研队伍当中的科研骨干、研究生导师,不仅能够承担或主持各类科学技术研究课题,还且还能够指导博士研究生、硕士研究生进行科学技术研究。因此,研究生毕业后留校或在科研机构工作能够有效提高所在单位的技术创新能力,加快单位所在区域的经济增长。(2)毕业后进入企业工作的研究生,通过不断地将学校积累的新知识、新技术转移到就业单位,往往能够参与甚至主持R & D项目,加快消化、吸收、模仿外部技术溢出的速度,直接提升所在单位的自主创新能力[22],进而促进区域经济增长。(3)毕业后的研究生作为高级教育人力资本直接投入到企业事业单位进行工作,将会直接促进所在区域经济增长,因为高级教育人力资本对区域经济增长的边际产出更大[23]。事实上,Cinnirella和Streb[24]、Barcenilla-Visús和López-Pueyo[25]分别对普鲁士经济演化、欧盟国家创新和技术追赶过程的研究也发现,高级教育人力资本不仅能够通过直接的生产渠道促进经济增长,而且还可通过技术创新来间接地促进经济增长。
三、研究设计 (一) 模型构建首先,本文整合了柯布-道格拉斯(Cobb-Douglas)生产函数和诺贝尔经济学奖得主荷兰学者丁伯根(Jan Tinbergen)的生产函数模型,将时间趋势和研究生教育变量纳入C-D生产函数,获取总量水平的基础动态模型如下:
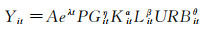
|
(1) |
其中Yit为第t(t=1, 2, …, T)期第i (i=1, 2, …, n)个地区的实际产出;K、L、PG、URB分别为物质资本存量、人力资本、研究生教育和城镇化水平;α、β、η和θ分别为对应的弹性系数;A为常数,eλt为时间趋势项。该模型表明随着时间的推移,某要素对经济增长的贡献呈指数形式变化。为便于回归分析,将式(1)两边取对数变换后的基础回归方程如下:
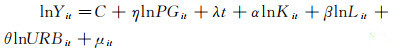
|
(2) |
其中C为常数,μit为残差项。
由于上述式(2)不能消除规模经济效益或者修正多重共线性等问题,本文借鉴黄海军和李立国(2012)[11]的做法,将式(1)取劳动力平均水平以控制地区规模经济(设定规模经济不变,即α+β=1)的影响。平均水平的基础动态模型如下:
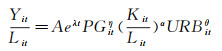
|
(3) |
同理,两边取对数变换后的基础回归方程如下:
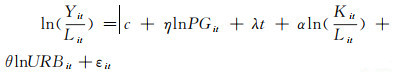
|
(4) |
其次,为了辨清我国研究生教育(PGit)是否通过技术创新(Pateit)对经济增长产生影响的问题,本文借鉴张秀武等(2018)[26]采用的中介效应检验方法,在式(2)的基础上逐步构建以下两个递归方程进行检验:
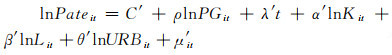
|
(5) |
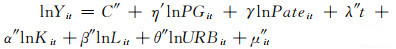
|
(6) |
同理在式(4)基础上逐步构建以下两个递归方程进行检验:

|
(7) |
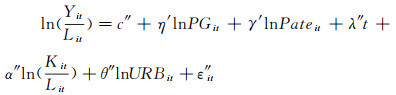
|
(8) |
最后,为了整个中介效应的检验过程更加全面,本文结合Sobel检验、Aroian检验和Goodman检验,具体分四个步骤展开:第一步,对总效应的检验。分别对式(1)和式(4)进行检验,若参数η统计显著,则继续下一步检验;否则,由于不具备中介效应的检验条件,可直接终止检验。第二步,分别对式(5)、式(6)和式(7)、式(8)进行检验,若参数ρ和γ′均统计显著,则满足中介效应必然存在的条件,继续进行下一步检验;否则,若其中有一个统计不显著,则直接跳到最后一步检验。第三步,依据上述检验结果,若参数η′统计不显著,表明存在完全中介效应,即自变量PGit对Yit产生影响只能通过中介变量Pateit才能起作用。若参数η′统计显著,表明存在部分中介效应,即在自变量PGit对Yit产生的影响中,有一部分是通过中介变量Pateit起作用的,且中介效应的大小为ργ′/(ργ′+η′)。第四步,进行Sobel检验、Aroian检验和Goodman检验,若检验结果统计显著,表明存在中介效应,可返回上述第三步计算参数值;否则,不存在中介效应。其中三种检验的统计量的值如下(其中Sγ′、Sρ分别为参数γ′和ρ的标准差):Sobel检验的Z值

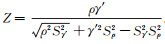
另外,本文采用计量经济学软件Eviews8.0对面板数据进行回归分析,采用统计软件SPSS18.0计算上述三种检验的Z值及其统计显著性。
(二) 数据的选择及描述性分析 1. 经济增长(Yit)现有学者使用频次最高的一个度量指标是实际国内生产总值[15, 22],本文也采用这一指标进行度量。为了剔除价格因素的影响,通过对2014—2018年的《中国统计年鉴》中30个省市(因数据缺失较多,西藏自治区的数据并未纳入其中)名义GDP进行了不变价格计算,获得以2013年为基期实际GDP(GDPit)。人均GDP则直接采用30个省市的以2013年为基期实际人均GDP(PGDPit),如表 1所示。
| 表 1 研究变量及其描述性统计结果 |
研究生入学率、在校生数或毕业生数等是现有研究测度研究生教育的常用度量指标,但是这些指标都只是研究生教育过程的不同横断面。事实上,研究生教育到底培育多少具有综合能力的研究生,最终体现在授予学位数量方面。因此,结合数据可得性问题,本文借鉴方超和罗英姿(2017)[17]选取的度量方式,采用30个省市高等学校(机构)年授予博士、硕士研究生学位数量作为度量变量,数据来源于中国教育部发展规划司的教育统计数据,时间跨度为2013—2017年。
3. 技术创新(Pateit)关于技术创新的代理变量,现有学者们广泛采用专利数量作为度量指标[27]。相比较于专利授权量,专利申请数量更加具有时效性,能够及时地反映出各地区的技术创新水平[28]。本文选用专利(含发明专利、实用新型专利和外观设计专利)申请数量作为技术创新的代理变量。数据来源于2014—2018年《中国统计年鉴》。
4. 控制变量首先,物质资本存量(Kit)。借鉴王小鲁等(2009)[29]做法,选用全社会固定资产投资作为度量物质资本投资的基本指标。同样,为了剔除价格因素的影响,本文通过对2014—2018年《中国统计年鉴》中30个省市"全社会固定资产投资实际到位资金"进行不变价格计算,获得以2013年为基期的实际物质资本投资。以戈登史密斯(Goldsmith)提出的永续盘存法进行测算:Kit=FIit+Kit-1*(1-σ),i、t同上;其中FI为实际物质资本投资,初始2013年K0等于FI0除以FI年均增长率和投资折旧率σ(取σ=15%)的和。其次,我国30个省市的人均物质资本存量(PKit)等于各地区物质资本存量(Kit)除以各地区年末人口数(Lit)。最后,本文还借鉴Cinnirella和Streb(2017)[24]的做法,将城镇化率(URBit)作为其中的一个控制变量,选取了"各地区年末城镇人口比重"进行度量。上述指标的数据均来源于2014—2018年《中国统计年鉴》。
四、实证分析 (一) 数据平稳性检验为了解决数据的不稳定性和可能存在的异方差性问题,结合上述构建的模型,本文对被解释变量、核心解释变量、中介变量和控制变量均采用了对数化处理,并采用统计软件Eviews8.0对其进行了面板数据单位根检验,结果发现所有变量均可认为具有较好的稳定性,如表 2所示。
| 表 2 变量的单位根检验 |
面板数据回归模型在一定程度上能够解决遗漏变量偏误的问题,故依据上述式(2)、式(4)~式(8),本文构建了含有个体的面板数据回归模型。首先,通过对构建的面板数据模型进行经典的豪斯曼(Hausman)检验,最终发现构建的所有含个体的面板数据模型接受原假设的概率均大于5%,因此,本文选用了含有个体的随机效应模型。此外,为了防止模型残差存在个体间的异方差和同期相关性,本文采用White截面加权法进行估计,如表 3所示。
| 表 3 研究生教育、技术创新与经济增长之间关系的回归结果 |
在未考虑中介效应模型I和模型IV中,研究生教育(PG)分别对实际地区生产总值(GDP)和实际人均地区生产总值(PGDP)均产生显著的积极影响,弹性系数估计值分别约为0.05和0.07,且都在0.01水平下统计显著。在考虑中介效应模型III和模型VI中,参数估计值分别约为0.04和0.05,且分别在0.05和0.01水平下统计显著。黄海军和李立国(2012)测算的1996—2009年我国研究生教育变量或知识资本的弹性系数介于0.018~0.033之间[11]。李锋亮和袁本涛(2013)测算的2003—2009年我国研究生教育的弹性系数为0.023,但东部地区的研究生教育弹性系数为0.04[12]。由此可以判定,无论是在未考虑中介效应的模型中还是在考虑中介效应的模型中,本文测算的2013—2017年我国研究生教育经济产出弹性系数基本上处于合理范围内。
2. 研究生教育通过技术创新对经济增长的间接效应依据式(5)~式(8)所构建的面板数据模型分别为表 3中模型Ⅱ、模型Ⅲ、模型Ⅴ和模型Ⅵ,目的是检验技术创新的中介效应。结果显示在模型Ⅱ和模型Ⅴ中,变量ln(PG)对ln(Pate)的影响系数分别在0.05、0.01水平下统计显著;并且在模型III和模型VI中,ln(Pate)对ln(GDP)、ln(PGDP)的影响系数分别在0.05、0.01水平下统计显著。表明无论是否剔除规模经济的影响,在研究生教育影响经济增长的过程中,技术创新的中介效应确实存在。为了进一步验证中介效应的存在,相应的Sobel检验、Aroian检验和Goodman检验值分别约为1.77、1.71、1.85和2.56、2.53、2.28,分别在0.01、0.01、0.01和0.05、0.05、0.001的置信水平统计显著。从而证实了研究生教育能够通过技术创新对经济增长产生间接效应,并且这一效应占总效应比例分别为21.74%和30.80%。一方面,研究生教育的目的之一是为社会培育大批综合型高端人才,加快社会高端人力资本的积累。与此同时,个体通过研究生阶段的学习,不断积累新知识和前沿新技术,加快提升自身人力资本质量。另一方面,通过研究生阶段的教育和培训,获得研究生相应学位的毕业生加入社会经济发展的过程中,直接参与新知识创造、技术研发、新产品开发等工作,从而通过技术创新能够间接地促进经济发展。
3. 控制变量对经济增长的影响首先,在构建的所有模型中,时间变量t对被解释变量(包括ln(GDP)、ln(PGDP)、ln(Pate))均具有显著的统计学意义,表明随着时间的推移,我国经济发展和技术创新已形成较为稳定的增长惯性。其次,在模型Ⅰ和模型Ⅲ中,物质资本存量(ln(K))、劳动力(ln(L))要素的平均经济产出弹性分别约为0.62和0.42,二者之和略等于1,基本上处于规模经济状态;城镇化率(ln(URB))的平均经济产出弹性约为0.55。值得注意的是,物质资本存量对经济增长的贡献显著大于劳动力要素的贡献。在模型IV和模型VI中,人均物质资本存量(ln(PK))的平均经济产出弹性约为0.57,以此推算出劳动力的经济产出弹性约为0.43。城镇化率(ln(URB))的平均经济产出弹性约为0.62。综上,尽管现有研究对发达国家资本存量的测算结果约在0.2~0.4之间,但是张秀武等(2018)对我国物质资本存量的经济产出弹性的估计为0.55~0.60之间[26]。郑鑫(2014)测算的1990—2011年我国城镇化的经济产出弹性范围在0.23~0.72[30]。因此,本文关于物质资本存量、劳动力和城镇化率对我国经济产出弹性的估计结果基本正确。在既定条件下,当资本、劳动力或城镇化分别变化1%时,将会分别引起经济发展变化率约为0.6%、0.4%和0.59%的变化。
4. 各要素对年均经济增长的贡献率研究生教育、技术创新等各要素对经济增长的贡献到底有多大?针对这一问题,本文对式(6)两端取全微分,则有: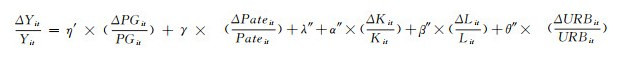

|
(9) |
其中y、pg、pate、k、l、urb分别是GDP年均增长率、研究生授予学位数年均增长率、专利申请年均增长率、资本存量年均增长率、劳动力年均增长率和城镇化年均增长率,如表 4所示。2013—2017年各变量的年均增长率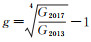
| 表 4 各指标年均增长率 |
| 表 5 各投入要素对我国经济增长的贡献率 |
对表 4和表 5进行观察不难发现:既定条件下,在2013—2017年间,首先,城镇化是我国经济增长的最大贡献者(全国平均值约为15.62%)。这表明近年来,随着新型城镇化战略的不断实施,诸如生态新城、大学城等各类新城新区的深入发展,城镇化强有力的拉动消费、扩大内需,已成为经济发展的巨大推动力[31]。其次,资本存量和技术创新对经济增长的贡献仅次于城镇化的贡献。尽管专利申请的弹性系数较小(约为0.035),但由于在2013—2017年间,全国专利申请数量年均增长率约达17. 31%,最终呈现技术创新对经济增长的贡献相对较大。这表明随着我国创新驱动发展战略的实施,诸如创新型/智慧型城市、创新中心等各类创新区域的蓬勃发展,技术创新强有力地推动了区域产业结构转型升级,不断缩短与前沿技术、国际领先技术的技术差距[18]以及关键攻关技术的突破,因此,技术创新对驱动经济发展的贡献将逐渐超过物质资本的贡献。最后,研究生教育对经济增长的贡献率约为4.71%,并且表现出在东部地区最大、依次向中西部地区递减的明显区域特征。尽管研究生教育的弹性系数较小(约为0.04),远低于资本存量和人力资本的弹性系数(分别约为0.62和0.42),但是近年来,研究生教育的快速扩张,不仅能够增强自身的技术创新能力,带动相关企业进行技术攻关,而且还为经济和社会发展提供了大量的创新型人才,从而有效地推动了我国经济快速发展。至于研究生教育对经济增长的贡献呈现明显的地区差异特征,主要的原因可能是研究生往往具有更频繁的流动性和更多地点的选择性。毕业于中、西部地区的研究生大部分选择去那些机遇较多、环境良好、待遇优厚的东部地区就业,即存在"孔雀东南飞"人才流失的现象,从而对本地区经济社会发展的带动作用远不及对东部地区的贡献。此外,劳动力对经济增长的贡献率最低,约为3.23%。该结论印证了,随着我国"人口红利"的不断消失,普通劳动者对经济发展的贡献将逐渐减少。
五、结论本研究基于2014—2018年《中国统计年鉴》中30个省市的面板数据,运用面板数据回归模型分析了研究生教育、技术创新与经济增长之间的关系。实证结果表明:
其一,我国研究生教育对经济增长(包括实际GDP和人均GDP)具有直接的促进作用,弹性系数大约在0.04~0.07之间。无论是否控制规模经济的影响,技术创新是研究生教育影响经济增长(包括实际GDP和人均GDP)的中介变量,并且这一效应占总效应的比例分别为21.74%和30.80%。从这一角度证实了许多地方尤其是那些缺乏"双一流"高校、科研院所的地方,政府出台相应政策吸引研究生教育机构入驻相对有效。
其二,各投入要素对经济增长贡献率的测算结果表明,城镇化是目前我国经济增长的最大贡献者(全国平均值约为15.62%),其次是资本存量和技术创新的贡献,并且物质资本存量对经济增长的贡献显著大于劳动力要素的贡献。研究生教育对经济增长的贡献率约为4.71%,并且表现出在东部地区最大、依次向中西部地区递减的明显区域特征。因此,进一步验证了随着我国新型城镇化战略的实施,目前城镇化强有力的拉动消费、扩大内需,并已成为经济发展的巨大推动力。
其三,控制变量的实证分析表明,在既定条件下,资本、劳动力和城镇化对经济增长均具有促进作用。随着时间推移,我国的经济发展和技术创新之间已经形成较为稳定的增长惯性。因此,进一步验证了随着我国创新驱动发展战略的实施,我国与前沿技术、国际领先技术的技术差距不断缩短,部分重大/关键攻关技术陆续得到突破,技术创新驱动我国经济发展的作用越来越大。
值得注意的是,本研究主要探讨了研究生教育、技术创新和经济增长之间的关系,由于数据的局限性,并未对研究生教育的空间布局、不同省市差异性、时段等进行控制。为此,在后续的研究中,需要进一步探讨研究生毕业后的空间配置、不同省市差异性或不同时段对研究生教育、技术创新和经济增长之间关系的影响。
注释:
① 以2000年国家制定西部大开发战略后的地区划分为准,其中东部地区包括北京市、天津市、河北省、辽宁省、上海市、江苏省、浙江省、福建省、山东省、广东省和海南省等11个省市;中部地区包括山西省、吉林省、黑龙江省、安徽省、江西省、河南省、湖北省和湖南省等8个省;西部地区包括四川省、重庆市、贵州省、云南省、陕西省、甘肃省、青海省、宁夏、新疆、广西和内蒙古等11个省市区。
| [1] |
Valero A, Reenen J V. The Economic Impact of Universities: Evidence from Across the Globe[J]. Economics of Education Review, 2019, 68(1): 53-67. |
| [2] |
崔玉平. 中国高等教育对经济增长率的贡献[J]. 北京师范大学学报(社会科学版), 2000(1): 1-5. |
| [3] |
樊星, 马树才. 中国区域高等教育对经济增长贡献率的时空特征研究——基于中国省域面板数据的实证分析[J]. 中国高教研究, 2017(8): 74-79. |
| [4] |
李锋亮, 王瑜琪. 研究生教育规模对经济增长影响的实证研究——基于国别面板数据[J]. 中国高教研究, 2020(8): 43-49. |
| [5] |
叶茂林, 郑晓齐, 王斌. 教育对经济增长贡献的计量分析[J]. 数量经济技术经济研究, 2003(1): 89-92. DOI:10.3969/j.issn.1000-3894.2003.01.019 |
| [6] |
Zhou G Y, Luo S M. Higher Education Input, Technological Innovation, and Economic Growth in China[J]. Sustainability, 2018(10): 1-15. |
| [7] |
吴东姣, 马永红. 我国研究生教育规模对第三产业经济发展影响的实证研究[J]. 学位与研究生教育, 2019(2): 18-23. |
| [8] |
杜育红, 赵冉. 教育在经济增长中的作用: 要素积累、效率提升抑或资本互补[J]. 教育研究, 2018, 39(5): 29. |
| [9] |
郭立强. "985工程"推动了地方经济发展吗?——基于双重差分和合成控制法的分析[J]. 教育与经济, 2019, 35(5): 77-84. |
| [10] |
毛洪涛, 马丹. 高等教育发展与经济增长关系的计量分析[J]. 财经科学, 2004(1): 92-95. DOI:10.3969/j.issn.1000-8306.2004.01.020 |
| [11] |
黄海军, 李立国. 我国研究生教育对经济增长的贡献率[J]. 高等教育研究, 2012(1): 57-64. |
| [12] |
李锋亮, 袁本涛. 研究生教育与我国经济增长的匹配关系[J]. 北京大学教育评论, 2013, 11(3): 78-84. DOI:10.3969/j.issn.1671-9468.2013.03.006 |
| [13] |
Barro R J, Lee J W. A New Data Set of Educational Attainment in the World, 1950~2010[J]. Journal of Development Economics, 2013, 104: 184-198. DOI:10.1016/j.jdeveco.2012.10.001 |
| [14] |
赖明勇, 张新, 彭水军, 等. 经济增长的源泉: 人力资本、研究开发与技术外溢[J]. 中国社会科学, 2005(2): 32-46. |
| [15] |
杨建芳, 龚六堂, 张庆华. 人力资本形成及其对经济增长的影响[J]. 管理世界, 2006(5): 10-18. |
| [16] |
聂娟, 辛士波. 我国高等教育质量差异化及对区域经济增长的效应分析[J]. 中国软科学, 2018(11): 58-65. DOI:10.3969/j.issn.1002-9753.2018.11.007 |
| [17] |
方超, 罗英姿. 研究生教育对我国经济增长的影响研究——兼论研究生人力资本的空间流动性[J]. 高等教育研究, 2017, 38(2): 52-60. DOI:10.3969/j.issn.1671-1653.2017.02.008 |
| [18] |
唐未兵, 傅元海, 王展祥. 技术创新、技术引进与经济增长方式转变[J]. 经济研究, 2014(7): 31-43. |
| [19] |
李苗苗, 肖洪钧, 赵爽. 金融发展、技术创新与经济增长的关系研究——基于中国的省市面板数据[J]. 中国管理科学, 2015, 23(2): 162-169. |
| [20] |
李成刚, 杨兵, 苗启香. 技术创新与产业结构转型的地区经济增长效应[J]. 科技进步与对策, 2019, 36(6): 33-42. |
| [21] |
The Committee for the Prize in Economic Sciences in Memory of Alfred Nobel. Economic Growth, Technological Change, and Climate Change[R/OL]. The Royal Swedish Academy of Sciences, 2018, https://www.nobelprize.org/prizes/Uncatego-rized/nobel-prizesand-laureates/.
|
| [22] |
Castellani D, Piva M, Schubert T, et al. R & D and Productivity in the US and the EU: Sectoral Specificities and Differences in the Crisis[J]. Technological Forecasting & #38; Social Change, 2019, 138: 279-291. |
| [23] |
Fleisher B, Li H Z, Zhao M Q. Human Capital, Economic Growth, and Regional Inequality in China[J]. Journal of Development Economics, 2010, 92(2): 230. |
| [24] |
Francesco C, Jochen S. The Role of Human Capital and Innovation in Economic Development: Evidence from Post-Malthusian Prussia[J]. Journal of Economic Growth, 2017, 22(2): 193-227. DOI:10.1007/s10887-017-9141-3 |
| [25] |
Barcenilla-Vis & #250;s S, L & #243;pez-Pueyo C. Inside Europe: Human Capital and Economic Growth Revisited[J]. Empirica, 2018, 45(4): 821-847. DOI:10.1007/s10663-017-9394-2 |
| [26] |
张秀武, 刘成坤, 赵昕东. 人口年龄结构是否通过人力资本影响经济增长——基于中介效应的检验[J]. 中国软科学, 2018(7): 149-158. DOI:10.3969/j.issn.1002-9753.2018.07.013 |
| [27] |
Bratti M, Conti C. The Effect of Immigration on Innovation in Italy[J]. Regional Studies, 2018, 52(7): 934-947. DOI:10.1080/00343404.2017.1360483 |
| [28] |
钱晓烨, 迟巍, 黎波. 人力资本对我国区域创新及经济增长的影响——基于空间计量的实证研究[J]. 数量经济技术经济研究, 2010(4): 107-121. |
| [29] |
王小鲁, 樊纲, 刘鹏. 中国经济增长方式转换和增长可持续性[J]. 经济研究, 2009(1): 44-47. |
| [30] |
郑鑫. 城镇化对中国经济增长的贡献及其实现途径[J]. 中国农村经济, 2014(6): 4-15. |
| [31] |
张莅黎, 赵果庆, 吴雪萍. 中国城镇化的经济增长与收敛双重效应[J]. 中国软科学, 2019(1): 98-116. DOI:10.3969/j.issn.1002-9753.2019.01.009 |
2. School of Economics and Management, Dalian University of Technology, Dalian, Liaoning 116024
 2021
2021