当前,我国研究生教育发展正在进入一个战略转型期,即从以规模发展为主转变为内涵式发展为主。在这一时期,全面提高研究生教育质量成为我国研究生教育的核心任务。研究生教育质量取决于研究生的学习过程,从教育心理学的视角分析,研究生学习的有效性影响着最终的培养质量。探讨研究生的有效学习不能仅限于关注研究生学习存在的问题,必须科学地研判影响研究生有效学习的具体因素,针对性地探讨提高研究生学习质量的途径与方法。关于有效学习,之前相关学者探讨了概念界定以及学习现状、学习适应、学习投入、学习倦怠等影响因素,但在实际学习环境中,研究生的学习存在的问题众多,如学习目标低、功利性太强、学习主动性不强,创造性不强、学习方法不变等。基于此,本文试图根据硕士研究生学习实际情况,从相关理论出发,并根据《全国研究生学习体验调查问卷》以及冯延勇等人编制的大学生学习适应量表对有效学习影响因素问卷进行编制、调整、整合,将有效学习细化为学习动机、学习态度、学习环境(氛围)、学习投入、学习收获这五个维度,定性构建有效学习影响模型,实证考察影响硕士研究生有效学习的因素以及这些因素之间的关系及强度。
一、 研究方法结构方程模型可分为测量方程 和结构方程两个部分。测量方程描述潜在变量与指标之间的关系,结构方程则描述潜在变量之间的关系。
(一) 测量模型对于指标与潜在变量间的关系,通常写成如下测量方程:
| $\begin{align} & x={{\Lambda }_{x}}\xi +\delta \text{ } \\ & y={{\Lambda }_{y}}\eta +\varepsilon \\ \end{align}$ |
其中,x—外源指标组成的向量;y—内生(endogenous)指标组成的向量;Λx—外源指标与外源潜在变量之间的关系,是外源指标在外源潜在变量上的因子负荷矩阵;Λy—内生指标与内生潜在变量之间的关系,是内生指标在内生潜在变量上的因子负荷矩阵;δ—外源指标的误差项;ξ—内生指标的误差项。
(二) 结构模型对于潜在变量的关系,通常写成如下的结构方程:
| $\eta =B\eta +\Gamma \xi +\zeta $ |
其中,η—内生潜在变量;ξ—外源潜在变量;B—内生潜在变量的关系;Γ—外源潜在变量对内生前在变量的影响;ζ—结构方程的残差项。
二、 问卷设计、数据收集和样本统计为了保证问卷的可靠性,首先对江苏师范大学的硕士研究生开展了前测工作,并对文学院、美术学院、教育学院的硕士研究生进行深度访谈,确定问卷的主体部分以及具体的指标问题。随后对问卷进行审查,让导师、专家提出修改的意见,对问卷进行修改及完善;其次,再对问卷进行被试,进一步地修正完善问卷;最后形成了硕士研究生有效学习影响因素的调查问卷,共37个指标题项。整个问卷分为五个维度,分别是学习动机(5个指标题项)、学习态度(4个指标题项)、学习环境(8个指标题项)、学习投入(11个指标题项)、学习收获(9个指标题项)。问卷采用了李克特(Likert)标准五点量表,1为非常不同意,2为不太同意,3为一般,4为比较同意,5为非常同意;其中学习投入维度的五点量表划分分别为:1表示从未,2表示很少,3表示较少,4表示有时,5表示经常。本次调查共发放调查问卷350份,其中回收的有效问卷325份,有效回收率为92.8%,样本基本情况统计见表 1。
| 表 1 样本的基本情况 |
由表 1可以看出,被调查的硕士研究生的人数女生相对而言多于男生,男生占总体比例的41%,女生为59%;而硕士研究生的专业分类以文科所占比例最高,多达43.7%,与理科及工科两者之和不相上下;对于硕士研究生的入学方式以统招为主,所占比例为84.4%,推免生仅为12.5%;非跨学科生源与跨学科生源的硕士研究生比例各占67.4%、32.6%;硕士研究生入学前就读的高校绝大多数是普通高校,占总体比例的87.2%,而“985”或“211”高校所占比例仅为12.8%。
三、 实证分析在对问卷调研数据进行分析之前,首先要对问卷进行信度和效度检验。运用SPSS20.0中的信度分析对问卷的信度进行检验。对整个问卷的信度分析表明,值为0.900,表明问卷具有较高的信度。而各个维度的信度分析结果表明:学习动机、学习态度、学习环境、学习投入、学习收获5个潜在变量的值分别为0.761、0.710、0.742、0.748和0.806,均满足大于0.70的要求,并且各个指标题项与潜在变量的相关系数比较高,该问卷具有较高的一致性和可靠性。
由于对潜在变量的测量具有良好的信度和效度,因此,本文进一步展开探索性因子分析。探索性因子分析主要是为了找出影响观测变量的因子个数以及各因子和各观测变量之间的相关程度。利用SPSS20.0对全部37个影响硕士研究生有效学习的因素进行分析,由统计结果得知取样适当性系数KMO值为0.848,表示变量间的共同因素很多,适合做因子分析。此外,球形检验值为4349,自由度为666,相伴概率Sig为0.000,达到显著,由此说明指标题项与潜在变量的相关矩阵间有共同因素存在,适合进行因素分析(见表 2)。随后,本文采用最大似然法作为因子的抽取方法,选择最大方差旋转Varimax方法获得更加清晰的因子解,在进行迭代式多轮主成分因子分析后,发现大于1的特征值有10个。采用方差最大化正交旋转,旋转后因子负载荷截公共因子上最大载荷小于0.35,共同度小于0.4的指标题项进行剔除。最后的分析结果见表 3所示。根据统计数据,累计因子贡献率为64.108%,说明37个变量可以用这五个维度(学习动机、学习态度、学习氛围、学习投入、学习收获)来解释,问卷各变量之间的结构设计是合理的。
| 表 2 KMO 和Bartlett的检验 |
| 表 3 硕士研究生有效学习影响因素探索性因子分析 |
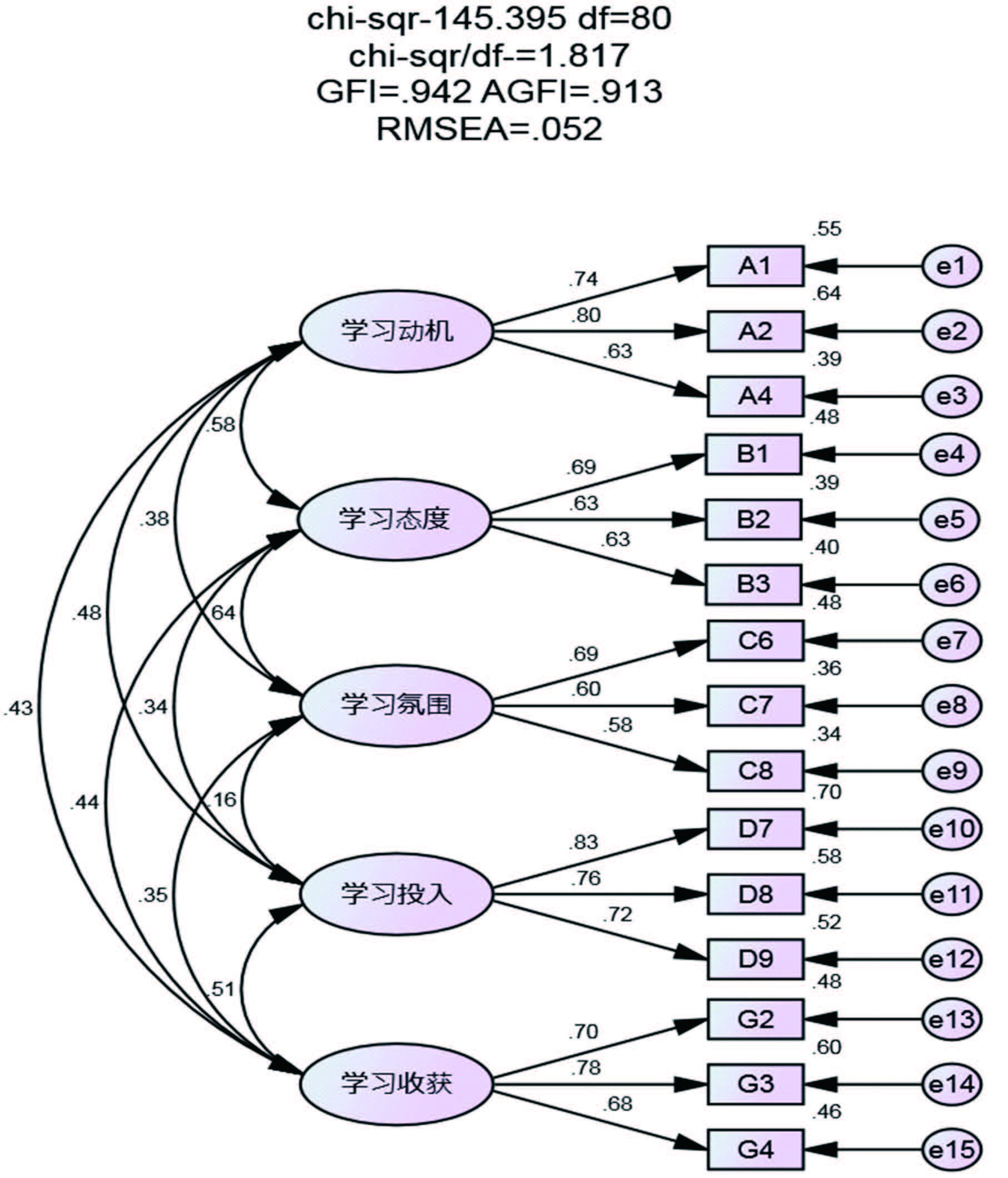
在运用探索性因子分析确定因素后,本文建立结构方程模型,进行验证性因子分析,分析的软件是Amos20.0。图 1是硕士研究生有效学习影响因素结构方程模型路径图,由图可知模型中潜在变量和观测指标之间的关系,并描述了模型路径系数。图中椭圆代表是潜在变量,矩形代表是观测变量。
|
图 1 硕士研究生有效学习影响因素结构方程模型路径图 |
为检验建立的结构方程模型是否合理,需要对一些拟合指标进行观察。在Amos中,模型迭代运算后,可从Output中查看Model Fit.从相关拟合指数评估的结果来看,拟合指数表明为一个很好的拟合数据虚拟结构。CFI为0.94,其TLI为0.91,RMSEA为0.05和90%,在0.04-0.08的置信区间。所有这3个值表示良好拟合。CFI和TLI可能低,RMSEA可能很高,可能都是来自样本的容量。所有维度加载统计显示出在对理论化的潜在变量没有修改的基础上的计算值(表 4),没有变量异常值或基于观测和复制数据的残差协方差矩阵,因此,可表明假定模型与样本数据模型适配。
四、 研究结果由图 1可知,第一,学习动机与学习态度(0.58)、学习氛围(0.38)、学习投入(0.48)、学习收获(0.43)之间呈显著正相关,各个维度之间的系数(皮尔逊相关系数)小于0.7,故维度之间没有受到共线性的影响。因此并未造成模型的卡方值上升,也没有得到负的方差及出现不合理的估计值。第二,学习态度与学习氛围(0.64)、学习投入(0.34)、学习收获(0.44)之间呈显著正相关。第三,学习氛围与学习投入(0.16)、学习收获(0.35)之间呈显著正相关。第四,学习策略与学习投入(0.51)之间呈显著正相关。
| 表 4 验证性因素分析 |
由表 4可知,估计值都大于0,没有负数出现,说明各个维度之间并没有违反估计;P值都达显著(P<0.001),说明模型与样本数据假设相一致;对于标准化状态下的各个维度之间的因素负荷量都大于0.6,说明各维度与指标题项之间显著相关;SMC(多元相关平方)的值在0.34-0.7之间,在可接受的标准范围内,因此说明模型研究假设成立。其次,各个维度都有其影响最大的指标系数,学习动机维度中指标题项系数最高的是A2(得到尊重0.80),说明观测变量A2对潜在变量(学习动机)的影响力最高;学习态度维度中指标题项系数最高的是B1(课程作业敷衍0.69),说明观测变量B1对潜在变量(学习态度)的影响力比其他的观测变量较高;学习氛围维度中指标题项系数最高的是C6(导师的激励0.69),说明观测变量C6对潜在变量(学习氛围)的影响力最大;学习投入维度中指标题项系数最高的是D7(阅读专业文献0.83),说明观测变量D7对潜在变量(学习投入)的影响力比其他的观测变量都高;学习收获维度中指标题项系数最高的是D3(管理时间能力0.78),说明观测变量D3对潜在变量(学习收获)的影响力比其他的观测变量都大。
综上所述,硕士研究生有效学习首先应从学习动机与学习氛围进行有效调整,使得正确的学习动机与学习氛围成正比;其次,从学习态度与学习投入方面进行加强,有一个端正的学习态度,是学习投入更有效的前提;同时还需从学习氛围与学习投入两者之间进行分析,使得学习环境更好,学习收获更多。
五、 对策建议基于以上的研究结果,为了更有效地促进研究生有效学习,特提出以下对策建议:
(一) 完善高校奖助学金制度,激发学习动机硕士研究生继续深造需要承担一定压力,尤为突出的便是经济压力。相当数量的硕士研究生放弃了原本优越的工作,来继续学习,在社会人向在校生转变的过程中,经济来源成为研究生需要考虑的一个重要因素。根据马斯洛需要层次理论,个体的生理需要得到满足是高层次需要得以实现的前提与保障,奖助学金作为满足硕士研究生生理需要的一项重要经济来源,特别是家庭经济困难研究生顺利完成学业的重要保障,作为我国现代研究生制度建设的重要内容,各高校应当给予足够重视,完善奖助学金制度,在保证公平公正的基础上,适度增加奖助学金数额、种类以及覆盖范围,以减缓硕士研究生生活压力,确保硕士研究生不会被经济问题所困扰,能够全身心地投入到学习过程中去,研究生的学习动机因此便会进一步提高,奖助学金制度成为硕士研究生有效学习的“催化剂”的效果得以更加显现。
(二) 积极参与课题讨论,培养良好学习态度硕士研究生的学习过程是自主的学习,导师或任课教师均是学习活动的客体,硕士研究生是学习主体。因此,在学习过程中,硕士研究生应当积极参与课堂讨论、学术论坛以及课题研究,在思想碰撞中摩擦出智慧的火花,在潜移默化中培养自身良好的学习态度,从而更加有效地学习。
(三) 强化导师激励作用,充分保障学术资源导师是研究生培养过程中一个重要的影响因素,导师在与研究生之间的交流合作过程中所体现的学术兴趣、治学态度、道德品质等对研究生学习都会产生潜移默化的影响。同时导师对研究生的激励作用也是不可小觑的,导师对研究生适时的鼓励及表扬将对研究生的精神层面产生莫大的鼓舞作用,进而对研究生的有效学习起到正向推动作用。因此,师生间的良好关系是硕士研究生建立正确的学习动机、学习态度、学习兴趣的有效助推器。学校的学术资源是硕士研究生进行有效学习的基本前提,学术资源不仅局限于图书资源,还有数据库资源、教学设备等,因此,学校需保障学术资源的宽度及深度,为硕士研究生有效学习提供广泛的资源。
(四) “专攻”与“博览”相结合,培养高效学习方式硕士研究生学习过程中要把“专攻”与“博览”有效结合,对于本专业的文献资料的学习需要“专攻”,而对于跨专业的知识则需“博览”,这样不仅增加了自我学习的广度及深度,也提高了自身的学术素养,更增强了学习能力。只有两者进行有效合理的结合,才会使得学习变得游刃有余。
本研究只选取了影响硕士研究生有效学习的五个维度进行分析,而硕士研究生有效学习影响因素中学习策略及学习风格等都会影响研究生有效学习,由于没有进行相关数据的调查而未纳入分析,后续研究中将会弥补这一缺陷。同时也会扩充样本数据的宽度及数量,在后续研究中还可在客观的统计建模分析的基础上,结合SEM的中介调节作用,用CMV进行共同方法变异检定,使得分析的结构模型及测量模型更稳定,以用于有效地提高硕士研究生有效学习影响因素的准确性。
| [1] | 候杰泰, 温忠麟, 成子娟著. 结构方程模型及其应用[M]. 北京: 教育科学出版社 , 2002 . |
| [2] | 谢晖, 雷井生. 知识型企业智力资本结构维度研究——基于知识创造过程的实证分析[J]. 科学学研究 , 2007 (7) : 1067–1076. |
| [3] | 宋志红, 范黎波. 模仿吸收能力和创新能力关系的实证研究[J]. 华东经济管理 , 2010 (9) : 153–157. |
| [4] | 张奇编. SPSS for windows在心理学与教育学中的应用[M]. 北京: 北京大学出版社 , 2008 : 301 . |
| [5] | 吴明隆. 结构方程模型——AMOS的操作与应用 重庆:重庆大学出版社[M]. 北京: 北京大学出版社 , 2010 : 21 -52. |
| [6] | 符洁.研究生学习倦怠与专业承诺关系及影响因素的研究[D].西北大学,2010. http://cdmd.cnki.com.cn/article/cdmd-10697-2010118853.htm |
| [7] | 仲雪梅.我国研究生学习投入的影响因素分析[D].华中师范大学,2011. |
| [8] | 陈燕.对当前大学生学习倦怠及其影响因素的研究[D].上海师范大学,2007. http://cdmd.cnki.com.cn/article/cdmd-10270-2007200266.htm |
| [9] | Hu L-T, BentlerPM. Cutoff criteria for fit indices in covariance structure analysis:conventional criteriaversus new alternatives[J]. StructEqu Model , 1999 (6) : 1–55. |
| [10] | Sivo SA, Fan X, Witta LE, Willse JT. The search for optimal cutoff properties:fit index criteria in structural equation modeling[J]. J ExpEduc , 2006, 74 (3) : 267–288. |
| [11] | James B.Schreiber, Ph.Schreiber, Ph .D. Core reporting practices in structural equation modeling[J]. Science direct:Research in social and Administrative Pharmacy 4 , 2008 : 83–97. |
 2016
2016