星载重轨干涉SAR是在星载SAR成像技术基础上的进一步应用，目前在全球范围的高程测绘和形变测量中起到关键作用(曾琪明 等，2018)。重轨干涉需要卫星对同一成像区域进行至少两次的重复观测，对观测角度、基线长度都有严格要求(鞠冰 等，2017)。然而由于全球观测的需要，卫星重访周期一般都在十几天到几十天，在此过程中卫星受到大气阻力、地球非球形引力、日月引力等摄动因素影响，飞行轨道会偏离预定轨道，造成重访轨道的偏移，直接影响了干涉基线的构形(包括长度和方向)。现有对卫星运行状态的控制基于单颗卫星的飞行状态，能够保证重访的时间和空间位置的一般要求，然而对于重轨干涉，由于至少两次的重访中基线的构形相对成像中卫星的位置有着更高的要求，基于单颗卫星的控制方法难以达到基线的精度和构形的要求，因此需要用相对轨道控制的方法来得到和保持基线构形。相对轨道运动最早由Clohessy和Wiltshire的C-W方程描述(Clohessy，1960)。该方程是在近圆轨道、无摄动且距离较近假设基础上的分析，在短时间有较高的精度，然而由于误差累积，误差随时间逐渐增大。在原始C-W方程的基础上，Vaddi等(2003)考虑了相对运动中高阶非线性项的影响，Schweighart提出了在大气阻力和J2摄动下的C-W方程(Sedwick和Schweighart，2001)。另外一类基于轨道根数的相对轨道控制方法，适用于对长周期的偏差进行补偿，采用相对轨道根数偏差，Naasz(2002)推导了几种相对轨道控制方法。由于轨道根数是卫星运动状态的积分项，在短周期内较为稳定，因此对卫星运行有较强的预测能力，并且在轨道控制策略制定时更能够全局规划，均衡控制。然而，在制定控制策略时必然要将根数偏差转换为位置速度，转换过程中可能存在精度损失，但随着摄动模型精度和计算能力的提高，基于相对轨道根数的控制方法得到了更广泛的应用(Rodriguez-Cassola 等，2011)。

受到摄动因素的影响，在一个重访周期内卫星偏移导致干涉基线变大而产生较大的去相干。为了达到SAR干涉要求的精度，飞行器的飞行轨迹必须保持在距离预定轨道一半临界基线之内。对于C波段卫星，例如RADARSAT-2，ENVISAT，干涉基线选取一般在1 km以下，并且多数在200 m以下(McLeod 等，1998)。对于基线稳定性较高，具有代表性的X波段SAR卫星TerraSAR-X，基线严格保持在250 m以内，当在50—100 m时具有最好的干涉效果(Krieger 等，2007；Montenbruck 等，2008)。高分三号是C波段SAR卫星，以高分三号的频率，高度等参数为例，为了兼顾获取相位对高程的敏感度(基线越长相位对高程越敏感)和基线去相干的影响(基线越长去相干越严重)，对应不同观测角，基线在200—400 m为最优。

在处理过程中，计算了高分三号在北京地区2017年3月30日—2018年1月14日的5景重访观测数据的垂直基线，最大达到了2312 m，平均为1136 m，标准差为1141 m，且小于500 m的比例较小，干涉基线相比国外先进卫星过长且稳定性有待提高。

在现有重轨观测卫星控制条件下，卫星已经可以达到相对参考轨道的近距离运动。对于近距离相对运动，在垂直于轨道平面方向，利用两次观测的轨道倾角之差和升交点赤经之差来描述是直观有效的方法。在轨道平面内，为避免引入奇异值，可以通过偏心率矢量来代表偏心率和近地点幅角。这种称为基于相对偏心率/倾角矢量的相对轨道运动模型在航天器编队相对控制中得到了广泛的应用(Spurmann和D’Amico，2011)，该模型能够直接观察到相对运动的主要参量，将可长时间观测并准确获得的轨道根数转化为相对运动的距离和速度，求得基线状态；另一方面，从干涉基线需求出发，用该模型易于得出对卫星的控制策略。本文首次将其应用在单星的重复轨道观测中，将前一次的飞行轨迹作为编队的另一颗卫星，能够直接应用已有的编队运动状态研究成果。在此轨道运动模型的基础上，分析了轨道根数偏差对于基线变化规律的影响，并用实际数据验证了理论模型的正确性。针对干涉基线这个特定的问题进行了详细分析，将相对位置转化为垂直基线长度，并给出了正算(从相对根数到基线)和反算(从基线到相对根数调整)的例子。更进一步，我们利用该模型制定了实现目标基线的轨道控制策略，并进行了仿真分析。

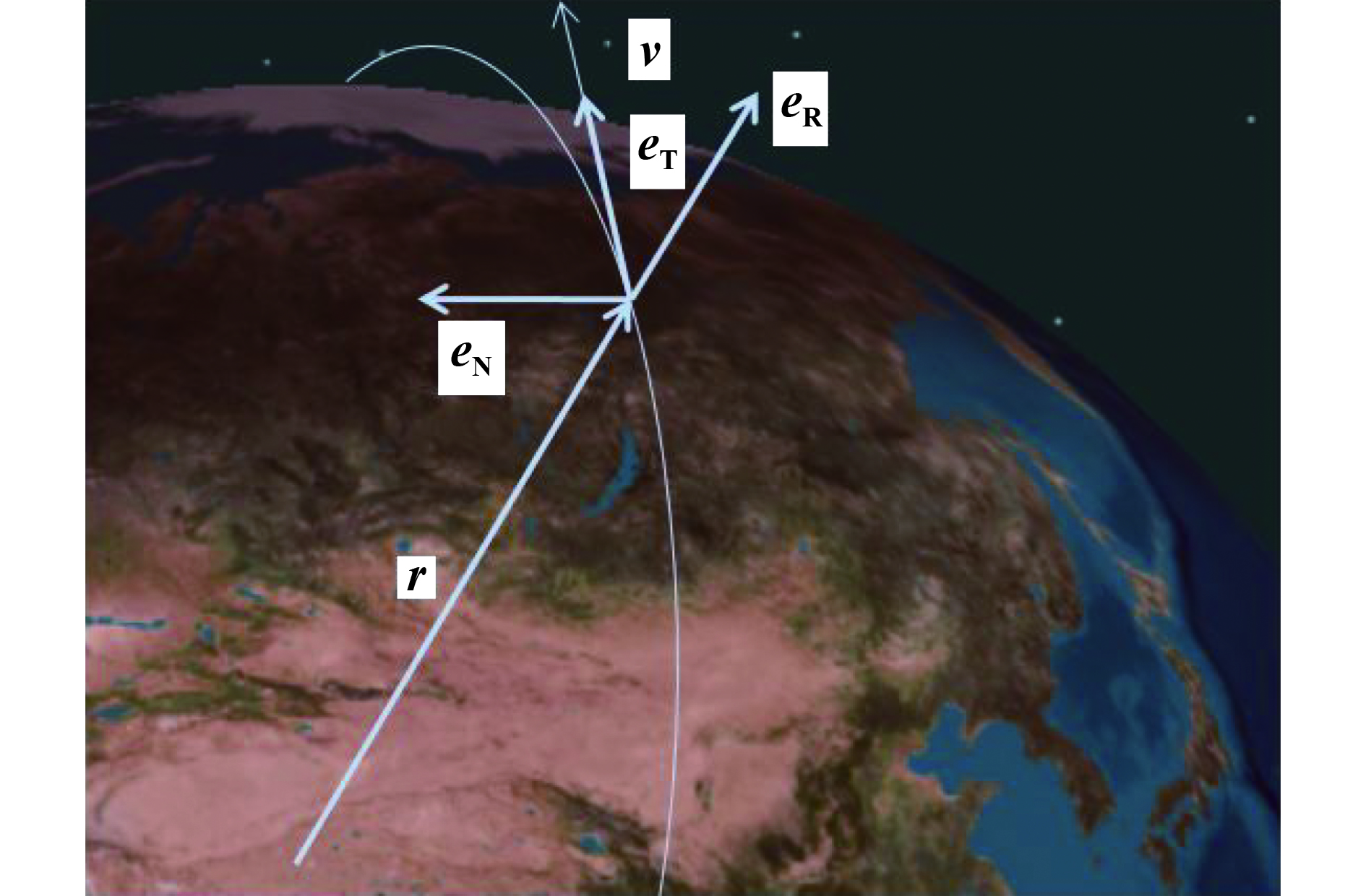
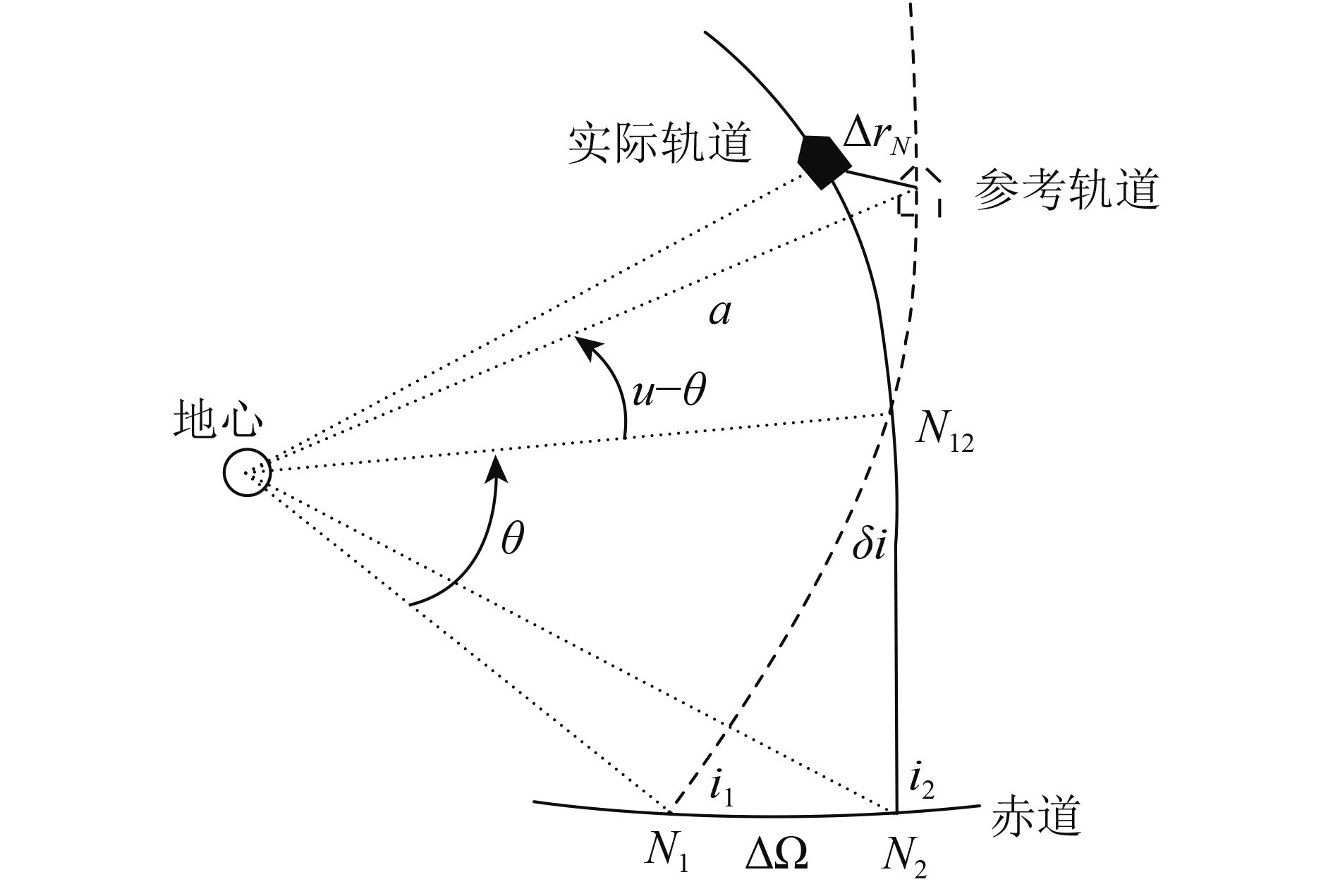
卫星飞行状态如图1所示，其中 ${v}$ 为卫星的速度， ${r}$ 为地球中心到卫星的矢量。从卫星飞行的RTN坐标系来分析卫星的运动状态，其中R的方向为从地心指向卫星， ${\rm{N}}$ 指向卫星角动量方向， ${\rm{T = N}} \times {\rm{R}}$ 指向运动方向。R, T, N方向的单位矢量分别为 ${{{e}}_{\rm{R}}}$ ， ${{{e}}_{\rm{T}}}$ ， ${{{e}}_{\rm{N}}}$ 。

设参考轨道卫星的位置在 ${{{r}}_1}$ ，卫星的实际位置为 ${{{r}}_2}$ ，则实际位置与参考轨道位置的偏差为

$\Delta {{r}} = {{{r}}_{\rm{2}}} - {{{r}}_{\rm{1}}} = \Delta {r_{\rm{R}}}{{{e}}_{\rm{R}}} + \Delta {r_{\rm{T}}}{{{e}}_{\rm{T}}} + \Delta {r_{\rm{N}}}{{{e}}_{\rm{N}}}$

(1)

式中， $\Delta \cdot $ 是差分符号。

计算在给定轨道根数的情况下 $\Delta {r_{\rm{N}}}$ 的值。后续分析需要满足两个条件，实际轨道和参考轨道都是近圆轨道( $e < \!\! < 1$ )且两者的轨道根数差分矢量 ${\rm{||(}}\Delta a/a,\Delta e,\Delta i,\Delta \Omega,\Delta \omega,\Delta u)|| < \!\! < 1$ 很小，其中a,e,i, $\varOmega,\omega,u$ 分别为半长轴，偏心率，轨道倾角，升交点赤经，近地点幅角和纬度幅角。只有在这种情况下，对于相对偏心率和两者相对位置的分析才有意义(Sengupta和Vadali，2007)。研究的近地观测SAR卫星，轨道偏心率 $e < 0.03$ ，满足近圆轨道的条件，并且在现有控制状态下，几个回归周期之内的偏差完全满足 ${\rm{||(}}\Delta a/a,\Delta e,\Delta i,\Delta \Omega,\Delta \omega,\Delta u)|| < \!\! < $ 1。

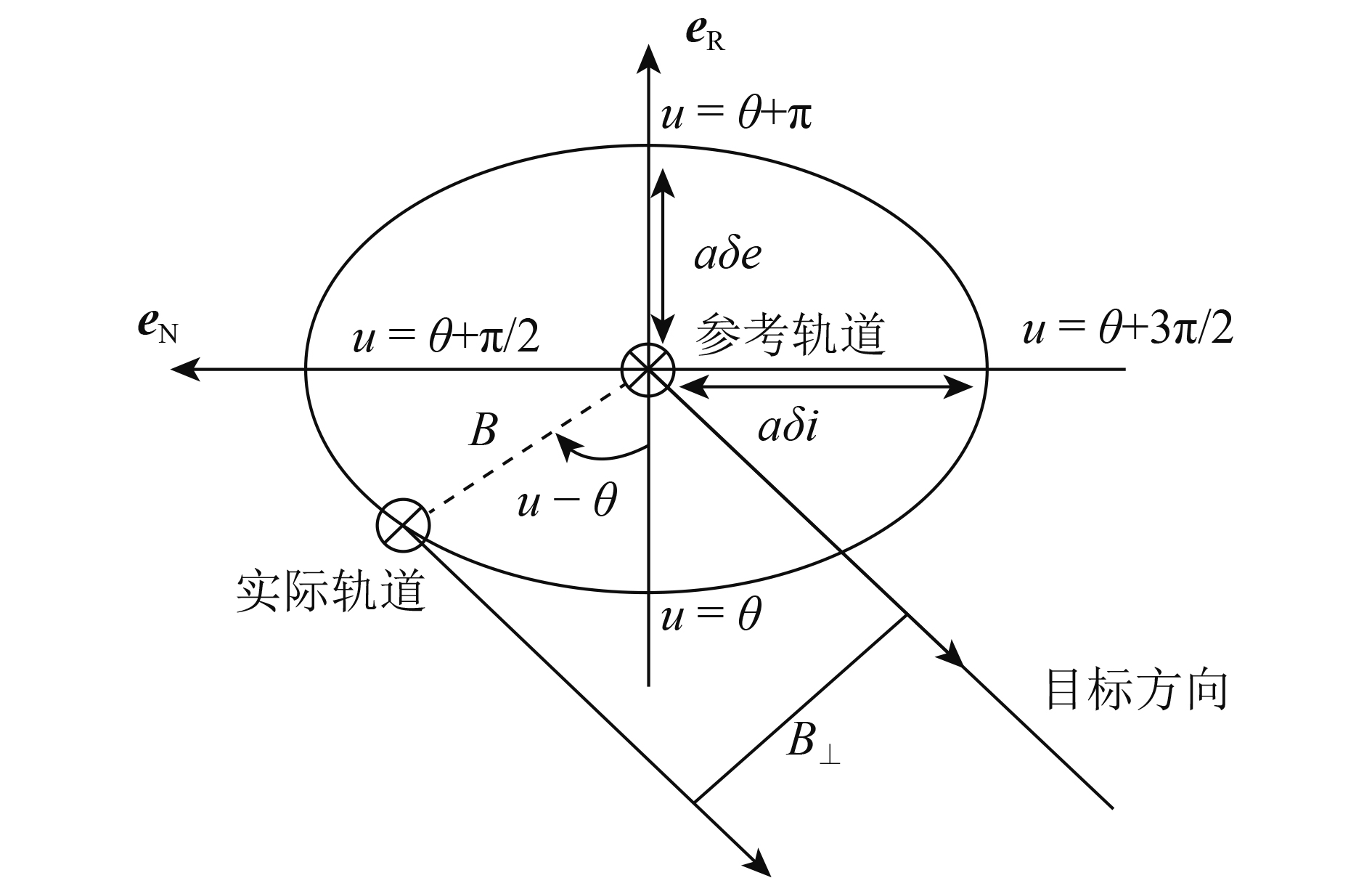
为了进一步分析受摄动因素影响下卫星的实际运行状态与参考轨道的偏差，如图2所示， $\theta $ 为实际轨道和参考轨道重合交叉点的幅角，称为相对升交点幅角， ${{{N}}_1}{\rm{,}}\;{{{N}}_{\rm{2}}}$ 分别为参考轨道和实际轨道的升交点， $\delta i$ 为轨道倾角的偏差值。

观察图2中的几何关系，可以得到

$\Delta {r_{\rm{N}}}/a = \sin (u - \theta)\sin (\delta i)$

(2)

将倾角矢量沿相对升交点幅角分解，在满足小偏差假设的条件下， $\delta i \approx \sin (\delta i)$ ， $\delta i$ 为 $\Delta {{i}}$ 的标量值，得到

$\Delta {{i}} = \left\{ {\begin{array}{*{20}{c}} {\Delta {i_{\rm{X}}}} \\ {\Delta {i_{\rm{Y}}}} \end{array}} \right\} = \delta i\left\{ {\begin{array}{*{20}{c}} {\cos \theta } \\ {\sin \theta } \end{array}} \right\} \approx \sin (\delta i)\left\{ {\begin{array}{*{20}{c}} {\cos \theta } \\ {\sin \theta } \end{array}} \right\}$

(3)

将式(3)代入式(2)，有

$\Delta {r_{\rm{N}}}/a = (- \Delta {i_{\rm{Y}}})\cos u + (\Delta {i_{\rm{X}}})\sin u$

(4)

由正余弦定理看，对顶点为 ${N_1},{N_2},{N_{12}}$ 的球面三角形，式(3)简化为

$\Delta i = \left\{ {\begin{array}{*{20}{c}} {\Delta i} \\ {\sin (i)\Delta \Omega } \end{array}} \right\}$

(5)

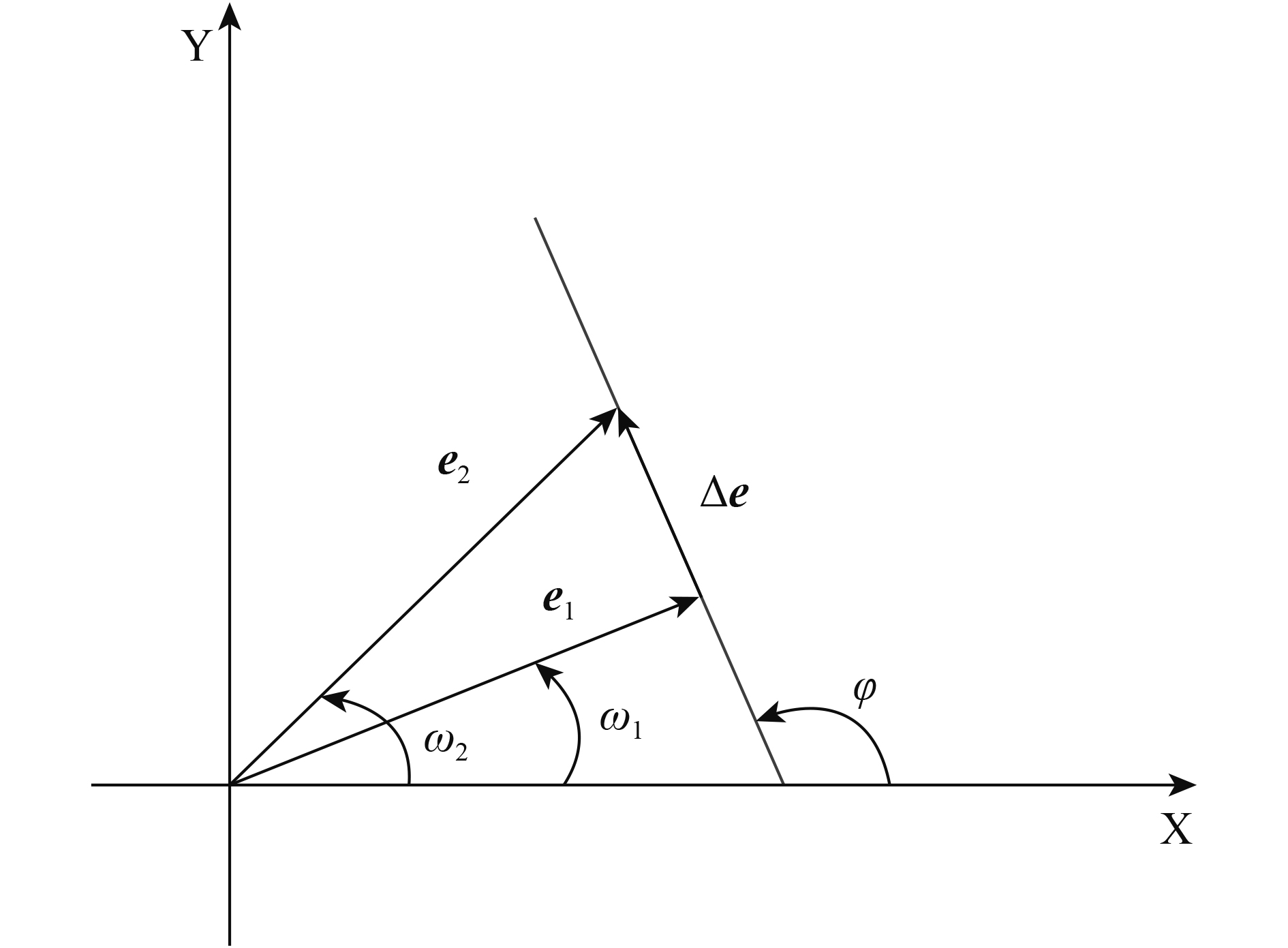
对于近圆轨道，偏心率和近地点幅角通常以偏心率矢量的形式表示

${{e}} = \left\{ {\begin{array}{*{20}{c}} {{e_{\rm{X}}}} \\ {{e_{\rm{Y}}}} \end{array}} \right\} = e \cdot \left\{ {\begin{array}{*{20}{c}} {\cos \omega } \\ {\sin \omega } \end{array}} \right\}$

(6)

在这种形式下可以避免奇点情况的存在，并且适合轨道摄动影响的分析(Cao 等，2013)。参考轨道和实际轨道的偏心率矢量差分可以表示为

$\Delta {e} = {{e}_2} - {{e}_1} = \left\{ {\begin{array}{*{20}{c}} {\Delta {e_{\rm{X}}}}\\ {\Delta {e_{\rm{Y}}}} \end{array}} \right\} = \delta e\left\{ {\begin{array}{*{20}{c}} {\cos \varphi }\\ {\sin \varphi } \end{array}} \right\}$

(7)

式中， $\varphi $ 如图3所示。

在轨道平面内，对于近圆轨道，真近点角 $f$ 和平近点角 $M$ 有(Jarnagin，1965)

$f - M = 2e\sin M = (- 2{e_{\rm{Y}}})\cos u + (2{e_{\rm{X}}})\sin u$

(8)

用平近点角表示的地心距离为

$r/a = 1 - e\cos M = (- {e_{\rm{X}}})\cos u - {e_{\rm{Y}}}\sin u$

(9)

对式(8)和式(9)分别进行差分，并在相近轨道假设下认为平近点角相同，得到

$\Delta {r_{\rm{T}}}/a \!=\! ({f_2} - {M_2}) - ({f_1} - {M_1}) \!=\! (- 2\Delta {e_{\rm{Y}}})\cos u + (2\Delta {e_{\rm{X}}})\sin u$

(10)

$\Delta {r_{\rm{R}}}/a = (- \Delta {e_{\rm{X}}})\cos u - \Delta {e_{\rm{Y}}}\sin u$

(11)

另外，在半长轴 $a$ 受到摄动的情况下， ${r_{\rm{R}}}$ 变化为摄动量 $\Delta a$ ，在卫星运行径向方向 ${r_{\rm{T}}}$ 为 $ - (3/2)\Delta a(u - {u_0})$ ，其中 ${u_0} = u({t_0})$ 为受到摄动时刻卫星的纬度幅角，在纬度幅角 $u$ 受到摄动的影响下， ${r_{\rm{R}}}$ 不变，径向 ${r_{\rm{T}}}$ 变化为 $\Delta u \cdot a$ ，结合式(11)，得

$\Delta {r_{\rm{T}}}/a \!=\! \Delta u - \frac{3}{2}(\Delta a/a)(u - {u_0}){\rm{ + }}(- 2\Delta {e_{\rm{Y}}})\cos u + (2\Delta {e_{\rm{X}}})\sin u$

(12)

$\Delta {r_{\rm{R}}}/a = \Delta a/a - (\Delta {e_{\rm{X}}}\cos u + \Delta {e_{\rm{Y}}}\sin u)$

(13)

在近圆轨道和小偏差假设的条件下，得到了轨道根数变化对RTN坐标系下卫星位置的影响。更进一步，将 $\Delta {{r}}$ 对时间微分，得到RTN坐标下的速度矢量 $\Delta {{v}}$ ，在参考轨道为参考下，实际轨道偏差量为

$ \begin{split} \left\{ {\begin{array}{*{20}{c}} \!\!\! {\Delta {r_{\rm{R}}}/a}\!\!\! \\ \!\!\! {\Delta {r_{\rm{T}}}/a}\!\!\! \\ \!\!\! {\Delta {r_{\rm{N}}}/a}\!\!\! \\ \!\!\! {\Delta {v_{\rm{R}}}/v}\!\!\! \\ \!\!\! {\Delta {v_{\rm{T}}}/v}\!\!\! \\ \!\!\! {\Delta {v_{\rm{N}}}/v}\!\!\! \end{array}} \right\} = &\left[ {\begin{array}{*{20}{c}} \!\!\! {\Delta a/a}&0&{ - \Delta {e_{\rm{X}}}}&{ - \Delta {e_{\rm{Y}}}}\!\!\! \\ \!\!\! {\Delta u}&{ - 3\Delta a/2a}&{ - 2\Delta {e_{\rm{Y}}}}&{2\Delta {e_{\rm{X}}}}\!\!\! \\ \!\!\! 0&0&{ - \Delta {i_{\rm{Y}}}}&{\Delta {i_{\rm{X}}}} \!\!\! \\ \!\!\! 0&0&{ - \Delta {e_{\rm{Y}}}}&{\Delta {e_{\rm{X}}}}\!\!\! \\ \!\!\! { - 3\Delta a/2a}&0&{2\Delta {e_{\rm{X}}}}&{2\Delta {e_{\rm{Y}}}} \!\!\!\\ \!\!\! 0&0&{\Delta {i_{\rm{X}}}}&{\Delta {i_{\rm{Y}}}} \!\!\! \end{array}} \right] \times \\ & \left\{ {\begin{array}{*{20}{c}} \!\!\! 1 \!\!\!\\ \!\!\! u\!\!\! \\ \!\!\! {\cos u} \!\!\!\\ \!\!\! {\sin u} \!\!\! \end{array}} \right\} \\[-20pt] \end{split} $

(14)

式中， $\Delta {v_{\rm{R}}},\Delta {v_{\rm{T}}},\Delta {v_{\rm{N}}}$ 分别为 $\Delta {{v}}$ 在RTN方向的分量。

通过给定高分三号卫星对同一目标重访观测的星历数据，验证模型的有效性，分析相对轨道根数转化为位置/速度时的误差，并分析误差产生的原因及解决方法。以下分析中，长度单位为m，速度单位为m/s，角度单位为度。

给定某地区重访观测时J2000坐标下的位置/速度，为

第一，二次观测的卫星位置

$\begin{split} &{{{P}}_1} = [ - 2093790.50,5882097.50,3437527.25]\\ & {{{P}}_2}{\rm{ = [}} - {\rm{2}}110568.50,5898703,3398725.50] \end{split}$

速度

$\begin{split} &{{V}_1} = [2802.01, - 2788.13,6455.62]\\ & {{V}_2}{\rm{ = [2790}}{\rm{.62,}} - {\rm{2746}}{\rm{.97,6478}}{\rm{.25]}} \end{split}$

得到RTN坐标下的方向矢量

$\begin{split} &{{e}_{\rm{R}}}{\rm{ = }}{P_1}/|{P_1}|\\ & {{e}_{\rm{T}}}{\rm{ = }}{V_1}/|{V_1}|\\ & {{e}_{\rm{N}}} = {{e}_{\rm{R}}} \times {{e}_{\rm{T}}} \end{split}$

对第一，第二次卫星的位置和速度差分并向RTN坐标方向投影，得到RTN坐标下的位置和速度差分

$\left\{ {\begin{array}{*{20}{c}} {\Delta {r_{\rm{R}}}} \\ {\Delta {r_{\rm{T}}}} \\ {\Delta {r_{\rm{N}}}} \\ {\Delta {v_{\rm{R}}}} \\ {\Delta {v_{\rm{T}}}} \\ {\Delta {v_{\rm{N}}}} \end{array}} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {8.0} \\ { - 4.5{\rm{E}}4} \\ {9.4} \\ {48.23} \\ { - 0.08} \\ {3.15} \end{array}} \right\}$

两次观测中卫星位置对应的轨道根数为

$\begin{split} {E_1} = & [{a_1},{e_1},{i_1},{\Omega _1},{\omega _1},{u_1}] = [{\rm{7}}{\rm{.30701E + 6,}} \\ & {\rm{0.0246219,101}}{\rm{.378,115}}{\rm{.955,32}}{\rm{.8085,29}}{\rm{.4695}}] \\ \end{split} $

$\begin{split} {E_2} = & [{a_2},{e_2},{i_2},{\Omega _2},{\omega _2},{u_2}] = [{\rm{7}}{\rm{.30730E + 6,}} \\ & {\rm{0.0246520,101}}{\rm{.399,115}}{\rm{.967,32}}{\rm{.4443,29}}{\rm{.1073}}] \\ \end{split} $

依照式(5)、式(7)转化为相对偏心率/倾角矢量，通过式(14)计算得到

$\left\{ {\begin{array}{*{20}{c}} {\Delta {r_{\rm{R}}}} \\ {\Delta {r_{\rm{T}}}} \\ {\Delta {r_{\rm{N}}}} \\ {\Delta {v_{\rm{R}}}} \\ {\Delta {v_{\rm{T}}}} \\ {\Delta {v_{\rm{N}}}} \end{array}} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {7.3} \\ { - 4.7{\rm{E4}}} \\ {11.4} \\ {49.29} \\ {0.13} \\ {3.18} \end{array}} \right\}$

通过式(14)相对轨道根数转换得到卫星轨道位置和速度与实际位置和速度的偏差为

$\left\{ {\begin{array}{*{20}{c}} {{\rm{d}}{r_{\rm{R}}}} \\ {{\rm{d}}{r_{\rm{T}}}} \\ {{\rm{d}}{r_{\rm{N}}}} \\ {{\rm{d}}{v_{\rm{R}}}} \\ {{\rm{d}}{v_{\rm{T}}}} \\ {{\rm{d}}{v_{\rm{N}}}} \end{array}} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {0.7} \\ {{\rm{1}}{\rm{.72E3}}} \\ { - 2.8} \\ { - 1.06} \\ { - 0.21} \\ { - 0.02} \end{array}} \right\}$

为了更进一步分析模型偏差，在4次重访观测的星历数据中读取1000次轨道位置和速度参数，并按照上述步骤计算两种方法得到的卫星位置和速度偏差，得到均方误差为

$\left\{ {\begin{array}{*{20}{c}} {\overline {{\rm{d}}{r_{\rm{R}}}} } \\ {\overline {{\rm{d}}{r_{\rm{T}}}} } \\ {\overline {{\rm{d}}{r_{\rm{N}}}} } \\ {\overline {{\rm{d}}{v_{\rm{R}}}} } \\ {\overline {{\rm{d}}{v_{\rm{T}}}} } \\ {\overline {{\rm{d}}{v_{\rm{N}}}} } \end{array}} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {4.3} \\ {{\rm{172}}} \\ {3.6} \\ {1.23} \\ {1.48} \\ {0.21} \end{array}} \right\}$

由于式(3)、式(5)、式(14)中近似和线性化引入的误差，相对轨道根数转化为卫星的位置和速度与GPS位置和速度转化为J2000坐标下的位置和速度有不同。另一方面，由于轨道根数和GPS位置定位间隔为1 s，卫星飞行速度在7.57 km/s，因此沿卫星飞行方向(T方向)的位置误差较大。然而在重轨干涉中，关注的是垂直于T方向的交轨基线，T方向的顺轨基线在配准时可以自动抵消。通过插值和更短时间间隔的GPS信息，可以进一步减小 ${\rm{d}}{r_{\rm{T}}}$ 。

对于国外先进的C波段SAR卫星，在进行重轨干涉实验时数据基线一般在几十米到几百米，相对轨道控制精度在百米量级(Snoeij 等，2012)。利用相对偏心率/倾角矢量的相对轨道运动模型，从轨道根数到卫星位置的转化误差小于10 m，相比轨道控制精度小一个数量级，因此对于卫星的控制是完全足够的。

为了更清楚的表达在根数偏差下基线的变化规律的几何意义，由式(3)、式(7)、式(14)得到

$\Delta {r_{\rm{R}}}/a = \Delta a/a - \delta e\cos (u - \varphi)$

(15)

$\Delta {r_{\rm{T}}}/a = - 3\Delta a/(2a) + 2\delta e\sin (u - \varphi)$

(16)

$\Delta {r_{\rm{N}}}/a = \delta i\sin (u - \theta)$

(17)

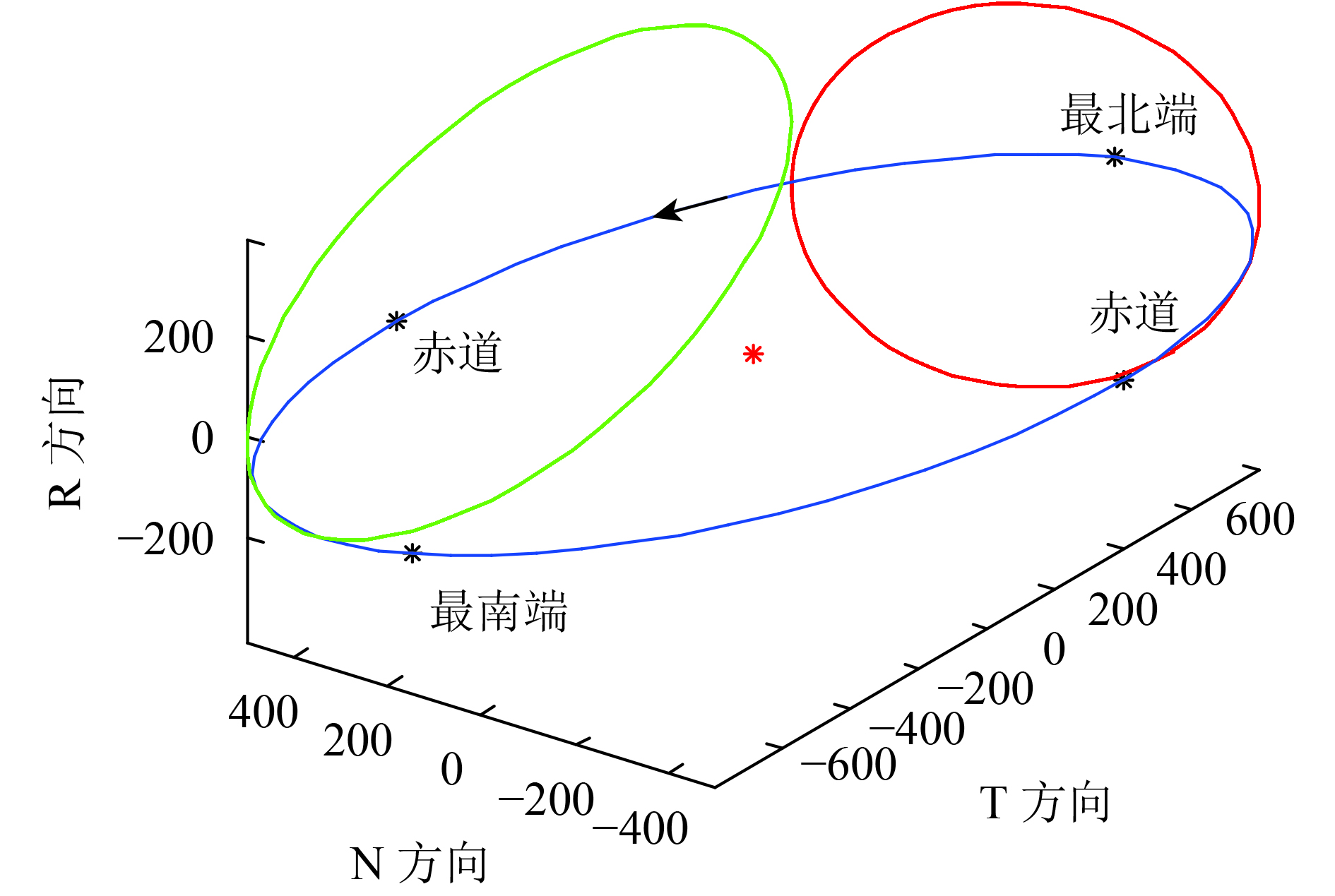
如图4，相对参考轨道，画出在交轨平面(RN平面)内，当偏心率和轨道倾角分别变化 $\delta e$ 和 $\delta i$ 时，实际轨道随着纬度幅角变化在以参考轨道为中心的椭球上变化。图4中只表示出RN平面的情况，当增加半长轴 $a$ 的变化，椭球在R方向移动 $\Delta a$ ，此处未表示出。

由椭圆几何关系得到，当卫星实际位置位于视线方向与椭圆的切点时，形成最长基线。

图5中蓝线给出当 $a\delta e = 400$ ， $a\delta i{\rm{ = }}500$ ， $\theta = $ $ - {142^ \circ } $ ， $\varphi = {58^ \circ }$ 时实际位置相对参考位置(红色星号)在绕地球一周的变化规律，右下角为卫星在赤道处相对参考卫星的位置，箭头方向表示卫星运动过程中相对位置随曲线的变化方向，图5中表示出赤道、北极、南极处的相对位置。红色曲线为卫星相对位置在RN平面的投影，绿色曲线为卫星的相对位置在TR平面的投影。

在RN平面内，当侧视角(地心与卫星连线和视线的夹角)为30°时，交轨基线长度的变化，其中蓝色曲线为图5中卫星相对位置的变化，红色曲线为在蓝色曲线基础上实际轨道 $\Delta a = 100$ 时的变化，实际卫星在N方向为正的方向基线长度为正。半长轴变化时RN平面内基线变化为(变化正负随半长轴变化正负)

$\Delta a \cdot \sin \vartheta $

(18)

式中， $\vartheta $ 为侧视角。对 $\Delta {r_{\rm{R}}},\Delta {r_{\rm{N}}}$ ，有

${B_ \bot } = \Delta {r_{\rm{R}}}\sin \vartheta - \Delta {r_{\rm{N}}}\cos \vartheta $

(19)

图6中红色曲线相比蓝色曲线增高 $\Delta a \cdot \sin \vartheta = $ $100 \cdot \sin {30^ \circ } = 50 $ 。

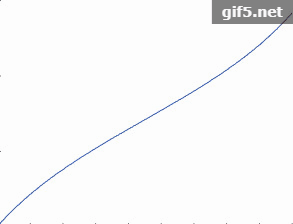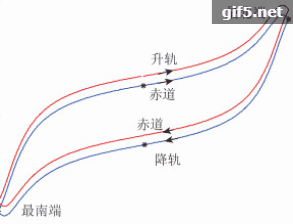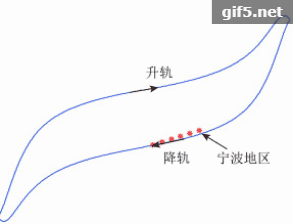
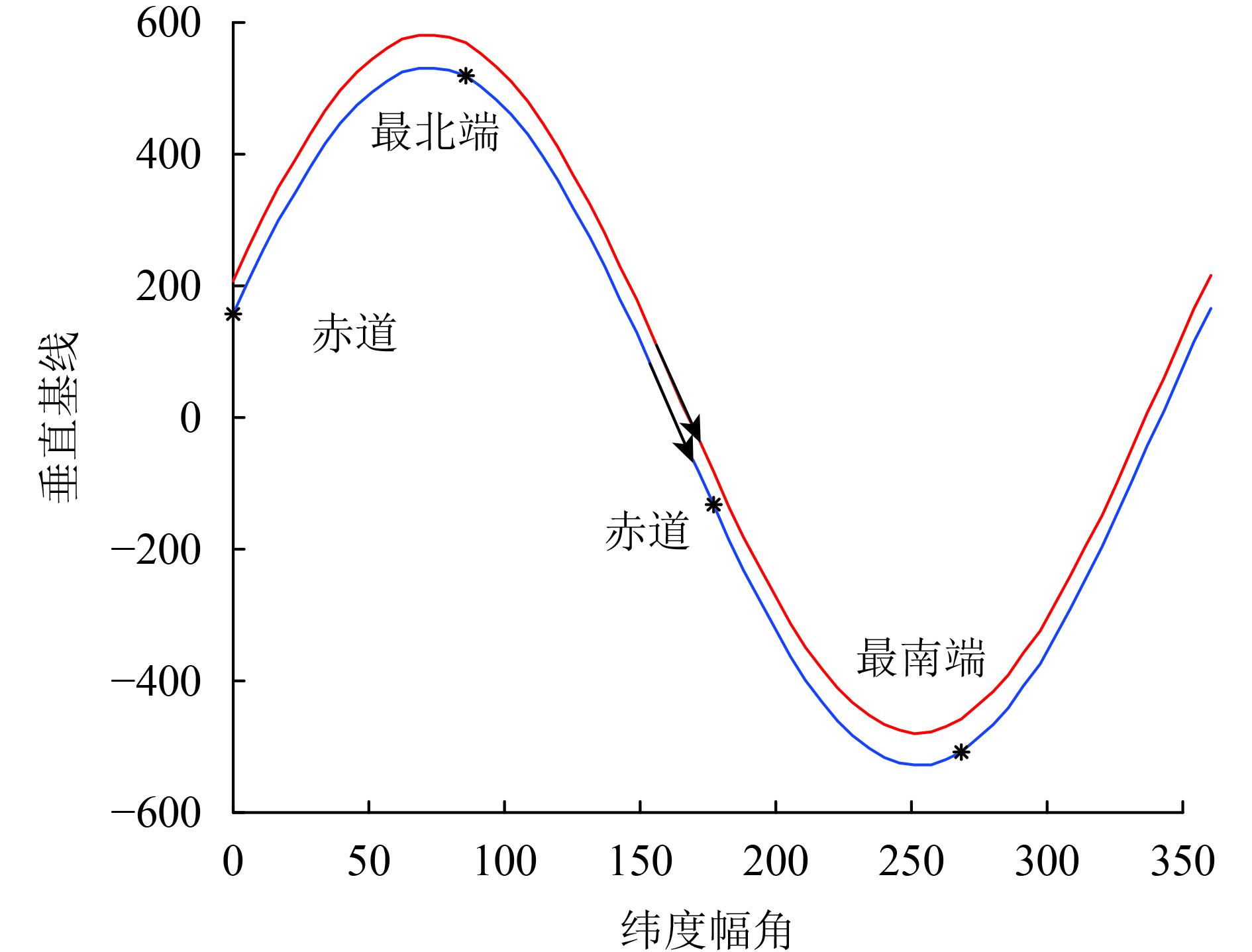
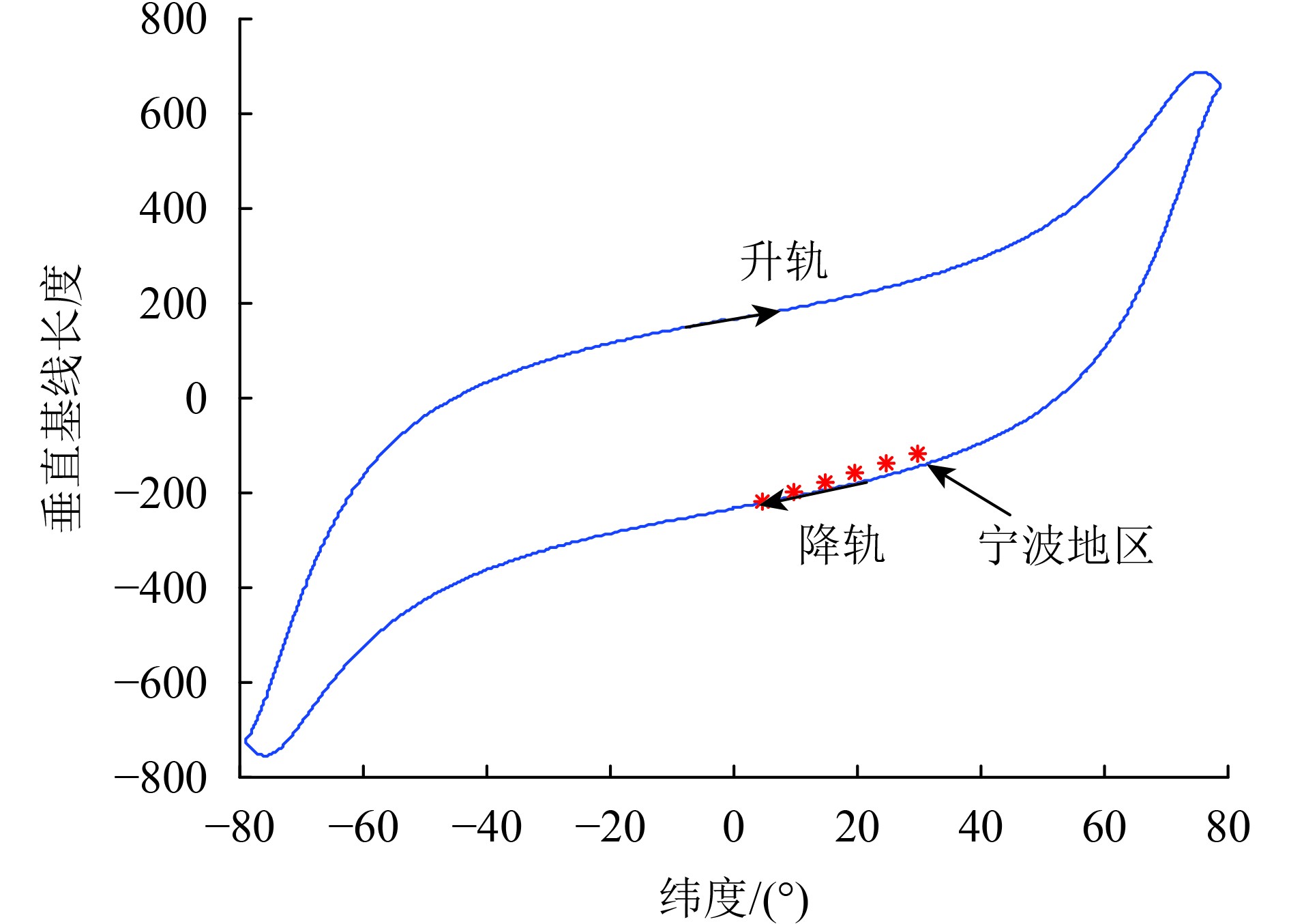
进一步将不同纬度幅角的基线长度以升轨和降轨时不同纬度的基线长度来展示，使得结果更加直观。图7中表示了纬度幅角 $u$ 和纬度 $\varphi $ 的几何关系。

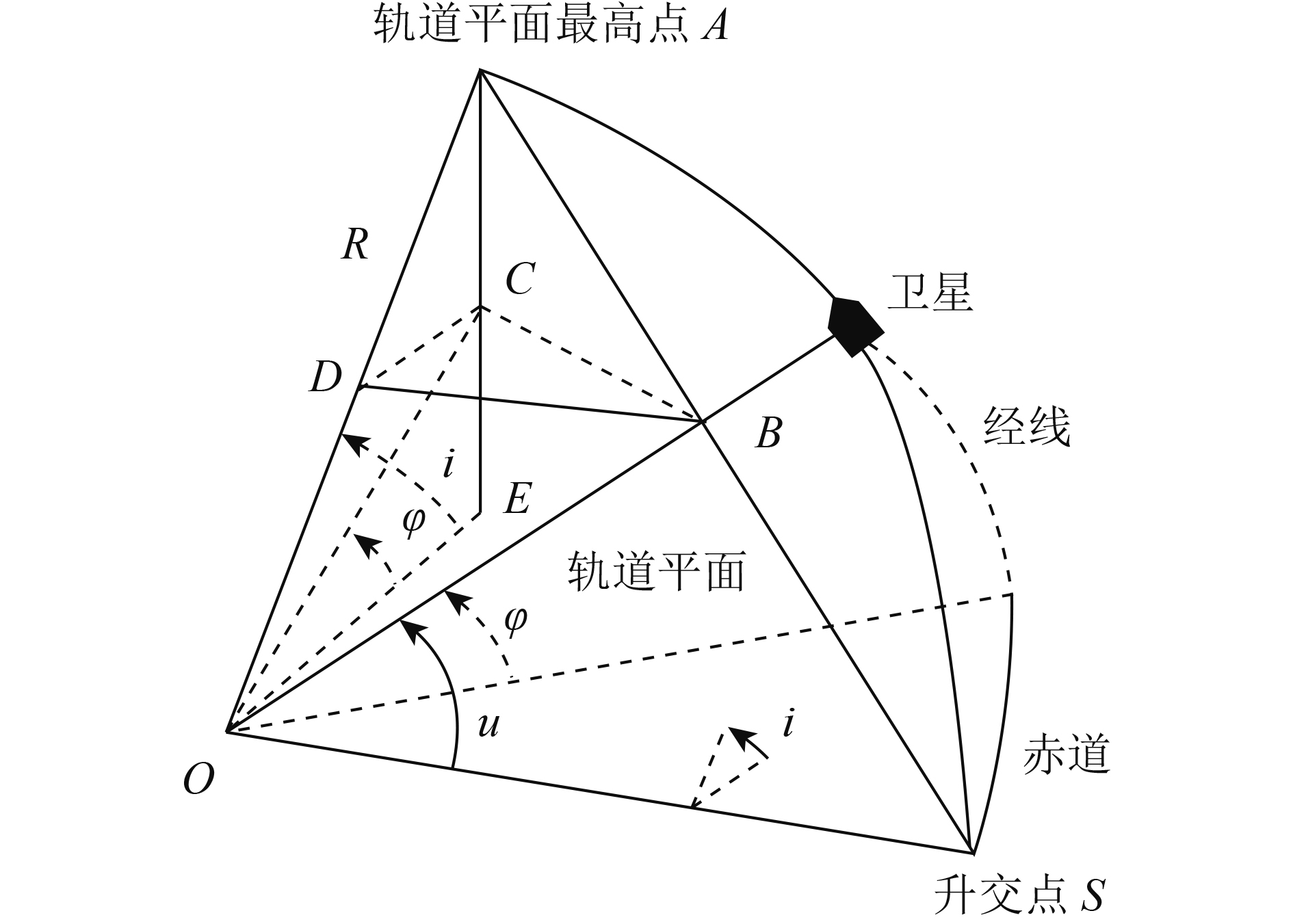
当已知纬度幅角 $u$ 和轨道倾角 $i$ ，由以下分析可以得到卫星所在的纬度 $\varphi $ 。 $A$ 为轨道平面最高点，因此∠ $AOS$ 为90°， $A$ 对赤道平面的垂线为 $AE$ ，则∠ $AOE$ 为轨道倾角 $i$ ，设地心与卫星连线和升交点与轨道平面最高点连线相交于 $B$ ，由 $B$ 对 $AE$ 做垂线，相交于 $C$ ，则Δ $ABC$ 与ΔASE成比例，则∠ $COE$ 为 $\varphi $ 。

设BS长度为 $x$ ， $BO$ 长度为 $y$ ，则在Δ $AOS$ 中，根据余弦定理，有

$\begin{gathered} {y^2} = {R^2} + {x^2} - 2xR\cos {45^ \circ } \\ {x^2} = {R^2} + {y^2} - 2yR\cos u \\ \end{gathered} $

(20)

可以求得BS长度

$x = R \cdot \left(\sqrt 2 + \frac{{\sqrt 2 \cos \phi \sqrt {(1 - \cos \phi)(1 + \cos \phi)} - \cos\phi }}{{2{{\cos }^2}\phi - 1}}\right)$

(21)

式中，

$\begin{split} & \phi = u, - {90^ \circ } \leqslant \phi \leqslant {90^ \circ },\\ & \phi ={\text{π}} - u,\phi {\text{为其他}}\\ & {\text{当}}\cos{^2}\phi = \frac{1}{2},x = R/\sqrt 2 \end{split}$

(22)

根据ΔABC与ΔASE比例关系，可以求得

$CE{\rm{ = abs(}}R\sin i\frac{x}{{\sqrt 2 R}})$

(23)

又 $OE = {\rm{abs}}(R\cos i)$ ，得到

$\begin{gathered} \varphi = u,i = {90^ \circ }; \\ \varphi {\rm{ = }}\arctan \frac{{CE}}{{OE}},0 \leqslant u \leqslant {180^ \circ },i \ne {90^ \circ }; \\ \varphi {\rm{ = }} - \arctan \frac{{CE}}{{OE}},{180^ \circ } < u < {360^ \circ },i \ne {90^ \circ } \\ \end{gathered} $

(24)

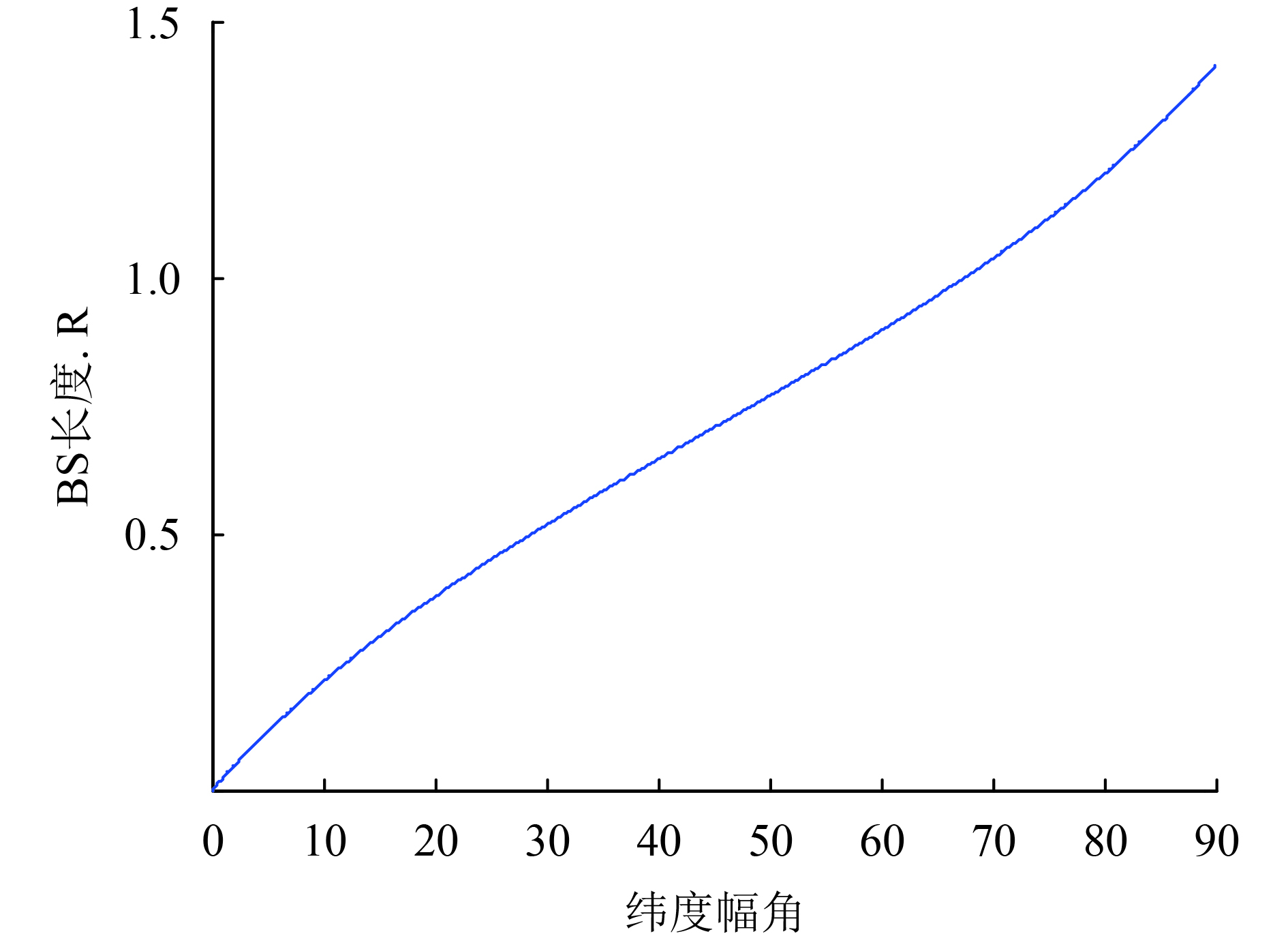
不同纬度幅角对应的BS长度如图8所示。

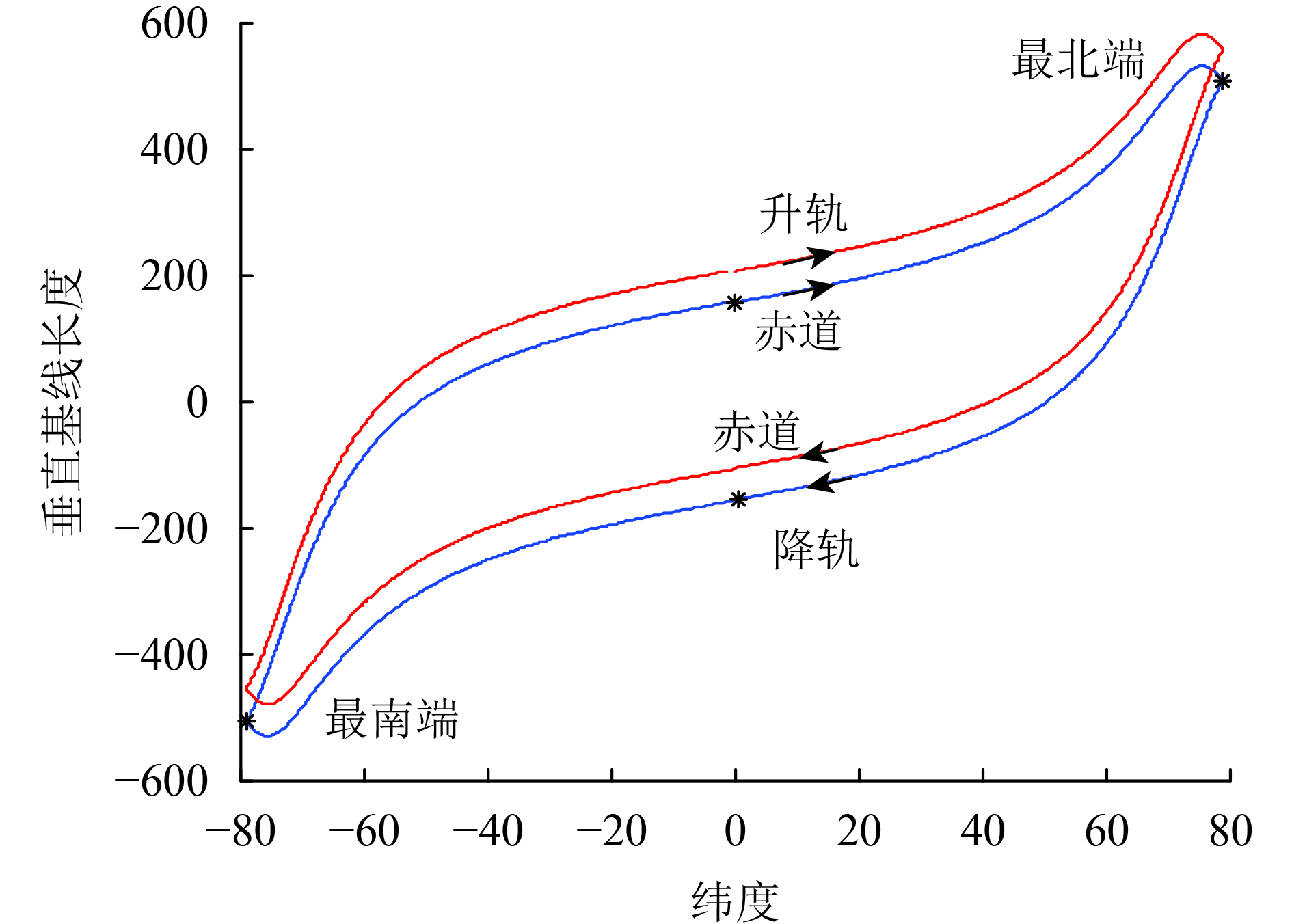
图9中给出图6所示基线在不同纬度时的长度。由图中可以看到，存在基线长度为0的时候，因此在根据观测目标进行轨道控制时，要尽量避免在观测的纬度形成的基线过短，以免相位对高程的敏感度降低而影响高程反演的精度。

在分析根数对RNT坐标下卫星位置影响的基础上，通过控制卫星的速度来实现卫星运动状态(位置和速度)的调整，保证重访时卫星位置满足干涉基线条件。

将式(14)写成轨道根数偏差对卫星RNT坐标下运动状态偏差的关系，得到式(25)、式(26)，在近圆轨道条件下求变换矩阵的逆矩阵，得到式(27)，为近圆轨道偏量的一阶线性解(Montenbruck 等，2004)。

$\left\{ {\begin{array}{*{20}{c}} \!\!\! {\Delta {r_{\rm{R}}}}\!\!\! \\ \!\!\! {\Delta {r_{\rm{T}}}}\!\!\! \\ \!\!\! {\Delta {r_{\rm{N}}}}\!\!\! \end{array}} \right\} = a{\left[ {\begin{array}{*{20}{c}} \!\!\! {1/a}&{ - (3/2)u/a}&0\!\!\! \\ \!\!\! { - \cos u}&{2\sin u}&0\!\!\! \\ \!\!\! { - \sin u}&{ - 2\cos u}&0\!\!\! \\ \!\!\! 0&0&{\sin u}\!\!\! \\ \!\!\! 0&0&{ - \cos u}\!\!\! \\ \!\!\! 0&1&0 \!\!\! \end{array}} \right]^{\rm{T}}} \times \left\{ {\begin{array}{*{20}{c}} \!\!\!{\Delta a} \!\!\!\\ \!\!\! {\Delta {e_{\rm{X}}}} \!\!\!\\ \!\!\! {\Delta {e_{\rm{Y}}}}\!\!\! \\ \!\!\! {\Delta {i_{\rm{X}}}}\!\!\! \\ \!\!\! {\Delta {i_{\rm{Y}}}}\!\!\! \\ \!\!\! {\Delta u} \!\!\! \end{array}} \right\}$

(25)

$\left\{ {\begin{array}{*{20}{c}} \!\!\! {\Delta {v_{\rm{R}}}} \!\!\! \\ \!\!\! {\Delta {v_{\rm{T}}}} \!\!\! \\ \!\!\! {\Delta {v_{\rm{N}}}} \!\!\! \end{array}} \right\} = v{\left[ {\begin{array}{*{20}{c}} \!\!\! 0&{ - (3/2)/a}&0 \!\!\! \\ \!\!\! {\sin u}&{2\cos u}&0 \!\!\! \\ \!\!\! { - \cos u}&{2\sin u}&0 \!\!\! \\ \!\!\! 0&0&{\cos u} \!\!\! \\ \!\!\! 0&0&{\sin u} \!\!\! \\ \!\!\! 0&0&0 \!\!\! \end{array}} \right]^{\rm{T}}} \times \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \!\!\! {\Delta a} \!\!\! \\ \!\!\! {\Delta {e_{\rm{X}}}} \!\!\! \\ \!\!\! {\Delta {e_{\rm{Y}}}} \!\!\! \\ \!\!\! {\Delta {i_{\rm{X}}}} \!\!\! \\ \!\!\! {\Delta {i_{\rm{Y}}}} \!\!\! \\ \!\!\! {\Delta u} \!\!\! \end{array}} \end{array}} \right\}$

(26)

$\left\{ {\begin{array}{*{20}{c}} \!\!\! {\Delta a} \!\!\! \\ \!\!\! {\Delta {e_{\rm{X}}}} \!\!\! \\ \!\!\! {\Delta {e_{\rm{Y}}}} \!\!\! \\ \!\!\! {\Delta {i_{\rm{X}}}} \!\!\! \\ \!\!\! {\Delta {i_{\rm{Y}}}} \!\!\! \\ \!\!\! {\Delta u} \!\!\! \end{array}} \right\} = \frac{1}{v}\left[ {\begin{array}{*{20}{c}} \!\!\! 0&{2a}&0 \!\!\! \\ \!\!\! {\sin u}&{2\cos u}&0 \!\!\! \\ \!\!\! { - \cos u}&{2\sin u}&0 \!\!\! \\ \!\!\! 0&0&{\cos u} \!\!\! \\ \!\!\! 0&0&{\sin u} \!\!\! \\ \!\!\! { - 2}&0&{ - \sin u/\tan i} \!\!\! \end{array}} \right] \times \left\{ {\begin{array}{*{20}{c}} \!\!\! {\Delta {v_{\rm{R}}}} \!\!\! \\ \!\!\! {\Delta {v_{\rm{T}}}} \!\!\! \\ \!\!\! {\Delta {v_{\rm{N}}}} \!\!\! \end{array}} \right\}$

(27)

式(27)反映了在纬度幅角为 $u$ 时，给定机动量，使得速度改变 ${{\rm{\{ }}\Delta {v_{\rm{R}}},\Delta {v_{\rm{T}}},\Delta {v_{\rm{N}}}{\rm{\} }}^{\rm{T}}}$ 时对轨道的修正的关系，据此可以得到满足需求的轨道控制解(Ilcev，2010)。

在轨道平面内，轨道偏心率偏差和半长轴偏差决定沿卫星飞行方向的机动，一般来说，通过在轨道平面两次对称的机动(用上标1,2表示)来调整轨道更加稳定和有效。式(26)虽然可以直接得到 $\Delta {v_T}$ ，但没有式(27)的解简洁直观，因此，这里依据式(27)，得到轨道平面内的控制方程为

$\begin{gathered} \Delta v_{\rm{T}}^1 = (v/4)(||D{{e}}|| + Da/a) \\ \Delta v_{\rm{T}}^2 = - (v/4)(||D{{e}}|| - Da/a) \\ \end{gathered} $

(28)

机动位置为

$\begin{gathered} u_{{\rm{in - plane}}}^1 = \arctan (D{e_{\rm{Y}}}/D{e_{\rm{X}}}) \\ u_{{\rm{in - plane}}}^2 = u_{{\rm{in - plane}}}^1 +{\text{π}} \\ \end{gathered} $

(29)

在垂直于轨道平面方向， $\Delta {v_{\rm{N}}}$ 能够调整轨道倾角的偏差，依据式(26)，得到两次对称机动的解为

$\begin{gathered} \Delta v_{\rm{N}}^1{\rm{ = (}}v/2)||D{{i}}|| \\ \Delta v_{\rm{N}}^2{\rm{ = (}}v/2)||D{{i}}|| \\ \end{gathered} $

(30)

机动位置为

$\begin{gathered} u_{{\rm{out - plane}}}^{\rm{1}} = \arctan (D{i_{\rm{Y}}}/D{i_{\rm{X}}}) \\ u_{{\rm{out - plane}}}^2 = u_{{\rm{out - plane}}}^1 + {\text{π}} \\ \end{gathered} $

(31)

式中， $D \cdot $ 代表相对轨道根数差分。

在给定观测目标纬度及升轨或降轨观测的条件下，根据当前轨道参数得到如图9的预测基线长度，然后依据式(15)、式(17)、式(19)得到目标基线时所需相对轨道根数与现有轨道根数的差分，再根据式(28)、式(29)、式(30)、式(31)得到使相对轨道根数满足基线需求的控制策略。在制定从现有基线到目标基线的过程中，相对轨道根数的差分要尽可能小。

以图10中宁波地区观测基线为例，现希望在对宁波地区观测时基线为−200 m，当根据相对轨道根数预测得到宁波地区观测基线为−160 m时，由图9及式(19)、式(15)可知，可以通过调整半长轴偏差来达到所需基线。

$\begin{gathered} D{B_ \bot } = - 200 - (- 160) \\ Da = {B_ \bot }/\sin \vartheta \\ \end{gathered} $

$Da = - 65.8$ ，再通过式(28)、式(29)计算得到

$\begin{gathered} \Delta v_{\rm{T}}^1 = - 0.017{\rm{ m/s}} \\ \Delta v_{\rm{T}}^2 = - 0.017{\rm{ m/s}} \\ \end{gathered} $

$\begin{gathered} u_{{\rm{in - plane}}}^1 = 0 \\− u_{{\rm{in - plane}}}^2 = {\text{π}} \end{gathered} $

此例中所需基线偏差较小，可以只通过调整半长轴来达到目标基线。当基线需调整较大，或其他参数有复杂的变动时，需要考虑式(15)、式(17)中偏心率矢量和轨道倾角矢量的大小和方向。

前文通过实际数据对模型精度进行了验证，对于变化规律进行了分析，并给出了得到相应变化的控制量的解。在此基础上，分析基线变化的规律和基线现有状态，计算了特定目的地处达到所需基线长度的控制方案。在编队控制中该模型已有成功的应用，因此理论和实践上都应认为控制方案是可行的。

相对偏心率/倾角矢量模型是在研究编队卫星运动中提出并一直用于编队卫星运动状态的分析的方法，本文首次将其应用在单星的重复轨道观测中，将前一次的飞行作为编队的另一颗卫星，能够直接应用已有的编队运动状态研究成果。以精确的相对轨道控制为出发点，建立了重轨干涉SAR卫星基线的运动模型，并用高分三号数据进行了模型的验证，在以1 s为间隔获取的轨道参数下，交轨基线的模型与实际偏差在10 m以下。在现有轨道控制的基础上，分析了基线在全球观测的变化规律，得出了不同纬度下基线的长度，为不同地区的观测基线分析提供了依据。针对干涉基线这个特定的问题进行了详细分析，将相对位置转化为垂直基线长度，并给出了正算(从相对根数到基线)和反算(从基线到相对根数调整)的例子。利用高分三号数据对基线长度模型进行了验证，实际基线运动规律符合模型分析。在分析基线运动规律的基础上，建立机动控制对相对轨道根数差分的调整模型，并制定了由预测基线到所需基线的控制策略。通过分析，可以在已知轨道根数的情况下预测重轨观测时对不同观测基线的长度，并采取控制策略调整观测基线满足需求。然而，现阶段检验该方法的实际数据较少，且真实效果有待实际卫星飞行控制的检验。