出版日期: 2019-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20198078
2019 | Volumn23 | Number 6
上一篇 | 下一篇

综述

广角水体体散射函数测量技术及其应用研究进展

徐聪辉^1,2 , 李彩¹

1. 中国科学院南海海洋研究所热带海洋环境国家重点实验室，广州 510301

2. 中国科学院大学，北京 100049

收稿日期: 2018-02-27; 预印本: 2018-04-09

基金项目: 国家自然科学基金(编号：41976181，41176083，41976172，41976170，41576030)；广州市科技计划重点项目(编号：201707020023，201607020041)；热带海洋环境国家重点实验室自主研究项目(编号：LTOZZ1602)

第一作者简介: 徐聪辉，1993年生，男，硕士研究生，研究方向为海洋光学技术。E-mail：xuconghui16@mails.ucas.edu.cn

通信作者简介: 李彩，1977年生，女，研究员，研究方向为海洋光学及海洋环境监测技术。E-mail：liclaire@scsio.ac.cn

摘要

水体体散射函数是描述水体中光在各方向散射特性的一个重要的固有光学参数，对水色遥感、水环境监测与保护、海气交互过程研究、水下军事目标跟踪等领域具有十分重要的意义。水体体散射函数测量尤其是覆盖0°—180°范围的广角体散射函数测量技术起步较晚，直接测量难度较大，一直以来都是一个棘手的科学难题。本文梳理了国内外广角水体体散射函数测量技术的发展历程，对于广角体散射函数测量技术，从原理上大致可以分为单一探测器转动式、多个固定探测器阵列式以及面阵CCD成像式等3大类，对不同测量原理下的测量技术进行详细分析，并对广角水体体散射函数测量技术在海洋生物光学、气泡跟踪、水色遥感等方面的相关应用进展进行总结和归纳，并对未来广角水体体散射函数的发展趋势和应用前景进行展望。

关键词

广角, 体散射函数, 测量技术, 水色遥感, 水环境监测

Progress of measurement technology and application of general-angle Volume Scattering Function of water

XU Conghui^1,2 , LI Cai¹

1.State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China

2.University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

In ocean optics, a Volume Scattering Function (VSF) is a fundamental inherent optical property parameter that describes the angular distribution of light scattered from an incident beam, and has considerable significance in studying ocean color remote sensing, underwater light radiation transmission, water environment monitoring and protection, air–sea interaction, and submarine target tracking. Despite its fundamental nature, the variability of the VSF is rarely reported, especially from 0° to 180° (i.e., general angle). This condition is mainly due to the extreme difficulty of performing direct measurements of general-angle VSF. With more than 50 years of development, the measurement technique of general-angle VSF remains in its infancy and is still being explored and improved. This study summarizes the research progress of measurement technology and application of the general-angle VSF of water and discusses the development status quo and the tendency of measurement technology and its application of general-angle VSF of water. On the basis of the measuring principle, the measurement technology of VSF can be divided into " mechanical rotating measurement by a single detector,” " synchronous measurement by array detectors,” and " photographic measurement by a plane array Charge-coupled Device.” The first instruments dedicated to measuring the general-angle VSF of water samples were developed in 1950—1960 and were still used up to this day. The principle of these instruments was principally based on either a light detector or a light source rotating around the sample volume. The angular distribution of scattered light can be measured with the rotation of a single detector or light source (or prism replacing the detector). The angular resolution of these instruments can reach 0.3°, regardless of measurement speed and data synchronization, and these instruments cannot be used in situ. Since the early 1990 s, the second-generation general-angle VSF instruments were built because of the significant advances in the fields of oceanic, optical, and electronics technology. This type of general-angle VSF instruments (referred to as " in situ concept” instruments) uses an array of several detectors that are located in the same plane with a monochromatic light source, which completes a rapid full measurement of VSF within 10 ms, and the angular resolution of these instruments can reach 10°. Some researchers have proposed a new optical approach to measuring the general-angle VSF through image detection. This type of instruments (operates in a laboratory environment) uses a combination of two reflectors and a CCD camera without changing the detector sensitivity and without moving any optical part, thereby allowing the simultaneous measurement of VSF at various angles with a few seconds. The application of direct measurement technology and instrument of general-angle VSF has gradually expanded to the bio-optical model, bubble trace, remote sensing of ocean color, radiative transfer, and upper-ocean heat balance. In the future, the direct measurement technology of general-angle VSF will play an important role in applying oceanic optics and its related field with the increase in application requirements and progress of measurement technology and theoretical methods.

Key words

general-angle, Volume Scattering Function(VSF), measurement technique, ocean color remote sensing, water environment monitoring

1 引　言

在海洋光学中，体散射函数VSF(Volume Scattering Function，β(ψ))是描述光在水体中某一散射体上散射光的角度分布的重要固有光学参数。利用水体体散射函数及吸收系数可以推算水体及其组分的所有特征性固有光学特性参数(c=a+b)及遥感反射率R(Duntley，1963；Mobley 等，2002)，水体体散射函数与水体组分直接相关，水体不同组分(如：藻类等浮游生物、气泡、悬浮泥沙等)对不同方向的体散射函数具有特征性贡献，随着人们对海洋研究的不断深入，水体体散射函数,尤其是广角(0°—180°范围)体散射函数在水色遥感(McLeroy-Etheridge和Roesler，1998；Lee 等，2002；Hubert等，2010)、水下军事目标跟踪(Rehm和McCormick，2011)、生态系统建模(Smith和Baker，1982)及近海灾害的预警预告(Hojerslev，1975；McLeroy-Etheridge和Roesler，1998；Ronald 等，2002)海洋学领域中越来越凸显出其重要性。

水体体散射函数可通过理论计算与直接测量两种方法获取。理论计算多基于Mie散射理论(Bohren和Huffman，1983；Pak 等，1971)，是建立在对颗粒物粒径、折射率等物理特性规则假设的条件之上，这种近似估算对确定颗粒物散射特性的研究非常有意义，但基于规则假设条件对于水体中不规则颗粒物散射特性的研究误差不可避免，事实上，人们无法完全了解水体中各种颗粒物的粒径分布、形状、折射率(包括内部的不均匀性)。水体的散射特性的直接测量相对理论研究就显得直接、可信。

对于体散射函数的直接测量，目前有一些商业化仪器被广泛应用，如Sequoia Scientific公司的LISST系列前向小角度散射仪(Agrawal，2005)，WetLabs公司的ECO系列及HOBI Labs公司的HydroSca系列后向散射系数测量仪等。上述前向或后向散射测量仪主要基于前向小角度体散射函数或后向某一固定角度体散射函数的测量结果计算获取颗粒物粒径分布或后向散射系数，无法得到水体的散射系数，更无法描述不同组分对光散射的方向性贡献—散射相函数。为了更加准确、全面地研究光进入水体后被散射进入不同方向的能量和概率以及不同角度体散射函数与水体及其所含组分之间的生物光学相关性，需要对0°—180°广角范围内不同角度的体散射函数(广角体散射函数)进行测量，测量的角度分辨率越高，所附带的信息越丰富；广角体散射函数的测量技术是海洋光学领域一个重要且棘手的科学难题，阻碍这一科学难题前进的原因主要有以下几点：(1)宽动态范围微弱光探测：体散射函数能量主要集中在前向小角度，后向能量极其微弱，前后向散射能量相差可达7个量级；同时，同一角度的散射光信号，在不同海区或不同剖面，其能量差距也可达4个数量级甚至更高；(2)杂散光消除，杂散光主要来自于仪器表面的散射、反射以及太阳背景光。理想状态下准直光束不会对前向小角度测量产生信号污染，但实际应用中的准直光源不能做到真正的准直。因此会对前向小角度散射信号产生污染，而对于后向角度的测量而言，因水体后向散射信号较弱，仪器表面的散射与反射光对水体的后向散射信号会带来较大影响；(3)体散射函数定标难度较大；此外，水体中的多重散射问题对体散射函数定标产生的影响一直以来难以得到很好解决。

虽然广角体散射函数的研究一直以来都受到国际海洋科学家的高度重视，但受散射信号自身特点及技术发展的限制，其发展过程相当缓慢，至今该项技术依然在不断探索完善中持续发展和改进。据报道，目前国际也仅有美国、德国、中国、乌克兰、日本等几个国家对海水广角体散射函数测量技术及应用开展了较多的研究，在国内，有关广角体散射函数测量技术及应用的研究甚少(李彩等，2004；Li 等，2012a，2012b，2015)，本文将从广角体散射函数测量原理出发，就0°—180°水体广角体散射函数测量方法、技术研究进展及其在海洋生物光学、水色遥感等方面的相关应用进展进行总结和归纳。

对于广角体散射函数测量技术，从原理上来分大体可以分为单一探测器转动式、多个探测器固定阵列式以及基于面阵CCD探测技术等3大类。

转动式广角体散射函数测量技术是基于单一光源、单一探测器，通过旋转光源或探测器或折光棱镜的方式实现0°—180°不同角度散射通量及体散射函数的测量；多探测器、阵列式广角体散射函数测量技术中光源、探测器均为固定部件，利用多个固定探测器实现不同角度散射通量及体散射函数的快速测量；基于面阵CCD照相式的广角体散射函数测量技术的核心即为面阵CCD，通过不同角度散射光在CCD面阵上的成像来实现0°—180°不同角度散射通量及体散射函数的测量。

2 广角水体体散射函数测量技术方法

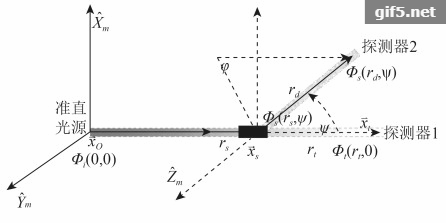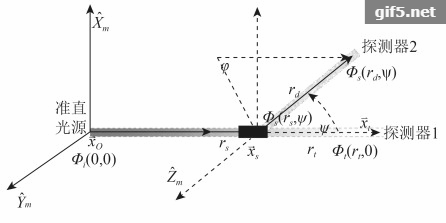
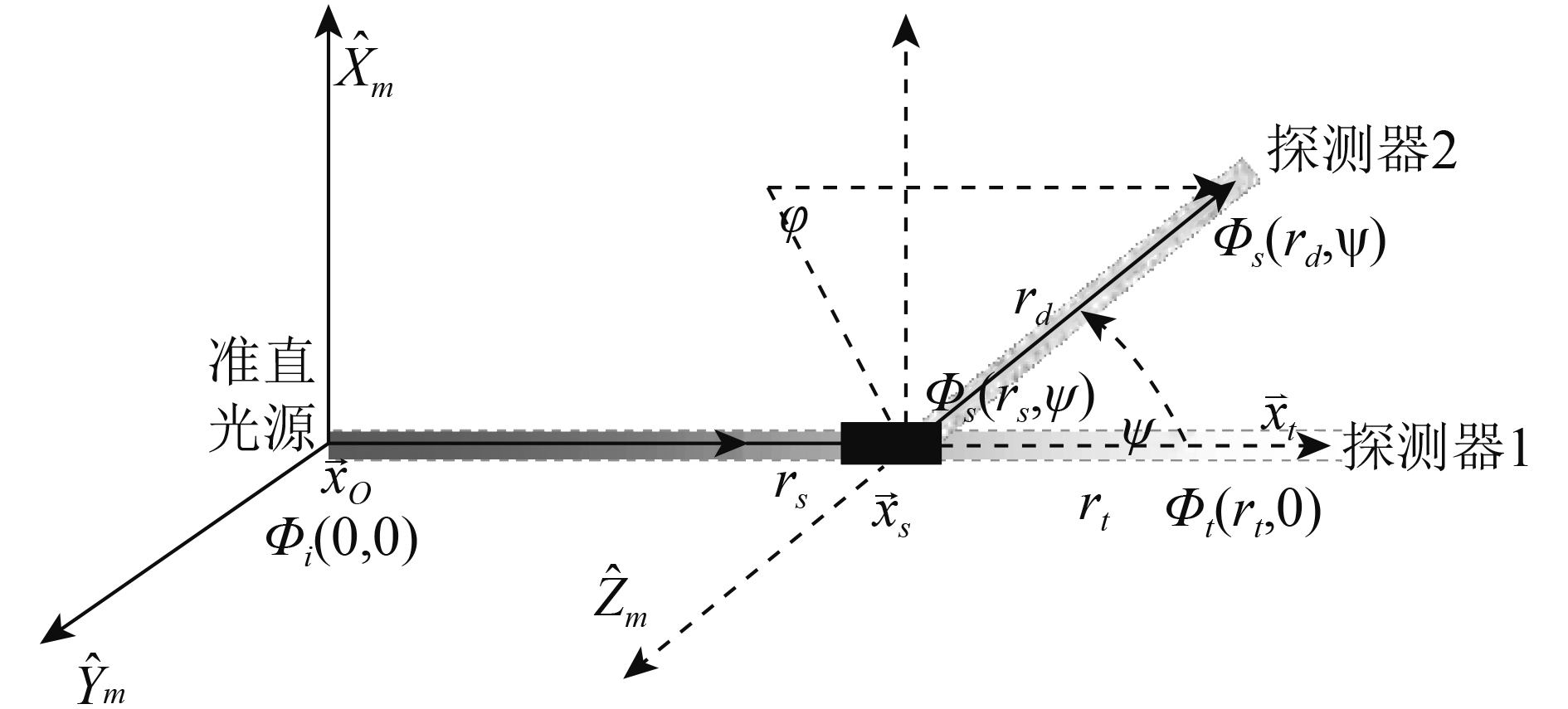
体散射函数的数学定义为某一散射体积V在散射角ψ方向上的散射通量对散射体积与散射立体角的二阶导数与入射辐照度E之比。单位为m⁻¹sr⁻¹。

$ \beta \left(\psi \right) = \frac{{{\partial ^2}\varPhi \left({\psi,{r_{\rm{s}}}} \right)}}{{E\partial \varOmega \partial V\left(\psi \right)}} $

(1)

式中，ψ为散射角，r_s表示散射光光程，即散射体与探测器间距离，Φ表示入射辐射通量， $\varOmega $ 表示散射立体角，E为入射辐射照度，散射体体积V随散射角变化而变化，β(ψ)虽然不含波长，但因波长的不同而不同。在水体中，β(ψ)还随时间和空间变化，一般表示为角度和深度的函数。图1所示为测量原理。

图 1 体散射函数测量原理

Fig. 1 Measuring principal of volume scattering function

对体散射函数进行不同角度范围的积分可得到散射系数b以及后向散射系数b_b。

$ {\rm{b}}=\iint\limits_{4{\text{π}}} {\beta \left(\psi \right){\rm{d}}\varOmega = 2{\text{π}}\int\nolimits_0^{\text{π}} {\beta \left(\psi \right)\sin \psi {\rm{d}}\psi } } $

(2)

$ {b_{\rm{b}}} = 2{\text{π}} \int\nolimits_{{\text{π}}/2}^{\text{π}} {\beta \left(\psi \right)\sin \psi {\rm{d}}\psi } $

(3)

以及无量纲归一化体散射相函数 $\tilde \beta \left(\psi \right) = \beta \left(\psi \right)/b$ 及后向散射比率b_b/b。

2.1 单一探测器转动式

多角度散射测量仪研究始于20世纪40年代。Dawson和Hulburt(1941)设计了第一台多角度散射测量仪，角度范围为22.5°—157.5°，角度分辨率为22.5°，光源固定，采用垂直和水平偏振光测量，仪器内置有球形玻璃容器作为样品池，探测器可机械式自动旋转，采用光电倍增管作为光电探测器件，基于对数放大电路对不同角度散射光进行放大。Dawson利用该仪器对四氯化碳、二硫化碳、乙烷、乙醚、纯水5种液体不同角度的散射通量进行探测，测量结果与瑞利散射理论计算结果具有较高的一致性，但目前尚未发现该仪器应用于自然水体体散射函数测量的记载。

Brice等(1950)设计了一种多角度散射仪(Brice-phoenix)，采用汞灯作为光源。通过旋转探测器实现45°—135°范围内散射光通量的测量，角度分辨率为45°，仪器内部有一六边形样品室，通过测量0°透射光、45°、90°以及135°散射光信号获取溶液的浊度(通过90°散射光0°透射光辐照度之比)以及高分子摩尔质量等信息。Spilhaus(1968)利用改进的Brice-phoenix散射计(角度范围为30°—135°，角度分辨率5°)对美国伍兹霍尔沿海、百慕大群岛、马尾藻海等5个海区进行测量。并根据30°—50°实测体散射函数值外推获得到0°—30°体散射函数，研究发现大洋清澈水体前向体散射小于近岸水体但曲线斜率更大，说明清澈水体颗粒物粒径相对较小，同时发现，清澈水体后向体散射函数分布中存在一些极大值和极小值点，而这种现象在沿海水体中并未观测到，由此推断出清澈水体的散射更倾向于单分散体系。Gibbs(1978)利用改进的Brice-phonix散射计(测量范围25°—140°，角度分辨率5°)，对碎石英，玻璃颗粒的体散射函数测量，研究发现不同形状颗粒的后向散射有很大区别，90°与140°体散射函数比值与颗粒物球度呈线性关系，并随着球度的增加而降低，由此，Gibbs认为通过该比值可以区分不同形状的颗粒，并通过实验区分并确定了高岭石，滑石和云母与石英，方解石、长石和煤灰等颗粒物，进一步验证了该结论。Sugihara和Tsuda(1979)利用该仪器对北太平洋的南部和北部水体体散射函数进行了测量，发现颗粒物散射系数与颗粒物浓度间有较大的相关性，但该相关系数也同时受颗粒物折射率和粒径分布的影响。Whitliock(1981)利用其自研的前向小角度散射仪(测量角度0.374°—1.5°)以及改进的Brice-phonix广角散射仪(测量角度25°—155°，角度分辨率5°)对弗吉尼亚的阿波马托克斯河以及后河的浑浊水域进行了测量，发现水体漫反射率R与后向散射系b和吸收系数a之比无明显的线性关系，而与b/(a+b)之间有线性相关性，但相关系数会随着水体的浊度以及太阳天顶角的变化而变化。

Tyler和Richardson(1958)设计了第一台真正意义上用于水体(海水)体散射函数测量的广角散射仪，测量范围20°—170°，该仪器的一个特点是散射体前段置有一旋转式光阑，在探测器旋转接收不同角度散射信号的同时该光阑也同步旋转(探测器和光阑并非同一光轴)，使不同角度的散射体体积保持近似相等，因此Tyler在定标体散射函数时没有对散射体体积进行校正，Tyler指出该仪器适用于浊度较低的大洋或海湾水体，而在混浊度较高的水体，海水会使得准直光束在入射到散射体之前被过量地散射，同时有效的散射体积也会增加，这会大大影响测量精度。同时，由于后向散射光信号十分微弱，光电探测器对后向散射探测地灵敏度不足，且光源的不完全准直对该仪器的测量结果也会产生一定的误差。因探测器接收的散射光通量先经过水体的衰减，基于体散射函数的数学定义，体散射函数定标需已知另一固有光学参数—衰减系数，Tyler(1961b)利用该仪器并搭配透射计，对太平洋沿海海域(圣佩德罗湾、圣卡特琳娜岛、圣克利门蒂岛)与内陆水体(庞多雷湖)以及纯水体散射函数和其他固有光学性质进行测量，发现沿海区域不同深度海水的衰减系数以及散射系数的变化率较高，达到25%左右，而前向散射率(前向散射系数与总散射系数之比)变化率小于2%，庞多雷湖的测量结果与该结果也较为一致，但前向散射率高于海水，而纯水中该值最低，他认为强的前向散射主要受大粒径颗粒的影响，清澈水体中主粒物粒径较小，因此其前向散射率较低，与此同时，Tyler研究发现，上述水体体散射函数最小值均出现在100°—120°。同年，Tyler(1961a)对不同浓度的脱脂牛奶溶液的体散射函数进行测量，发现45°体散射函数值与散射系数之间的相关性达到0.9以上，因此对含有相同类型悬浮颗粒物的水体而言，可以用45°体散射值来计算总散射系数。

受早期光电探测能力及仪器设计结构的限制，转动式探测器式仪器无法对10°内前向小角度散射光信号进行测量，Duntley(1963)设计了一款测量0.5°体散射函数的散射仪。也是已知的第一个测量前向小角度体散射的散射仪。其测量原理是准直光束经散射体后发生散射，小角度散射光与透射光经一凸透镜聚焦在焦平面上，焦点处有一不透明遮光板遮挡0°透射光，焦平面上还置有一孔径光阑使其后方的光电探测器接收0.5°散射信号，同年，Duntley设计了一种基于转动式测量原理的广角散射仪，测量范围为20°—160°，角度分辨率为5°，利用两种仪器对美国新罕布什尔州温尼珀索基湖进行了测量，对两种仪器测得的不同角度的体散射函数进行曲线拟合并将其与Dawson、Tyler等不同学者在不同海区的实测与理论结果进行对比(Dawson和Hulburt，1941；Hulburt，1945；Jerlov，1961；Tyler，1961b；Tyler和Austin，1964)，并对所测得的体散射函数进行90°的标准化处理，发现这些标准化的体散射函数( $\beta \left( \psi \right)/\beta \left( {90^\circ } \right)$ )在前向范围内具有很高的一致性，而在后向变化则较大，因此，他认为自然水体的大部分散射是由水体中的大粒径颗粒物和透明有机物的折射与反射导致的，而对入射光波长的依赖性不大。

Kullenberg(1968)设计了一款前向小角度散射仪，通过平行移动两楔形反射镜，使探测器接收并测量1°、2.5°、3.5°的散射信号，Kullenberg利用该仪器以及自研的转动式广角散射仪(10°—165°)和Jerlov等设计的可测量45°和90°的体散射函数的散射仪对大西洋马尾藻海水体散射函数进行了测量并与其他研究者对不同海域以及不同方法(实测与理论计算)得到的数据进行对比，发现45°体散射值与散射系数具有较大相关性，约为3.3 ×10⁻², 但Hodkinson(1962)认为对于不同的悬浮颗粒这一比值会有较大变化，通过实验研究发现当悬浮颗粒为透明石英颗粒时，这一比值为3.5 ×10⁻²，当悬浮颗粒为生煤颗粒时，该比值为2.0 ×10⁻²，这表明水质的不同可能会导致该比值发生较大变化，Kullenberg(1968)研究的区域为较清澈的大洋水体，对于浊度较高的水域如港口等需要进一步的研究论证。

Petzold(1972)研究设计了两款体散射仪，一款(LASM)测量前向小角度(包括0.0859°、0.169°、0.338°。其中，对于清澈水域，0.0859°测量的体散射值太小而无法使用，该角度的测量适用于更为浑浊的水体)，其测量原理与Duntley于1963年设计的前向小角度散射仪原理相似(Duntley，1963)，另一款广角测量仪器(GASM)测量范围10°—170°，角度分辨率10°，探测器一端固定，光源一端可机械式转动，Petzold提出多重散射对于水体尤其是对浊度较高水体的体散射函数测量带来较大误差，并提出一种迭代方法对该误差影响进行校正。基于自主研制的两套仪器，Petzold对3类典型海域(深海、近岸、浑浊的港口)海水体散射函数进行了测量发现3类水体体散射函数有明显的不同，呈现为港口>近岸>深海，Petzold的测量结果作为经典体散射函数沿用至今。

Kullenberg(1978a)设计了一款探测器旋转式体散射测量仪(工作波长520 nm、650 nm)，测量角度8°—160°，角度分辨率1°，视场角固定为1°，Kullenberg通过实验测试发现，探测器水下转动的角度误差对体散射函数的测量带来较大的影响，其中60°—100°体散射函数测量的最大误差可达到25%，而90°—100°的最大误差达到40%，40°—60°和110°—130°的误差达到15%。其他值达到10%，Kullenberg分别于1976年、1977年对德雷克海峡以及秘鲁上升流海区800 m以深的40个不同深度的水体体散射函数进行研究后发现(Kullenberg, 1978b,1984)，在100 m水深范围内，散射系数及体散射函数随深度显著变化，且具有较为显著的区域性特点。且上升流海区由于富含营养物质其体散射值高于其他区域，同时也发现大粒径颗粒对前向散射的影响大于波长对前向散射的影响，而前向散射中小于20°的体散射在散射系数中所占比重可达90%以上，因此其认为大粒径颗粒物浓度很大程度上决定了散射系数。

德国学者Reuter(1980)对德国波罗的海富伦斯堡峡湾水域22 m深的海水样本进行采集，利用自研的探测器旋转式广角散射仪(5°—170°)对含有不同粒径大小的泥浆颗粒、石英颗粒、伊利石颗粒的海水样本进行测量(Reuter，1980)，发现高折射率、大粒径的悬浮颗粒其后向散射较强，颗粒物形状对其影响较小。且大粒径泥浆颗粒体散射函数明显高于Mie理论估计值，Reuter认为这是由于测量的大粒径泥浆颗粒(6 μm—20 μm)通常由多个小粒径泥浆颗粒集聚组成，而这些小颗粒并不紧密相连，集聚体比较疏松，作为其组成部分的小颗粒也会各自产生散射，从而使得测量体散射函数值明显大于理论估计值。

Volten等(1998)研究设计了一款探测器转动式的散射仪，角度分辨率为5°，测量范围20°—160°，仪器内置有圆柱形样品室，由于0°透射光在样品室内壁发生多次反射，反射光经过散射体产生的散射对测量结果会产生较大影响，这种影响也广泛存在于含有样品室的如Brice以及Dawson等设计的广角散射仪中(Dawson和Hulburt，1941；Brice 等，1950；Spilhaus，1968；Whitlock 等，1981)，而前人对此误差并未进行校正，Volten对由样品室内壁多次反射产生的误差进行了计算和校正，利用其自研的散射仪，Volten对来自沿海与内陆的15种不同类型浮游植物以及2种河口沉积物的泥沙颗粒进行了体散射函数测量，发现颗粒物的不同外部形状(近球形与细长圆柱形)对体散射函数的影响并不明显，对于浮游植物，体内气囊的有无及大小对其体散射函数影响显著，体内含有气囊的微囊藻的体散射函数在近前向角度的衰减程度明显大于不含气囊的微囊藻。

Lee和Lewis(2002)设计了一套光源与探测器固定，采用旋转棱镜的方法测量0.3°—177.3°体散射函数的测量仪—MVSM，测量的角度间隔为0.3°。该光路设计可以较好的避免背景光对前向小角度探测的影响，通过引入吸光性玻璃板大大减少仪器表面镜面散射和反射对后向散射的影响，采用高灵敏度的光电倍增管以及自动调节探测器增益系数的方法(对数放大电路)适应宽动态范围的探测。Chami(2006)对克里米亚半岛沿海地区不同深度海水样本进行采集，利用MVSM测量水样的体散射函数分布,分别以实测体散射函数与Fournier-Forand体散射函数作为输入参数，利用Hydrolight计算水体不同角度的遥感反射率，发现实测体散射函数与FF体散射函数在0°—180°范围内有一定的差异，这种差异对遥感反射率的影响可达到20%，同时通过计算水体多重散射对不同角度的遥感反射率的影响，发现水体越浑浊，其前向散射产生的多重散射对遥感反射率的贡献越大，纯水中多重散射对遥感反射率的贡献约为16%，而当水体的b_b/a>0.3(后向散射系数与吸收系数之比)，多重散射的贡献可达94%，这一试验结果与Mobley和Park等前人的理论研究结果基本一致(Mobley 等，2002；Park和Ruddick，2005)。Shybanov等结合MVSM并搭配HS-6、ECO-VSF等仪器测量黑海沿海区域海水的光学性质(Chami 等，2005)，利用MVSM测得的后向散射系数(90°—180°积分得到)与HS-6(经验推算)以及ECO-VSF测量(经验推算)的后向散射系数相差小于10%，根据Twardowski等(2001)的经验公式，通过实测后向散射率反演得到的该研究区域颗粒物平均折射率分布在1.12—1.20，而石英与云母颗粒的折射率分别为1.15与1.20，因此Shybanov等(2006)认为该研究区域海水的散射系数与后向散射系数主要由非藻类矿物颗粒所决定，同时发现4°的体散射函数与散射系数间的相关性达到0.96，其比值平均值为9.3±4.3%， $\beta (45^\circ)/{b_{\rm{bp}}}$ 较依赖于水体中的颗粒物组成， $\;\beta (4^\circ)/{b_{\rm{bp}}}$ 能适用于不同类型的水体。

Zhang等(2011)基于MVSM对新泽西海岸沿海水体体散射函数实测数据，结合Mie理论反演并分析了该海区颗粒物粒径分布情况，研究发现测量的海水样本中含有5个不同中值粒径的颗粒群，其中小于0.1 μm的颗粒物对水体前向散射的贡献非常小，而对后向散射的贡献可以达到20%—40%，且这一趋势随着水体营养化程度增加而增加，折射率对亚微米粒径颗粒的体散射函数影响很小；而对于粒径大于20 μm的颗粒物，其体散射函数贡献主要依赖于颗粒物折射率与浓度，粒径大小对其影响很小。

研究表明,水体后向散射系数 ${b_{\rm{b}}}$ 与后向某一角度体散射函数之间存在很好的线性关系(Oishi，1990)，Chami(2006)利用MVSM(测量波长为443 nm、490 nm、555 nm)对黑海的沿岸水体进行测量，发现相关因子 ${\chi _{\rm{p}}}$ 在140°时变化率最低( ${\chi _{\rm{p}}}(140^\circ)$ =1.21±5.1%； ${\chi _{\rm{p}}}(120^\circ)$ =1.29±5.5%)，利用 ${\chi _{\rm{p}}}(140^\circ)$ 估算的颗粒物后向散射系数平均误差为7.1%。但通过对不同类型的藻类培养液的测量发现， ${\chi _{\rm{p}}}(140^\circ)$ 的估计误差达到25.8%,因此Chami认为 ${\chi _{\rm{p}}}(140^\circ)$ 不适用于对富营养化水体的后向散射系数估算。

Zhang等(2002)通过MVSM实测和Mie理论估算对存在气泡的海水体散射函数进行研究，发现对于被有机质覆盖的气泡，其外层有机质会大大增加气泡的后向散射，而前向散射几乎不受影响，气泡对海水总体散射函数的贡献达5%，而对海水后向散射系数贡献达到40%,这一结论或许解释了Morel(1991)、Stramski等(2001)观察到的海水后向系数突增的现象。研究同时发现无论是被有机质覆盖的气泡还是纯净气泡，当半径大于入射波长时，体散射函数在60°—80°会出现一峰值，随着半径的减小这一现象将逐渐消失。这一现象的存在也为跟踪海水气泡提供了一种有效的光学手段。但MVSM的测量频率(90 s/次)无法对水体中瞬息万变的气泡长消过程进行快速捕获。

美国Sequoia公司研发了一款可用于剖面测量的广角体散射剖面仪LISST-VSF(Slade 等，2013)，该仪器也是目前已知的唯一一款商业化广角体散射函数仪器，测量角度范围0.1°—150°，其中0.088°—14.36°范围采用32个环形固定探测器探测，15°—150°范围的测量通过转动“眼球探测器”模式的光学扫描，接收不同角度的散射光信号，角度分辨率1°，入射光经偏振分束器以及半波片的作用形成水平偏振光或垂直偏振光并先后经散射体散射形成两个线性极化偏振分量被两个光电倍增管探测。测量数据可以计算出体散射函数和线偏振度(穆勒矩阵M11和M12)。将该仪器对聚苯乙烯微珠测得的体散射函数和线偏振度与Mie理论估计值对比发现，二者具有很高的一致性。Harmel利用LISST-VSF(0.1°—150°)、I-VSF(8°—172°)、POLVSM(1°—179°)对聚苯乙烯微珠的VSF进行测量(Harmel 等，2016)，并与Mie散射估计值进行对比，3个仪器测量结果与理论估计值平均差异率分别为13.1%、3.1%、3.1%，且I-VSF与POLVSM在大于25°测得的VSF与Mie散射估计值有着高度的一致性，但通过对5种不同种类的浮游藻类测量后发现，这两类仪器测得的体散射函数在大于150°后均显著高于理论估计值(1个量级以上)，Harmel认为该现象的主要原因是浮游生物内部构造较为复杂，内部折射率与表面折射率不同(内部折射率大于表面)，而理论估计模型并没有考虑这些因素。

Chami(2014)设计了基于偏振光测量的广角散射仪—POLVSM，该仪器的光源和探测器前端分别置有可旋转的起偏器和检偏器，探测器与样品室紧密相连，随圆柱形样品室的水平转动接收1°—179°偏振散射光信号，角度分辨率1°，可测量包括体散射函数在内的穆勒矩阵中的9个元素，完成1°—179°测量的时间(包括3个偏振方向)约为10 min，该仪器的一大特点是样品室内有两反射棱镜P1，P2,入射光通过P1棱镜的反射进入样品室中，再通过P2棱镜反射出样品室外，该棱镜系统的设计使得入射光与被测的散射光(探测器转动平面)处于不同平面，有效地减少了镜面反射产生的杂散光影响，同时也大大增加了测量的角度范围。Chami利用该仪器进行测量发现，颗粒物的后向散射尤其是大于150 °的后向散射会随着颗粒物折射率的增大而增大，随颗粒物粒径的增大而减小。该发现与Twardowski等(2001)、Zhou等(2012)基于理论模型研究结论一致，同时Chami还发现，折射率的增大会导致其线偏振度M12降低，1°—179°范围内矿物颗粒线偏振度的最大值为0.8，而浮游植物只有0.5。

转动式广角体散射函数测量技术因其结构限制，多应用于实验室或在线测量。早期转动式广角体散射函数测量技术通过单一光源或探测器一端固定，另一端机械式旋转实现不同角度散射光信号探测。21世纪后，随着技术的发展，转动式测量仪有了较大的改进，如MVSM、LISST-VSF等，探测器与光源均固定，通过棱镜的转动将不同角度的散射反射入探测器中，转动式散射仪具有高角度分辨率及宽角度测量范围等优点，但其测量速度较慢，目前测量最快的转动式测量仪也只有0.25 Hz(LISST-VSF)，对于瞬息万变的海洋环境，这种结构的采样频率是其瓶颈，且转动和探测功耗大，供电复杂，角度分辨率的重复性和稳定性均较差(Kullenberg，1978a)，因此大多无法适用于海水的原位测量。

2.2 多固定探测器、阵列式

据目前已有文献记载，第一款多固定探测器、阵列式散射仪诞生于1992年，美国Wyatt Technology Corporation 公司设计了一种散射计—DAWN(Wyatt，1993)，采用18个固定探测器(硅光电二极管)同步测量22.5°—147°(18个角度，22.5°—147°，角度分辨率不固定：4°—9°)范围内18个角度的散射光信号。该仪器起初用来测量液体中大分子或胶质物的摩尔质量(Wyatt, 1993，1997，1998；Turquois和Gloria，2000)，并广泛应用于生物化学领域中，直到1999年，该仪器才被应用到海水体散射函数测量中，Balch等(1999)首先利用流式细胞仪对美国缅因州西布斯贝港的海水样本中不同种类的钙化藻类进行分类提取(实验对象为颗石藻，在非活动期，细胞膜外部钙化，形成许多碳酸钙晶体—方解石，而在活动期则无晶体覆盖)，然后利用DAWN对不同种类的样本颗石藻进行了测量，发现颗石藻后向散射系数 ${b_{\rm{bp}}}$ 随着um级藻类中碳酸钙浓度(mol/L)的相关性大于0.85，个别藻类可达到0.99，但不同藻类该相关系数不同。通过对活动期无方解石晶体的颗石藻测量得到的后向散射系数 ${b_{\rm{b}}}$ 反演，可得到叶绿素浓度，进而得到颗粒有机碳(POC)浓度信息。对钙化的颗石藻进行酸化脱钙处理，测量脱钙颗石藻后向散射系数 ${b_{\rm{bp1}}}$ ，利用未经酸化处理的钙化颗石藻后向散射系数之差( ${b_{\rm{bp}}} - {b_{\rm{bp1}}}$ )反演颗石藻中颗粒无机碳(PIC)浓度，但测量误差最大可达38%。Reynolds等(2006)利用DOWN、LISST-100X，ECO-VSF3、HS-6对不同粒径的聚乙烯微粒进行体散射函数测量拟合，发现实测值在0.5°—120°范围内与Mie散射估计值有较高的相关性，DOWN实测的大于120°的后向散射明显高于Mie理论估计值和HS-6与ECO-VSF3的实测值,Reynolds等认为这是由于样品室内壁与仪器表面的反射导致后向散射测量值剧增引起的。Reynold等(2006)利用上述仪器组对圣地亚哥帝国海滩码头海水进行了测量，与Petzold(1972)的实测数据进行比对发现该海区海水体散射函数与Petzold所测的浑浊港口数据具有较高的一致性，但2005年—2006年不同时期同一海区海水体散射函数变化超过两个量级，2005年7月该海区赤潮期间体散射函数达到最高值。Babin等(2012)对DAWN的光源部分进行了调整，提出了新的定标方法，校正样品室界面的反射以测定体散射函数，支持检测的悬浮颗粒最大粒径理论上为6.2 um。但相关应用未见报道。

2000年，美国的HOBI labs公司设计了一款阵列式散射仪—Hydrobeta(Dana和Maffione, 2000, https://www.hobilabs.com/cmsitems/attachments/3/HydroBetaOOXVExtendedAbstract.pdf[2018-02-27]),该仪器利用12个探测器同时测量11个角度体散射和0°透射光，支持体散射函数水下原位测量，为适应不同角度散射光信号的强度，不同角度的探测器对应着不同的视场角以及不同的增益系数来适应宽动态范围信号的测量，仪器定标是通过在光源和探测器之间插入漫射体，并移动测量确定一个只与仪器光机电结构相关的综合性权重响应函数，这种定标方法无需散射体校正，但关于该仪器的应用方面的记载尚未发现。

李彩等(2004)年设计了一套可用于测量20°—160°范围内7个不同角度的阵列式体散射函数及0°透射光测量仪样机(Li 等，2012b)，角度分辨率20°，测量频率6 Hz。测量仪可实现水体衰减系数以及不同角度体散射函数的剖面测量，采用无线数据下载方式,实现测量仪与上位机之间的无线通讯。利用该散射剖面测量仪对我国大亚湾沿岸和离岸南海海域不同类型海水体散射函数进行剖面测量(Li 等，2012a)，结果发现受岸边泥沙注入以及较高浓度的浮游植物的影响，大亚湾东山口附近水体体散射函数远大于大亚湾核电站附近水域(约1个量级)。而海洋底质界面体散射函数高于表层海水，对于大洋开放水体，前向小角度的体散射函数有较为显著的变化，后向散射变化较小，通过对台风前后水体体散射函数实测结果研究发现，台风过境前后海表层体散射函数在60°—80°会有一个显著地变化，具体表现为台风过境后60°—80°体散射函数会出现一个非常显著的峰值(Li 等，2015)，这一结论与Zhang等(2011)的研究结论相吻合。

2009年，美国WET labs公司研制了一款支持水下原位测量的广角体散射仪样机—MASCOT(Sullivan和Twardowski，2009)，17个探测器同步测量10°—170°角度范围内17个角度的体散射函数，角度间隔10°，为减少杂散光，采用双反射光路的准直光源，并尽量保证探测器及其他容易发生镜面反射的光学部件最小化，同时在10°探测器附近加入一个光阱避免可能的反射。但该仪器不能同步测量衰减系数，需搭配其他仪器如ACS等同步测量体散射函数。Twardowski(2012)利用MASCOT对加州斯科利普斯栈桥附近碎浪带区域进行了测量。通过10°—170°体散射函数反演海水颗粒物粒径分布与折射率分布情况，反演方法与Zhang等(2011)相似，但在具体散射相函数构建上，Zhang等(2011)的方法基于球形颗粒的Mie理论估计，而Twardowski(2012)除球形颗粒物还添加了非球形颗粒如非对称六面体的石英颗粒以及被有机质包裹的不同厚度、不同粒径气泡的散射相函数。通过反演发现，海水沉积颗粒物的10°与120°体散射函数比值随着海水沉积物折射率的升高而降低。同时Twardowkiski提出，虽然利用近前向散射光信号可以反演粒径分布情况(如LISST-100X)，但却无法获取颗粒物组分等信息，而颗粒物的组分以及结构对后向散射有着十分重要的影响，利用MASCOT等广角散射仪可以获取颗粒物折射率分布以及总悬浮物(TSM)、颗粒有机物(POM)、颗粒无机物(POM)含量等，进而能深入地了解颗粒物生物化学特性等信息。

Zhang等(2002，2011)曾利用MVSM对海水气泡进行VSF测量，但由于海水中的气泡往往会在短时间内破裂消失，而MVSM一次完整的测量需要90 s，导致其不能有效获取海水气泡的体散射函数信息。Czerski等(2011)利用高采样频率(20 Hz)的MASCOT对夏威夷南部表层海水中气泡的体散射函数进行测量，反演了粒径小于30 um气泡的粒径分布情况，并将其与声学探测方法反演的结果进行比较，发现气泡表面覆盖的有机质成分及有机质膜的厚度对气泡的体散射函数、以及粒径分布的反演都有较大影响，对小于5 um的气泡，气泡有机质膜的厚度对体散射函数影响占主导(主要体现在后向散射)，折射率对其影响相对较小。且通过计算发现，当该研究区域气泡的平均折射率以及包裹的膜平均厚度分别取1.18 nm与10 nm时，通过体散射函数反演得到的气泡粒径分布情况与声学方法得到的结果一致性最高，该结论也与Glazman(1983)、Aas(1996)等的研究结果一致。同时，Czerski通过研究发现，Zhang等(2002)所发现的气泡体散射函数在60°—80°存在峰值的现象对于粒径小于5 μm的气泡并不明显。Twardowkiski等(2012)利用MASCOT对美国加州斯科利普斯栈桥附近的碎浪带海区进行测量发现，um级以上的大粒径气泡浓度与 $\beta (70^\circ )/\beta \left( {120^\circ } \right)$ 有着较好的相关性。

Sullivan和Twardowski(2009)利用MASCOT仪器对10个不同地区的海域测量得到的数据分析，以1°的间隔进行3次样条插值得到体散射函数曲线，结果发现110°—120°范围内颗粒物体散函数与后向散射系数之比在不同区域内的变化率均小于2%， ${\chi _p}$ 在113°的变化率最小，但考虑到仪器噪声等测量误差，Sullivan认为推算后向散射系数最佳角度也可能出现在110°—120°范围的其他角度，Sullivan的这一结论与Oishi(1990)与Boss和Pegau(2001)的研究结果基本一致。

阵列式散射仪是在光电检测技术飞速发展以及人们对海洋认识的不断深入的背景下诞生的，这种基于多个探测器同步测量的阵列式散射仪具有测量速度快(目前最快可达20 Hz)、同步性好、稳定性好、功耗低、设计灵活、适应性强等适用于体散射函数快速剖面测量的优点。但阵列式散射仪与转动式体散射函数测量仪相比，角度分辨率低，角度范围方面受限，且至目前，受光电检测技术限制，探测器均采用硅光电二极管，致使其检测灵敏度受限，对微弱的后向散射信号探测能力较弱。

2.3 面阵CCD成像式

日本学者Tan等(2013)设计了一种测量方法与前者具有较大区别的体散射仪—I-VSFM。(测量范围8°—172°，角度分辨率1°)采用面阵CCD作为光电探测器，入射光经样品池内散射体发生散射，各角度散射光在一锥形反射镜表面上反射并通过半环形狭缝，经过狭缝的不同角度散射光再经过两次精准反射进入到CCD中，CCD不同像元接收不同角度散射光，形成散射光的半环形图像。在狭缝0°—25°位置放置中性滤光片(透过率1.5%),以减弱小角度散射光信号强度，避免过饱和的同时为减少样品池表面反射问题，在样品室的光线出射端加入了带有倾斜角的光阱和滤光片，大部分透射光被吸收，只有约0.4%的反射光，从样品上方反射出去。仅大约0.01%的反射光反射回样品内，因此能大大减少样品室边界的散射对测量结果带来的影响。

Tan等(2015)利用I-VSF(8°—172°，入射波长400—600 nm)测量了大洋一类水体、沿岸浑浊水体、以及含有不同浮游植物的培养液的不同角度的 ${\chi _{\rm{p}}}$ ，结果表明，对于自然水体以及沿岸水体 ${\chi _{\rm{p}}}(1{\rm{2}}0^\circ)$ 与 ${\chi _p}(140^\circ)$ 均表现出较好的相关性，其变化率均小于5%,但对于不同种类的藻类培养液 ${\chi _p}(120^\circ)$ 平均变化率为20.3%， ${\chi _{\rm{p}}}(140^\circ)$ 的变化率为17.3%，这意味着对于富营养化或营养程度较高的水体，单一角度的体散射函数不能很好的推算海水颗粒物后向散射系数，Tan发现，通过引入 $\;{\beta _{\rm{p}}}(120^\circ)/{\beta _{\rm{p}}}(170^\circ)$ 与 $\;{\beta _{}}(120^\circ)/\beta (170^\circ)$ ，能够准确地推算颗粒物以及水体的后向散射系数， ${b_{\rm{bp}}}$ 、 ${b_{\rm{b}}}$ ：

$ {b_{\rm{bp}}} = 0.9743{{\rm{e}}^{0.0684{\beta _{\rm{p}}}(120)/{\beta _{\rm{p}}}(170)}}{\beta _{\rm{p}}}(120) $

(4)

$ {b_{\rm{b}}} = 0.9939{{\rm{e}}^{0.0686{\beta _{}}(120)/{\beta _{}}(170)}}{\beta _{}}(120)) $

(5)

式中，b_bp表示水体中颗粒物后向散射系数，b_b表示水体后向散射系数，根据该表达式对所研究水体推算的 ${b_{\rm{bp}}}$ 与 ${b_{\rm{b}}}$ 平均误差约为3%。基于面阵CCD测量的成像式散射仪具有宽角度范围、高角度分辨率的特点，且仪器稳定性高、功耗低、能同步测量水体不同角度的体散射函数。但该结构采用单一CCD实现不同角度体散射函数测量，灵敏度和动态范围均受限，后向微弱散射光信号探测能力较弱，虽然该散射仪在前向散射较强的方向上对应放置一定透过率的中性滤光片以减弱较强的前向散射光信号，但对于方向性特点极其显著的散射光而言，CCD每个像素检测能力一定，增益系数固定，依然不可避免会产生不同角度测量过饱和或灵敏度低等影响测量精度和可靠性的问题。目前，成像式散射仪仅支持实验室测量。

3 结　语

广角水体体散射函数测量技术自20世纪40年代发展至今，依然在不断探索和改进中前行，转动式、阵列式及CCD成像式3大类测量技术正在齐头并进，每一种技术都在不断改进和完善之中，转动式测量角度范围和分辨率高，但测量频率和角度的重复性和稳定性限制了其适用范围；阵列式测量稳定性高、速度快、同步性好，但现有技术致使其角度分辨率和角度范围受限；CCD成像式的测量速度快、同步性、角度分辨率高，但单一探测器及单一放大增益致使其测量动态范围和灵敏度较低。为更好地顺应海洋光学的发展，对瞬息万变的海洋环境进行监测，毋庸置疑，广角体散射函数测量技术应该向小型化、高测量频率、高灵敏度、高精度、高角度分辨率、宽动态范围、水下快速剖面方向发展。新兴发展起来的微型、高灵敏度、低功耗、低压工作的类光电倍增管的出现能够在很大程度上推进和优化广角体散射函数测量技术向小型化、高灵敏、宽动态范围的方向发展，同时，深入研究体散射函数测量过程中多重散射机制与校正模型的研究能很大程度上提升散射测量的精准度。中国在广角水体体散射函数的研究上与国际先进国家差距甚大，国内海洋光学及海洋物理相关专家高度重视广角体散射函数测量技术的进展和贡献，这一应用需求可以促进中国在广角体散射函数测量技术上的进步和突破。

目前，广角体散射函数测量技术在海水光学特性及其相关领域的研究正在不断深入，对湖泊、河流等内陆水体的研究较少(Tyler，1961b；Duntley，1963)，目前还主要集中在后向某一角度体散射或后向散射系数的测量研究以及广角水体体散射函数的理论估计(Effler 等，2013；Kalenak 等，2013；黄昌春等，2011；孙德勇等，2008)，随着测量技术的不断发展，内陆水体也应成为未来广角水体体散射函数测量的重要研究对象。将体散射函数实测数据与Mie理论、Fournier-Forand模型及MonteCarlo 辐射传输理论等理论模型相结合，研究直接测量过程中水体多重散射机制与校正模型以及体散射函数与水体各组分(如：气泡、浮游藻类、沉积物等)的物化特性(如：折射率、粒径分布、颗粒物组成结构及浓度等)之间的相关关系及水体不同组分对不同角度散射的特征性贡献是广角体散射函数的一个重点研究和应用方向，可促进水体散射特性等固有光学特性更好地在水下光辐射传输、水色遥感、水环境监测与保护、海气交互过程研究及水下目标的光学探测等光学海洋学应用领域发挥更为显著的作用。

参考文献(References)

Aas E. 1996. Refractive index of phytoplankton derived from its metabolite composition. Journal of Plankton Research, 18 (12): 2223–2249. [DOI: 10.1093/plankt/18.12.2223]

Agrawal Y C. 2005. The optical volume scattering function: temporal and vertical variability in the water column off the New Jersey coast. Limnology and Oceanography, 50 (6): 1787–1794. [DOI: 10.4319/lo.2005.50.6.1787]

Babin M, Stramski D, Reynolds R A, Wright V M and Leymarie E. 2012. Determination of the volume scattering function of aqueous particle suspensions with a laboratory multi-angle light scattering instrument. Applied Optics, 51 (17): 3853–3873. [DOI: 10.1364/AO.51.003853]

Balch W M, Drapeau D T, Cucci T L, Vaillancourt R D, Kilpatrick K A and Fritz J J. 1999. Optical backscattering by calcifying algae: separating the contribution of particulate inorganic and organic carbon fractions. Journal of Geophysical Research, 104 (C1): 1541–1558. [DOI: 10.1029/1998JC900035]

Bohren C F and Huffman D R. 1983. Absorption and Scattering of Light by Small Particles. New York: Wiley: 328

Boss E and Pegau W S. 2001. Relationship of light scattering at an angle in the backward direction to the backscattering coefficient. Applied Optics, 40 (30): 5503–5507. [DOI: 10.1364/AO.40.005503]

Brice B A, Halwer M and Speiser R. 1950. Photoelectric light-scattering photometer for determining high molecular weights. Journal of the Optical Society of America, 40 (11): 768–778. [DOI: 10.1364/JOSA.40.000768]

Chami M, Marken E, Stamnes J J, Khomenko G and Korotaev G. 2006a. Variability of the relationship between the particulate backscattering coefficient and the volume scattering function measured at fixed angles. Journal of Geophysical Research, 111 (C5): C05013 [DOI: 10.1029/2005JC003230]

Chami M, McKee D, Leymarie E and Khomenko G. 2006b. Influence of the angular shape of the volume-scattering function and multiple scattering on remote sensing reflectance. Applied Optics, 45 (36): 9210–9220. [DOI: 10.1364/AO.45.009210]

Chami M, Shybanov E B, Churilova T Y, Khomenko G A, Lee M E G, Martynov O V, Berseneva G A and Korotaev G K. 2005. Optical properties of the particles in the Crimea coastal waters (Black Sea). Journal of Geophysical Research, 110 (C11): C11020 [DOI: 10.1029/2005JC003008]

Chami M, Thirouard A and Harmel T. 2014. POLVSM (Polarized Volume Scattering Meter) instrument: an innovative device to measure the directional and polarized scattering properties of hydrosols. Optics Express, 22 (21): 26403–26428. [DOI: 10.1364/OE.22.026403]

Czerski H, Twardowski M, Zhang X and Vagle S. 2011. Resolving size distributions of bubbles with radii less than 30 μm with optical and acoustical methods. Journal of Geophysical Research, 116 (C7): C00H11 [DOI: 10.1029/2011JC007177]

Dana D R and Maffione R A. 2000. HydroBeta: a new instrument for measuring in-situ profiles of the volume scattering function from 10 to 170 degrees. Ocean Optics XV.https //www.hobilabs.com/cmsitems/attachments/3/HydroBetaOOXVExtendedAbstract.pdf

Dawson L H and Hulburt E O. 1941. Angular distribution of light scattered in liquids. Journal of the Optical Society of America, 31 (8): 554–558. [DOI: 10.1364/JOSA.31.000554]

Duntley S Q. 1963. Light in the sea. Journal of the Optical Society of America, 53 (2): 214–233. [DOI: 10.1364/JOSA.53.000214]

Effler S W, Peng F, O'Donnell D M and Strait C. 2013. The backscattering coefficient and its components in the Great Lakes: a review and synthesis. Journal of Great Lakes Research, 39 (S1): 108–122. [DOI: 10.1016/j.jglr.2013.02.002]

Gibbs R J. 1978. Light scattering from particles of different shapes. Journal of Geophysical Research, 83 (C1): 501–502. [DOI: 10.1029/JC083iC01p00501]

Glazman R E. 1983. Effects of adsorbed films on gas bubble radial oscillations. Journal of the Acoustical Society of America, 74 (3): 980–986. [DOI: 10.1121/1.389844]

Harmel T, Hieronymi M, Slade W, Röttgers R, Roullier F and Chami M. 2016. Laboratory experiments for inter-comparison of three volume scattering meters to measure angular scattering properties of hydrosols. Optics Express, 24 (2): A234–A256. [DOI: 10.1364/OE.24.00A234]

Hodkinson J. R. 1962. Light scattering and extinction by irregular particles larger than the wavelength. Ices Electromagnetic Scattering. Postdam: Milton Kerer : 87–100.

Hojerslev N. 1975. A spectral light absorption meter for measurements in the sea. Limnology and Oceanography, 20 (6): 1024–1034. [DOI: 10.4319/lo.1975.20.6.1024]

Huang C C, Li Y M, Sun D Y, Le C F and Jin X. 2011. Research of scattering spectrum characteristic and formative mechanism of Taihu lake waters. Acta Optica Sinica, 31 (5): 0501003 ( 黄昌春, 李云梅, 孙德勇, 乐成峰, 金鑫. 2011. 太湖水体散射光谱特性及其形成机理研究. 光学学报, 31 (5): 0501003 )

Hubert L, Lubac B, Dessailly D, Duforet-Gaurier L and Vantrepotte V. 2010. Effect of inherent optical properties variability on the chlorophyll retrieval from ocean color remote sensing: an in situ approach . Optics Express, 18 (20): 20949–20959. [DOI: 10.1364/OE.18.020949]

Hulburt E O. 1945. Optics of distilled and natural water. Journal of the Optical Society of America, 35 (11): 698–705. [DOI: 10.1364/JOSA.35.000698]

Jerlov N G. 1961. Optical measurements in the eastern North Atlantic. (" Discovery II” expedition of August and September 1959). Meddelanden från Oceanografiska Institutet i Göteborg. 30. 22-32.

Kalenak D, Boss E and Effler S W. 2013. Inherent optical properties of suspended particulates in four temperate lakes: application of in situ spectroscopy. Hydrobiologia, 713 (1): 127–148. [DOI: 10.1007/s10750-013-1498-5]

Kullenberg G. 1968. Scattering of light by Sargasso Sea water. Deep Sea Research and Oceanographic Abstracts, 15 (4): 423–432. [DOI: 10.1016/0011-7471(68)90050-8]

Kullenberg G. 1978a. light-scattering observations in frontal zones. Journal of Geophysical Research, 83 (C9): 4683–4690. [DOI: 10.1029/JC083iC09p04683]

Kullenberg G. 1978b. Light scattering observations in the northwest African upwelling region. Deep Sea Research, 25 (6): 525–542. [DOI: 10.1016/0146-6291(78)90641-0]

Kullenberg G. 1984. Observations of light scattering functions in two oceanic areas. Deep Sea Research Part A. Oceanographic Research Papers, 31 (3): 295–316. [DOI: 10.1016/0198-0149(84)90106-7]

Lee Z P, Carder K L and Arnone R A. 2002. Deriving inherent optical properties from water color: a multiband quasi-analytical algorithm for optically deep waters. Applied Optics, 41 (27): 5755–5772. [DOI: 10.1364/AO.41.005755]

Li C, Cao W X and Yang Y Z. 2012a. Optical scattering property: spatial and angle variability in Daya Bay. Chinese Optics Letters, 10 (S2): S20101

Li C, Cao W X, Yang Y Z and Xu Z T. 2015. The optical scattering property: spatial and angle variability in Northern South China Sea//Proceedings of SPIE 9449, The International Conference on Photonics and Optical Engineering. Xi'an, China: SPIE [DOI: 10.1117/12.2075865]

Li C, Cao W X, Yu J, Ke T C, Lu G X, Yang Y Z and Guo C Y. 2012b. An instrument for In situ measuring the volume scattering function of water: design, calibration and primary experiments . Sensors, 12 (4): 4514–4533. [DOI: 10.3390/s120404514]

Li C, Ke T C, Cao W X, Lu G X, Yang Y Z and Guo C Y. 2004. An instrument for measuring in-situ profiles of the Volume Scattering Function of seawater//Proceedings of 2004 National Symposium on Optics and Photoelectronics, 2005 National Symposium on Optics and Photoelectronics, and the Collection of Papers at the 20th Anniversary of the Establishment of Guangxi Optical Society. Yantai: China ordnance Society, Optics Committee of China Military Engineering Society, Guangxi Society of Optics, Optical Technology Magazine (李彩, 柯天存, 曹文熙, 卢桂新, 杨跃忠, 郭超英. 2004. 水体体散射函数剖面仪//2004全国光学与光电子学学术研讨会、2005全国光学与光电子学学术研讨会、广西光学学会成立20周年年会论文集. 烟台: 中国兵工学会, 中国兵工学会, 中国兵工学会光学专业委员会, 广西光学学会, 《光学技术》杂志社)

McLeroy-Etheridge S L and Roesler C S. 1998. Are the inherent optical properties of phytoplankton responsible for the distinct ocean colors observed during harmful algal blooms?. Ocean Optics : 14

Mobley C D, Sundman L K and Boss E. 2002. Phase function effects on oceanic light fields. Applied Optics, 41 (6): 1035–1050. [DOI: 10.1364/AO.41.001035]

Morel A. 1991. Light and marine photosynthesis: a spectral model with geochemical and climatological implications. Progress in Oceanography, 26 (3): 263–306. [DOI: 10.1016/0079-6611(91)90004-6]

Oishi T. 1990. Significant relationship between the backward scattering coefficient of sea water and the scatterance at 120°. Applied Optics, 29 (31): 4658–4665. [DOI: 10.1364/AO.29.004658]

Pak H, Ronald J, Zaneveld V and Beardsley Jr G F. 1971. Mie scattering by suspended clay particles. Journal of Geophysical Research, 76 (21): 5065–5069. [DOI: 10.1029/JC076i021p05065]

Park Y J and Ruddick K. 2005. Model of remote-sensing reflectance including bidirectional effects for case 1 and case 2 waters. Applied Optics, 44 (7): 1236–1249. [DOI: 10.1364/AO.44.001236]

Petzold T J. 1972. Volume Scattering Functions for Selected Ocean Waters. San Diego: Scripps Institution of Oceanography, 1-30.

Rehm E and McCormick N J. 2011. Inherent optical property estimation in deep waters. Optics Express, 19 (25): 24986–25005. [DOI: 10.1364/OE.19.024986]

Reuter R. 1980. Characterization of marine particle suspensions by light scattering II. Experimental results. Oceanologica Acta, 3 (3): 325–332.

Reynolds R A, Stramski D and Wright V M. 2006. Measurement of the volume scattering function using a multi-instrument approach. Applied Optics, 36 : 6057–6067.

Ronald J, Zaneveld V, Twardowski M S, Shifrin K S, Pegau W S, Boss E and Zolotov I. 2002. Inversion of light scattering measurements to obtain biogeochemical parameters. Ocean Optics XVI, 1-19

Slade W H, Agrawal Y C and Mikkelsen O A. 2013. Comparison of measured and theoretical scattering and polarization properties of narrow size range irregular sediment particles//Proceedings of 2013 Oceans - San Diego. San Diego, USA: IEEE [DOI: 10.23919/OCEANS.2013.6740987]

Smith R C and Baker K S. 1982. Oceanic chlorophyll concentrations as determined by satellite (nimbus-7 coastal zone color scanner). Marine Biology, 66 (3): 269–279. [DOI: 10.1007/BF00397032]

Spilhaus Jr A F. 1968. Observations of light scattering in seawater. Limnology and Oceanography, 13 (3): 418–422. [DOI: 10.4319/lo.1968.13.3.0418]

Stramski D, Bricaud A and Morel A. 2001. Modeling the inherent optical properties of the ocean based on the detailed composition of the planktonic community. Applied Optics, 40 (18): 2929–2945. [DOI: 10.1364/AO.40.002929]

Sugihara S and Tsuda R. 1979. Light scattering and size distribution of particles in the surface waters of the North Pacific Ocean. Journal of the Oceanographical Society of Japan, 35 (2): 82–90. [DOI: 10.1007/BF02108519]

Sullivan J M and Twardowski M S. 2009. Angular shape of the oceanic particulate volume scattering function in the backward direction. Applied Optics, 48 (35): 6811–6819. [DOI: 10.1364/AO.48.006811]

Sun D Y, Li Y M, Wang Q, Le C F, Huang C C and Wu L. 2008. The scattering characteristics of Lake Taihu waters. Journal of Lake Sciences, 20 (3): 389–395. [DOI: 10.18307/2008.0320] ( 孙德勇, 李云梅, 王桥, 乐成峰, 黄昌春, 伍蓝. 2008. 太湖水体散射特性及其空间分异. 湖泊科学, 20 (3): 389–395. [DOI: 10.18307/2008.0320] )

Tan H, Doerffer R, Oishi T and Tanaka A. 2013. A new approach to measure the volume scattering function. Optics Express, 21 (16): 18697–18711. [DOI: 10.1364/OE.21.018697]

Tan H, Oishi T, Tanaka A and Doerffer R. 2015. Accurate estimation of the backscattering coefficient by light scattering at two backward angles. Applied Optics, 54 (25): 7718–7733. [DOI: 10.1364/AO.54.007718]

Turquois T and Gloria H. 2000. Determination of the absolute molecular weight averages and molecular weight distributions of alginates used as ice cream stabilizers by using multiangle laser light scattering measurements. Journal of Agricultural and Food Chemistry, 48 (11): 5455–5458. [DOI: 10.1021/jf000003v]

Twardowski M, Zhang X D, Vagle S, Sullivan J, Freeman S, Czerski H, You Y, Bi L and Kattawar G. 2012. The optical volume scattering function in a surf zone inverted to derive sediment and bubble particle subpopulations. Journal of Geophysical Research, 117 (C7): C00H17 [DOI: 10.1029/2011JC007347]

Twardowski M S, Boss E, Macdonald J B, Pegau W S, Barnard A H, and Zaneveld J R V. 2001. A model for estimating bulk refractive index from the optical backscattering ratio and the implications for understanding particle composition in case I and case II waters. Journal of Geophysical Research, 106 (C7): 14129–14142. [DOI: 10.1029/2000JC000404]

Tyler J E. 1961a. Measurement of the scattering properties of hydrosols. Journal of the Optical Society of America, 51 (11): 1289–1293. [DOI: 10.1364/JOSA.51.001289]

Tyler J E. 1961b. Scattering properties of distilled and natural waters. Limnology and Oceanography, 6 (4): 451–456. [DOI: 10.4319/lo.1961.6.4.0451]

Tyler J E and Austin R W. 1964. Scattering meter for deep water. Applied Optics, 3 (5): 613–620. [DOI: 10.1364/AO.3.000613]

Tyler J E and Richardson W H. 1958. Nephelometer for the measurement of volume scattering function In situ . Journal of the Optical Society of America, 48 (5): 354–357. [DOI: 10.1364/JOSA.48.000354]

Volten H, de Haan J F, Hovenier J W, Schreurs R, Vassen W, Dekker A G, Hoogenboom H J, Charlton F and Wouts R. 1998. Laboratory measurements of angular distributions of light scattered by phytoplankton and silt. Limnology and Oceanography, 43 (6): 1180–1197. [DOI: 10.4319/lo.1998.43.6.1180]

Whitlock C H, Poole L R, Usry J W, Houghton W M, Witte W G, Morris W D and Gurganus E A. 1981. Comparison of reflectance with backscatter and absorption parameters for turbid waters. Applied Optics, 20 (3): 517–522. [DOI: 10.1364/AO.20.000517]

Wyatt P J. 1993. Light scattering and the absolute characterization of macromolecules. Analytica Chimica Acta, 272 (1): 1–40. [DOI: 10.1016/0003-2670(93)80373-S]

Wyatt P J. 1997. Multiangle light scattering: the basic tool for macromolecular characterization. Instrumentation Science and Technology, 25 (1): 1–18. [DOI: 10.1080/10739149709351443]

Wyatt P J. 1998. Submicrometer particle sizing by multiangle light scattering following fractionation. Journal of Colloid and Interface Science, 197 (1): 9–20. [DOI: 10.1006/jcis.1997.5215]

Zhang X D, Lewis M, Lee M, Johnson B and Korotaev G. 2002. The volume scattering function of natural bubble populations. Limnology and Oceanography, 47 (5): 1273–1282. [DOI: 10.4319/lo.2002.47.5.1273]

Zhang X D, Twardowski M and Lewis M. 2011. Retrieving composition and sizes of oceanic particle subpopulations from the volume scattering function. Applied Optics, 50 (9): 1240–1259. [DOI: 10.1364/AO.50.001240]

Zhou W, Wang G F, Sun Z H, Cao W X, Xu Z T, Hu S B and Zhao J. 2012. Variations in the optical scattering properties of phytoplankton cultures. Optics Express, 20 (10): 11189–11206. [DOI: 10.1364/OE.20.011189]

摘要

关键词