|
收稿日期: 2017-11-27; 预印本: 2018-05-16
基金项目: 国家自然科学基金项目(编号:61675051)
第一作者简介: 赵亮,1987年生,女,博士研究生,研究方向为高光谱遥感图像波段选择技术。E-mail:zl_zhaoliang_zl@163.com
通信作者简介: 王立国,1974年生,男,教授,研究方向为高光谱遥感图像处理技术。E-mail:wangliguo@hrbeu.edu.cn
|
摘要
为降低高光谱遥感数据光谱空间的冗余度,提出一种快速的波段选择方法。该方法在波段子空间下进行,依次选择各子空间中方差最大的波段作为初始波段,设定目标函数,然后逐子空间替换波段使得目标性能更加优化,直至没有替换可以使得目标更优为止。在两个公开高光谱影像数据集上对比3种常用波段选择方法(ABC、AP、ABS)来验证提出方法的有效性,实验结果表明:(1)在印第安纳数据上,本文方法与ABC、AP、ABS所选波段子集相比平均相关性分别降低22.04%、52.61%、55.71%,最佳指数分别提高0.58%、51.73%、0.95%,总体分类精度分别提高0.16%、1.39%、23.07%,在搜索效率上与同类型的ABC方法相比提高6.61%—69.02%;(2)在帕维亚大学数据上,本文方法与ABC、AP、ABS所选波段子集相比平均相关性分别降低2.38%、0.51%、32.83%,最佳指数分别提高1.34%、17.97%、12.92%,总体分类精度分别提高0.31%、0.69%、8.53%,在搜索效率上与同类型的ABC方法相比提高19.13%—86.34%。本文提出的波段选择方法能够选择合适的波段子集满足不同的应用需要,是一种有效的波段选择方法。
关键词
遥感, 高光谱, 波段选择, 子空间划分, 准则函数, 分类,搜索策略
Abstract
Hyperspectral remote sensing data have a wealth of spectral information that can describe objects in detail. However, redundancy occurs due to the high correlation of adjacent bands in the narrow-band continuous spectrum space. This redundancy leads to high computational complexity and dimension disaster in data analysis. As an important means of dimension reduction, band selection can reduce these negative effects. The goal of band selection is to retain the relevant information needed in practical applications with as few bands as possible. Therefore, two aspects of discussion are involved: selection criteria and selection methods (search methods). A new band search method based on band subspace is proposed to improve band searching efficiency. This method needs to input the required number of bands without any other parameter settings. First, the spectral space of hyperspectral data is partitioned according to the block characteristics of band correlation coefficient matrix image and the adjacent transitive correlation, which is partitioned as a first subspace. Then, on the basis of the actual demand band number, the first subspace is divided secondary according to the proportion of the subspace size, and the final band subspace is obtained. Second, a band is selected according to certain rules (e.g., the maximum standard deviation) in each final band subspace to form an initial band subset. Lastly, after the objective function (e.g., the average correlation of the band subsets, the best index, the overall classification accuracy) is set, bands are replaced by each subspace to increase (or decrease) the value of objective function until no replacement can improve the goal further, which is the final band subset we pursued. The other three band selection methods are compared with our method on two opened hyperspectral data to verify the validity of the proposed method. Experimental results show that as a fast search strategy, the computational time of the proposed method is much less than the exhaustive band combination. The proposed method has faster search efficiency and convergence than the artificial bee colony algorithm for all kinds of objective functions. Moreover, compared with band selection method based on spectral clustering and adaptive band selection, this method can flexibly transform the target function for specific applications and obtain more suitable band subsets for different requirements. The correlation of spectral space of hyperspectral data is flexibly used in this study. It substantially reduces the computational complexity of the search algorithm in the band selection that combined the subspace partition with band search. Moreover, few parameters are used to simplify the complexity of the model and reduce the time spent in parameter tuning. For different application requirements, the proposed method flexibly transforms the objective function so that the searched bands’ combination becomes suitable for these requirements.
Key words
remote sensing, hyperspectral images, band selection, subspace partition, criterion function, classification, search strategy
1 引 言
与传统的遥感数据相比,高光谱遥感数据具有近乎连续的光谱特征和纳米级的光谱分辨率。光谱分辨率的提高一方面可以增强地物分辨能力,另一方面也带来了数据冗余,导致数据分析时产生较高的计算复杂度以及维数灾难现象(Pal和Foody,2010)。因而高光谱遥感数据分析前,降维预处理常常是十分必要的。
降维方法一般可分为两类:特征提取和波段选择。特征提取是用映射的方法将原始数据变换为较少的新特征,包括主成分分析PCA(Principal Component Analysis)(Agarwal 等,2007)、独立成分分析ICA(Independent Component Analysis)(Wang和Chang,2006)、局部线性嵌入LLE(Locally Linear Embedding)(Li 等,2012)等方法。与特征提取不同,波段选择可以在保留原始数据的物理意义及光谱特性的同时降低数据维度,因而被广泛应用。其中,依目的波段搜索方法相较其他无监督的依单波段指标排序(Chang和Wang,2006)、波段聚类(Sun 等,2015)等方法,前者在有、无监督情况下均适用,因此本文主要研究此类方法。
现有的波段搜索方法分为最优搜索算法与次优搜索算法。最优搜索算法是利用穷举法在光谱空间中遍历所有波段组合,虽然可以找到最优解,但实施困难。因而实际应用中,一般使用次优搜索算法(Pudil 等,1994)。次优搜索算法以准则函数为评价依据,通过特定的方法从原始特征集中选择一组性能较好,但不一定是最好的特征组合。已有的次优搜索算法包括顺序前向选择法、顺序后向选择法、顺序前向浮动选择法和顺序后向浮动选择法(Serpico和Bruzzone,2001)、最速上升法、遗传算法(赵冬和赵光恒,2009)、拟态物理学算法(王立国和魏芳洁,2013)、人工蜂群算法ABC(Artificial Bee Colony algorithm)(王立国 等,2015)等。顺序前向选择法和顺序后向选择法的运算速度较快,但这两种方法所选波段组合冗余较多,性能较差,并且一旦某一波段被选(或剔除),就无法更改。顺序前向浮动选择法和顺序后向浮动选择法是对顺序前向选择法和顺序后向选择法的改进,能够动态地改变选入或者剔除的波段数,但计算复杂。最速上升法较顺序前向浮动选择法可获得性能更好的波段组合,但计算复杂度提高,并且结果对初始值敏感,随着维度的增加其性能会呈现下降趋势,鲁棒性较差。遗传算法、拟态物理学算法、人工蜂群算法均属于智能优化方法,这类方法虽可以针对目标函数获得具有倾向性的波段组合,但一般要设置较多参数,导致模型复杂性提高。
鉴于以上方法的优势与不足,本文提出一种只需输入待选波段子集大小,而无需设置其他参数的波段搜索策略,同时为进一步降低算法的计算复杂度,将子空间划分引入该方法中,通过逐子空间搜索替换的方式获取波段子集来满足监督与无监督两种情况下的降维需求。
2 算法描述
本文方法预先对波段子空间进行划分,得到相关性较弱的几个波段子空间,而后利用提出的搜索方法根据相应搜索准则在各波段子空间内搜索波段子集。
2.1 子空间划分
2.1.1 划分依据
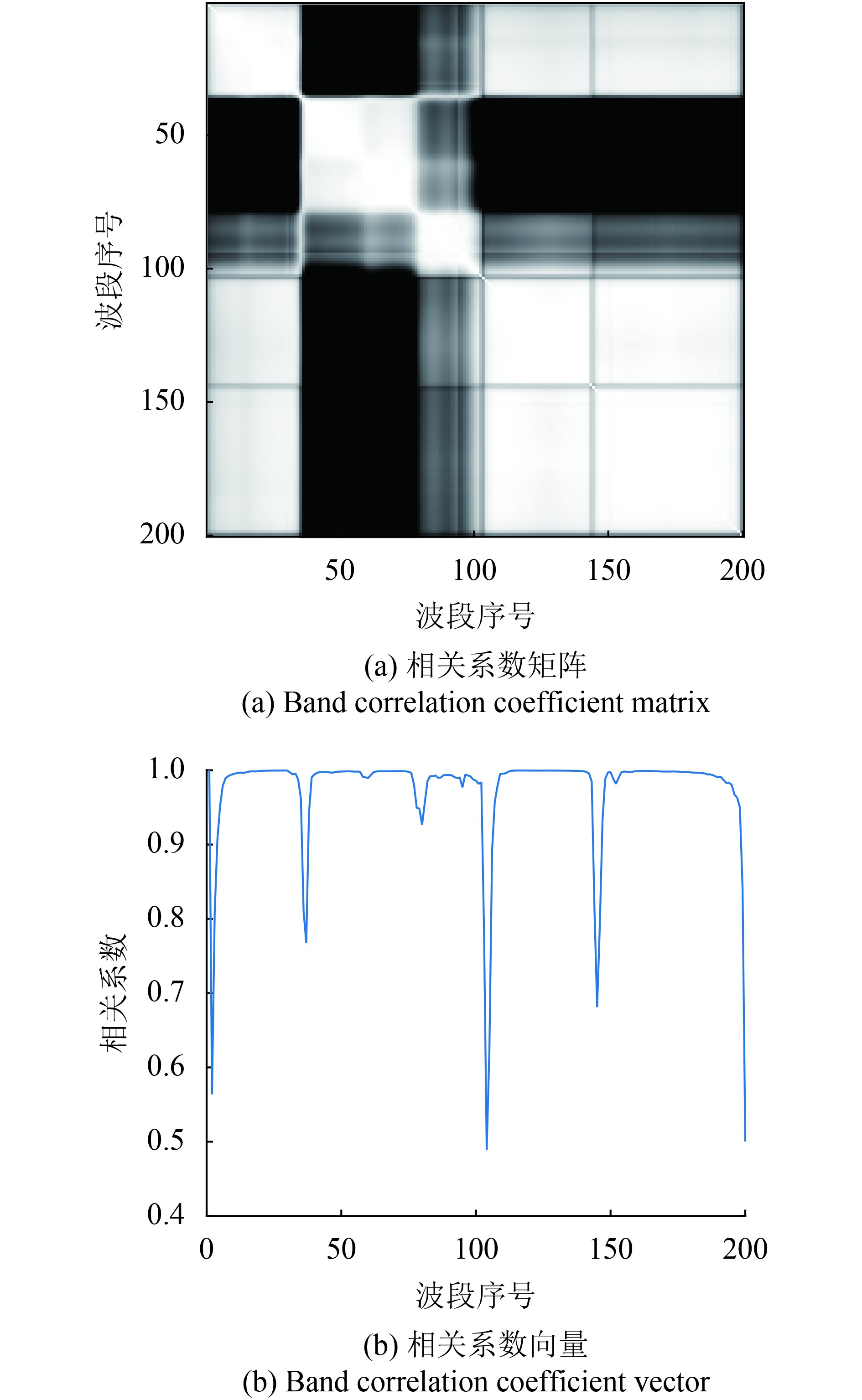
更加精细的光谱划分是高光谱数据的特点,这使得数据在光谱域具有较强相关性,这里的谱间相关性是指:空间上同一位置的地物,相邻波段的波段图像具有相似性。产生谱间相似的原因主要为:同一地物在相邻波段的光反射率是非常相近的,因此产生了一定的相关性。这种相关性可以用相关系数矩阵来描述(谷延锋和张晔,2003),以AVIRIS采集的印第安纳农林数据为例,计算其相关系数矩阵和相关系数向量,并将得到的矩阵和向量进行可视化(图1):
图1(a)是以灰度图像的形式呈现,由灰度图像的取值特点可知,越明亮的区域相关系数越大,而明亮区域主要集中于主对角线,因此可以说明相邻波段间的相关性更强,而从图1(b)可以直观看到相关性较强的各个波段范围。依据高光谱数据的这种波段聚集特性,可以将这些具有较大相关性的波段进行划分,以便加速后续处理。
2.1.2 自动子空间划分方法
自动子空间划分的方法主要是根据波段相关系数矩阵图像分块特性及近邻可传递相关性来进行高光谱数据空间划分,具体步骤如下:
步骤1 将二维波段图像转换为一维的波段向量;
步骤2 计算所有波段的相关系数得到高光谱数据的相关系数矩阵R,其定义为R=[r1,1,r1,2,…,r1, j;r2,1,r2,2,…,r2, j;…;r j,1,r j,2,…,r j,j];
步骤3 从相关矩阵中提取出近邻可传递相关矢量rNTR,其定义为rNTR=[r1,2,r2,3,…r i,i+1,…r j−2,j−1,r j−1,1]T,对近邻可传递相关矢量进行处理得到c−1个局部相关的极小值;
步骤4 根据得到的c−1个极小值将高光谱数据空间划分c个适合的数据子空间。
经过划分后可以得到不同维度的子空间,每个子空间内的波段数据具有相近的光谱特性。
2.2 搜索准则
波段搜索准则与波段的评价手段相关,针对不同的评价方式可以选择不同的搜索准则或目标函数,对于高光谱遥感数据,波段子集的评价主要包括信息量、各波段间相关性以及类别可分性。其中以最佳指数、波段子集平均相关性和整体分类精度为目前常用评价指标,也可根据实际应用进行调整。
为验证搜索算法的有效性,将以上述各评价指标分别作为目标搜索准则,下面介绍各准则的计算方法。
(1)平均相关性。波段子集平均相关性的计算方式如式(1)(王立国和魏芳洁,2013)所示。
| $\bar R = \frac{1}{{{M^2}}}\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {{R_{ij}}} } $ | (1) |
式中,N为波段总数,M为样本总数,Rij为波段i和波段j的相关系数,其计算方式如式(2)(谷延锋和张晔,2003)所示。
| ${R_{ij}} = \frac{{\sum\limits_{k = 1}^M {\left({{x_{ik}} - {{\bar x}_i}} \right)} \left({{x_{jk}} - {{\bar x}_j}} \right)}}{{\sqrt {\sum\limits_{k = 1}^M {{{\left({{x_{ik}} - {{\bar x}_i}} \right)}^2}\sum\limits_{k = 1}^M {{{\left({{x_{jk}} - {{\bar x}_j}} \right)}^2}} } } }}$ | (2) |
式中,
(2)最佳指数。最佳指数(Chavez 等,1982)采用了波段的标准差与波段间相关性的比值进行计算,其计算方式如式(3)所示。
| ${O_{{\rm{OIF}}}} = \frac{{\sum\limits_{i = 1}^N {{S_i}} }}{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left| {{R_{ij}}} \right|} } }}$ | (3) |
式中,Si是第i波段的标准差,Rij同上。波段的标准差是衡量波段信息量的一种手段,标准差越大则信息量越大。另如上文所述,波段间相关性越小冗余越小,综合这两个值来看,波段子集的最佳指数越大越好。
(3)总体分类精度。高光谱数据的总体分类精度计算方式如式(4)(童庆禧 等,2006)所示。
| ${O_{{\rm{OA}}}} = \frac{{\sum\limits_{i = 1}^C {{m_{ii}}} }}{M}$ | (4) |
式中,mii为
2.3 搜索方法
2.2节中介绍了波段选择所追求的几种目标,波段搜索最终就是实现在所选波段子集下某目标函数值的最大或者最小化。为此,算法首先在各波段子空间提取一个波段(本文选择每个子空间中方差最大的波段),构成大小为K的波段子集,并相应地计算由该初始子集下的目标函数值。然后,固定K−1个波段子空间,只变化余下的一个子空间中的波段,用该子空间中的波段依次替换当前选择的波段,如果某个替换能够得到更大(或更小)的目标函数值,那么该次替换就作为有效替换得以保留,否则作为无效替换而被淘汰。当得到有效替换后,跳出该子空间,进入下一子空间重复这样的择优替换过程,直到没有任何替换能够使得目标函数值增加(或减小)为止。此时,所选择的波段组合则为最终输出的波段子集。
值得注意的是,当所需波段数目大于根据2.1节中计算得到的子空间个数时,需要对子空间进行二次划分。这里,将2.1节介绍的划分称为一级划分,一级划分得到的子空间称为一级子空间;对一级子空间进行再划分的过程称为二级划分,得到的各子空间称为二级子空间。二级划分方法分为两步:首先,按照各一级子空间大小的比例分配每个一级子空间所需选择的波段数目;然后,对每个一级子空间按待选波段数目进行均分,得到二级子空间。
2.4 算法总体流程
现将2.1—2.3节所介绍内容总结为下面的步骤:
步骤1 根据所需的波段数目K对数据在光谱空间进行波段子空间划分;
步骤2 在各子空间内各选取一个方差最大的波段进行波段子集初始化;
步骤3 计算初始波段子集下的目标函数值G;
步骤4 固定K−1个子空间的已选波段,在剩余的一个子空间中按顺序对波段子集进行更新,计算新的波段子集下目标函数值Gg;
步骤5 比较G与Gg的大小,若G<Gg则返回步骤4,若G>Gg则保留该次替换,同时按标号顺序更换进行迭代替换的波段子空间;
步骤6 重复步骤5,直至没有任何一次替换使得目标函数改变,输出最终的波段子集,算法结束。
3 实验与分析
为验证本文方法的可行性与有效性,进行了以下实验:与基于ABC算法的波段选择方法进行有监督与无监督两种情况下的对比;与基于反向传播AP(Affinity Propagation)算法的波段选择,自适应波段选择ABS(Adaptive Band Selection)算法进行无监督情况对比。基于AP算法的波段选择是基于聚类方法的波段选择,而ABS算法则是同时考量了信息量与相关性的波段选择方法。
实验环境为AMD双核处理器,主频2.47 Hz,有效内存8 GB,开发环境为Matlab R2008a。实验数据为去除噪声波段的200波段的AVIRIS印第安纳农林数据和103波段的ROSIS帕维亚大学数据:
(1)印第安纳农林数据。该数据的波长范围为0.4—2.5 µm,空间分辨率为17 m,共有144×144个像素点。数据中剔除背景共包含16类地物,主要农作物是生长期的玉米和大豆,结合地面实际测量数据,其中7种地物样本量过少,对于该数据不具有代表性,因此选取另9种样本数目较多的代表性地物作为实验用地物。
(2)帕维亚大学数据。该数据的波长范围为0.43—0.86 µm,空间分辨率为1.3 m,共有610×340个像素点,共包含9类地物,实验中9种地物均作为实验用地物。
两组数据所对应的假彩色图像与真值数据如图2、图3所示,9种地物类型及数目如表1所示。
表 1 地物类别及数目表
Table 1 Land-covers for Indian Pines and University of Pavia
| 印第安纳农林数据
地物类别(数目) |
帕维亚大学数据
地物类别(数目) |
| Corn-notill(1434) | Asphalt(6641) |
| Corn-min(834) | Meadows(18649) |
| Grass/Pasture(497) | Gravel(2099) |
| Soybeans-notill(968) | Trees(3064) |
| Soybeans-clean(614) | Metal Sheets(1345) |
| Grass/Trees(747) | Soil(5029) |
| Hay-windrowed(489) | Bitumen(1330) |
| Soybeans-min(2468) | Bricks(3682) |
| Woods(1294) | Shadows(947) |
3.1 印第安纳农林数据实验
印第安纳农林数据按照2.1节进行子空间划分后得到5个子空间,分别为:(1—36)、(37—79)、(80—103)、(104—144)、(145—200),于每个子空间内各选择一个波段,获得相关性较低的5波段组合。
对于多光谱数据通过穷举法可以获取最优波段子集,但对于高光谱数据,这是一个惊人的计算过程。以印第安纳农林数据为例,5个子空间的大小分别为:36、43、24、41、56,若遍历所有的组合方式,则要进行85300922次运算,这在实际应用中很难实现。而本文方法对目标函数进行搜索时可通过少量计算得到较优的波段子集,下面进行具体的实验分析。
(1)搜索次数比较。从本文方法搜索3种目标函数时所计算的组合次数中数据可以看出(表2),本文方法通过计算远少于穷举组合的次数的波段组合方式即可以收敛到一个较优的波段组合。
表 2 搜索次数比较
Table 2 Comparison of searching times
| 目标函数 | 计算次数 |
| 平均相关性 | 3789 |
| 最佳指数 | 2121 |
| 总体分类精度 | 742 |
(2)指标评价比较。将本文方法与ABC算法,AP算法与ABS算法所得波段子集的各目标函数值与计算时间列于表3、表4中(表中数据均是进行20次实验的统计平均结果)。表中“总体分类精度(目标函数)”一项为本文方法与ABC算法在有监督情况下将分类精度作为目标函数进行波段选择时的总体分类精度。将总体分类精度作为目标函数时,监督数据的选择方式为各地物均匀抽取200个像素点,再将200个像素点均分为2份,每份100个像素分别作为此过程的训练与测试数据。AP算法与ABS算法为无监督波段选择方法,因此在这一项不做比较。表中“总体分类精度(最终评价)”一项为各方法所获取的波段子集在整个数据集上进行地物分类的结果,这里训练样本同样均匀抽取200像素点,剩余像素点为测试数据。而表4中只对本文方法与ABC方法针对不同目标函数进行搜索时间的对比,而不对只根据单一准则进行搜索的ABS算法与AP算法进行比较。
表 3 各方法的指标评价
Table 3 Indexes evaluation of different method
| 目标函数 | 本文方法 | ABC | AP | ABS |
| 平均相关性 | 0.2600 | 0.3335 | 0.5486 | 0.5871 |
| 最佳指数 | 4.3455+E5 | 4.3203+E5 | 2.8573+E5 | 4.3043+E5 |
| 总体分类精度
(目标函数) |
0.8078 | 0.8065 | 无 | 无 |
| 总体分类精度
(最终评价) |
0.7111 | 0.7099 | 0.7013 | 0.5778 |
表 4 波段搜索时间对比
Table 4 Comparison of computational time for searching band
| 目标函数 | 本文方法/s | ABC/s |
| 平均相关性 | 11.92 | 19.98 |
| 最佳指数 | 25.63 | 27.46 |
| 总体分类精度(目标函数) | 160.08 | 516.78 |
从表3中可以看出针对不同需求进行搜索的本文方法与ABC算法相较AP算法与ABS算法可以得到更适应需求的波段组合。这是因为AP算法与ABS算法均是按照单一的准则进行子集选取的,在面向不同的需求时,无法灵活应对。
通过表4进一步分析本文方法与ABC算法的搜索效率可以看出本文方法在搜索时间上的花费更少,效率更高。并且本文方法所搜索得到的波段组合具有唯一解,而基于ABC算法所得到的波段组合则具有随机性,这是由ABC算法的随机初始化特性所决定的。
3.2 帕维亚大学数据实验
帕维亚大学数据经过子空间划分得到3个子空间,分别为:(1—73)、(74—84)、(85—103),于每个子空间内各选择一个波段,获得相关性较低的3波段组合。这3个子空间的大小分别为:73、11、19,若穷举所有波段组合方式,则有15257种组合。
采用同样的对比实验进行本文方法有效性的验证,将实验结果分别列于表5、表6、表7中。
表 5 搜索次数比较
Table 5 Comparison of searching times
| 目标函数 | 计算次数 |
| 平均相关性 | 114 |
| 最佳指数 | 660 |
| 总体分类精度 | 508 |
表 6 各方法的指标评价
Table 6 Indexes evaluation of different method
| 目标函数 | 本文方法 | ABC | AP | ABS |
| 平均相关性 | 0.3322 | 0.3403 | 0.3339 | 0.4946 |
| 最佳指数 | 1.9669+E6 | 1.9408+E6 | 1.6672+E6 | 1.7417+E6 |
| 总体分类精度
(目标函数) |
0.7778 | 0.7767 | 无 | 无 |
| 总体分类精度
(最终评价) |
0.7431 | 0.7408 | 0.7380 | 0.6847 |
表 7 波段搜索时间对比
Table 7 Comparison of computational time for searching band
| 目标函数 | 本文方法/s | ABC/s |
| 平均相关性 | 7.65 | 56.01 |
| 最佳指数 | 62.05 | 76.73 |
| 总体分类精度(目标函数) | 161.27 | 223.35 |
(1)搜索次数比较。将本文方法搜索4种目标函数时所计算的组合次数列于表5中,从表中数据可以看出,本文方法通过计算远少于穷举组合的次数的波段组合方式即可以收敛到一个较优的波段组合。
(2)指标评价比较。与印第安纳农林数据实验的方式相同,将本文方法与ABC算法,AP算法与ABS算法进行比较分析,每种方法各进行20次实验,将统计平均的结果列于表5、表6中。从表中可以看出本文方法与ABC算法在有针对性的应用时相较另外两种方法能获得性能更优的波段子集。同时,在搜索效率上本文方法与ABC算法相比更高。
通过对两个实际高光谱数据集的实验结果可以看出,本文方法在两组数据上可以得到一致的性能评价,证明了本文方法的有效性。
4 结 论
本文针对高光谱数据光谱空间特征冗余问题,提出了一种子空间下的波段选择方法,该方法可以按照实际需要快速地选择出一个性能优良的波段子集,算法设置参数极少,并且通过子空间划分既可以降低波段组合的冗余度,同时又能加速搜索过程。针对两种实际高光谱数据集进行实验,结果证明了该方法的可行性与有效性。
未来的研究工作可以从以下两个方向进行展开:(1)本文在所需波段数目较多时,采用的是按比例对一级子空间进行平均再分的方式,这种方式简单易行,但是没有进一步挖掘一级子空间的光谱特性来进行二次划分,因此对初步子空间划分后的各波段区间进行再分析是一个重要的研究方向;(2)文中各子空间中波段替换方式是按顺序进行的,然而面对不同应用时波段子集的初始化应采用不同的方法以加速收敛,因此寻求更灵活的替换机制同样是一个待研究的问题。
志 谢 此实验的数据为普度大学与帕维亚大学所提供的公开数据集,在此衷心地表达感谢。
参考文献(References)
-
Agarwal A, El-Ghazawi T, El-Askary H and Le-Moigne J. 2007. Efficient hierarchical-PCA dimension reduction for hyperspectral image//Proceedings of 2007 IEEE International Symposium on Signal Processing and Information Technology. Giza, Egypt: IEEE: 353-356
-
Chang C I and Wang S. 2006. Constrained band selection for hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 44 (6): 1575–1585. [DOI: 10.1109/TGRS.2006.864389]
-
Chavez P S, Berlin G L and Sowers L B. 1982. Statistical method for selecting Landsat MSS ratios. Journal of Applied Photographic Engineering, 8 (1): 23–30.
-
Gu Y F and Zhang Y. 2003. Feature extraction based on automatic subspace partition for hyperspectral images. Remote Sensing Technology and Application, 18 (6): 384–387. [DOI: 10.11873/j.issn.1004-0323.2003.6.384] ( 谷延锋, 张晔. 2003. 基于自动子空间划分的高光谱数据特征提取. 遥感技术与应用, 18 (6): 384–387. [DOI: 10.11873/j.issn.1004-0323.2003.6.384] )
-
Li W, Prasad S, Fowler J E and Bruce L M. 2012. Locality-preserving dimensionality reduction and classification for hyperspectral image analysis. IEEE Transactions on Geoscience and Remote Sensing, 50 (4): 1185–1198. [DOI: 10.1109/TGRS.2011.2165957]
-
Pal M and Foody G M. 2010. Feature selection for classification of hyperspectral data by SVM. IEEE Transactions on Geoscience and Remote Sensing, 48 (5): 2297–2307. [DOI: 10.1109/TGRS.2009.2039484]
-
Pudil P, Novovičová J and Kittler J. 1994. Floating search methods in feature selection. Pattern Recognition Letters, 15 (11): 1119–1125. [DOI: 10.1016/0167-8655(94)90127-9]
-
Serpico S B and Bruzzone L. 2001. A new search algorithm for feature selection in hyperspectral remote sensing image. IEEE Transactions on Geoscience and Remote Sensing, 39 (7): 1360–1367. [DOI: 10.1109/36.934069]
-
Sun K, Geng X R and Ji L Y. 2015. Exemplar component analysis: a fast band selection method for hyperspectral imagery. IEEE Geoscience and Remote Sensing Letters, 12 (5): 998–1002. [DOI: 10.1109/LGRS.2014.2372071]
-
Tong Q X, Zhang B and Zheng L F. 2006. Hyperspectral Remote Sensing. Beijing: Higher Education Press (童庆禧, 张兵, 郑兰芬. 2006. 高光谱遥感——原理、技术与应用. 北京: 高等教育出版社)
-
Wang J and Chang C I. 2006. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Transactions on Geoscience and Remote Sensing, 44 (6): 1586–1600. [DOI: 10.1109/TGRS.2005.863297]
-
Wang L G and Wei F J. 2013. Artificial physics optimization algorithm combined band selection for hyperspectral imagery. Journal of Harbin Institute of Technology, 45 (9): 100–106. [DOI: 10.11918/j.issn.0367-6234.2013.09.018] ( 王立国, 魏芳洁. 2013. 结合APO算法的高光谱图像波段选择. 哈尔滨工业大学学报, 45 (9): 100–106. [DOI: 10.11918/j.issn.0367-6234.2013.09.018] )
-
Wang L G, Zhao L and Liu D F. 2015. Artificial bee colony algorithm-based band selection for hyperspectral imagery. Journal of Harbin Institute of Technology, 47 (11): 82–88. [DOI: 10.11918/j.issn.0367-6234.2015.11.014] ( 王立国, 赵亮, 刘丹凤. 2015. 基于人工蜂群算法高光谱图像波段选择. 哈尔滨工业大学学报, 47 (11): 82–88. [DOI: 10.11918/j.issn.0367-6234.2015.11.014] )
-
Zhao D and Zhao G H. 2009. Band selection of hyperspectral image based on improved genetic algorithm. Journal of the Graduate School of the Chinese Academy of Sciences, 26 (6): 795–802. ( 赵冬, 赵光恒. 2009. 基于改进遗传算法的高光谱图像波段选择. 中国科学院研究生院学报, 26 (6): 795–802. )