出版日期: 2019-09-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20198391
2019 | Volumn23 | Number 5
上一篇 | 下一篇

遥感应用

全球海洋次表层温度异常遥感反演的季节时空变化特征

杨欣¹ , 苏华¹ , 黎文娥¹ , 黄琳瑾¹ , 汪小钦¹ , 严晓海²

1. 福州大学卫星空间信息技术综合应用国家地方联合工程研究中心空间数据挖掘与信息共享教育部重点实验室，福州 350116

2. 厦门大学—美国特拉华大学近海海洋研究与管理联合研究所，厦门 361005

收稿日期: 2018-10-09; 预印本: 2018-12-13

基金项目: 国家自然科学基金(编号：41971384，41601444，41630963)；福建省高校杰出青年科研人才培育计划(编号：KJ2017-17)；福建省自然科学基金(编号：2017J01657)；海西政务大数据应用协同创新中心资助(编号：2015750401)；中央引导地方科技发展专项(编号：2017L3012)

第一作者简介: 杨欣，1994年生，女，硕士研究生，研究方向为海洋环境遥感。E-mail：1792502127@qq.com

通信作者简介: 苏华，1985年生，男，副研究员，研究方向为海洋环境遥感。E-mail：suhua@fzu.edu.cn

摘要

卫星遥感反演海洋内部多时相、大尺度热力结构信息对于了解海洋内部复杂、多维的动力过程有重要意义。本文采用随机森林回归模型，利用卫星遥感观测的海表参量(海表高度异常(SSHA)、海表温度异常(SSTA)、海表盐度异常(SSSA)和海表风场异常(SSWA))，反演不同季节、不同深度层位(1000 m深度以上)的海洋次表层温度异常(STA)，并用Argo实测数据作精度验证，采用均方根误差(RMSE)、归一化均方根误差(NRMSE)以及决定系数(R²)评价模型在全球及洋盆尺度上的反演精度。结果显示，全球海洋16个深度层位的平均R²在春、夏、秋、冬四季分别为0.53、0.60、0.54、0.66，NRMSE分别为0.051、0.031、0.043、0.044。随着季节的变化，模型反演性能有所波动。模型在印度洋的反演效果最佳，不同季节、不同深度层位上的平均R²和RMSE分别为0.71和0.18 ℃，而大西洋的反演精度最低，平均R²和RMSE分别为0.46和0.25 ℃。研究表明随机森林模型适用于全球不同季节的STA遥感反演，且在不同洋盆上均有较好的反演效果；不同季节上，上层STA有明显变化信号，空间异质性显著，但300 m以深，STA信号较弱且基本不随季节变化。本研究可为长时序、大尺度海洋内部参量信息遥感反演与重建提供依据，有助于进一步发展深海遥感方法。

关键词

遥感, 全球海洋次表层, 温度异常, 随机森林, 遥感反演, 季节时空变化

Seasonal-spatial variations in satellite-derived global subsurface temperature anomalies

YANG Xin¹ , SU Hua¹ , LI Wen’e¹ , HUANG Linjin¹ , WANG Xiaoqin¹ , YAN Xiaohai²

1.Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education, National & Local Joint Engineering Research Center of Satellite Geospatial Information Technology, Fuzhou University, Fuzhou 350116, China

2.Xiamen University/University of Delaware Joint Institute for Coastal Research and Management (Joint-CRM), Xiamen University, Xiamen 361005, China

Abstract

Improving ocean interior observation resolution via satellite remote sensing is essential because of the limitation and sparsity of ocean interior observation. Retrieving the multi-temporal and large-scale thermal structure information of the subsurface ocean on the basis of satellite remote sensing is of great importance in understanding the complex and multi-dimensional dynamic processes within the ocean. This task requires a robust model with strong spatiotemporal applicability to provide technical support based on satellite observations. This study adopts a random forest regression model, namely, an advanced machine learning algorithm, to predict global Subsurface Temperature Anomaly (STA) at different depth levels (upper 1,000 m) in different seasons in 2010 from multisource sea surface parameters (sea surface height anomaly, SSHA; sea surface temperature anomaly, SSTA; sea surface salinity anomaly, SSSA; sea surface wind anomaly, SSWA) based on satellite observations. We use the in-situ Argo data for performance measurement and accuracy validation by combined use of the root mean square error (RMSE), normalized root-mean-square error (NRMSE) and coefficient of determination (R²) at global and ocean basin scales. For model accuracy, the results show that the average R² and NRMSE of 16 depth levels are 0.53/0.60/0.54/0.66 and 0.051/0.031/0.043/0.044 for global ocean in spring/summer/autumn/winter. With the evolution of seasons, the model performance promotes first, declines, and then promotes, a trend that may be caused by the El Niño and La Niña phenomena and the transformation between them. The best performance of the model occurs in the Indian Ocean with the average R² and RMSE of 0.71 and 0.18 °C, respectively, whereas accuracy in the Atlantic is the lowest, with average R² and RMSE of 0.46 and 0.25 °C at different depth levels in different seasons. This study suggests that the random forest model is suitable for retrieving ocean subsurface temperature anomalies in different seasons and can achieve good performance in different ocean basins. STA has distinctive variation signal in the upper ocean (above 300 m) and spatial heterogeneity is considerable in different seasons. However, in the subsurface and deeper layers (below 300 m), STA variation signal is weak over different seasons. This study can provide a basis for remote sensing estimation of STA and further promote the reconstruction of long-term and large-scale ocean internal parameter information (such as thermohaline structure). It can also help develop the subsurface and deeper ocean remote sensing technique.

Key words

remote sensing, global ocean, subsurface temperature anomaly, Random Forest, remote sensing inversion, seasonal-spatial variation

1 引　言

自20世纪70年代以来，卫星传感器提供了大量高空间、高时间分辨率的、长时间序列上大范围观测的遥感数据。虽然遥感技术在海洋领域应用成效显著，但遥感观测仅限于海洋表面，无法直接探测海洋内部信息。例如，热红外传感器探测海表温度，微波辐射计测量海表盐度，雷达高度计测量海表高度，雷达散射计测量海表风场等。海洋内部动力过程复杂，具有多维多尺度动态特征，了解其变化过程和机制亟需多时空尺度海洋内部观测数据支持。此外，大量研究表明，全球中深层海洋(300—2000 m)的热量变化及其再分配过程在全球变化过程中起重要作用(Balmaseda 等，2013；Chen和Tung，2014；Drijfhout 等，2014)。海洋内部观测对了解整个海洋系统的动力过程和机制至关重要(Meehl 等，2011)。然而，现有的海洋内部浮标观测资料虽然准确性较高，但是稀疏有限、时空分辨率较低(刘磊，2016)，远远满足不了多尺度海洋过程的观测要求，阻碍了我们对海洋内部真实动力过程的了解。如何有效结合表层卫星遥感观测和有限的浮标实测数据间接地推演海洋次表层关键动力信息对于了解海洋内部动态过程至关重要。

现阶段，随着海洋表层多源遥感观测和Argo实测数据集的不断丰富和进展，越来越多的研究人员通过建立动力模型、经验统计模型或者通过数据同化和模拟方法(Akbari 等，2017)，建立海表观测信息与海洋内部实测数据之间的关系，从而提取了海洋内部热盐结构等重要环境信息。Oke等(2005)运用BRAN模型将卫星测高数据、海表温度和现场观测数据进行同化，对澳大利亚地区海洋涡流进行反演，效果较好。Wang等(2013)提出了“内部+表面准地转方程”(isQG)动力学方法，Liu等(2017)运用此方法对墨西哥湾的一子区域进行研究，提取次表层密度和流场异常信息。但是，由于海洋动力模型框架的不完备，动力模型往往只能运用在小范围区域，而且动力模型不具备变量间的相互协调的反馈机制，导致其结果过于依赖输入参量。数值模拟结合现场观测数据同样较难提供大空间尺度的准实时海洋次表层环境信息(Fiedler，1988)。Takano等(2009)基于一个两层模型的假设利用准实时的卫星高度计资料开发出一种估算海洋中尺度三维温度结构的经验方法。但是这种统计关系过于简单和依赖于海表高度数据，输入模型参量较为单一，不能充分利用现有的丰富的海表遥感数据。Chapman和Charantonis(2017)运用迭代自组织神经网络(ISOM)结合卫星所提供的海表参量对南大洋1000 m深度的流场进行反演，并在建模过程中考虑了地理位置信息。Su等(2015)、Su等(2018b)利用高级机器学习方法，基于多源海表卫星观测数据(SSH, SST, SSS, SSW)准确地反演了海洋次表层温度异常，且发现在全球尺度上随机森林模型估算精度优于支持向量回归模型，构建了适合大尺度的海洋内部热力结构遥感反演模型。Wu等(2012)应用自组织神经网络模型(SOM)，结合海表温度异常(SSTA)和海表高度异常(SSHA)反演了北大西洋时序海洋内部温度结构。Su等(2018a)考虑海洋表层与次表层参量的空间非平稳性，基于局部差异化建模思想，引入了地理加权回归模型(GWR)反演了不同季节的印度洋次表层温度异常，反演精度相比全局普通线性回归模型(OLS)得到了较大提高。但是，过往研究缺乏对模型的区域反演精度的评价，模型的区域适用性有待进一步验证。同时，模型也欠缺在不同季节上的应用，对区域和季节变化的敏感性有待深入考量。

本研究基于海表多源卫星观测数据，运用随机森林回归模型，反演了全球海洋不同季节的次表层温度异常(STA)，并使用Argo实测数据评价模型反演精度。此外，本文分析了模型在不同季节、不同洋盆上的反演精度，评价模型在不同季节、不同区域受不同气候环境影响下的可靠性和稳定性，同时分析了模型反演误差的空间分布特征。

2 研究区及数据

2.1 研究区概况

海洋作为全球气候变化的敏感区，对气候变化既有响应又有调节。此外，全球海洋的热容量很大，具有储热、缓冲的功能，地球系统获得的大多数热量都被储存于海洋之中。本文的研究区域包括印度洋、太平洋和大西洋(180°W—180°E，78.375°S—77.625°N)。

2.2 海表遥感观测与Argo实测数据

使用的海表遥感观测及Argo实测数据如下：(1)海表高度数据(SSH)，由AVISO卫星高度计观测而得，空间分辨率为0.25°×0.25°(https://www.aviso.altimetry.fr [2018-06-14])；(2)海表温度数据(SST)，使用AQUA卫星的AMSR-E传感器获取的海表温度数据产品SST，空间分辨率为0.25°×0.25°(http://www.remss.com/measurements/sea-surface-temperature/ [2018-06-14])；(3)海表盐度数据(SSS)，选取欧空局(ESA)的SMOS(自2009年起)海表盐度产品，空间分辨率为1°×1°(https://earth.esa.int/web/guest/pi-community[2018-06-14])；(4)海表风场数据(SSW)，采用美国国家大气研究中心(NCAR’s RDA)发布的多卫星融合资料CCMP海表风场数据集(融合了QuikSCAT、ADEOS-Ⅱ、AMSR-E、TRMM TMI和SSM/I等多种卫星探测海表风产品)(Atlas 等，2011；詹思玙等，2017)，空间分辨率为0.25°×0.25°(https://rda.ucar.edu/datasets [2018-06-16])；(5)格网化Argo分层实测数据，时间跨度为2005年1月至2015年12月，分辨率为1°×1°，从海表0— 2000 m深度共有27个标准层位，各层位均包括了绝对动力高度、温度和盐度等观测信息(http://apdrc.soest.hawaii.edu/projects/Argo/data/gridded/On_standard_levels [2018-06-16])。各海表遥感参量的气候态数据来自Argo空间格网化数据集产品。

2.3 数据预处理

为了便于模型计算，需进行数据预处理，确保数据的时空一致性。首先将所有数据时间、空间分辨率分别统一为每月、1°×1°，然后将所有表层遥感参量(包括SSH、SST、SSS与SSW)与Argo实测温度(ST)均减去各自气候平均态后得到各参量异常值(Anomaly)(SSHA、SSTA、SSSA、SSWA与STA)，避免混入气候态季节变动信号对机器学习建模产生干扰(黎文娥等，2017)。此外，由于不同海表参量的度量单位以及取值范围不一致，故将模型输入参量进行归一化处理，使其绝对值变成相对值，这样可有效地提高模型反演结果的可靠性。

图1展示了2010年7月经预处理的海表遥感数据以及Argo实测的表层STA数据，其中SSHA(变动范围为−0.2—0.3 m)，SSTA(变动范围为−4—3 ℃)，SSSA(变动范围为−1.5—1 psu)，SSWA(变动范围为−7—7 m/s)，STA(变动范围为−3—2 ℃)。这些参量都表现出显著的空间异质性，如海表高度在太平洋赤道中东部呈现异常低值，在印度洋南部则呈现异常高值(图1(a))；海表温度在太平洋赤道中东部呈现异常低温，西部异常高温(图1(b))，这是因为拉尼娜(La Nina)现象所引起的(Nino3.4指数为−1.0 ℃)(National Climate Center，2010)。热带印度洋西部温度低于热带印度洋东部，这是因为印度洋偶极子(IOD)处为负相位(李崇银和穆明权，2001)(图1(b))；海表盐度(图1(c))呈现较均匀纬向带状分布；海表风场也呈纬向带状分布，并且在北大西洋和北太平洋呈现异常低值,而在北印度洋却呈现异常高值(图1(d))。

图 1 卫星遥感观测的多源海表参量，空间分辨率统一到1°×1°，时间均为2010年7月

Fig. 1 The monthly SSHA, SSTA, SSSA, SSWA (the sea surface parameters) and Argo STA for the global ocean from satellite remote sensing observations with the unified 1°×1° spatial resolution on July 2010

3 方　法

随机森林(RF)是由Breiman(2001)年提出的一种集成学习算法，其基本思想是以决策树构建Bagging(一种自助采样数据集来训练分类器的技术)进行集成，进一步在决策树基础上引入了随机属性(周志华，2016)。RF模型训练速度快，实现简单，性能良好，且能有效地抵抗过拟合现象，在遥感信息提取与应用研究中备受青睐，得到很好地应用(Feng 等，2015；Belgiu和Drăguţ，2016；Wang 等，2016；沈润平等，2017；齐雁冰等，2017)。

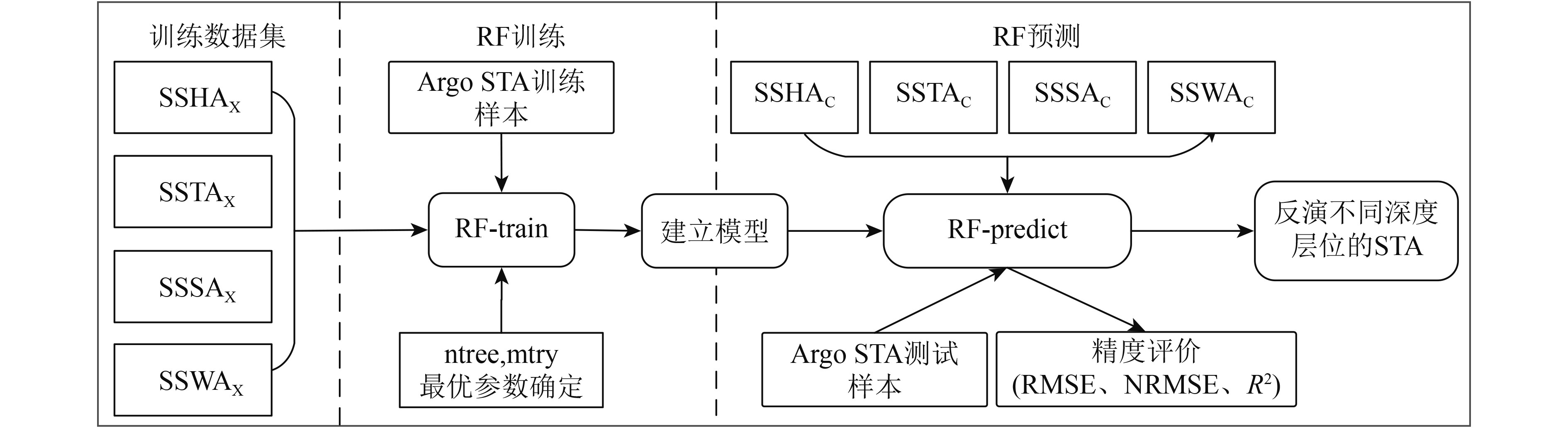
本文使用MATLAB软件中的Random Forest开发包实现RF的回归建模。图2展示了基于RF模型反演全球海洋次表层温度异常的技术流程图。

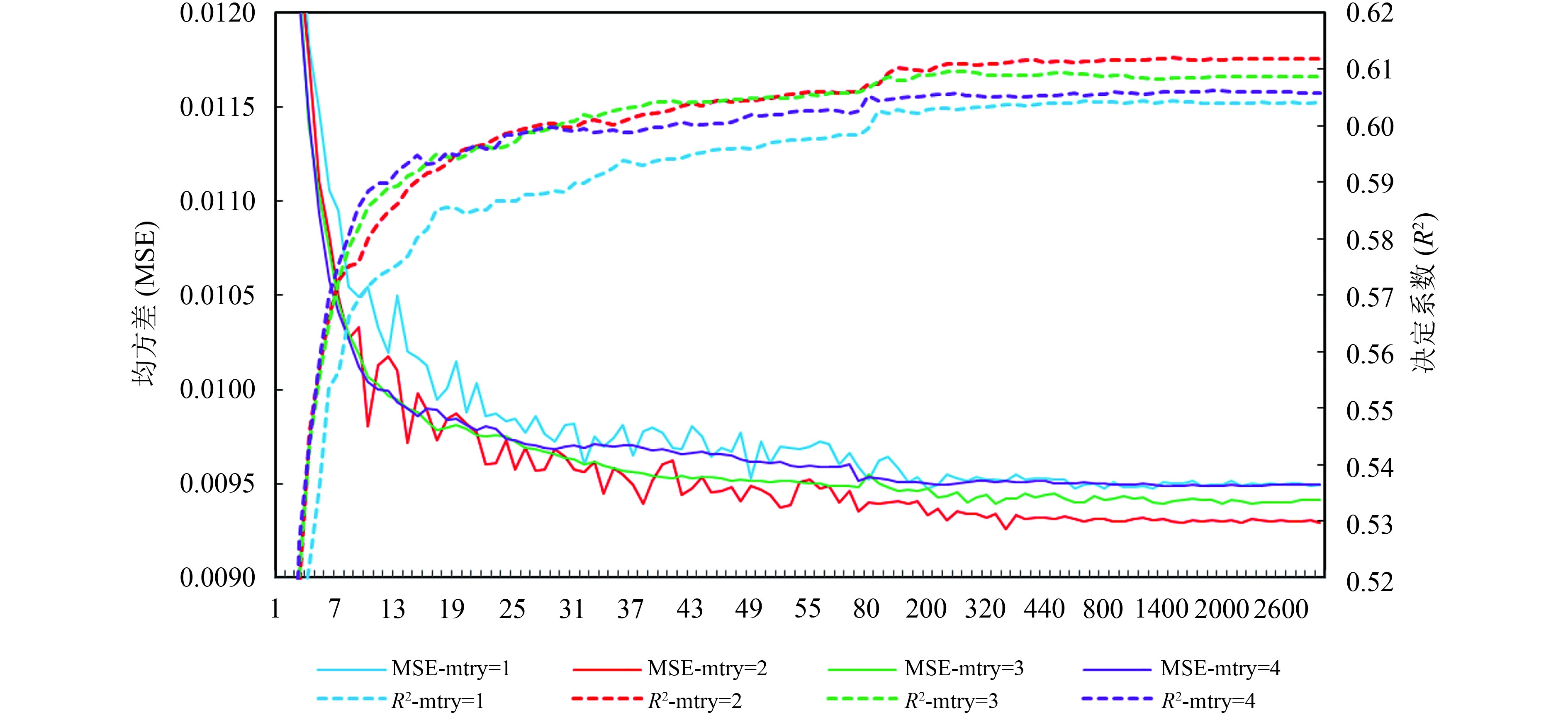
图 2 运用RF模型反演全球海洋次表层不同层位温度异常(STA)技术路线图

Fig. 2 Flowchart for STA (at different levels) inversion in the Global Ocean using a Random Forest (RF) regression approach

构建RF回归模型包含3个步骤：训练数据集的构建；RF回归模型的训练；RF模型的预测及验证。其中，训练数据集和验证数据集完全相互独立，按照6∶4的比例进行随机划分。RF建模过程中涉及到两个重要的参数：mtry和ntree，其中mtry即随机选取的特征数，ntree即生成的决策树数量，也就是自助采样的次数。为了确定模型的最优参数从而构建适用于不同季节的反演模型，采用格网搜索方法，利用Argo实测数据验证，得到模型反演精度与模型参数之间的敏感关系(图3)，可分析模型精度随参数变化及收敛情况，并最终确定最优参数组合。

图 3 RF模型最优参数(mtry、ntree)确定依据

Fig. 3 Determination basis for optimal parameters (mtry, ntree) in RF model

由图3可知，当mtry与ntree的取值分别为2与500时，模型性能达到相对较好的预测效果(最低的MSE和最高的R²)；同时随着ntree的增大，模型都收敛且趋于稳定；当ntree小于200，且mtry较小时(mtry=1, mtry=2)，均方差(MSE)变动较大，这可能是因为RF在构建决策树时从m个变量数中随机选取的变量较少，变量组合可能性就变多，同时决策树数量有限，导致模型不够稳定，精度波动误差偏大。当ntree大于200，且mtry较大时(mtry=3, mtry=4)，MSE波动减小，模型逐渐收敛并趋于稳定。本研究以SSHA、SSTA、SSSA和SSWA为输入变量，选取ntree=500，mtry=2来构建最优的、具有较强时空适用性的RF遥感反演模型。

4 结果与分析

本研究采用随机森林回归方法构建模型，反演全球海洋4个不同季节(1月(冬季)、4月(春季)、7月(夏季)、10月(秋季))分层位(30 m、50 m、75 m、100 m、125 m、200 m、250 m、300 m、400 m、500 m、600 m、700 m、800 m、900 m、1000 m)STA，然后对比分析不同洋盆反演精度。

4.1 不同季节的反演结果分析

4.1.1 定性分析

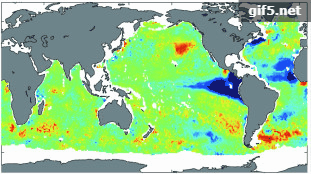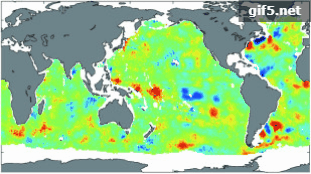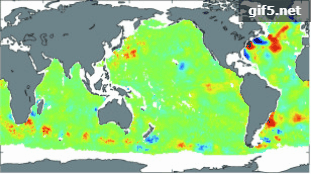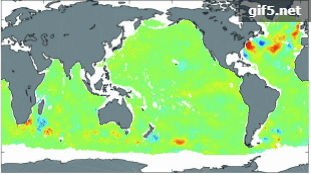
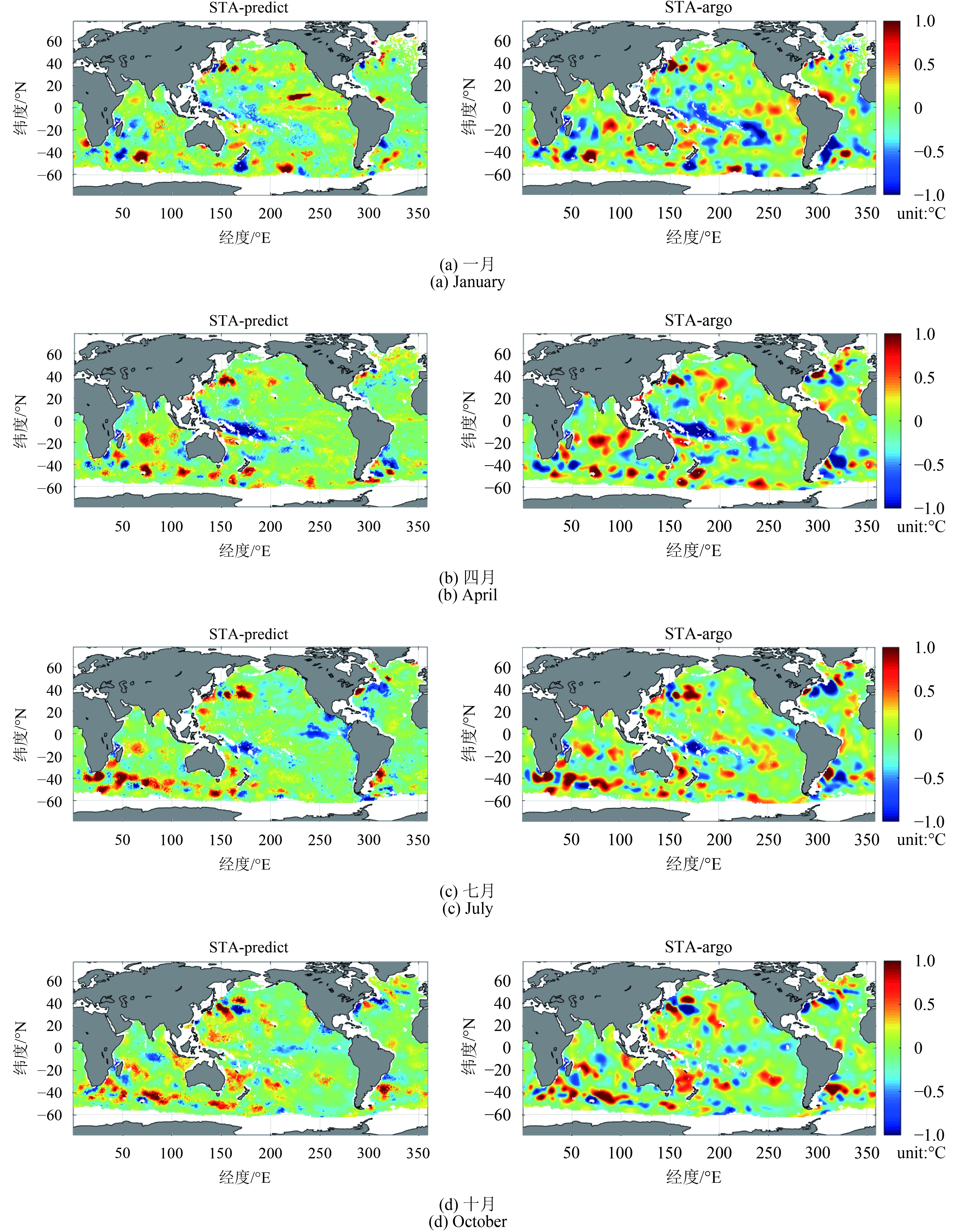
图4展示了部分深度层位(100 m(a)、300 m(b)、700 m(c)、1000 m(d))4个季节基于RF反演全球海洋内部的温度异常值的空间分布图。可直观看出，在同一深度层位，基于RF方法反演的全球海洋次表层温度异常能够较好地与实测Argo数据的STA相吻合。除了100 m深度层，其他深度层(300 m以深)上，4个不同季节的STA空间分布均无较大变动，这是因为随着深度的增加，中深层海洋内部热力环境逐渐趋于稳定，几乎不受季节变化的影响。其次，不同深度层上，4个季节均呈现100 m深度层(上层)比其他深度层(300—1000 m，中深层)的STA空间分布差异大，且STA变动范围随着深度增加逐渐减小，空间分布差异越来越不明显，这与海洋表层及内部的动力差异、层化状态有关。

图 4 2010年不同季节在100 m深度层位的RF反演的STA与Argo实测的STA空间分布图

Fig. 4 Spatial distribution of RF-retrieved STA and Argo STA at 100 m in different seasons of 2010

图4展示了100 m深度层上4个季节的STA空间分布，不同季节的空间分布差异很大。1月(冬季)印度洋南部出现异常高温值，赤道太平洋中东部出现异常高温值，异常值高达2 ℃，这是因为2010年1月出现厄尔尼诺现象，Nino3.4指数为1.5 ℃(http://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/[2018-10-09])。4月(春季)印度洋南部和太平洋的异常高温现象明显减弱，直至7月(夏季)赤道太平洋中东部出现与1月相反的现象，10月(秋季)这一现象得以加剧，此时赤道太平洋中东部出现拉尼娜现象，Nino3.4指数为−1.7 ℃。但同时赤道印度洋东部以及赤道太平洋西部温度出现异常高值，且印度洋海温异常呈东正西负的分布状态，这是由于印度洋偶极子正处于负相位时期。

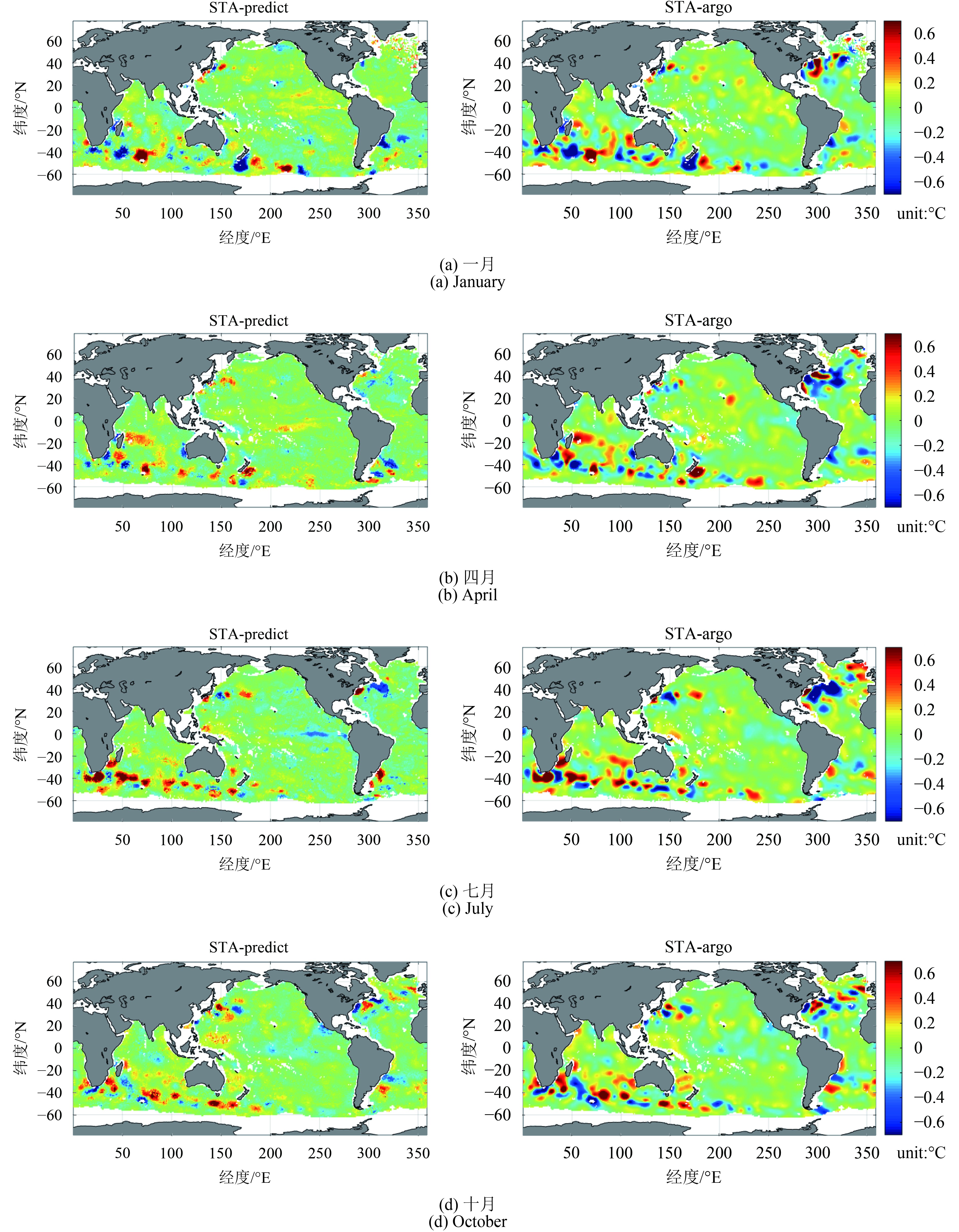
在300 m深度，1月(冬季)与10月(秋季)赤道中东太平洋仍分别存在厄尔尼诺与拉尼娜信号，但是与100 m深度相比，信号强度弱得多(图5)，这是因为海洋次表层(300 m)相对于表层，其热力结构更趋稳定；而当深度达700 m及1000 m时，海表ENSO信号几乎毫无表征。此外，受边界流的影响，300 m以深，相对于洋盆中心，洋盆边界附近的温度异常信号更加显著，且受季节影响较小。700 m以深，STA呈纬向带状分布，在南大洋南极绕极流区域和北大西洋墨西哥湾流区域信号最为显著(图6，图7)，这是由于这两个区域存在强烈的动力过程(南极绕极流和墨西哥湾流，并伴随着丰富的中尺度涡)，且受季节的影响不显著。

图 5 2010年不同季节在300 m深度层位的RF反演的STA与Argo实测的STA空间分布图

Fig. 5 Spatial distribution of RF-retrieved STA and Argo STA at 300 m in different seasons of 2010

图 6 2010年不同季节在700 m深度层位的RF反演的STA与Argo实测的STA空间分布图

Fig. 6 Spatial distribution of RF-retrieved STA and Argo STA at 700 m in different seasons of 2010

图 7 2010年不同季节在1000 m深度层位的RF反演的STA与Argo实测的STA空间分布图

Fig. 7 Spatial distribution of RF-retrieved STA and Argo STA at 1000 m in different seasons of 2010

总体上，300 m以浅，STA空间分布受季节影响较大；300 m以深，随着深度的增加，海洋内部热力结构受季节的影响越来越不显著。上层海洋的STA主要是受印太暖池和厄尔尼诺/拉尼娜现象影响，分布在热带海洋；对于中深层海洋，STA显著的地方主要发生在南大洋(南极绕极流)，北大西洋(墨西哥湾流)以及西北太平洋(黑潮暖流)等区域，这些区域都具有强烈的洋流运动和中尺度过程(如中尺度涡)(图4—图7)。

4.1.2 定量评价

定量上，我们采用均方根误差(RMSE)、归一化均方根误差(NRMSE)与决定系数(R²)评价模型反演精度(表1，图8)。其中RMSE可反映每个深度层位的STA反演的真实误差大小。由于不同深度层位的STA值的变动范围(甚至量级)不同，模型反演真实误差RMSE范围亦因深度层位变化而不同。为了提升模型精度在不同深度层位上的可比性，将真实误差值(RMSE)进行了归一化，这样在各个深度层位上都得到一个对应的相对误差即归一化均方根误差(NRMSE，为当前深度层位的RMSE除以当前深度层位的Argo实测STA的范围)(Kim 等，2018)来描述模型反演精度随深度的变化，从而更加直观地比较和分析不同深度层位上的反演精度。

表 1 不同深度层位、不同季节下RF反演的STA所对应的均方根误差(RMSE)和决定系数(R²)
Table 1 Root mean square error (RMSE) and coefficient of determination (R²) of STAs estimated by RF in different depth levels and different seasons

下载CSV

不同深度层位	RMSE/℃				R²
不同深度层位	冬季	春季	夏季	秋季	冬季	春季	夏季	秋季
30 m	0.38	0.31	0.31	0.35	0.84	0.61	0.57	0.66
50 m	0.40	0.35	0.29	0.46	0.79	0.56	0.63	0.56
75 m	0.46	0.39	0.36	0.45	0.71	0.56	0.61	0.63
100 m	0.46	0.39	0.38	0.51	0.66	0.62	0.61	0.60
125 m	0.49	0.41	0.34	0.46	0.69	0.57	0.66	0.63
150 m	0.50	0.42	0.37	0.40	0.71	0.58	0.63	0.61
200 m	0.37	0.45	0.34	0.31	0.68	0.60	0.61	0.53
250 m	0.26	0.34	0.28	0.27	0.69	0.64	0.64	0.52
300 m	0.23	0.28	0.24	0.25	0.66	0.63	0.66	0.53
400 m	0.20	0.23	0.21	0.23	0.65	0.56	0.65	0.54
500 m	0.18	0.21	0.20	0.19	0.63	0.48	0.59	0.55
600 m	0.17	0.19	0.18	0.16	0.60	0.43	0.56	0.53
700 m	0.16	0.17	0.17	0.14	0.59	0.43	0.54	0.49
800 m	0.16	0.15	0.15	0.12	0.58	0.44	0.54	0.46
900 m	0.13	0.13	0.13	0.11	0.57	0.40	0.56	0.42
1000 m	0.11	0.11	0.10	0.09	0.54	0.37	0.54	0.37
平均值	0.29	0.28	0.25	0.28	0.66	0.53	0.60	0.54

图 8 基于RF模型的全球海洋16个不同深度层位、不同季节的STA反演结果的精度评价，折线图(R²)、柱状图(NRMSE)

Fig. 8 Accuracy evaluation of STA retrieving results of 16 different depths and different seasons of global ocean based on RF model, line (R²), histogram (NRMSE)

表1直观地展示了4个季节在不同深度层位上STA的真实反演误差值的大小以及对应R²的大小。

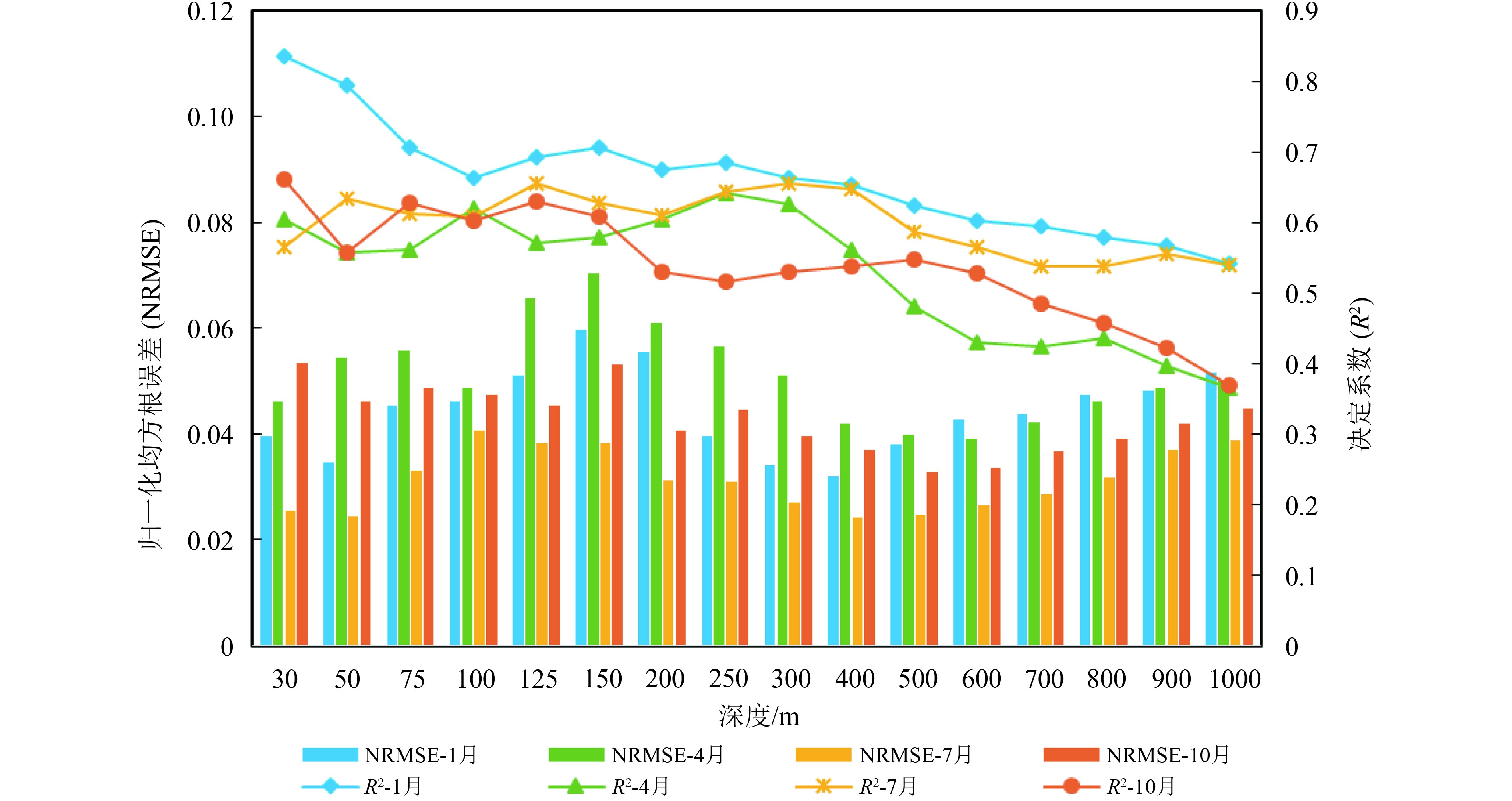
图8展示了模型在4个季节反演精度随深度的变化。整体上，不同季节的NRMSE总体均呈现先增后减再增趋势，R²则先波动，后随着深度的增加而降低，说明随着深度的增加，RF的预测能力下降，这可能与混合层与温跃层的扰动等海洋内部复杂的动力过程密切相关。1月(冬季)模型反演的精度最高，平均R²为0.66，平均NRMSE为0.044，其次是7月(夏季)，平均R²为0.60，平均NRMSE为0.031，接着是10月(秋季)，平均R²为0.54，平均NRMSE为0.043，精度最低的是4月(春季)，平均R²为0.53，平均NRMSE为0.051。模型在不同季节上总体反演精度均较高，因此RF方法适用于构建全球海洋不同季节的STA反演模型。

1月(冬季)，在不同层位反演的R²均高于其他季节，且R²随深度变化趋势较为稳定。其中，在30 m深度，R²达到最大(R²=0.84)。在150 m以浅，R²波动变化较大，可能是因为1月太平洋正处于强厄尔尼诺状态，上层海洋动力环境不稳定。150 m以深，R²呈缓慢下降趋势，可能由于冬季温度较低，海洋内部过程较为缓和，且层化趋于稳固。整体上，1月(冬季)R²呈现平缓下降趋势(图8)。4月(春季)，模型反演精度最低，可能是由于4月太平洋正处于厄尔尼诺现象减弱而拉尼娜现象开始增强的交替阶段，其海洋内部过程较复杂且异常信号较不稳定，造成模型的预测性能下降，但仍能较好地提取全球海洋STA信息(图8)，R²在250 m深度处达到最高(R²=0.64)。

7月(夏季)，由于表层与浅层海洋温度较高，上层海洋运动较为剧烈，因此，无论是NRMSE还是R²在300 m以浅的混合层中波动都较大，但总体精度较高。在300 m以深的中深层，海水层化明显，状态较为稳定，精度波动较小，但总体精度逐层下降。10月(秋季)，随着深度的增加，R²和NRMSE先出现波动，而后在500 m以深，呈现R²减小而NRMSE增大的趋势，即模型反演能力在500 m以深逐渐下降，这是由于中深层海水层化明显且异常信号较难在海表体现。

4.2 不同洋盆的模型反演精度比较

RF方法可以较好地反演全球海洋不同深度层、不同季节上的次表层温度异常，但这只针对模型全局(全球)的反演精度进行评估，缺乏对模型区域(洋盆)预测效果的评价。这里我们结合不同洋盆的区域特征，分析RF方法在不同洋盆(印度洋、大西洋和太平洋)的STA反演精度，从而更加全面地评估RF方法的区域反演效果。

从图4—图7可直观地看到印度洋的局部反演结果与Argo实测的STA之间的吻合程度相对于其他两大洋更高，这可能是由于其几乎全部位处于南半球，气候特征相比其他大洋更加单一，动力环境更加稳定，物理机制更容易学习所致；随着深度的增加，三大洋盆的预测效果均逐渐下降，这是海洋表层及内部的动力差异所致。

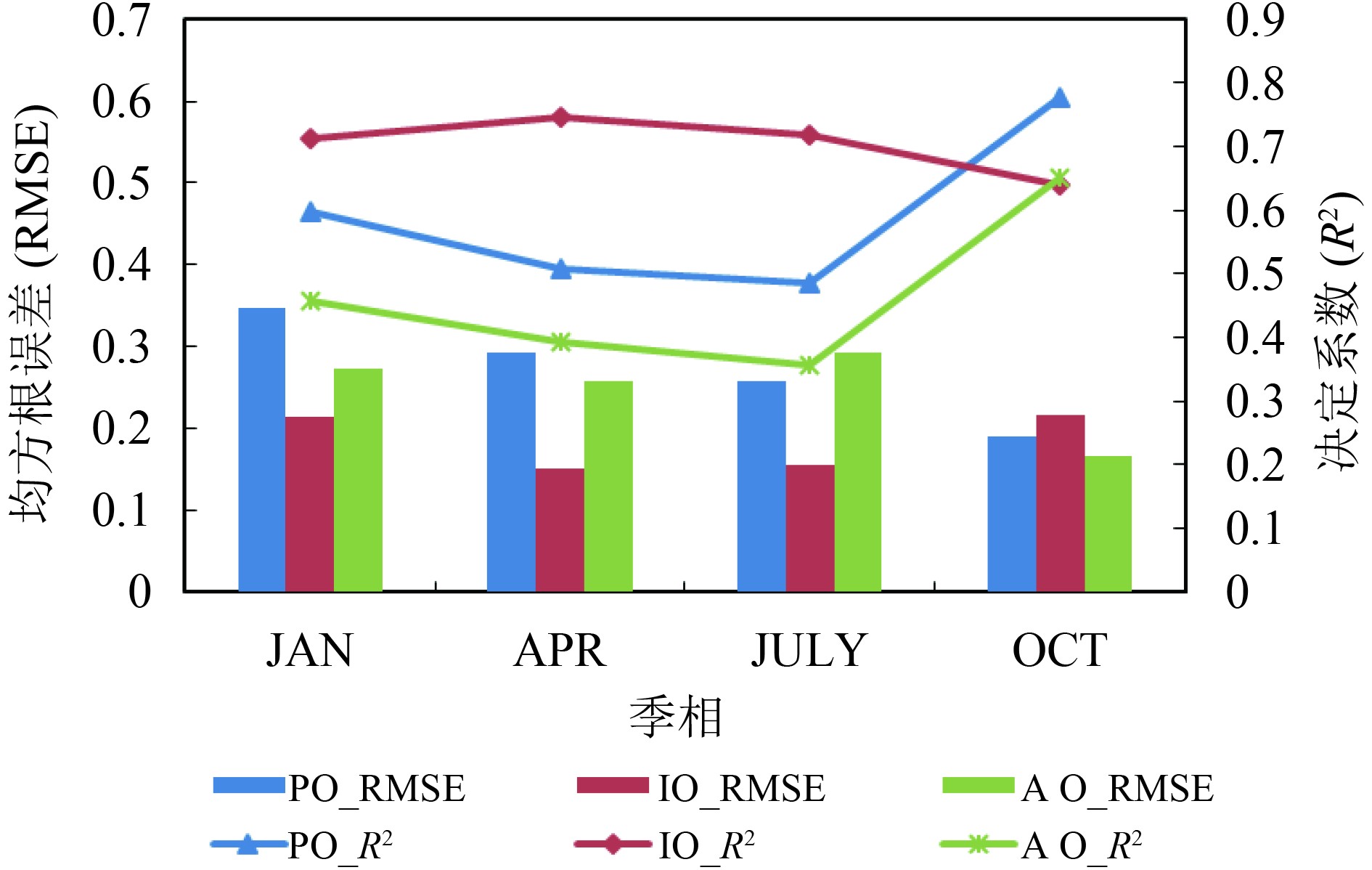
图9为在不同洋盆上RF模型反演的STA不同季节、不同深度层的平均R²和RMSE，由图可直观地得出：在1月(冬季)、4月(春季)和7月(夏季)，印度洋不同深度层的平均R²均高于其他洋盆，此时平均RMSE也都低于其他洋盆，这与印度洋相对简单的气候特征和动力环境相关。大西洋和太平洋横跨南北半球，具有多种气候特征和复杂动力过程，故其变化规律相对印度洋，模型较难学习。而在10月(秋季)，印度洋的反演精度相比其他月份并无绝对优势，平均R²下降较为剧烈，平均RMSE则相应地上升，此时太平洋精度最高，平均R²为0.77，这可能是由印度洋气—陆—海相互作用所引发偶极子现象(2010年10月印度洋偶极子处于负相位)引起的。

图 9 基于RF模型的全球海洋不同洋盆在不同季节的STA反演结果的精度评价(蓝色(太平洋)、红色(印度洋)、绿色(大西洋)，折线图(R²)、柱状图(RMSE))

Fig. 9 Accuracy evaluation of STA retrieving results of different oceanic basins in different seasons based on RF model (blue (Pacific Ocean), red (Indian Ocean), green (Atlantic Ocean), line (R²), histogram (RMSE))

4.3 反演误差的空间分布分析

结合4.1的内容可得，4月(春季)RF反演的STA精度最低，因此这里主要分析4月(春季)RF反演的STA误差空间分布特征。用RF反演的STA值减去Argo实测的STA值即为反演误差，见图10。

图 10 不同深度RF方法反演的STA误差空间分布

Fig. 10 Spatial distribution of errors of STA retrieved by RF methods in different depths

图10分别展示了30 m、250 m、600 m和1000 m深度的RF方法反演的STA误差空间分布。整体上，不同深度层的误差空间分布图大面积均呈现绿色，即模型预测值均接近实际参考值，这再一次验证了基于RF方法能较好地反演STA信息。在海洋上层(30 m深度)赤道东太平洋ENSO异常信号出现低估，ENSO信号转换(厄尔尼诺转拉尼娜)导致模型预测精度有所降低。此外，STA反演误差还较明显发生在各个大洋盆边界，如北大西洋(强墨西哥湾暖流影响)，南大洋(南极绕极流影响)；随着深度的增加(250 m深度)，赤道太平洋低估现象减弱，这是因为随着深度的增加，海表ENSO信号随之减弱，但此时大西洋仍存在较为明显的STA高估和低估交替现象；在600 m和1000 m的中深层，太平洋无明显反演误差，主要误差较均匀地分布在北大西洋和南大洋，这是由于在这两个区域的中深层存在着较显著的STA信号，模型反演过程中出现了高估和低估经向交替。因此，从海洋上层到中深层，大西洋在不同层位的平均估算误差相对太平洋更高，反演精度更低(图9)。但是，总体上，误差变动范围不大，在600 m和1000 m层位的误差变动范围分别为−1—1 ℃和−0.8—0.8 ℃。

5 结　论

本文利用海表卫星观测数据(SSH、SST、SSS及SSW)，运用随机森林(RF)的机器学习方法，反演全球海洋次表层(1000 m深度以浅)温度异常信息。本研究以Argo实测的海洋内部各深度层的STA数据做验证，使用均方根误差(RMSE)和决定系数(R²)进行精度评价，比较分析了4个季节(1月(冬季)、4月(春季)、7月(夏季)及10月(秋季))、3个洋盆(印度洋、太平洋及大西洋)在不同深度层的RF方法反演结果。

结果显示：(1)RF方法能够较好地反演全球次表层温度异常，不同季节不同深度上的R²值均达0.5以上，平均RMSE均小于等于0.29 ℃，Su等(2018)反演了2010年10月(秋季)的全球海洋STA，其结果与此结果相似；(2)不同季节下，浅层海洋内部温度异常空间异质性较大，但到300 m以深，海洋内部温度异常信息基本不随季节变化，因为海洋中深层热力结构相对于浅表层更加稳定；(3)每个洋盆反演精度与全球海洋反演结果一致，其中印度洋反演精度最高，平均R²可达0.78，平均RMSE为0.20 ℃，这是因为印度洋具有独特的地理位置和气候特征；(4)该方法低估了在海洋上层赤道东太平洋ENSO异常信号，这是因为ENSO信号转换(厄尔尼诺转拉尼娜)导致模型预测精度有所降低。

综上，随机森林(RF)适用于全球尺度不同季节的海洋内部热力结构信息反演。此外，本文分析了反演精度随季节与洋盆的时空变化，更细致地探讨了模型在季节尺度上的时空适用性。本研究有助于构建长时序的海洋内部动力参量遥感反演模型，可为中深海遥感研究提供有力的技术支持，有利于更全面地认识海洋内部动力环境信息及其演变过程，优化当前全球变化过程中的海洋内部时空变异(如暖化)分析。

志谢此次研究所用的海表高度数据由AVISO提供，AMSR-E海表温度数据由遥感系统(RSS)提供，海表盐度数据由欧空局(ESA)提供，CCMP海表风场数据由美国国家大气研究中心(NCAR’s RDA)提供，Argo格网数据是由国际太平洋研究中心(IPRC)提供，在此表示衷心的感谢！

参考文献(References)

Akbari E, Alavipanah S K, Jeihouni M, Hajeb M, Haase D and Alavipanah S. 2017. A review of ocean/sea subsurface water temperature studies from remote sensing and non-remote sensing methods. Water, 9 (12): 936 [DOI: 10.3390/w9120936]

Atlas R, Hoffman R N, Ardizzone J, Leidner S M, Jusem J C, Smith D K and Gombos D. 2011. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bulletin of the American Meteorological Society, 92 (2): 157–174. [DOI: 10.1175/2010BAMS2946.1]

Balmaseda M A, Trenberth K E and Källén E. 2013. Distinctive climate signals in reanalysis of global ocean heat content. Geophysical Research Letters, 40 (9): 1754–1759. [DOI: 10.1002/grl.50382]

Belgiu M and Drăguţ L. 2016. Random forest in remote sensing: a review of applications and future directions. ISPRS Journal of Photogrammetry and Remote Sensing, 114 : 24–31. [DOI: 10.1016/j.isprsjprs.2016.01.011]

Breiman L. 2001. Random forests. Machine Learning, 45 (1): 5–32. [DOI: 10.1023/A:1010933404324]

Chapman C and Charantonis A A. 2017. Reconstruction of subsurface velocities from satellite observations using iterative self-organizing maps. IEEE Geoscience and Remote Sensing Letters, 14 (5): 617–620. [DOI: 10.1109/LGRS.2017.2665603]

Chen X Y and Tung K K. 2014. Varying planetary heat sink led to global-warming slowdown and acceleration. Science, 345 (6199): 897–903. [DOI: 10.1126/science.1254937]

Drijfhout S S, Blaker A T, Josey S A, Nurser A J G, Sinha B and Balmaseda M A. 2014. Surface warming hiatus caused by increased heat uptake across multiple ocean basins. Geophysical Research Letters, 41 (22): 7868–7874. [DOI: 10.1002/2014GL061456]

Feng Q L, Liu J T and Gong J H. 2015. UAV remote sensing for urban vegetation mapping using random forest and texture analysis. Remote Sensing, 7 (1): 1074–1094. [DOI: 10.3390/rs70101074]

Kim B, Kang S, Eom J and Lee S. 2018. Evaluation of respiratory-correlated 4D digital tomosynthesis imaging technique for image-guided radiation therapy. Optik, 171 : 247–252. [DOI: 10.1016/j.ijleo.2018.06.060]

Li C Y and Mu M Q. 2001. The dipole in the equatorial Indian Ocean and its impacts on climate. Chinese Journal of Atmospheric Sciences, 25 (4): 433–443. [DOI: 10.3878/j.issn.1006-9895.2001.04.01] ( 李崇银, 穆明权. 2001. 赤道印度洋海温偶极子型振荡及其气候影响. 大气科学, 25 (4): 433–443. [DOI: 10.3878/j.issn.1006-9895.2001.04.01] )

Li W E, Su H, Wang X Q and Yan X H. 2017. Estimation of global subsurface temperature anomaly based on multisource satellite observations. Journal of Remote Sensing, 21 (6): 881–891. [DOI: 10.11834/jrs.20177026] ( 黎文娥, 苏华, 汪小钦, 严晓海. 2017. 多源卫星观测的全球海洋次表层温度异常信息提取. 遥感学报, 21 (6): 881–891. [DOI: 10.11834/jrs.20177026] )

Liu L. 2016. Inversion of the Internal State of the Ocean Using Satellite Remote Sensing Sea Surface Information. Beijing: University of Chinese Academy of Sciences (刘磊. 2016. 利用卫星遥感海表信息对海洋内部状态的反演研究. 北京: 中国科学院大学)

Liu L, Peng S Q, Huang R X. 2017. Reconstruction of ocean's interior from observed sea surface information. Journal of Geophysical Research: Oceans, 122 (2): 1042–1056. [DOI: 10.1002/2016JC011927]

Meehl G A, Arblaster J M, Fasullo J T, Hu A X and Trenberth K E. 2011. Model-based evidence of deep-ocean heat uptake during surface-temperature hiatus periods. Nature Climate Change, 1 (7): 360–364. [DOI: 10.1038/nclimate1229]

National Climate Center. ENSO Report (No. 41)[EB/OL]. (2010-07-28). http://www.doc88.com/p-9117178739656.html" (中国气象局国家气候中心. ENSO监测简报(第41期)[EB/OL]. (2010-07-28). http://www.doc88.com/p-9117178739656.html")

Oke P R, Schiller A, Griffin D A and Brassington G B. 2005. Ensemble data assimilation for an eddy‐resolving ocean model of the Australian region. The Quarterly Journal of the Royal Meteorological Society, 131 (613): 3301–3311. [DOI: 10.1256/qj.05.95]

Qi Y B, Wang Y Y, Chen Y, Liu J J and Zhang L L. 2017. Soil organic matter prediction based on remote sensing data and random forest model in Shaanxi province. Journal of Natural Resources, 32 (6): 1074–1086. [DOI: 10.11849/zrzyxb.20160623] ( 齐雁冰, 王茵茵, 陈洋, 刘姣姣, 张亮亮. 2017. 基于遥感与随机森林算法的陕西省土壤有机质空间预测. 自然资源学报, 32 (6): 1074–1086. [DOI: 10.11849/zrzyxb.20160623] )

Shen R P, Guo J, Zhang J X and Li L X. 2017. Construction of a drought monitoring model using the random forest based remote sensing. Journal of Geo-Information Science, 19 (1): 125–133. [DOI: 10.3724/SP.J.1047.2017.00125] ( 沈润平, 郭佳, 张婧娴, 李洛晞. 2017. 基于随机森林的遥感干旱监测模型的构建. 地球信息科学学报, 19 (1): 125–133. [DOI: 10.3724/SP.J.1047.2017.00125] )

Su H, Wu X B, Yan X H and Kidwell A. 2015. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: a support vector machine approach. Remote Sensing of Environment, 160 : 63–71. [DOI: 10.1016/j.rse.2015.01.001]

Su H, Huang L J, Li W E, Yang X and Yan X H. 2018a. Retrieving ocean subsurface temperature using a satellite-based geographically weighted regression model. Journal of Geographical Research: Oceans, 123 (8): 5180–5193. [DOI: 10.1029/2018JC014246]

Su H, Li W E and Yan X H. 2018b. Retrieving temperature anomaly in the global subsurface and deeper ocean from satellite observations. Journal of Geophysical Research: Oceans, 123 (1): 399–410. [DOI: 10.1002/2017JC013631]

Takano A, Yamazaki H, Nagai T and Honda O. 2009. A method to estimate three-dimensional thermal structure from satellite altimetry data. Journal of Atmospheric and Oceanic Technology, 26 (12): 2655–2664. [DOI: 10.1175/2009JTECHO669.1]

Wang J B, Flierl G R, LaCasce J H, McClean J L and Mahadevan A. 2013. Reconstructing the ocean’s interior from surface data. Journal of Physical Oceanography, 43 (8): 1611–1626. [DOI: 10.1175/JPO-D-12-0204.1]

Wang L A, Zhou X D, Zhu X K, Dong Z D and Guo W S. 2016. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. The Crop Journal, 4 (3): 212–219. [DOI: 10.1016/j.cj.2016.01.008]

Wu X B, Yan X H, Jo Y H, Liu W T. 2012. Estimation of subsurface temperature anomaly in the North Atlantic using a self-organizing map neural network. Journal of Atmospheric and Oceanic Technology, 29 (11): 1675–1688. [DOI: 10.1175/JTECH-D-12-00013.1]

Zhan S Y, Qi L L and Lu W. 2017. Analysis of sea surface wind in Northwest Pacific based on CCMP satellite data. Marine Forecasts, 34 (2): 10–20. [DOI: 10.11737/j.issn.1003-0239.2017.02.002] ( 詹思玙, 齐琳琳, 卢伟. 2017. 基于CCMP资料和现场观测资料的西北太平洋海面风场特征分析. 海洋预报, 34 (2): 10–20. [DOI: 10.11737/j.issn.1003-0239.2017.02.002] )

Zhou Z H. 2016. Machine Learning. Beijing: Tsinghua University Press: 178-188 (周志华. 2016. 机器学习. 北京: 清华大学出版社: 178-188)

摘要

关键词