出版日期: 2019-07-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20197330
2019 | Volumn23 | Number 4
上一篇 | 下一篇

综述

基于FY-2F数据的中国区域地表温度日变化模型评价及特征研究

孟翔晨 , 刘昊 , 程洁

1. 北京师范大学遥感科学国家重点实验室，北京 100875

2. 北京师范大学地理科学学部遥感科学与工程研究院，北京 100875

收稿日期: 2017-08-14; 预印本: 2018-02-19

基金项目: 国家自然科学基金(编号：41771365)；遥感科学国家重点实验室自由探索项目(编号：17ZY-02)

第一作者简介: 孟翔晨，1990年生，男，博士研究生，研究方向为热红外地表温度反演的理论和应用。E-mail：xiangchenmeng@yeah.net

通信作者简介: 程洁，1981年生，男，副教授，研究方向为热红外定量遥感。E-mail：Jie_Cheng@bnu.edu.cn

摘要

地表温度日变化模型作为非常重要的输入参数在气象、水文、生态等领域研究中具有重要意义。风云二号(FY-2F)静止气象卫星的地表温度产品的时间分辨率为1小时，这为拟合精确的地表温度日变化(DSTC)模型提供了可能。本文首先利用194个气象站点对应的2014年的FY-2F地表温度产品评价了GOT01、VAN06、JNG06、INA08、GOT09和GEM_V这6种地表温度日变化模型在中国区的模拟精度，对不同时间窗口和不同地表覆盖类型拟合精度的差异进行了分析；其次，选用JNG06模型探究了中国区域地表温度随经纬度、季节和地表覆盖类型的日变化规律。研究结果表明：在不同时间窗口内，GOT09模型获得了全局最优的拟合精度，均方根误差为0.89 K；JNG06和GEM_V模型精度次之，均方根误差分别为0.92 K和0.94 K；GOT01、INA08和VAN06模型精度最差；各模型在城市和建筑区、农用地和自然植被以及常绿阔叶林这3类地表覆盖类型的拟合精度最好，其均方根误差在0.89—0.92 K，在其余地表覆盖类型的拟合精度在1.0 K以上。JNG06模型模拟的地表温度在4种典型的地表类型随纬度的变化规律较为明显，地表温度在1月份随纬度变化较为剧烈，在7月份整体波动较为平缓。综上所述，使用FY-2F地表温度产品建立的DSTC模型在中国区域具有较高的精度，模拟的地表温度随着纬度变化的规律较为明显。使用本文模型既可以纠正现有模型又可获取归一化地表温度产品，同时可以检验和标定陆面模式地表温度模拟结果。

关键词

遥感, FY-2F, MCD12C1, 地表温度, 日变化模型, 气象站点

Evaluation and characteristic research in diurnal surface temperature cycle in China using FY-2F data

MENG Xiangchen , LIU Hao , CHENG Jie

1.State Key Laboratory of Remote Sensing Science, Beijing Normal University, Beijing 100875, China

2.Institute of Remote Sensing Science and Engineering, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China

Abstract

Diurnal Surface Temperature Cycle (DSTC) model is an important input parameter in the field of meteorology, hydrology, and ecology. In the past 20 years, various DSTC models under clear-sky conditions have been developed on the basis of Spinning Enhanced Visible and Infrared Imager (SEVIRI) and Geostationary Operational Environment Satellite (GOES) satellites. However, only a few related studies have focused on China due to its complex topography, geomorphology, and climatic conditions. This situation restricts the application and development of DSTC models in the region. Although the DSTC model is mature, its evaluation is often based on the data of a certain point or day, which lacks verification at a large range of time and spatial scales. Moreover, the free variable setting of the DSTC model cannot meet the need at large time and spatial scales. Thus, the variable setting of the DSTC model must be expanded. In this study, six DSTC models were evaluated on the basis of FY-2F land surface temperature product at the monthly average and large space scales for China. In addition, JNG06 model was used to analyze the diurnal variation characteristics of Land Surface Temperature (LST) with the changes in seasonality, latitude and longitude, and land cover types. Semi-empirical model is simple and convenient and has a wide range of applications. Physical model is close to the actual physical condition of the surface. Therefore, five semi-empirical models, namely, GOT01, VAN06, JNG06, INA08, and GOT09, and the GEM-V physical model were used for DSTC simulation and analysis. On the basis of the geographical location of 194 meteorological stations, the corresponding FY-2F LST data were extracted, and the average monthly and hourly LST data after quality control were set as the model initial value. To evaluate the fitting accuracy of DSTC model in China, the model evaluation was divided into two parts: 1) the fitting of DSTC model was divided into five time periods, and the precision of DSTC model was analyzed; and 2) the fitting accuracy of each model under different land cover types was statistically explored on the basis of the land cover types of 194 stations. JNG06 model was also used to analyze the diurnal variation characteristics of LST with the changes in seasonality, latitude and longitude, and land cover types. Analysis of the average root mean square error (RMSE) of five time windows showed that GOT09 model obtained the global optimal fitting accuracy with an RMSE of 0.89 K, followed by JNG06 and GEM_V models with RMSEs of 0.92 and 0.94 K, respectively. GOT01, INA08, and VAN06 models obtained the worst accuracy. Each model had the best fitting precision in urban and built-up, cropland/natural vegetation mosaic, and evergreen broadleaf forest with an RMSE between 0.89 and 0.92 K. The fitting precision in mixed forest and cropland followed with an RMSE of around 1.0 K. Each model had the worst fitting precision in barren or sparse vegetation and savannas with an RMSE of above 1.3 K. From the results, we can conclude that the accuracies of GOT01, VAN06, and INA08 are poor in all land cover types and time windows, and the remaining models are relatively robust with close accuracy. The land surface temperature simulated by JNG06 model in four land cover types vary with the changes in latitude and longitude. The rule of LST varies with the change in latitude and but is unaffected by the change in longitude. The DSTC model can be used as the input parameter of climate and hydrological models. The model can also be used as reference for future studies on the DSTC model and its applications.

Key words

remote sensing, FY-2F, MCD12C1, LST (Land Surface Temperature), diurnal surface temperature cycle, meteorology stations

1 引　言

地表温度LST(Land Surface Temperature)决定了地表辐射能量平衡中的长波辐射，能够提供地表能量平衡状态的时空变化信息，是气候、水文、生态和生物地球化学模式以及数据同化的关键参量(Cheng 等，2010；Norman和Becker，1995；Li 等，2013；Liang 等，2016)。地表温度日变化模型DSTC(Diurnal Surface Temperature Cycle)作为非常重要的输入参数在气候学和气象学研究中有广泛应用，如用于热惯量和土壤水分的反演(Ignatov和Gutman，1999；Price，1977)。传统的地面定点测量获取的地表温度受到人员、精力、地域的限制，导致其测量的温度无法满足各种应用需求，卫星遥感能够获取大范围、空间连续的地表温度，这为地表温度日变化模型的研究提供了数据支持。同时，DSTC模型与卫星数据的结合能够有效改善现有地表温度产品存在的时空限制问题(Van Den Bergh 等，2006；Inamdar 等，2008；刘紫涵等，2017；薛兴盛和吴艳兰，2017)，为区域变化动态监测、地表过程模型、地表参数反演提供有利的数据支撑。

目前，DSTC模型根据其形式，可大致分为以下4类：第1类为纯物理模型。该类方法以由地面气象站或卫星获取的高精度地表参量和大气参量作为输入参数模拟DSTC模型(Dickinson 等，1993)。Kahle(1977)结合大气测量结果，发展了简化的地表模型，用以计算热惯量和模拟地表温度的变化。Jin和Dickinson(1999)、Jin(2000)以CCM3/BATS气候模型为基础，建立由纬度、BATS地表类型、季节和时间共同决定的查找表，然后结合实际地表温度对DSTC模型插值修正。Sun和Pinker(2005)使用GOES数据代替Jin和Dickinson(1999)的方法中CCM3 (Community Climate Model)/BATS (Biosphere-Atmosphere Transfer Scheme)模拟的地表温度建立了DSTC模型。第2类为物理模型。这类模型基于地表能量平衡方程，将地表热惯量、长波辐射、感热通量、潜热通量等地表辐射相关参数与DSTC模型结合在一起。Zhan等(2012a)通过同化空气温度以获取线性边界条件，从而改善城市环境的DSTC模型模拟。Huang等(2014)发展了基于地表能量平衡方程、通过参数化地表热通量反演地表温度的前向模型，并根据观测数灵活设置未知参数个数，拟合精度为0.33—1.71 K。陈颖等(2016)针对极轨卫星热红外数据利用热传导方程建立了3参数的地表温度日变化模型，结果表明模拟精度优于3 K。第3类是半经验模型。半经验模型采用一些与温度隐性相关的变量如日间温度变化振幅、残余温度、大气光学厚度等建立DSTC模型，直接拟合温度变化曲线的形状。Parton和Logan(1981)最先提出使用正弦函数/指数函数模拟温度在白天/夜间变化的DSTC模型。Göttsche和Olesen(2001)使用热扩散方程构建谐波方程拟合白天的温度变化曲线，选择指数函数来模拟自然地表夜晚的温度变化曲线(以下称GOT01模型)。Duan等(2012)提出了简化版的GOT01模型(以下称GOT01_0模型)，该模型和Schädlich等(2001)提出的模型有类似的表达形式，但考虑了衰减系数，模型更为简单但精度有所下降。Van Den Bergh等(2006)在GOT01模型基础上，采用两个余弦函数分别描述白天温度上升过程和温度下降过程的地表温度的变化情况(以下称VAN06模型)。Jiang等(2006)增加了GOT01模型自由变量的个数，增强了GOT01模型对拟合数据的依赖性(以下称JNG06模型)。Inamdar等(2008)使用双曲线函数代替GOT01模型中的指数函数来描述描述夜间的地表温度变化(以下称INA08模型)。Göttsche和Olesen(2009)以地表能量平衡方程取代热扩散方程，考虑了大气总光学厚度的影响，建立了改进的DSTC模型，提高了日出前后的温度估计精度和整体精度(以下称GOT09模型)。朱琳清等(2017)针对航空热红外遥感影像在GOT01模型基础上发展了一种考虑风速影响的温度日变化模型，改进后的模型精度能提高0.3—0.6 K。Duan等(2012)使用地表实测数据和MSG-SEVIRI反演地表温度检验了这6个典型DSTC模型的性能，结果显示JNG06和GOT09模型均方根误差在0.5 K，GOT01、VAN06、INA08模型均方根误差在0.8 K左右，GOT01_0模型表现最差。第4类是统计模型。统计模型是不使用地表能量平衡方程或热传导方程，通过对测量的地表温度作统计分析，或建立地表温度与地理信息的关系建立DSTC模型(Aires 等，2004)。例如：以MODIS 地表温度产品为基础，通过建立地表温度和相关参数(图像获取时间、地理位置和高程等)的回归关系，可以得到大范围的日地表温度(Coops 等，2007；Crosson 等，2012)。

近20年来，国内外基于SEVIRI (Spinning Enhanced Visible and Infrared Imager)、GOES (Geostationary Operational Environment Satellite)等卫星已发展了多种晴天条件下地表温度日变化模型，且取得了初步的应用成果(Sun和Pinker，2005；Duan 等，2014)。由于中国静止卫星发展较晚，地形地貌和气候条件比较复杂，类似的研究工作开展较少，极大地制约了地表温度日变化模型在中国区域的应用发展。尽管日变化模型算法相对成熟，但学者对日变化模型的评估往往是基于某点、某天的数据，缺乏更大范围时间尺度和空间尺度的验证；其次，地表温度日变化模型的自由变量设置不能满足更大时间尺度和空间尺度的需求，需要拓展地表温度日变化模型规律研究的变量设置。中国自主研制的风云二号(FY-2F)静止气象卫星的地表温度产品的时间分辨率为1 h，能够真实反映地表温度的时间变化情况，这为拟合精确的DSTC模型提供了可能。本研究以中国陆地区域为研究区，以FY-2F地表温度产品为数据基础，将模型评估范围拓展到月平均尺度和面尺度来评价现有几类典型DSTC模型的拟合精度，为用户在中国区域使用DSTC模型提供参考，便于用户选择合适自己的模型。在评价DSTC模型在中国区域精度的基础上，选取具有物理意义的代表性DSTC模型，对中国区域不同经纬度、不同地表覆盖类型和不同季节的像元作DSTC模型拟合，探究其随地理位置、地物类型、季节的变化规律。使用FY-2F地表温度产品建立的DSTC模型与实测地表温度结合，可以纠正现有DSTC模型从而预测其他时间的地表温度，结合卫星反演的地表温度可获得归一化后的地表温度产品，同时可以检验和标定陆面模式地表温度模拟结果。

2 研究区概况及数据说明

2.1 研究区概况

由于中国幅员广阔，国土范围跨度较大，逐像元对比DSTC模型在中国区的拟合精度并不现实，故本文以194个基准气候站的地理位置为基础，提取FY-2F对应像元上的温度数据分析DSTC模型的精度。国家基准气候站是指获取标准气候资料的气候站，是全国气候站网中的骨干和基准点，根据国家气候区划以及全球观测系统的要求，为获取具有充分代表性的长期、连续气候资料而设置观测站。因此国家基准气候站对中国区域的条件具有代表性。站点的具体信息可参考刘昊和程洁(2016)发表的论文，194个气象站点在MODIS地表覆盖分类数据中的分布情况如下：水体(12)、常绿阔叶林(2)、混交林(15)、多树草原(10)、草地(51)、农用地(54)、城市和建筑区(34)、农用地和自然植被(6)、裸地或稀疏植被(10)。194个站点覆盖了中国主要的地表覆盖类型，其拟合结果能够基本代表中国地区各地表覆盖类型的拟合情况，同时可为选择合适的DSTC模型研究中国区域DSTC模型规律性变化提供先验知识。

2.2 数据说明

2.2.1 FY-2F地表温度产品

FY-2F是中国自行研制的第一代地球静止轨道气象卫星中的第4颗业务星，该星搭载可见光红外自旋扫描辐射仪，星下点经度为112°E，星下点空间分辨率为5 km，只在陆地覆盖范围内有数据。本文使用国家气象卫星中心提供的2014年标称格式1小时地表温度产品，UTC时间每个“半点”获得一景数据(http://www.nsmc.org.cn/NewSite/NSMC/Home/Index.html[2015-06])。

2.2.2 MODIS地表覆盖分类数据

MODIS地表覆盖类型产品是利用监督决策树分类算法得到的全球土地覆盖类型数据。MODIS官网提供500 m、1 km和0.05°共3种不同分辨率的产品，为了便于风云卫星数据的匹配，本文选择0.05°的产品即MCD12C1。MCD12C1产品包含3种分类方案：国际地圈生物圈计划(IGBP)分类方案，马里兰大学(UMD)植被分类方案和MODIS反演LAI/FPAR的分类方案(Friedl 等，2010)。本文选择IGBP的分类方案作为研究数据基础，各地表覆盖类型如下所示：水体、常绿针叶林、常绿阔叶林、落叶针叶林、落叶阔叶林、混交林、稠密灌丛、稀疏灌丛、多树草原、热带稀树草原、草地、永久湿地、农用地、城市和建筑区、农用地和自然植被、雪和冰以及裸地或稀疏植被。

3 模型介绍

半经验模型简单便捷且应用较为广泛，物理模型更接近地表真实物理情况，因此本节选择GOT01，VAN06，JNG06，INA08和GOT09这5种半经验模型和GEM-V物理模型进行DSTC的模拟与分析，并给出了几种模型的初始参数。

3.1 GOT01模型

为了描述太阳照射的影响和夜间地表温度的自然下降趋势，Göttsche和Olesen(2001)使用热扩散方程构建谐波方程拟合白天的温度变化曲线，选择指数函数来模拟自然地表夜晚的温度变化曲线。该模型属于半经验模型，建立该模型有3个要求：(1)晴空条件且风速没有明显变化；(2)模型建立于两次日出之间；(3)在定义的时间 ${t_{\rm{s}}}$ 之后，地表温度自由降低。模型描述如下

$ \left\{\!\!\!\!\!\! {\begin{array}{*{20}{c}} {{T_1}(t) = {T_0} + {T_{\rm{a}}}\cos \left({\dfrac{\text{π}}{\omega }(t - {t_{\rm{m}}})} \right)}\!\!&\!\!{t < {t_{\rm{s}}}} \\ {{T_2}(t) = ({T_0} + \delta T) \!+\! \left( {{T_{\rm{a}}}\cos \left({\dfrac{\text{π}}{\omega }({t_{\rm{s}}} - {t_{\rm{m}}})} \right) - \delta T} \right){{\rm{e}}^{\frac{{ - (t \!-\! {t_{\rm{s}}})}}{k}}}}\!\!&\!\!{t \geqslant {t_{\rm{s}}}} \end{array}} \right. $

(1)

式中， ${T_1}/{T_2}$ 是模型中分别代表白天/夜晚温度的两个部分。其中t是时间， ${T_0}$ 是日出前后的残余温度， ${T_{\rm{a}}}$ 是温度振幅， $\omega $ 是余弦函数半周期宽度， ${t_{\rm{m}}}$ 是温度到达最大值的时间， ${t_{\rm{s}}}$ 是温度开始自由衰减的时间， $\delta {\rm{T}}$ 是 ${T_0}$ 和 $T (t \to \infty) $ 的差值，k是衰减常数。模型中有5个自由变量 ${T_0},{T_{\rm{a}}},{t_{\rm{m}}},{t_{\rm{s}}}$ 和 $ \delta {\rm{T}}$ 。模型中的 $\omega $ 定义为有太阳能量输入的时长，由纬度 $\phi $ 和太阳倾斜角 $\delta $ 决定，其表示为

$ \begin{split} & \omega = \frac{2}{{15}}{\cos ^{ - 1}}(- \tan \phi \tan \delta)\\ & \delta = 23.45\sin \left(360\frac{{284 + n}}{{365}}\right) \end{split}$

(2)

由于DSTC模型曲线连续，白天和夜晚的温度模拟函数在 ${t_{\rm{s}}}$ 处的导数应相同，由此可获得衰减常数

$ k = \frac{\omega }{\text{π}}\left( {{{\tan }^{ - 1}}\left({\frac{\text{π}}{\omega }\left({{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right) - \frac{{\delta T}}{{{T_{\rm{a}}}}}{{\sin }^{ - 1}}\left({\frac{\text{π}}{\omega }\left({{t_{\rm{s}}} - {t_{\rm{m}}}} \right)} \right)} \right) $

(3)

3.2 VAN06模型

Van Den Bergh等(2006)在GOT01模型基础上，采用两个余弦函数分别描述白天温度上升过程和温度下降过程的地表温度的变化情况，新模型包含6个自由变量 ${T_0},{T_{\rm{a}}},{t_{\rm{m}}},{t_{\rm{s}}},{\omega _1}$ 和 $ {\omega _2}$ ，新模型描述如下

$ \left\{ {\begin{array}{*{20}{l}} {{T_1}(t) = {T_0} + {T_{\rm{a}}}\cos \left( {\dfrac{\text{π}}{{{\omega _1}}}(t - {t_{\rm{m}}})} \right)}&{t < {t_{\rm{m}}}}\\ {{T_2}(t) = {T_0} + {T_{\rm{a}}}\cos \left( {\dfrac{\text{π}}{{{\omega _2}}}(t - {t_{\rm{m}}})} \right)}&{{t_{\rm{m}}} \leqslant t < {t_{\rm{s}}}}\\ k = \dfrac{{{\omega _2}}}{\text{π}}{\tan ^{ - 1}}\left( {\dfrac{\text{π}}{{{\omega _2}}}({t_{\rm{s}}} - {t_{\rm{m}}})} \right)\\ {{T_3}(t) = {T_0} + {T_{\rm{a}}}\cos \left( {\dfrac{\text{π}}{{{\omega _2}}}({t_{\rm{s}}} - {t_{\rm{m}}})} \right){{\rm{e}}^{\frac{{ - (t - {t_{\rm{s}}})}}{k}}}}&{t \geqslant {t_{\rm{s}}}} \end{array}} \right. $

(4)

式中，T₁，T₂，T₃分别表示白天温度上升过程、温度下降过程、夜晚3个时间段，以温度达到最高值 ${t_{\rm{m}}}$ 和温度自由下降的 ${t_{\rm{s}}}$ 两个时间点为分界。

3.3 JNG06模型

Jiang等(2006)在GOT01的模型基础上自由拟合参数 $\omega $ 和k，同样地保留地表温度在 ${t_{\rm{s}}}$ 时刻处温度连续且一阶导数连续，该模型表达为

$ \left\{ {\begin{array}{*{20}{l}} {{T_1}(t) = {T_0} + {T_{\rm{a}}}\cos \left( {\beta (t - {t_{\rm{m}}})} \right)}&{t < {t_{\rm{s}}}}\\ {{T_2}(t) = {b_1} + {b_2}{{\rm{e}}^{\alpha (t - {t_{\rm{s}}})}}}&{t \geqslant {t_{\rm{s}}}} \end{array}} \right. $

(5)

式中， $\begin{array}{*{20}{l}}{{b_2} = [ - \beta {T_{\rm{a}}}\sin\left( {\beta ({t_{\rm{s}}} - {t_{\rm{m}}})} \right)]/\alpha }\\{{b_1} = {T_0} + {T_{\rm{a}}}\cos \left( {\beta ({t_{\rm{s}}} - {t_{\rm{m}}})} \right) - {b_2}}\end{array} $

与VAN06相同，JNG06模型包含6个自由参数 ${T_0},{T_{\rm{a}}},{t_{\rm{m}}},{t_{\rm{s}}},\alpha $ 和 $\,\,\beta $ 。对比GOT01模型和JNG06模型可以看出，在GOT01模型中，当 $\omega = {\text{π}}/\beta $ 且 $k = - 1/\alpha $ 时，GOT01模型与JNG06模型等效。

3.4 INA08模型

Inamdar等(2008)认为双曲线函数比指数函数能更好地描述夜间的地表温度变化，即 ${{t}} \geqslant {t_{\rm{s}}}$ 时GOT01模型可表示为

$ {T_2}(t) = ({T_0} + \delta T) + \left( {{T_{\rm{a}}}\cos \left({\frac{\text{π}}{\omega }({t_{\rm{s}}} - {t_{\rm{m}}})} \right) - \delta T} \right)\frac{k}{{k + t - {t_{\rm{s}}}}} $

(6)

式中，k的表达式与GOT01模型相同，INA08模型的5个自由参数 ${T_0},{T_{\rm{a}}},{t_{\rm{m}}},{t_{\rm{s}}}$ 和 $\delta {{T}}$ 也与GOT01模型保持一致。

3.5 GOT09模型

GOT01模型既没有描述单日温度变化曲线峰值附近的温度变化，也没有模拟出日出前后地表温度的平缓变化，同时GOT01模型没有考虑气溶胶的影响，对实际地表温度变化的模拟误差较大。为了解决这些问题，Göttsche和Olesen(2009)以地表能量平衡方程取代热扩散方程，建立了新的DSTC模型

$ \left\{ {\begin{array}{*{20}{l}} {\begin{aligned} & {T_2}(\theta) = ({T_0} + \delta T) + \\ & \left( {{T_{\rm{a}}} \cdot \cos \left({{\theta _{{\textit{z}}s}}} \right) \cdot \frac{{{{\rm{e}}^{\tau ({m_{\min }} - m({\theta _{{\textit{z}}s}}))}}}}{{\cos ({\theta _{{\textit{z}}, \min }})}} - \delta T} \right) \cdot {{\rm{e}}^{\frac{{ - 12}}{{{\text{π}}k}}(\theta - {\theta _s})}} \end{aligned}}&{t \geqslant {t_{\rm{s}}}} \\ {{T_1}(\theta) = {T_0} + {T_{\rm{a}}} \cdot \cos \left({{\theta _{\textit{z}}}} \right) \cdot \dfrac{{{{\rm{e}}^{\tau ({m_{\min }} - m({\theta _{\textit{z}}}))}}}}{{\cos ({\theta _{{\textit{z}}, \min }})}}}&{t < {t_{\rm{s}}}} \end{array}} \right. $

(7)

式中， $\tau $ 是大气总光学厚度； $\theta $ 表示“热时角”； ${\theta _{{s}}}$ 是 ${{t}} = {t_{\rm{s}}}$ 时的热时角； ${\theta _{\textit{z}}}$ 是太阳天顶角； ${\theta _{{{\textit{z}}s}}}$ 是 $\theta {\rm{ = }}{\theta _{{s}}}$ 时的热天顶角； ${\theta _{{\textit{z}}, \min }}$ 是最小热天顶角；m是相对大气质量，是太阳天顶角的函数； ${m_{\min }}$ 是最小相对大气质量。各项参数计算为

$ \begin{array}{l} \theta = \dfrac{\text{π}}{{12}}\left({t - {t_m}} \right) \\ {\theta _z} = \arccos (\sin (\delta)\sin (\phi) + \cos(\delta)\cos(\phi)\cos (\theta)) \\ m({\theta _z}) = - \dfrac{{{{R} _{\rm E}}}}{H}\cos ({\theta _z}) + \sqrt {{{\left({\dfrac{{{{R} _{\rm E}}}}{H}\cos ({\theta _z})} \right)}^2} + 2\dfrac{{{{R} _{\rm E}}}}{H} + 1} \end{array} $

(8)

式中， ${R_{\rm E}}$ 是地球半径，H是大气标高， $\phi $ 代表纬度， $\delta $ 代表黄赤交角。

3.6 GEM-V模型

Huang等(2014)基于地表能量平衡方程，参数化地表热通量建立反演地表温度的前向模型GEM(Generic Framework Model)。该方法可以模拟任意起始时刻的地表温度日变化而不局限于从日出到下一个日出的时间范围内，地表温度日变化模型表示为

$ \begin{aligned} & T(0, t) = \overline T + \sum\limits_{n - 1}^\infty {{M_n} \cdot g(t)} \\ & {M_{{n}}} = {\left(n{\omega _L}{P^2} + \sqrt {2n{\omega _L}} P \cdot {h_1} + {h_1}^2 \right)^{ - 1/2}} \\ & g(t) = {A_n}\cos (n{\omega _L}t - {\phi _n}) + {B_n}\sin (n{\omega _L}t - {\phi _n}) \\ & {\phi _n} = \arctan \left[P\sqrt {n{\omega _L}} \cdot {(\sqrt 2 {h_0} + P\sqrt {n{\omega _L}})^{ - 1}}\right] \end{aligned} $

(9)

式中， $P$ 是热惯量， ${A_n}$ 和 ${B_n}$ 是短波净辐射近似值和热通量残差项的傅里叶级数展开第n阶系数， ${\omega _L}$ 对应连续多日周期， ${h_0}$ 和 ${h_1}$ 是上行热通量的两个系数。考虑到地表温度在多日周期内并不呈现严格的周期变化，上行热通量系数可表达为时间的线性函数： ${h_1} = {\eta _0} + {\eta _1}t$ 。前向模型GEM待确定系数有四个基本参数，包括 $P,\overline T ,{\eta _0}$ 和 ${\eta _1}$ ，分别表示热惯量、日均地表温度和上行热通量系数。

3.7 模型参数设置

在模型参数设置之前需要对提取FY-2F的地表温度做质量控制，因为除了受到薄云和反演误差的影响，数据中也会存在偶尔产生的由反常因素造成的测量数值超出正常范围的小概率误差，含有此类误差会干扰对实验结果的分析甚至歪曲实验结果。本文采用格拉布斯准则剔除异常值，其判别方法如下(Xiong和Wu，2010)：将呈正态分布的等精度多次测量样本按从小到大排列，统计临界系数G(a，n)的值为G₀，进而计算G₁、G_n

$ {G_1}{\rm{ = }}\left( {\bar X - {X_1}} \right)/\sigma ;{G_n} = \left( {{X_n} - \bar X} \right)/\sigma $

(10)

若 ${G_1} \geqslant {G_n}$ 且 ${\rm{ }}{G_1} > {G_0}$ ，剔除X₁；若 ${G_n} \geqslant {G_1}$ 且 ${G_n} > {G_0}$ ，剔除X_n；若 ${G_1} \geqslant {G_0}$ 且 ${G_n} < {G_0}$ ，则不存在坏值，无须剔除。然后用剩余数据重复上述步骤进行判断，直到所有数据都不存在坏值。

由于地表温度日变化模型是拟合从日出之后到下一个日出之前这段时间的地表温度变化情况，起始拟合时间的判断就显得尤为重要。本研究中首先通过日出方程式计算太阳在不同赤纬时，不同经纬度位置的日出时间(T_sr)、日落时间(T_ss)的精确时间，而后以日出后的第一次观测作为拟合的起始时间，日出之后24次观测作为完整的观测数据(刘昊和程洁，2016)。所有模型均为非线性模型，本研究使用Levenberg-Marquargt最小二乘法对模型参数进行求解。GEM_V由于其模型设置较为复杂，且与其他模型参数的物理意义相差较大，参考Huang等(2014)的研究将GEM_V模型的拟合初始值设置为：1500(热惯量)、300(日均地表温度)和0(上行热通量系数)。对其他几种模型的初始值作了改进，使其更符合真实地表情况，从而收敛速度更快。具体模型参数设置如下：T₀设置为日出后第一次观测数据， ${t_{\rm{s}}}$ 为日落前一小时观测数据， ${t_{\rm{m}}}$ 为正午后一小时观测数据，剩余参数和Duan等(2012)参考文献一致，其初值取值如表1所示。虽然我们对模型参数的初值进行了改进，但模型的晴空假设会对非晴空下的拟合结果产生一定的影响。根据Göttsche和Olesen(2009)的研究，完全晴空大气条件下，考虑大气总光学厚度的GOT09模型的平均误差为0.55 ℃，GOT01模型的平均误差为0.6 ℃。而在混合大气条件下，考虑大气总光学厚度的GOT09模型的平均误差为0.8 ℃，GOT01模型的平均误差为1.82 ℃。此外，根据Duan等(2012)的研究，当高斯分布的随机误差(平均值为0 K，标准差为1 K)加入地表温度后，随机误差对不同模型具有相似的影响，其中GOT09模型的大气光学厚度的偏差和均方根误差分别为0.01和0.09。

表 1 5个DSTC模型的参数初始值
Table 1 Initial parameters for five DSTC models

下载CSV

参数/ 模型	GOT01	VAN06	JNG06	INA08	GOT09
T₀	T(1)	T(1)	T(1)	T(1)	T(1)
T_a	T_max−T_min	T_max−T_min	T_max−T_min	T_max−T_min	T_max−T_min
t_m	(T_ss+T_sr)/2+1	(T_ss+T_sr)/2+1	(T_ss+T_sr)/2+1	(T_ss+T_sr)/2+1	(T_ss+T_sr)/2+1
t_s	T_ss−1	T_ss−1	T_ss−1	T_ss−1	T_ss−1
δT	0.5			0.5	0.5
ω₁		ω
ω₂		ω
α			−0.3
β			π/ω
τ					0.03

4 研究结果与分析

本文分为两个部分对模型进行评价：(1)地表温度日变化模型在中国气象站点的适应性分析。以194个站点的地理位置为基础，提取2014年FY-2F对应像元上的地表温度数据，对逐月逐小时的数据做质量控制后取平均值，作为该月逐小时的平均温度，根据设置的模型初始值，评估DSTC模型在中国区域的拟合精度。首先，将DSTC模型的拟合分为5个时间段，分析DSTC模型的拟合精度。其次，根据194个站点所在的地表覆盖类型统计各模型在每一种地表类型下的拟合精度。(2)中国区域地表温度日变化规律探究。选用地表覆盖类型比例较高的4种地表类型以及具有一定物理意义的、拟合收敛速度快、精度较高的JNG06模型作为研究基础，分析中国区域地表温度在季节性、经纬度和地表覆盖类型的日间变化特征。

4.1 不同时间窗口下DSTC模型精度评价

陈颖等(2016)研究发现，地表温度日变化模型在日出时刻附近和18—21时段内具有较大的拟合误差；朱琳清等(2017)分析表明风速对不同时间段内DSTC模型时间归一化的影响有所差异。本文按照拟合起始时间后的1—4、5—9、10—14、15—19和20—24小时分为5个时间窗口对DSTC模型的精度进行评价。为了直观理解变化趋势，在作图时统一将地方时5时表示为起始时间，5个时间窗口分别为6—9时、10—14时、15—19时、20—24时和1—5时，分别代表日出前后、温度高峰前后、温度下降期、前半夜晚间和后半夜晚间5个部分。图1为6种DSTC模型在不同时间窗口下的RMSE月平均值曲线图。从图1可以看出，各模型总体拟合精度最佳的时间窗口是15—19时和20—24时，全年各模型拟合精度相近且不超过1.5 K，其中GOT01和INA08模型表现略逊于其他几种模型。在6—9时日出前后的时间窗口，GOT01、INA08和VAN06模型表现较差，全年RMSE基本都在1.5 K以上且波动较大，最高达到3 K以上，剩余几种模型全年RMSE均在1.5 K以下，波动较小。在10—14时时间窗口内，GOT01、INA08和VAN06模型表现欠佳，其中VAN06模型在2—6月和7—12月的RMSE都基本持平；其他模型在全年表现都较为稳定，RMSE维持在1.5 K以下，1月和12月的RMSE最小在0.5 K左右。在1—5时时间窗口内，各模型的RMSE年变化均较大，在2月、4月和10月RMSE尤甚，其中4月的总体拟合精度最差。在整个拟合时段内，几种模型变化趋势基本一致，GOT01、INA08和VAN06效果较差，RMSE均高于其他几种模型，全年RMSE均大于1 K，剩余几种模型的表现基本一致。从5个时间窗口的平均RMSE来看，GOT09模型具有最高的精度，RMSE为0.89 K，其次为JNG06和GEM_V模型，RMSE分别为0.92 K和0.94 K，GOT01、INA08和VAN06模型精度最差，RMSE均在1.33 K左右。

图 1 DSTC模型在不同时间窗口的拟合精度

Fig. 1 The fitting precision of DSTC model at different time windows

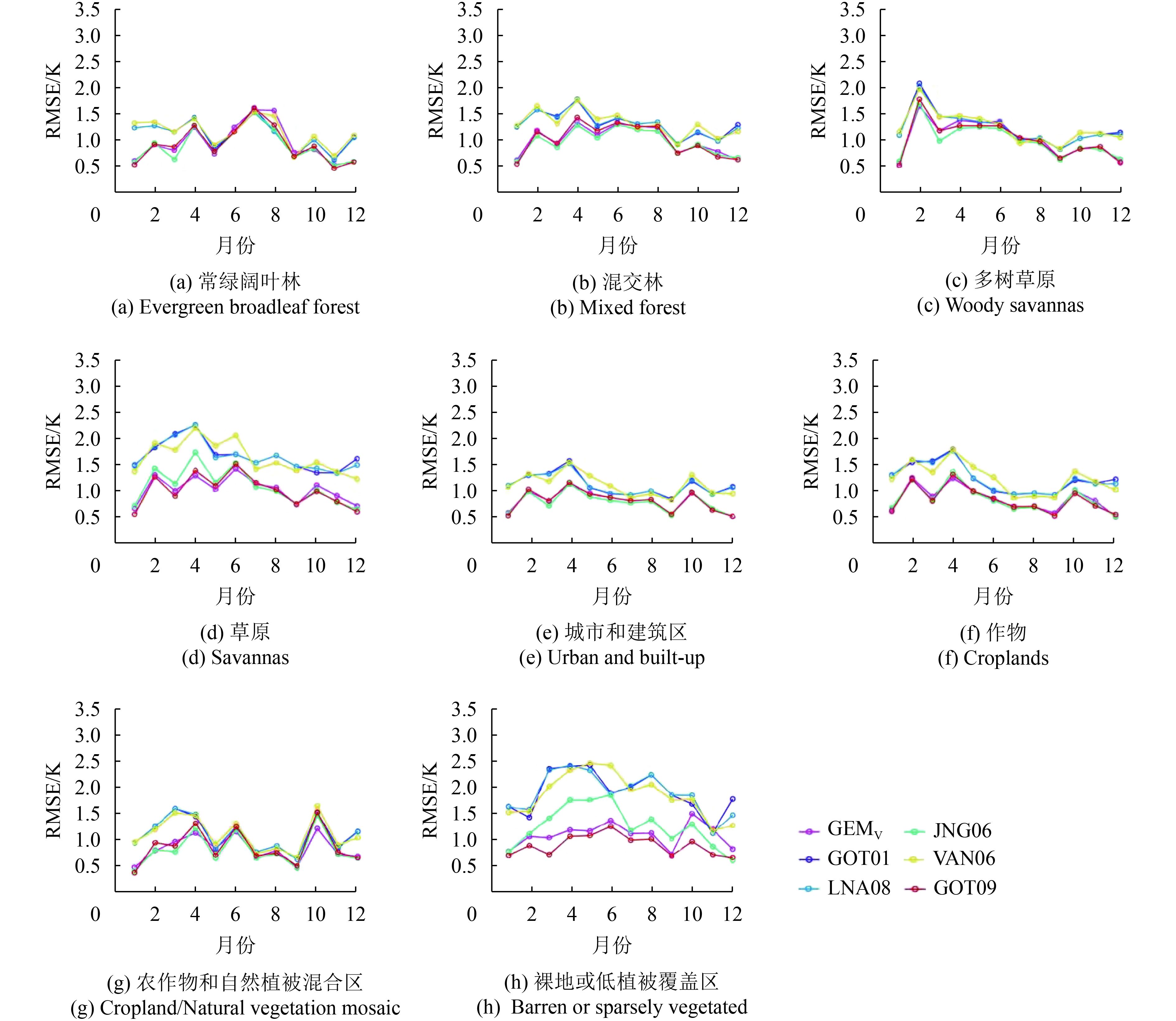
4.2 不同地表覆盖类型下DSTC模型精度评价

由于FY-2F LST产品在水体区域为空值，故剩余站点所在区域主要有8种地表类型，分别为常绿阔叶林、混交林、多树草原、草地、农用地、城市和建筑区(城市等)、农用地和自然植被(农用地等)以及裸地或稀疏植被(裸地等)。图2为整个拟合时间段内6种DSTC模型在8种地表类型的拟合结果。对于常绿阔叶林这一地表类型，GOT01、VAN06和INA08这3个模型在1、2、3和12月这4个月份的拟合精度与其他模型差异较大，其余几个月份则比较接近，同时在7月份各模型RMSE均达到最大值。在城市和建筑区、混交林、草地和农用地这4种地表覆盖类型中，整体拟合趋势比较接近，除草地这一地表覆盖类型外，其余3种类型的整体拟合精度也较为一致，RMSE大部分都在1.5 K以下。GOT01、VAN06和INA08这3种模型在裸地或稀疏植被这一地表覆盖类型拟合精度最差；JNG06模型的拟合结果波动较大，精度有所下降。各模型在多树草原这一地表覆盖类型的拟合精度一致，GOT01、VAN06和INA08这3种模型的拟合精度稍差，各模型在二月份的RMSE均达到最高值。综合各模型在不同地表覆盖类型的模拟精度，模型在草地和裸地或稀疏植被这两种地表覆盖类型的拟合精度最差，RMSE在1.3 K以上；在混交林和农用地这两类地表覆盖类型表现次之，RMSE在1.0 K左右；在城市和建筑区、农用地和自然植被以及常绿阔叶林这3类地表覆盖类型的拟合精度最好，其RMSE在0.89—0.92 K。总体而言，GOT01、VAN06和INA08这3种模型在所有地表覆盖类型及各月份的模拟精度均较差，剩余几种模型表现较为稳健，在各地表覆盖类型的模拟精度均相近。

图 2 DSTC模型在不同地表覆盖类型的拟合精度

Fig. 2 The fitting precision of DSTC model at different land cover type

4.3 地表温度日变化特征

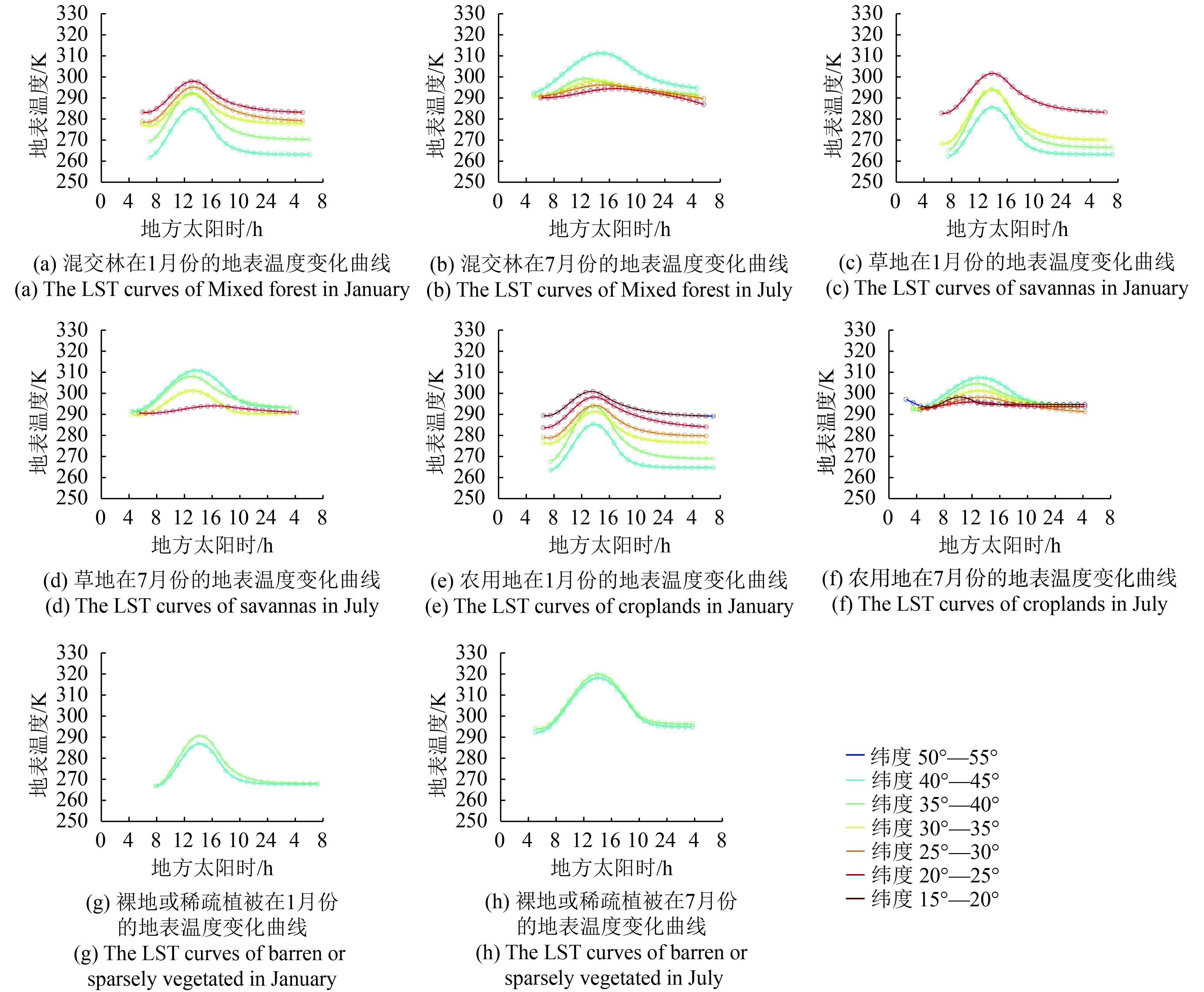
通过统计MCD12C1几种地表覆盖类型像元在中国的分布，选用地表覆盖类型比例较高的四种地表类型(草地、裸地或稀疏植被、农用地和混交林)以及具有一定物理意义的、拟合收敛速度快、精度较高的JNG06模型作为研究基础，分析中国区域地表温度在季节性、经纬度和地表覆盖类型的日间变化特征。在Jin和Treadon(2003)的研究基础上，对经度和纬度同时作5°分带(建立DSTC模型经纬网格查找表)，选取2014年1月和7月的数据，探究在不同地理位置下的地表温度日变化差异。在每个网格内对每种地表类型的DSTC模型参数做中值提取(Göttsche和Olesen，2001)，作为该类别在网格内的DSTC模型参数，生成DSTC模型参数在中国区的查找表。

如图3所示是4种地表类型在东经105°—110°区间内，DSTC模型拟合的地表温度曲线在1月和7月随纬度变化情况。图3(a)、(c)、(e)和(g)依次为混交林、草地、农用地、裸地或稀疏植被在1月份的变化情况，图3(b)、(d)、(f)、(h)依次为混交林、草地、农用地、裸地或稀疏植被在7月份的变化情况。由图3可见，模型模拟的地表温度在四种地表类型均展现了规律性变化趋势：4种地表类型的地表温度在1月份北半球冬季的变化特征较为一致，在整个拟合时间内低纬度的地表温度要高于高纬度的地表温度，随着纬度升高，地表温度最大值呈下降趋势。地表温度在1月份波动较为剧烈，在35°—40°N内变化幅度最大，且4种地表类型在35°—45°N的变化范围基本一致。混交林、草地和农用地这3类地表类型的地表温度在7月份整体波动较为平缓，纬度在30°N以下的地表温度在整个拟合区间基本持平，纬度在北纬30°以上时，随着纬度升高，地表温度最大值呈上升趋势。裸地或稀疏植被这类地表类型在7月份的地表温度变化较为剧烈，在整个拟合时间段，两个纬度区间的地表温度基本没有差别，温度最大值也基本一致。

图 3 4种地表类型在105°—110°E内，DSTC模型拟合的地表温度曲线在1月和7月随纬度变化情况

Fig. 3 In the range of 105 °—110 °E, the LST curves of the DSTC model are latitudinal changes in January and July

在1月份北半球冬季，混交林、草地和农用地这3类地表类型的残余温度在不同纬度相差较大。1月份北半球冬季，随纬度升高，地表接受到的太阳下行辐射降低，日照时间减少，故随着纬度降低地表温度和残余温度也升高。以混交林为例，20°—25°N和40°—45°N内的日出前后残余温度相差达到17.7 K，温度变化振幅相差4.3 K。在7月份北半球夏季，4种地表类型的残余温度在纬度均没有明显变化，不同纬度的残余温度基本相等。在低纬度地区，地表温度值以及变化幅度都低，原因可归于以下几点：(1)相对于高纬度地区裸露地表而言，低纬度地区植被覆盖度高，土壤含水量大，热容量大，因此地表温度偏低；(2)由于蒸散和遮蔽效应影响，浓密植被地区温度变化幅度较小(Göttsche和Olesen，2001)；(3)数据质量控制采取的统计学方法无法完全去除薄云及其他异常值的影响。陈颖等(2016)研究表明在云的影响下的地表温度日变化模型的模拟精度较低，均方根误差大于3 K。

在低纬度地区几乎不可能出现全天无云的情况，而DSTC的拟合只适合全天无云的情况，故模拟误差无可避免，但本文模拟的是5°×5°范围内月平均尺度上的地表温度日变化情况，这种模拟相对于单日尺度上的模拟会有较多的晴空数据。文中使用的模型只有5—6个自由参数，理论上，只需要5—6个地表温度数据作为模型输入，就可以描述一天中地表温度随时间的变化(陈颖等，2016)。一方面，本文使用的是月平均处理能够增加一定数量的地表温度数据；另一方面，5°×5°范围内取中值既能够去除部分异常值的影响又能在一定程度上增加网格内数据的可用性。因此，即使在云量较多的低纬度地区夏季也有足够的晴空数据(大于6)作为DSTC模型的输入来描述地表温度日周期变化。

5 结　论

本文以中国区域为研究范围，以FY-2F卫星实测数据为基础，首先从月平均尺度和面尺度评估了现有6种地表温度日间变化模型在中国区域的精度。从5个时间窗口的平均RMSE来看，GOT09模型获得了全局最优的拟合精度，RMSE为0.89 K，其次为JNG06和GEM_V模型，RMSE分别为0.92 K和0.94 K，GOT01、INA08和VAN06模型精度最差。各模型在城市和建筑区、农用地和自然植被以及常绿阔叶林这3类地表覆盖类型的拟合精度最好，其RMSE在0.89—0.92 K，在混交林和农用地这两类地表覆盖类型表现次之，RMSE在1.0 K左右；在草地和裸地或稀疏植被这两种地表覆盖类型的拟合精度最差，RMSE在1.3 K以上。其次，利用JNG06模型得到了晴空条件下中国区域地表温度日变化曲线随地理位置、地物类型、季节的变化特征，生成了地表温度日变化模型各参数的查找表。利用该查找表，结合实测地表温度数据可以纠正现有DSTC模型从而预测其他时间的地表温度，结合反演的地表温度可获得归一化的地表温度产品。4种地表类型的地表温度在1月份随纬度变化较为剧烈，在7月份整体波动较为平缓。在1月份，低纬度的地表温度要高于高纬度的地表温度，随着纬度升高，地表温度最大值呈下降趋势，7月份趋势则相反。

综上所述，DSTC模型在中国区域具有较高的精度，随着纬度的变化特征较为明显。使用FY-2F地表温度产品建立的DSTC模型结合实测地表温度，可以纠正现有DSTC模型从而预测其他时间的地表温度，结合卫星反演的地表温度可获得归一化后的地表温度产品，同时可以检验和标定陆面模式地表温度模拟结果。虽然利用FY-2F地表温度产品对DSTC模型进行了精度评价，也得到了较高的精度，但未使用地面实测数据对模型验证或进行规律解析。其次，虽采取统计学方法对数据质量进行控制，如何更有效地判断未被识别的薄云像元值及存在质量问题的像元值，在本研究以及日后地表温度变化模型的模拟中均是值得探讨的问题。

参考文献(References)

Aires F, Prigent C and Rossow W B. 2004. Temporal interpolation of global surface skin temperature diurnal cycle over land under clear and cloudy conditions. Journal of Geophysical Research: Atmospheres, 109 (D4): D04313 [DOI: 10.1029/2003JD003527]

Chen Y, Duan S B, Leng P, Chen Y Y and Han X J. 2016. Modeling of diurnal cycle of land surface temperature based on polar orbiting satellite thermal infrared data. Remote Sensing Information, 31 (6): 7–14. [DOI: 10.3969/j.issn.1000-3177.2016.06.002] ( 陈颖, 段四波, 冷佩, 陈媛媛, 韩晓静. 2016. 极轨卫星热红外地表温度日变化模拟. 遥感信息, 31 (6): 7–14. [DOI: 10.3969/j.issn.1000-3177.2016.06.002] )

Cheng J, Liang S L, Wang J D and Li X W. 2010. A stepwise refining algorithm of temperature and emissivity separation for hyperspectral thermal infrared data. IEEE Transactions on Geoscience and Remote Sensing, 48 (3): 1588–1597. [DOI: 10.1109/TGRS.2009.2029852]

Coops N C, Duro D C, Wulder M A and Han T. 2007. Estimating afternoon MODIS land surface temperatures (LST) based on morning MODIS overpass, location and elevation information. International Journal of Remote Sensing, 28 (10): 2391–2396. [DOI: 10.1080/01431160701294653]

Crosson W L, Al-Hamdan M Z, Hemmings S N J and Wade G M. 2012. A daily merged MODIS Aqua-Terra land surface temperature data set for the conterminous United States. Remote Sensing of Environment, 119 : 315–324. [DOI: 10.1016/j.rse.2011.12.019]

Dickinson R E, Henderson-Sellers A and Kennedy P J. 1993. Biosphere-atmosphere Transfer Scheme (BATS) Version 1E As Coupled to the NCAR Community Climate Model. NCAR Technical Note NCAR/TN-387+STR. NCAR [DOI: 10.5065/D67W6959]

Duan S B, Li Z L, Tang B H, Wu H and Tang R L. 2014. Generation of a time-consistent land surface temperature product from MODIS data. Remote Sensing of Environment, 140 : 339–349. [DOI: 10.1016/j.rse.2013.09.003]

Duan S B, Li Z L, Wang N, Wu H and Tang B H. 2012. Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satellite data . Remote Sensing of Environment, 124 : 15–25. [DOI: 10.1016/j.rse.2012.04.016]

Friedl M A, Sulla-Menashe D, Tan B, Schneider A, Ramankutty N, Sibley A and Huang X M. 2010. MODIS collection 5 global land cover: algorithm refinements and characterization of new datasets. Remote Sensing of Environment, 114 (5): 168–182. [DOI: 10.1016/j.rse.2009.08.016]

Göttsche F M and Olesen F S. 2001. Modelling of diurnal cycles of brightness temperature extracted from METEOSAT data. Remote Sensing of Environment, 76 (3): 337–348. [DOI: 10.1016/S0034-4257(00)00214-5]

Göttsche F M and Olesen F S. 2009. Modelling the effect of optical thickness on diurnal cycles of land surface temperature. Remote Sensing of Environment, 113 (11): 2306–2316. [DOI: 10.1016/j.rse.2009.06.006]

Huang F, Zhan W F, Duan S B, Ju W M and Quan J L. 2014. A generic framework for modeling diurnal land surface temperatures with remotely sensed thermal observations under clear sky. Remote Sensing of Environment, 150 : 140–151. [DOI: 10.1016/j.rse.2014.04.022]

Ignatov A and Gutman G. 1999. Monthly mean diurnal cycles in surface temperatures over land for global climate studies. Journal of Climate, 12 (7): 1900–1910. [DOI: 10.1175/1520-0442(1999)012<1900:MMDCIS>2.0.CO;2]

Inamdar A K, French A, Hook S, Vaughan G and Luckett W. 2008. Land surface temperature retrieval at high spatial and temporal resolutions over the southwestern United States. Journal of Geophysical Research: Atmospheres, 113 (D7): D07107 [DOI: 10.1029/2007JD009048]

Jiang G M, Li Z L and Nerry F. 2006. Land surface emissivity retrieval from combined mid-infrared and thermal infrared data of MSG-SEVIRI. Remote Sensing of Environment, 105 (4): 326–340. [DOI: 10.1016/j.rse.2006.07.015]

Jin M L. 2000. Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle: 2. Cloudy‐pixel treatment. Journal of Geophysical Research: Atmospheres, 105 (D3): 4061–4076. [DOI: 10.1029/1999JD901088]

Jin M L and Dickinson R E. 1999. Interpolation of surface radiative temperature measured from polar orbiting satellites to a diurnal cycle: 1. Without clouds. Journal of Geophysical Research, 104 (D2): 2105–2116. [DOI: 10.1029/1998JD200005]

Jin M L and Treadon R.E. 2003. Correcting the orbit drift effect on AVHRR land surface skin temperature measurements. International Journal of Remote Sensing, 24 (22): 4543–4558. [DOI: 10.1080/0143116031000095943]

Kahle A B. 1977. A simple thermal model of the Earth’s surface for geologic mapping by remote sensing. Journal of Geophysical Research, 82 (11): 1673–1680. [DOI: 10.1029/JB082i011p01673]

Li Z L, Tang B H, Wu H, Ren H Z, Yan G J, Wan Z M, Trigo I F and Sobrino J A. 2013. Satellite-derived land surface temperature: Current status and perspectives. Remote Sensing of Environment, 131 : 14–37. [DOI: 10.1016/j.rse.2012.12.008]

Liang S L, Cheng J, Jia K, Jiang B, Liu Q, Liu S H, Xiao Z Q, Xie X H, Yao Y J, Yuan W P, Zhang X T and Zhao X. 2016. Recent progress in land surface quantitative remote sensing. Journal of Remote Sensing, 20 (5): 875–898. [DOI: 10.11834/jrs.20166258] ( 梁顺林, 程洁, 贾坤, 江波, 刘强, 刘素红, 肖志强, 谢先红, 姚云军, 袁文平, 张晓通, 赵祥. 2016. 陆表定量遥感反演方法的发展新动态. 遥感学报, 20 (5): 875–898. [DOI: 10.11834/jrs.20166258] )

Liu H and Cheng J. 2016. Construction of Diurnal Surface Temperature Cycle Model and Probe about the Regular Pattern of the Model in China. Beijing: Beijing Normal University: 21 (刘昊, 程洁. 2016. 中国区域地表温度日变化模型的构建及规律探究. 北京: 北京师范大学: 21)

Liu Z H, Wu P H, Wu Y L, Shen H F and Zeng C. 2017. Robust reconstruction of missing data in Feng Yun geostationary satellite land surface temperature products. Journal of Remote Sensing, 21 (1): 40–51. [DOI: 10.11834/jrs.20176003] ( 刘紫涵, 吴鹏海, 吴艳兰, 沈焕锋, 曾超. 2017. 风云静止卫星地表温度产品空值数据稳健修复. 遥感学报, 21 (1): 40–51. [DOI: 10.11834/jrs.20176003] )

Norman J M and Becker F. 1995. Terminology in thermal infrared remote sensing of natural surfaces. Remote Sensing Reviews, 12 (3/4): 159–173. [DOI: 10.1080/02757259509532284]

Parton W J and Logan J A. 1981. A model for diurnal variation in soil and air temperature. Agricultural meteorology, 23 : 205–216. [DOI: 10.1016/0002-1571(81)90105-9]

Price J C. 1977. Thermal inertia mapping: a new view of the earth. Journal of Geophysical Research, 82 (18): 2582–2590. [DOI: 10.1029/JC082i018p02582]

Schädlich S, Göttsche F M and Olesen F S. 2001. Influence of land surface parameters and atmosphere on METEOSAT brightness temperatures and generation of land surface temperature maps by temporally and spatially interpolating atmospheric correction. Remote Sensing of Environment, 75 (1): 39–46. [DOI: 10.1016/S0034-4257(00)00154-1]

Sun D L and Pinker R T. 2005. Implementation of GOES-based land surface temperature diurnal cycle to AVHRR. International Journal of Remote Sensing, 26 (18): 3975–3984. [DOI: 10.1080/01431160500117634]

Van Den Bergh F, Van Wyk M A and Van Wyk B J. 2006. Comparison of data-driven and model-driven approaches to brightness temperature diurnal cycle interpolation//Proceedings of the 17th Annual Symposium of the Pattern Recognition Association of South Africa. Parys, South Africa: [s.n.]

Xiong Y Y and Wu X Q. 2010. The generalizing application of four judging criterions for gross errors. Physical Experiment of College, 23 (1): 66–68. [DOI: 10.3969/j.issn.1007-2934.2010.01.022] ( 熊艳艳, 吴先球. 2010. 粗大误差四种判别准则的比较和应用. 大学物理实验, 23 (1): 66–68. [DOI: 10.3969/j.issn.1007-2934.2010.01.022] )

Xue X S and Wu Y L. 2017. A comparison of missing data reconstruction methods for Feng Yun geostationary satellite land surface temperature products. Journal of Anhui Agricultural University, 44 (2): 308–315. [DOI: 10.13610/j.cnki.1672-352x.20170419.028] ( 薛兴盛, 吴艳兰. 2017. 面向风云静止卫星地表温度产品的缺失数据修复方法对比. 安徽农业大学学报, 44 (2): 308–315. [DOI: 10.13610/j.cnki.1672-352x.20170419.028] )

Zhan W F, Chen Y H, Voogt J, Zhou J, Wang J F, Liu W Y and Ma W. 2012a. Interpolating diurnal surface temperatures of an urban facet using sporadic thermal observations. Building and Environment, 57 : 239–252. [DOI: 10.1016/j.buildenv.2012.05.005]

Zhu L Q, Zhou J, Liu S M and Li G Q. 2017. Temporal normalization research of airborne land surface temperature. Journal of Remote Sensing, 21 (2): 193–205. [DOI: 10.11834/jrs.20176103] ( 朱琳清, 周纪, 刘绍民, 李国全. 2017. 航空遥感地表温度时间归一化. 遥感学报, 21 (2): 193–205. [DOI: 10.11834/jrs.20176103] )

摘要

关键词