|
收稿日期: 2017-12-20; 预印本: 2018-07-20
基金项目: 国家自然科学基金(编号:41571432)
第一作者简介: 李烁,1990年生,男,博士研究生,研究方向为数字摄影测量和数字图像处理。E-mail:
chxyls@163.com
通信作者简介: 王慧,1968年生,女,教授,研究方向为航空航天信息获取与处理。E-mail:
zzch0908@163.com
|
摘要
针对区域范围内多幅待镶嵌影像之间的色彩差异问题,提出一种基于GPU的分块加权Wallis并行匀色算法。首先,根据变异系数对影像自适应分块并利用双线性插值确定每一个像素的变换参数,利用加权Wallis变换消除影像间的色彩差异。然后,为了控制区域整体的匀色质量,利用Voronoi图和Dijkstra算法确定影像间的处理顺序。最后,利用GPU技术进行并行任务设计并从配置划分、存储器访问和指令吞吐量等方面进行优化,提高算法运算效率。实验结果表明,本文方法既能有效地消除影像间色彩差异,又能消除影像间的对比度差异。与CPU串行算法相比,GPU并行算法显著减少了计算时间,加速比最高达到60倍以上。
关键词
遥感, 影像匀色, GPU并行, 自适应分块, Wallis变换, 归约求和
Abstract
Mosaicked remote sensing images that cover large areas are important in image analysis and application. However, different degrees of color and contrast differences are observed between images due to the influence of sensor and external factors, such as light and fog, which complicate image mosaicking. Therefore, eliminating the differences between adjacent images and ensuring consistent colors in the large area (i.e., color balancing) are becoming increasingly significant. The acquisition cycle of remote sensing data is shortened and the amount of data is increased dramatically with the development of the sensor technology. The changes bring challenges to the efficiency of color balancing of remote sensing images. The traditional serial processing model based on CPU also cannot meet the requirements of fast processing mass data to handle emergency response. To solve the aforementioned problems, a parallel color balancing method based on adaptive block Wallis algorithm for image mosaicking was proposed. First, the images were adaptively divided into blocks depending on the coefficients of variation. Bilinear interpolation was used to determine the transformation parameters of each pixel, and the Wallis transform was adopted to eliminate the color differences between adjacent images. Second, Voronoi diagram was generated to determine the adjacent relation of images. Dijkstra algorithm was used to calculate the shortest path and determine the processing sequence for controlling the color consistency of the entire region. Finally, GPU technology was used to parallelize the proposed method for improving the efficiency. Bilinear interpolation and linear transformation are repetitive and dense computing tasks, which were directly assigned to each thread and executed simultaneously. The reduction method was adopted to parallelize the calculation of mean and standard deviation. Moreover, configuration, memory access, and instruction throughput were optimized to further improve the efficiency. Two groups of experiments were implemented on orthoimages to verify the effectiveness and efficiency of the proposed method. Experimental results showed that the proposed method was superior to the traditional Wallis method and Inpho in visual effect and quantitative evaluation. Moreover, the highest speed-up of the proposed parallel algorithm based on GPU could be more than 60 times that of the serial color balancing method based on CPU. The proposed method can effectively eliminate the color and contrast differences between adjacent images, thereby decreasing the difficulty in seamline detection. Meanwhile, the efficiency of the method is improved dramatically with the proposed parallel acceleration strategy. The performance of the proposed method is excellent in improving the quality and efficiency of color balancing and reducing the difficulty in image mosaicking. Moreover, the proposed method is sufficiently efficient to meet the requirements of fast color balancing of remote sensing images.
Key words
remote sensing, color balancing, GPU parallel, adaptive block, Wallis transformation, reduction of sum
1 引 言
在遥感领域中,大范围的镶嵌影像是影像分析和应用中的重要数据源。但是,受获取时刻光照、天气以及时相等条件的影响,待镶嵌影像之间存在着不同程度的色彩差异和对比度差异,使影像镶嵌更为复杂,也更为困难。因此,对区域范围内的多幅影像进行匀色,也称色彩一致性处理(吴炜 等,2012),消除影像之间色彩差异,使测区内影像在色调上保持一致,降低影像镶嵌的难度,具有重要的现实意义。
现有方法可以分为两类,一类是非线性方法,如直方图匹配法(Helmer和Ruefenacht,2005;陈建乐 等,2007)和Gamma校正法(Zhou 等,2015);另一类是线性变换法(Canty和Nielsen,2008;吴炜 等,2013),也是最受关注的方法,这类方法倾向于从影像的重叠区域选取不变像素作为样本参与统计,然后利用线性模型进行相对辐射校正。对于像素样本的筛选,张鹏强等(2006)采用人工选取的方法,Chen等(2014)使用迭代加权的多元变化检测法,Zhang等(2014)利用迭代慢特征分析法,Lin等(2015)采用加权主成分分析法。这些方法虽然可以不同程度地解决色彩不一致问题,但是通常不能很好地消除对比度不一致现象。然而进行大范围的影像镶嵌时,影像之间常有色彩不一致和对比度不一致同时存在的情况。因此,一种基于均值和方差的特殊线性变换即Wallis变换,引入到色彩一致性处理中。李治江(2005)采用全局Wallis变换对相邻影像进行色调匹配。王密和潘俊(2006)提出了一种兼顾整体与局部的匀色方法,在利用Wallis变换对影像进行处理后,采用直方图匹配法对重叠区域进一步处理。孙明伟(2009)在Wallis变换基础上提出了基于最小二乘区域网平差的匀色处理方法,整体计算区域中每幅影像的色调调整参数。李烁等(2016)针对正射影像提出了一种基于重叠区域的Wallis匀色方法,根据相邻影像有效区域的重叠区域的均值和方差信息进行匀色处理。上述方法本质上都是基于Wallis变换且利用同一线性关系进行匀色处理,但是影像中的地物复杂多样,色彩差异程度也不相同,采用同一个线性关系不能很好地消除影像之间的色彩差异。
此外,随着遥感数据获取方式朝着多平台、多轨道、多传感器、多光谱、高分辨率、短周期访问等方向发展,使得获取的遥感数据呈爆炸性增长(闸旋,2013),使影像匀色处理的效率面临挑战。传统基于CPU的串行处理模式运算能力已明显不足,无法满足在应急应用领域中对海量遥感数据快处理需求(方留杨 等,2013)。随着GPU(Graphic Processing Unit)通用计算能力的不断增强,为提高遥感数据处理效率提供了新的有效手段。基于GPU的并行技术在遥感领域中的应用日益广泛,越来越多的算法以并行结构被重新设计(王宗跃 等,2014;常方正 等,2016),但是在影像匀色处理中应用相对较少。
针对上述问题,本文在Wallis变换的基础上,提出一种基于GPU的自适应分块加权Wallis并行匀色方法。一方面,综合利用线性模型和非线性模型的优势,从整体和局部两方面提高匀色处理的质量。另一方面,对匀色方法的并行性进行分析并设计相应的并行算法,提高匀色处理的效率。
2 自适应分块加权Wallis匀色
2.1 Wallis匀色原理
Wallis匀色法是一种特殊的线性变换法,通过将待处理影像的均值和标准偏差映射到参考影像的均值和标准偏差,实现不同影像间的色彩均衡。线性数学模型如下
| $f(x, y) = g(x, y){r_1} + {r_0}$ | (1) |
式中,
| ${r_0} = b{m_f} + (1 - b - {r_1}){\kern 1pt} {m_g}$ | (2) |
| ${r_1} = \frac{{c{s_f}}}{{c{s_g} + (1 - c){s_f}}}$ | (3) |
式中,
Wallis变换的目的是将处理影像的灰度均值和标准偏差分别被强制到
| $f(x, y) = \left( {g(x, y) - {m_g}} \right) \cdot \left({s_f}/{s_g}\right) + {m_f}$ | (4) |
2.2 自适应分块Wallis匀色法
由式(4)可知,Wallis匀色法是根据影像整体的均值和标准偏差,利用同一个线性关系对影像的每一个像素进行处理。但是影像中的地物复杂多样,颜色信息也各不相同,影像整体的均值和标准偏差无法准确地反映局部地物色彩特征,采用同一个线性关系显然是不合理的。
为了解决上述问题,本文将待处理影像进行分块并统计各块的均值和标准偏差,然后利用双线性插值获取每一个像素对应的线性变换参数,对不同像素采用不同的线性关系进行处理。
2.2.1 影像自适应分块
采用分块策略时,匀色处理的质量受分块数目影响。若分块数目太多,即各影像块太小时,容易过度校正造成地物失真偏色并且计算量较大;若分块数目太少,即各影像块太大时,统计的均值方差不能准确反映地物分布,不能很好地消除影像之间的色彩差异。
为了提高匀色处理的质量,本文利用变异系数(Zhang 等,2017)自适应确定分块大小。变异系数是标准偏差与均值之比,也称离散系数,可以描述影像内地物的丰富程度。当变异系数越大时,影像内地物种类越丰富,对应的分块数目应该越大即影像块越小,才能获得较好地匀色效果。因此,本文采用如下公式计算自适应确定最优分块数目
| $W = r \times w, {\kern 1pt} {\kern 1pt} {\kern 1pt} H = r \times h$ | (5) |
| $r = \frac{{CV}}{{C{V_{{\rm{Ref}}}}}}$ | (6) |
式中,
2.2.2 加权Wallis匀色
在确定影像分块大小后,计算各影像块的灰度均值和标准偏差。为了避免出现“块效应”,在对各影像块处理时,考虑相邻影像块的均值和标准偏差,利用双线性插值计算每一个像素的线性变换参数。具体步骤如下:
(1) 将待处理影像分为互不重叠的
(2) 计算各影像块角点对应的均值和标准偏差,若角点只属于一个影像块,则将该影像块的均值和标准偏差赋给该角点;若角点为多个相邻影像块之间的公共角点,则将所属多个影像块参数的平均值赋给该角点。
(3) 将所属影像块的四个角点按照距离赋予不同的权值相加,即利用双线性插值计算每一个像素对应的均值和标准偏差。
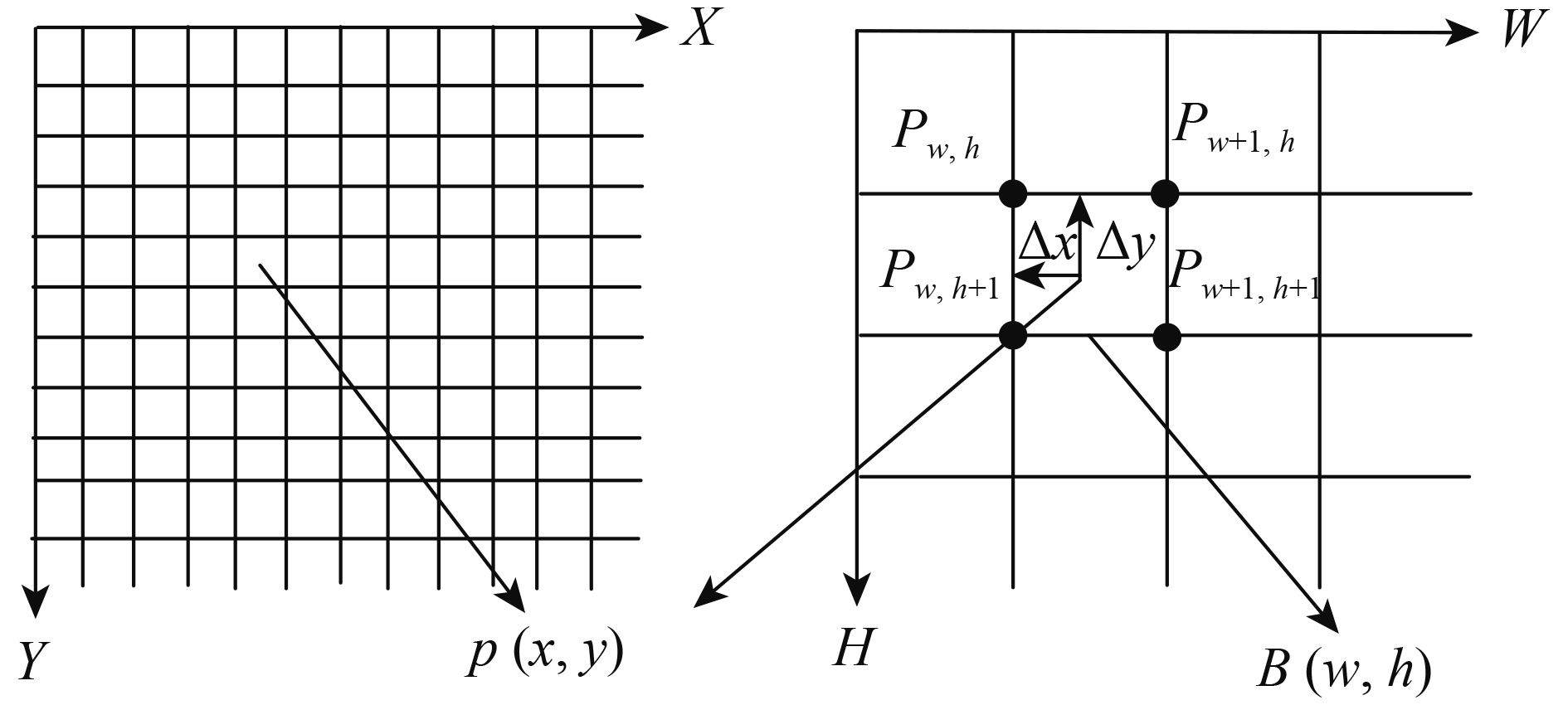
对于影像块
| $\begin{split} m(x, y) = & \left(1 - \frac{{\Delta x}}{X}\right)\left(1 - \frac{{\Delta y}}{{{Y}}}\right)m(w, h) + \\ & \frac{{\Delta x}}{X}\left(1 - \frac{{\Delta y}}{{{Y}}}\right)m(w + 1, h) + \\ & \left(1 - \frac{{\Delta x}}{X}\right)\frac{{\Delta y}}{{{Y}}}m(w, h + 1) + \\ & \frac{{\Delta x\Delta y}}{{XY}}m(w + 1, h + 1) \end{split}$ | (7) |
| $\begin{split} s(x, y) =& \left(1 - \frac{{\Delta x}}{X}\right)\left(1 - \frac{{\Delta y}}{{{Y}}}\right)s(w, h) + \\ & \frac{{\Delta x}}{X}\left(1 - \frac{{\Delta y}}{{{Y}}}\right)s(w + 1, h)+ \\ & \left(1 - \frac{{\Delta x}}{X}\right)\frac{{\Delta y}}{{{Y}}}s(w, h + 1) + \\ & \frac{{\Delta x\Delta y}}{{XY}}s(w + 1, h + 1) \end{split} $ | (8) |
式中,
(4) 根据计算出每个像素的
| $f(x, y) = \left( {g\left(x, y\right) - m\left(x, y\right)} \right) \cdot \left({s_f}/s(x, y)\right) + {m_f}$ | (9) |
利用双线性内插计算每个像素的线性变换参数,可以保证相邻影像块之间的平滑性。此外,利用影像的各角点而非中心点参与计算,可以避免影像边缘的分块出现锯齿现象。
2.3 最短传递路径
在利用Wallis匀色时,如果待处理影像与参考影像的影像内容差距较大,处理结果容易偏色或退化。区域范围内的多幅影像之间的内容往往变化较大,单一的参考影像不适合区域内多幅影像之间的匀色处理。根据相邻影像之间具有相同或相似内容的性质,可采用多次调整参考影像两两处理相邻影像的方法。由于区域范围内多幅影像间的邻近关系复杂,空间分布不规则,影像之间的处理顺序即传递路径直接影响匀色的质量。
为了解决上述问题,本文采用Voronoi图与Dijkstra算法相结合的方法确定匀色处理顺序。根据影像中心点位置构造Voronoi图,对区域范围内的影像有效的组织,便于邻近关系的查询。利用Dijkstra算法计算最短传递路径(李烁 等,2016),对应处理的相邻影像具有较大重叠区域的相邻影像,传递次数较少,可以减少传递过程中的误差(Pan 等,2010),提高区域内影像之间的色彩一致性。具体步骤如下:
(1) 选取初始参考影像。初始参考影像的质量会影响区域内影像的整体质量,本文选取具有最大清晰度的影像作为初始参考影像。清晰度是利用影像的平均梯度来衡量影像在纹理和细节方面表达能力的质量评价参数,其值越大表示影像越清晰,影像质量越高,计算公式为
| $D = \frac{1}{{(M - 1)(N - 1)}}\sum\limits_{x = 1}^{M - 1} {\sum\limits_{y = 1}^{N - 1} {\sqrt {\frac{{\Delta _x^2 + \Delta _y^2}}{2}} } } $ | (10) |
| ${\Delta _x} = f(x + 1, y) - f(x, y)$ | (11) |
| ${\Delta _y} = f(x, y + 1) - f(x, y)$ | (12) |
式中,
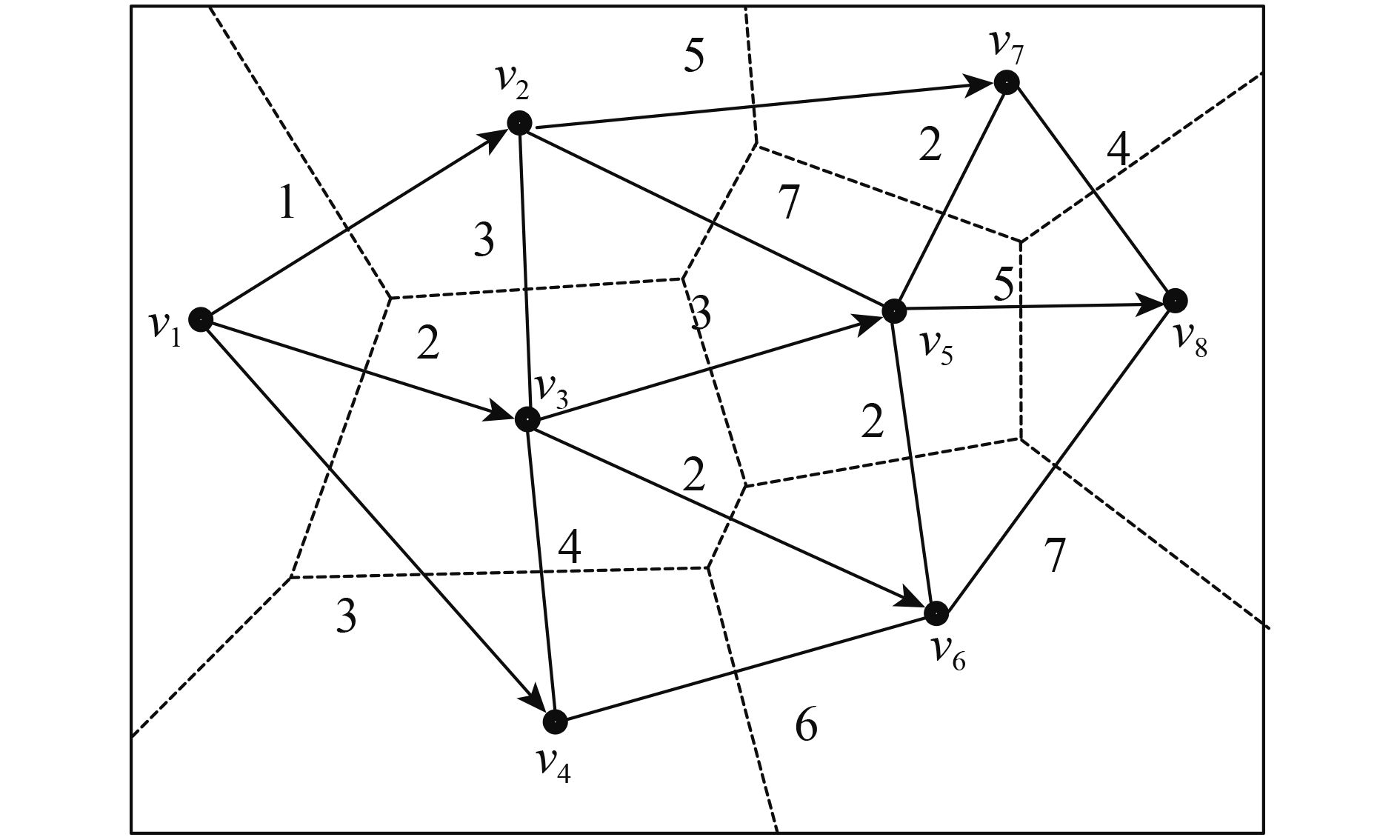
(2) 根据区域内影像的中心点构建Voronoi图,如图2中虚线所示,每个中心点对应一个Voronoi多边形。根据Voronoi多边形之间是否存在公共边,即可判断对应的影像是否相邻。由于Voronoi图是以距离中心点最近为原则划分的,可以合理地判断多度重叠影像之间的邻近关系,只有距离较近的影像才会判断为相邻,对应影像的重叠度较大,可以提高匀色效果。
(3) 利用Dijkstra算法计算初始参考影像中心点到其他影像中心点的最短路径,即图2中
(4) 利用分块Wallis匀色法两两处理。为了避免多次传递导致的色彩偏移,保持区域内影像整体的色彩一致性,利用初始参考影像的均值和标准偏差对新的参考影像的均值和标准进行约束。设影像
| ${m_f} = w{m_{j'}} + (1 - w){m_1}$ | (13) |
| ${s_f} = w{s_{j'}} + (1 - w){s_1}$ | (14) |
式中,
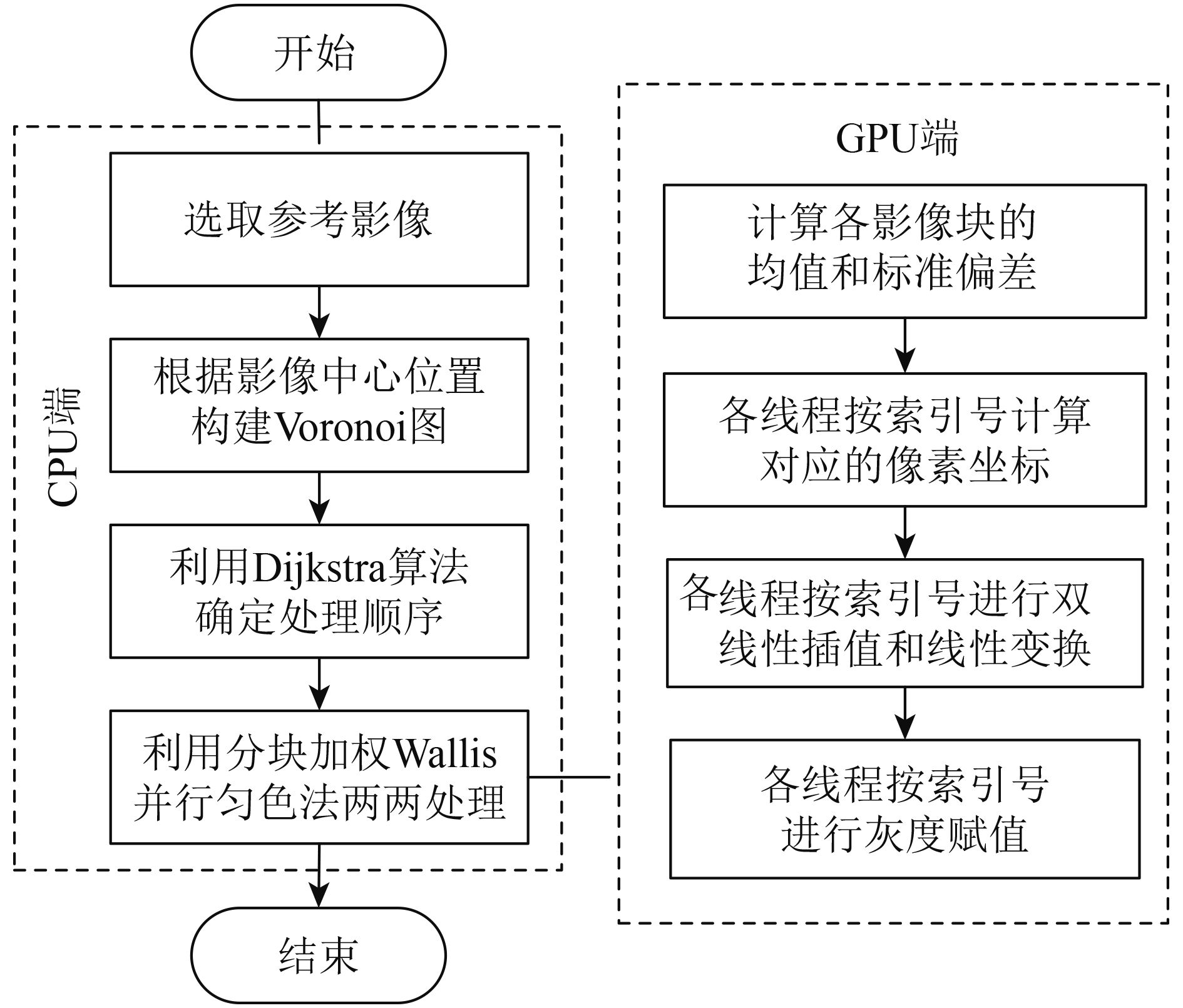
3 基于GPU的并行加速策略
分块Wallis匀色法的主要计算任务包括3个步骤:计算各影像块的均值和标准偏差、逐像素双线性插值和线性变换计算新的灰度值。分析可知:
(1) 双线性插值和线性变换需要逐像素计算,是计算量最大的部分,各像素的计算是相互独立的,非常适合GPU并行处理,一个线程执行一个像素点的计算任务。
(2) 影像块均值和标准偏差的本质均为累计求和计算,耦合度低,不能直接进行并行设计。本文采用归约求和的方式进行优化,利用共享存储器在每一个线程块中进行并行运算。
3.1 并行双线性插值和线性变换
双线性插值和线性变换为重复的密集计算任务,并行化比较简单,可以直接分配给各个线程同时计算,满负荷利用计算资源,可以大幅度缩短计算时间。
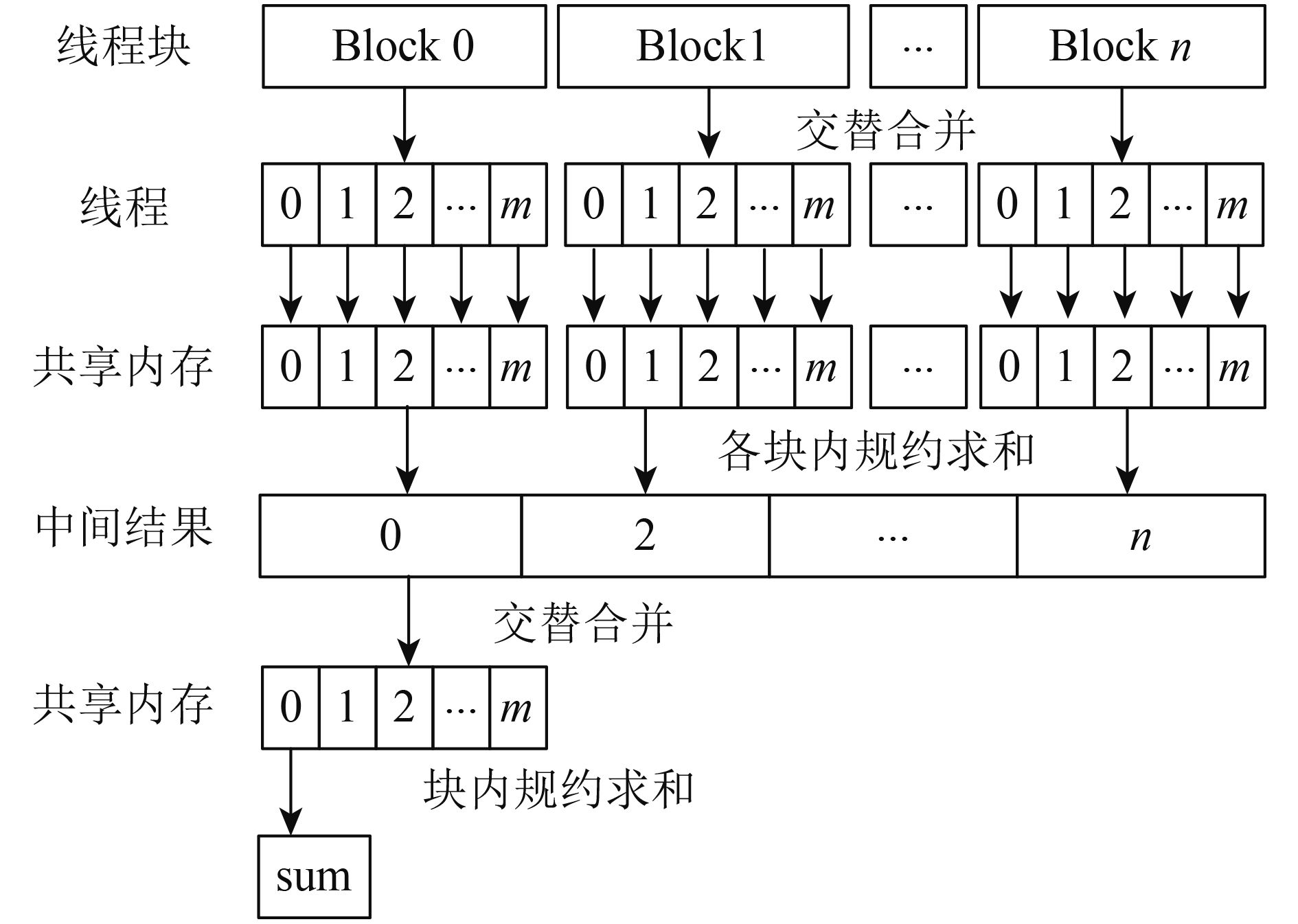
线程是GPU的最小执行单元,具体执行时,按照“线程格网—线程块—线程”的层次结构进行组织,如图3所示。假设待处理影像大小为
3.2 并行归约求和
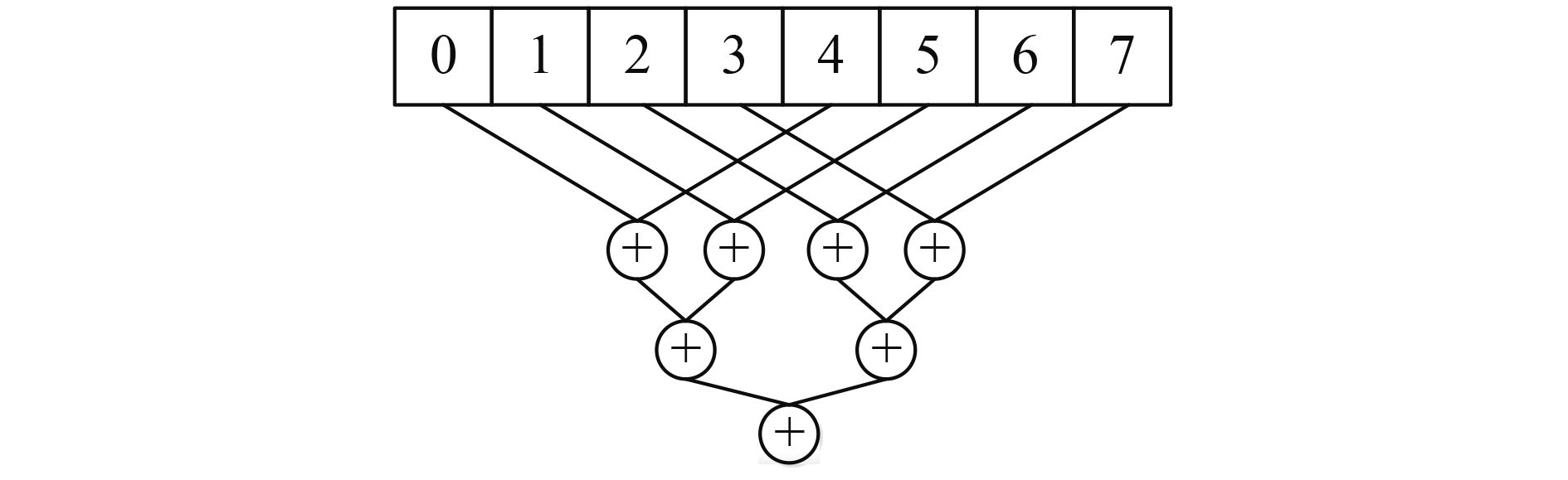
归约求和是一种缩减计算方法,基于对数步长交替两两求和,如图4所示,可以将求和的时间复杂度由
针对GPU的层次结构,本文采用两遍归约求和策略。第一阶段内核执行
(1) 对输入数组落入每个线程中的数据进行求和。每个线程把它得到的累计值写入共享内存,交替因子为
(2) 对共享内存中的值进行对数步长的归约操作。共享内存中后半部分的值被加到前半部分,即
(3) 线程块的和写入全局内存。
利用并行规约求和方法计算影像像素值之和以及像素个数,即可求出影像均值,同理可求标准偏差。
3.3 并行策略优化
为了达到尽可能高的并行加速比,本文结合算法的自身特点,从配置划分、存储器带宽和指令吞吐量等方面进行优化。具体如下:
(1) 合理组织线程。GPU中线程块独立被调度到流式多处理器中,来自同一个线程块的线程在同一个流式多处理器中执行。为了使流式多处理器的性能达到最优,流式多处理器中线程块的数量要小于8、线程数等于1536,线程块中的线程数要小于1024 (Kirk 等,2010)。分析可知,当线程块大小设置为256或512时,流式多处理器的性能最优,可以提高并行算法的运算速度。
(2) 存储器优化。由于常量存储器的访问速度明显优于全局存储器,合理利用常量存储器代替全局存储器可以有效地减少内存流量和内存带宽(闸旋,2013)。双线性插值中的四个角点的均值和标准偏差和线性变换中的参考均值和参考标准偏差数据量不大且每个线程都会读取,将这些参数分配为常量内存,可以大大加速访问数据速度和减少内存带宽,有效地提升程序的运行效率。
针对共享内存中的归约求和,为了减少不必要的线程同步,使用线程束同步优化。由于每个线程块中的线程束是按照锁步方式执行每条指令的,当线程块中的活动线程数低于硬件线程束的大小32时,无须再调用_syncthreads()内置函数。线程束同步可以避免每个Warp中出现分支导致效率低下,减小线程的闲置,提高并行度。
(3) 指令优化。为了使指令吞吐量最大化,在满足精度的前提下,尽可能使用单精度float类型代替双精度double类型,使用硬件函数代替常规函数,用最少的指令完成相同的运算。
4 实验与分析
为了验证本文方法的有效性和高效性,本文设计两组对比实验分别从匀色质量和匀色效率两个方面进行验证。
实验硬件环境为Intel(R) Core(TM) i5-6300HQ CPU 2.30 GHz、8 GB内存、NVIDIA GeForce GTX960M显卡和2 GB显存的便携式计算机。
软件环境为Windows 7操作系统、Microsoft Visual Studio 2010开发环境、C++编程语言和Cuda 7.5并行开发包。
4.1 匀色质量对比实验
为了验证本文方法的匀色质量,分别利用全局Wallis匀色法、商业软件Inpho5.6以及本文方法对两组航空正射影像进行对比实验,结果如图7和图8所示,图9和图10为图8中区域1和区域2的局部放大图。第一组实验数据(数据Ⅰ)为4幅存在明显的色彩不一致和对比度不一致的彩色影像,两两重叠度约为40%,如图7(a)所示。第二组实验数据(数据Ⅱ)为5条航带的234张影像,航向重叠度约为70%—80%,旁向重叠度约为40%—50%,如图8(a)所示。为了直观对比3种方法的匀色质量,图7—图10均为几何镶嵌的结果,未进行镶嵌缝羽化处理。
可以看出,全局Walllis匀色法只能在一定程度上减小影像间的色彩差异,影像间仍存在明显的色调差异,如图7(b)和图9(b)所示,这是由于影像整体的统计信息无法代表影像局部的地物特征。并且采用单一参考影像会产生过增强或偏色现象,如图10(b)所示。Inpho能够较好地消除影像间的色彩差异,使区域影像整体色调一致,但是影像整体对比度下降并且色调与原始影像产生了一定的偏差,如图8(c)所示。同时,当影像的色调与区域整体色调差异较大时,Inpho的处理结果不理想,如图7(c)中右下角影像。相比而言,本文方法对两组影像的处理结果都比较理想,在使区域影像整体色彩和对比度一致的同时消除或减小了相邻影像重叠区域的局部差异,并且没有产生偏色现象。同时,本文自动选取了清晰度最大的影像作为参考影像,区域内影像整体清晰度较高,具有较好的目视效果。
为了对匀光影像进行定量评价,统计区域范围内相邻影像重叠区域的灰度均值之差的平均值
| $\overline {\Delta m} = \frac{{\sum {\left| {{m_{ij}} - {m_{ji}}} \right|} }}{n}, (i \ne j)$ | (15) |
| $\overline {\Delta s} = \frac{{\sum {\left| {{s_{ij}} - {s_{ji}}} \right|} }}{n}, (i \ne j)$ | (16) |
式中,
由表1可知,数据Ⅰ的原始影像的
由上可知,本文方法在目视效果评价和定量评价两方面均优于全局Wallis匀色法和Inpho,可以同时有效地消除影像间的色彩差异和对比度差异,体现了明显的优势。
表 1 数据Ⅰ匀色结果的定量评价
Table 1 The quantitative evaluation of the results with different methods of dataset imageⅠ
| 指标 | 波段 | 原始影像 | 全局Wallis | Inpho | 本文方法 |
|
|
R | 25.20 | 16.26 | 1.99 | 1.42 |
| G | 28.80 | 16.23 | 1.68 | 1.49 | |
| B | 28.75 | 15.74 | 1.58 | 1.17 | |
|
|
R | 6.19 | 4.55 | 5.81 | 1.11 |
| G | 5.36 | 3.94 | 6.88 | 1.27 | |
| B | 3.92 | 2.53 | 6.61 | 1.07 |
表 2 数据Ⅱ匀色结果的定量评价
Table 2 The quantitative evaluation of the results with different methods of dataset Ⅱ
| 指标 | 波段 | 原始影像 | 全局Wallis | Inpho | 本文方法 |
|
|
R | 6.64 | 7.81 | 2.09 | 1.76 |
| G | 6.43 | 7.21 | 1.81 | 1.60 | |
| B | 6.03 | 6.64 | 1.82 | 1.56 | |
|
|
R | 2.73 | 2.83 | 3.50 | 1.00 |
| G | 2.54 | 2.78 | 3.74 | 0.93 | |
| B | 2.49 | 2.68 | 3.37 | 1.02 |
4.2 匀色效率对比实验
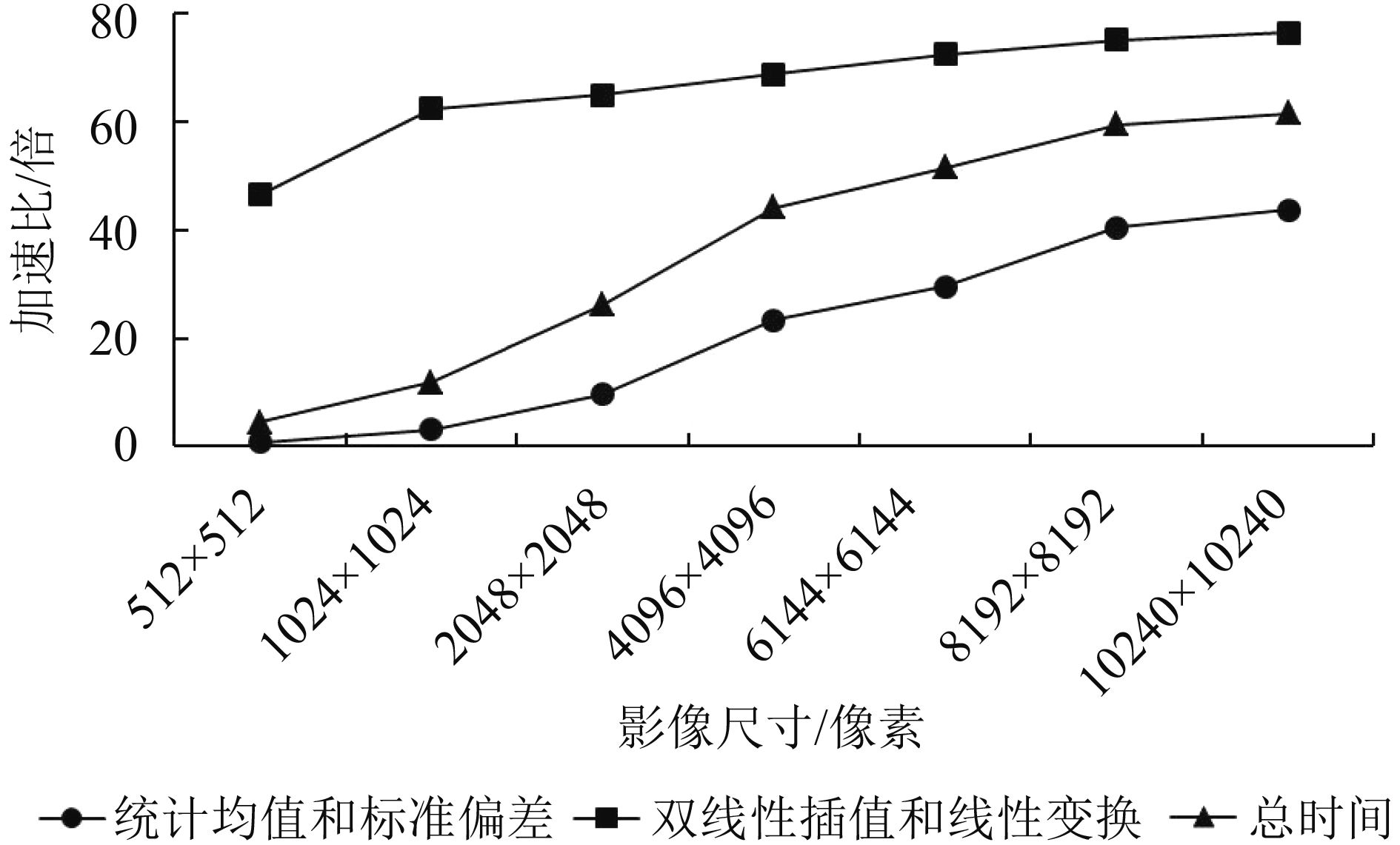
为了验证本文并行加速策略的有效性,分别统计CPU串行算法和GPU并行算法处理不同尺寸影像的运行时间和加速比,如表3和图11所示。实验影像为数据Ⅱ的缩放影像,加速比为CPU串行算法运行时间与GPU并行算法运行时间的比值。统计的运行时间不包括硬盘与内存之间数据传输消耗的时间,统计均值和标准偏差的运行时间为统计影像整体均值和标准偏差以及统计分块均值和标准偏差的运行时间之和,分块数目均设置为8×8。
表 3 不同尺寸影像CPU与GPU的运行时间对比
Table 3 Comparison of runtime in CPU and GPU with different image size
| 影像大小 | CPU处理时间/s | GPU处理时间/s | 加速比/倍 | ||||||||
| 统计均值
标准偏差 |
双线性插值和
线性变换 |
总时间 | 统计均值
标准偏差 |
双线性插值和
线性变换 |
总时间 | 统计均值
标准偏差 |
双线性插值和
线性变换 |
总时间 | |||
| 512×512 | 0.016 | 0.093 | 0.109 | 0.022 | 0.002 | 0.024 | 0.73 | 46.50 | 4.54 | ||
| 1024×1024 | 0.093 | 0.312 | 0.405 | 0.029 | 0.005 | 0.034 | 3.21 | 62.40 | 11.91 | ||
| 2048×2048 | 0.436 | 1.233 | 1.669 | 0.045 | 0.019 | 0.064 | 9.69 | 64.89 | 26.08 | ||
| 4096×4096 | 1.966 | 4.945 | 6.911 | 0.084 | 0.072 | 0.157 | 23.40 | 68.68 | 44.02 | ||
| 6144×6144 | 4.373 | 11.228 | 15.601 | 0.148 | 0.155 | 0.303 | 29.54 | 72.43 | 51.48 | ||
| 8192×8192 | 9.522 | 21.669 | 31.191 | 0.236 | 0.289 | 0.525 | 40.35 | 74.98 | 59.41 | ||
| 10240×10240 | 14.642 | 30.761 | 45.403 | 0.336 | 0.403 | 0.739 | 43.58 | 76.33 | 61.44 | ||
(1) 当影像尺寸较小如512×512时,统计影像均值和标准偏差的串行算法比并行算法快。这是由于统计每一个影像块的均值和标准偏差时都存在内存与显存之间的数据传输,而GPU并行的加速时间小于数据传输消耗的时间。但是,双线性插值和线性变换的并行加速效果较好,因此,整个过程GPU并行算法的运行时间仍优于CPU串行算法的运行时间。
(2) 随着影像尺寸的增加,GPU的计算资源得到更充分的利用,GPU并行算法的优势越来越明显,加速比越来越大。
(3) 当影像尺寸增加到一定程度时,GPU并行算法的加速比趋于稳定不再明显增加,最高加速比可以达到60倍以上。
5 结 论
针对区域范围内多幅影像之间的色彩不一致问题,本文提出一种基于GPU的自适应分块加权Wallis并行匀色方法。采用分块策略和双线性加权方法对Wallis变换进行改进,对不同像素采用不同的线性关系进行处理,可以在局部更好地消除相邻影像间的色彩差异和对比度差异。同时,本文采用最短传递路径确定匀色处理顺序,可以有效地保证区域内影像整体的色彩一致性。此外,本文结合GPU并行技术,设计了并行加速策略,大幅度提高了匀色处理的效率。与CPU串行算法相比,最高加速比可以达到60倍以上。本文方法有效地提高了匀色处理的质量和效率,能够降低影像镶嵌的难度,提高影像镶嵌的质量,同时可以满足海量遥感影像快速处理和应急响应的需求。
但是,在试验中也发现了本文方法的不足,本文未考虑遥感影像中的特殊区域(如水域和阴影等),下一步应当对参与计算的像素进行检测和筛选,进一步提高影像匀色的质量。另外,随着多核GPU的出现,下一步可研究如何利用多核GPU实现影像匀色,进一步提高算法的效率。
参考文献(References)
-
Canty M J and Nielsen A A. 2008. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sensing of Environment, 112 (3): 1025–1036. [DOI: 10.1016/j.rse.2007.07.013]
-
Chang F Z, Zhao Y D and Liu S L. 2016. CUDA parallel algorithm for CVA change detection of remote sensing imagery. Journal of Remote Sensing, 20 (1): 114–128. [DOI: 10.11834/jrs.20164311] ( 常方正, 赵银娣, 刘善磊. 2016. 遥感影像CVA变化检测的CUDA并行算法设计. 遥感学报, 20 (1): 114–128. [DOI: 10.11834/jrs.20164311] )
-
Chen C, Chen Z J, Li M C, Liu Y X, Cheng L and Ren Y B. 2014. Parallel relative radiometric normalisation for remote sensing image mosaics. Computers and Geosciences, 73 : 28–36. [DOI: 10.1016/j.cageo.2014.08.007]
-
Chen J L, Liu J L, Ye J H and Chen Y S. 2007. Luminance and chrominance correction for multi-view video using overlapped local histogram matching. Journal of Image and Graphics, 12 (11): 1992–1999. [DOI: 10.3969/j.issn.1006-8961.2007.11.008] ( 陈建乐, 刘济林, 叶建洪, 陈妤姗. 2007. 多视点视频中基于局部直方图匹配的亮度和色差校正. 中国图象图形学报, 12 (11): 1992–1999. [DOI: 10.3969/j.issn.1006-8961.2007.11.008] )
-
Fang L Y, Wang M and Li D R. 2013. A CPU-GPU co-processing orthographic rectification approach for optical satellite imagery. Acta Geodaetica et Cartographica Sinica, 42 (5): 668–675. ( 方留杨, 王密, 李德仁. 2013. CPU和GPU协同处理的光学卫星遥感影像正射校正方法. 测绘学报, 42 (5): 668–675. )
-
Helmer E H and Ruefenacht B. 2005. Cloud-free satellite image mosaics with regression trees and histogram matching. Photogrammetric Engineering and Remote Sensing, 71 (9): 1079–1089.
-
Li S, Wang H, Wang L Y, Cheng T and Wang C Y. 2016. Color consistency processing of orthoimages based on the minimum transfer path. Journal of Geomatics Science and Technology, 33 (6): 593–598. [DOI: 10.3969/j.issn.1673-6338.2016.06.009] ( 李烁, 王慧, 王利勇, 程挺, 王重阳. 2016. 最小传递路径的正射影像色彩一致性处理方法. 测绘科学技术学报, 33 (6): 593–598. [DOI: 10.3969/j.issn.1673-6338.2016.06.009] )
-
Li Z J. 2005. Theory and Practice on Tone Reproduction of Color Photos. Wuhan: Wuhan University (李治江. 2005. 彩色影像色调重建的理论与实践. 武汉: 武汉大学)
-
Lin C H, Lin B Y, Lee K Y and Chen Y C. 2015. Radiometric normalization and cloud detection of optical satellite images using invariant pixels. ISPRS Journal of Photogrammetry and Remote Sensing, 106 : 107–117. [DOI: 10.1016/j.isprsjprs.2015.05.003]
-
Pan J, Wang M, Li D R and Li J L. 2010. A network-based radiometric equalization approach for digital aerial orthoimages. IEEE Geoscience and Remote Sensing Letters, 7 (2): 401–405. [DOI: 10.1109/LGRS.2009.2037442]
-
Sun M W. 2009. Research on Key Technology of Automatical and Fast DOM Generation. Wuhan: Wuhan University (孙明伟. 2009. 正射影像全自动快速制作关键技术研究. 武汉: 武汉大学)
-
Wang M and Pan J. 2006. A new color balance method for large-scale seamless image database. Remote Sensing for Land and Resources, 18 (4): 10–13. [DOI: 10.6046/gtzyyg.2006.04.03] ( 王密, 潘俊. 2006. 面向无缝影像数据库应用的一种新的光学遥感影像色彩平衡方法. 国土资源遥感, 18 (4): 10–13. [DOI: 10.6046/gtzyyg.2006.04.03] )
-
Wang Z Y, Ma H C and Ming Y. 2014. GPGPU-based parallel algorithm for full waveform decomposition. Journal of Remote Sensing, 18 (6): 1217–1222. [DOI: 10.11834/jrs.20144027] ( 王宗跃, 马洪超, 明洋. 2014. 基于GPGPU的全波形并行分解算法. 遥感学报, 18 (6): 1217–1222. [DOI: 10.11834/jrs.20144027] )
-
Wu W, Luo J C, Li J L, Yang H P and Shen Z F. 2012. Support vector regression color normalization method for image mosaic. Journal of Image and Graphics, 17 (12): 1561–1567. [DOI: 10.11834/jig.20121215] ( 吴炜, 骆剑承, 李均力, 杨海平, 沈占锋. 2012. 面向遥感影像镶嵌的SVR色彩一致性处理. 中国图象图形学报, 17 (12): 1561–1567. [DOI: 10.11834/jig.20121215] )
-
Wu W, Shen Z F, Li J L, Yang H P and Luo J C. 2013. Ridge of joint probability density based color normalization method for image mosaic. Acta Geodaetica et Cartographica Sinica, 42 (2): 247–252. ( 吴炜, 沈占锋, 李均力, 杨海平, 骆剑承. 2013. 联合概率密度脊提取的影像镶嵌色彩一致性处理方法. 测绘学报, 42 (2): 247–252. )
-
Zha X. 2013. Research on Parallel Processing Technologies of Remote Sensing Data Based on CPU+GPU under Single-Computer. Zhengzhou: Information Engineering University (闸旋. 2013. CPU+GPU单机异构环境下遥感数据并行处理技术研究. 郑州: 解放军信息工程大学)
-
Zhang L P, Wu C and Du B. 2014. Automatic radiometric normalization for multitemporal remote sensing imagery with iterative slow feature analysis. IEEE Transactions on Geoscience and Remote Sensing, 52 (10): 6141–6155. [DOI: 10.1109/TGRS.2013.2295263]
-
Zhang P Q, Yu X C, Liu Z, Li J S and Wan G. 2006. A study on relative radiometric correction of multitemporal remote sensing images. Journal of Remote Sensing, 10 (3): 339–344. [DOI: 10.3321/j.issn:1007-4619.2006.03.009] ( 张鹏强, 余旭初, 刘智, 李建胜, 万刚. 2006. 多时相遥感图像相对辐射校正. 遥感学报, 10 (3): 339–344. [DOI: 10.3321/j.issn:1007-4619.2006.03.009] )
-
Zhang Y J, Yu L, Sun M W and Zhu X Y. 2017. A mixed radiometric normalization method for mosaicking of high-resolution satellite imagery. IEEE Transactions on Geoscience and Remote Sensing, 55 (5): 2792–2984. [DOI: 10.1109/TGRS.2017.2657582]
-
Zhou X G. 2015. Multiple auto-adapting color balancing for large number of images. International Archives of the Photogrammetry Remote Sensing and Spatial Information Sciences, XL-7/w3: 735-742