出版日期: 2019-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20198018
2019 | Volumn23 | Number 3
上一篇 | 下一篇

技术方法

GNSS-R DDM波形仿真的时延与多普勒间隔研究

夏俊明^1,2 , 吴学睿^3,4 , 白伟华^1,2,5 , 孙越强^1,2,5 , 骆黎明^1,2,5 , 杜起飞^1,2 , 王先毅^1,2 , 柳聪亮^1,2 , 孟祥广^1,2 , 赵丹阳^1,2 , 王迎强⁶

1. 中国科学院国家空间科学中心空间环境探测研究室，北京 100190

2. 北京市天基空间环境探测重点实验室，北京 100190

3. 中国科学院上海天文台，上海 200030

4. 中国科学院行星科学重点实验室，上海 200030

5. 中国科学院大学天文学院，北京 100190

6. 解放军理工大学气象学院，南京 211101

收稿日期: 2018-01-23; 预印本: 2018-04-24

基金项目: 国家重点研发计划(编号：2017YFB0502800，2017YFB0502802)；国家自然科学基金(编号：41606206，41405039，41405040，41505030，41501384)

第一作者简介: 夏俊明，1986年生，男，副研究员，研究方向为GNSS-R的理论和应用。E-mail：xiajunming10@126.com

通信作者简介: 白伟华，1982年生，男，研究员，研究方向为GNSS遥感技术。E-mail：bjbwh@163.com

摘要

DDM波形是GNSS-R技术用于反演地球物理参量的基本观测量，其仿真结果的可靠性直接影响GNSS-R的理论研究及项目工程参数设计。利用GREEPS仿真软件分析了时延间隔与多普勒间隔对DDM波形仿真结果可靠性的影响，得到了用于获取可靠DDM仿真波形的时延与多普勒间隔参数。研究表明，时延和多普勒间隔越小，DDM仿真波形与理论波形吻合度越高；当时延间隔取1/16个GPS L1 C/A码元、多普勒间隔取50 Hz时，DDM仿真波形与理论波形几乎完全吻合，二者的相关系数大于0.99；时延间隔对DDM仿真波形峰值位置的影响远大于对峰值信噪比的影响；而多普勒间隔对DDM仿真波形峰值位置与信噪比的影响相当。

关键词

GNSS-R, 时延—多普勒波形, 时延间隔, 多普勒间隔, GREEPS

Research on the effects of delay and Doppler intervals on GNSS-R DDM simulation

XIA Junming^1,2 , WU Xuerui^3,4 , BAI Weihua^1,2,5 , SUN Yueqiang^1,2,5 , LUO Liming^1,2,5 , DU Qifei^1,2 , WANG Xianyi^1,2 , LIU Congliang^1,2 , MENG Xiangguang^1,2 , ZHAO Danyang^1,2 , WANG Yingqiang⁶

1.National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China

2.Beijing Key Laboratory of Space Environment Exploration, Beijing 100190, China

3.Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China

4.Key laboratory of Planetary Sciences, Chinese Academy of Sciences, Shanghai 200030, China

5.School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 100190, China

6.College of Meteorology and Oceanology, National University of Defense Technology, Nanjing 211101, China

Abstract

Global Navigation Satellite System Reflectometry (GNSS-R) uses GNSS signals reflected by the Earth’s surface to detect the Earth surface parameters, including sea surface wind field, sea surface height, soil moisture, sea ice range, and snow depth. GNSS-R is a new Earth remote sensing technology, and it has been a research focus in recent years. Delay-Doppler Mapping (DDM) is a significant GNSS-R observation for retrieving geophysical parameters. The reliability of GNSS-R DDM simulation results directly affects GNSS-R theoretical research and satellite mission engineering parametric design. In this thesis, the effects of delay and Doppler intervals on a simulated DDM is investigated, and the suitable parameters for both intervals is determined to generate a reliable DDM simulation result. GREEPS, which was a GNSS-R simulator based on Z-V models and was developed by the National Space Science Center of the Chinese Academy of Sciences, is currently used to simulate DDM waveforms with different delay and Doppler intervals. To evaluate the accuracy of the simulated DDM waveforms, the 1D delay mapping with 0 Hz Doppler and the peak’s signal-to-noise ratio (SNR) and position of the simulated DDM are compared with theoretical ones. The results shows that the smaller the delay and Doppler intervals are, the higher the correlation coefficient of the simulated DDM waveform and the theoretical waveform will be. When the delay interval is less than 1/16 GPS L1 C/A code chips, the correlation coefficient of the simulated DDM waveform and the theoretical waveform is greater than 0.99. The relative deviation of the peak SNR of the simulated DDM waveform is approximately 0.1% when the delay interval is set to be 1/16 GPS L1 C/A code chips. However, the relative deviation of the peak position of the simulated DDM waveform is extremely high. Even if the delay interval is set to be 1/64 GPS L1 C/A code chips, the relative deviation of the peak position of the simulated DDM is just 2.3%. When the Doppler interval is less than 200 Hz, the correlation coefficient of the simulated DDM waveform and the theoretical waveform is close to 1. When the Doppler interval is less than 50 Hz, the relative deviation of the peak SNR and the peak position is less than 0.1%. It is can be concluded that the smaller the delay and Doppler intervals are, the higher the coincidence degree of the simulated DDM and the theoretical DDM will be. When the delay interval and the Doppler interval are set to be 1/16 GPS L1 C/A code chips and 50 Hz, respectively, the simulated waveforms and the theoretical waveforms highly coincide with one another. The correlation coefficient is more than 0.99, and the relative deviation of the peak SNR of DDM is less than 0.1%. The effect of the delay interval on the peak’s position of DDM is greater than that of the Doppler interval. The relative deviation of the position of the peak SNR is greater than 2% even if the delay interval is set to 1/64 GPS L1 C/A code chips.

Key words

GNSS-R, delay-Doppler mapping, delay interval, Doppler interval, GREEPS

1 引　言

GNSS反射信号遥感技术GNSS-R(Global Navigation Satellite System Reflectometry)是一种新型对地观测技术，利用经地面反射的GNSS信号对海洋、陆地、冰冻圈等地表参数进行遥感探测，在海面风场、海面高度、土壤湿度、海冰范围及雪深测量等领域具有重要应用前景，是近年来的研究热点(Zavorotny 等，2014)。2003年英国国家空间中心发射了第一颗搭载了GPS反射信号接收机装置的UK-DMC灾难探测卫星，成功地验证了在低地球轨道LEO(Low Earth Orbit)卫星高度上，可以接收到来自海洋、冰雪区域甚至陆地的GPS反射信号(Gleason 等，2005；Clarizia 等，2009)，但是该星提供的GPS反射数据非常少。继UK-DMC卫星之后，2014年英国萨利卫星公司成功发射了一颗名为TechDemonsat-1的技术验证卫星，与UK-DMC卫星携带的GNSS-R软件接收机不同，该星携带的是可以在星上实时生成时延—多普勒相关功率波形DDM(Delay-Doppler Mapping)的GNSS-R硬件接收机，迄今为止该星已经获得了大量的DDM波形数据，研究人员利用这些实测数据，对海面风速的反演精度达到了2.2 m/s (Foti 等，2015；Soisuvarn 等，2016)。2016年12月美国宇航局NASA成功发射了一个由轨道倾角为35°的8颗小卫星组成的名为CYGNSS的卫星星座，该星座采用了GNSS-R技术，通过加强对热带气旋中心的观测，提高人们对热带气旋的认识和对热带气旋强度的预报能力(Ruf 等，2013；Morris和Ruf，2017；Warnock 等，2017；Saïd 等，2017)。由中国研制的国际上首个GNSS-R与GNSS掩星兼容的天基载荷GNOS II预计将于2020年随风云三号气象卫星的E星发射升空，该载荷由中国科学院国家空间科学中心研制，GNOS II的GNSS-R功能兼容了北斗与GPS导航系统，未来将在国际上推动星载北斗导航卫星反射信号遥感技术的应用(Sun 等，2017)。GNSS-R DDM波形仿真软件是开展GNSS-R项目工程参数设计及物理参数反演的重要工具(Addabbo 等，2017；Marchan-Hernandez 等，2009)。目前，国内外的研究团队已经开发出了多个此类仿真软件，如CYGNSS E2ES软件(O’Brien和Johnson，2017)，P2EPS仿真软件(Park 等，2017)，GREEPS仿真软件(Bai 等，2016)和SAVERS仿真软件(Pierdicca 等，2014)等。对于这些仿真软件，时延间隔和多普勒间隔是DDM波形仿真过程中的两个重要的输入参量，理论上，时延间隔与多普勒间隔设置的越小，所模拟出来的DDM越精确，然而，当间隔变小之后，计算机仿真所需要的时间也会大幅增加。因此，为了既能保障DDM波形的仿真精度又能尽量降低计算机仿真所需的时间，仿真软件的时延间隔与多普勒间隔需设置为合适的参数值。然而，目前，国内外关于这一问题的相关研究报道相对较少，本文基于中科院国家空间科学中心开发的GREEPS仿真软件(Bai 等，2016)，研究了DDM波形仿真过程中的时延和多普勒间隔的参数设置问题。

2 理论基础与仿真方法

2.1 理论基础

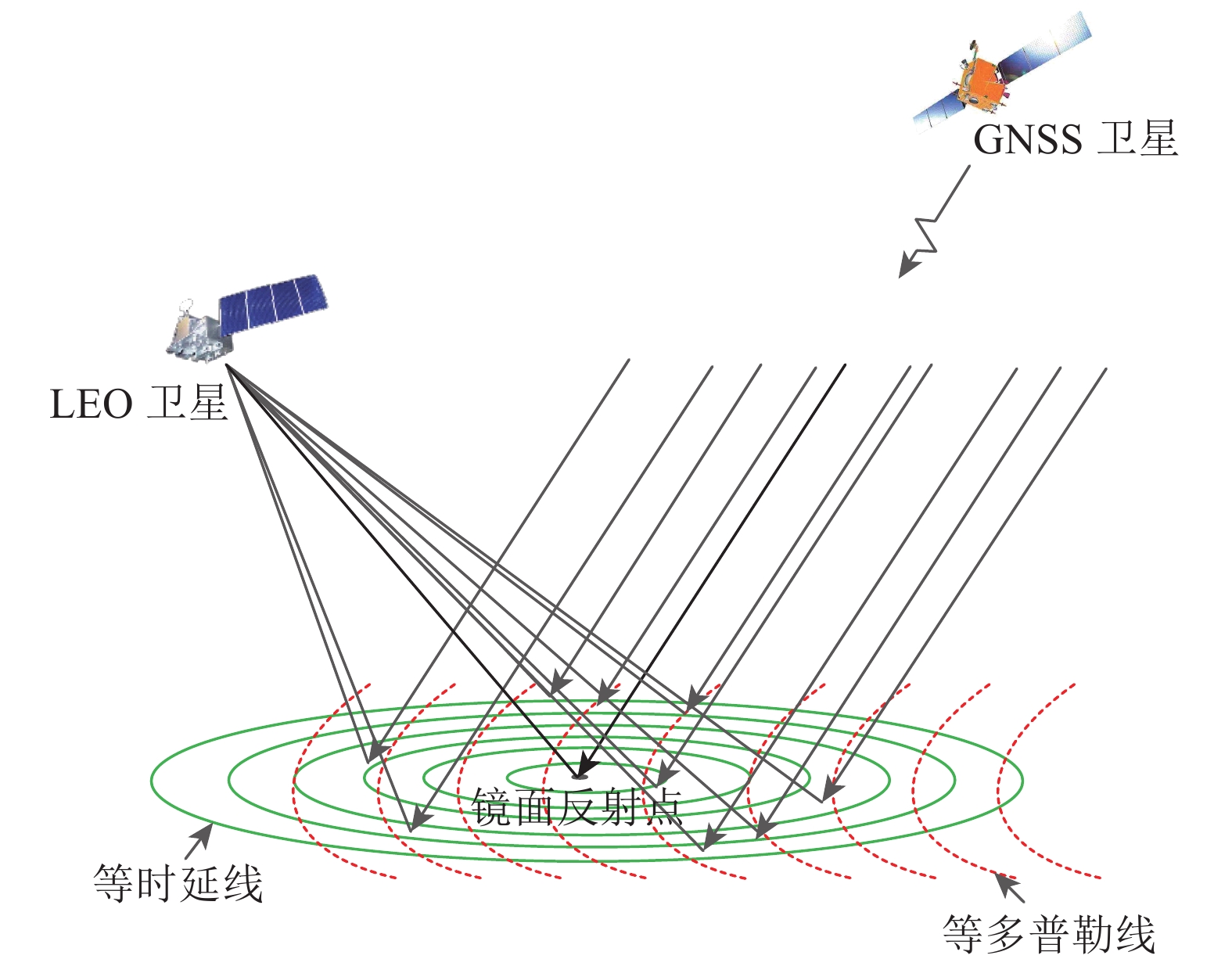
GNSS-R对地遥感的工作模式属于双基地雷达模式，GNSS卫星、地面与LEO卫星接收机一起构成的双基雷达几何模型如图1所示。由于地面的反射面通常是粗糙的，因此，图1中LEO卫星接收到的GNSS地面反射信号，其本质上是经镜面反射点周围地面大片区域反射后的一系列多径信号，这些多径信号由于传播路径不同及接收机平台的运动，而具有不同的时延和多普勒值。因此，利用一系列的等时延—等多普勒线可以将反射面划分成大量小反射面元，这些等时延—等多普勒线的时延和多普勒间隔的大小决定了这些划分得到的小反射面元的大小。图2是在LEO卫星高度为830 km，GPS卫星高度角为60°条件下，在同一反射区域上，利用不同时延间隔的等时延—等多普勒线划分后的反射区域，图2中多普勒间隔固定为500 Hz，图2(a)的时延间隔大小为1/4个GPS L1 C/A码元，图2(b)的时延间隔大小为1/8个GPS L1 C/A码元，图2(c)的时延间隔为1/16个GPS L1 C/A码元。由图2可知，时延间隔越小，由等时延—等多普勒线分割后的反射面小面元的面积越小。多普勒间隔大小对被分割后的小面元面积大小的影响与时延间隔大小的影响同理。

图 1 GNSS-R双基雷达几何模型

Fig. 1 GNSS-R Bistatic radar geometry model

图 2 不同时延间隔的等时延—等多普勒线

Fig. 2 Isochronous delay-Doppler lines with different delay intervals

GNSS反射信号遥感技术的理论基础是Z-V模型(Zavorotny和Voronovich，2000)，该模型又称为GNSS反射信号的双基雷达方程，它给出了描述GNSS多径反射信号与接收机产生的本地伪随机码相关后的相关功率的解析式

$\left\langle{\left| {Y\left( {\tau , f} \right)} \right|^2}\right\rangle = \frac{{{{\textit{λ}} ^2}T_i^2}}{{{{\left( {4{\text{π}} } \right)}^3}}}{P_t}{G_t}\mathop \int\!\!\!\int \nolimits^ \frac{{{G_r}{\varLambda ^2}\left( \tau \right){S^2}\left( f \right)}}{{R_t^2R_r^2}}{\sigma _0}{\rm{d}}s$

式中，等式左侧表示GNSS多径反射信号中时延大小为τ、多普勒频率为f的反射信号分量与接收机本地伪随机码之间的相关功率。等式右侧的T_i是接收机的相干积分时间；λ是GNSS信号的载波波长；P_t为GNSS卫星发射功率，G_t为GNSS卫星发射天线的增益，P_tG_t表示GNSS卫星的有效全向辐射功率EIRP(Effective Isotropic Radiated Power)，该值通常在GNSS镜面反射点周围积分的海面区域内变化不大，可近似为常数值；G_r为GNSS反射信号接收天线的增益，对于天基GNSS-R，该值通常在GNSS镜面反射点周围区域内也变化不大，也可近似为常数值；Λ²(τ)S²( f )是GNSS-R双基雷达的模糊度函数WAF(Woodward Ambiguity Function)，描述了相关功率对多普勒频率f和时延τ的选择性；R_t和R_r分别表示GNSS卫星和反射信号接收机到反射面元ds的空间距离；σ₀表示反射面的归一化双基雷达散射截面，在基尔霍夫—几何光学近似条件下，海面的σ₀可表示为

${\sigma _0} = {\Re ^2}\left( {S, T} \right){\text{π}}P\left( { - \frac{{{q_ \bot }}}{{{q_{\rm{z}}}}}} \right)\frac{{{q^4}}}{{q_{\rm{z}}^4}}$

式中， $\Re$ 是GNSS信号在海面的菲涅尔反射系数，S，T分别为海面海水的盐度和温度，对于GNSS信号，这两个因素对 $\Re$ 的影响通常可以忽略不计(Cardellach，2002)；q是一个用于描述GNSS卫星、反射面元与LEO卫星三者之间的反射几何关系的向量，通常称为散射向量，式中的q，q_z和q_⊥分别为散射向量q的模、q的法向分量的模和q的水平分量的模；P是海面均方倾斜概率密度函数，可用海浪谱模型来计算，本文仿真过程中采用的是Elfouhaily二维海浪谱模型(Elfouhaily 等，1997)。P在一定程度上反映了海面的粗糙程度与海面风场密切相关，从而也决定了归一化双基雷达散射截面σ₀与海面风场的依赖关系，这是GNSS-R技术可用于反演海面风场的理论基础。

2.2 仿真方法

为了研究时延与多普勒间隔对DDM波形仿真结果的影响，以天基GNSS海面反射信号的应用为背景，利用中国科学院国家空间中心开发的GREEPS仿真软件，首先，在固定的多普勒间隔条件下，评估了不同的时延间隔对DDM波形仿真结果的影响。然后，在固定的时延间隔条件下，评估了多普勒间隔对DDM波形仿真结果的影响。GREEPS仿真软件的理论基础是式(1)所示的GNSS-R双基雷达方程，仿真中涉及到的主要输入参数，如表1所示。

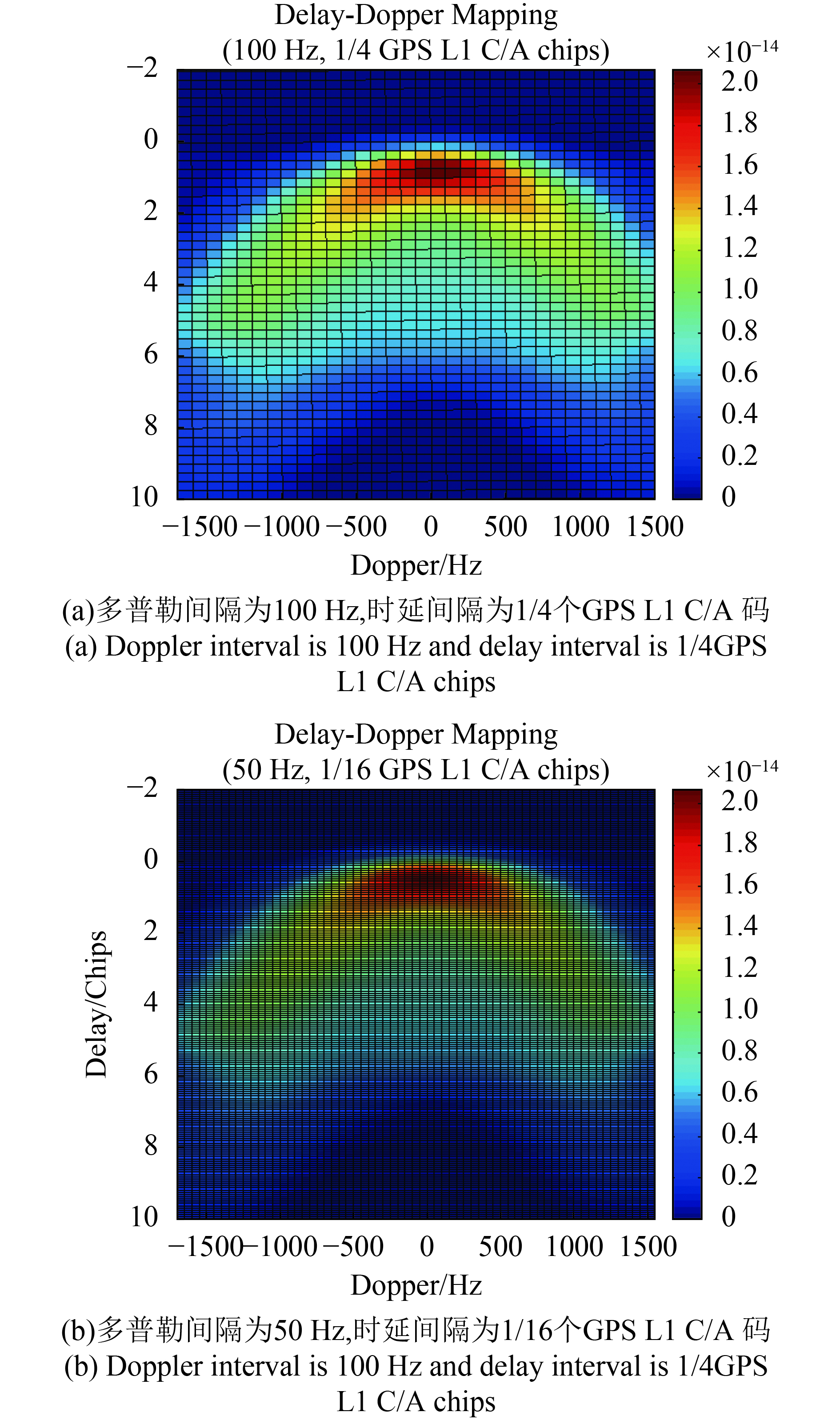
在上述条件下，利用GREEPS仿真软件仿真的DDM波形如图3所示，其中图3(a)仿真时的时延和多普勒间隔为100 Hz，1/4个GPS L1C/A码；图3(b)仿真时的时延和多普勒间隔为50 Hz，1/16个GPS L1C/A码。对比图3(a)与图3(b)可知，当时延与多普勒间隔变小后，仿真得到的DDM波形变得更加精细。

表 1 主要的输入参数表
Table 1 The main input parameter list for simulation

下载CSV

参数	计量单位	数值[范围]
GNSS系统及频率	—	GPS L1
GNSS卫星速度	km/s	3.87
GNSS卫星高度	km	20200
GNSS卫星高度角	°	60
LEO卫星高度	km	830
LEO卫星速度	km/s	7.44 km/s
海面积分区域范围	km²	100×100
海水温度	℃	30
海水盐度	psu	35
海水相对磁导率	1	1
地球半径	km	6378.137
海面风速	m/s	10
海面风向	°	0
接收天线增益	dB	14.78
GPS卫星EIRP	dBm	58.81
相干积分时间	ms	1
信号损耗	dB	2.78
噪声功率	dBm	–172.69

图 3 不同时延、多普勒间隔条件下仿真得到DDM波形

Fig. 3 The simulated DDMs with different delay and Doppler intervals

GNSS-R DDM波形仿真结果可靠性的评估，主要依据的是GNSS-R技术在实际应用中通常用到的两个主要观测量：

(1) DDM波形的0 Hz多普勒频率所对应的一维时延波形DM(Delay-Mapping)；

(2) DDM波形的峰值。在利用DDM波形的峰值评估仿真结果可靠性的过程中，既评估了DDM波形峰值信噪比SNR(Signal Noise Ratio)的可靠性，又评估了DDM波形峰值的位置(即DDM波形峰值对应的时延)的可靠性。

3 仿真结果与分析

3.1 时延间隔影响的仿真结果与分析

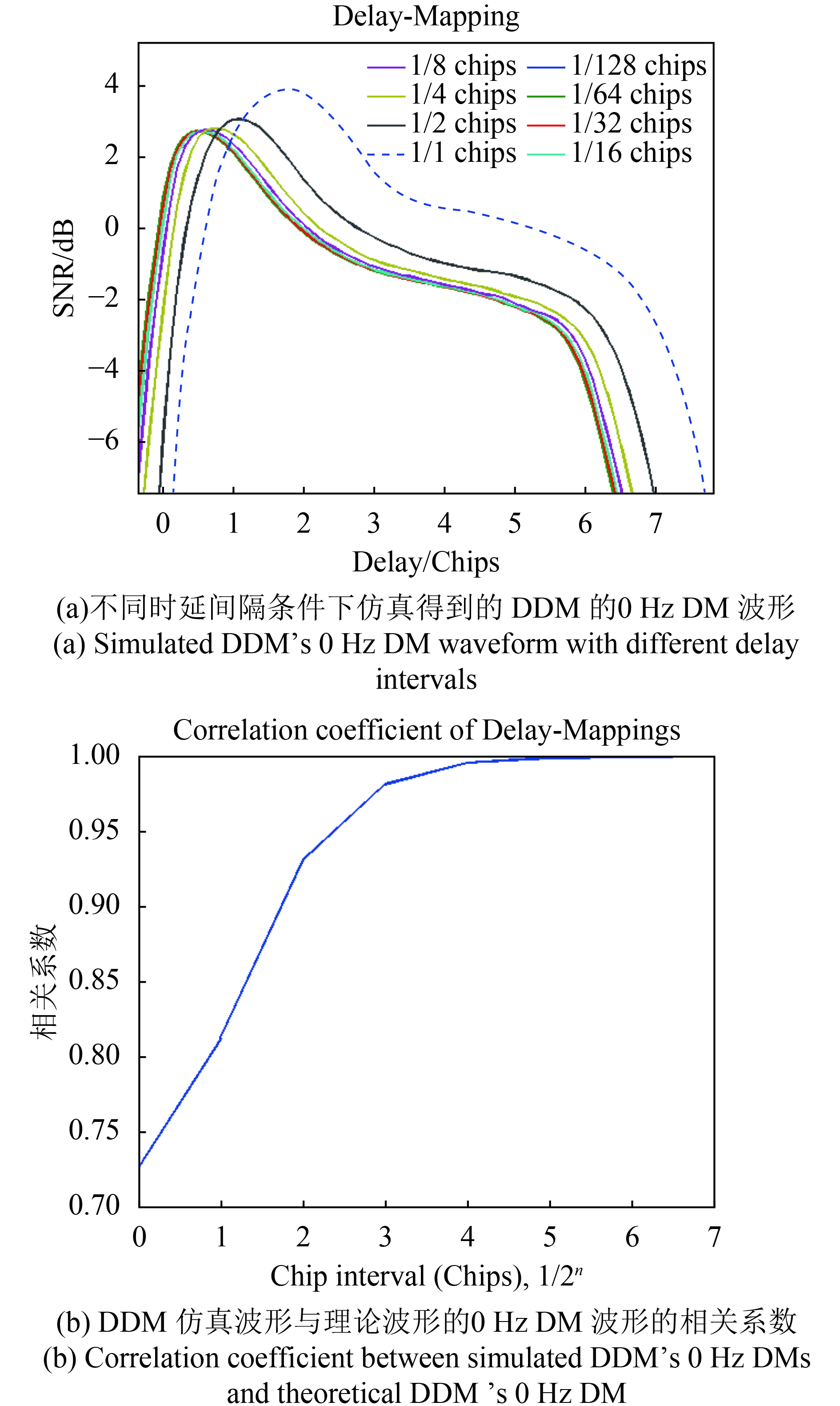
将多普勒间隔固定为5 Hz，利用表1中的输入参数，仿真得到了时延间隔分别为1、1/2、1/4、1/8、1/16、1/32、1/64、1/128个GPS L1C/A码元时的DDM波形。图4(a)为仿真得到的DDM波形的0 Hz多普勒频率对应的DM波形。为了便于对比分析，将1/128个GPS L1C/A码元间隔时的DDM波形作为DDM理论波形，利用二维插值的方法将1、1/2、1/4、1/8、1/16、1/32、1/64个GPS L1C/A码元间隔的DDM仿真波形都插值为1/128个GPS L1C/A码元间隔的波形，并与DDM理论波形进行对比。图4(b)是相关计算得到不同时延间隔的DDM仿真波形与理论波形的相关系数，横轴表示不同的时延间隔，需要说明的是横轴坐标值n对应的是1/2ⁿ的时延间隔，例如横轴等于3的位置，实际上对应的是1/2³的时延间隔，即1/8个GPS L1 C/A码元，下文中图5的横轴与之相同，不再重复说明；图4(b)的纵轴表示的是DDM仿真波形与理论波形的相关系数，相关系数值越接近1，表示二者吻合度越高。由于采用了1/128个GPS L1 C/A码元的DDM波形作为了理论值，因此，图4(b)中横坐标为7时，对应的相关系数为1。由图4(b)可知，时延间隔越小(图4(b)中横轴值越大)，DDM仿真波形与理论波形相关系数越接近于1；当时延间隔小于等于1/16个GPS L1 C/A码元时，相关系数大于0.996；当时延间隔取1/64个GPS L1 C/A码元时，相关系数达到了0.9999。

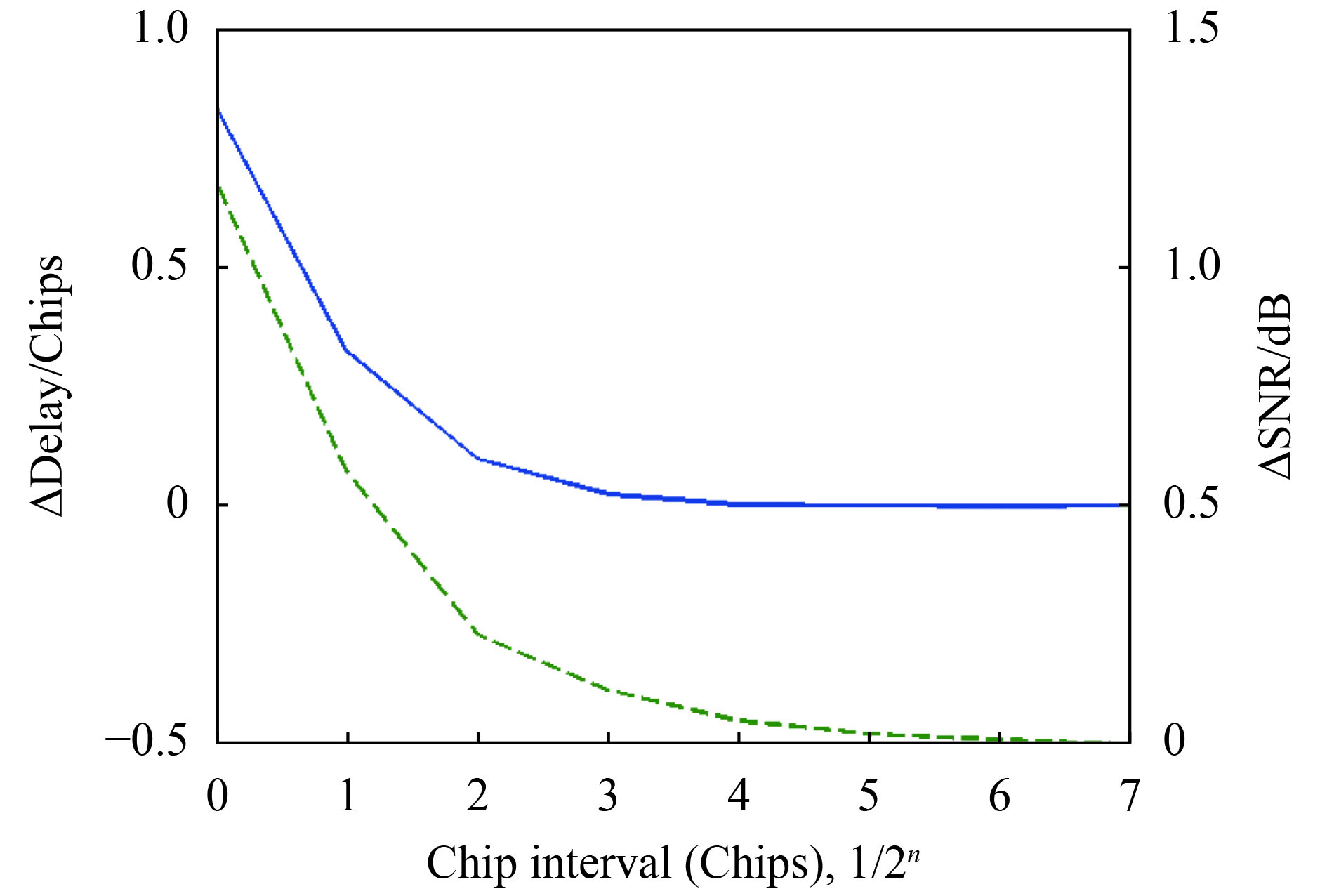
图 4 不同时延间隔条件下，DDM仿真波形的0 Hz DM波形的相关系数

Fig. 4 The correlation coefficient of the 0 Hz DM waveform of simulated DDMs with different delay intervals

DDM仿真波形与理论波形的峰值信噪比与时延的对比结果如图5所示。图5中绿色虚线是不同时延间隔条件下，DDM波形峰值SNR的对比结果，其纵轴表示仿真波形与理论波形的峰值信噪比的差ΔSNR，ΔSNR越接近0 dB表示仿真波形越可靠，其中，理论波形的峰值SNR为3.01 dB。由于采用了1/128个GPS L1 C/A码元的DDM波形作为了理论波形，因此横坐标为7时的峰值信噪比的差ΔSNR等于0 dB。由图5中绿色虚线可知，时延间隔越小，仿真波形与理论波形的峰值信噪比的差ΔSNR越小；当时延间隔等于1/16码元时，ΔSNR约为0.003 dB，与理论值的相对偏差为0.1%；当时延间隔取1/64 个GPS L1 C/A码元时，ΔSNR约为0.0004 dB，相对偏差约为0.01%。图5中蓝色实线是不同时延间隔条件下，DDM波形峰值时延的对比结果，其纵轴是仿真波形与理论波形峰值时延的差ΔDelay，ΔDelay越接近0码片表示波形仿真结果越准确，其中理论波形的参考值为0.435码片。同样，由于采用了1/128个GPS L1 C/A码元的DDM波形作为了参考值，横坐标为7的位置所对应的峰值时延的差ΔDelay等于0码片。由图5中蓝色实线可知，时延间隔越小，仿真波形与理论波形的峰值时延差ΔDelay越接近于0码片，当时延间隔等于1/16 个GPS L1 C/A码元时，DDM仿真波形的ΔDelay约为0.05 个码片，相对偏差为11.4%；当时延间隔取1/64个GPS L1 C/A码元时，ΔDelay为0.010个码片，相对偏差为2.3%。

图 5 不同时延间隔条件下，DDM仿真波形与理论波形峰值时延及信噪比的比较

Fig. 5 Comparison of the peak’s position and SNR of simulated DDMs with different delay intervals and those of theoretical DDM peak

综上可知，时延间隔越小，DDM仿真波形与理论波形吻合度越高，当时延间隔小于等于1/16 个GPS L1 C/A码元时，DDM仿真波形与理论波形的相关系数大于0.99；时延间隔对DDM仿真波形峰值位置的影响远大于对峰值信噪比的影响，当时延间隔取1/16个GPS L1 C/A码元时，DDM仿真波形的峰值SNR的相对偏差约等于0.1%，但是，即使时延间隔取1/64 个GPS L1 C/A码元时，DDM仿真波形的峰值位置的相对偏差也达到了2.3%。

3.2 多普勒间隔影响的仿真结果与分析

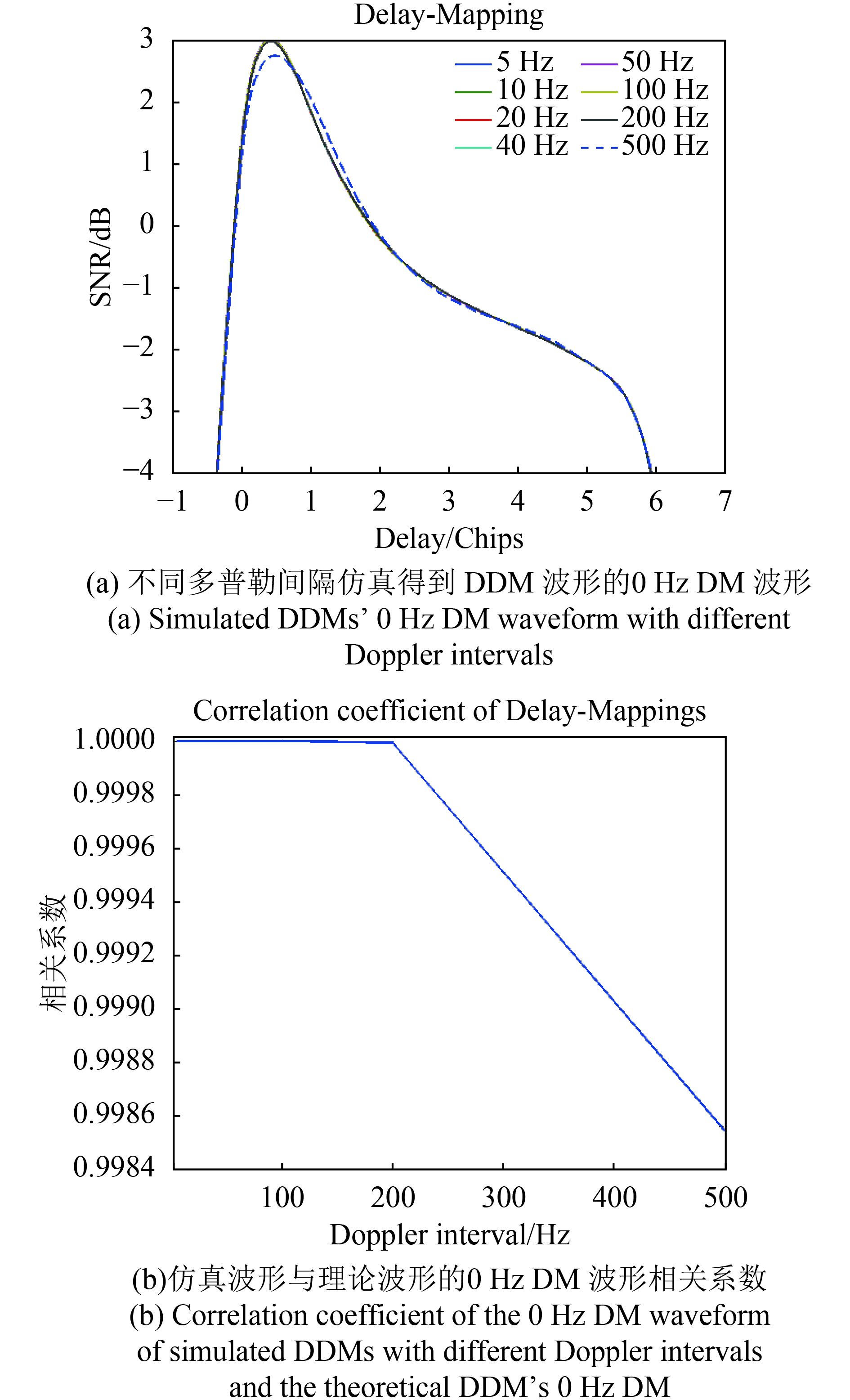
将时延间隔固定为1/128 个GPS L1 C/A码元，仿真得到了多普勒间隔分别为5 Hz、10 Hz、20 Hz、40 Hz、50 Hz、100 Hz、200 Hz和500 Hz的DDM波形。图6(a)为不同多普勒间隔条件下，仿真得到DDM波形的0 Hz多普勒频率对应的一维DM波形。为了便于对比分析，将5 Hz多普勒间隔的DDM仿真波形，作为DDM理论波形，并利用二维插值方法将10 Hz、20 Hz、40 Hz、50 Hz、100 Hz、200 Hz和500 Hz间隔的DDM仿真波形都插值为5 Hz多普勒间隔的DDM波形，并与DDM理论波形进行对比。图6(b)是不同多普勒间隔的DDM仿真波形与理论波形的相关系数，其横轴表示不同的多普勒间隔，纵轴表示仿真波形与理论波形的相关系数，相关系数值越接近1，表示二者吻合度越高。由于采用了5 Hz多普勒间隔的DDM波形作为了理论波形，因此，图6(b)中横轴为5 Hz时的相关系数值为1。由图6(b)可知多普勒间隔越小，DDM仿真波形与理论波形的相关系数值越接近于1。当多普勒间隔取最大的500 Hz时，仿真波形与理论波形的相关系数便可达到0.9984；当多普勒间隔小于等于200 Hz时，相关系数非常接近于1。

图 6 不同多普勒条件下，DDM仿真波形的0 Hz DM波形的相关系数

Fig. 6 The correlation coefficient of the 0 Hz DM waveform of simulated DDMs with different Doppler intervals

DDM仿真波形与理论波形的峰值时延和信噪比的对比结果如图7所示。图7中的绿色虚线是不同多普勒间隔条件下，DDM仿真波形与理论波形峰值SNR的差。图7中的横轴表示不同的多普勒间隔，纵轴是DDM仿真波形与理论波形峰值SNR的差ΔSNR，ΔSNR越接近0 dB表示波形仿真结果越准确，其中理论波形的参考值仍然为3.01 dB。同样，由于采用了5 Hz多普勒间隔的DDM波形作为了理论波形，横坐标为5 Hz多普勒间隔时的峰值SNR的差ΔSNR等于0 dB。由图7中绿色虚线可知，多普勒间隔越小，DDM仿真波形与理论波形的峰值SNR的差ΔSNR越接近于0 dB；当多普勒间隔取100 Hz时，仿真波形与理论波形峰值信噪比SNR的差ΔSNR约为–0.009 dB，与参考值的相对偏差为0.3%；当多普勒间隔取50 Hz时，仿真波形与理论波形峰值信噪比SNR的差ΔSNR约为0.0025 dB，相对偏差为0.1%；当多普勒间隔取20 Hz时，ΔSNR约为–0.002 dB，相对偏差为0.01%。图7中蓝色实线是不同多普勒间隔条件下，DDM仿真波形与理论波形峰值位置的差。图7中的横轴表示不同的多普勒间隔，纵轴是仿真波形与理论波形峰值信噪比对应时延的差ΔDelay，ΔDelay越接近0 chips表示波形仿真结果越准确，其中理论波形的参考值仍然为0.435 chips。同样，由于采用了5 Hz间隔的DDM波形作为了参考值，横坐标为5 Hz多普勒间隔的DDM波形峰值位置的偏差ΔDelay等于0 Chips。由图7中蓝色实线可知，多普勒间隔越小，DDM仿真波形与理论波形的峰值时延差ΔDelay越接近0 chips；当多普勒间隔等于100 Hz时，DDM仿真波形与理论波形峰值位置的偏差ΔDelay等于 0.0007 chips，与参考值的相对偏差约为0.2%；当多普勒间隔等于50 Hz时，ΔDelay等于0.0003 chips，与参考值的相对偏差约为0.1%；当多普勒间隔等于20 Hz时，ΔDelay等于0.0001 chips，相对偏差约为0.02%。

综上可知，多普勒间隔越小，DDM仿真波形与理论波形吻合度越高，当多普勒间隔为200 Hz时，DDM仿真波形与理论波形的相关系数便接近于1；当多普勒间隔取50 Hz时，DDM仿真波形与理论波形的峰值信噪比及峰值位置的相对偏差都已降至约0.1%。

图 7 不同多普勒间隔条件下，DDM仿真波形与理论波形峰值时延及信噪比的比较

Fig. 7 Comparison of the peak’s position and SNR of simulated DDMs with different Doppler intervals and those of theoretical DDM peak

4 结　论

本文利用GREEPS仿真软件评估了时延间隔和多普勒间隔对GNSS-R DDM仿真波形的影响，得出如下结论：

(1)时延间隔与多普勒间隔的大小影响GNSS-R DDM仿真波形的可靠性，影响规律为：时延间隔和多普勒间隔越小，DDM仿真波形与理论波形吻合度越高；

(2)对于固定的多普勒间隔，时延间隔对DDM波形峰值位置的影响，远大于对峰值信噪比的影响。当多普勒频率固定为5 Hz，时延间隔取1/64个GPS L1 C/A码元时，DDM仿真波形的峰值SNR的相对偏差不足0.1%，而DDM仿真波形峰值位置的相对偏差却仍有2.3%。

(3)对于固定的时延间隔，多普勒间隔对DDM波形峰值位置和对峰值大小的影响相当。当时延间隔固定为1/128个GPS L1 C/A码元，多普勒间隔取50 Hz时，DDM仿真波形与理论波形的峰值信噪比及峰值位置的相对偏差都只有约0.1%。

因此，在DDM波形仿真过程中，应根据应用需求，选择合适的时延与多普勒间隔参数。

参考文献(References)

Addabbo P, Giangregorio G, Galdi C and Di Bisceglie M. 2017. Simulation of TechDemoSat-1 delay-Doppler maps for GPS ocean reflectometry. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 10 (9): 4256–4268. [DOI: 10.1109/JSTARS.2017.2703163]

Bai W H, Xia J M, Zhao D Y, Sun Y Q, Meng X G, Liu C L, Du Q F, Wang X Y, Wang D W, Wu D, Wu C J, Liu C and Cai Y R. 2016. GREEPS: an GNSS-R end-to-end performance simulator//2016 IEEE International Geoscience and Remote Sensing Symposium. Beijing: IEEE: 4831–4834 [DOI: 10.1109/IGARSS.2016.7730260]

Cardellach E. 2002. Sea surface determination using GNSS reflected signals. Barcelona: Polytechnical University of Catalonia: 37–38

Clarizia M P, Gommenginger C P, Gleason S T, Srokosz M A, Galdi C and Di Bisceglie M. 2009. Analysis of GNSS-R delay-Doppler maps from the UK-DMC satellite over the ocean. Geophysical Research Letters, 36 (2): L02068 [DOI: 10.1029/2008GL036292]

Elfouhaily T, Chapron B, Katsaros K and Vandemark D. 1997. A unified directional spectrum for long and short wind-driven waves. Journal of Geophysical Research, 102 (C7): 15781–15796. [DOI: 10.1029/97JC00467]

Foti G, Gommenginger C, Jales P, Unwin M, Shaw A, Robertson C and Roselló J. 2015. Spaceborne GNSS reflectometry for ocean winds: first results from the UK TechDemoSat-1 mission. Geophysical Research Letter, 42 (13): 5435–5441. [DOI: 10.1002/2015GL064204]

Gleason S, Hodgart S, Sun Y P, Gommenginger C, Mackin S, Adjrad M and Unwin M. 2005. Detection and Processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing. IEEE Transactions on Geoscience and Remote Sensing, 43 (6): 1229–1241. [DOI: 10.1109/TGRS.2005.845643]

Marchan-Hernandez J F, Camps A, Rodriguez-Alvarez N, Valencia E, Bosch-Lluis X and Ramos-Perez I. 2009. An efficient algorithm to the simulation of delay–Doppler maps of reflected global navigation satellite system signals. IEEE Transactions on Geoscience and Remote Sensing, 47 (8): 2733–2740. [DOI: 10.1109/TGRS.2009.2014465]

Morris M and Ruf C S. 2017. Determining tropical cyclone surface wind speed structure and intensity with the CYGNSS satellite Constellation. Journal of Applied Meteorology and Climatology, 56 (7): 1847–1865. [DOI: 10.1175/JAMC-D-16-0375.1]

O’Brien A and Johnson T J. 2017. Comparing the CYGNSS simulator forward scattering model with TDS-1 and CYGNSS on-orbit DDMS//2017 IEEE International Geoscience and Remote Sensing Symposium. Fort Worth, TX, USA: IEEE: 2657–2658 [DOI: 10.1109/IGARSS.2017.8127542]

Park H, Camps A, Pascual D, Kang Y J, Onrubia R, Querol J and Alonso-Arroyo A. 2017. A generic level 1 simulator for spaceborne GNSS-R Missions and application to GEROS-ISS ocean reflectometry. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 10 (10): 4645–4659. [DOI: 10.1109/JSTARS.2017.2720625]

Pierdicca N, Guerriero L, Giusto R, Brogioni M and Egido V. 2014. SAVERS: a simulator of GNSS Reflections from bare and vegetated soils. IEEE Transactions on Geoscience and Remote Sensing, 52 (10): 6542–6554. [DOI: 10.1109/TGRS.2013.2297572]

Ruf C, Unwin M, Dickinson J, Rose R, Rose D, Vincent M and Lyons A. 2013. CYGNSS: enabling the future of hurricane prediction. IEEE Geoscience and Remote Sensing Magazine, 1 (2): 52–67. [DOI: 10.1109/MGRS.2013.2260911]

Saïd F, Katzberg S J and Soisuvarn S. 2017. Retrieving hurricane maximum winds using simulated CYGNSS power-versus-delay waveforms. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 10 (8): 3799–3809. [DOI: 10.1109/JSTARS.2017.2695878]

Soisuvarn S, Jelenak Z, Said F, Chang P S and Egido A. 2016. The GNSS reflectometry response to the ocean surface winds and waves. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 9 (10): 4678–4699. [DOI: 10.1109/JSTARS.2016.2602703]

Sun Y Q, Liu C L, Du Q F, Wang X Y, Bai W H, Kirchengast G, Xia J M, Meng X G, Wang D W, Cai Y R, Zhao D Y, Wu C J, Li W and Liu C. 2017. Global navigation satellite system occultation sounder II (GNOS II)//2017 IEEE International Geoscience and Remote Sensing Symposium. Fort Worth, TX, USA: IEEE: 1189–1192 [DOI: 10.1109/IGARSS.2017.8127170]

Warnock A M, Ruf C S and Morris M. 2017. Storm surge prediction with CYGNSS winds//2017 IEEE International Geoscience and Remote Sensing Symposium. Fort Worth, TX, USA: IEEE: 2975–2978 [DOI: 10.1109/IGARSS.2017.8127624]

Zavorotny V U, Gleason S, Cardellach E and Camps A. 2014. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geoscience and Remote Sensing Magazine, 2 (4): 8–45. [DOI: 10.1109/MGRS.2014.2374220]

Zavorotny V U and Voronovich A G. 2000. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Transactions on Geoscience and Remote Sensing, 38 (2): 951–964. [DOI: 10.1109/36.841977]

摘要

关键词