出版日期: 2018-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187070
2018 | Volumn22 | Number 3
上一篇  |  下一篇
综述 
定量遥感升尺度转换方法研究进展
expand article info 郝大磊1,2 , 肖青1,2 , 闻建光1,2 , 游冬琴1 , 吴小丹1,3 , 林兴稳1,2 , 吴胜标1,2
1. 中国科学院遥感与数字地球研究所 遥感科学国家重点实验室，北京 100101
2. 中国科学院大学，北京 100049
3. 兰州大学 资源环境学院，兰州 730000
收稿日期: 2017-03-14
基金项目: 国家自然科学基金(编号: 41671366)
第一作者简介: 郝大磊(1993—　)，男，硕士研究生，研究方向为山区定量遥感。E-mail：haodl@radi.ac.cn
通讯作者简介: 肖青(1971—　)，男，研究员，研究方向为定量遥感反演机理和模型。E-mail：xiaoqing@radi.ac.cn
中图分类号: P237
文献标识码: A

摘要

尺度效应是地理科学中普遍存在的现象，制约着遥感等空间科学的发展。发展合理的尺度转换方法以促进遥感技术的全面应用迫在眉睫。本文分别从面—面升尺度转换、点—面升尺度转换两个角度对目前定量遥感领域存在的升尺度转换方法进行综述。其中，面—面升尺度转换方法按照转换原理可分为先反演后聚合、先聚合后反演两种；点—面升尺度转换方法依据定权策略可分为简单平均法、经验回归法、地统计方法、贝叶斯方法等。不同的升尺度转换方法具有各自的特点和优势，本文分别从模型构架、基本原理、特点、局限性和适用条件等方面对现有升尺度转换方法进行分析和讨论，并从离散型与连续型、统计型与物理型、普适型与针对型以及先验知识有和无4个方面总结了现有研究中存在的不足，剖析了升尺度转换研究中存在的问题与挑战，并预测了可能的发展方向。

关键词

升尺度转换, 尺度效应, 尺度纠正, 真实性检验, 定量遥感

Advances in upscaling methods of quantitative remote sensing
expand article info HAO Dalei1,2 , XIAO Qing1,2 , WEN Jianguang1,2 , YOU Dongqin1 , WU Xiaodan1,3 , LIN Xingwen1,2 , WU Shengbiao1,2
1.Skate Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Bejing 100101, China
2.University of Chinese Academy of Sciences, Bejing 100049, China
3.College of Earth Environmental Sciences, Lanzhou University, Lanzhou 730000, China

Abstract

The scale effect is a common phenomenon in geography that restricts the development of space science, such as remote sensing. Scale issues have elicited increasing attention from scientists due to the development of quantitative remote sensing. Developing a reasonable scaling method to promote the extensive application of remote sensing technology is urgent. In this study, existing upscaling methods in quantitative remote sensing are reviewed from two aspects, namely, pixel-to-pixel and point-to-pixel upscaling. The methods are analyzed and compared in terms of the construction, basic principles, characteristics, limitations, and applicable conditions of the corresponding models. Pixel-to-pixel upscaling methods can be divided into two types, namely, inversion–aggregation and aggregation–inversion, according to the conversion mechanism. Inversion–aggregation methods are classified as mathematics and physics based. Mathematics-based methods consist of classic image process approaches, empirical regression methods, and fractal-based methods. The principle of inversion–aggregation methods is explicit and clear, and the values acquired by such methods are generally considered true values. However, these methods require a pixel-by-pixel inversion process, which leads to low operational efficiency. Aggregation–inversion methods are categorized as input parameter-, model-, and output parameter-based approaches. Pixel-by-pixel retrieval is avoided in such methods. From the perspective of the power determination strategy, point-to-pixel upscaling methods can be classified as simple average, empirical regression, geostatistical, and Bayesian. Simple average methods depend on a reasonable evaluation of spatial heterogeneity and an efficient sampling strategy. Empirical regression methods build the empirical statistical relationship on the basis of a large amount of sample data. Geostatistical methods consider the spatial autocorrelation and spatial distribution characteristics of variables. Bayesian methods integrate high-spatial-resolution remote sensing data and prior knowledge to acquire an optimal estimation of land surface parameters at a low spatial resolution. Different point-to-pixel upscaling methods present different advantages and characteristics. Combining the temporal–spatial distribution characteristics of parameters, prior knowledge, and applicability of upscaling methods is necessary to select reasonable upscaling methods in practical applications. On the basis of this analysis, we summarize the problems in existing scaling research from four aspects, namely, discrete and continuous model, statistical and physical model, universal and targeted model, and use of prior knowledge or not. Several other problems, such as the definition of true value, uncertainty analysis, and scale domain and scale threshold determination, have rarely been discussed in upscaling research and require the attention of scientists. We also provide several possible development directions of upscaling methods in quantitative remote sensing. These directions provide important guidance to scaling theory research and its practical application.

Key words

upscaling, scale effect, scale correction, validation, quantitative remote sensing

1 引　言

地球表面空间作为一个具有很高复杂性的巨系统，在某一尺度上观测到的现象、总结出的规律，在另一尺度上可能有效、可能相似，而更多需要修正(李小文 等，2002)，这就是地理学中普遍存在的尺度问题。遥感中的尺度问题是一种特殊的地理学可变面元问题(MAUP)(Marceau和Hay，1999)，是导致95%的海量遥感数据无法得到有效利用、早期卓有成效的遥感应用难以再上新台阶的根本原因之一(苏理宏 等，2001)。目前在定量遥感领域，绝大多数模型和算法均是在特定像元尺度上建立的，盲目地将这些模型应用于其他分辨率遥感数据，必然带来很大的误差，甚至是错误(Raffy 等，1992)。尺度问题已成为遥感数据在传统地理学应用中面临的一个突出问题。在遥感产品的真实性检验中，盲目地利用地面“点”测量数据去直接验证“面”特征的遥感数据，很难得出客观的评价结论。广义上讲，尺度效应是地理现象或地理实体不可避免的本质特征，无法消除，例如海岸线的长度测量问题就是地学描述中的最典型的尺度问题。从狭义上讲，定量遥感反演中的尺度效应可定义为同一区域、同一时间、同样遥感模型、同类遥感数据、同等成像条件，只是分辨率不同导致的遥感反演地表参量不一致，且这种地表参量属于存在物理真值的可标度量(刘良云，2014a)。这种狭义上的尺度效应，本质上是由于某一像元尺度遥感反演模型在其他像元尺度数据上的不适用性导致的。

很多研究表明，遥感尺度问题的根源在于地表的空间异质性、反演算法的非线性以及传感器成像过程中的空间响应函数的非线性。在不考虑传感器成像因素的情况下，只有在地表均质(不存在空间异质性)或者遥感反演模型为线性形式时，尺度效应才不存在(Hu和Islam，1997a；Wu和Li，2009；Wu 等，2013)。在实际应用中，尤其是区域性和全球性问题，非均质是常态，因此必须考虑这种尺度效应。解决方案是构建合适的不同尺度间的尺度转换方法。尺度转换通常包括时间尺度和空间尺度转换两个方面，本文主要针对狭义上的尺度效应，对现有的空间尺度转换方法进行归纳总结。

空间尺度转换是将数据或信息从一个尺度转换到另一个尺度的过程。通常，称由高分辨率到低分辨率的尺度转换为升尺度转换或尺度上推(upscaling)，称由低分辨率到高分辨率的尺度转换为降尺度或尺度下推(downscaling)(Liang，2004)。目前在遥感领域，无论是从实际应用还是从真实性检验的角度考虑，升尺度转换更有意义。随着遥感技术的发展，获取更高空间分辨率的遥感数据成为可能，但是对于遥感研究和应用而言，并非分辨率越高越好，一方面更高的分辨率意味着更高的数据量和运算量，另一方面虽然遥感技术的发展为多圈层中陆面过程和边界层研究提供了有力的工具，但在多模型耦合、系统集成等方面要求遥感数据的分辨率与应用模型(如气候模型等)的较低分辨率相匹配，面临着升尺度转换问题带来的挑战。同时，真实性检验能够为遥感数据产品算法的研发和应用效果评价提供重要的佐证，基于高分辨率数据的多尺度验证、基于地面采样的直接升尺度验证及不同空间尺度遥感产品间的交叉验证的难点在于尺度不匹配问题。解决以上问题的关键为升尺度转换。从数据的获取、模型难度、可行性分析等方面分析，升尺度转换能够成为尺度效应等尺度问题研究的突破口，这对于揭示和把握复杂的生态地理变化规律具有重要的意义。相对于升尺度转换，降尺度转换往往难度更大，目前这方面的研究也相对较少。因此，本文将着眼于定量遥感的升尺度转换过程，主要对高分辨率遥感信息到低分辨率遥感信息的面—升尺度转换、地面定点观测数据到遥感信息的点—面升尺度转换进行归纳分析、探讨总结。

2 尺度转换概念

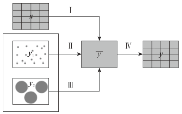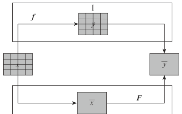
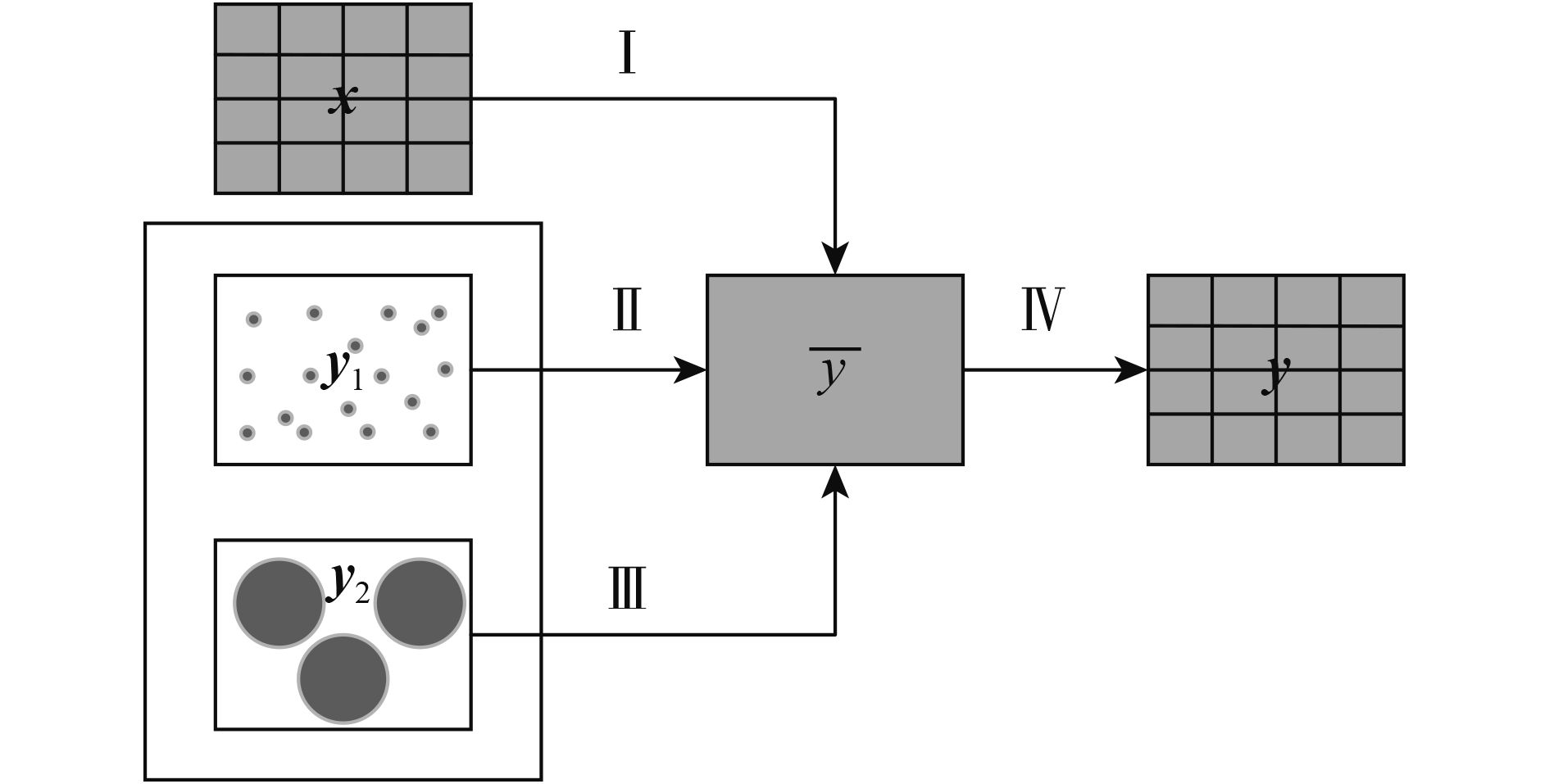
定量遥感中涉及的尺度转换过程如图1所示，其中x表示高分辨率遥感信息；y1表示地面点采样数据，y2表示地面足迹观测数据， $\bar y$ 表示低分辨率遥感信息，y表示高分辨率遥感信息。由x、y1、y2到 $\bar y$ 的转换过程Ⅰ、Ⅱ、Ⅲ均属于升尺度转换，由 $\bar y$ 到y属于降尺度转换。


图 1 定量遥感中的尺度转换
Fig. 1 Scaling of quantitative remote sensing

x、y1、y2均属于遥感相关信息量，其中x为具有连续面特征的遥感信息；地面点采样数据y1具有点状特征，这里的“点”特征是相对于较大尺度的“面”而言的，如安装于高度为4 m的塔上的CNR4辐射表，其观测范围为半径为32 m的圆形区域，相对于1 km的MODIS影像而言可认为是点；足迹观测数据y2，10通量塔观测数据等，其足迹范围近600 m，与1 km“面”数据具有一定的可比性。但y1、y2均属于离散的定点观测数据，不具备x的连续面特征，因此本文将y1、y2统称为“点”数据，将y1、y2涉及的升尺度转换过程Ⅱ、Ⅲ称为点—面升尺度转换，将x涉及的升尺度转换过程Ⅰ称为面—面升尺度转换。

3 面—面升尺度转换方法

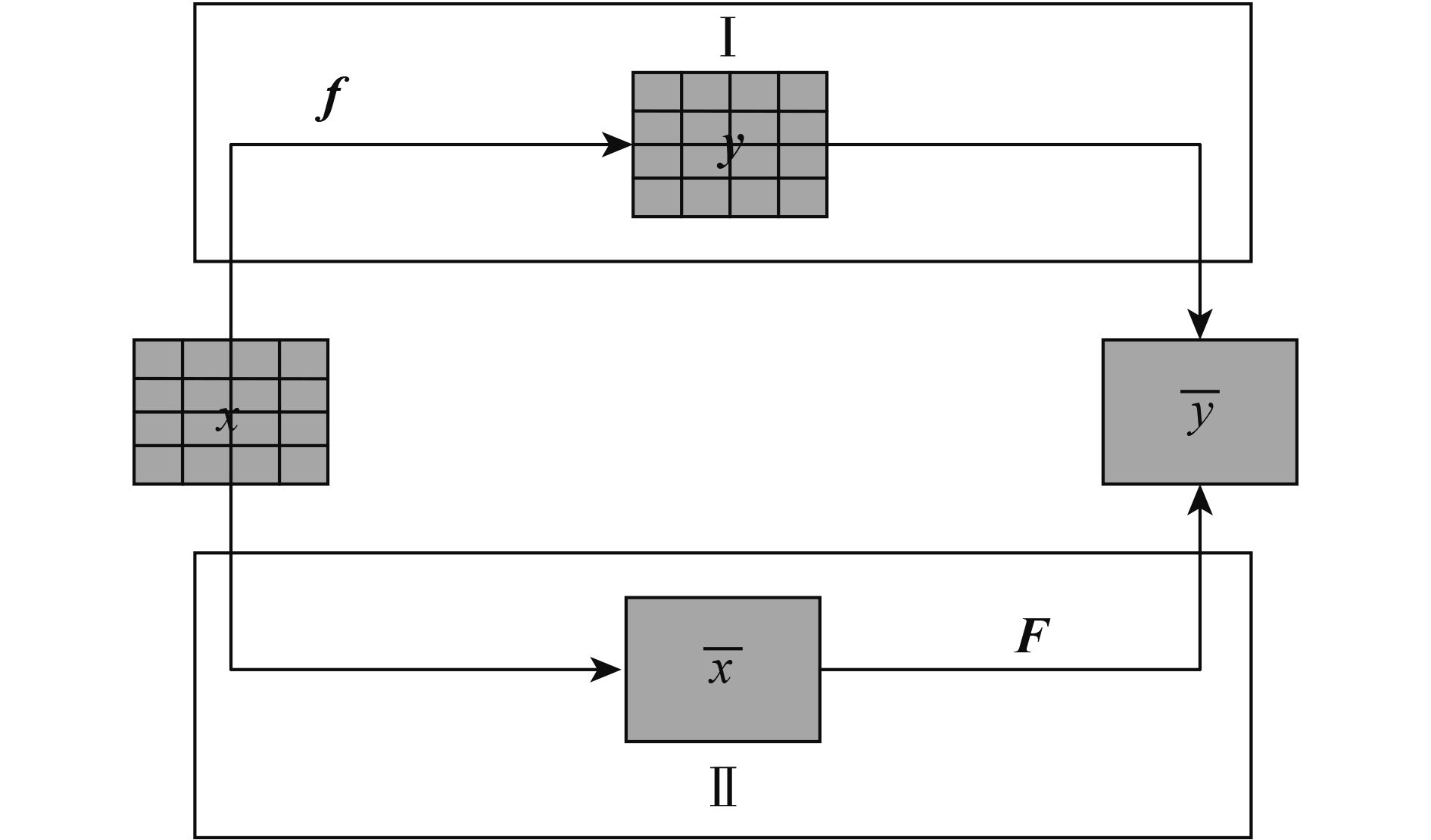
面—面升尺度转换是指从高分辨率遥感信息向低分辨率遥感信息的尺度转换过程，可用式(1)表示。升尺度转换的关键在于尺度转换函数S的确定，根据S确定原理的不同，面—面升尺度转换方法可分为两类(图2)第1类方法如图2过程Ⅰ所示，先反演后聚合，即这种方法首先利用高分辨率信息x通过高分辨率尺度的遥感反演模型f(f代表适用于地表均一分布的遥感反演模型)反演得到高分辨率的遥感信息y，然后利用一定的聚合方法实现遥感信息由高分辨率到低分辨率的尺度转换。第2类方法如图2过程Ⅱ所示，先聚合后反演，即这种方法首先将高分辨率遥感信息x聚合得到低分辨率遥感信息 $\bar x$ ，然后利用一定的模型方法F实现低分辨率遥感信息 $\bar x$ 到低分辨率遥感信息 $\bar y$ 的反演。

$\bar y = S({{x}})$ (1)


图 2 面—面升尺度转换方法示意图
Fig. 2 Pixel-to-pixel upscaling methods

3.1 先反演后聚合

先反演后聚合式的尺度转换方法分为两个阶段，第1阶段中利用高分辨率反演模型f获取高分辨率遥感信息y，第2阶段为高分辨率信息到低分辨率信息的聚合过程。根据聚合方式确定方法的不同，这类尺度转换方法主要分为数学方法与物理机制法，其中数学方法主要包括经典图像处理方法、经验回归法、分形法等。

基于经典图像处理的尺度转换方法借鉴图像处理中的经典方法实现遥感信息的尺度上推，主要包括局部平均、最近邻法、双线性插值、三次卷积、中值采样等重采样方法(周觅和张杰林，2011)、点扩散函数(Gao和Huete，2000)、小波变换法(An 等，2015)等图像变换方法。这种方法没有考虑地表参数的物理意义及其地学性质，也未考虑高分辨率像元之间可能存在的彼此能量交换过程，属于一种纯数学上的处理。如果在尺度上推过程中结合遥感参数自身的特点，借鉴图像处理中的数学技巧，也能够达到很理想的效果，但一般情况下不考虑地学描述的经典图像处理方法会使遥感信息的升尺度转换产生较大偏差(Hay 等，1997)。

基于经验回归的尺度转换方法从数据本身出发，建立地表参数遥感信息不同尺度间的回归关系，已被广泛应用于NDVI(Aman 等，1992)、反照率(Liang，2000)、林地面积(Lu 等，2011)、森林覆盖比例(Mayaux和Lambin，1995)等。这种方法从数据本身出发，舍弃了繁琐的物理过程，原理比较简单，易于实现，在研究示范区域亦能达到足够高的精度，但这种方法需要大量的样本数据，没有明确的物理意义，缺乏足够的外推能力和可移植性，特别是当把经验公式应用于其他区域时精度往往较低。这种方法仅适用于统计关系所建立的几个离散尺度，属于离散型尺度转换模型。如果不同尺度间参数的空间代表性不能很好的匹配，这种方法产生的结果也会出现偏差，可靠性降低。

基于分形的尺度转换方法则从统计分形的角度出发，利用定量遥感地表参数体现出的不同尺度间的自相似性实现尺度转换(苏理宏 等，2001；徐希孺，2005)，已被应用于遥感影像(郭建明，2008)、NDVI(栾海军 等, 2013a, b，2015)、LAI(Zhang 等，2010；Wu 等，2015a，b )。分形方法充分利用地表参数的分形特征，模型简洁明晰，属于连续型尺度转换模型，能够实现尺度域内任意尺度的尺度上推，不仅仅受限于几个离散的尺度间的转换。目前已取得一定的进展，但是还存在很多问题，例如对地表参数分形特征认识不够、对分形自相似性尺度域还缺乏研究，对分形的物理机制认识也不明确等。当地表参数的分形特征不明显或者根本没有分形特征时，这种方法将难以应用。

基于物理机制的尺度转换方法从地表参数的物理意义及地学性质出发，根据物质守恒、能量守恒等原则建立相应的模型进行尺度上推，已被应用于LAI(Tian 等，2003)、BRDF/反照率(Liu 等，2006；闻建光，2008；Wen 等，2009)等。这种方法建立在对地表参数的物理意义及地学过程完全认识的基础上，模型较为复杂，理论上讲精度最高。但目前对于某些地表参数的像元尺度真值还缺乏明确的认识，定义难以统一，导致模型构建与反演困难，同时这种方法也存在模型假设与真实场景不一致、模型适用性等问题，导致这种方法应用受限。

3.2 先聚合后反演

先聚合后反演式的尺度转换方法的关键在于模型方法F的构建。从输入参数、反演模型、输出参数3种函数组成要素的角度考虑，该方法可分为基于遥感信息x、基于遥感模型F、基于遥感信息y 3类。

3.2.1 基于遥感信息x

基于遥感信息x的尺度转换方法，从输入参数的角度出发，通过对遥感信息x进行合适的异质性参数化表达和重新定义，实现反演模型的尺度不变性，主要包括等效参数法。

等效参数法从参数的角度出发，通过对输入参数的重新定义，使得高分辨率遥感模型f可用于低分辨率遥感参数反演，这种方法通过重构自变量间接实现了反演模型的尺度不变性，即此时F=f，已应用于地表温度(Becker和Li，1995)、方向间隙率(Ma 等，2008)、LAI(吴骅 等，2008)等的尺度转换中。如何定量描述等效参数同高分辨率尺度参数均值或其他统计值之间的关系是该方法的难点所在，同时如何理解等效参数的物理意义也是亟待解决的难题。

3.2.2 基于遥感模型F

基于遥感模型F的尺度转换方法，从反演模型角度出发构建考虑地表参数空间异质性的反演模型F，主要包括计算几何法和物理模型法两种。

计算几何法是基于几何学中凸集的概念发展而来，它利用凸集的思想构建模型F，最先由Raffy(1992)引入到定量遥感尺度转换领域，目前主要应用于LAI的尺度上推中(马灵玲，2008；吴骅，2010)。它对反演函数的数学性质没有要求，适用于非连续、不可导、非线性程度大的反演函数，同时该方法只需要利用自变量的范围获取上下包络线，并不需要完整的高分辨率数据，仅仅需要高分辨率数据的参数范围，即可实现尺度转换，但是当反演函数拥有多个自变量时，包络线的确定将变成一个难题。这种方法也对给定的参数的空间域有较高的要求，当空间域范围过大时，这种方法精度会很低，同时它也没有很好的考虑地表参数的空间异质性特征，限制了该方法的应用。

物理模型法是建立在对不同尺度的物理过程的理解基础上的，根据物理过程来构建函数F，主要分为两种模式，第1种为在不同的尺度上建立不同的模型，第2种为建立尺度不变模型，可适用于不同的尺度。第1种模式中最具代表性的就是传统的定量遥感模型，如叶片尺度的PROSPECT模型，冠层尺度的几何光学模型，公里尺度的混合像元模型等。第2种模式往往难度更大，如Tian等人(2003)以电磁波在介质中的辐射传输过程为基础，考虑到光子邻边位移(lateral migration)平均长度、依赖尺度的吸收和散射特性以及像元异质性，构建了尺度依赖的LAI反演模型。这种方法基于物理过程建立，物理意义明确，但由于其本身构建的复杂性以及模型反演的困难性，同时也受到模型假设以及参数不确定性的影响，阻碍了它的发展和应用。

3.2.3 基于遥感信息y

基于遥感信息y的尺度转换方法从输出参数的角度出发，首先，利用高分辨率遥感模型f将低分辨率遥感信息 $\bar x$ 反演得到低分辨率遥感信息y′于尺度效应Δ的存在，y′与真值 $\bar y$ 存在差异，必须通过一定的方法来计算尺度效应Δ，并最终得到不受尺度效应影响的遥感信息 $\bar y$ 。这种方法的关键在于Δ描述方法的不同，这类尺度转换方法主要包括泰勒展开法、校正因子补偿法以及二者的混合方法、小波—分形法4种。

泰勒级数展开法最早由Becker和Li(1995)应用于等效温度和比辐射率的尺度转换研究中，它利用泰勒展开技术来定量描述尺度效应Δ，Hu和Islam人(1997b)提出了基于泰勒展开方法的普适性尺度纠正方法框架。Li等人(1999)和李小文等人(1999)基于泰勒展开方法研究了非同温黑体表面普朗克定律尺度效应，并将普朗克定律的尺度纠正推广到一般的非同温3维结构非黑体表面(Li 等，1999, 2000；李小文 等，1999)。之后众多研究学者采用这种方法研究了遥感反演的地表特征参数的尺度效应和尺度转换规律，如归一化差分植被指数NDVI(Hu和Islam，1997b)、叶面积指数LAI(Garrigues 等，2006；吴骅 等，2009；刘良云，2014b)、地表温度(吴骅，2010)、显热和潜热(Pelgrum，2000)等。泰勒展开法可适用于多种地表参数类型，合理解释了尺度效应的产生原因(地表空间异质性与反演函数的非线性)，原理简单明确，但要求高分辨率反演函数连续并存在二阶导数，而且这种方法忽略了二阶以上的高级项，这些都限制了它的精度和应用范围。当反演函数非线性程度较大时，这种方法将会导致较大的误差(Pelgrum，2000)。

校正因子补偿法是一种基于亚像元类型信息的尺度纠正方法，它假设尺度效应Δ主要是由地表特征不连续变化引起的，同一特征类型内地表参数的异质性造成的影响可忽略不计。换言之它假设尺度效应是由于仅仅考虑占主导的特征类型而忽略其他类型造成的。这种方法已广泛应用于LAI(Chen，1999；田庆久和金震宇，2006)、NPP(Zelic 等，2002；Simic 等，2004；王莉雯 等，2010；王培娟 等，2007；Chen 等，2013)、蒸散ET(El Maayar和Chen，2006)的尺度上推中。校正因子补偿法计算简单，考虑了亚像元类型变化带来的尺度效应，但是其物理机制不够明确，对造成尺度效应的异质性因子的选择也是一个关键问题。此外根据统计回归得到的类型比例和校正因子之间的关系与选取的反演函数有关，导致其可移植性不高。

混合方法综合了泰勒展开法以及校正因子补偿法的思想，同时考虑了地物类型变化以及同一地物类型内地表参数的异质性产生的尺度效应Δ。泰勒展开法仅仅考虑了同种地物类型下地表参数异质性造成的影响，忽略了不同地物类型的影响，校正因子补偿法则恰恰相反，仅仅考虑了不同地物类型造成的影响。顾名思义，混合方法则将两种方法有机结合起来，它首先对不同组分分别基于泰勒展开法进行尺度效应计算，然后在通过组分比例对尺度效应进行综合，最终实现尺度纠正。Wu等人(2013)首次提出这种方法，并利用它进行了LAI的尺度纠正，证明了该方法的可行性和有效性。混合方法综合了泰勒展开法以及校正因子补偿法的各自的优势，同时考虑了参数的密度、结构等空间变化所带来的影响，但同样也无法避免这两种方法存在的问题。

小波—分形法是利用小波—分形理论来定量刻画尺度效应Δ，实现尺度纠正的方法。小波分析将地表参数数据分解为低频与高频的信息，高频信息往往是造成尺度效应的原因，分形理论能够挖掘高频信息内在的自相似性，获取连续尺度上空间信息变化规律。从信号分解的角度看，泰勒级数分解实际上是把函数或者信号分解到无线维的空间中，每一项的系数是函数或者信号在这个维度空间中分配的能量。但这种分配能量的方式并不是正交，每一项描述的尺度效应可能存在交叉，造成描述尺度效应的偏差。正交小波分解法不存在这种问题。在正交小波分解基础上，分形法可定量描述分解后的高频信息所导致的尺度效应。Jiang等人(2015)利用该方法实现了LAI的尺度纠正，证明了该方法的可行性。小波—分形法充分挖掘小波正交分解后的高频信息中内在的自相似性，避免了泰勒展开中的信息交叉问题，模型简单，虽然取得了一定的进展，但是还存在很多问题，如小波函数的选择、小波阈值、分形维度的确定等，还需要进一步的研究。

3.3 分析与讨论

如表1所示，这几种方法具有不同的特点和优势，不同分辨率的地表参数之间不是简单平均的关系，而是与地表物性空间分布状况相关，必须建立可靠、便捷、自洽的尺度转换方法，才能满足用户的需求。先反演后聚合方法原理清晰，需要进行逐像元反演，运算量大，效率较低。随着计算机云计算等技术的发展，这类方法将得到广泛的应用。先聚合后反演方法与先反演后聚合方法相比，不需要高分辨率尺度上的逐像元反演，计算效率较高。这两类从不同角度出发的尺度转换方法本身并不孤立，而是相辅相成的。每类方法都有其各自的优势，需要从数据现状、应用需求等方面考虑，根据每种方法的特点来选择合适的满足要求的方法进行升尺度转换。

4 点—面升尺度转换方法

点—面升尺度转换是指从“点”尺度的地面观测值向卫星像元尺度的参数地表真值的升尺度转换过程，如图1过程Ⅱ、Ⅲ所示。在空间异质性较大的区域，直接用单点测量值或者多点采样平均值来代表像元尺度的真值是常用的简单方法，但会造成很大的不确定性。因此，通过发展和建立有效的点—面升尺度转换方法以获取像元尺度的真值对于像元尺度遥感模型的建立以及遥感反演地表参数产品的真实性检验都具有重要的意义。这种升尺度转换方法的选择不仅与地表参数的时空异质性有关，还与地面采样策略(包括采样的空间分布模式、密度、方向等)有关。本文从升尺度模型参数估计角度对现有的点—面升尺度转换方法进行分类总结。像元尺度参数值可表示地面点观测值向量y的函数，如式(2)所示，升尺度过程可表示为函数f。

$\bar y = f({{y}})$ (2)

表 1 面—面升尺度转换方法特点总结
Table 1 Characteristics of different pixel-to-pixel upscaling methods

下载CSV 
基本原理 具体方法 优点 缺点
先反演后聚合 数学方法 经典图像处理方法 方法简单，数学原理清晰 没有考虑参数的物理定义和地学性质，效果较差，应用较少
经验回归法 舍弃了繁琐的物理过程，原理比较简
单，精度适当，易于实现，属于离散
型升尺度转换模型 		需要大量的样本数据，没有明确的物理意义，缺乏足够的外推能力与可移植性
分形法 模型简洁明晰，属于连续型升尺度转换
模型 		要求参数具有分形特征，适用性有限，生物物理机制认识不明确，自相似性尺度域较难确定
物理机制法 物理意义明确，理论上精度最高 模型复杂，较难构建，适用性有限，受到模型假设与真实场景不一致等问题的影响
先聚合后反演 基于遥感信息x 等效参数法 实现了反演模型的尺度不变性 等效参数定义较难，同时等效参数的物理意义较难理解
基于遥感模型F 计算几何法 适用于非连续、不可导、非线性程度
大的反演模型，不需要完整的高分辨
率遥感信息 		自变量较多时，包络线较难确定，对参数的空间域先验知识要求较高，没有很好的考虑地表参数的空间异质性
物理模型法 物理意义明确 模型复杂，较难构建，受到模型假设以及参数不确定性的影响
基于遥感信息y 泰勒展开法 普适性较强，原理简单明确，解释了尺
度效应产生的机制 		要求反演函数连续并存在二阶导数，忽略了高阶展开项，反演函数非线性程度较大时误差较大
校正因子补偿法 计算简单，考虑了亚像元类型特征带来
的影响 		物理机制不明确，异质性因子的选择较难，可移植性不高
混合方法 同时考虑了参数的密度、结构等空间变
化产生的影响 		继承了泰勒展开法与校正因子补偿法各自的缺点
小波—分形法 避免了泰勒展开中的信息交叉问题，模
型简单 		小波函数难以选择、小波阈值、分形维度较难确定，研究还不够透彻

升尺度后的像元尺度参数值与地面测量值一般具有相同的物理含义，因此一般f为线性函数，则式(3)可简化为式(3)，其中w代表对应地面采样点的权重向量。

$\bar y = {{{w}}^{\rm{T}}}{{y}}$ (3)

因此升尺度的关键就在于权重w的确定。而w必须通过先验知识来确定，先验知识包括基本假设(如地理学第一定律)、历史累积数据、辅助统计信息等。根据w的定权策略，点—面升尺度转换方法可分为简单平均法、经验回归法、地统计方法、贝叶斯方法等。

4.1 简单平均法

简单平均法是将地面采样点值直接进行算术平均或者按照面积或足迹范围进行加权平均的方法。它使用的前提是地表的均一程度较高或者采样站点具有良好的空间代表性，换言之这种方法很大程度上依赖于采样点的分布与所在像元的空间异质性程度。这种方法主要包括算术平均法(Wang 等，2004；Riihelä 等，2010)、时间稳定性法(Cosh 等，2006；Crow 等，2012；Zhao 等，2013；Wu 等，2015b)、面积加权平均法(Hufkens 等，2008；Shi 等，2015；Liu 等，2016；Greifeneder 等，2016)、足迹加权平均法(Ezzahar 等，2007；彭谷亮 等，2008；Timmermans 等，2009；卢俐 等，2010)等。

算术平均法仅仅适用于相对均一的地表，或者采样点对遥感像元具有足够高的代表性，适用性有限；时间稳定性法的本质是通过时间序列分析选择能够代表地表特征参数区域平均值的采样点，实际上是一种基于地表参数分布状况一段时间内稳定不变假设的布点策略；面积加权法(足迹加权法)的基本思想是根据每一采样点所能代表的区域面积来对采样数据进行加权平均，当地表参数具有规则的空间结构时，这种方法可在一定程度上减小尺度上推误差，但随着时间的推移各个点的权重需根据下垫面的实际变化情况进行调整或者重新计算。

4.2 经验回归法

经验回归法是利用历史累积的样本数据通过最小二乘法等手段来获取各采样点所占权重的方法。当存在其他类型先验知识时，也可通过正则化方法将其引入到权重系数的计算中。下面分别从回归模型、样本选择以及回归模型中自变量3种角度对经验回归法进行分析。

从回归模型角度看，经验回归法包括普通最小二乘法、逆回归分析、主轴回归法(RMA)(Smith，2009)、全最小二乘法等。Cohen等人(2003)比较了多种回归模型，结果显示RMA回归方法效果更好。在BigFoot工程中，RMA方法被视为估计LAI的标准方法(Berterretche 等，2005)。不同的回归方法的统计学假设存在差异，在实际应用过程中应结合实际数据的特点进行方法的选择。

根据样本数据获取的手段，经验回归法可分为高分辨率数据法(Shi 等，2014；Wu 等，2016b)、陆地表面模型法(Crow 等，2005)、辅助变量法(Qin 等，2013)。高分辨率数据法是指通借助高分辨率数据获取像元尺度的真值，精度依赖于高分辨率数据的可靠性。陆表模型法是指在不具高分辨率数据的情况下，利用相关的陆表模型生成对应参数的高分辨率产品，然后进行相应的尺度间的经验关系构建，精度依赖于陆地表面模型的可靠程度。辅助变量法是指在高分辨率数据难以获取，陆地表面模型法精度难以保证、难以表达相关要素的空间异质性的情况下，利用相关的先验信息进行经验拟合或者物理公式推导计算来获取像元尺度的真值。

根据自变量的不同，回归模型可分为基于原始变量，以及基于变量与趋势面的残差两种。基于趋势面残差的回归法与基于原始变量的经验回归方法相比，其经验关系是在趋势面的基础构建的，其余步骤和解法均相同。其中趋势面可来源于高分辨率数据或者陆地表面模型等，如Crow等人(2005)利用这种方法实现了土壤湿度的尺度转换。当参数的空间变异性较大时，使用第一种方法的拟合效果往往较差。引入趋势面后，趋势面残差的空间变异性往往比较小，因此利用其进行拟合，效果也会更好，构建的经验关系也更加鲁棒。而对于具体采用哪种方法需要结合先验知识、采样策略、数据条件以及参数信息等知识来综合确定。这两种经验回归法的精度也很大程度上依赖于历史数据的精度和可靠性，具有统计模型的通病——可移植性较差。

4.3 地统计方法

地统计学以区域化变量理论为基础，以变异函数为主要工具，可用来研究空间上既有随机性又有结构性，或具有空间相关性和依赖性的自然现象(刘爱利 等，2012)。Atkinson和Tate(2000)综述了地统计方法在空间尺度问题中的应用。地统计方法主要包括传统的地统计方法(如克里金插值)以及地统计回归方法。传统的地统计方法由于其不仅利用了采样点的实地观测数据，而且还利用了地表参数的空间结构信息，被广泛应用于地面采样点数据的尺度上推过程中。地统计回归方法综合了经验回归方法以及传统的地统计方法的优点。与经验回归方法相比，地统计回归方法引入了地表参量残差的时空相关性(Hengl 等，2007)；与传统的地统计方法相比，地统计回归法通过引入辅助数据来提高精度。目前地统计回归方法已被应用于积雪覆盖(Erickson 等，2005)、土壤水分(Kang 等，2015)、LAI(He 等，2016)等参量的估计中。

地统计方法中以克里金方法最为典型。克里金法也称空间局部估计，是建立在变异函数理论及结构分析基础上，在有限区域内对区域化变量的一种无偏最优估计。根据引入先验信息的方式，应用于定量遥感点—面尺度上推中的克里金方法主要分为块克里金(冉有华和李新，2009；Ding 等，2014；Wang 等，2014；Kang 等，2017)、协同克里金(Gao 等，2014)、回归克里金方法(Ge 等，2015；Hu 等，2015；Kang 等，2015；Wang 等；2015)3种。块克里金方法没有引入相关辅助数据，它的精度仅依赖于采样点的密度和分布。协同克里金方法通过线性方式引入了相关的辅助变量作为先验知识，要求辅助变量与目标变量相关性较高，当协变量对目标参数的影响较小时，其效果与普通克里金的效果基本上相同(Asli和Marcotte，1995；Wu 等，2009)。回归克里金方法通过回归方式构建趋势面，充分利用了先验信息，同时结合了采样点的观测数据实现最优估计，更加完整的考虑了地表参数的空间异质性。

4.4 贝叶斯方法

贝叶斯方法是一种综合先验信息与样本信息来推断未知参数的最优化估计方法。贝叶斯最大熵法则是在贝叶斯框架下结合信息论中的熵的概念来认识与处理时空变量，是现代时空地统计学的重要组成部分，具有坚实的认识论框架和方法学基础。它是一种更通用的非线性估计器，并且适用于空间上非正态分布或者异质性比较强的地表参数估计(Christakos和Li，1998；Christakos，1990；Christakos 等，2001)。

BME的基本流程如图3所示，主要包括基于熵的先验分布确定阶段、基于特定知识(包括硬数据、软数据)的贝叶斯条件化阶段以及基于贝叶斯定理的最优化参数确定阶段。目前，BME在尺度上推领域的应用仍然需要进一步挖掘。具有代表性的工作主要包括：Christakos等人(2004)综合臭氧站点观测数据以及遥感数据进行了臭氧分布制图；Li等人(2011, 2013)进行了基于贝叶斯最大熵方法的多源定量遥感产品(LAI、SST)融合研究；Gao等人(2014)采用这种方法融合了土壤水分传感器网络观测数据(作为硬数据)和ASTER地表温度数据(作为软数据)，成功实现了土壤水分的尺度上推；Fan等人(2015)利用这种方法实现了土壤水分无线传感器网络观测数据、ASTER土壤蒸散发数据、灌溉统计数据以及被动微波土壤水分数据的多源多尺度数据融合。


图 3 BME分析流程(改自(D’Or D, 2003))
Fig. 3 BME analysis process (adapted from(D’Or D, 2003))

4.5 分析与讨论

如表2所示，各种点—面升尺度转换方法具有不同的优势和不足。简单平均法能够有效实现尺度上推的基础是合理的时空异质性评价与采样策略。因此，根据地表参数的时空异质性特征合理布设采样点是这种方法的关键所在，当地表站点的空间代表性较差或地表站点的分布过于稀疏时，这种方法难以适用；经验回归法没有利用地表参数的时空分布特性及空间自相关特征，仅仅利用数学手段来拟合经验关系，而且升尺度精度很大程度上依赖于样本数据集的可靠性，某一区域构建的经验关系往往难以适用于其他区域；地统计方法通常对地表参数分布有统计假设，例如克里金方法的正态分布与二阶平稳假设，然后在相关统计假设基础上利用统计优化理论实现稀疏观测的尺度上推，这种方法本质上是一种线性优化算法，对某些类型的先验信息，如不确定性较大的目标变量的先验分布等，不能做到很好的融合；贝叶斯最大熵方法实际上是在经典地统计学的基础之上借助于贝叶斯和最大熵观点建立了一个更加宏大的理论和方法学框架，与传统的空间估计方法相比，这种方法可集成不确定性数据，如专家经验、推理、误差较大的观测数据等均可作为有价值的辅助数据，极大扩充了辅助数据的范畴；贝叶斯最大熵方法属于最优无偏估计，克里金方法仅仅是它的特例，它对地表参数的空间分布没有要求，能够通过合理的概率描述来融合各类先验信息，提高升尺度转换的精度。这种方法的关键在于先验知识的概率化表达，如何更合理的引入先验信息是将来需要探索的方向。

表 2 点—面升尺度转换方法特点总结
Table 2 Characteristics of different point-to-pixel upscaling methods

下载CSV 
定权策略 具体方法 优点 缺点
简单平均 算术平均法 简单实用 要求地表参数的均一性程度高
时间稳定性法 利用了地表参数的时序特征，选择的采样
点具有区域代表性 		假设地表参数分布状况一段时间内稳定不变，不适用于时变特征明显的地表参数
面积或足迹加权平均法 引入了采样点的代表区域信息，适用于具
有规则的空间结构的地表参数 		仅仅考虑了类型变化，未考虑每一类型内地表参数的异质性的影响
经验回归 基于原始变量 简单实用 空间异质性较大时，拟合效果差
基于趋势面残差 引入了趋势面，提高了拟合模型的鲁棒性 趋势面的质量会影响到模型的精度
地统计思想
(以克里金方法为例) 		块克里金 不仅利用了测量数据，而且考虑了地表参
数的空间相关性与变异性 		没有利用其他辅助信息，依赖于采样点的分布与测量精度
协同克里金 相比块克里金方法，引入点状特征的相关
辅助变量信息 		仅仅通过线性组合的方式进行优化有局限性，只能考虑具有点状特征的辅助变量，要求辅助变量相关性较高
回归克里金 充分利用各种点状、面状特征的先验知识，更加完整的考虑了地表参数的空间异质性 由于引入了更多的先验信息，从而也引入了更多的误差来源和不确定性
贝叶斯思想 贝叶斯最大熵法 可融合各种先验信息，对先验知识的分布
没有要求 		先验知识的概率化表达与组织较难，研究还不成熟

当然，这些方法也不是相互独立的，特别是在多种先验知识可利用的情况下，可结合多种定权策略，融合多种尺度上推方法，实现最好的效果，尽可能减小尺度上推过程中的不确定性。除上述几类典型的方法，学者还提出了一些其他方法，如刘艳等人(2014)将应用于面—面尺度纠正的泰勒级数展开模型进行改进后用于地面点测量数据到像元尺度LAI的尺度转换；de Lannoy等人(2007)利用累积概率函数匹配法进行了土壤湿度的尺度上推，得到了较好的结果。3.2.2节介绍的计算几何法也可直接用于点—面尺度转换。黑河生态水文遥感试验(HiWATER)初步建立了从采样设计、多尺度观测、代表性误差的度量、尺度上推新方法到真实性检验的研究框架，在点—面升尺度转换方面取得了较大的进展(李新 等，2016)。

5 存在的问题

虽然目前定量遥感升尺度转换方法取得一定的进展，但还存在很多问题和不足，特别是在实际应用还是以简单取平均的聚合方式进行尺度上推为主。结合现有升尺度转换方法的特点(如表1、2所示)，分别从离散型与连续型、统计型与物理型、普适型与针对型以及先验知识有和无4个方面考虑，总结现有研究中存在的问题：

(1) 离散型与连续型：离散型模型如一般的统计回归模型等仅能够适用于有限几个尺度间的转换，如30 m分辨率TM产品向1 km分辨率MODIS产品的尺度转换，而无法实现尺度域内任意尺度间的转换，但是这种模型构建的难度较小，也易于操作；连续型模型如分形模型等则能够实现连续尺度的转换，从理论上讲这种模型能够真正揭示尺度转换规律，从应用上看它也能够推动遥感产品系统的智能化和自动化进程。但是这种机制更加复杂，构建难度太大。研究连续型尺度转换模型是今后发展的趋势，具有重大的理论研究和实际应用价值。结合现状，一方面，可通过不断深入研究结合物理认识和数学工具积极探索构建简单实用的连续型模型；另一方面，也可利用已有离散型模型，从中总结升尺度转换的规律，在此基础上尝试实现离散型模型向连续型模型的转换。

(2) 统计型与物理型：统计型模型如面—面升尺度转换中的分形法、校正因子补偿法以及点—面升尺度转换中常用的经验回归方法、地统计方法等均在一定的统计学假设基础上构建，模型简单，易于计算，但缺乏对物理机理的理解和认知，可移植性较差，如将基于某一区域大量样本数据构建的LAI校正补偿经验公式应用于其他区域时会产生一定偏差(Chen，1999)，需要针对不同区域构建不同的经验模型；物理型模型是对尺度转换过程的抽象化表达，物理机制清晰，较为复杂，但往往物理模型的假设与实际情况不符合，适用性有限，如Wen等人(2009)提出的山区BRDF/反照率尺度转换模型忽略了天空漫散射及邻近地表散射的影响以及地表的混合像元问题，并且尺度转换效果依赖于DEM及相关地形因子的精度。因此，如何结合这两种模型的优势，对物理模型进行简化和近似，参数化关键性因子，降低模型复杂度，构建既计算简便又有一定物理意义的半经验模型是值得探索的研究方向。

(3) 普适型与针对型：针对型模型是指模型仅仅针对某些特定的地表参数类型而建立，无法适用于其他地表参数；普适型模型强调模型的适用范围，研究价值更高，泰勒级数展开法、几何级数法等具有一定的普适性，但也都存在一定的限制(如泰勒级数展开法要求反演函数连续可导等)。由于地表参数种类繁多，地表空间异质性普遍存在，构建地表参数耦合的针对型转换模型不仅任务量繁重，而且不适合于业务化产品的生产和应用。王祎婷等人(2014)提出构造地理要素趋势面的基本构想，搭建了一个普适性尺度转换方法框架。在普适性尺度转换概念模型的指导下，构建普适性的、独立于地表参数的、统一的尺度转换模型方法具有很重要的意义。

(4) 先验知识有和无：理论上讲，没有先验信息是无法实现尺度转换的，这里的有和无仅仅是相对的概念，如块克里金方法引入了空间变异信息，回归克里金方法则在此基础上引入了更多的先验趋势面信息。虽然理论上讲引入更多的先验信息意味着精度会更高，但本身先验信息的引入也会带来更多的误差和不确定性来源，在某些情况下，先验信息的引入反而会降低尺度转换的误差。因此，如何选择合适的先验信息、如何合理的控制先验信息的误差以及不确定性、如何合理的组织和表达先验知识是需要重视的问题。贝叶斯方法能够综合各种先验信息与样本信息，在其他领域得到了广泛的应用，或许是一种可靠的值得探索的提升尺度转换精度的方法。

此外，现有的升尺度转换研究中对像元尺度的真值定义问题还没解决，同时也缺乏对尺度域与尺度阈值、不确定性等方面的考虑。进行升尺度转换的首要核心问题就是定量遥感反演地表参量的像元尺度真值的定义问题。目前对于像元尺度真值的定义方式主要包括根据物理意义定义参数真值、从地表参量应用的实用性和便捷性的角度进行定义以及借鉴地图综合的思路进行定义三种。李新(2013)认为宏观尺度上的参数的准确估值只能从统计意义上定义，并建议宏观尺度上的参数真值可定义为无偏最优估计。只有在明确像元尺度的真值定义基础上才能有效实现定量遥感升尺度转换，但目前关于像元尺度的真值定义还没达成统一的共识，需要进一步的研究。尺度域与尺度阈值问题是尺度问题中的另一难题，同一尺度域内的决定地理现象的主导因素相似，不同尺度域间的主导机制往往相差较大(Wu和Li，2009)。同一尺度域内的尺度转换模型往往适用性强，精度较高，当跨越尺度域时，尺度转换将变得十分复杂，但现有的研究中往往忽略了尺度域的影响，要实现更好的效果，尺度转换研究需要考虑尺度域、尺度阈值等相关问题。不确定性是定量认识陆地表层系统的最大挑战之一(李新，2013)，定量遥感升尺度转换过程中也存在很大的不确定性，它的精度会受到原始数据精度、先验信息精度、模型精度以及误差传播等方面的影响，但是目前的研究往往是在规避很多不确定因素的基础上进行的，与实际情况不符，如研究中往往忽略了遥感影像成像时间、几何校正、大气校正、配准精度、定标质量以及噪声等因素的影响，下一步需要加强升尺度转换过程中不确定性的量化及控制、误差传递规律等方面的研究。

6 结　语

尺度问题是地理学中存在的基本问题，也是定量遥感领域的核心问题之一。尺度转换是解决定量遥感尺度效应问题的重要方法(栾海军 等，2013c)。本文针对定量遥感升尺度转换方法，分别从面—面升尺度转换、点—面升尺度转换两个角度对目前定量遥感领域中存在的升尺度转换方法进行综述，并分析了升尺度转换方法发展中存在的问题，提出了未来可能的发展方向。此外，从理论发展以及实际应用的角度来看，升尺度转换方法在以下几个方面还存在很大的发展空间和应用需求：

(1) 加强多尺度数据的遥感观测试验：尺度问题的理论和方法的发展严重受限于稀缺的多尺度观测数据，针对此问题国际上已进行了一系列大型观测试验，获取了覆盖地面—航空—卫星的多尺度数据，如BigFoot、BSRN、SURFRAD、FLUXNET等。国内2012年启动的黑河生态水文遥感试验(HiWATER)获取了大量的多尺度观测数据，对于推进尺度转换理论方法的研究具有重要意义。

(2) 多种尺度上推方法的耦合：不同的升尺度转换方法具有各自的特点和适用范围，如何在实际应用中结合各种方法的优势，通过优化组合来实现尺度转换的最优效果，以减小尺度上推过程中存在的不确定性也是需要进一步研究的方向。

(3) 探索分形、贝叶斯等数学手段在尺度转换中的应用：目前，学者已经在尝试利用小波变换、分形几何等数学手段来定量描述尺度效应，但在方法适用性、参数选择、尺度阈值等方面还存在很多问题，需要进一步研究。如何利用数学手段，结合定量遥感地表参数反演的特点，实现尺度效应的公式化描述和连续型尺度转换模型的构建，是值得探索的方向。

(4) 普适性概念模型的具体化：王祎婷等人(2014)提出的构造地理要素趋势面的概念模型，充分利用地表环境要素时间、空间上的信息作为先验知识，通过关联遥感观测新信息和先验趋势面生成指定时空尺度的地表要素产品，为解决原数据信息量不足时引入额外信息和保留关键信息两个关键问题提供了思路。岩石圈、水圈、生物圈和大气圈等多圈层模型耦合是地学发展的最新趋势，各个圈层模型的空间尺度差异性很大，多变量的空间尺度转换将是其中最关键的技术难点。构造地理要素趋势面的普适性尺度转换概念模型，综合考虑了多种时空要素之间的联系，有希望成为解决多模型耦合中尺度转换问题的新途径。

为解决现有升尺度转换过程中存在的问题，升尺度转换研究需要结合自上而下的演绎方法和自下而上归纳方法(李小文和王祎婷，2013)，不断融入多学科交叉知识，借鉴地图综合的思路保留关键信息，依据贝叶斯等思想在原数据信息量不足时引入多源先验信息，循序渐进，分阶段、逐步深入构建严谨、统一、自洽的升尺度转换模型，以期实现遥感尺度问题研究的突破。

志 谢 中国科学院寒区旱区环境与工程研究所李新研究员、审稿专家提出了宝贵意见，在此一并致谢。

参考文献(References)

  • Aman A, Randriamanantena H P, Podaire A and Frouin R. 1992. Upscale integration of normalized difference vegetation index: the problem of spatial heterogeneity. IEEE Transactions on Geoscience and Remote Sensing, 30 (2): 326–338. [DOI: 10.1109/36.134082]
  • An N, Ma Y and Bao Y H. 2015. Image and spectral fidelity study of hyperspectral remote sensing image scaling up based on wavelet transform//Proceedings of SPIE 9669, Remote Sensing of the Environment: 19th National Symposium on Remote Sensing of China. Xi’an, China: SPIE: 96690A [DOI: 10.1117/12.2204853]
  • Asli M and Marcotte D. 1995. Comparison of approaches to spatial estimation in a bivariate context. Mathematical Geology, 27 (5): 641–658. [DOI: 10.1007/BF02093905]
  • Atkinson P M and Tate N J. 2000. Spatial scale problems and geostatistical solutions: a review. The Professional Geographer, 52 (4): 607–623. [DOI: 10.1111/0033-0124.00250]
  • Becker F and Li Z L. 1995. Surface temperature and emissivity at various scales: definition, measurement and related problems. Remote Sensing Reviews, 12 (3/4): 225–253. [DOI: 10.1080/02757259509532286]
  • Berterretche M, Hudak A T, Cohen W B, Maiersperger T K, Gower S T and Dungan J. 2005. Comparison of regression and geostatistical methods for mapping Leaf Area Index (LAI) with Landsat ETM+ data over a boreal forest. Remote Sensing of Environment, 96 (1): 49–61. [DOI: 10.1016/j.rse.2005.01.014]
  • Chen J M. 1999. Spatial scaling of a remotely sensed surface parameter by contexture. Remote Sensing of Environment, 69 (1): 30–42. [DOI: 10.1016/S0034-4257(99)00006-1]
  • Chen J M, Chen X and Ju W. 2013. Effects of vegetation heterogeneity and surface topography on spatial scaling of net primary productivity. Biogeosciences Discussions, 10 (3): 4225–4270. [DOI: 10.5194/bgd-10-4225-2013]
  • Christakos G. 1990. A Bayesian/maximum-entropy view to the spatial estimation problem. Mathematical Geology, 22 (7): 763–777. [DOI: 10.1007/BF00890661]
  • Christakos G and Li X Y. 1998. Bayesian maximum entropy analysis and mapping: a farewell to kriging estimators?. Mathematical Geology, 30 (4): 435–462. [DOI: 10.1023/a:1021748324917]
  • Christakos G, Kolovos A, Serre M L and Vukovich F. 2004. Total ozone mapping by integrating databases from remote sensing instruments and empirical models. IEEE Transactions on Geoscience and Remote Sensing, 42 (5): 991–1008. [DOI: 10.1109/tgrs.2003.822751]
  • Christakos G, Serre M L and Kovitz J L. 2001. BME representation of particulate matter distributions in the state of California on the basis of uncertain measurements. Journal of Geophysical Research: Atmospheres, 106 (D9): 9717–9731. [DOI: 10.1029/2000JD900780]
  • Cohen W B, Maiersperger T K, Gower S T and Turne D P. 2003. An improved strategy for regression of biophysical variables and Landsat ETM+ data. Remote Sensing of Environment, 84 (4): 561–571. [DOI: 10.1016/S0034-4257(02)00173-6]
  • Cosh M H, Jackson T J, Starks P and Heathman G. 2006. Temporal stability of surface soil moisture in the Little Washita River watershed and its applications in satellite soil moisture product validation. Journal of Hydrology, 323 (1/4): 168–177. [DOI: 10.1016/j.jhydrol.2005.08.020]
  • Crow W T, Berg A A, Cosh M H, Loew A, Mohanty B P, Panciera R, de Rosnay P, Ryu D and Walker J P. 2012. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Reviews of Geophysics, 50 (2): RG2002 [DOI: 10.1029/2011rg000372]
  • Crow W T, Ryu D and Famiglietti J S. 2005. Upscaling of field-scale soil moisture measurements using distributed land surface modeling. Advances in Water Resources, 28 (1): 1–14. [DOI: 10.1016/j.advwatres.2004.10.004]
  • de Lannoy G J M, Houser P R, Verhoest N E C, Pauwels V R N and Gish T J. 2007. Upscaling of point soil moisture measurements to field averages at the OPE3 test site . Journal of Hydrology, 343 (1/2): 1–11. [DOI: 10.1016/j.jhydrol.2007.06.004]
  • Ding Y L, Ge Y, Hu M G, Wang J F, Wang J H, Zheng X M and Zhao K. 2014. Comparison of spatial sampling strategies for ground sampling and validation of MODIS LAI products. International Journal of Remote Sensing, 35 (20): 7230–7244. [DOI: 10.1080/01431161.2014.967889]
  • D’Or D. 2003. Spatial Prediction of Soil Properties, the Bayesian Maximum Entropy Approach. Louvain-la-Neuve: Université Catholique de Louvain
  • El Maayar M and Chen J M. 2006. Spatial scaling of evapotranspiration as affected by heterogeneities in vegetation, topography, and soil texture. Remote Sensing of Environment, 102 (1/2): 33–51. [DOI: 10.1016/j.rse.2006.01.017]
  • Erickson T A, Williams M W and Winstral A. 2005. Persistence of topographic controls on the spatial distribution of snow in rugged mountain terrain, Colorado, United States. Water Resources Research, 41 (4): W04014 [DOI: 10.1029/2003wr002973]
  • Ezzahar J, Hoedjes J C B and Chehbouni A. 2007. On the application of scintillometry over heterogeneous grids. Journal of Hydrology, 334 (3/4): 493–501. [DOI: 10.1016/j.jhydrol.2006.10.027]
  • Fan L, Xiao Q, Wen J G, Liu Q, Jin R, You D Q and Li X W. 2015. Mapping high-resolution soil moisture over heterogeneous cropland using multi-resource remote sensing and ground observations. Remote Sensing, 7 (10): 13273–13297. [DOI: 10.3390/rs71013273]
  • Gao S G, Zhu Z L, Liu S M, Jin R, Yang G J and Tan L. 2014. Estimating the spatial distribution of soil moisture based on Bayesian maximum entropy method with auxiliary data from remote sensing. International Journal of Applied Earth Observation and Geoinformation, 32 : 54–66. [DOI: 10.1016/j.jag.2014.03.003]
  • Gao X and Huete A R. 2000. Validation of MODIS land surface reflectance and vegetation indices with multi-scale high spatial resolution data//Proceedings of 2000 IEEE International Geoscience and Remote Sensing Symposium. Honolulu, HI: IEEE: 533–535 [DOI: 10.1109/igarss.2000.861620]
  • Garrigues S, Allard D, Baret F and Weiss M. 2006. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sensing of Environment, 105 (4): 286–298. [DOI: 10.1016/j.rse.2006.07.013]
  • Ge Y, Liang Y Z, Wang J H, Zhao Q Y and Liu S M. 2015. Upscaling sensible heat fluxes with area-to-area regression kriging. IEEE Geoscience and Remote Sensing Letters, 12 (3): 656–660. [DOI: 10.1109/lgrs.2014.2355871]
  • Greifeneder F, Notarnicola C, Bertoldi G, Niedrist G and Wagner W. 2016. From point to pixel scale: an upscaling approach for in situ soil moisture measurements. Vadose Zone Journal, 15(6) [DOI: 10.2136/vzj2015.03.0048] (in press)
  • Guo J M. 2008. An Analysis on Scale Transformation in Remote Sensing-Based on Fractal Theory. Xi’an: Northwest University (郭建明. 2008. 分形理论在遥感影像空间尺度转换中的应用研究. 西安: 西北大学)
  • Hay G J, Niernann K O and Goodenough D J. 1997. Spatial thresholds, image-objects, and upscaling: a multiscale evaluation. Remote Sensing of Environment, 62 (1): 1–19. [DOI: 10.1016/S0034-4257(97)81622-7]
  • He Y Q, Bo Y C, Chai L L, Liu X L and Li A H. 2016. Linking in situ LAI and fine resolution remote sensing data to map reference LAI over cropland and grassland using geostatistical regression method. International Journal of Applied Earth Observation and Geoinformation, 50 : 26–38. [DOI: 10.1016/j.jag.2016.02.010]
  • Hengl T, Heuvelink G B M and Rossiter D G. 2007. About regression-kriging: from equations to case studies. Computers and Geosciences, 33 (10): 1301–1315. [DOI: 10.1016/j.cageo.2007.05.001]
  • Hu M G, Wang J H, Ge Y, Liu M X, Liu S M, Xu Z W and Xu T R. 2015. Scaling flux tower observations of sensible heat flux using weighted area-to-area regression kriging. Atmosphere, 6 (8): 1032–1044. [DOI: 10.3390/atmos6081032]
  • Hu Z L and Islam S. 1997a. Effects of spatial variability on the scaling of land surface parameterizations. Boundary-Layer Meteorology, 83 (3): 441–461. [DOI: 10.1023/A:1000367018581]
  • Hu Z L and Islam S. 1997b. A framework for analyzing and designing scale invariant remote sensing algorithms. IEEE Transactions on Geoscience and Remote Sensing, 35 (3): 747–755. [DOI: 10.1109/36.581996]
  • Hufkens K, Bogaert J, Dong Q H, Lu L, Huang C L, Ma M G, Che T, Li X, Veroustraete F and Ceulemans R. 2008. Impacts and uncertainties of upscaling of remote-sensing data validation for a semi-arid woodland. Journal of Arid Environments, 72 (8): 1490–1505. [DOI: 10.1016/j.jaridenv.2008.02.012]
  • Jiang J L, Liu X N, Liu C H, Wu L, Xia X P, Liu M L and Du Z H. 2015. Analyzing the spatial scaling bias of rice leaf area index from hyperspectral data using wavelet-fractal technique. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8 (6): 3068–3080. [DOI: 10.1109/jstars.2014.2346251]
  • Kang J, Jin R and Li X. 2015. Regression kriging-based upscaling of soil moisture measurements from a wireless sensor network and multiresource remote sensing information over heterogeneous cropland. IEEE Geoscience and Remote Sensing Letters, 12 (1): 92–96. [DOI: 10.1109/LGRS.2014.2326775]
  • Kang J, Jin R, Li X and Zhang Y. 2017. Block kriging with measurement errors: a case study of the spatial prediction of soil moisture in the Middle Reaches of Heihe River Basin. IEEE Geoscience and Remote Sensing Letters, 14 (1): 87–91. [DOI: 10.1109/LGRS.2016.2628767]
  • Li A H, Bo Y C and Chen L. 2011. Bayesian Maximum Entropy data fusion of field observed LAI and Landsat ETM+ derived LAI//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver, BC: IEEE: 2617–2620 [DOI: 10.1109/igarss.2011.6049739]
  • Li A H, Bo Y C, Zhu Y X, Guo P, Bi J and He Y Q. 2013. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sensing of Environment, 135 : 52–63. [DOI: 10.1016/j.rse.2013.03.021]
  • Li X. 2013. Characterization, controlling, and reduction of uncertainties in the modeling and observation of land-surface systems. Science China Earth Sciences, 43 (11): 1735–1742. [DOI: 10.1007/s11430-013-4728-9] ( 李新. 2013. 陆地表层系统模拟和观测的不确定性及其控制. 中国科学: 地球科学, 43 (11): 1735–1742. [DOI: 10.1007/s11430-013-4728-9] )
  • Li X, Jin R, Liu S M, Ge Y, Xiao Q, Liu Q H, Ma M G and Ran Y H. 2016. Upscaling research in HIWATER: progress and prospects. Journal of Remote Sensing, 20 (5): 921–932. [DOI: 10.11834/jrs.20166241] ( 李新, 晋锐, 刘绍民, 葛咏, 肖青, 柳钦火, 马明国, 冉有华. 2016. 黑河遥感试验中尺度上推研究的进展与前瞻. 遥感学报, 20 (5): 921–932. [DOI: 10.11834/jrs.20166241] )
  • Li X W, Strahler A H and Friedl M A. 1999. A conceptual model for effective directional emissivity from nonisothermal surfaces. IEEE Transactions on Geoscience and Remote Sensing, 37 (5): 2508–2517. [DOI: 10.1109/36.789646]
  • Li X W, Wang J D and Strahler A H. 1999. Scale effect of Planck’s law over nonisothermal blackbody surface. Science in China Series E: Technological Sciences, 29 (5): 422–426. [DOI: 10.3321/j.issn:1006-9275.1999.05.007] ( 李小文, 王锦地, Strahler A H. 1999. 非同温黑体表面上Planck定律的尺度效应. 中国科学(E辑), 29 (5): 422–426. [DOI: 10.3321/j.issn:1006-9275.1999.05.007] )
  • Li X W, Wang J D and Strahler A H. 2000. Scale effects and scaling-up by geometric-optical model. Science in China Series E: Technological Sciences, 43 (S1): 17–22. [DOI: 10.1007/BF02916574]
  • Li X W and Wang Y T. 2013. Prospects on future developments of quantitative remote sensing. Acta Geographica Sinica, 68 (9): 1163–1169. [DOI: 10.11821/dlxb201309001] ( 李小文, 王祎婷. 2013. 定量遥感尺度效应刍议. 地理学报, 68 (9): 1163–1169. [DOI: 10.11821/dlxb201309001] )
  • Li X W, Zhao H R, Zhang H and Wang J D. 2002. Global change study and quantitative remote sensing for land surface parameters. Earth Science Frontiers, 9 (2): 365–370. [DOI: 10.3321/j.issn:1005-2321.2002.02.015] ( 李小文, 赵红蕊, 张颢, 王锦地. 2002. 全球变化与地表参数的定量遥感. 地学前缘, 9 (2): 365–370. [DOI: 10.3321/j.issn:1005-2321.2002.02.015] )
  • Liang S L. 2000. Numerical experiments on the spatial scaling of land surface albedo and leaf area index. Remote Sensing Reviews, 19 (1/4): 225–242. [DOI: 10.1080/02757250009532420]
  • Liang S L. 2004. Quantitative Remote Sensing of Land Surfaces. Hoboken, NJ, USA: Wiley-Interscience
  • Liu A L, Wang P F and Ding Y Y. 2012. Introduction to Geostatistics. Beijing: Science Press (刘爱利, 王培法, 丁园圆. 2012. 地统计学概论. 北京: 科学出版社)
  • Liu L Y. 2014a. Vegetation Quantitative Remote Sensing Principles and Applications. Beijing: Science Press (刘良云. 2014a. 植被定量遥感原理与应用. 北京: 科学出版社)
  • Liu L Y. 2014b. Simulation and correction of spatialscaling effects for leaf area index. Journal of Remote Sensing, 18 (6): 1158–1168. [DOI: 10.11834/jrs.20144103] ( 刘良云. 2014b. 叶面积指数遥感尺度效应与尺度纠正. 遥感学报, 18 (6): 1158–1168. [DOI: 10.11834/jrs.20144103] )
  • Liu S M, Xu Z W, Song L S, Zhao Q Y, Ge Y, Xu T R, Ma Y F, Zhu Z L, Jia Z Z and Zhang F. 2016. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agricultural and Forest Meteorology, 230-231 : 97–113. [DOI: 10.1016/j.agrformet.2016.04.008]
  • Liu Y, Wang J D, Zhou H M and Xue H Z. 2014. Upscaling approach for validation of LAI products derived from remote sensing observation. Journal of Remote Sensing, 18 (6): 1189–1198. [DOI: 10.11834/jrs.20144084] ( 刘艳, 王锦地, 周红敏, 薛华柱. 2014. 用地面点测量数据验证LAI产品中的尺度转换方法. 遥感学报, 18 (6): 1189–1198. [DOI: 10.11834/jrs.20144084] )
  • Liu Y B, Hiyama T and Yamaguchi Y. 2006. Scaling of land surface temperature using satellite data: a case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sensing of Environment, 105 (2): 115–128. [DOI: 10.1016/j.rse.2006.06.012]
  • Lu D S, Batistella M, Moran E, Hetrick S, Alves D and Brondizio E. 2011. Fractional forest cover mapping in the Brazilian Amazon with a combination of MODIS and TM images. International Journal of Remote Sensing, 32 (22): 7131–7149. [DOI: 10.1080/01431161.2010.519004]
  • Lu L, Liu S M, Xu Z W, Bai J and Wang J M. 2010. The scale relationship of sensible heat flux measured by large aperture scintillometer and eddy covariance system. Advances in Earth Science, 25 (11): 1273–1282. [DOI: 10.11867/j.issn.1001-8166.2010.11.1273] ( 卢俐, 刘绍民, 徐自为, 白洁, 王介民. 2010. 大孔径闪烁仪和涡动相关仪观测显热通量之间的尺度关系. 地球科学进展, 25 (11): 1273–1282. [DOI: 10.11867/j.issn.1001-8166.2010.11.1273] )
  • Luan H J, Tian Q J, Gu X F, Yu T and Hu X L. 2013a. Establishing continuous scaling of NDVI based on fractal theory and GEOEYE-1 image. Journal of Infrared and Millimeter Waves, 32 (6): 538–544, 549. [DOI: 10.3724/sp.j.1010.2013.00538] ( 栾海军, 田庆久, 顾行发, 余涛, 胡新礼. 2013a. 基于分形理论与GEOEYE-1影像的NDVI连续空间尺度转换模型构建及应用. 红外与毫米波学报, 32 (6): 538–544, 549. [DOI: 10.3724/sp.j.1010.2013.00538] )
  • Luan H J, Tian Q J, Yu T, Gu X F, Huang Y, Hu X L and Yang Y J. 2015. Establishing continuous spatial scaling model of NDVI on fractal theory and five-index estimation system. Journal of Remote Sensing, 19 (1): 116–125. [DOI: 10.11834/jrs.20153340] ( 栾海军, 田庆久, 余涛, 顾行发, 黄彦, 胡新礼, 杨闫君. 2015. 根据分形理论与五指标评价体系构建NDVI连续空间尺度转换模型. 遥感学报, 19 (1): 116–125. [DOI: 10.11834/jrs.20153340] )
  • Luan H J, Tian Q J, Yu T, Hu X L, Huang Y, Du L T, Zhao L M, Wei X, Han J, Zhang Z W and Li S P. 2013b. Modeling continuous scaling of NDVI based on fractal theory. Spectroscopy and Spectral Analysis, 33 (7): 1857–1862. [DOI: 10.3964/j.issn.1000-0593(2013)07-1857-06] ( 栾海军, 田庆久, 余涛, 胡新礼, 黄彦, 杜灵通, 赵利民, 魏曦, 韩杰, 张周威, 李少鹏. 2013b. 基于分形理论的NDVI连续空间尺度转换模型研究. 光谱学与光谱分析, 33 (7): 1857–1862. [DOI: 10.3964/j.issn.1000-0593(2013)07-1857-06] )
  • Luan H J, Tian Q J, Yu T, Hu X L, Huang Y, Liu L, Du L T and Wei X. 2013c. Review of up-scaling of quantitative remote sensing. Advances in Earth Science, 28 (6): 657–664. [DOI: 10.11867/j.issn.1001-8166.2013.06.0657] ( 栾海军, 田庆久, 余涛, 胡新礼, 黄彦, 刘李, 杜灵通, 魏曦. 2013c. 定量遥感升尺度转换研究综述. 地球科学进展, 28 (6): 657–664. [DOI: 10.11867/j.issn.1001-8166.2013.06.0657] )
  • Ma L L. 2008. Study on Spatial Scaling Bias Analyses and Transformation Method of Land Parameters Retrived from Remote Sensing Data. Beijing: Institute of Remote Sensing Applications, Chinese Academy of Sciences (马灵玲. 2008. 遥感可反演地表参数的空间尺度效应分析及转换方法研究. 北京: 中国科学院遥感应用研究所)
  • Ma L L, Li C R, Tang B H, Tang L L, Bi Y Y, Zhou B Y and Li Z L. 2008. Impact of spatial LAI heterogeneity on estimate of directional gap fraction from SPOT-satellite data. Sensors, 8 (6): 3767–3779. [DOI: 10.3390/s8063767]
  • Marceau D J and Hay G J. 1999. Remote sensing contributions to the scale issue. Canadian Journal of Remote Sensing, 25 (4): 357–366. [DOI: 10.1080/07038992.1999.10874735]
  • Mayaux P and Lambin E F. 1995. Estimation of tropical forest area from coarse spatial resolution data: a two-step correction function for proportional errors due to spatial aggregation. Remote Sensing of Environment, 53 (1): 1–15. [DOI: 10.1016/0034-4257(95)00038-3]
  • Pelgrum H. 2000. Spatial Aggregation of Land Surface Characteristics: Impact of Resolution of Remote Sensing Data on Land Surface Modelling. Netherlands: Wageningen Universiteit
  • Peng G L, Liu S M, Cai X H, Lu L and Xu Z W. 2008. Footprint analysis of turbulent flux measurement over heterogeneous surface. Chinese Journal of Atmospheric Sciences, 32 (5): 1064–1070. [DOI: 10.3878/j.issn.1006-9895.2008.05.06] ( 彭谷亮, 刘绍民, 蔡旭晖, 卢俐, 徐自为. 2008. 非均匀下垫面湍流通量观测的印痕分析. 大气科学, 32 (5): 1064–1070. [DOI: 10.3878/j.issn.1006-9895.2008.05.06] )
  • Qin J, Yang K, Lu N, Chen Y Y, Zhao L and Han M L. 2013. Spatial upscaling of in-situ soil moisture measurements based on MODIS-derived apparent thermal inertia. Remote Sensing of Environment, 138 : 1–9. [DOI: 10.1016/j.rse.2013.07.003]
  • Raffy M. 1992. Change of scale in models of remote sensing: a general method for spatialization of models. Remote Sensing of Environment, 40 (2): 101–112. [DOI: 10.1016/0034-4257(92)90008-8]
  • Ran Y H and Li X. 2009. Up scaling of point soil moisture measurements to pixel averages based on block kriging. Journal of Glaciology and Geocryology, 31 (2): 275–283. ( 冉有华, 李新. 2009. 基于块克里金的土壤水分点观测向像元尺度的尺度上推研究. 冰川冻土, 31 (2): 275–283. )
  • Riihelä A, Laine V, Manninen T, Palo T and Vihma T. 2010. Validation of the Climate-SAF surface broadband albedo product: comparisons with in situ observations over Greenland and the ice-covered Arctic Ocean. Remote Sensing of Environment, 114 (11): 2779–2790. [DOI: 10.1016/j.rse.2010.06.014]
  • Shi Y C, Qu Y H, Wang J D and Zhou H M. 2014. Upscaling in-situ leaf area index measurements to obtain the representative ground-truth of the heterogeneous land surface//Proceedings of the 3rd International Conference on Agro-Geoinformatics. Beijing, China: IEEE: 1–5 [DOI: 10.1109/Agro-Geoinformatics.2014.6910621]
  • Shi Y C, Wang J D, Qin J and Qu Y H. 2015. An upscaling algorithm to obtain the representative ground truth of LAI time series in heterogeneous land surface. Remote Sensing, 7 (10): 12887–12908. [DOI: 10.3390/rs71012887]
  • Simic A, Chen J M, Liu J and Csillag F. 2004. Spatial scaling of net primary productivity using subpixel information. Remote Sensing of Environment, 93 (1/2): 246–258. [DOI: 10.1016/j.rse.2004.07.008]
  • Smith R J. 2009. Use and misuse of the reduced major axis for line-fitting. American Journal of Physical Anthropology, 140 (3): 476–486. [DOI: 10.1002/ajpa.21090]
  • Su L H, Li X W and Huang Y X. 2001. An review on scale in remote sensing. Advance in Earth Sciences, 16 (4): 544–548. [DOI: 10.3321/j.issn:1001-8166.2001.04.016] ( 苏理宏, 李小文, 黄裕霞. 2001. 遥感尺度问题研究进展. 地球科学进展, 16 (4): 544–548. [DOI: 10.3321/j.issn:1001-8166.2001.04.016] )
  • Tian Q J and Jin Z Y. 2006. Research on calculation and spatial scaling of forest leaf area index from remote sensing image. Remote Sensing Information, 21 (4): 5–11. [DOI: 10.3969/j.issn.1000-3177.2006.04.003] ( 田庆久, 金震宇. 2006. 森林叶面积指数遥感反演与空间尺度转换研究. 遥感信息, 21 (4): 5–11. [DOI: 10.3969/j.issn.1000-3177.2006.04.003] )
  • Tian Y H, Wang Y J, Zhang Y, Knyazikhin Y, Bogaert J and Myneni R B. 2003. Radiative transfer based scaling of LAI retrievals from reflectance data of different resolutions. Remote Sensing of Environment, 84 (1): 143–159. [DOI: 10.1016/S0034-4257(02)00102-5]
  • Timmermans W J, Su Z and Olioso A. 2009. Footprint issues in scintillometry over heterogeneous landscapes. Hydrology and Earth System Sciences, 13 (11): 2179–2190. [DOI: 10.5194/hess-13-2179-2009]
  • Wang J H, Ge Y, Heuvelink G B M and Zhou C H. 2015. Upscaling in situ soil moisture observations to pixel averages with spatio-temporal geostatistics . Remote Sensing, 7 (9): 11372–11388. [DOI: 10.3390/rs70911372]
  • Wang J H, Ge Y, Song Y Z and Li X. 2014. A geostatistical approach to upscale soil moisture with unequal precision observations. IEEE Geoscience and Remote Sensing Letters, 11 (12): 2125–2129. [DOI: 10.1109/lgrs.2014.2321429]
  • Wang K C, Liu J M, Zhou X J, Sparrow M, Ma M, Sun Z A and Jiang W H. 2004. Validation of the MODIS global land surface albedo product using ground measurements in a semidesert region on the Tibetan Plateau. Journal of Geophysical Research: Atmospheres, 109 (D5): D05107 [DOI: 10.1029/2003JD004229]
  • Wang L W, Wei Y X and Niu Z. 2010. Spatial scaling of net primary productivity model based on remote sensing. Journal of Remote Sensing, 14 (6): 1074–1089. [DOI: 10.11834/jrs.20100602] ( 王莉雯, 卫亚星, 牛铮. 2010. 净初级生产力遥感估算模型空间尺度转换. 遥感学报, 14 (6): 1074–1089. [DOI: 10.11834/jrs.20100602] )
  • Wang P J, Xie D H, Zhang J H, Zhu Q J and Chen J M. 2007. Spatial scaling of net primary productivity based on process model in Changbai Mountain Natural Reserve. Acta Ecologica Sinica, 27 (8): 3215–3223. [DOI: 10.3321/j.issn:1000-0933.2007.08.015] ( 王培娟, 谢东辉, 张佳华, 朱启疆, 陈镜明. 2007. 基于过程模型的长白山自然保护区森林植被净第一性生产力空间尺度转换方法. 生态学报, 27 (8): 3215–3223. [DOI: 10.3321/j.issn:1000-0933.2007.08.015] )
  • Wang Y T, Xie D H and Li X W. 2014. Universal scaling methodology in remote sensing science by constructing geographic trend surface. Journal of Remote Sensing, 18 (6): 1139–1146. [DOI: 10.11834/jrs.20144108] ( 王祎婷, 谢东辉, 李小文. 2014. 构造地理要素趋势面的尺度转换普适性方法探讨. 遥感学报, 18 (6): 1139–1146. [DOI: 10.11834/jrs.20144108] )
  • Wen J G. 2008. Study on Retrival of Land Surface BRDF/Albedo and Its Scale Effects in Complex Terrain. Institute of Remote Sensing Applications. Beijing: Institute of Remote Sensing Applications, Chinese Academy of Sciences (闻建光. 2008. 复杂地形条件下地表BRDF/反照率遥感反演与尺度效应研究. 北京: 中国科学院遥感应用研究所)
  • Wen J G, Liu Q, Liu Q H, Xiao Q and Li X W. 2009. Scale effect and scale correction of land-surface albedo in rugged terrain. International Journal of Remote Sensing, 30 (20): 5397–5420. [DOI: 10.1080/01431160903130903]
  • Wu C F, Wu J P, Luo Y M, Zhang L M and DeGloria S D. 2009. Spatial prediction of soil organic matter content using cokriging with remotely sensed data. Soil Science Society of America Journal, 73 (4): 1202–1208. [DOI: 10.2136/sssaj2008.0045]
  • Wu H. 2010. Study on Scale Effects and Scaling Method for Land Surface Key Parameters: Case Studies for Leaf Area Index and Surface Temperature. Beijing: Graduate University of Chinese Academy of Sciences (吴骅. 2010. 地表关键特征参数的尺度效应与尺度转换方法研究: 以叶面积指数和地表温度为例. 北京: 中国科学院研究生院)
  • Wu H, Jiang X G, Xi X H, Li C R and Li Z L. 2009. Comparison and analysis of two general scaling methods for remotely sensed information. Journal of Remote Sensing, 13 (2): 183–189. [DOI: 10.11834/jrs.20090235] ( 吴骅, 姜小光, 习晓环, 李传荣, 李召良. 2009. 两种普适性尺度转换方法比较与分析研究. 遥感学报, 13 (2): 183–189. [DOI: 10.11834/jrs.20090235] )
  • Wu H and Li Z L. 2009. Scale issues in remote sensing: a review on analysis, processing and modeling. Sensors, 9 (3): 1768–1793. [DOI: 10.3390/s90301768]
  • Wu H, Tang B H, Jiang X G, Bi Y Y and Li Z L. 2008. A novel scaling method based on equivalent parameters for remote sensing data//2008 Remote Sensing Symposium Across Taiwan Strait. Guilin: Institute of Remote Sensing Applications, Chinese Academy of Sciences (吴骅, 唐伯惠, 姜小光, 毕于运, 李召良. 2008. 基于等效参数的遥感信息尺度转换方法研究//2008海峡两岸遥感大会论文集. 桂林: 中国科学院遥感应用研究所)
  • Wu H, Tang B H and Li Z L. 2013. Impact of nonlinearity and discontinuity on the spatial scaling effects of the leaf area index retrieved from remotely sensed data. International Journal of Remote Sensing, 34 (9/10): 3503–3519. [DOI: 10.1080/01431161.2012.716537]
  • Wu L, Liu X N, Zheng X P, Qin Q M, Ren H Z and Sun Y J. 2015a. Spatial scaling transformation modeling based on fractal theory for the leaf area index retrieved from remote sensing imagery. Journal of Applied Remote Sensing, 9 (1): 096015 [DOI: 10.1117/1.jrs.9.096015]
  • Wu L, Qin Q M, Liu X N, Ren H Z, Wang J H, Zheng X P, Ye X and Sun Y J. 2016a. Spatial up-scaling correction for leaf area index based on the fractal theory. Remote Sensing, 8 (3): 197 [DOI: 10.3390/rs8030197]
  • Wu X D, Wen J G, Xiao Q, Liu Q, Peng J J, Dou B C, Li X H, You D Q, Tang Y and Liu Q H. 2016b. Coarse scale in situ albedo observations over heterogeneous snow-free land surfaces and validation strategy: a case of MODIS albedo products preliminary validation over northern China. Remote Sensing of Environment, 184 : 25–39. [DOI: 10.1016/j.rse.2016.06.013]
  • Wu X D, Xiao Q, Wen J G, Liu Q, You D Q, Dou B C, Tang Y and Li X W. 2015b. Optimal nodes selectiveness from WSN to fit field scale albedo observation and validation in long time series in the Foci experiment areas, Heihe. Remote Sensing, 7 (11): 14757–14780. [DOI: 10.3390/rs71114757]
  • Xu X R. 2005. Physical Principles of Remote Sensing. Beijing: Beijing University Press (徐希孺. 2005. 遥感物理. 北京: 北京大学出版社)
  • Zelic A, Chen J M, Liu J and Csillag F. 2002. Algorithms for spatial scaling of net primary productivity using subpixel information//Proceedings of 2002 IEEE International Geoscience and Remote Sensing Symposium. Toronto, Ontario, Canada: IEEE: 1066–1068 [DOI: 10.1109/igarss.2002.1025777]
  • Zhang R H, Tian J, Li Z L, Su H B, Chen S H and Tang X Z. 2010. Principles and methods for the validation of quantitative remote sensing products. Science China Earth Sciences, 53 (5): 741–751. [DOI: 10.1007/s11430-010-0021-3]
  • Zhao L, Yang K, Qin J, Chen Y Y, Tang W J, Montzka C, Wu H, Lin C G, Han M L and Vereecken H. 2013. Spatiotemporal analysis of soil moisture observations within a Tibetan mesoscale area and its implication to regional soil moisture measurements. Journal of Hydrology, 482 : 92–104. [DOI: 10.1016/j.jhydrol.2012.12.033]
  • Zhou M and Zhang J L. 2011. Review on scale transformation for remote sensing image and selection of optimal spatial resolution. World Nuclear Geoscience, 28 (2): 94–98. [DOI: 10.3969/j.issn.1672-0636.2011.02.006] ( 周觅, 张杰林. 2011. 遥感影像尺度转换及最优尺度选择探讨. 世界核地质科学, 28 (2): 94–98. [DOI: 10.3969/j.issn.1672-0636.2011.02.006] )
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体