出版日期: 2018-03-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20186461
2018 | Volumn22 | Number 2
上一篇 | 下一篇

技术方法

风能方向性参量遥感反演

朱晓辉^1,2 , 杨晓峰¹ , 杜延磊^1,2 , 井成^1,3 , 刘桂红¹ , 李紫薇¹

1. 中国科学院遥感与数字地球研究所遥感科学国家重点实验室，北京 100101

2. 中国科学院大学，北京 100049

3. 中国空间电子信息技术研究院，西安 710199

收稿日期: 2016-12-08

基金项目: 国家自然科学基金(编号: 41371355)

第一作者简介: 朱晓辉(1993—　)，男，硕士研究生，研究方向为海洋遥感。E-mail：zhuxh@radi.ac.cn

通讯作者简介: 李紫薇(1960—　)，女，研究员，研究方向为海洋遥感、GNSS-R海面风场遥感。E-mail：lizw@radi.ac.cn

中图分类号: TP79

文献标识码: A

摘要

目前可遥感反演的海上风能参量主要为平均风速和平均风功率密度，缺乏对风能方向性参量的反演。本文建立了以风向频率、风能密度方向分布为核心的风能方向性参量体系及相应的反演方法，使用2007年—2016年ASCAT星载散射计观测数据进行了反演实验，并利用海上现场观测数据对反演结果进行比较验证，通过理论分析和模拟实验对反演方法的数据量需求和误差传递进行了分析。结果表明，90%的反演结果通过了所有的同一性检验，验证了其有效性和准确性；风向频率和风能密度方向分布准确反演所需的最小数据量分别为350条和800条；遥感反演的风速风向数据的误差使得最终反演的风能方向性参量趋于离散，真实的风能方向分布越集中，对其影响越敏感。

关键词

风能, 风能方向性参量, ASCAT, 风向频率, 风能密度方向分布, 海面风场, 方向统计

Estimation of directional distribution of wind energy from satellite observations

ZHU Xiaohui^1,2 , YANG Xiaofeng¹ , DU Yanlei^1,2 , JING Cheng^1,3 , LIU Guihong¹ , LI Ziwei¹

1.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Science, Beijing 100101, China

2.University of Chinese Academy of Sciences, Beijing 100049, China

3.China Academy of Space Technology, Xi’an 710199, China

Abstract

The offshore wind energy industry has surged in recent years as a main source of clear energy. Meanwhile, remote sensing can retrieve sea surface wind data and provide valuable information to locate suitable offshore wind power plants. Published studies mostly focus on the retrieval of average wind speed and average wind power density. However, wind directional distribution is also required in locating potential offshore wind power plants. Therefore, a method is proposed to retrieve the directional distribution of wind energy from satellite scatterometer observations. According to Chinese national standard (GB/T 18710-2002), wind directional frequency and directional distribution of wind energy density are used to delineate the directional distribution of wind energy. In addition, certain circular statistical parameters of wind energy, circular mean, and circular standard deviation are selected to depict the characteristic of wind energy. Wind speed and directional data in certain timespans are used as input in the proposed method. These wind data can be obtained from satellite observations or reanalysis datasets. Then, 0.1°×0.1° global maps of wind energy directional distribution parameters are retrieved by the proposed method from 2007—2016 advanced scatterometer (ASCAT) wind products. These retrieval results are accordant with antecedent research and scientific facts. To test and verify these retrieved results, they are compared with parameters calculated from 20 NDBC buoys. First, the ASCAT wind products and buoy data are screened for quality control. Then, all buoy-measured winds are converted to 10 m height to match the ASCAT wind retrievals. Subsequently, a time and spatial matchup dataset of ASCAT and buoy data are built, and the differences between them are calculated. A non-parametric hypothesis test is also implied to assess the accuracy of circular error statistics. A total of 80% of the test dataset pairs passed all hypothesis tests and satisfied all assessment criteria (total difference <10%). Meanwhile, 100% of the dataset pairs satisfied the criteria and passed the test in which only wind direction parameters were considered. Furthermore, 90% of the dataset pairs passed the test for wind energy circular statistical parameters. In addition, 80% of the dataset pairs satisfied the total difference criteria of directional distribution wind energy. One model was constructed to describe the relation between the retrieval accuracy of wind directional distributions and record number using the law of large numbers and a basic understanding of the remote sensing process. The function that expresses the relation between record number and retrieval accuracy was obtained, and the minimal record number required to obtain reliable retrieval results was calculated with the aforementioned function by numerical stimulation and curve fitting. Moreover, the impact of the time characteristic of remote sensing data (fixed local time) was considered in the analysis. Models were built to describe the retrieval error of the remote sensing process and the actual offshore wind directional distributions on the basis of normal distribution and circular statistics. These models enabled us to understand the effect of the retrieval error of remote sensing quantitatively and qualitatively. Thus, the deconvolution algorithm was designed to eliminate this effect. Conclusion: (1) The proposed parameter systems can be retrieved by remote sensing data to depict the directional characteristics of wind energy thoroughly. (2) Two methods, namely, the total difference and the Kuiper test, were effectively used to test and verify the difference among the directional distributions. The Kuiper test results showed that the total difference identical criterion of the two directional distributions was built. (3) The validation demonstrated the effectivity and accuracy of the new method and the data product produced by this model. (4) At least 800 records were required for the reliable retrieval of DDED, and the number for DF was 350. (5) The error in the retrieval of wind direction from remote sensing data influenced not only the final retrieval accuracy of the directional distribution of wind energy but also the distribution itself. The more dispersed the distribution, the less the effect of the retrieval error of wind direction on the accuracy of directional distribution retrieval.

Key words

offshore wind energy, wind directional distribution, ASCAT, wind direction frequency, wind power density, sea surface wind vector, direction statistics

1 引　言

为满足中国增长的能源需求，应对气候变化，十三五期间在国家战略和政策导向上鼓励和推动风能产业的发展(朱明，2015)。近年来，风能产业在中国获得了巨大而快速的发展(中国可再生能源学会风能专业委员会，2016)。海上风电的单机发电功率更高，更为稳定，距离电力需求也更近，有着自身发展的独特优势(郑崇伟等，2014)。随着限制海上风电发展的技术难题逐渐解决，风电场水深和离岸距离都不断增加，海上风电发展潜力巨大(夏云峰，2016)。

风电场的选址，对于其成本和收益有着巨大的影响(娜仁花，2015)。遥感数据具有较高空间分辨率和大面积同步观测两大不可替代的优势，已经开始在海上风电场选址中发挥出重要作用(Heckenbergerova 等, 2015)。

根据国家标准《GBT 18710-2002风电场风能资源评估方法》，用于风能评估的参量除了用于评估风能大小的平均风速和平均风功率密度，还包括用于评估风能方向性分布的风向频率和风能密度方向分布。但是，目前基于遥感数据进行的海面风能研究，其主要反演参数为平均风速和平均风功率密度。Doubrawa等人(2015)、Chang等人(2015)和Hasager等人(2015a, 2005b)综合使用SAR和微波散射计数据分别对美国五大湖区、中国南海和欧洲北部海域的风能状况进行了评估，他们使用的评价指标均为平均风速和平均风功率密度。Hasager等人(2015b)使用遥感数据对4个浮标站位的风向频率玫瑰图进行了计算并和浮标观测的风向频率玫瑰图进行了对比，但这种视觉对比还是非常主观的、无法定量评价的。总体说来目前对于风能方向性参量的研究还处于起步状态，尚无系统地针对海面风场的总体风能方向性进行评价的参量体系，也没有对应的定量反演和评价方法。

本文基于数理统计模型，提出可描述风能方向性的遥感参量，并利用ASCAT海面风场产品数据计算了全球海面风能方向性参数，为了验证结果的准确性，利用海面浮标的风场实测数据对其进行精度检验。进一步地，通过误差分析和最小数据量需求分析，论证了风能方向性遥感反演方法的实用性和可靠性，为近岸风能的方向性评估提供了理论基础和技术手段。

2 风能方向性参量的定义与计算方法

2.1 风向频率和风能密度方向分布

在气象学上，风向共有16个方位。风向频率和风能密度方向分布对于风场的风能方向特征的统计和描述正是基于这16个方位的。

风向频率DF (wind direction frequency)是表征风向特征的一种统计性方向分布。它统计了某特定地点不同方位风向在过去某特定时间段内，出现次数占总观测次数的百分比(中华人民共和国国家质量监督检验检疫总局，2002)。

类似的，风能密度方向分布DDED (direction distributions of wind energy density)统计了特定地点在过去一段时间内，各方位风能密度与全方位总风能密度的百分比(中华人民共和国国家质量监督检验检疫总局，2002)。

风向频率和风能密度方向分布是反映特定数据在不同类别上分布情况的一组数值，而不是像温度、平均风速等数值型参量一样的单一参数。因此，它们的表达方式并不像数值型参量一样直观。通常，这两个参量都借由玫瑰图来进行表达。玫瑰图是极坐标体系下的柱状图或者折线图，不同的方位角区间来表示风向的不同方位。

2.2 风能方向性分布的特征参数

在统计上，平均值和标准差可以用来直观得了解一组数据的总体特征。对于风能方向分布，统计参数也可以用来把握其总体特征。对于风向这样的具有循环特性的角度数据，需要使用圆域分布(circular distribution)统计方法计算其平均值和标准差。在使用风向数据计算平均风向和风向标准差计算过程中加入风能密度作为权重，所获得的结果可以反映风能密度方向分布的统计特征。

圆域均值(circular mean)表征了分布在角度域上平均值出现的位置。当风向或者风能密度呈单峰分布时，其圆域均值尤为重要。圆域标准差(circular standard deviation)(Batschelet，1981)表征了分布在圆域上的离散性和集中度。圆域标准差越大，表征了数据越离散，在整个圆域上分布越均衡，可能存在多峰分布。

平均风向或平均风能方向 $\bar \alpha $ (Pewsey 等，2013)

${x_i} = \cos {\alpha _i}, {y_i} = \sin {\alpha _i}$

(1)

$\bar x = \sum\limits_{i = 1}^n {({x_i} \times {D_{{wei}}})} /\sum\limits_{i = 1}^n {{D_{{wei}}}} $

(2)

$\bar y = \sum\limits_{i = 1}^n {({y_i} \times {D_{{wei}}}})/\sum\limits_{i = 1}^n {{D_{{wei}}}} $

(3)

$\bar \alpha = \left\{ \begin{aligned}& {{arctg}}(\bar y/\bar x), \bar x > 0\\ & 180^\circ + {{arctg}}(\bar y/\bar x), \bar x < 0\\ & 90^\circ, \bar x = 0, \bar y > 0\\ & 270^\circ, \bar x = 0, \bar y < 0\\ & \text{不定}, \bar x = 0, \bar y = 0\end{aligned} \right.$

(4)

式中， $\alpha {}_i$ 为第i条数据的风向， ${D_{{wei}}}$ 为第i条数据的风能密度，当计算平均风向时 ${D_{{wei}}}{{ = }}1$ ，即消除其对计算结果的影响。

风向标准差或风能方向标准差s (Pewsey 等，2013)

$s = \sqrt { - \ln ({{\bar x}^2} + {{\bar y}^2})} $

(5)

同样的，计算风向标准差时， $\bar x$ 和 $\bar y$ 的计算中的 ${D_{{wei}}}{{ = }}1$ 。

3 数　据

3.1 卫星遥感数据

3.1.1 数据源

风能方向性参量的反演必须基于大量高空间分辨率的风向数据。虽然多种微波遥感手段都可以进行海面风场反演，但高度计和普通微波辐射计不具备风向反演能力，并不适合此应用目的。微波散射计和合成孔径雷达的空间分辨率和风向风速反演精度均较高(Yang 等，2011, 2014)，是风能方向性参量遥感反演的较为适宜的数据源。

考虑到风能方向性参量的准确计算需要长期连续观测数据，本文使用了美国RSS(Remote Sensing Systems)生产的MetOp-A卫星ASCAT散射计海面风场产品，数据获取时间为2007-03-01—2016-02-29(Ricciardulli和Wentz, ，2016)。该产品利用EUMETSAT(European Organization for the Exploitation of Meteorological Satellites)提供的L1B级数据，使用针对ASCAT开发的C-2015地球物理模式函数生产。

3.1.2 数据预处理

海面风场数据在使用前先，根据RSS提供的数据文档中建议的质量控制流程和数据产品中附带的质量控制辅助数据进行了质量控制，剔除了刈幅外围的数据、对地球物理模式函数(C-2015)拟合效果不好的数据和可能存在降雨干扰的数据(Ricciardulli和Wentz，2016)。根据ASCAT用户手册，大于25 m/s的风速可信性较低，本文进行了剔除，这一测风范围有效规避了风速大于风机安全阈值的无效样本。

通过上述筛选，保证了研究中所采用的遥感数据具有较高的数据质量和可信度。

3.2 固定浮标站位数据

3.2.1 数据源

为了验证基于卫星遥感数据计算的风能方向性参数的准确性，以及通过模拟实验分析遥感数据的样本量和样本代表性对反演结果的影响，本文使用了大量固定浮标站位数据。

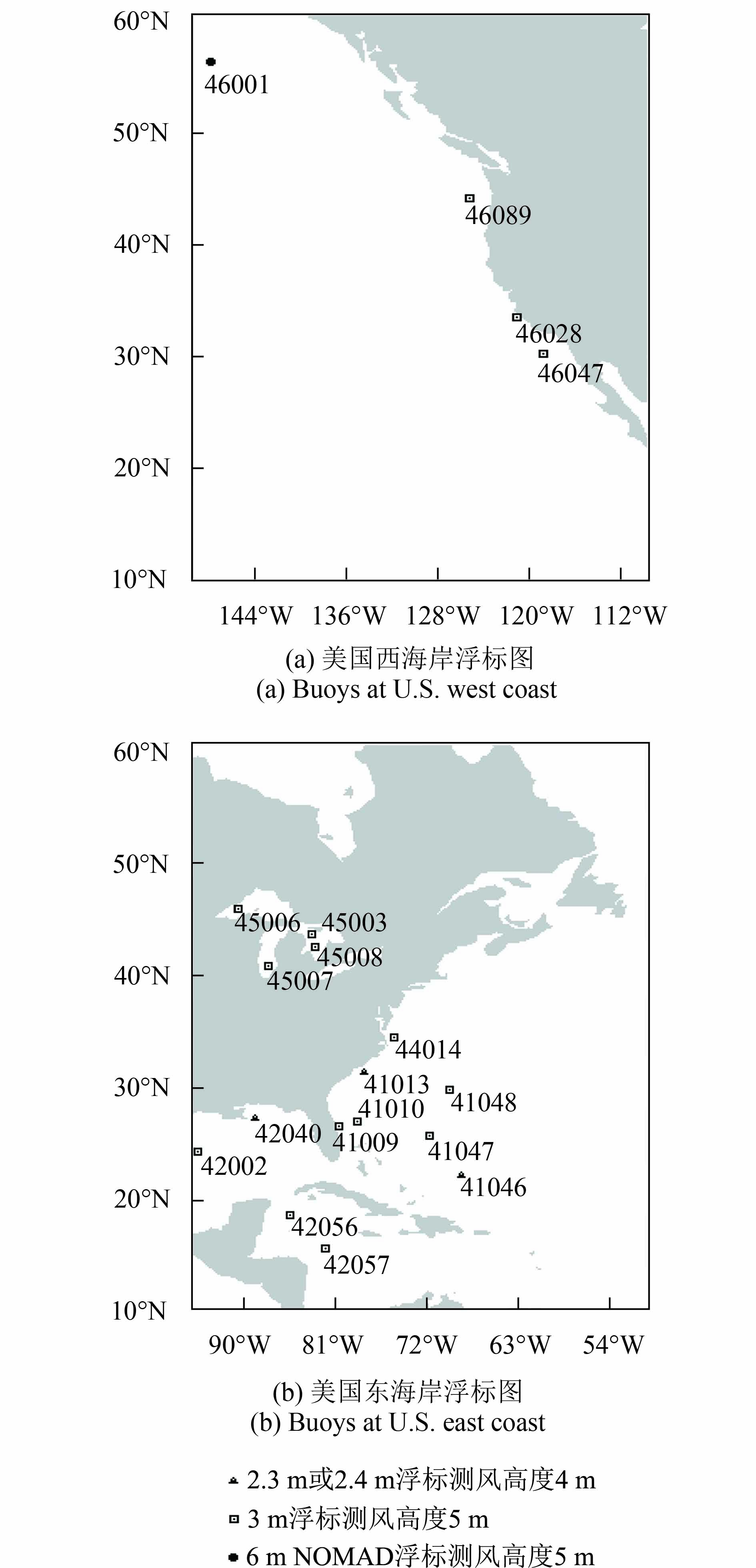
在反演结果的准确性验证部分，从美国大气海洋局NOAA(National Ocean and Atmosphere Administrator)国家浮标数据中心NDBC(National Data Buoy Center)选取了在2007-03—2016-03具有连续数据、且数据质量合格率大于80%的20个固定浮标站位。选取的20个浮标来自于美国东海岸、西海岸、墨西哥湾、五大湖区以及加勒比海(图1)。选取的浮标具有纬度、海陆关系、气压带和风带的多样性，保证了验证的全面性和可靠性。

图 1 浮标位置和相关信息

Fig. 1 The locations of buoys used in this study

在最小数据量分析的模拟实验部分，在美国东西海岸以及墨西哥湾内各选择了一个浮标。其中，东海岸的浮标41048具有近岸风场的一般特征，即风向变化较大，风速相对较小。墨西哥湾内的浮标42040，有时会受到飓风的影响，记录有极端高风速数据。西海岸的浮标46001离岸较远，风向较为恒定，风速也较大。此3个浮标涵盖了较为多元的海面风场情况。

3.2.2 数据预处理

为了保证所采用的浮标数据的质量，剔除较为明显的误差，采取下列标准剔除可靠性较低的数据：

$\left\{ \begin{array}{c}\left| { u} \right| < 0.4m{s^{ - 1}}\\[6pt]\left| { u} \right| > 75m{s^{ - 1}}\\[6pt]\forall \left| {{{{{u}}_i}} } \right| > 15m{s^{ - 1}},\\[6pt]\left| {{{{{u}}_i}} } \right| > \left| {{{{{u}}_{i - 1}}} } \right| \times 1.5 \vee \left| {{{{{u}}_i}} } \right| > \left| { {{{{u}}_{i + 1}}} } \right| \times 1.5\\[6pt]{0^\circ } > \theta > {360^\circ }\end{array} \right.$

(6)

式中， $\left| { u} \right|$ 是风矢量 $ u$ 的模，即风速， $ {{{{u}}_{i - 1}}} $ 和 $ {{{{u}}_{i + 1}}} $ 分别代表第i条风矢量 $ {{{{u}}_i}} $ 前后1小时的风矢量， $\theta $ 是风向的角度。式(6)依次剔除了风速过小的数据，因为由于浮标的机械摩擦，在风速较小时，其风向可能存在较大误差；剔除了可能存在错误的风速过大的记录，这种风速范围即来源于机械转速的极限也源于对海面风速的理解 (Estévez 等，2011)；剔除了在高风速情况下的孤立数据(Doubrawa 等，2015)；剔除了在风向方面记录明显错误的数据。

3.3 数据匹配

在使用固定浮标站位数据对风能方向性参量的反演结果进行精度评价的过程中，必须对二者进行数据匹配，以实现他们在时间、空间和测风高度上的吻合。

ASCAT海面风场产品为10 m高度处的风场，而NDBC风速现场观测值根据浮标测风仪安装高度的不同，测量的是海面不同高度下的风速，浮标观测值需按照NDBC建议的公式(Hsu 等，1994)转化为海面以上10 m高处的风速。

数据的空间匹配以浮标数据的经纬度为标准，选取以其为中心的0.1°×0.1°经纬网格内的遥感数据进行风能方向性参量计算，并与浮标数据的对应参量进行比较。

4 反演结果与精度分析

4.1 反演过程与计算结果

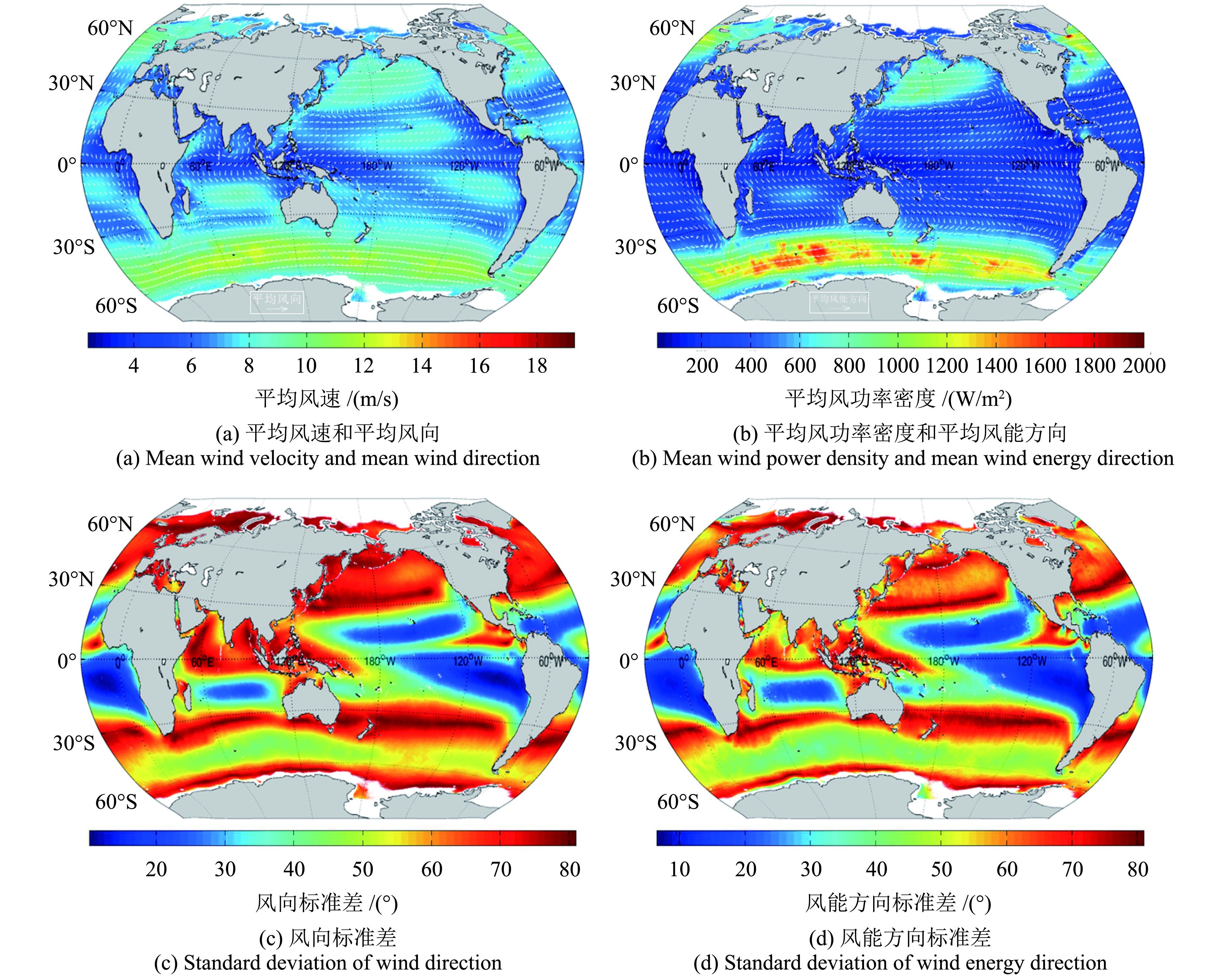
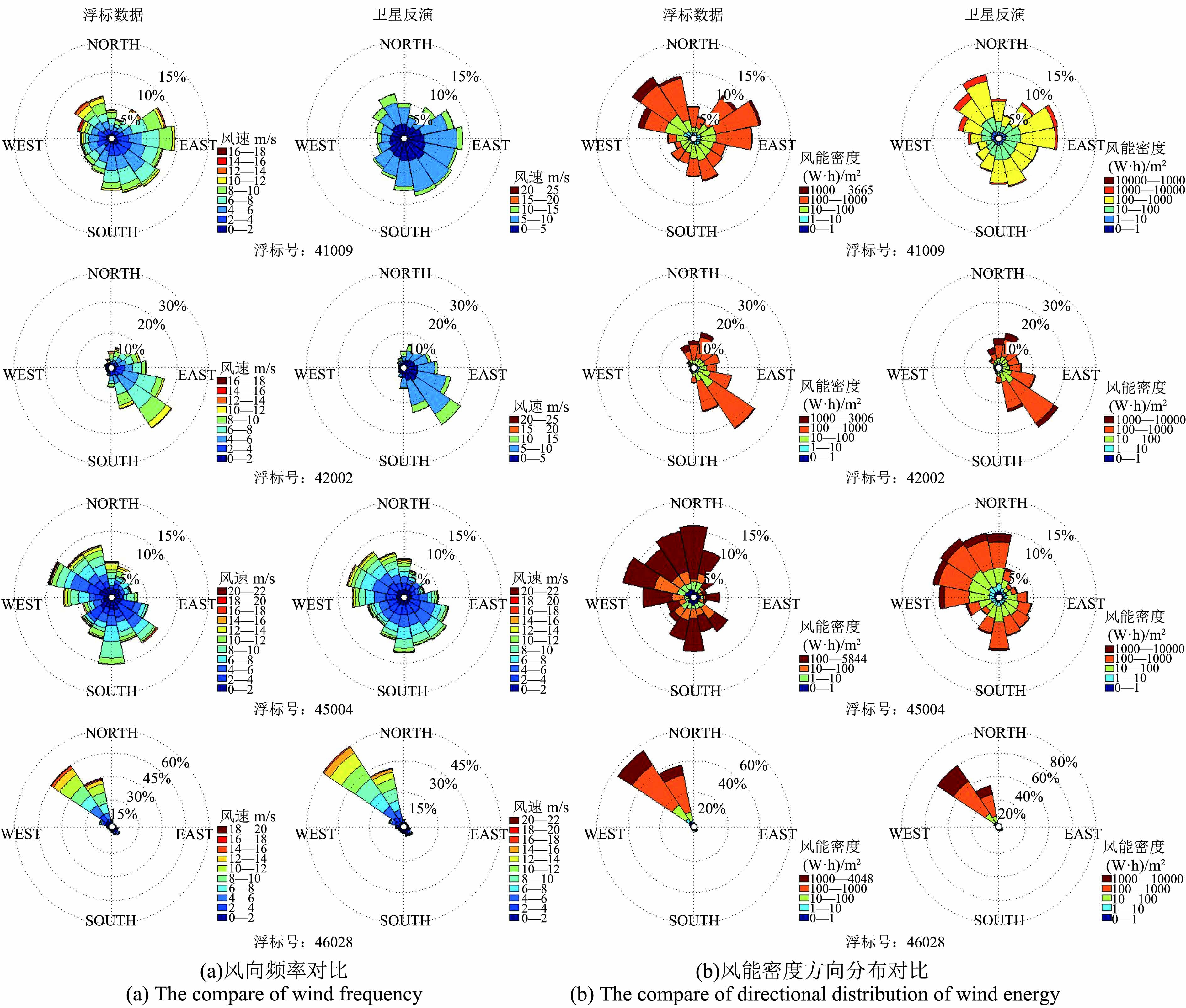
在对RSS生产的ASCAT海面风场产品进行质量控制之后，根据本文所述计算方法，基于0.1°×0.1°经纬网格，对全球海域的风能方向性参量进行了计算。全球海域的风能方向性参数反演结果见图2，其中4个浮标站位的风向频率反演结果请见图3(a)，风能密度方向分布反演结果请见图3(b)。

图 2 风能方向性参量反演结果

Fig. 2 The retrieval results of parameters of wind directional distribution

利用ASCAT海面风场产品计算的平均风速和平均风能密度与利用数值模式长时序模拟数据得到的全球风能评估结果较为吻合(郑崇伟和潘静，2012)。平均风向和平均风能方向在全球尺度也符合目前对于全球大气环流的基本认知。侧面验证了基于遥感数据计算的全球风能方向性参量的正确性。

分析图2可知，西风带尤其是南半球西风带是全球海域中风能蕴藏最为丰富的区域，其平均风能密度能达到1200 W/m²以上，部分区域在2000 W/m²以上。南半球西风带风向也较为稳定，风向标准差在40°—60°。北半球西风带风向较不稳定，但其风能方向标准差明显小于风向标准差，说明虽然风向不稳定，但蕴含较多风能的高速风的风向却较为稳定。除北印度洋区域外信风带风向常年稳定，其风向标准差小于10°，但其稳定的东风风速较低，蕴藏的风能也较小。副热带高气压带和副极地高气压带的风向标准差和风能标准差都较高，此区域的风向稳定性差，没有较为明显的稳定主风向。

由卫星反演的风向频率和风能密度方向分布玫瑰图(图3)可知，42002和46028号浮标所处海域风向常年稳定，具有明显的主方向，不存在显著的季节变化和日内变化。而41009和45004所处海域风向不稳定，存在多个主风向，甚至主风向不明显，并且多个主风向间风能密度存在差异，存在频次高而能量密度低的风向。

图 3 浮标数据与卫星反演结果对比

Fig. 3 The compare of wind rose between buoys and satellite retrieval

4.2 精度检验方法

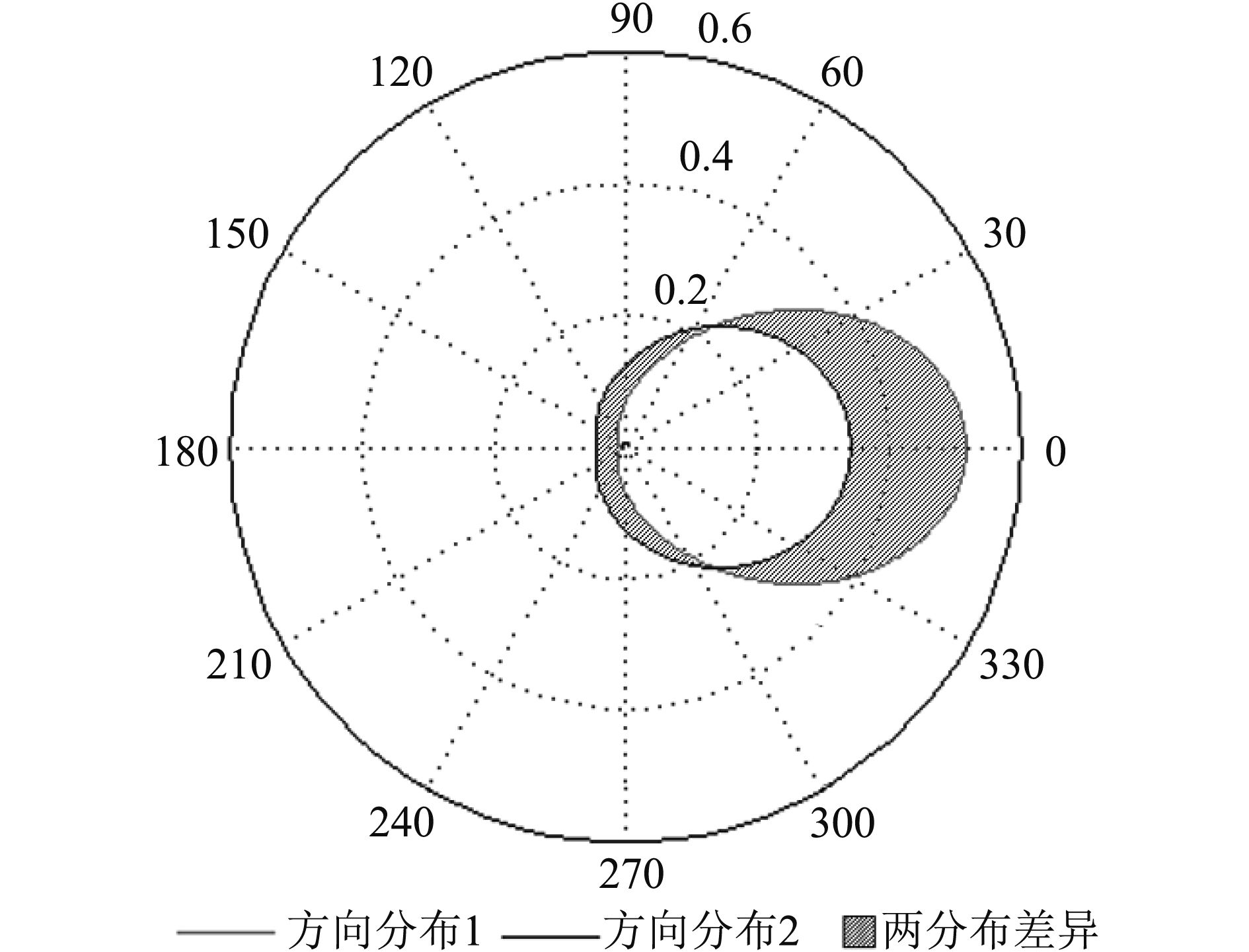
评估两个方向分布的差异需要在它们的分布域内进行。两个方向分布的差异如图4所示，此差异可以通过积分进行计算。因为对差异的积分过程中，通过取绝对值对同一差异重复计算了两次，理论最大值为2。对差异积分后应除以2进行归一化，消除重复计算的影响。

图 4 两个方向分布的差异

Fig. 4 The difference of two directional distributions

本文中风向频率和风能密度方向分布都是16维离散数据，针对此情况我们对积分过程进行了离散化，提出了评价指标归一化总偏差 ${\delta _D}$ 。总偏差通过对两个方向分布参量对应方位所占百分比之差的绝对值求和来计算。归一化总偏差 ${\delta _D}$ 计算公式如下：

${\delta _D} = \frac{1}{2}\sum\limits_{j = 1}^{16} {\left| {D{'_j} - {D_j}} \right|} $

(7)

式中， $D{'_j}$ 是卫星反演的方向分布参数在j方位所占百分比； ${D_j}$ 是浮标数据对应方位所占百分比。

同时，运用循环数据的非参数检验方法Kuiper test(Kuiper，1960)对卫星反演的结果和浮标实测数据的风向频率和风能密度方向分布进行对比互校，判断其是否具有相同的分布。分布的任何一个特征(如均值、方差)上的不一致都会导致Kuiper检验的失败，因此通过检验的两个风向频率或风能密度方向分布在特征参数上也相一致。

4.3 精度检验结果

使用ASCAT产品计算的风能方向性参量与NDBC浮标实测结果之间的误差评定和反演精度评价如表1所示。图3同时展示了4个现场观测站位利用浮标数据和卫星数据分别计算得到的风向频率和风能密度方向分布。从图3中可以看到，遥感反演的玫瑰图与浮标实测的玫瑰图之间差异很小，可以有效反映真实的海面风场的风能方向分布情况。

从表1可知，基于ASCAT产品计算获得的风能方向性参量与实测参量之间的误差较小：80%的结果风向与风能总偏差均低于10%，90%的结果通过了风向与风能分布同一性测试。其中，45003的风能密度方向分布总偏差大于10%，但仍然通过了同一性检验，这是由于在进行离散化的过程中，实际上方向非常接近的数据被分到了不同的方位，增大了归一化总偏差，但实际上分布是相似的。所有与风向频率相关的测试都得到了通过，优于风能方向分布相关的测试结果。这是由于，在风能相关的参数反演中，不仅风向误差，风速误差也对结果产生了影响，增大了误差的积累。

表 1 反演结果误差表
Table 1 The statistic results of retrieval errors

下载CSV

浮标号	风向频率总偏差/%	风向频率 Kuiper 检验	风能密度方向分布总偏差/%	风能密度方向分布 Kuiper检验	反演所用数据量
41009	5.02	通过	8.40	通过	1778
41010	5.24	通过	5.70	通过	1437
41013	6.78	通过	9.17	通过	1315
41046	5.01	通过	9.82	通过	1298
41047	4.41	通过	6.30	通过	1393
41048	4.40	通过	8.72	通过	1503
42002	4.98	通过	3.91	通过	1357
42040	6.74	通过	6.65	通过	1523
42056	3.23	通过	3.54	通过	2020
42057	4.85	通过	4.27	通过	1294
44014	6.16	通过	7.52	通过	1228
45003	5.32	通过	12.48(>10%)	通过	1095
45004	6.65	通过	9.65	通过	946
45006	5.31	通过	9.61	通过	1199
45007	5.44	通过	9.40%	通过	1089
45008	8.32	通过	12.56(>10%)	未通过	971
46001	5.66	通过	10.29(>10%)	通过	1157
46028	5.48	通过	5.69	通过	1364
46047	3.88	通过	2.47	通过	1215
46089	4.42	通过	11.40(>10%)	未通过	1703

总体而言，本文计算的全球海域风能方向性参量的准确性和有效性得到了验证。

5 数据量需求与误差分析

5.1 最小数据量分析

风能方向性分布作为分布类参量对于统计样本量有着较高的需求。正确理解反演精度与数据量的关系，确定最小数据量的需求，对于今后的反演工作有着重要的意义。

5.1.1 数据量与反演精度的关系

现在主流的散射计反演的海面风速误差小于2 m/s，偏差小于0.5 m/s。对于风向的反演也符合这一规律，虽然单次反演的误差仍然较大，但总体偏差却很小。根据RSS提供的ASCAT产品报告，ASCAT风向产品与NCEP(National Centers for Environmental Prediction)再分析风向数据的风向频率分布基本吻合，总体偏差很小。

所以，微波散射计对海面风场的反演结果可以视为对风场真值的一种无偏估计。虽然在目前的技术水平下，单次反演的误差仍然可能较大，但在大量观测的条件下，对于总体的平均情况的估计是没有偏差的，观测值的期望与真实值相等。

与总体分布均值的反演相类比，数据量对于方向分布整体情况的反演的影响也是相似的。在风场产品反演的风速风向不存在误差的情况下，随着数据密度的增加，最终反演的风能方向分布与真实的方向分布是相同的。风场产品反演的风速风向存在无偏的误差时，通过增大数据密度，非系统性的误差之间可以相互抵消。因为风能方向分布的反演精度随着数据密度的增加而提高，存在一个最小数据密度，当数据密度大于此值时，反演精度可以获得Kuiper检验的认可，认为反演是准确的。

对于遥感数据来说，虽然年数据密度无法改变，但风能的方向分布却不存在显著的年际变化。而且，在工程应用中还需要对多年风能情况进行平均。所以通过使用多年遥感数据来增大数据密度，以此来提高反演精度是可行的，与最小数据密度相对应，存在着准确反演的最小数据量。

5.1.2 遥感数据观测时间特征的影响

进行风能方向性参量的反演过程中使用的风场产品的观测时间并不是随机的。由于卫星散射计通常搭载于太阳同步轨道，其获取的海面风场数据只局限于特定的一些地方时(Zhu和Yang，2016)。而近岸海面风场，在海陆相互作用下展现出了明显的日内变化规律(Barthelmie 等，1996)。

因此，即使通过增加数据量，最终反演的风能方向分布也不能等同于真实的方向分布，而是等同于特定地方时区间的风能方向分布。但是，根据精度评价结果可知，并不是要求两个方向分布完全相同才意味数学上的一致。当这个特定地方时区间的风能方向分布与真实分布差异小于一定程度时，通过增大数据量获取的风能方向分布仍然能够与真实分布相一致。

遥感数据观测时间特征的存在提醒我们进行数据量影响分析、确定最小数据量时应该充分考虑这一特征的影响，尽量模拟真实的遥感过程。

5.1.3 模拟实验

为了研究数据量对于方向性参量反演精度的影响，本文进行了以下模拟实验：通过概率取样确定此次取样的地方时，其中地方时取样概率模拟了遥感数据的采样时间特征(图6)。确定了此次取样的地方时后，从这个地方时的真实观测浮标数据中随机抽取一条观测记录加入模拟数据集。独立重复确定地方时并随机取样的过程，建立起数据量n从21至800(约为浮标数据集年数据量的十分之一)递增的模拟遥感数据集。对于每一个数据量为n的数据集，均建立100个独立的含有n条记录的模拟数据子集。

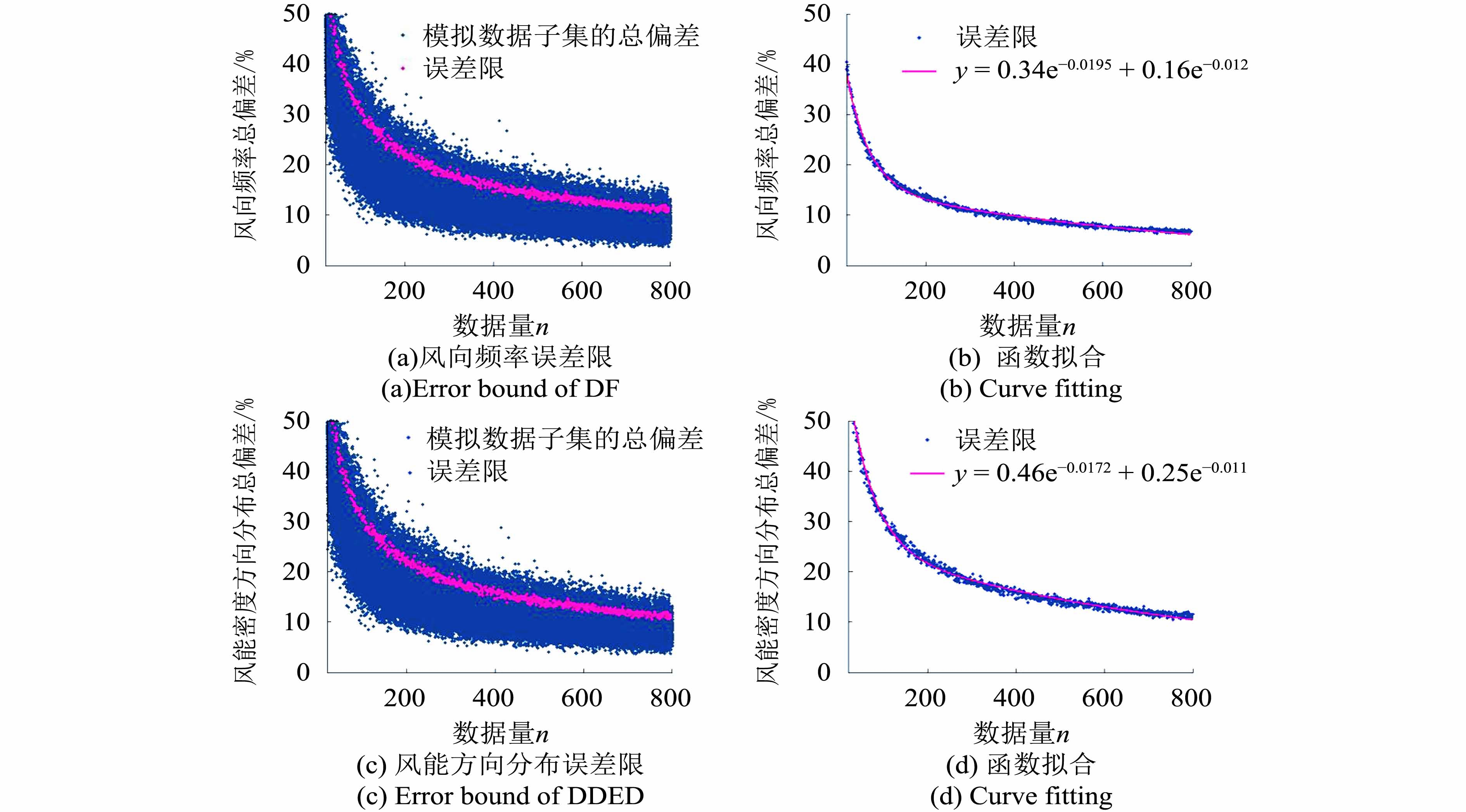
然后，计算生成的模拟数据子集的风向频率和风能密度方向分布，并计算其与真实数据集的风向频率和风能密度方向分布在16个方位向上的归一化总偏差。为了剔除极端数据对于总体情况的影响，对数据量n的100组模拟数据子集的总偏差进行排序，选取上侧十分位数作为在此数据量下的误差限(Barthelmie和Pryor，2003)。

本文选取二项指数函数对误差限进行拟合，利用拟合函数，可以计算误差限降至不同的总偏差值时对应的数据量需求。基于表1中实例反演的精度评价结果，发现当归一化总偏差小于10%，反演结果一定能通过分布的同一性检验，因此，本文规定10%的归一化总偏差为精确反演的理论精度上限。图5为根据上述方法建立数据量与反演精度关系的过程示例。

图 5 总偏差和数据量关系

Fig. 5 The relationship between total difference and records number

本实验中所用3个固定浮标站位对应的ASCAT遥感数据的采样时间特征如图6，取样时间能覆盖4到6个地方时并且不同地方时数据量存在差异。

图 6 ASCAT 采样时间特征

Fig. 6 The characteristic of the time of ASCAT observation

5.1.4 模拟实验结果

基于41048、42040和46001这3个浮标，对于精确反演的数据量需求研究结果见表2。从表2中可知，风能密度分布所需样本量明显大于风向频率。风向稳定区域所需精确反演数据量明显较小。

表 2 准确反演风向频率风和能密度方向分布所需最小数据量
Table 2 The minimum number of records to get reliable retrieval DF and DDED

下载CSV

年份	浮标号：41048		浮标号：42040		浮标号：46001
年份	DF	DDED	DF	DDED	DF	DDED
2005	—	—	366	941	404	704
2006	—	—	373	838	331	745
2007	—	—	363	729	289	548
2008	372	723	370	904	366	785
2009	348	783	329	590	344	800
2010	366	734	365	828	344	688
2011	380	982	377	845	317	710
2012	341	710	373	821	350	763
2013	377	691	367	780	339	545
2014	384	830	372	800	—	—
平均	367	779	366	808	343	699
注：实验通过剔除风速大于25 m/s的数据，消除了热带气旋的极端影响。DF：风向频率；DDED：风能密度方向分布。

根据表中信息可知，即使在不存在风速风向误差的情况下，为了反演较为可信的风能方向性参量，数据量需要在800以上。根据表1所示，真实的准确反演所用的数据量确实大于800，印证了本结论。并且，为了避免风场季节变化对于整体分布的影响，数据的使用必须以年为单位，年内采样也应该较为均匀。这为风能方向性参量反演的数据源提出了较高的要求。

5.2 遥感反演误差分析

在通过遥感手段对海面风场的风速风向进行反演的过程中不可避免得会引入误差。而这种误差的引入对于风能方向性参量的反演是否会带来系统性的误差，并且使得通过遥感手段反演的风能方向性参量与真实参量间存在偏差需要进一步的分析。

5.2.1 基于总体特征的误差分析

由于遥感反演带来的风速风向误差是无偏的，为了简化分析过程，假设此误差是随机并且独立于所反演参数的，因此可以认为误差满足正态分布 $N(0, {\mu ^2})$ ，则遥感反演获得的风速 ${v_i}'$

${v_i}' = {v_i} + N(0, {\mu ^2})$

(8)

式中，真实风速为 ${v_i}$ ， $\mu $ 为遥感反演风速误差的标准差。

因此，根据遥感反演的风速数据，风速分布的平均风速 $E({v_i}')$ 和风速方差 $D({v_i}')$ 分别为

$E({v_i}') = E({v_i})$

(9)

$D({v_i}') = D({v_i}) + {\mu ^2}$

(10)

式中， $E({v_i})$ 为真实的平均风速， $D({v_i})$ 为真实的风速方差。根据式(10)，遥感反演的平均风速与真实平均风速间不存在偏差，但遥感反演的风速方差比真实风速方差多了一个风速误差的方差 ${\mu ^2}$ 。

同理，对于风能方向分布的参数平均风向和风向标准差，遥感反演带来的风向误差也存在类似影响。遥感反演获得的风向 ${\alpha _i}'$

${\alpha _i}' = {\alpha _i} + N(0, {\mu ^2})$

(11)

式中，真实风向为 ${\alpha _i}$ ， $\mu $ 为遥感反演风向误差的标准差。

根据理论推导，遥感反演的风向标准差 $s'$

$s' = \sqrt {s + {\mu ^2}} $

(12)

式中，s为真实风向标准差。

由于平均风向的最终运算中含有 $\displaystyle\frac{{\bar y'}}{{\bar x'}}$ ， ${{{e}}^{ - \frac{{{\mu ^2}}}{2}}}$ 被约去，故最终 $\bar \alpha ' = \bar \alpha $ 。

根据式(12)，遥感反演的平均风向与真实平均风向间不存在偏差，但遥感反演的风向方差比真实风向方差多了一个风向误差的方差 ${\mu ^2}$ 。

5.2.2 基于方向分布参量的误差分析

基于上述结论，为了进一步分析遥感反演过程对于风能方向分布反演的影响，需建立海面风场的风向分布模型。循环正态分布是风能方向分布案例研究中最常用的概率分布(Carta 等，2008；Heckenbergerová，2013；Masseran 等，2013)。当海面风场具有多个主风向时，通常也可以用广义循环正态分布(Generalized von Mises Distribution)或者多元循环正态分布(Multivariate von Mises Distribution)进行拟合。所以，在此选择循环正态分布作为分析遥感反演过程对于风向分布影响的理想模型，并且假设其平均风向为0，风向方差为 $1/\kappa $

$f(x) = \frac{{{{{e}}^{\kappa \cos (x)}}}}{{2{\text{π}}{I_0}(\kappa)}}$

(13)

式中， ${I_0}(\kappa)$ 为0阶第一类修正贝塞尔函数(Modified Bessel functions of 1st kind)。

由于最终反演得到的风向，为真实风向上叠加一个随机误差，是两个变量相加。独立变量之和的概率密度是两个变量概率密度的卷积。所以，将理想模型的风向分布函数与遥感反演的误差分布函数相卷积可以获得遥感反演影响下的风向分布。由于，正态分布的概率密度在角度域上积分不为1，现选取循环正态分布作为误差模型与理想模型进行卷积。由于，遥感反演是无偏的，故平均误差应为0，现假设误差方差为 $1/\kappa '$ 。

遥感反演风向分布为

$f'(x) = \int_{ - {\text{π}}}^{\text{π}} {\frac{{{{{e}}^{\kappa \cos (\tau)}}}}{{2{\text{π}}{I_0}(\kappa)}}} \times \frac{{{{{e}}^{\kappa '\cos (x - \tau)}}}}{{2{\text{π}}{I_0}(\kappa ')}}{{d}}\tau $

(14)

此卷积没有解析解，现基于数值方法对遥感反演误差进行分析。

遥感反演带来的总偏差函数

$\begin{array}{l}\delta (\kappa, \kappa ')\\\;\; = \displaystyle\int_{ - {\text{π}}}^{\text{π}} {\left| {\displaystyle\int_{ - {\text{π}}}^{\text{π}} {\displaystyle\frac{{{{{e}}^{\kappa \cos (\tau)}}}}{{2{\text{π}}{I_0}(\kappa)}}} \times \displaystyle\frac{{{{{e}}^{\kappa '\cos (x - \tau)}}}}{{2{\text{π}}{I_0}(\kappa ')}}{{d}}\tau - \displaystyle\frac{{{{{e}}^{\kappa \cos (x)}}}}{{2{\text{π}}{I_0}(\kappa)}}} \right|{{d}}x} \end{array}$

(15)

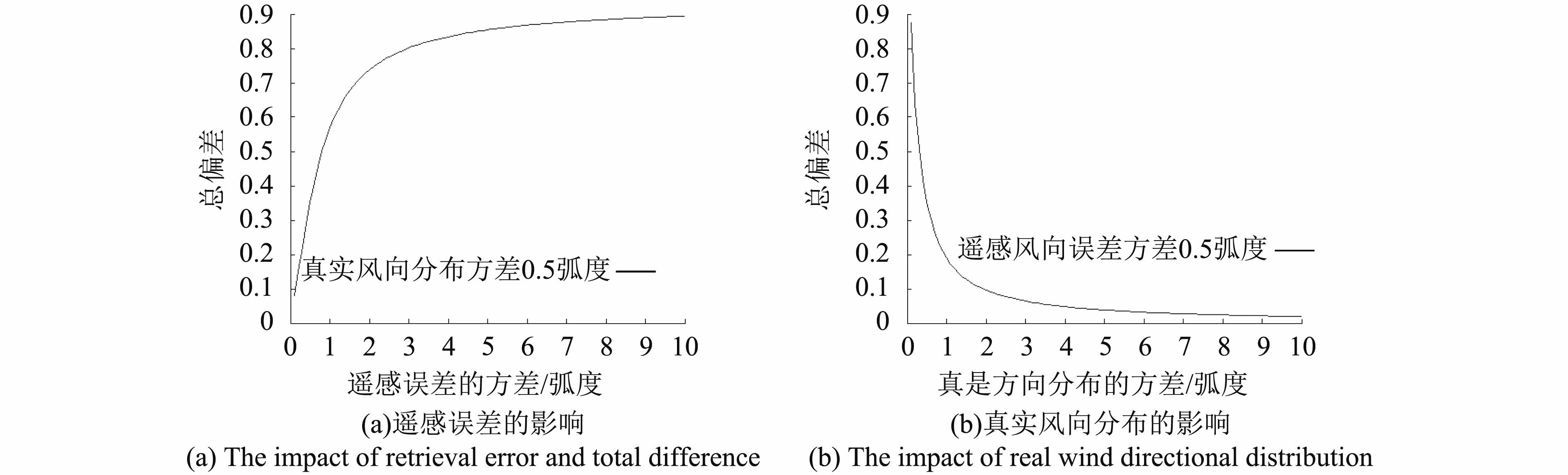
分别视 $1/\kappa $ 和 $1/\kappa '$ 为自变量，并保持另一个量不变，研究两者对于总偏差的影响。

其结果如图7所示。图7(a)展示了真实分布的方差保持在0.5弧度(28.65°，标准差5.35°)不变的情况下，总偏差随遥感误差方差变化的情况。图7(b)展示了遥感误差方差保持在0.5弧度(28.65°，标准差5.35°)不变的情况下，总偏差随着真实方向分布的方差变化的情况。

图 7 遥感误差对风向分布的影响

Fig. 7 The impact of retrieval error of wind direction on directional distribution

根据图中结果可知，在真实方向分布方差不变的情况下，遥感误差的方差越大总偏差越大，但这种影响随着方差增大逐渐放缓。在方差无限大时，方向分布为圆域上的均匀分布，所以遥感误差带来的总偏差最终应收敛于 $\displaystyle\int_{ - {\text{π}}}^{\text{π}} {\displaystyle\frac{{{{{e}}^{\kappa \cos (\tau)}} - {I_0}(\kappa)}}{{2{\text{π}}{I_0}(\kappa)}}} {{d}}\tau $ 。而当遥感误差的方差不变时，真实方向分布的方差越大，所受影响越小。并且，这种变化也是逐渐放缓的，最终总偏差应收敛于0。

6 结　论

在风能资源评估和风电场选址过程中，需要充分考虑风能方向性分布对风能利用的影响。它决定了风电场中风机的排布模式，影响着风机的之间的尾流干扰，但目前尚缺少关于此类参量遥感反演方法的研究。基于此，本文建立了以风向频率和风能密度方向分布为主要反演参数的风能方向性参量反演方法，并对准确反演所需的最小数据量和反演过程中的误差传递进行了分析。

(1)本文建立了全球海域风能方向性参量的遥感计算方法，其空间分辨率较高，与浮标观测一致性较好，具有实际应用价值。

(2)风能方向性参量的反演误差随数据量的增长呈指数衰减。不考虑风向和风速反演所包含的误差，风向频率的准确反演最少需要约350条数据，而风能密度方向分布最少需要约800条数据。根据本文验证结果星载微波散射计观测数据能满足风能方向性参量反演数据量要求。

(3)风向和风速数据的反演误差对于均值类的参量反演没有影响，但增大了方差类参量的误差，其在风向方差和风速方差的反演结果上均叠加了一个自身反演中误差的方差。

风向和风速数据的反演误差对于风能方向分布类参量存在系统性的影响，这种系统性影响增大了分布的方差，使得分布趋于离散，但这种影响在理论上可以通过反卷积算法进行消除。这种影响的大小不仅取决于反演误差而且取决于真实的海面风能方向分布自身，真实分布越离散，所受影响越小。

参考文献(References)

Barthelmie R J, Grisogono B and Pryor S C. 1996. Observations and simulations of diurnal cycles of near-surface wind speeds over land and sea. Journal of Geophysical Research: Atmospheres, 101 (D16): 21327–21337. [DOI: 10.1029/96jd01520]

Barthelmie R J and Pryor S C. 2003. Can satellite sampling of offshore wind speeds realistically represent wind speed distributions?. Journal of Applied Meteorology, 42 (1): 83–94. [DOI: 10.1175/1520-0450(2003)042<0083:CSSOOW>2.0.CO;2]

Batschelet E. 1981. Circular Statistics in Biology. London: Academic Press: 28

Carta J A, Bueno C and Ramírez P. 2008. Statistical modelling of directional wind speeds using mixtures of von Mises distributions: case study. Energy Conversion and Management, 49 (5): 897–907. [DOI: 10.1016/j.enconman.2007.10.017]

Chang R, Zhu R, Badger M, Hasager C B, Xing X H and Jiang Y R. 2015. Offshore wind resources assessment from multiple satellite data and WRF modeling over South China Sea. Remote Sensing, 7 (1): 467–487. [DOI: 10.3390/rs70100467]

Chinese Wind Energy Association. 2016. The statistics of installed wind power capacity of China in 2015. Wind Energy (2): 48–63. ( 中国可再生能源学会风能专业委员会. 2016. 2015年中国风电装机容量统计. 风能 (2): 48–63. )

Doubrawa P, Barthelmie R J, Pryor S C, Hasager C B, Badger M and Karagali I. 2015. Satellite winds as a tool for offshore wind resource assessment: the Great Lakes Wind Atlas. Remote Sensing of Environment, 168 : 349–359. [DOI: 10.1016/j.rse.2015.07.008]

Estévez J, Gavilán P and Giráldez J V. 2011. Guidelines on validation procedures for meteorological data from automatic weather stations. Journal of Hydrology, 402 (1/2): 144–154. [DOI: 10.1016/j.jhydrol.2011.02.031]

General Administration of Quality Supervision, Inspection and Quarantine of the People′s Republic of China. 2002. GB/T 18710-2002 Methodology of wind energy resource assessment for wind farm. Beijing: Standards Press of China: 6 (中华人民共和国国家质量监督检验检疫总局. 2002. GB/T 18710-2002风电场风能资源评估方法. 北京: 中国标准出版社: 6)

Hasager C B, Mouche A, Badger M, Bingöl F, Karagali I, Driesenaar T, Stoffelen A, Peña A and Longépé N. 2015a. Offshore wind climatology based on synergetic use of Envisat ASAR, ASCAT and QuikSCAT. Remote Sensing of Environment, 156 : 247–263. [DOI: 10.1016/j.rse.2014.09.030]

Hasager C B, Vincent P, Badger J, Badger M, Di Bella A, Peña A, Husson R and Volker P J H. 2015b. Using satellite SAR to characterize the wind flow around offshore wind farms. Energies, 8 (6): 5413–5439. [DOI: 10.3390/en8065413]

Heckenbergerova J, Musilek P and Krömer P. 2015. Optimization of wind direction distribution parameters using particle swarm optimization//Abraham A, Krömer P and Snasel V, eds. Afro-European Conference for Industrial Advancement. Cham: Springer: 15–26 [DOI: 10.1007/978-3-319-13572-4_2]

Heckenbergerová J, Musilek P, Mejznar J and Vančura M. 2013. Estimation of wind direction distribution with genetic algorithms//Proceedings of the 26th IEEE Canadian Conference on Electrical and Computer Engineering. Regina, SK, Canada: IEEE: 78–81 [DOI: 10.1109/CCECE.2013.6567681]

Hsu S A, Meindl E A and Gilhousen D B. 1994. Determining the power-law wind-profile exponent under near-neutral stability conditions at sea. Journal of Applied Meteorology, 33 (6): 757–765. [DOI: 10.1175/1520-0450(1994)033<0757:dtplwp>2.0.co;2]

Kuiper N H. 1960. Tests concerning random points on a circle. Indagationes Mathematicae (Proceedings), 63 : 38–47. [DOI: 10.1016/S1385-7258(60)50006-0]

Masseran N, Razali A M, Ibrahim K and Latif M T. 2013. Fitting a mixture of von Mises distributions in order to model data on wind direction in Peninsular Malaysia. Energy Conversion and Management, 72 : 94–102. [DOI: 10.1016/j.enconman.2012.11.025]

Na R H. 2015. Researching on Location of Wind Power Farm based on Fuzzy Comprehensive Evaluation Model. Beijing: North China Electric Power University: 1–2 (娜仁花. 2015. 基于模糊综合评价模型的风电场选址研究. 北京: 华北电力大学: 1–2)

Pewsey A, Neuhäuser M and Ruxton D G. 2013. Circular Statistics in R. Oxford, UK: Oxford University Press: 22, 27

Ricciardulli L and Wentz F J. 2016. Remote sensing systems ASCAT C-2015 daily ocean vector winds on 0.25 deg grid, version 02.1, [0000 to 49024]. Santa rosa, CA: Remote Sensing Systems. www.remss.com/missions/ascat. [2016-04-05]

Xia Y F. 2016. The increase interconnection capacity of European offshore wind power in 2015 is more than 3 GW. Wind Energy (2): 64–69. [DOI: 10.3969/j.issn.1674-9219.2016.02.019] ( 夏云峰. 2016. 2015年欧洲海上风电新增并网容量超过3GW. 风能 (2): 64–69. [DOI: 10.3969/j.issn.1674-9219.2016.02.019] )

Yang X F, Li X F, Pichel W G and Li Z W. 2011. Comparison of ocean surface winds From ENVISAT ASAR, MetOp ASCAT scatterometer, buoy measurements, and NOGAPS model. IEEE Transactions on Geoscience and Remote Sensing, 49 (12): 4743–4750. [DOI: 10.1109/TGRS.2011.2159802]

Yang X F, Liu G H, Li Z W and Yu Y. 2014. Preliminary validation of ocean surface vector winds estimated from China′s HY-2A scatterometer. International Journal of Remote Sensing, 35 (11/12): 4532–4543. [DOI: 10.1080/01431161.2014.916049]

Zheng C W, Hu Q L, Su Q and Yang Y. 2014. The review of progress of global offshore wind energy. Ocean Development and Management, 31 (6): 25–32. [DOI: 10.3969/j.issn.1005-9857.2014.06.07t] ( 郑崇伟, 胡秋良, 苏勤, 杨艳. 2014. 国内外海上风能资源研究进展. 海洋开发与管理, 31 (6): 25–32. [DOI: 10.3969/j.issn.1005-9857.2014.06.07t] )

Zheng C W and Pan J. 2012. Wind energy resources assessment in global ocean. Journal of Natural Resources, 27 (3): 364–371. [DOI: 10.11849/zrzyxb.2012.03.002] ( 郑崇伟, 潘静. 2012. 全球海域风能资源评估及等级区划. 自然资源学报, 27 (3): 364–371. [DOI: 10.11849/zrzyxb.2012.03.002] )

Zhu M. 2015. To transform the role of wind energy and other renewable energy from complementary energy to alternative energy is the fundamtion of the thirteenth Five-Year Plan. Wind Energy (11): 18–19. [DOI: 10.3969/j.issn.1674-9219.2015.11.003] ( 朱明. 2015. 实现风电等可再生能源从补充能源向替代能源转变是" 十三五”规划的主基调. 风能 (11): 18–19. [DOI: 10.3969/j.issn.1674-9219.2015.11.003] )

Zhu X H and Yang X F. 2016. Uncertainties in directional offshore wind distribution estimate from satellite remote sensing. Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium. Beijing, China: IEEE: 4623–4626 [DOI: 10.1109/IGARSS.2016.7730206]

摘要

关键词