出版日期: 2018-03-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20187302
2018 | Volumn22 | Number 2
上一篇 | 下一篇

国产卫星

双星敏感器在轨相对热变形分析及修正

钟金凤 , 郭思岩 , 吴敬玉 , 裴甲瑞 , 贾艳胜

上海航天控制技术研究所上海市空间智能控制技术重点试验室，上海 201109

收稿日期: 2017-07-20

基金项目: 第四届高分青年基金项目(编号：GFZX04061502)

第一作者简介: 钟金凤(1985—　)，工程师，研究方向为卫星控制系统。E-mail：zhongjinfeng822@126.com

中图分类号: V448

文献标识码: A

摘要

为了获取高质量的对地观测遥感图像，除了有效载荷成像的高分辨率外，还需要卫星平台姿态具有高精度。在双星敏联合姿态确定时，星敏感器之间的相对热变形会对姿态确定带来不利影响，需对热变形误差进行辨识与修正。通过对某遥感卫星在轨遥测数据进行分析，建立了星敏感器在轨结构热变形模型，并对星敏感器热变形进行了在轨修正。采用辨识得到的傅里叶级数的热变形模型参数，对星敏热变形进行在轨修正后，提高了星敏感器的测量精度，减小了星敏感器之间的热变形误差对姿态确定精度的影响，对得到高质量的对地观测遥感图像具有很大的工程应用价值。

关键词

遥感卫星, 双星敏感器, 热变形, 在轨修正, 测量精度

Correction of the relative thermal deformation of dual star sensors for remote-sensing satellites

ZHONG Jinfeng , GUO Siyan , WU Jingyu , PEI Jiarui , JIA Yansheng

Shanghai Institute of Spaceflight Control Technology, Shanghai Key Laboratory of Spacecraft Intelligent Control Technology, Shanghai 201109, China

Abstract

A high-accuracy satellite platform is required to obtain remote-sensing images that meet the requirements of high image quality and high resolution for payload imaging. In practical engineering applications, the thermal deformation error caused by the thermal environment of star sensors is always neglected. Therefore, relative thermal deformation between star sensors will negatively affect altitude determination by dual sensors. Thus, the thermal deformation error must be identified and corrected. In this study, the thermal deformation model is established on the basis of satellite remote-sensing data and then corrected. The parameters of the thermal deformation model established using the Fourier series reflect the real results of on-orbit thermal deformation, and the magnitudes of sinusoidal and cosine functions in the Fourier series are determined. Then, the estimated parameters are used to compensate for the output of star sensors. Comparing the altitude error of star sensors before and after correction revealed that measurement precision improved by 40% after correction. Results showed that the proposed method for thermal deformation correction can improve the measurement precision of star sensors and reduce the influence of slow-frequency error on the precisions of altitude determination. The proposed method has potential engineering applications for obtaining high-quality images.

Key words

remote sensing satellite, dual star sensors, thermal deformation, on-orbit correction, measurement precision

1　引　言

遥感卫星在轨运行时，对成像质量的要求越来越高，除了有效载荷成像高分辨率外(邓云凯等，2012)，还必须要求卫星平台姿态具有高精度。星敏感器是高精度的卫星姿态测量敏感器，它的测量精度直接决定了卫星的姿态确定精度，其测量精度主要受星敏感器的测量噪声、安装矩阵标定误差及卫星结构热变形等因素影响。

目前，针对星敏感器自身精度、安装支架和系统姿态确定算法改进等方面的研究较多(孙婷等，2013；江帆等，2014；江帆等，2015；张春青等，2014；边志强等，2014)，通过补偿热变形提高星敏感器精度的研究尚处于探索状态。在实际工程应用中，尤其是星敏感器安装环节受空间热环境影响产生的热变形误差往往被忽略。由于太阳照射角度周期性变化产生的冷热交变的热环境，能引起星敏感器安装结构形变，从而产生周期信号的热变形误差。据报道，在PROBA，CHAMP，ALOP，天绘一号等多个航天器上都发现了周期性的热变形误差的影响(Jørgensen 等，2005a，2005b；Iwata 等，2007；王兴涛等，2012)。周期性的热变形误差难以用现有的姿态确定卡尔曼滤波算法予以消除，会存在于姿态确定结果中，从而影响姿态确定精度(熊凯等，2014)。因此，为了获取高精度的卫星姿态，需要对星敏感器的热变形误差进行研究及补偿。

本文通过对某遥感卫星在轨遥测数据进行分析处理，对星敏感器在轨结构热变形的真实情况进行评估，建立了星敏感器的热变形模型，并对星敏感器进行了在轨修正。

2 在轨热变形评估

高精度卫星控制系统采用双星敏感器融合技术进行姿态确定时，除了星敏感器自身的测量噪声误差、低频误差、星敏感器光学测量基准与整星控制基准之间的安装偏差、有效载荷与整星基准之间的安装偏差外，当保证星敏感器在良好的温控条件下工作时，由于热变形而导致的星敏感器之间的慢变误差也会对姿态确定产生不利影响。

星敏感器随卫星入轨后，由于缺少外部基准，如何分析评估星敏感器的测量误差、有效载荷的安装参数误差、卫星结构变形等，还没有成熟的方法。虽然设计过程中保证了星敏感器与微波载荷之间的良好布局，由于星敏感器安装位置不同，与载荷间的相对变形会存在一定的差异，需要根据载荷成像数据，将星敏相对载荷的常值偏差进行修正。同时通过对星敏感器进行多次精测，得到星敏感器相对微波载荷的历次误差数据，找出误差变化最小、最稳定的星敏感器作为整星测量的主星敏感器。该卫星在轨运行状态选择星敏感器1为主星敏感器，通过星敏互修，实时修正了其他星敏感器与主星敏感器之间的安装误差、应力释放、星敏自身常偏导致的星敏姿态不一致项，既保证了星敏相对载荷的常值偏差较小，又保证了多台星敏姿态数据的一致性。

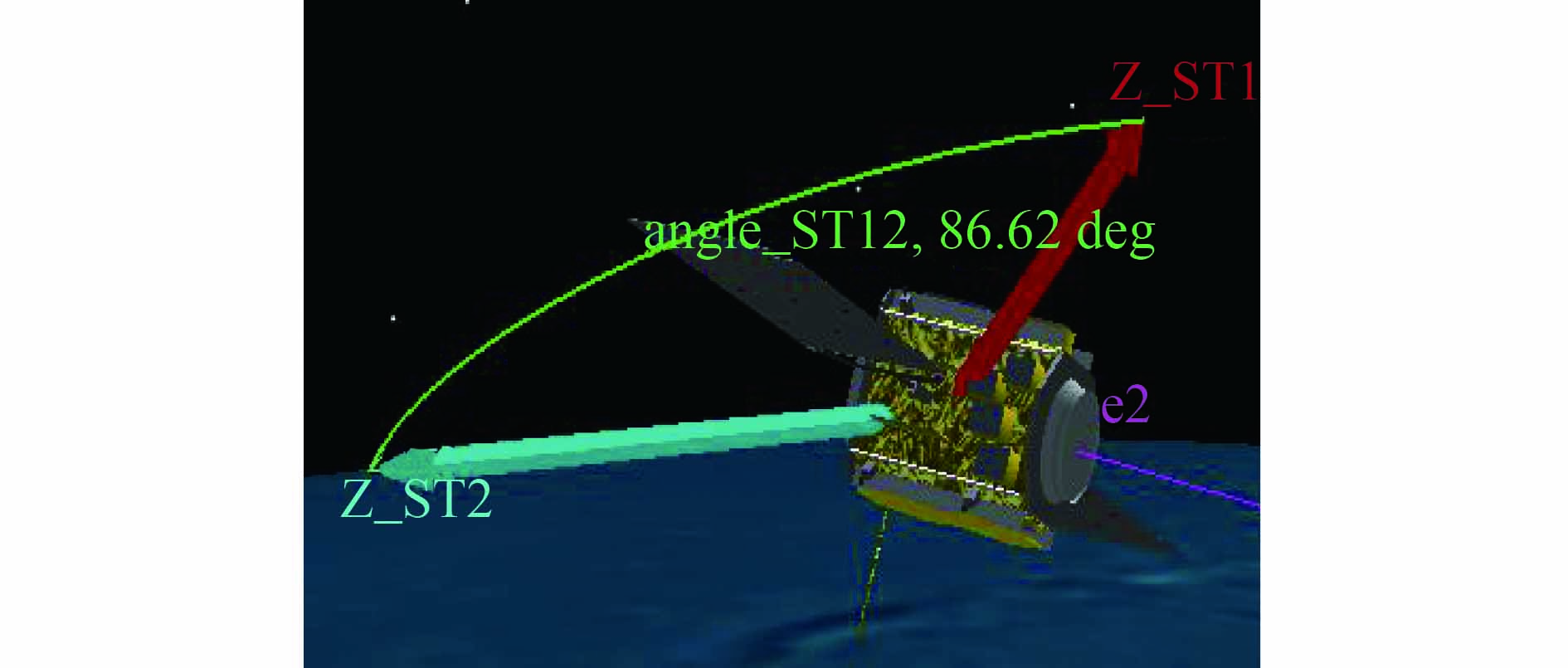
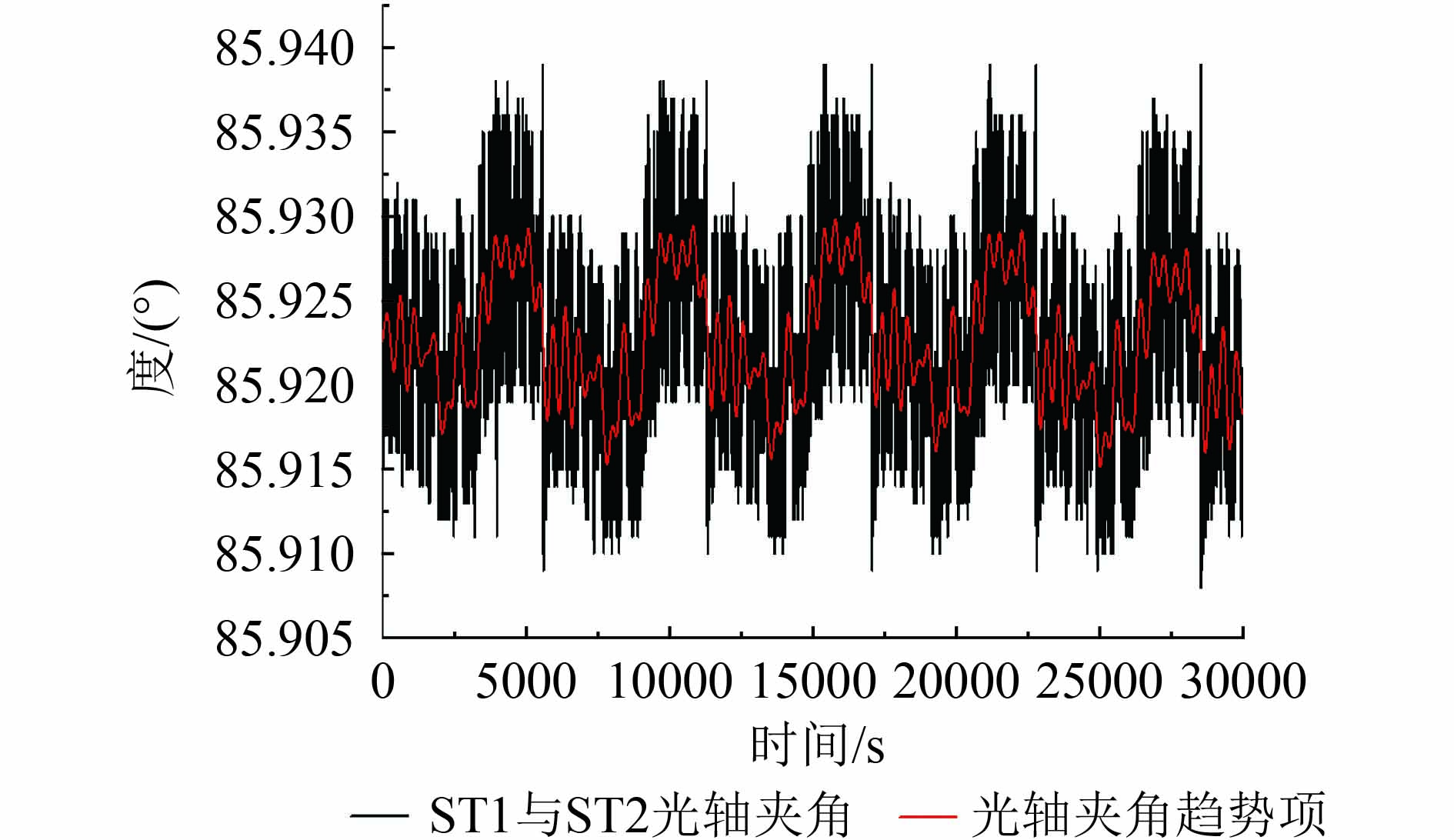
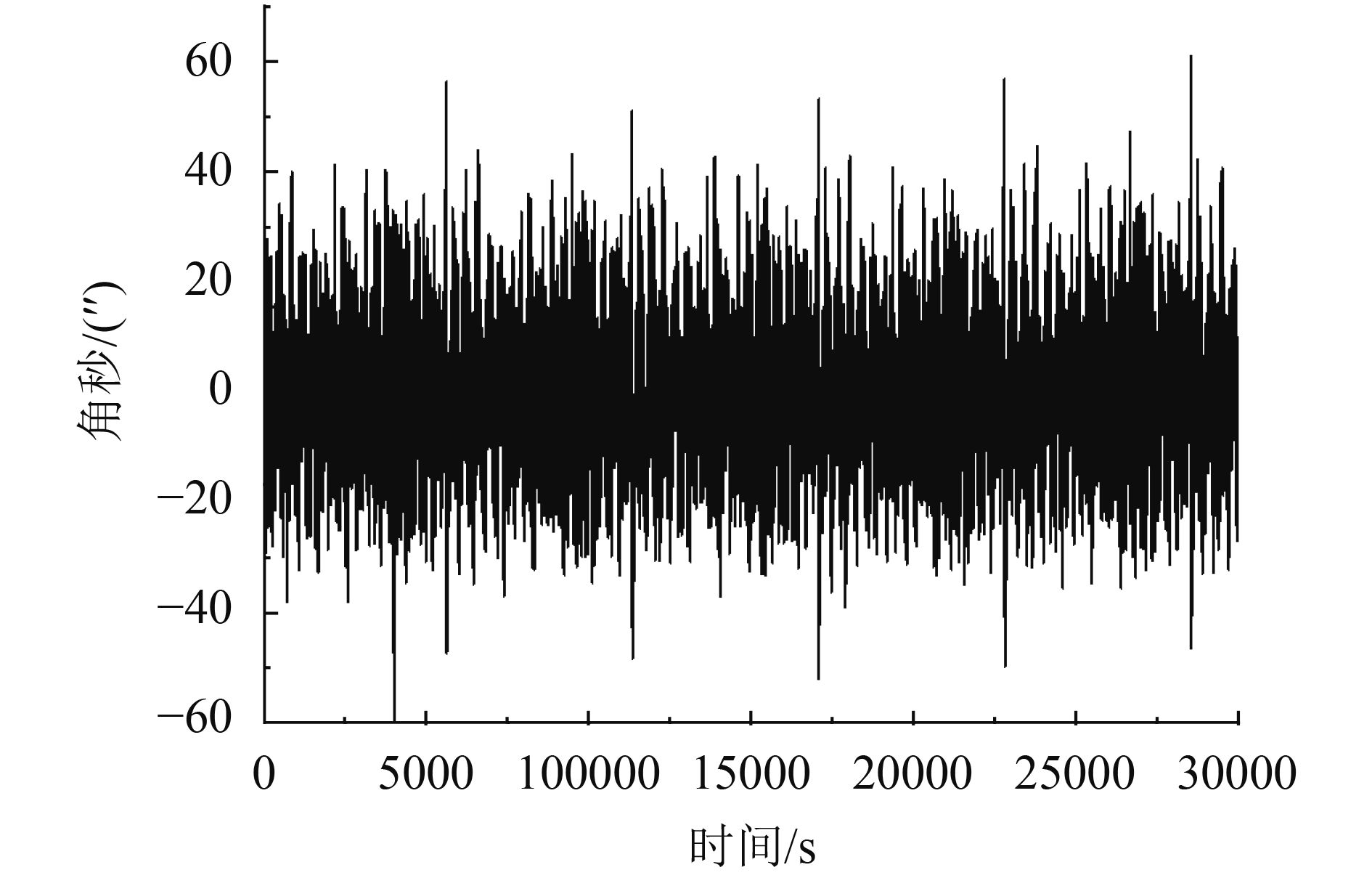
利用在轨遥测数据计算两星敏光轴指向夹角，上述误差特性会对光轴夹角有影响。理论上，如果卫星结构没有变形，两个星敏感器光轴夹角客观上在惯性空间应保持不变，如图1所示。在轨飞行过程中由于结构热变形等原因引起的星敏感器光轴夹角具有明显的周期性变化，存在长周期项和短周期项，如图2所示，长周期项是影响系统指向精度的主要因素。星敏感器1与星敏感器2光轴指向夹角在85.91°—85.94°范围内波动，采用低通滤波滤去高频测量噪声，光轴指向夹角的噪声见图3。

图 1 星敏感器光轴夹角指向示意图

Fig. 1 Optical axis angle pointing of star sensors

图 2 星敏感器1和2 光轴夹角

Fig. 2 Optical axis angle between star sensor 1 and 2

图 3 星敏感器1和2 光轴夹角噪声

Fig. 3 Optical axis angle noise between star sensor 1 and 2

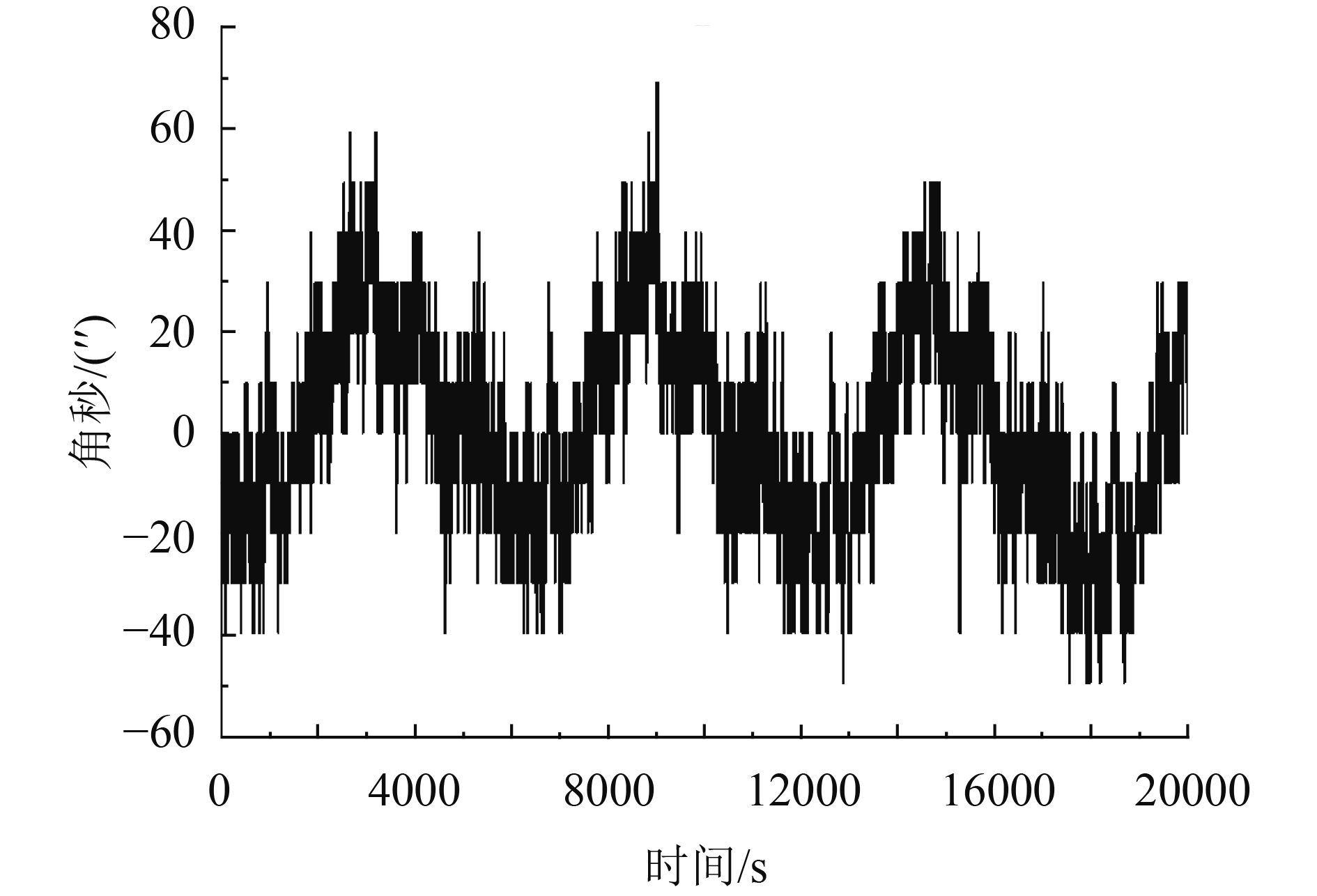
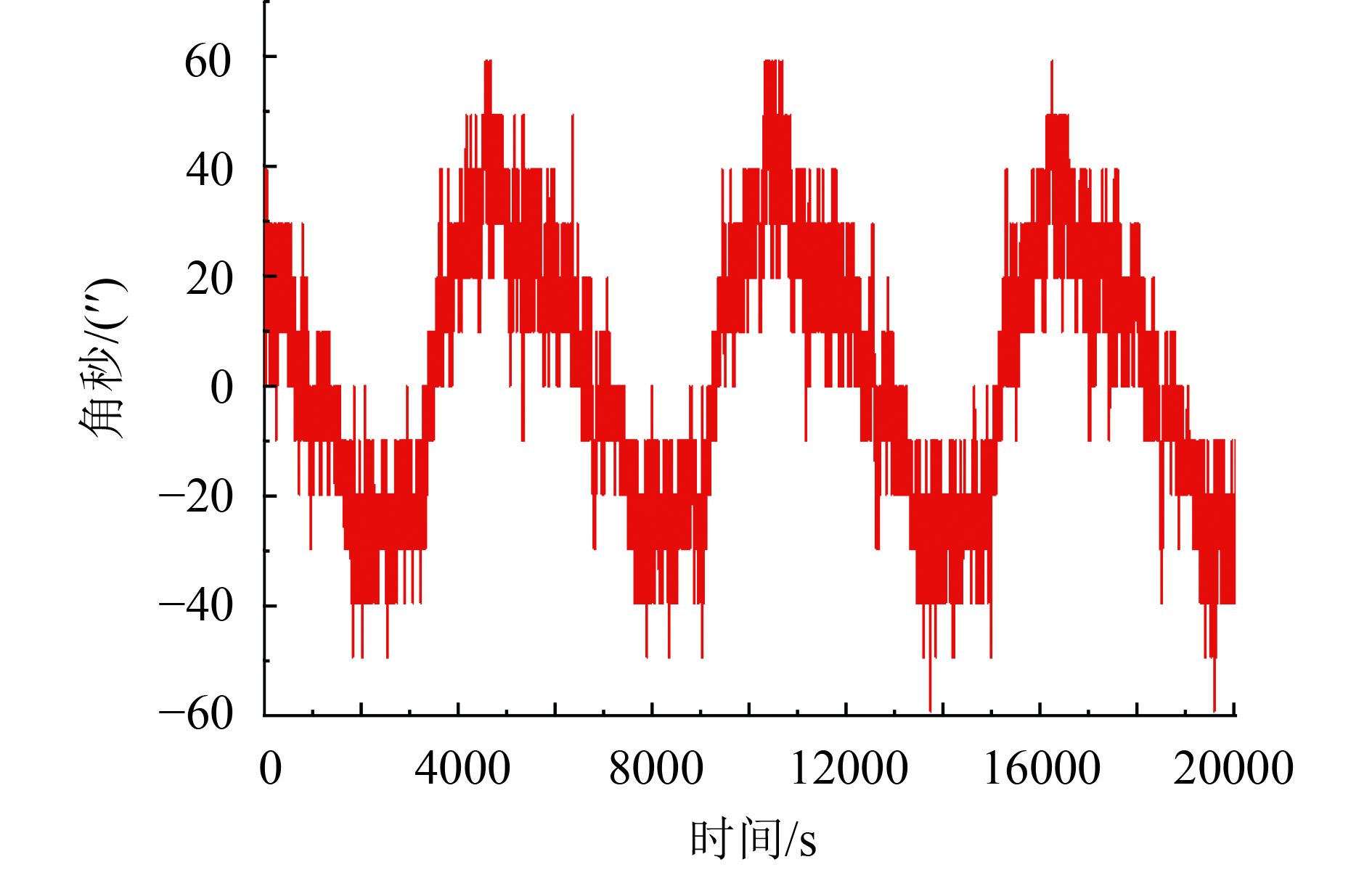
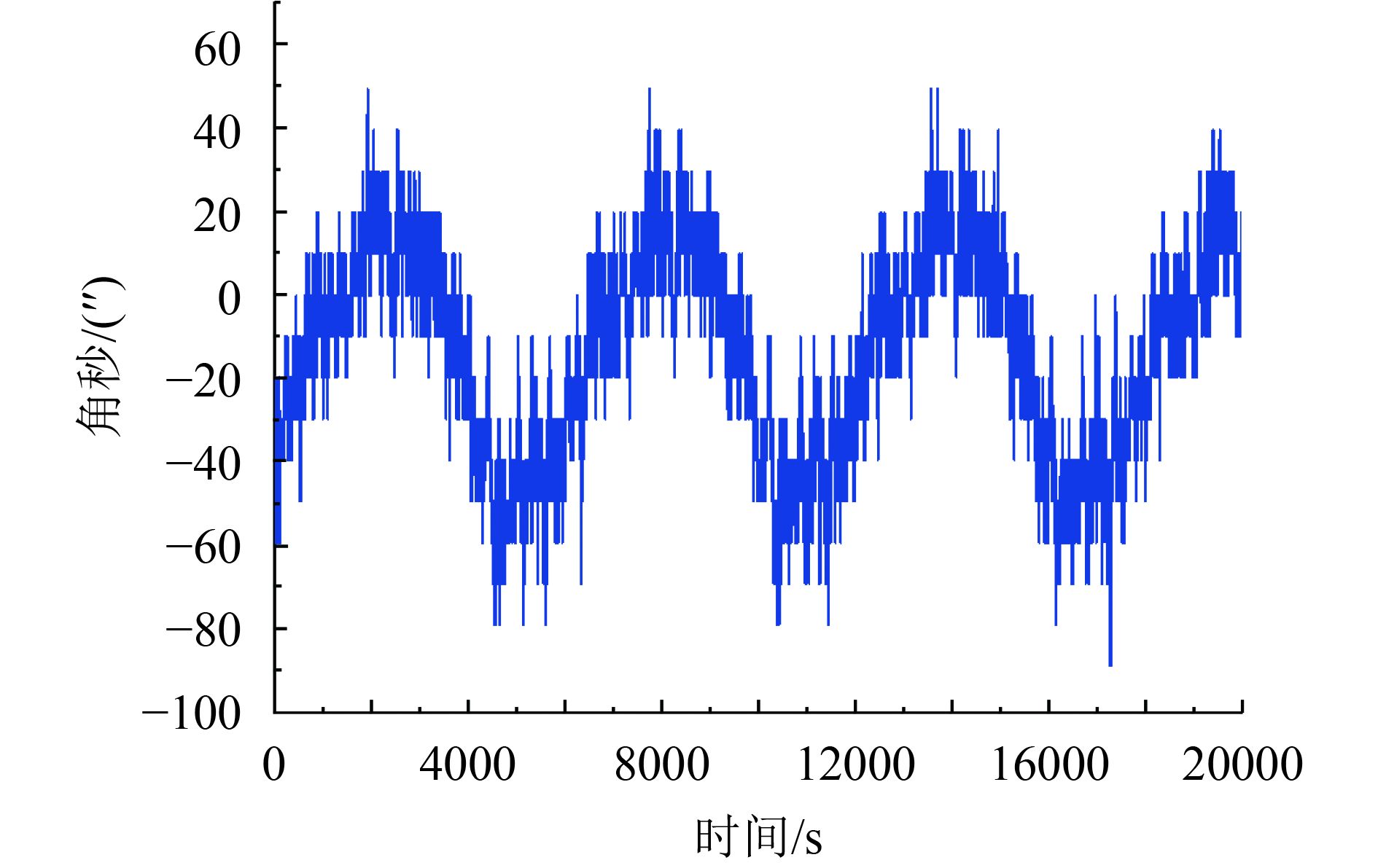
分析星敏感器之间的三轴姿态误差变化(遥测采集数据周期为2 s)如图4—6所示。

图 4 星敏感器X向姿态误差曲线

Fig. 4 X-axis attitude error of star sensors

图 5 星敏感器Y向姿态误差曲线

Fig. 5 Y-axis attitude error of star sensors

由图4—6可见，星敏感器输出的姿态误差存在有规律的周期性变化，其变化周期与轨道周期(一个轨道周期约为97 min)完全吻合。星敏感器输出的三轴姿态误差幅值变化约在20″—30″之间，而由星敏感器自身温度变化引起的焦距误差等带来的测量误差约为0.2″/℃，在轨温度变化范围10℃左右引起的偏差仅为2″。

图 6 星敏感器Z向姿态误差曲线

Fig. 6 Z-axis attitude error of star sensors

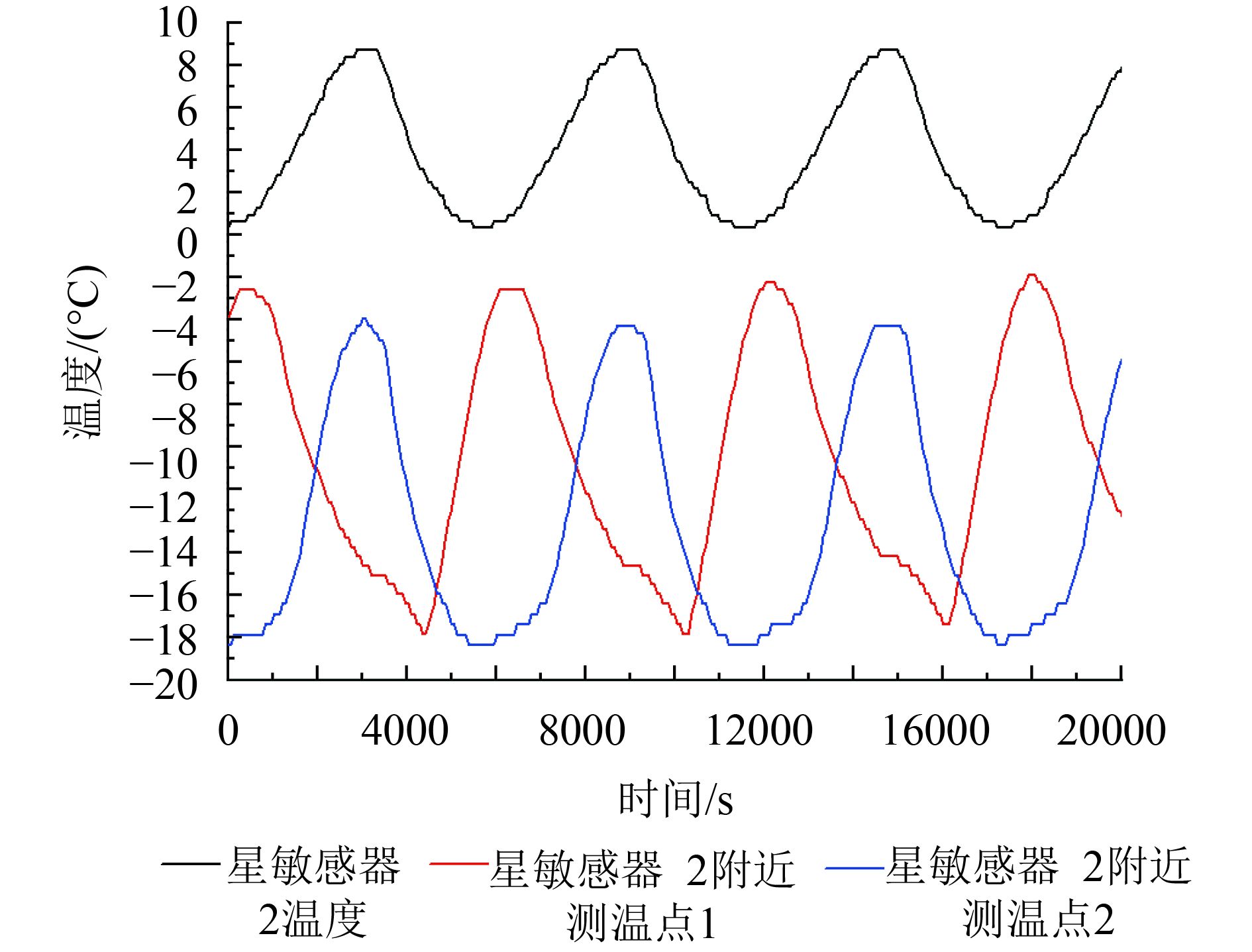
星敏感器在轨热环境较为复杂，由于卫星轨道周期性受太阳光照，阳照区温度升高，阴影区温度降低，结合热控系统加热器的开关和星敏感器制冷器开关等综合作用，会产生周期性的温度变化。取星敏感器温度及安装位置附近测温点的温度数据(遥测采集数据周期为64 s)进一步分析，如图7、8所示。

图 7 星敏感器1温度及安装位置附近温度变化曲线

Fig. 7 Temperature changes near installation position of star sensor 1

由图7、8可知，星敏感器温度出现周期性变化，星敏感器1附近测温点的温度波动不超过2℃，而星敏感器2安装位置两侧的两个测温点的温度明显出现冷热交变现象，从而会引起星敏感器2安装位置的结构形变，导致星敏感器测量姿态出现偏差。姿态误差极值点和温度偏差极值点出现的时刻基本吻合，说明星敏姿态数据之间的差异主要是由星敏器2安装位置的温度变化带来的结构热变形引起的。

图 8 星敏感器2温度及安装位置附近温度变化曲线

Fig. 8 Temperature changes near installation position of star sensor 2

3 热变形实时修正方法

对星敏感器之间的三轴姿态误差作进一步分析，由于遥测下传的姿态角信息进行了低通滤波，采用星敏感器原始数据进行姿态解算及数据分析，星敏感器测量姿态四元数 ${{{q}}_{{{st}}}}$ 表达式为

${{{q}}_{{{st}}}} = {{atti\_q}} \otimes {{{q}}_{{e}}} \otimes {{{q}}_{{r}}}$

(1)

式中， ${{atti\_q}}$ 为星敏感器输出四元数， ${{{q}}_{{e}}}$ 为星敏感器安装误差四元数， ${{{q}}_{{r}}}$ 为热变形补偿四元数，由在轨数据分析计算后计算得到，初值 ${{{q}}_{{r}}} = \left[ \!\!\! {\begin{array}{*{20}{c}} 0 \! & \! 0 \! & \! 0 \! & \! 1 \end{array}} \!\!\! \right]_{}^{{T}}$ 。

星敏感器本体坐标系相对惯性系的姿态四元素表达式 ${{q}}_{{{bi}}}^{}$ 为

${{q}}_{{{bi}}}^{} = {{{q}}_{{{st}}}} \otimes {{{q}}_{{{bs}}}}$

(2)

式中， ${{{q}}_{{{bs}}}}$ 为星敏感器安装四元数. 根据遥测下传轨道信息，得到轨道坐标系相对于地心惯性系的姿态四元数 ${{{q}}_{{{oi}}}}$ ，计算卫星本体坐标系相对于轨道坐标系的姿态四元数 ${{{q}}_{{{bo}}}}$

${{{q}}_{{{bo}}}} = {{q}}_{{{oi}}}^{{{ - 1}}} \otimes {{q}}_{{{bi}}}^{}$

(3)

将用四元数 ${{{q}}_{{{bo}}}}$ 表示的卫星姿态信息转换为用欧拉角表示的卫星三轴姿态信息 $\varphi $ 、 $\theta $ 、 $\psi $

$\begin{gathered} \varphi = \arcsin \left({2 \times \left({{q_{_2}}{q_{_3}} + {q_{_1}}{q_{_4}}} \right)} \right) \hfill \\ \theta = a\tan 2\left({ - 2 \times \left({{q_{_1}}q{}_{_3} - {q_{_2}}{q_{_4}}} \right), - q_1^2 - q_2^2 + q_3^2 + q_4^2} \right) \hfill \\ \psi = a\tan 2\left({ - 2 \times \left({{q_{_1}}{q_{_2}} - {q_{_3}}{q_{_4}}} \right), - q_1^2 + q_2^2 - q_3^2 + q_4^2} \right) \hfill \\ \end{gathered} $

(4)

分析在轨遥测数据认为，结构热变形引起的姿态周期性变化规律可用傅里叶级数表述，建立星敏相对热变形模型的3个方向分量 ${\phi _{r1}}$ 、 ${\theta _{r1}}$ 、 ${\psi _{r1}}$

$\begin{gathered} {\phi _r}{{ = }}{\phi _{c0}}{{ + }}{{{A}}_x}\cos \left({u/180 \times pi} \right) + {B_x}\sin \left({u/180 \times pi} \right) + \\ {{{C}}_x}\cos \left({2 \times u/180 \times pi} \right) + {D_x}\sin \left({2 \times u/180 \times pi} \right) \\ {\theta _r}{{ = }}{\theta _{c0}}{{ + }}{{{A}}_y}\cos \left({u/180 \times pi} \right) + {B_y}\sin \left({u/180 \times pi} \right) + \\ {C_y}\cos \left({2 \times u/180 \times pi} \right) +{D_y}\sin \left({2 \times u/180 \times pi} \right) \\ {\psi _r}{{ = }}{\psi _{c0}}{{ + }}{{{A}}_z}\cos \left({u/180 \times pi} \right) + {B_z}\sin \left({u/180 \times pi} \right) + \\ {C_z}\cos \left({2 \times u/180 \times pi} \right) + {D_z}\sin \left({2 \times u/180 \times pi} \right) \\ \end{gathered} $

(5)

式(5)包括二阶谐波项， $u$ 表示纬度幅角，常数项 ${\phi _{c0}}$ 、 ${\theta _{c0}}$ 、 ${\psi _{c0}}$ 表示常值误差， ${A_x} \text{—} {D_z}$ 表示了由结构热变形引起的周期性变化幅值。其中 ${A_x}$ 、 ${A_y}$ 、 ${A_z}$ 为一阶余弦幅值， ${B_x}$ 、 ${B_y}$ 、 ${B_z}$ 为一阶正弦幅值， ${C_x}$ 、 ${C_y}$ 、 ${C_z}$ 为二阶余弦幅值， ${D_x}$ 、 ${D_y}$ 、 ${D_z}$ 为二阶正弦幅值。

计算热变形补偿四元数 ${q_r}$ 为

${{{q}}_{{r}}} = \left[ {\begin{array}{*{20}{c}} 0 \\ [5pt] 0 \\ [5pt] {\sin \left({\displaystyle\frac{{{{ - }}{\psi _r}}}{2}} \right)} \\ [12pt] {\cos \left({\displaystyle\frac{{{{ - }}{\psi _r}}}{2}} \right)} \end{array}} \right] \otimes \left[ {\begin{array}{*{20}{c}} 0 \\ [5pt] {\sin \left({\displaystyle\frac{{{{ - }}{\theta _r}}}{2}} \right)} \\ [12pt] 0 \\ [5pt] {\cos \left({\displaystyle\frac{{{{ - }}{\theta _r}}}{2}} \right)} \end{array}} \right] \otimes \left[ {\begin{array}{*{20}{c}} {\sin \left({\displaystyle\frac{{{{ - }}{\phi _r}}}{2}} \right)} \\ [12pt] 0 \\ [5pt] 0 \\ [5pt] {\cos \left({\displaystyle\frac{{{{ - }}{\phi _r}}}{2}} \right)} \end{array}} \right]$

(6)

通过在轨数据进行傅里叶级数拟合得到的热变形模型是卫星在轨星敏感器结构热变形的真实情况。地面根据拟合函数按321转序转换成对应的热变形补偿四元数 ${{{q}}_{{r}}}$ ，将计算得到的 ${{{q}}_{{r}}}$ 代入式(1)即可完成在轨热变形修正，得到修正后的星敏姿态数据。

4 热变形实时修正效果分析

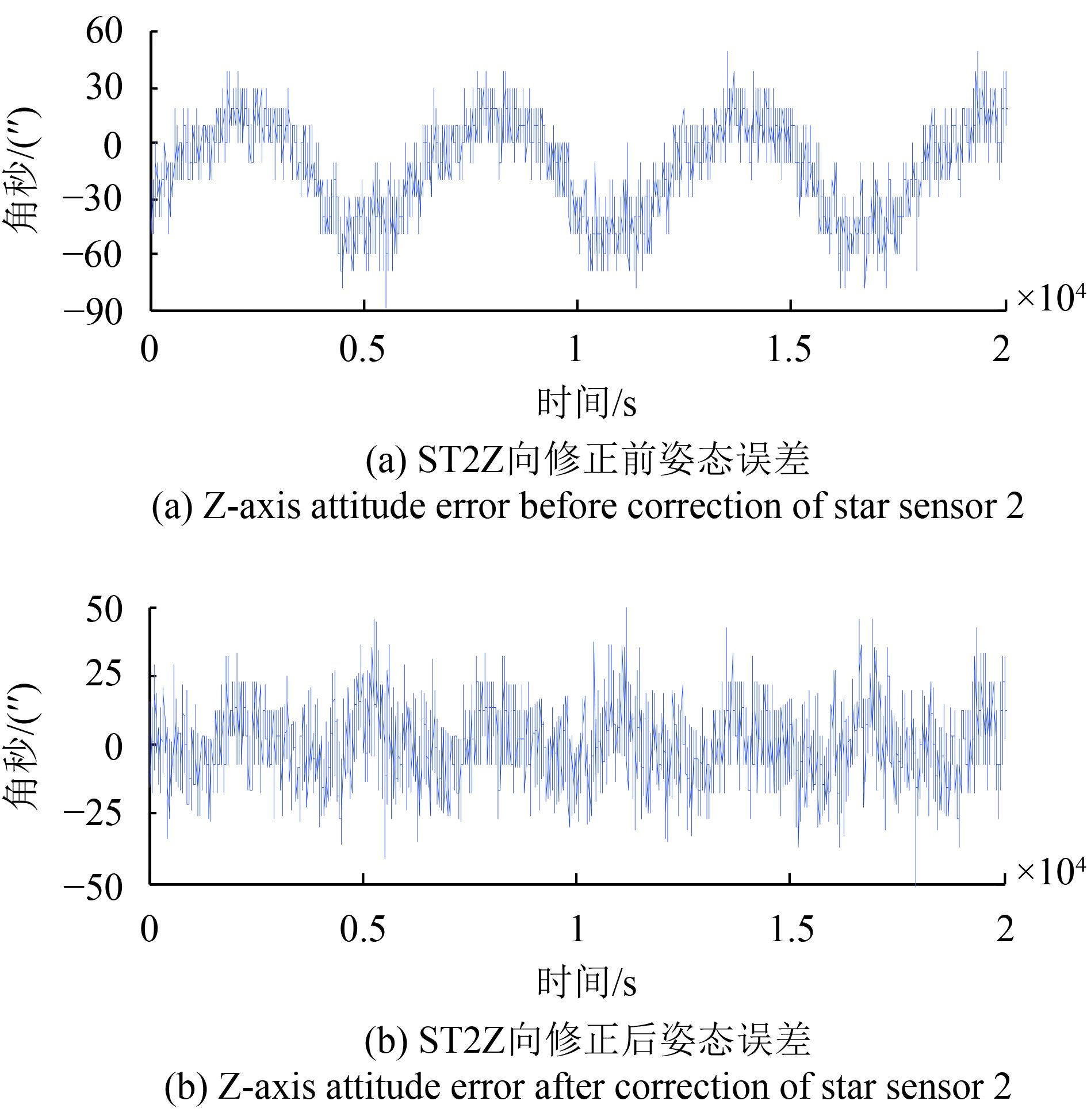
根据在轨遥测数据，得到傅里叶级数的热变形模型参数，按照上述修正方法对热变形进行了修正，修正后的星敏感器2姿态输出误差，如图9—11所示。

修正前后的星敏感器输出姿态误差如表1所示，修正前三轴姿态角误差约为19″—25″，修正后三轴姿态角误差约为9″—13″。通过修正前后的比对结果，可以看出，对在轨数据分析拟合的热变形模型进行补偿后，显著减小了星敏感器之间周期性的热变形误差，星敏感器的测量精度提高了约40%。

从修正后的星敏感器输出姿态可以看出，输出姿态仍然呈现有周期性的波动，由于星敏感器的姿态误差是多方面误差特性共同叠加影响的，有待进一步研究。

图 9 星敏感器2 X向姿态角修正前后误差

Fig. 9 X-axis attitude error before and after correction

图 10 星敏感器2 Y向姿态角修正前后误差

Fig. 10 Y-axis attitude error before and after correction

图 11 星敏感器2 Z向姿态角修正前后误差

Fig. 11 Z-axis attitude error before and after correction

表 1 修正前后星敏感器输出姿态误差对比
Table 1 Comparison of attitude error output of star sensor before and after correction

下载CSV

星敏感器输出姿态误差	修正前均方差/(″)	修正前均值/(″)	修正后均方差/(″)	修正后均值/(″)
X向姿态角误差	19.2532	3.5876	11.4483	0.0169
Y向姿态角误差	23.5029	3.6787	9.1023	0.0230
Z向姿态角误差	24.7655	14.3417	12.2721	0.1486

5 结　论

由于空间热环境的原因，造成暴露在舱外的星敏感器结构产生热变形，导致星敏感器输出姿态中含有热变形误差，影响姿态确定的精度。

基于在轨遥测数据，对星敏感器在轨结构热变形的真实情况进行评估，采用傅里叶级数建立热变形模型并进行参数辨识，根据辨识得到的模型参数对星敏感器进行了在轨修正。

研究表明，通过热变形修正后能够显著减小周期性的热变形误差，有效提高了星敏感器的测量精度。本方法在工程应用中易于实现，可为星敏感器热变形误差的补偿提供设计和参考。

除了本文研究的轨道周期的热变形误差，星敏感器的低频误差主要还有视场观测误差等，也是高精度姿态确定的关键技术，需要进一步研究。

参考文献(References)

Bian Z Q, Cai C S, Lyu W and Shen Y L. 2014. High accuracy and high stability control technology of remote sensing satellite. Aerospace Shanghai, 31 (3): 24–33, 38. [DOI: 10.3969/j.issn.1006-1630.2014.03.005] ( 边志强, 蔡陈生, 吕旺, 沈毅力. 2014. 遥感卫星高精度高稳定度控制技术. 上海航天, 31 (3): 24–33, 38. [DOI: 10.3969/j.issn.1006-1630.2014.03.005] )

Deng Y K, Zhao F J and Wang Y. 2012. Brief analysis on the development and application of spaceborne SAR. Journal of Radars, 1 (1): 1–10. [DOI: 10.3724/SP.J.1300.2012.20015] ( 邓云凯, 赵凤军, 王宇. 2012. 星载SAR技术的发展趋势及应用浅析. 雷达学报, 1 (1): 1–10. [DOI: 10.3724/SP.J.1300.2012.20015] )

Iwata T, Hoshino H, Yoshizawa T and Kawahara T. 2007. Precision attitude determination for the advanced land observing satellite (ALOS): design, verification, and on-orbit calibration. AIAA 2007-7482. Hilton Head: AIAA [DOI: 10.2514/6.2007-6817]

Jiang F, Wang Z S, Chen L H, Wu Q W and Guo L. 2014. Thermal design of star sensor assembly. Infrared and Laser Engineering, 43 (11): 3740–3745. [DOI: 10.3969/j.issn.1007-2276.2014.11.041] ( 江帆, 王忠素, 陈立恒, 吴清文, 郭亮. 2014. 星敏感器组件的热设计. 红外与激光工程, 43 (11): 3740–3745. [DOI: 10.3969/j.issn.1007-2276.2014.11.041] )

Jiang F, Wu Q W, Wang Z S, Miao J Y, Guo L, Chen L H and Yang X W. 2015. Analysis and verification of structure stability and thermal stability of a bracket of star sensors. Infrared and Laser Engineering, 44 (11): 3463–3468. [DOI: 10.3969/j.issn.1007-2276.2015.11.049] ( 江帆, 吴清文, 王忠素, 苗健宇, 郭亮, 陈立恒, 杨献伟. 2015. 星敏感器支架的结构/热稳定性分析及验证. 红外与激光工程, 44 (11): 3463–3468. [DOI: 10.3969/j.issn.1007-2276.2015.11.049] )

Jørgensen J L, Denver T, Betto M and Van den Braembussche P. 2005a. The PROBA satellite star tracker performance. Acta Astronautica, 56 (1/2): 153–159. [DOI: 10.1016/j.actaastro.2004.09.011]

Jørgensen P S, Jørgensen J L, Denver T and Betto M. 2005b. In-flight quality and accuracy of attitude measurements from the CHAMP advanced stellar compass. Acta Astronautica, 56 (1/2): 181–186. [DOI: 10.1016/j.actaastro.2004.09.012]

Sun T, Xing F and You Z. 2013. Optical system error analysis of high accuracy star trackers. Acta Optica Sinica, 33 (3): 323003 [DOI: 10.3788/aos201333.0323003] ( 孙婷, 邢飞, 尤政. 2013. 高精度星敏感器光学系统误差分析. 光学学报, 33 (3): 323003 [DOI: 10.3788/aos201333.0323003] )

Wang X T, Li Y C and Li X Y. 2012. Mapping satellite-1 star sensor accuracy analysis. Journal of Remote Sensing, 16 (S1): 90–93. [DOI: 10.11834/jrs.20120018] ( 王兴涛, 李迎春, 李晓燕. 2012. " 天绘一号”卫星星敏感器精度分析. 遥感学报, 16 (S1): 90–93. [DOI: 10.11834/jrs.20120018] )

Xiong K, Zong H and Tang L. 2014. On star sensor low frequency error in-orbit calibration method. Aerospace Control and Application, 40 (3): 8–13. [DOI: 10.3969/j.issn.1674-1579.2014.03.002] ( 熊凯, 宗红, 汤亮. 2014. 星敏感器低频误差在轨校准方法研究. 空间控制技术与应用, 40 (3): 8–13. [DOI: 10.3969/j.issn.1674-1579.2014.03.002] )

Zhang C Q, Wang S Y and Chen C. 2014. A high-precision relative attitude determination method for satellite. Aerospace Control and Application, 40 (3): 19–24. [DOI: 10.3969/j.issn.1674-1579.2014.03.004] ( 张春青, 王淑一, 陈超. 2014. 卫星高精度相对姿态确定技术. 空间控制技术与应用, 40 (3): 19–24. [DOI: 10.3969/j.issn.1674-1579.2014.03.004] )

摘要

关键词