出版日期: 2018-03-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20186420
2018 | Volumn22 | Number 2
上一篇  |  下一篇
技术方法 
特征级高分辨率遥感图像快速自动配准
expand article info 何梦梦1,2 , 郭擎1 , 李安1 , 陈俊1 , 陈勃1 , 冯旭祥1
1. 中国科学院遥感与数字地球研究所，北京 100094
2. 中国科学院大学，北京 100049
收稿日期: 2016-11-07
基金项目: 国家自然科学基金(编号：61771470)；中国科学院遥感与数字地球研究所所长基金(编号：Y3SJ6400CX)；中国科学院青年创新促进会人才项目(编号：2014054)
第一作者简介: 何梦梦(1990—　)，女，硕士研究生，研究方向为遥感图像处理。E-mail：hemm@radi.ac.cn
通讯作者简介: 郭擎(1980—　)，女，副研究员，研究方向为遥感图像信息提取与处理、图像配准、图像融合和图像加密等。E-mail：guoqing@radi.ac.cn
中图分类号: TP751
文献标识码: A

摘要

随着遥感图像分辨率的日益提高，遥感图像的尺寸和数据量也不断地增大，同时随着遥感应用的发展，对图像配准的性能也提出越来越高的要求，基于此，提出一种特征级高分辨率遥感图像快速自动配准方法。首先，对图像进行Haar小波变换，基于小波变换后的近似图像进行配准以提高配准速度；其次，根据不同的遥感图像来源使用不同的特征提取方法(光学图像使用Canny边缘提取算子，SAR图像使用Ratio Of Averages算子)，并将线特征转化为点特征；然后，依据特征点间最小角与次小角的角度之比小于某一阈值来确定初始匹配点对；最后，利用改进的随机抽样一致性算法滤除错误匹配点对，并结合分块思想均匀选取匹配点对计算仿射变换参数，进一步提高配准精度。为了验证本文方法的有效性，选择高分辨率WorldView-2图像、Pleiades图像和TerraSAR图像进行了实验，并与典型的SIFT算法、SURF算法进行比较分析，采用匹配率、匹配效率、均方根误差和时间消耗4个定量评价指标来客观评价算法的配准性能。实验结果表明，本文方法具有较好的有效性，且在不同的情况下具有较高的配准精度。本文提出的特征级高分辨率遥感图像快速自动配准方法，多组高分辨率遥感图像数据的配准实验结果表明该方法能快速实现并具有较高的配准精度和较好的鲁棒性。

关键词

遥感图像配准, 高分辨率遥感图像自动配准, 图像匹配, 特征匹配, 特征提取

Automatic fast feature-level image registration for high-resolution remote sensing images
expand article info HE Mengmeng1,2 , GUO Qing1 , LI An1 , CHEN Jun1 , CHEN Bo1 , FENG Xuxiang1
1.Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China
2.University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

The size and amount of remote sensing images constantly increase with the improving resolution of remote sensing images. Meanwhile, the development of remote sensing applications also requires high image registration performance. Therefore, an automatic fast feature-level image registration method for high-resolution remote sensing images is proposed. The method includes five steps. First, the reference image and the image to be registered are processed by Haar wavelet transform to obtain the low-frequency approximate images to match. Then, the original images are registered according to the matching result of the approximate images, thereby potentially effectively reducing calculation and improving registration speed. Second, edges in the optical image are extracted by the Canny operator, and edges in the SAR image are extracted by the Ratio Of Averages (ROA) operator. Then, the edge line features are transformed into point features. The use of edge point features can achieve positioning accuracy and acquire stable features. Third, in the feature matching session, the main and auxiliary directions of the point features are considered such that each point feature has multiple directions to enhance the robustness of image registration. Then, the initial matching points are determined by the ratio of the minimum angle to the second minimum angle, which is less than a threshold. Fourth, in the matching point pair filtering session, the random sample consensus is enhanced to improve registration accuracy by adding the constraint condition. The high-quality matching point pairs are selected to fit the model parameters. Finally, in the affine session, the block thought is used to uniformly select matching point pairs to be evenly distributed in the image to avoid the local optimal problem on the registration and further improve image registration accuracy. To verify the efficiency of the method, experiments are conducted under the following conditions: the same sensor optical image registration and sensor SAR image registration, image registration among different bands, image registration with different resolutions, and image registration of different satellite sensors with large size. High resolution WorldView-2, Pleiades, and TerraSAR images are used to perform the experiments. The proposed method is compared with the typical SIFT and SURF algorithms. Four quantitative evaluation indexes, namely, Matching Ratio (MR), Matching Efficiency (ME), Root Mean Square Error (RMSE), and time consumed are used for the registration result evaluation. Experimental results show that the proposed method effectively achieves high registration accuracy under the different conditions. An automatic fast feature-level image registration method for high-resolution remote sensing images is proposed. Multiple datasets of registration experimental results for high-resolution remote sensing images indicate that the proposed method can be rapidly implemented and has high accuracy and strong robustness.

Key words

remote sensing registration, high resolution remote sensing image automatic registration, image matching, feature matching, feature extraction

1 引　言

图像配准是将相同区域的不同类型的图像传感器、不同时间、不同视角及不同拍摄条件下获取的两幅或两幅以上图像进行匹配的过程，其目的是将参考图像和待配准图像进行对准(刘小军 等，2007)，获得更为全面的图像描述供观察或进一步处理。

遥感图像配准是众多遥感信息提取与处理技术中的一个基本问题，是实现同场景多幅遥感图像分析和处理的前提和基础，在应用领域中发挥着重要作用。目前，遥感图像配准已经是多传感器图像融合、遥感图像镶嵌、目标识别、目标变换检测、3D重建、遥感定量信息分析等应用中的关键处理环节。而且，很多后期的理论和应用都是在假设配准问题已解决的前提下展开的，图像配准的精度将直接影响后续应用成果的精度和应用效果。

现有的遥感图像配准方法大致分为两类：基于灰度的遥感图像配准方法和基于特征的遥感图像配准方法(Zitová和Flusser，2003；Zhang 等，2015；Zhu 等，2014)。基于灰度的遥感图像配准直接利用图像的灰度值来确定配准的空间变换，常用的匹配方法有互相关匹配方法、投影匹配方法、基于傅里叶变换的相位相关匹配方法和互信息匹配方法(Eastman 等，2007；Chen 等，2003；Suri和Reinartz，2010；Ma 等，2010；Holia和Thakar，2012)。基于特征的遥感图像配准不直接利用灰度信息，主要依靠图像内部的共同特征进行匹配，这种方法受噪声影响小，计算量小，稳定性强，适应性广，更适合于遥感图像之间的配准，也是目前遥感图像配准领域研究的重点(Fan 等，2013；尤红建和胡岩峰，2014；Bay 等，2006；Li 等，2016；Gu 等，2016；Sedaghat和Ebadi, 2015a, b )。常用的特征配准方法有基于点特征(Lowe, 1999, 2004；Ke和Sukthankar，2004；Kupfer 等，2015)、基于边缘特征(Zhao和Goshtasby，2016；Ma 等，2015)和基于区域特征的方法(Merkle 等，2015；Liu 等，2016；Nagarajan和Schenk，2016)。点特征定位准确，并且匹配后的特征点坐标可以直接用来计算图像之间的空间变换关系；边缘特征较为稳定，但易出现断裂、提取不完整的现象；区域特征含有更多有用的信息，只是在提取之前要对图像进行分割，并且区域特征不容易得到。因此，利用边缘点特征来进行遥感图像配准，既可以准确定位，又可以获得稳定的特征。

另外，遥感数据应用范围广，数据量庞大，实现遥感图像的自动配准以及提高配准的效率对遥感数据分析具有重要意义，也是学者们关注的焦点(李晓明 等，2006；Murphy 等，2016；Paul和Pati，2016)。目前基于点特征自动配准的主流方法是Scale Invariant Feature Transform(SIFT)算法和Speeded Up Robust Features(SURF)算法。Lowe教授在1999年第一次提出了尺度不变特征变换(SIFT)算法，并于2004年将其完善，该方法基于尺度空间，将图像之间的匹配转化为在多尺度空间上点特征的匹配，实现了尺度不变性，该方法在噪声干扰、仿射变换等方面还具有良好的鲁棒性。但SIFT采用欧氏距离对特征点进行匹配，会产生较多的误匹配点对，降低图像匹配效果。Ke和Sukthankar(2004)提出PCA-SIFT算法，虽然简化了SIFT算法的描述子，提高了速度，但是匹配效果没有SIFT好。Pramote和Piamsa-nga(2015)在立体图像匹配方面应用了SIFT算法。Lei等人(2016)将SIFT算法和最小二乘法进行结合，实现了无人机遥感图像的自动配准。Bay等人(2008)提出了加速稳健特征(SURF)算法，该算法引入了积分图像，在尺度和仿射变换下既保持了SIFT的不变性，又优化了配准时间，但是SURF算法存在特征点检测数目少，匹配点对数量少，匹配率较低的缺陷。

又随着遥感图像分辨率的提高，遥感图像配准的研究也逐渐从中低分辨率转向高分辨率(Huang 等，2016；项盛文 等，2015)。但是，高分辨率遥感图像信息更多，细节和纹理更复杂，相对于成熟的中低分辨率遥感图像的配准要难很多，尤其是亚米级高分辨率遥感图像的配准要更难。而且，对高分辨率遥感图像配准适用的方法一定对低分辨率适用，反之却不一定。因此，本文面向细节纹理信息丰富的高分辨率光学及SAR遥感图像，提出了一种特征级高分辨率遥感图像快速自动配准方法，相比目前常用的SIFT方法，在配准精度与计算时效性方面都有了显著提高。本文方法主要包括4个方面：(1)对参考图像与待配准图像都进行一级Haar小波变换，分离图像细节信息的同时保留图像主要空间结构，在变换后的低频近似图像上实现匹配，然后根据匹配结果完成原图的配准，从而有效减少计算量，提高配准速度；(2)依据不同种类遥感图像的特性使用不同的特征提取算法，对于光学图像，使用Canny边缘检测算法(Canny，1986)，对于SAR图像，使用Ratio Of Averages(ROA)边缘检测算法(Touzi 等，1988)，并将边缘线特征转化为点特征；(3)参考图像上每个特征点分别与待配准图像上每个特征点计算角度，通过特征点最小与次小角度之比小于某一阈值来确定初始匹配点对；(4)使用改进的随机抽样一致性算法(RANSAC)滤除错误匹配点，从而提高配准精度，并结合分块思想，均匀选取匹配点对计算仿射变换参数，进一步提高配准精度。

2 特征级高分辨率遥感图像配准方法

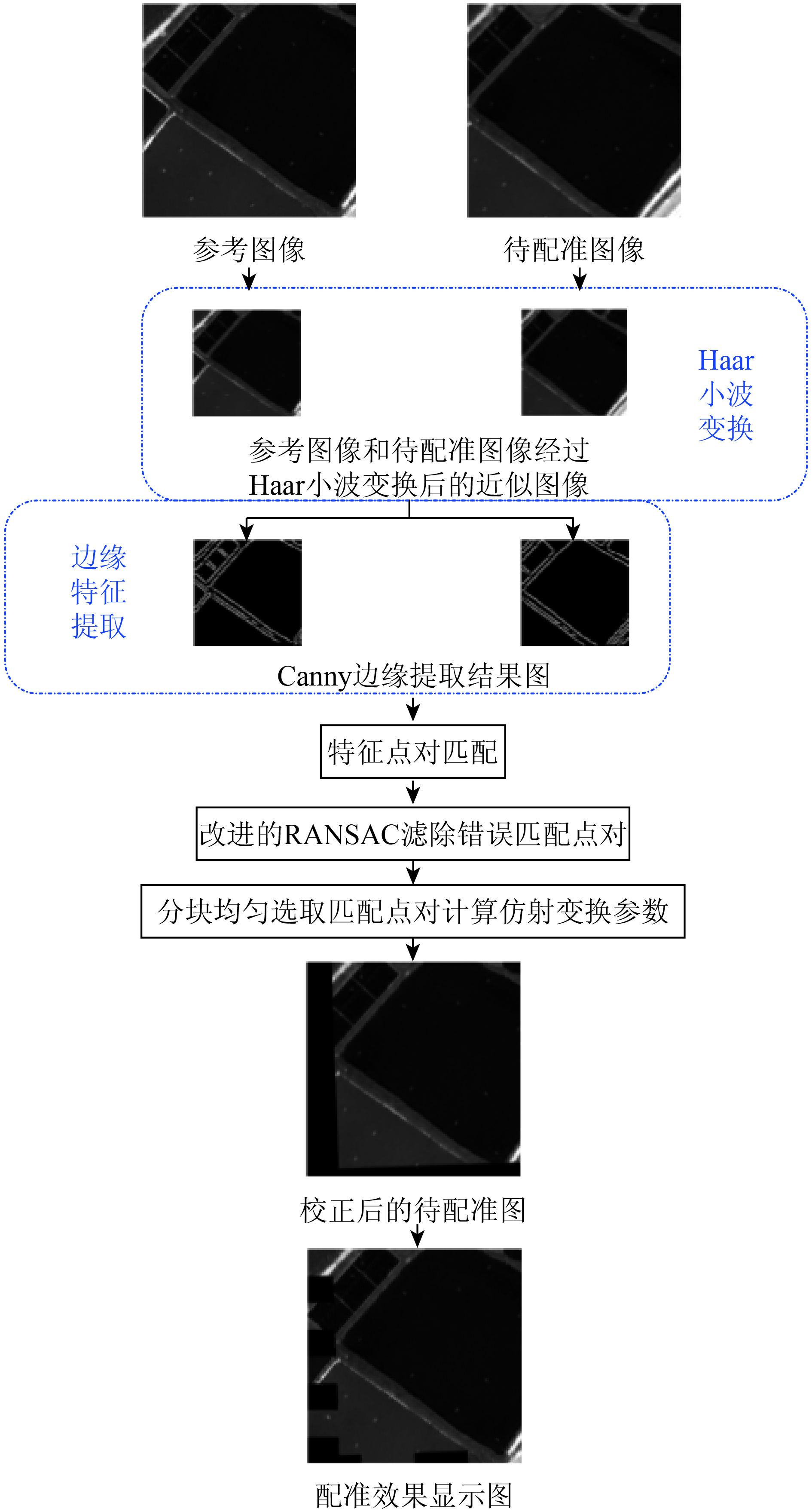
本文提出的方法主要包括Haar小波变换、边缘特征提取、特征点对匹配、错误匹配点对滤除和仿射变换参数计算等步骤。根据遥感图像的来源不同，该方法选择相适合的边缘检测方法。详细的光学图像配准技术路线如图1。其中，若将光学图像的Canny边缘提取方法改为ROA边缘提取方法，则为SAR图像的配准技术路线。


图 1 光学图像配准流程图
Fig. 1 The workflow of optical image registration

为了降低相干斑噪声对SAR图像的影响，本文在对SAR图像进行小波变换前，使用增强的Frost滤波算法实现了滤波预处理。增强的Frost滤波算法针对每一个图像像元根据滤波窗口中像元的方差、像元的灰度平均值、噪声的相对标准差确定不同的权重值，即不同的像元其权重值不同，自适应地平滑掉斑点噪声；而且根据滤波窗口的特性，调整参与滤波运算的权值，有效地抑制斑点噪声和保留边缘细节信息。

2.1 Haar小波变换

在之前的图像配准研究方法中，大多数方法在读取图像后便进行特征提取。但随着遥感图像分辨率越来越高，其图像尺寸也越来越大，直接对图像进行特征提取，会增加数据计算量，降低图像配准效率。小波具有多尺度分析能力，可把图像信号按不同尺度分成保留图像主要空间结构的低频近似图像和3个方向的高频细节信息图像。Haar小波变换函数作为最简单的正交小波变换函数，因其构造简单，计算方便的特点被广泛应用。本文在特征提取之前先对图像进行Haar小波变换得到其低频近似图像，在低频近似图像基础上进行后续处理来提高图像配准的速率。

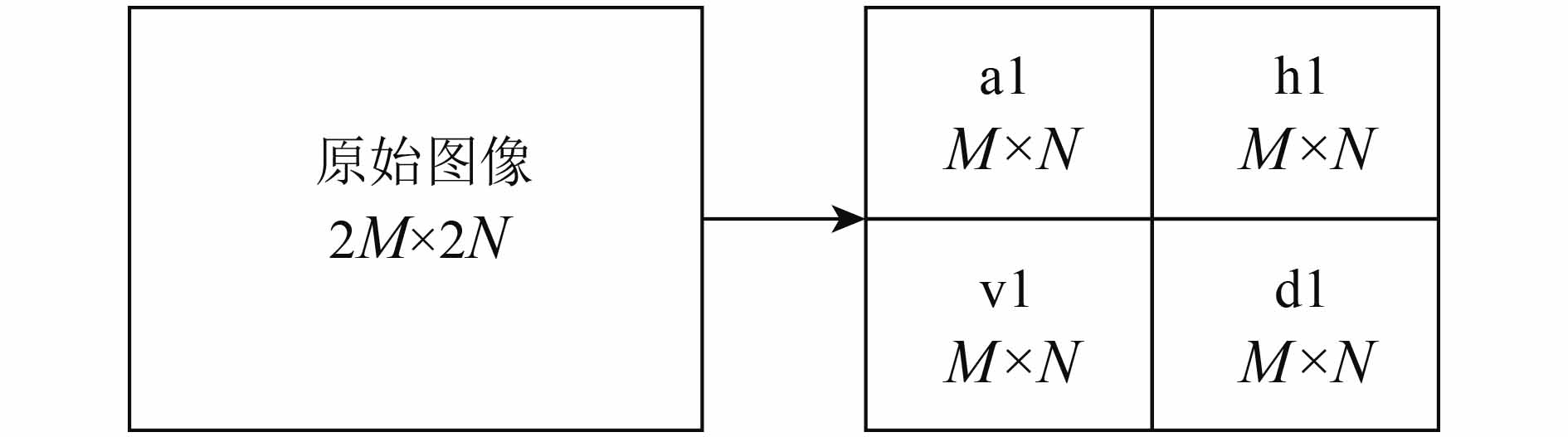
图像经过Haar小波一级分解后可得到4幅子带图(图2)，分别为低频近似图像(a1)、水平细节图像(h1)、垂直细节图像(v1)和对角细节图像(d1)。图2给出了Haar小波一级变换分解示意图。


图 2 Haar小波一级变换分解
Fig. 2 The level 1 decomposition of Haar wavelet transform

2.2 边缘特征提取

常用的提取图像边缘特征的算子有Canny、Roberts、Sobel和Prewitt等算法(Rong 等，2014)。这些算子对存在加性噪声的光学图像适应性好，而对于存在较强乘性相干斑噪声且很难准确定位边缘位置的SAR图像并不适合。

其中，Roberts算子提取的边缘有明显的边缘不连续和部分边缘现象；Sobel和Prewitt算子对弱边缘的检测效果不好，导致检测出的边缘往往不完全；Canny算子既可以控制边缘的细节信息，又能抑制噪声，且使用两个阈值来检测强边缘和弱边缘，可以很好地检测出真正的弱边缘。ROA算子对图像中的乘性噪声具有很好的抑制作用，可以保持边缘检测的稳定性，适用于SAR图像的边缘检测。所以，本文选择Canny算子和ROA算子分别提取光学图像和SAR图像的边缘特征。

2.2.1 Canny边缘提取算子

对于光学图像，首先，将图像的Haar小波低频近似图像 $I\left({x, y} \right)$ 进行高斯滤波，得到平滑后的图像 ${I_{{s}}}\left({x, y} \right)$ 。

${I_{{s}}}\left({x, y} \right) = I\left({x, y} \right)*G\left({x, y} \right)$ (1)

式中， $G\left({x, y} \right)$ 是2维高斯函数， $\sigma $ 是高斯滤波器参数。

$G\left({x, y} \right) = \frac{1}{{2{\text{π}}{\sigma ^2}}}{{{e}}^{\frac{{ - \left({{x^2} + {y^2}} \right)}}{{2{\sigma ^2}}}}}$ (2)

接着，计算图像 ${I_{{s}}}\left({x, y} \right)$ 中各个像元的梯度方向 $H\left({x, y} \right)$ 和梯度幅值 $M\left({x, y} \right)$ 。 ${k_x}\left({x, y} \right)$ 和 ${k_y}\left({x, y} \right)$ 分别为沿x和y方向的偏导数，即

${k_x}\left({x, y} \right) = \frac{{\left[ {I\left({x, y + 1} \right) - I\left({x, y} \right) + I\left({x + 1, y + 1} \right) - I\left({x + 1, y} \right)} \right]}}{2}$ (3)
${k_y}\left({x, y} \right) = \frac{{\left[ {I\left({x, y} \right) - I\left({x + 1, y} \right) + I\left({x, y + 1} \right) - I\left({x + 1, y + 1} \right)} \right]}}{2}$ (4)
$M\left({x, y} \right) = \sqrt {k_x^2\left({x, y} \right) + k_y^2\left({x, y} \right)} $ (5)
$H\left({x, y} \right) = \arctan \left({\frac{{{k_y}\left({x, y} \right)}}{{{k_x}\left({x, y} \right)}}} \right)$ (6)

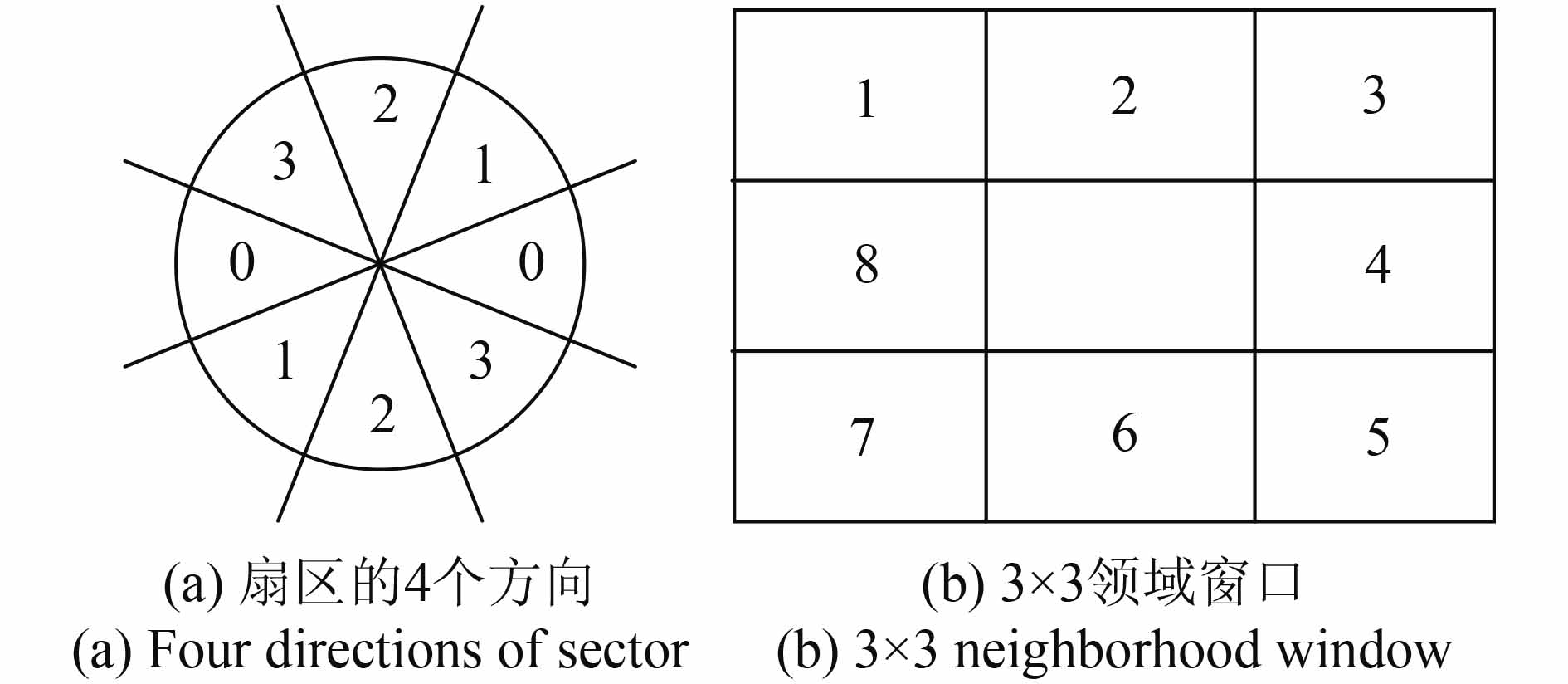
再次，将梯度方向合并到扇区的4个方向(如图3，标号为0, 1, 2, 3)，利用非极大值抑制找到边缘位置。即用一个3×3的邻域窗口作用于梯度幅值阵列 ${M}$ ，每个中心像元的邻域像元必然在其中的一个扇区内，比较中心像元的梯度幅值 ${M_{{{center}}}}\left({x, y} \right)$ 和其梯度方向所在扇区的两个相邻像元的梯度幅值 ${M_{{{near1}}}}\left({x, y} \right)$ 和 ${M_{{{near2}}}}\left({x, y} \right)$ 。若 ${M_{{{center}}}}\left({x, y} \right) > {M_{{{near1}}}}\left({x, y} \right)$ 并且 ${M_{{{center}}}}\left({x, y} \right) > {M_{{{near2}}}}\left({x, y} \right)$ ，则将该中心像元标记为候选边缘像元， ${M_{{{center}}}}\left({x, y} \right)$ 保持不变；反之，该中心像元为非边缘像元， ${M_{{{center}}}}\left({x, y} \right) = 0$ 。


图 3 非极大值抑制
Fig. 3 Non-maximal suppression

最后，制定双阈值(高阈值 ${T_{{{high}}}}$ 和低阈值 ${T_{{{low}}}}$ )来滤除非边缘像元。如果像元的梯度幅值 $M\left({x, y} \right)$ 大于 ${T_{{{high}}}}$ ，则此像元为边缘像元；如果小于 ${T_{{{low}}}}$ ，则此像元是非边缘像元。对于处于 ${T_{{{high}}}}$ 和 ${T_{{{low}}}}$ 之间的像元，若其与边缘像元邻接，则认为是边缘像元，否则是非边缘像元，很好地体现了只有强弱边缘相接时才输出真正的弱边缘。

2.2.2 ROA边缘提取算子

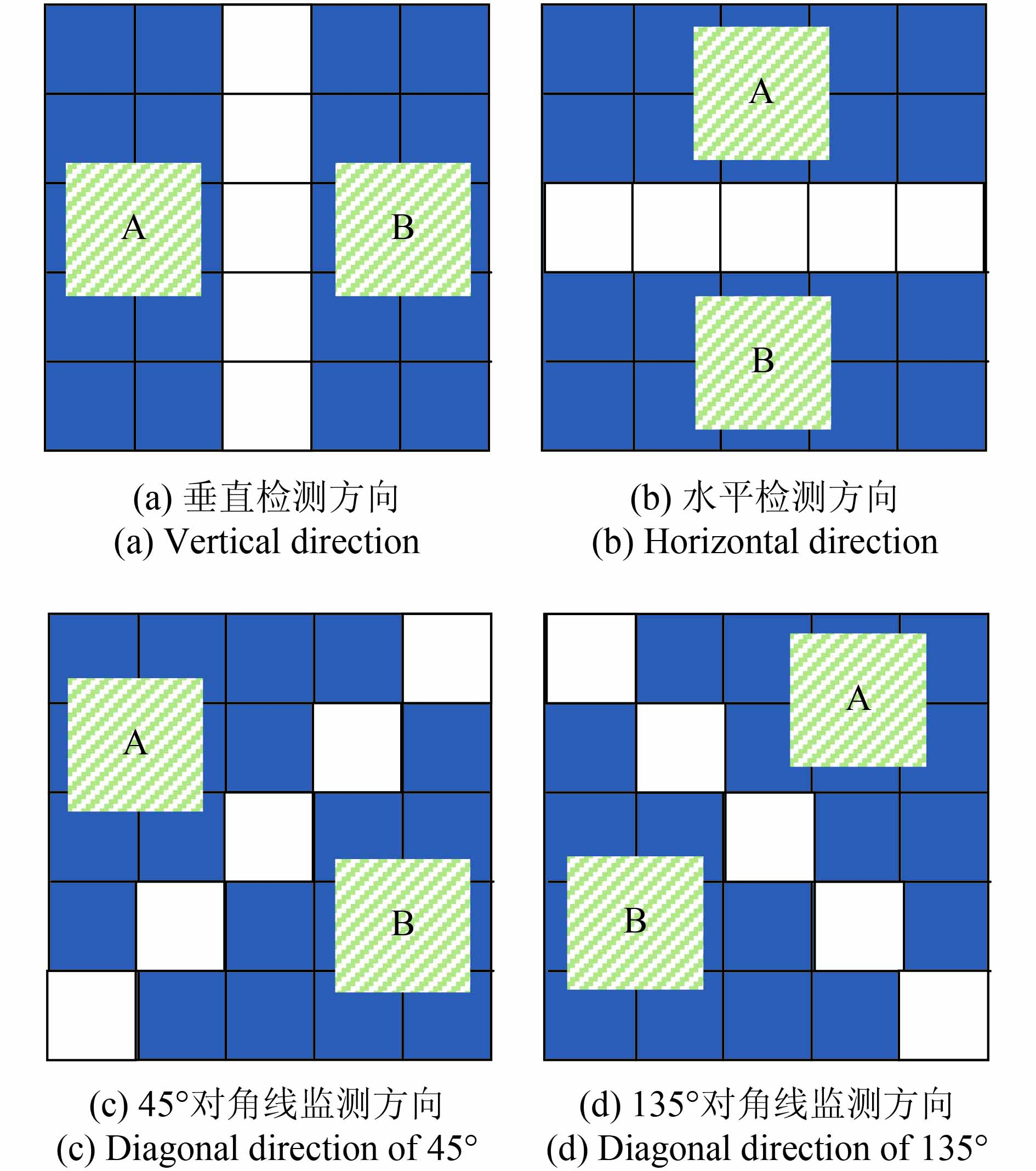
ROA将两个相邻区域的像元灰度均值比作为检测特征量(Touzi 等，1988)。对于SAR图像，取一定尺寸的滑动窗口的中心像元点作为边缘待检测点，则过该点的某直线将滑动窗口划分为A和B两个区域，计算两区域内所有待检测点的灰度均值 ${\mu _{{A}}}$ 与 ${\mu _{{B}}}$ 。令

${r_i} = \max \left\{ {\frac{{{\mu _{{A}}}}}{{{\mu _{{B}}}}}, \frac{{{\mu _{{B}}}}}{{{\mu _{{A}}}}}} \right\}$ (7)

则有两区域灰度均值比值的最大值 ${r_i} \geqslant 1$ ( $i = \left\{ {1, 2, 3, 4} \right\}$ ；分别表示图4中4个边缘方向)。 ${r_i}$ 越趋近于1，即A和B两区域的均值越接近，则它们很可能属于同一区域，从而待检测点越不可能处于A和B的边界上；反之 ${r_i}$ 越大，则A和B的差别越大，待检测点处于两区域间边界上的可能性也越大。因边缘走向不同，故按图4所示的4个边缘方向各检测一次，则待检测点的ROA梯度强度 $r$ 为最大值，有 $r = \max \left({{r_1}, {r_2}, {r_3}, {r_4}} \right)$ 。


图 4 ROA的4种主要检测方向(以5×5窗口为例)
Fig. 4 Four main directions (5×5) of ROA

由于 $r$ 值仅与两区域均值之比有关，而与区域具体的均值大小无关，故可选一个全局阈值T与 $r$ 值进行比较。当 $r$ 值大于T值时，将该点判断为边缘点。

2.3 特征匹配

经过边缘特征提取后分别得到参考图像和待配准图像低频近似图像的二值图像，根据二值图像的属性分别提取边缘点信息作为初始待匹配特征点集。

在匹配之前，需要先确定特征点的方向和描述。本文借鉴SIFT算法思想，提出了基于角度的特征匹配算法。首先，利用特征点邻域像元的梯度方向分布特性为每个特征点指定方向参数，使匹配算子具备旋转不变性。其次，对于每幅低频近似图像 ${{I}}\left({x, y} \right)$ ，在以边缘特征点为中心的3×3邻域窗口内按式(8)(9)计算其梯度值 $m\left({x, y} \right)$ 和梯度方向 $\beta \left({x, y} \right)$ 。再次，将梯度方向的取值范围[0, 2π]分为36段，分别统计梯度幅值直方图，其峰值代表该边缘特征点的主方向。在梯度方向直方图中，当某梯度幅值达到主方向峰值80%以上时，将此方向作为该点的辅方向。因此，一个特征点可能具有多个方向，这可以增强匹配的鲁棒性。对任意一个特征点，将梯度方向变换到以特征点主方向为基准的坐标系中，并将以特征点为中心的16×16邻域均匀分成4×4个子区域，对每个子区域分别统计8个方向的梯度直方图，则构成一个128维的特征向量，然后将该特征向量长度归一化，该向量就是特征点描述。

$m\left({x, y} \right) \!=\! \sqrt {{{\left[ {I\left({x \!+\! 1, y} \right) \!-\! I\left({x \!-\! 1, y} \right)} \right]}^2} \!+\! {{\left[ {I\left({x, y \!+\! 1} \right) \!-\! I\left({x, y \!-\! 1} \right)} \right]}^2}} $ (8)
$\beta \left({x, y} \right) = {\tan ^{ - 1}}\frac{{I\left({x, y + 1} \right) - I\left({x, y - 1} \right)}}{{I\left({x + 1, y} \right) - I\left({x - 1, y} \right)}}$ (9)

最后，通过利用特征向量计算角度对特征点进行匹配，即将近似参考图像(参考图像经过Haar小波变换后的近似图像)上的每个特征点的特征向量 ${a}$ 分别与近似待配准图像(待配准图像经过Haar小波变换后的近似图像)上的每个特征点的特征向量 ${b}$ 做内积得到角度值 $\theta $ ，如式(10)。若特征点的最小角度值 ${\theta _{{{min}}}}$ 与次小角度值 ${\theta _{{{sec}}}}$ 之比小于某一个阈值t，如式(11)，则认为这两个特征点是一对匹配点对。

$\cos \theta = \frac{{{a} \bullet {b}}}{{\left| {a} \right| \times \left| {b} \right|}}$ (10)
$\frac{{{\theta _{\min }}}}{{{\theta _{\sec }}}} < t$ (11)

2.4 改进的RANSAC滤除错误匹配点对

早先学者的研究中，往往直接利用RANSAC算法(Fischler和Bolles，1981)滤除错误匹配点对。RANSAC是一种随机参数估计算法，其目标函数因问题的不同而不同，它的具体步骤为(1)从初始匹配点对集中随机选取8个匹配点对作为样本初始化模型，确定一个模型的参数；(2)用此模型检测初始匹配点对集，找到满足该模型阈值的所有内点(符合模型的数据)；(3)统计由该模型得到的内点数量；(4)重复步骤(1)—(3)，当得到的内点数量最多、误差最小时停止；(5)输出最多的内点集，该内点集即为经过RANSAC筛选后的匹配点对集。

虽然RANSAC算法可以在很大程度上过滤掉误差较大的错误匹配点对，但是它不考虑匹配点对质量的好坏，每次都要随机抽取匹配点对，迭代次数较多，计算复杂度较大，浪费时间。并且当初始匹配点对中误匹配点对较多时或者抽取的匹配点对中含有较多的误匹配点对时就会对图像配准造成误差。

为此本文提出了改进的RANSAC算法来滤除错误匹配点对：将特征匹配中得到的特征点最小角和次小角的角度比值作为匹配点对质量好坏的定量表示(即比值越小则质量越好)。不从匹配点对中随机选取8个匹配点对作为样本进行模型参数拟合，而是根据匹配点对质量的好坏进行排序，在模型参数拟合时选择质量最好的前8个匹配点对进行估计，然后选择距该模型一定距离阈值内的匹配点对作为最终的匹配点对。上述改进解决了多次选择样本集带来的时间耗费问题，并且能够有效减少因选择错误匹配点对而造成的图像配准误差，提高图像配准的精度。

改进的RANSAC算法筛选匹配点对的主要步骤是：首先，对得到的初始特征匹配点对集按特征点最小角度值 ${\theta _{{{min}}}}$ 和次小角度值 ${\theta _{{{sec}}}}$ 之比由小到大排序，选择其中比值最小的8个匹配点对作为样本。其次，将样本进行模型参数拟合，得到符合这些数据的一个基本模型M。再次，用模型M检验特征匹配点对中的所有点，如果该点距模型M的距离小于某个阈值，则此点属于内点(符合模型的数据)，否则为外点(不符合模型的数据)。最后，得到筛选后的匹配点对集。

2.5 仿射变换参数计算

两幅影像经过改进的RANSAC后得到了质量较好(此处质量的标准与RANSAC中一致)的匹配点对，传统方法往往是从这些质量好的匹配点对中随机选取3对来计算仿射变换参数。由于选取的匹配点对可能集中在图像上的某一区域，求解出来的参数容易陷入局部最优而无法整体最优，影响图像配准精度。本文针对这一问题提出了分块均匀提取匹配点对的方法：首先根据图像尺寸的大小，利用双阈值方法进行分块，若匹配点对的行列坐标值均小于低阈值，则归为第1块；若匹配点对的行列坐标值均大于高阈值，则归为第2块；剩下的匹配点对归为第3块。其次在每一块中按质量好坏对匹配点对进行排序，分别选择其中质量最好的一对，最终使选取的匹配点对均匀分布在图像上。

因这些匹配点对均是在低频近似图像上得到的，低频近似图像的尺寸是原图尺寸的一半(本文采用一级小波分解)，所以在计算仿射变换参数前要将这些匹配点对的坐标值乘以2。即将选取的3组匹配点对 ${T_1}\left({{i_1}, {j_1}, {x_1}, {y_1}} \right)$ 、 ${T_2}\left({{i_2}, {j_2}, {x_2}, {y_2}} \right)$ 、 ${T_3}\left({{i_3}, {j_3}, {x_3}, {y_3}} \right)$ (其中， ${T_n}\left({{i_n}, {j_n}, {x_n}, {y_n}} \right)$ ( ${n} = \left\{ {1, 2, 3} \right\}$ )表示特征匹配点对在参考图像中的坐标 $\left({{i_n}, {j_n}} \right)$ 和在待配准图像中的坐标 $\left({{x_n}, {y_n}} \right)$ )坐标值分别乘以2，再计算仿射变换参数，才是原图的变换参数。

首先，将所选匹配点对代入仿射变换式(12)。

$\left( {\begin{array}{*{20}{c}} {\mathop x\nolimits_n } \\[3pt] {\mathop y\nolimits_n } \end{array}} \right) = s \cdot \left( {\begin{array}{*{20}{c}} {\cos \alpha \quad-\sin \alpha } \\ [3pt] {\sin \alpha \quad \cos \alpha } \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\mathop i\nolimits_n } \\ [3pt] {\mathop j\nolimits_n } \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {\mathop d\nolimits_x } \\ [3pt] {\mathop d\nolimits_y } \end{array}} \right)$ (12)

式中，s表示影像的缩放比例； ${d_x}$ 和 ${d_y}$ 分别表示影像在x和y方向上的平移量；α表示影像的旋转角度， $\left({{x_n}, {y_n}} \right)$ 和 $\left({{i_n}, {j_n}} \right)$ 分别为待配准影像和参考影像上匹配特征点对的坐标。

其次，通过解算得到仿射变换的参数。最后，对原始的待配准图像运用得到的仿射变换参数进行双线性插值，得到校正后的图像，完成配准。

3 实验与结果分析

针对本文提出的特征级高分辨率遥感图像配准方法，使用WorldView-2(4级产品，成像时间为2014年10月11日，湛江市某区域)的全色影像数据(分辨率为0.5 m)和多光谱影像数据(分辨率为2 m)，Pleiades的全色影像数据(分辨率0.5 m，成像时间为2016年11月14日，湛江市某区域)以及TerraSAR影像数据(HH，分辨率为0.5 m，成像时间为2014年4月8日，湛江市某区域)进行实验。

为了更好地验证本文方法的有效性，分4种不同的情况来进行实验，分别为不同传感器图像的自身配准、不同波段间的图像配准、不同分辨率的图像配准以及大尺寸不同传感器不同时相的图像配准。实验1到实验4中影像尺寸均为512×512，实验环境为Intel酷睿I5四核处理器，内存为8 GB，操作系统为Windows 7，Matlab 2014a。实验5采用了尺寸为2000×2800的遥感图像，以更好地支持本文方法的通用性和适用性。将本文方法与比较典型的SIFT算法、SURF算法进行比对，采用匹配率(MR)、匹配效率(ME)、均方根误差(RMSE)和时间(T)这4个定量评价指标来客观评价算法的配准结果。

${{MR}} = \frac{{{{SMPP}}}}{{{{MPP}}}}$ (13)

式中，SMPP是筛选后匹配点对数，MPP是匹配点对数。

${{ME}} = \frac{{{{MR}}}}{T}$ (14)
${{RMSE}} = \sqrt {\frac{1}{k}\sum {\left({{{\left({{x_p} - {x_q}} \right)}^2} + {{\left({{y_p} - {y_q}} \right)}^2}} \right)} } $ (15)

式中， $k$ 是选取的点数，p∈[1, k]，q∈[1, k]， ${x_p}$ , ${y_p}$ 是配准图像上匹配点的坐标， ${x_q}$ , ${y_q}$ 是参考图像上对应匹配点的坐标。RMSE越小说明配准精度越高，若RMSE小于1，则配准精度达到亚像素级。

3.1 高分辨率遥感图像不同传感器的自身配准

实验1：图5分别为参考图像(WorldVIew-2的全色波段影像数据)和待配准图像(变换后的World View-2全色波段影像数据)以及Haar小波变换后的低频近似图像和Canny边缘提取图像(为了显示效果，把近似图像和基于近似图像的处理结果都拉伸到与原图一样大小的尺寸)。经过一级Haar小波变换后，低频近似图像的尺寸缩小为原来的一半，尽管丢失了部分细节信息，但Canny算法很好地提取了边缘特征。另外，采用参考图像和待配准图像的低频近似图像(一级小波分解)来提取特征信息进行配准，理论上速度可提升4倍。


图 5 WorldView-2全色图像配准输入图
Fig. 5 The input images for WorldView-2 panchromatic image registration

图6给出了近似图像间经改进的RANSAC筛选前后的匹配点对情况。可以看出，筛选后，错误的匹配点对几乎都被滤除了。为了验证理论上速度提升的正确性，我们分别对原始图像和经Haar小波变换后的近似图像提取特征点和配准。表1中记录了WorldView-2全色波段图像和经过Haar小波变换的配准信息。其中，从近似参考图像(参考图像经过Haar小波变换后的近似图像)、近似待配准图像(待配准图像经过Haar小波变换后的近似图像)、参考图像和待配准图像上提取出来的特征点个数分别为6318、6104、22808和21050，近似图像间的匹配点对是303对，除去不符合要求和错误的匹配点对后，最终为74对匹配点对，而原始图像间的初始匹配点对为803对，筛选后为71对。


图 6 近似图像间经改进的RANSAC筛选前后的匹配点对情况
Fig. 6 The match points of approximate image after the improved RANSAC

同时表1给出了用不用Haar小波变换的配准精度和配准时间的比较。从表1中可以看出，近似图像和原图的RMSE均达到亚像素配准精度，但原始图像的配准时间却远远大于经Haar小波变换后近似图像的配准时间，是其的将近5倍。这主要是因为经过Haar小波变换后，从近似图像上提取的特征点数量减少，从而大幅度降低了特征点匹配计算量，提高了配准速度。

表 1 WorldView-2全色波段原始图像与小波变换后近似图像的配准信息比较
Table 1 The registration information comparison between the WorldView-2 panchromatic original image and the approximate image after Haar wavelet transform

下载CSV 
图像 特征
点数 		匹配点
对数 		筛选后匹
配点对数 		时间/
s 		RMSE/
像元
近似参考图像 6318 303 74 10.463 0.6376
近似待配准图像 6104
原始参考图像 22808 803 71 51.223 0.4092
原始待配准图像 21050

图7给出了配准结果及其显示效果图。图7(a)为待配准图像经过仿射变换得到的校正图像，图7(b)是将参考图像与校正图像叠加在一起并分块显示，从块与块的拼接线是否平滑来展示配准效果。由于原始图像尺寸均为512×512，待配准图像校正时保证图像尺寸不变，所以参考图像与校正图像叠加后大小依然为512×512。将叠加图像平均分割为64块子图像，每一块子图像的尺寸为8×8，其中参考图像和校正图像各占有32块子图像，奇数行的奇数列和偶数行的偶数列为参考图像，剩下的为校正图像。也即每一块参考图像子图像的上、下、左、右均为校正图像子图像，每一块校正图像子图像的上、下、左、右也都为参考图像子图像。为了更清楚地显示配准叠加结果，本文又将参考图像和校正图像先进行伪彩色处理(蔡铁峰 等，2015)后再按上述方法分块叠加显示(图7(c))，以红紫为主要颜色的子图像是参考图像，以蓝绿为主要颜色的子图像是校正图像。

结合图7(b)和图7(c)来看，参考图像和校正图像可以很好地拼接在一起，且接缝处平滑没有差别。


图 7 WorldView-2全色图像配准结果
Fig. 7 The registration result of WorldView-2 panchromatic image

表2给出了SIFT算法、SURF算法和本文方法的对比。从表中可以看出，SIFT算法虽然筛选后得到的匹配点对数最多，但是其配准时间最长，匹配效率最低；SURF算法虽然配准时间最快，但是其匹配率低，均方根误差(RMSE)最大，配准精度最低；而本文方法在匹配率和配准精度上均高于SIFT算法和SURF算法，性能最好。

表 2 WorldView-2全色波段图像的3种算法配准性能比较
Table 2 Three algorithms registration performance comparison of the WorldView-2 panchromatic image

下载CSV 
方法 图像 特征点数 匹配点对数 筛选后匹配点对数 匹配率/% 时间/s 匹配效率/% RMSE/像素
SIFT 参考图像 3742 2343 309 13.2 12.245 1.1 0.8669
待配准图像 3383
SURF 参考图像 1167 293 35 11.9 4.067 2.9 0.9877
待配准图像 1140
本文方法 参考图像 6318 303 74 24.4 10.463 2.3 0.6376
待配准图像 6104

实验2：参考图像为TerraSAR影像数据，待配准图像为变换后的TerraSAR影像数据。图8给出了参考图像、待配准图像以及对应的边缘提取结果图像。

与实验1不同的是，SAR图像需要事先利用增强Frost滤波进行斑点噪声去除，然后进行Haar小波变换，再对经过Haar小波变换后的近似图像进行ROA边缘提取。

图9是校正后的图像和参考图像与校正图像的叠加图像，图9(b)和图9(c)的显示方式与图7(b)和图7(c)相同。从叠加图像上去看，拼接处平滑过度，宛如一幅图像，其RMSE为0.4825。


图 8 TerraSAR图像配准输入图
Fig. 8 The input images for TerraSAR image registration


图 9 TerraSAR图像配准结果
Fig. 9 The registration result of TerraSAR image

从表3中可以看出，SURF算法配准时间最快，SIFT算法配准时间最慢，而本文方法在配准时间上和SURF算法相差不多，但是在匹配率和匹配效率上远远高于SIFT算法和SURF算法；在均方根误差上，本文方法不到0.5，低于SIFT算法和SURF算法，配准精度最好。可见本文方法的配准性能优于SIFT算法和SURF算法。

表 3 TerraSAR图像的3种算法配准性能比较
Table 3 Three algorithms registration performance comparison of the TerraSAR image

下载CSV 
方法 图像 特征点数 匹配点对数 筛选后匹配点对数 匹配率/% 时间/s 匹配效率/% RMSE/像元
SIFT 参考图像 8222 5533 3686 66.6 18.397 3.6 0.6363
待配准图像 8262
SURF 参考图像 1312 423 197 46.6 5.422 8.5 0.7868
待配准图像 1242
本文方法 参考图像 5583 1064 1035 97.3 7.552 12.9 0.4825
待配准图像 5168

3.2 高分辨率光学遥感图像不同波段的配准

实验3：如图10，参考图像为WorldView-2多光谱影像数据中的第5波段，待配准图像为World View-2多光谱影像数据中的第3波段。

配准结果仍然选择参考图像和待配准图像直接叠加显示，图10(c)和10(d)分别给出了本文方法的校正图和配准结果显示图。图10(d)中，地物及纹理在拼接处十分平滑和自然。


图 10 Worldview-2多光谱影像不同波段配准输入图及结果
Fig. 10 The input images for different bands registration and result of WorldView-2 multi-spectral image

实验将SIFT算法、SURF算法与本文方法作对比(表4)，SIFT算法分别从参考图像和待配准图像上提取28417和24630个特征点，找到4125对匹配点对，经原始的RANSAC提纯后为4028对，减少了97对；SURF算法从参考图像和待配准图像上分别提取特征点数为1595和1590，共得到匹配点对数327对，筛选后降为125对，减少了202对；而本文方法从参考近似图像和待配准近似图像上提取的特征点数量依次为14137个和14029个，匹配点对数量经改进的RANSAC提纯后为50对，减少了55对。

对比本文方法与SIFT算法和SURF算法的RMSE可知，本文方法的RMSE为0.8652，SURF算法RMSE为1.2655，而SIFT算法的RMSE存在不稳定情况，有时为0.8994，有时又为0.9854，甚至有时超过1个像素。原因则是SIFT计算配准参数时任意选取3对特征点对，有可能选到不理想的匹配点对从而增大配准误差，达不到满意的效果；其次经原始的RANSAC随机选点滤除的效果也可能不太好。综上可见，在多光谱影像不同波段配准情况下，本文方法比SIFT算法和SURF算法好。

表 4 WorldView-2多光谱影像不同波段的3种算法配准性能比较
Table 4 Three algorithms registration performance comparison of WorldView-2 multi-spectral image

下载CSV 
方法 图像 特征点数 匹配点对数 筛选后匹配点对数 匹配率/% 时间/s 匹配效率/% RMSE/像元
SIFT 参考图像 28417 4125 4028 97.6 33.460 2.9 0.8994
待配准图像 24630
SURF 参考图像 1595 327 125 38.2 7.876 4.9 1.2655
待配准图像 1590
本文方法 参考图像 14137 105 50 47.6 19.080 2.5 0.8652
待配准图像 14029

3.3 高分辨率光学遥感图像不同分辨率的配准

实验4：本组实验的参考图像和待配准图像分别为WorldView-2的全色影像数据和多光谱影像数据中的第5波段影像(图11)，主要为不同分辨率0.5 m和2 m间的配准。


图 11 WorldView-2不同分辨率配准输入图
Fig. 11 The input images for different resolutions registration of Worldview-2

图12给出了全色影像与校正后的多光谱影像的配准结果及其叠加显示图，虽然参考图像和待配准图像分辨率相差4倍，仍然可以从参考图像和待匹配图像上检测出一定数量的匹配点对，且本文方法初始匹配对数和滤除后的匹配对数分别为122对和115对。从图12(b)中看，地物和纹理在拼接处还是很自然的。而由于SIFT随意选择匹配点对，图12(d)中明显看出接缝处的地物有错位现象，没有很好的目视效果。


图 12 WorldView-2不同分辨率配准结果
Fig. 12 The different resolutions registration result of WorldView-2 image

由表5看出，SIFT算法配准所耗时间是SURF算法的2.7倍，是本文方法的1.5倍；在匹配率方面，本文方法最优，SIFT算法次之，SURF算法最低；在匹配效率方面，SIFT算法和SURF算法差不多，本文方法最好为13.6%，是SIFT算法和SURF算法的1.7倍；从最重要的配准精度上看，本文方法更是好于SIFT算法和SURF算法。

表 5 WorldView-2全色波段与多光谱图像的3种算法配准性能比较
Table 5 Three algorithms registration performance comparison of WorldView-2 panchromatic and multi-spectral image

下载CSV 
方法 图像 特征点数 匹配点对数 筛选后匹配点对数 匹配率/% 时间/s 匹配效率/% RMSE/像元
SIFT 参考图像 3630 1656 1379 83.3 10.384 8.0 2.8471
待配准图像 5077
SURF 参考图像 1132 47 15 31.9 3.904 8.2 5.3557
待配准图像 1184
本文方法 参考图像 7460 122 115 94.3 6.937 13.6 1.7423
待配准图像 6760

3.4 大尺寸高分辨率遥感图像不同传感器不同时相的配准

实验5：本组实验的参考图像和待配准图像分别为WorldView-2的全色影像数据(2014年10月11日)和Pleiades全色影像数据(2016年11月14日)(图13)。


图 13 WorldView-2和Pleiades配准输入图
Fig. 13 The input images for Worldview-2 and Pleiades

表6给出了3种算法的配准性能比较。虽然SIFT算法检测出的特征点数和得到的匹配点对数都是最多的，但同时也含有最多的误匹配点对数，匹配率仅为7.4%；本文方法检测的特征点数多于SURF算法，虽然得到的匹配点对数少于SIFT算法和SURF算法，但是本文方法包含的误匹配点对数是3种算法中最少的，而且匹配率和匹配效率都是最高的；在RMSE方面，本文方法也低于SIFT算法和SURF算法，配准精度最好。因此，相对于SIFT和SURF算法，本文方法在大尺寸高分辨率遥感图像不同传感器不同时相配准中性能最优。

表 6 WorldView-2全色波段与Pleiades全色波段的3种算法配准性能比较
Table 6 Three algorithms registration performance comparison of WorldView-2 panchromatic and Pleiades panchromatic

下载CSV 
方法 图像 特征点数 匹配点对数 筛选后匹配点对数 匹配率/% 时间/s 匹配效率/% RMSE/像元
SIFT 参考图像 155678 779 58 7.4 2291.859 0.003 1.8450
待配准图像 202627
SURF 参考图像 31650 106 31 29.2 466.417 0.06 4.0573
待配准图像 31095
本文方法 参考图像 97392 40 28 70 965.404 0.07 0.5676
待配准图像 106443

为了更好地比较配准结果，本组实验给出了WorldView-2全色影像与Pleiades全色影像配准前叠加的局部放大图(图14(c))，可以看到很明显的错位现象。从本文方法的配准结果叠加图14(b)中看，虽然参考图像和待配准图像的传感器和时相均不同，但是地物和纹理在拼接处连接自然平滑。而SIFT算法和SURF算法的配准结果没有很好的目视效果，图14(d)和14(e)中地物在接缝处仍有错位。


图 14 WorldView-2和Pleiades配准结果
Fig. 14 The registration result of WorldView-2 and Pleiades image

4 结　论

本文提出了一种特征级高分辨率遥感图像快速自动配准方法，解决了高分辨遥感图像配准的自动化处理问题，同时提高了配准效率与配准精度。常用的SIFT算法和SURF算法虽然在尺度、平移和旋转方面具有不变性，但SIFT算法耗时长且会产生较多的误匹配点对，SURF算法又有特征点检测数目少和匹配率较低的缺陷。而本文方法运用Haar小波变换缩小图像尺寸的同时保留图像主要空间结构，减少匹配的计算量，提高图像的配准速度。特征匹配中对特征点添加方向时，选择主辅方向一起添加，一个特征点拥有多个方向以增强图像配准的鲁棒性。在筛选匹配点对方面，对随机抽样一致性算法进行改进，添加约束条件，即将匹配点对最小角和次小角的角度比值作为匹配点对质量好坏的依据，优先选择质量好的匹配点对进行模型参数拟合，以此提高图像配准的精确度。其次，在计算最重要的仿射变换参数时，采取分块选取匹配点对的方法，挑选均匀分布在图像中的匹配点对进一步提高图像配准精度。4种情况下高分辨率遥感图像的实验结果也证明了这一方法的有效性、可靠性和适用性，光学传感器图像、SAR传感器图像、不同波段图像和大尺寸不同传感器不同时相图像的配准精度均达到亚像素级。

高分辨率SAR遥感图像和光学遥感图像有着不可或缺的互补优势，但由于成像条件的差异等问题导致配准较难，这也是下一步要深入研究的问题。

参考文献(References)

  • Bay H, Ess A, Tuytelaars T and Van Gool L. 2008. Speeded-up robust features (SURF). Computer Vision and Image Understanding, 110 (3): 346–359. [DOI: 10.1016/j.cviu.2007.09.014]
  • Bay H, Tuytelaars T and Van Gool L. 2006. Surf: speeded up robust features//Proceedings of the 9th European Conference on Computer Vision. Graz, Austria: Springer: 404–417 [DOI: 10.1007/11744023_32]
  • Cai T F, Zhu F, Hao Y M and Fan H J. 2015. Pseudo-color processing of gray images for human visual detection and recognition. Infrared and Laser Engineering, 44 (S1): 213–219. [DOI: 10.3969/j.issn.1007-2276.2015.z1.039] ( 蔡铁峰, 朱枫, 郝颖明, 范慧杰. 2015. 面向人眼探测识别的灰度图像伪彩色化方法. 红外与激光工程, 44 (S1): 213–219. [DOI: 10.3969/j.issn.1007-2276.2015.z1.039] )
  • Canny J. 1986. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-8(6): 679–698 [DOI: 10.1109/TPAMI.1986.4767851]
  • Chen H M, Varshney P K and Arora M K. 2003. Performance of mutual information similarity measure for registration of multitemporal remote sensing images. IEEE Transactions on Geoscience and Remote Sensing, 41 (11): 2445–2454. [DOI: 10.1109/TGRS.2003.817664]
  • Eastman R D, Le Moigne J and Netanyahu N S. 2007. Research issues in image registration for remote sensing//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN, USA: IEEE: 1–8 [DOI: 10.1109/CVPR.2007.383423]
  • Fan B, Huo C L, Pan C H and Kong Q Q. 2013. Registration of optical and SAR satellite images by exploring the spatial relationship of the improved sift. IEEE Geoscience and Remote Sensing Letters, 10 (4): 657–661. [DOI: 10.1109/LGRS.2012.2216500]
  • Fischler M A and Bolles R C. 1981. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24 (6): 381–395. [DOI: 10.1145/358669.358692]
  • Gu Y J, Ren K, Wang P C and Gu G H. 2016. Polynomial fitting-based shape matching algorithm for multi-sensors remote sensing images. Infrared Physics and Technology, 76 : 386–392. [DOI: 10.1016/j.infrared.2016.03.019]
  • Holia M S and Thakar V K. 2012. Mutual information based image registration for MRI and CT SCAN brain images//Proceedings of 2012 International Conference on Audio, Language and Image Processing. Shanghai, China: IEEE: 78–83 [DOI: 10.1109/ICALIP.2012.6376590]
  • Huang F H, Mao Z Y and Shi W Z. 2016. ICA-ASIFT-based multi-temporal matching of high-resolution remote sensing urban images. Cybernetics and Information Technologies, 16 (5): 34–49. [DOI: 10.1515/cait-2016-0050]
  • Ke Y and Sukthankar R. 2004. PCA-SIFT: a more distinctive representation for local image descriptors//Proceedings of 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC, USA: IEEE: 506–513 [DOI: 10.1109/CVPR.2004.1315206]
  • Kupfer B, Netanyahu N S and Shimshoni I. 2015. An efficient SIFT-based mode-seeking algorithm for sub-pixel registration of remotely sensed images. IEEE Geoscience and Remote Sensing Letters, 12 (2): 379–383. [DOI: 10.1109/LGRS.2014.2343471]
  • Lei T J, Li L, Kan G Y, Zhang Z B, Sun T, Zhang X L, Ma J W and Huang S F. 2016. Automatic registration of unmanned aerial vehicle remote sensing images based on an improved sift algorithm//Proceedings of SPIE Volume 10033, Eighth International Conference on Digital Image Processing. Chengdu, China: SPIE: 10033 [DOI: 10.1117/12.2245126]
  • Li J Y, Hu Q W and Ai M Y. 2016. Robust feature matching for remote sensing image registration based on Lq-estimator . IEEE Geoscience and Remote Sensing Letters, 13 (12): 1989–1993. [DOI: 10.1109/LGRS.2016.2620147]
  • Li X M, Zheng L and Hu Z Y. 2006. SIFT based automatic registration of remotely-sensed imagery. Journal of Remote Sensing, 10 (6): 885–892. [DOI: 10.3321/j.issn:1007-4619.2006.06.009] ( 李晓明, 郑链, 胡占义. 2006. 基于SIFT特征的遥感影像自动配准. 遥感学报, 10 (6): 885–892. [DOI: 10.3321/j.issn:1007-4619.2006.06.009] )
  • Liu F Q, Bi F K, Chen L, Shi H and Liu W. 2016. Feature-area optimization: a novel SAR image registration method. IEEE Geoscience and Remote Sensing Letters, 13 (2): 242–246. [DOI: 10.1109/LGRS.2015.2507982]
  • Liu X J, Zhou Y, Ling J G, Shen H B and Yang J. 2007. Patch-based SAR image automatic registration. Computer Engineering, 33 (4): 176–178. [DOI: 10.3969/j.issn.1000-3428.2007.04.061] ( 刘小军, 周越, 凌建国, 沈红斌, 杨杰. 2007. 基于轮廓特征的SAR图像自动配准. 计算机工程, 33 (4): 176–178. [DOI: 10.3969/j.issn.1000-3428.2007.04.061] )
  • Lowe D G. 1999. Object recognition from local scale-invariant features. Proceeding of the 7th International Conference on Computer Vision. Kerkyra, Greece: IEEE: 1150–1157 [DOI: 10.1109/ICCV.1999.790410]
  • Lowe D G. 2004. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 60 (2): 91–110. [DOI: 10.1023/B:VISI.0000029664.99615.94]
  • Ma J L, Chan J C W and Canters F. 2010. Fully automatic subpixel image registration of multiangle CHRIS/proba data. IEEE Transactions on Geoscience and Remote Sensing, 48 (7): 2829–2839. [DOI: 10.1109/TGRS.2010.2042813]
  • Ma J Y, Zhou H B, Zhao J, Gao Y, Jiang J J and Tian J W. 2015. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Transactions on Geoscience and Remote Sensing, 53 (12): 6469–6481. [DOI: 10.1109/TGRS.2015.2441954]
  • Merkle N, Müller R, Schwind P, Palubinskas G and Reinartz P. 2015. A new approach for optical and SAR satellite image registration. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, II-3/W4: 119–126 [DOI: 10.5194/isprsannals-II-3-W4-119–2015]
  • Murphy J M, Moigne J L and Harding D J. 2016. Automatic image registration of multimodal remotely sensed data with global shearlet features. IEEE Transactions on Geoscience and Remote Sensing, 54 (3): 1685–1704. [DOI: 10.1109/TGRS.2015.2487457]
  • Nagarajan S and Schenk T. 2016. Feature-based registration of historical aerial images by Area Minimization. ISPRS Journal of Photogrammetry and Remote Sensing, 116 : 15–23. [DOI: 10.1016/j.isprsjprs.2016.02.012]
  • Paul S and Pati U C. 2016. Remote sensing optical image registration using modified uniform robust SIFT. IEEE Geoscience and Remote Sensing Letters, 13 (9): 1300–1304. [DOI: 10.1109/LGRS.2016.2582528]
  • Pramote O U and Piamsa-nga P. 2015. Improve accuracy of disparity map for stereo images using sift and weighted color model//Proceedings of the 7th International Conference on Knowledge and Smart Technology. Chonburi, Thailand: IEEE: 109–114 [DOI: 10.1109/KST.2015.7051470]
  • Rong W B, Li Z J, Zhang W and Sun L N. 2014. An improved canny edge detection algorithm//Proceedings of 2014 IEEE International Conference on Mechatronics and Automation. Tianjin, China: IEEE: 577–582 [DOI: 10.1109/ICMA.2014.6885761]
  • Sedaghat A and Ebadi H. 2015a. Distinctive order based self-similarity descriptor for multi-sensor remote sensing image matching. ISPRS Journal of Photogrammetry and Remote Sensing, 108 : 62–71. [DOI: 10.1016/j.isprsjprs.2015.06.003]
  • Sedaghat A and Ebadi H. 2015b. Remote sensing image matching based on adaptive binning SIFT descriptor. IEEE Transactions on Geoscience and Remote Sensing, 53 (10): 5283–5293. [DOI: 10.1109/TGRS.2015.2420659]
  • Suri S and Reinartz P. 2010. Mutual-information-based registration of terraSAR-X and Ikonos imagery in urban areas. IEEE Transactions on Geoscience and Remote Sensing, 48 (2): 939–949. [DOI: 10.1109/TGRS.2009.2034842]
  • Touzi R, Lopes A and Bousquet P. 1988. A statistical and geometrical edge detector for SAR images. IEEE Transactions on Geoscience and Remote Sensing, 26 (6): 764–773. [DOI: 10.1109/36.7708]
  • Xiang S W, Wen G J, Gao F and Wu Y J. 2015. High resolution remote sensing image registration method based on multi-model representation. Transducer and Microsystem Technologies, 34 (10): 22–24, 28. [DOI: 10.13873/J.1000-9787(2015)10-0022-03] ( 项盛文, 文贡坚, 高峰, 伍颖佳. 2015. 基于多模型表示的高分辨率遥感图像配准方法. 传感器与微系统, 34 (10): 22–24, 28. [DOI: 10.13873/J.1000-9787(2015)10-0022-03] )
  • You H J and Hu Y F. 2014. Investigation on fine registration for SAR and optical image. Journal of Radars, 3 (1): 78–84. [DOI: 10.3724/SP.J.1300.2014.13154] ( 尤红建, 胡岩峰. 2014. SAR和光学图像精配准技术的研究. 雷达学报, 3 (1): 78–84. [DOI: 10.3724/SP.J.1300.2014.13154] )
  • Zhang Q, Cao Z G, Hu Z W, Jia Y H and Wu X L. 2015. Joint image registration and fusion for panchromatic and multispectral images. IEEE Geoscience and Remote Sensing Letters, 12 (3): 467–471. [DOI: 10.1109/LGRS.2014.2346398]
  • Zhao C Y and Goshtasby A A. 2016. Registration of multitemporal aerial optical images using line features. ISPRS Journal of Photogrammetry and Remote Sensing, 117 : 149–160. [DOI: 10.1016/j.isprsjprs.2016.04.002]
  • Zhu H, Li Y F, Yu J M, Leung H and Li Y H. 2014. Ensemble registration of multisensor images by a variational bayesian approach. IEEE Sensors Journal, 14 (8): 2698–2705. [DOI: 10.1109/JSEN.2014.2315838]
  • Zitová B and Flusser J. 2003. Image registration methods: a survey. Image and Vision Computing, 21 (11): 977–1000. [DOI: 10.1016/S0262-8856(03)00137-9]
数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献
  • 多媒体 多媒体