|
收稿日期: 2017-06-12
基金项目: 国家自然科学基金(编号:41501394);中国科学院遥感与数字地球研究所研究生所长基金;中国科学院青年创新促进会(编号:2017086);陆地生态系统碳监测卫星工程
第一作者简介: 张立福(1967— ),男,研究员,研究方向为高光谱遥感技术和应用。E-mail:zhanglf@radi.ac.cn
中图分类号: TP701
文献标识码: A
|
摘要
利用卫星遥感探测区域和全球尺度太阳诱导叶绿素荧光SIF(Solar-Induced chlorophyll Fluorescence)近年来成为研究热点。由于地球大气吸收和散射的影响,卫星尺度的SIF反演问题较为复杂,科学界对该问题一直存在争议,不同科学团队提出了众多方法。本文介绍了大气层顶SIF反演的机理、难点及思路,总结了近10年来最新发展的大气层顶SIF反演算法,并将这些算法归纳为3类:基于辐射传输方程的算法、简化的物理模型算法和数据驱动算法,分析讨论了各算法的特点及适用性;以应用最广泛的数据驱动算法为例,基于GOME-2数据详细介绍了算法的中间环节及注意事项;最后回顾了卫星遥感反演SIF的发展历程,汇总了目前及未来具有荧光探测能力的星载传感器,并依据数据源的特点相应地给出了适用的SIF反演算法,为今后基于航空和卫星高光谱数据的SIF反演提供了依据。
关键词
太阳诱导叶绿素荧光(SIF), 高光谱遥感, 辐射传输方程, 数据驱动算法
Abstract
Solar-Induced chlorophyll Fluorescence (SIF) is directly related to photosynthesis and therefore considered a promising tool for grossprimary productivityestimation and vegetation environmental stress monitoring. Interest in SIF has increased since satellite remote sensing of SIF became feasible, especially after the first global SIF map was depicted in 2011. However, methods for retrieving SIF at Top-Of-Atmosphere (TOA) are still under investigation and argumentation, as decoupling SIF from total at-sensor radiance is challenging in the presence of atmospheric scattering and absorption. This paper aims to review the methods proposed for SIF retrieval at TOA over the past 10 years, to illustratethe advantages/disadvantages of those methods and to provide a technical instruction for remote sensingof SIF at airborne/space level. All the methods were categorized into three types: methods based on Radiative Transfer (RT) calculations, simplified physically-based methods and data-driven approaches. Methods based on RT calculations, including improved Fraunhofer Line Discrimination (FLD) methods and Spectral Fitting Methods (SFM), aim to retrieve SIF using atmospheric absorption lines. Atmosphere is characterized through RT calculations and then the TOA problem is converted to Bottom-Of-Atmosphere (BOA). These methods are applicable in situations with medium to low spectral resolution (0.3—5 nm) whereas imperfect characterization of atmosphere and RT process will lead to retrieval errors. Physically-based methods utilize single or several solar Fraunhofer Lines located in atmospheric windows, using solar irradiance spectra (measured or simulated through spectra convolution) as reference, decoupling SIF signal from earth radiances. Atmosphere scattering and absorption are neglected under these situations. Physically-based methods were developed for high spectral resolution measurements (e.g. 0.025 nm for GOSAT) and are sensitive to noise. Data driven approaches consider any fluorescent radiance spectrum consists non-fluorescent portion and SIF signal. Features extracted from large training dataset consisting non-fluorescent spectra (cloud, ice/snow, desert…) are used to express the non-fluorescent portion in the fluorescent spectra while SIF signal is expressed as mathematical function or spectra with fixed shape. Data driven approaches are popular because they do not require RT calculations while are applicable for medium to high spectral resolution situations. The performance of data driven approaches depends on the representativeness of training dataset and other empirical settings of the model, including the number of features used, function used to describe SIF spectrum and retrieval window selected. With several satellite sensors with medium spectral resolution (0.3—0.5 nm) being available for SIF retrieval (including currently available ones and scheduled to be launched in near future ones), including MetOp-GOME-2, Sentinel-5-TROPOMI and the FLuorescence EXplorer (FLEX) mission, RT-based methods and data-driven approaches are considered most promising SIF retrieval methods in the future. The RT-based methods are mainly developed by the FLEX team and are applicable for low spectral resolution and airborne data, but the performance of these methods on global SIF retrieval needs to be validated with real satellite data. On the other hand, several global SIF products have been generated using data driven approaches. However, representative training dataset needs to be built carefully and optimal parameters need to be determined according to different sensors.
Key words
SIF retrieval, hyperspectral remote sensing, radiative transfer, data-driven approaches
1 引 言
处于自然光照条件下的绿色植物在进行光合作用时释放一种波长位于650—800 nm的光,称为太阳诱导叶绿素荧光SIF(Solar-Induced chlorophyll Fluorescence)。SIF是光合作用的副产品,源于吸收的光合有效辐射APAR(Absorbed Photosynthetically Active Radiation),与植被光合固碳及热耗散同根同源,因此同植被总初级生产力GPP(Gross Primary Productivity)和植被受胁迫状态密切相关(Porcar-Castell 等,2014)。
利用卫星遥感的方法探测全球尺度SIF成为近年来研究热点,欧洲空间局(ESA)的Fluorescence Explorer (FLEX)于2015年打败CarbonSat,正式被选为ESA第八届对地观测计划卫星;美国国家宇航局(NASA)开展了大量航空飞行进行SIF探测实验,并在第二代碳监测卫星(OCO-2)指标设计中充分考虑全球SIF探测的需求;中国于2016年底发射的二氧化碳监测卫星(TanSat)和欧盟将于2017年7月发射的哨兵5号卫星也具有荧光探测能力。利用SIF进行区域、全球植被监测,对于精确把握植被生长状态、准确了解全球碳汇分布和进一步理解陆表植被对气候变化的响应具有重要意义。
作为一种微弱的冠层发射信息(通常不足吸收光子能量的5%,Van Der Tol 等,2014),SIF与反射能量同时被遥感器捕获,将SIF从总入瞳辐亮度中剥离的过程称为SIF的遥感反演。遥感反演则成为进一步利用SIF进行植被监测的前提。
1.1 SIF的遥感反演机理
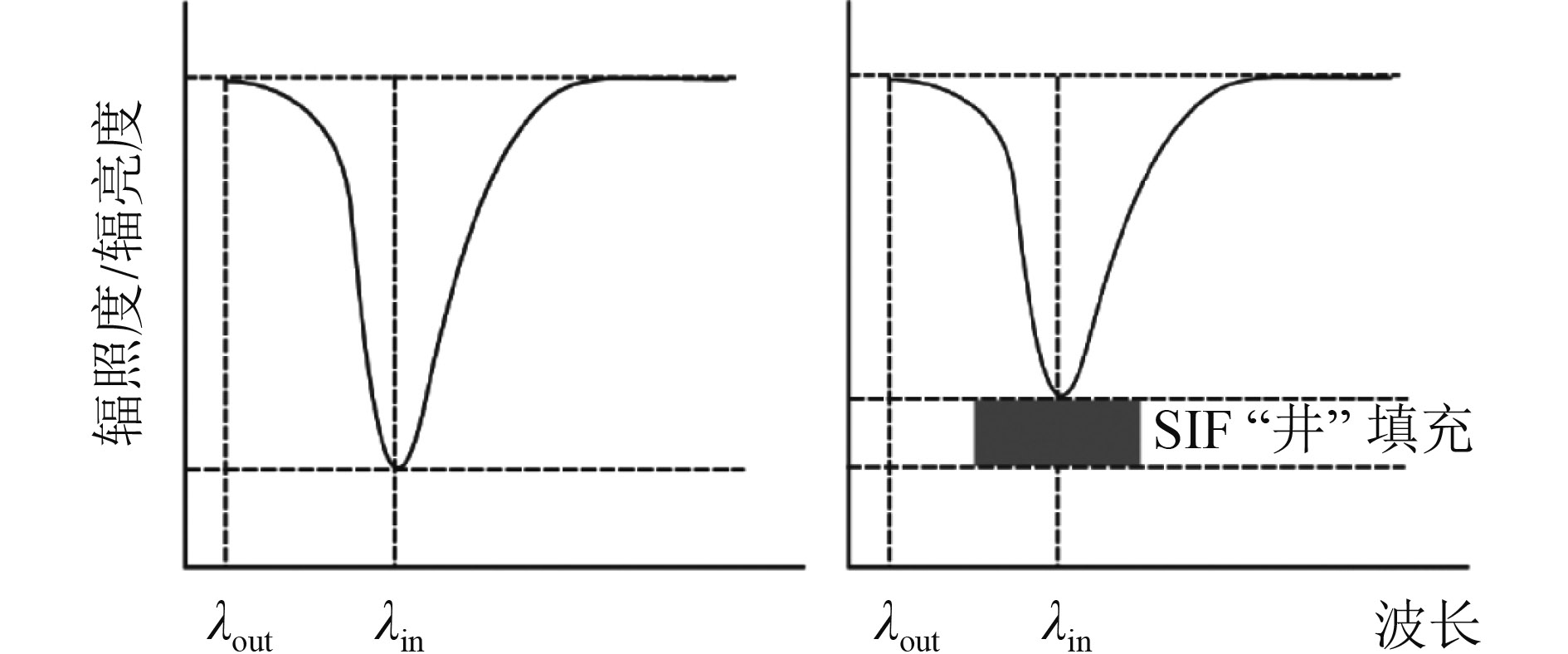
太阳辐射亮度谱线经过太阳大气和地球大气中各成分的吸收,到达传感器时存在宽度不等(0.1 nm至10 nm,胡姣婵 等,2015)、深度不同的吸收谷,称为夫琅和费暗线(Fraunhofer Lines)。SIF作为地表发射信号,叠加于反射信息之上,改变了夫琅和费暗线的深度,利用SIF对夫琅和费暗线的“井”填充效应(图1),通过比对原始暗线深度及经SIF填充后的暗线深度,可以实现SIF的遥感反演(刘良云 等,2006)。由于反演SIF至少利用一条夫琅和费暗线,且对于任意一条暗线,传感器的光谱分辨率愈高,观测得到的原始暗线深度愈深,SIF对暗线的填充效应愈明显,则SIF反演的鲁棒性愈强。因此,SIF的遥感反演需要在高光谱分辨率条件下实现,其核心问题为如何准确得到未被荧光填充的原始暗线和被荧光填充后的暗线。
近地面的叶绿素荧光遥感反演较为容易实现,利用余弦接收器对天空观测或利用裸光纤对标准反射白板观测获得未被荧光填充的暗线,忽略传感器至植被冠层路径内大气对荧光上行辐射的吸收和散射,通过假设夫琅和费暗线内外的冠层反射率和荧光光谱满足特定的条件,反演得到冠层释放的SIF。Meroni等人(2009)总结了近地面利用单条夫琅和费暗线反演SIF的算法,包括FLD(Fraunhofer Line Discrimination)系列算法和光谱拟合算法SFMs(Spectral Fitting Methods)。由于SIF与APAR密切相关,随光照条件变化而变化,SIF从而具有瞬时性,因此SIF的时空分布特性比其绝对值更具指示意义(Köhler 等,2015b;Zhang 等,2016),空间连续分布的多时相SIF则需借助航空、卫星平台搭载的传感器观测数据。然而,由于受地球大气的影响,相对于近地面,大气层顶的SIF反演问题更为复杂。
1.2 大气层顶SIF反演的难点
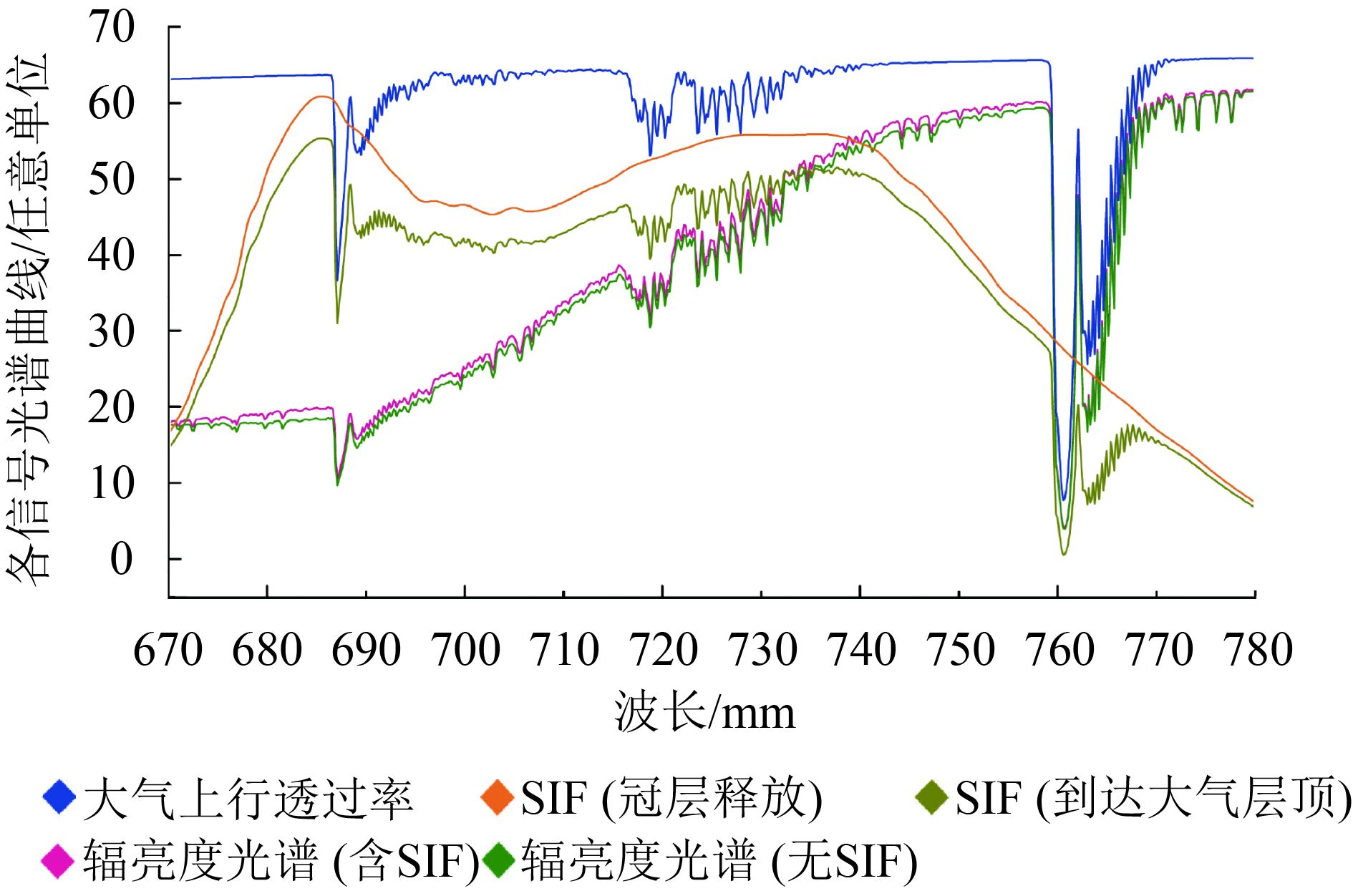
利用地球大气暗线进行SIF反演(如O2-A或O2-B)面临两个主要问题。以O2-A波段为例,一方面,到达地表的太阳辐射光谱中的O2-A暗线无法直接观测,即未被SIF填充的真实暗线深度未知,只能通过模拟估计;另一方面,冠层释放的SIF在传输过程中被大气中的O2吸收,改变了原始荧光谱线特征,在强吸收波段甚至可能导致荧光信号完全被吸收(Frankenberg 等,2011),给SIF反演带来不确定性。图2展示了0.3 nm光谱分辨率条件下冠层释放的SIF、到达大气层顶的SIF、大气上行透过率和传感器入瞳辐亮度。
利用位于大气窗口的太阳夫琅和费暗线进行荧光反演无需考虑地球大气的影响,但太阳大气暗线的宽度通常较窄,在同等光谱分辨率条件下深度较浅,因此对传感器的光谱分辨率及信噪比提出了更高要求;此外,在超高光谱分辨率条件下,地球大气中的非弹性散射(转动拉曼散射RRS(Raman Rotational Scattering))、传感器杂散光等对夫琅和费暗线的填充效应更加明显(Vasilkov 等,2013),为SIF反演带来系统误差。
因此,需针对上述主要问题改进近地表SIF反演算法或发展新的大气层顶SIF反演算法。
1.3 大气层顶SIF反演的思路
目前大气层顶的SIF反演主要有3种思路。
第1种条思路仍试图利用地球大气夫琅和费暗线进行SIF反演,通过对太阳辐射及大气吸收和散射的定量化描述建立耦合荧光发射和地表反射的大气辐射传输方程,将大气层顶的荧光反演问题转化至大气层底,再利用近地表SIF反演算法求解荧光。这类算法主要由ESA的FLEX团队提出,包括改进的FLD系列算法(Damm 等,2014;Guanter 等,2007;Guanter 等,2010)和基于严密辐射传输方程的SFM算法(Cogliati 等,2015;Verhoef 等,2014)。这类算法的优势在于对传感器光谱分辨率的要求不高(通常优于4 nm即可),且FLEX团队开展了大量基于模拟数据和航空数据的算法测试实验,对算法的不确定性有较完备评估;其劣势在于反演的精度取决于对大气状态描述的准确程度及建立的辐射传输方程的严密程度,容易产生系统误差。
第2种思路则完全避开地球大气吸收线,通过大气层顶观测或光谱卷积模拟得到未经荧光填充的暗线,并利用大气窗口内的一条或少数几条太阳夫琅和费暗线进行荧光反演。由于避开了大气吸收线,并将大气程辐射视为大气对太阳辐射的平滑反射,则变为与近地表SIF反演相同的问题,这类算法称为简化的物理模型荧光反演算法(Frankenberg 等,2011;Joiner 等,2011;Köhler 等,2015a;刘新杰和刘良云,2013)。简化的物理模型荧光反演算法的主要优势在于无需考虑大气的影响,反演模型简单;劣势在于对传感器光谱分辨率的要求极高(通常优于0.1 nm),且对噪声敏感。
第3种思路则综合利用地球暗线和大气窗口内的太阳暗线,将传感器观测到的入瞳辐亮度视为非荧光信号和荧光信号的线性叠加,利用大量非荧光目标(海上浓云、沙漠、冰雪等)光谱构成训练集,对其光谱进行特征提取,用提取的少量特征表达任意观测的非荧光信号,再利用简化的辐射传输方程进行荧光信号的分离,这类算法称为数据驱动算法。数据驱动算法的优势在于对传感器的光谱分辨率要求低于简化的物理模型算法,通常亚纳米即可满足,在降低了硬件需求的同时避免了辐射传输计算进而提高了算法效率,数据驱动算法已经应用于全球卫星荧光提取并发布了时间序列荧光产品(Joiner 等,2013;Köhler 等,2015b);数据驱动算法的缺点是算法中需要经验参数设置,不同数据源可能需采用不同反演窗口并需要改变参数设置,且算法表现依赖于选择的训练集的代表性(Zhang 等,2017)。
表1总结了目前大气层顶SIF反演的主要算法、应用的数据和涉及的主要文献。表2列出了目前具有荧光探测能力的主要卫星及传感器的参数,包括已经在轨运行的和列入发射日程的卫星。
表 1 大气层顶(航空、卫星)SIF遥感反演的主要算法、选取波段、所用传感器数据及参考文献
Table 1 State of the art of SIF retrieval methods at top-of-atmosphere (the selected retrieving window, data used and references are also listed)
| 算法类型 | 算法名称 | 反演窗口 | 传感器 | 参考文献 |
| 基于大气辐射传输方程的算法 | FLD算法 | O2-A | MERIS/CASI | Guanter 等,2007 |
| 系数FLD算法 | FLEX-FIMAS | Guanter 等,2010 | ||
| ASD(机载) | Damm 等,2014 | |||
| SFM算法 | O2-A/B | FLEX-FLORIS | Cogliati 等,2015 | |
| 简化的物理模型算法 | IMAP-DOAS | 756—759 nm | GOSAT-FTS | Frankenberg 等,2011 |
| — | 769.9—770.2 nm | Joiner 等,2011 | ||
| 带权最小二乘算法 | 刘新杰和刘良云,2013 | |||
| — | 755—759 nm | Köhler 等,2015a | ||
| 数据驱动算法 | SVD算法 | 756—759 nm 769—771 nm | GOSAT-FTS | Guanter 等,2012 |
| 758—759 nm 770.1 nm | OCO-2 | Frankenberg 等,2014 | ||
| 各潜在窗口 | TROPOMI | Guanter 等,2015 | ||
| 非线性PCA算法 | 712—783 nm | GOME-2、SCIAMACHY | Joiner 等,2013 | |
| 682—692 nm | Joiner 等,2016 | |||
| 712—783 nm | Sanders 等,2016 | |||
| 线性PCA算法 | 720—758 nm | Köhler 等,2015b | ||
| 注:所用FLEX-FIMAS、FLEX-FLORIS和TROPOMI传感器数据为依据传感器光谱响应函数和信噪比生产的模拟数据。 | ||||
综上所述,SIF的大气层顶遥感反演是进一步利用荧光进行大尺度植被监测的基础,且存在较大不确定性。针对大气层顶SIF反演中存在的主要问题,近年来众研究团队及科学家提出了不同的解决思路并发展了众多算法,这些算法各有优劣,适用性不同。本文的主要目的是总结目前已发展的主流大气层顶SIF反演方法,并在充分介绍各算法基本原理的基础上,评价各算法的优劣及适用性,为今后基于航空、卫星高光谱数据的SIF反演工作提供依据。
2 大气层顶SIF反演算法
大气层顶SIF反演算法包括基于大气辐射传输方程的算法、简化的物理模型算法和数据驱动算法。
2.1 基于大气辐射传输方程的SIF反演算法
近地面的SIF的遥感反演最初在地球大气暗线波段实现,因此,大气层顶SIF反演最直接的思路是沿用近地面提取SIF的方法并考虑大气的吸收和散射效应。这类方法包括改进的FLD系列算法和光谱拟合算法。
2.1.1 FLD系列算法
假设地表反射与冠层SIF发射均为各向同性,位于大气层顶的传感器入瞳辐亮度(LTOA)可表示为
| ${L_{\rm{TOA}}} = {L_0} + \frac{{\left[ {{E_{\rm{tot}}}\displaystyle\frac{\rho _{\rm{s}}}{\text{π}} + F_{\rm{s}}} \right]{T_ \uparrow }}}{{1 - S{\rho _{\rm{s}}}}}$ | (1) |
式中,L0为大气程辐射亮度,Etot为到达地表的总太阳辐射能量(包括直射光和散射光),T↑为大气上行透过率,S为大气球面反照率,ρs为地表反射率,Fs为冠层释放的SIF。其中,L0、Etot、T↑及S均与太阳天顶角、大气模式、水汽含量、气溶胶及地表高程等参数有关,可通过大气辐射传输模型(如MODTRAN、6S等)模拟得到,则式(1)中的未知数为地表反射率ρs和冠层荧光Fs。Guanter等人(2007)基于MERIS数据,在波段10(753.8 nm附近)和波段11(760.6 nm附近)分别建立式(1),借用标准FLD算法思想,假设两个波段的地表反射率及荧光相等,得到
| $\left. \begin{aligned}L_{\rm{TOA}}^{\rm{o}} = L_0^{\rm{o}} + \displaystyle\frac{{{E^{\rm{o}}}\displaystyle\frac{{{\rho _{\rm{s}}}}}{\text{π}} + F_{\rm{s}}T_ \uparrow ^{\rm{o}}}}{{1 - {S^{\rm{o}}}{\rho _{\rm{s}}}}}\\[5pt]L_{\rm{TOA}}^{\rm{i}}= L_0^{\rm{i}} + \displaystyle\frac{{{E^i}\displaystyle\frac{{{\rho _{\rm{s}}}}}{\text{π}} + F_{\rm{s}}T_ \uparrow ^{\rm{i}}}}{{1 - {S^{\rm{i}}}{\rho _{\rm{s}}}}}\end{aligned} \right\}$ | (2) |
| ${F_{\rm{s}}} = \frac{{{X^i}({E^o} + {X^o}{S^o}) - {X^o}({E^i} + {X^i}{S^i})}}{{T{}_ \uparrow ^i({E^o} + {X^o}{S^o}) - T{}_ \uparrow ^o({E^i} + {X^i}{S^i})}}$ | (3) |
式中,上标i/o表示夫琅和费暗线内/外(对应MERIS波段11/10)
| ${X^j} = \text{π} (L_{\rm{TOA}}^j - L_0^j),{\rm{ }}j ={\rm{i}},{\rm{o}}$ | (4) |
通过MODTRAN辐射传输模型模拟得到式(3)中的各参数,Guanter等人(2007)首次利用卫星数据实现了SIF反演。
由于MERIS数据光谱分辨率较低,夫琅和费暗线内、外波段中心波长相距较远,因此,选取的2波段的地表反射率及荧光可能相差较大,对夫琅和费暗线内、外波段地表反射率和荧光相等的假设对反演结果带来较大误差。基于上述事实,Guanter等人(2010)借用iFLD(improved FLD)算法的思想,加入系数A、B,改进得到
| $F_{\rm{s}}^{\rm{i}} = B\left[ {\frac{{{X^{\rm{i}}}({E^{\rm{o}}} + {X^{\rm{o}}}{S^{\rm{o}}}) - A{X^{\rm{o}}}({E^{\rm{i}}} + {X^{\rm{i}}}{S^{\rm{i}}})}}{{T_ \uparrow ^{\rm{i}}B({E^{\rm{o}}} + {X^{\rm{o}}}{S^{\rm{o}}}) - T_ \uparrow ^{\rm{o}}A({E^{\rm{i}}} + {X^{\rm{i}}}{S^{\rm{i}}})}}} \right]$ | (5) |
式中,系数A、B的定义为
| $\left. \begin{array}{l}A = \frac{{\rho _{{\rm{app}}}^{\rm{i}}}}{{\rho _{{\rm{app}}}^{\rm{o}}}}\\B = \frac{{F{s^{\rm{i}}}}}{{F{s^{\rm{o}}}}}\end{array} \right\}$ | (6) |
式中,ρapp为大气层顶表观反射率,系数B根据夫琅和费暗线内外波段选取的位置确定,通常取常数。Damm等人(2014)借用3-FLD(3-bands FLD)算法的思想,重新定义系数A
| $A = \frac{{\rho _{\rm{l}}^{\rm{o}}{\omega _1} + \rho _{\rm{r}}^{\rm{o}}{\omega _2}}}{{\rho _{\rm{l}}^{\rm{o}}}},{\omega _1} = \frac{{\lambda _{\rm{r}}^{\rm{o}} - {\lambda ^{\rm{i}}}}}{{\lambda _{\rm{r}}^{\rm{o}} - \lambda _{\rm{l}}^{\rm{o}}}},{\omega _2} = \frac{{{\lambda ^{\rm{i}}} - \lambda _{\rm{l}}^{\rm{o}}}}{{\lambda _{\rm{r}}^{\rm{o}} - \lambda _{\rm{l}}^{\rm{o}}}}$ | (7) |
式中,下标l/r指示选取的暗线外左/右参考波段。
2.1.2 SFM算法
FLD算法通常仅利用夫琅和费暗线内外的少数几个波段,而SFM算法的思想是,在较宽的窗口内,基于SIF与反射率谱线的自然光谱特性,利用多个波段进行最小二乘拟合,反演得到窗口内连续的SIF光谱曲线。大气层顶利用SFM算法进行SIF反演需要进行严密的大气订正,将问题转换为近地表的SIF反演。忽略SIF信号进行大气程辐射订正得到近地表表观反射率
| $\begin{aligned}& {L_{{\rm{TOA}}}} = {L_0} + \frac{{\frac{{{E_{{\rm{tot}}}}}}{{\text{π}}} \cdot {R_{{\rm{app}}}} \cdot {T_ \uparrow }}}{{1 - S \cdot {R_{{\rm{app}}}}}},\\ & \Rightarrow {R_{{\rm{app}}}} = \frac{{{L_{{\rm{TOA}}}} - {L_0}}}{{({L_{{\rm{TOA}}}} - {L_0}) \cdot S + \frac{{{E_{{\rm{tot}}}}}}{{\text{π}}} \cdot {T_ \uparrow }}}\end{aligned}$ | (8) |
式中,Rapp为近地表表观反射率,包含SIF的贡献。假设存在地面标准白板,则标准板的近地表辐亮度(LWLR)为
| ${L_{\rm{WLR}}} = \frac{{{E_{\rm{tot}}}}}{{\text{π} \cdot (1 - S \cdot {R_{\rm{app}}})}}$ | (9) |
则经大气订正后的近地表辐亮度(LTOC)为
| ${L_{{\rm{TOC}}}} = {R_{{\rm{app}}}} \cdot {L_{{\rm{WLR}}}}$ | (10) |
至此,将大气层顶问题完全转化至大气层底,利用近地表传感器观测辐亮度基本公式
| ${L_{{\rm{TOC}}}}{\rm{ = }}\rho (\lambda ) \cdot {L_{{\rm{WLR}}}}(\lambda ) + {F_{\rm{s}}}(\lambda )$ | (11) |
并假设地表反射率和荧光光谱满足特定的数学函数(如线性、高次多项式或高斯函数等),结合最小二乘原则式 (12)进行荧光的光谱拟合反演。
| $\min \sum {{{({L_{{\rm{TOC}}}}(\lambda ) - \rho (\lambda ) \cdot {L_{{\rm{WLR}}}}(\lambda ) - {F_{\rm{s}}}(\lambda ))}^2}} $ | (12) |
SFM算法被选为FLEX计划标准荧光反演算法(Vicent 等,2016),Cogliati等人(2015)基于FLEX-FLORIS模拟数据(Verhoef 等,2014),在O2-A、O2-B波段应用多种SFM算法进行了大气层顶SIF反演,并评价了各算法的表现及精度。SFM算法对光谱分辨率的要求高于FLD系列算法,其优势在于可以获取拟合窗口内的全谱段荧光光谱,具有较好的抗噪能力;劣势在于需要进行十分严格的大气订正,对大气辐射传输模拟的精度要求较高,且未基于真实卫星数据测试。
2.1.3 基于大气辐射传输方程的SIF反演算法特点
基于大气辐射传输方程的SIF反演算法是最早被提出用于大气层顶SIF提取的算法,通过对大气辐射传输的定量化描述将近地表SIF反演理论推广至大气层顶。由于主要利用地球大气暗线进行SIF反演,且O2-A波段的大气暗线深度较深,宽度在10 nm左右,因此对数据源的光谱分辨率要求较低,现有的卫星高光谱数据如MERIS、Hyperion数据均可用于O2-A波段的SIF反演,航空平台搭载光谱仪(如ASD)亦可满足该波段SIF反演的需求。
基于大气辐射传输方程的SIF反演算法精度依赖于对大气状态及大气辐射传输过程描述的准确程度,Liu和Liu(2014)基于FLD算法进行了敏感性分析,提出现有的大气参数产品(MODIS气溶胶光学厚度(AOD)产品、水汽产品)尚难满足O2波段的SIF反演需求;Guanter等人(2010)基于FLD算法和SFM算法进行了SIF的端对端反演模拟,发现噪声、AOD、表面压力等误差源造成的O2-A波段SIF反演绝对误差在0.5—1.0 mW/m2/Sr/nm(此波段SIF数量级大约在0.5—3.0 mW/m2/Sr/nm),而SFM算法的精度高于FLD算法;此外,逐像元的大气辐射传输计算也限制了SIF反演效率。然而,最近FLEX团队开发的端对端模拟器(Vicent 等,2016)的模拟结果表明,在FLEX各传感器参数条件下,SFM算法能够用于反演得到可靠的SIF;Guanter等人(2010)和Damm等人(2014)利用同一场景内的临近非荧光像元有效消除了大气辐射计算误差带来的SIF反演偏差。
总体来说,基于大气辐射传输方程的算法对大气订正精度要求高,而对光谱分辨率要求较低;目前常规的大气订正精度难以满足SIF反演的要求,而利用场景内临近的非荧光目标光谱可以有效提高SIF反演精度;SFM算法的总体精度高于FLD算法。
2.2 简化的物理模型算法
2.2.1 简化的物理模型算法原理
简化的物理模型算法指利用荧光对位于大气窗口内的太阳夫琅和费暗线的填充,忽略地球大气的影响的SIF反演方法。对大气层顶的任意观测,式 (1)的另一种形式为
| ${L_{{\rm{TOA}}}} = {L_0} + \frac{{\frac{{{I_{{\rm{sol}}}} \cdot {\mu _0}}}{\text{π} } \cdot {T_ \downarrow } \cdot {\rho _{\rm{s}}} \cdot {T_ \uparrow } + {F_{\rm{s}}} \cdot {T_ \uparrow }}}{{1 - S \cdot {\rho _{\rm{s}}}}}$ | (13) |
式中,Isol为大气层外的太阳辐照度,T↓为大气下行透过率,μ0为太阳天顶角余弦。由于位于大气窗口,忽略大气的吸收和球面反射,则T↓=T↑=1,S=0;大气程辐射实际为大气对太阳辐射的后向散射,以反射形式(ρ0)描述L0,则式 (13)可进一步改写为
| ${L_{{\rm{TOA}}}} = \frac{{{I_{{\rm{sol}}}} \cdot {\mu _0}}}{\text{π} } \cdot ({\rho _0} + {\rho _{\rm{s}}}) + {F_{\rm{s}}}$ | (14) |
在较窄(2—5 nm)的大气窗口内,大气后向散射和地表反射均可视为连续,则可将二者表达为波长的多项式函数,则式(14)最终改写为
| ${L_{{\rm{TOA}}}} = {I_{{\rm{sol}}}} \cdot \sum\limits_{i = 0}^n {({\lambda ^i} \cdot {a_i})} + {F_{\rm{s}}}$ | (15) |
式中,n为多项式的次数,依据窗口的位置或宽度通常取1—2。由于Isol可由位于大气层顶的传感器直接观测太阳获取(如GOSAT-FTS,GOME-2等传感器均有对太阳辐射的观测),或根据太阳辐射光谱库和传感器光谱响应函数卷积得到,则求解SIF变为线性最小二乘求解问题。
2.2.2 简化的物理模型算法特点
简化的物理模型算法避开了地球大气吸收波段,忽略地球大气对SIF反演的影响,从而避免了辐射传输计算,在大气层顶直接应用近地表SIF反演原理。表1的“简化的物理模型算法”部分给出了常用的包含太阳夫琅和费暗线的SIF反演窗口。简化的物理模型算法对光谱分辨率要求极高,目前只应用于GOSAT-FTS传感器(光谱分辨率约0.025 nm)。算法对传感器噪声敏感,为了提高算法鲁棒性,一种做法是增加太阳夫琅和费暗线内波段的权重,使SIF对暗线的填充对方程求解贡献更大(Joiner 等,2011;刘新杰和刘良云,2013);另一种做法是采用较宽窗口,利用窗口内的多条太阳夫琅和费暗线进行反演(Frankenberg 等,2011;Köhler 等,2015a)。
总体来讲,简化的物理模型算法的实现较为简单,但仅适用于超高光谱分辨率条件下的SIF反演(通常二氧化碳监测卫星的光谱分辨率可满足需求),对传感器信噪比要求较高;此外,该算法对除SIF外的其他夫琅和费暗线填充源(如杂散光、费弹性散射等)敏感。
简化的物理模型算法仅可利用大气窗口内的太阳夫琅和费暗线,且需要获取大气层顶的太阳辐照度光谱,传感器对太阳的直接观测可能带来与对地观测不同类型的噪声,而光谱卷积过程中原始太阳光谱数据源的选择和对传感器光谱响应函数的近似描述则会带来系统误差。基于上述问题,Guanter等人(2012)发展了数据驱动算法。
2.3 数据驱动算法
数据驱动算法主要包括基于SVD(Singular Vector Decomposition)的荧光反演算法(简称SVD算法)和基于PCA(Principle Component Analysis)荧光反演算法(简称PCA算法)。
2.3.1 SVD算法
将式(13)改写为非荧光光谱与荧光光谱叠加的形式:
| ${L_{{\rm{TOA}}}} = \frac{{{\mu _0} \cdot {I_{{\rm{sol}}}}}}{\text{π} }\left[ {{\rho _0} + \frac{{{\rho _{\rm{s}}} \cdot {T_{ \uparrow \downarrow }}}}{{1 - S \cdot {\rho _{\rm{s}}}}}} \right] + \frac{{{F_{\rm{s}}} \cdot {T_ \uparrow }}}{{1 - S \cdot {\rho _{\rm{s}}}}}$ | (16) |
式中,右边第1项为非荧光光谱,第2项为荧光光谱。SVD算法认为,荧光目标的非荧光光谱部分可进一步分解为低频信息和高频信息,其中低频信息由大气后向散射(ρ0)、大气球面反射(S)和地表反射(ρs)贡献,高频信息则由太阳大气和地球大气分子的吸收贡献(即夫琅和费暗线)。低频信息平滑,可表达为波长的高次多项式函数;高频信息具有特定的变化规律,可视为少量统计特征的线性叠加,这些特征则由传感器对非荧光目标观测的光谱进行特征提取(SVD)得到。荧光信号则可表达为特定的数学函数或具有固定光谱形状的谱线。因此,式(16)可改写为
| ${L_{{\rm{TOA}}}} = \left( {\sum\limits_{i = 0}^{{n_p}} {{a_i} \cdot {\lambda ^i}} } \right) \cdot \sum\limits_{j = 1}^{{n_v}} {{\alpha _j} \cdot {v_j}} + {F_{\rm{s}}} \cdot {h_{\rm{F}}} \cdot {T_ \uparrow }$ | (17) |
式中,np为多项式次数,nv为使用非荧光特征个数(通常只取前几个主要特征),vj为训练得到的高频变化特征,ai和αj为拟合参数,hF为荧光形状函数,通常取高斯函数或通过模型模拟得到,因此,一旦得到大气上行透过率,则式(17)中的自由变量为ai、αj和Fs,则求解SIF变为线性最小二乘求解问题。
SVD算法首先应用于基于GOSAT卫星数据的大气窗口内SIF反演,此时作近似T↑=1 (Guanter 等,2012),vj仅包含太阳夫琅和费暗线高频信息。Frankenberg等人(2014)沿用了SVD算法,利用模拟的OCO-2数据实现了全球SIF反演。SVD算法本质上仍是利用SIF对夫琅和费暗线的填充进行SIF反演,当数据光谱分辨率不够高时,需要拓宽反演窗口以囊括更多高频(暗线)信息,因此不可避免地包括了一些大气吸收波段。此时首先应进行大气上行透过率的估算
| ${T_{ \uparrow \downarrow }} = \frac{{{L_{{\rm{TOA}}}} \cdot \text{π} }}{{{I_{{\rm{sol}}}} \cdot {\mu _0}}},{T_ \uparrow } = \exp \left[ {\ln ({T_{ \uparrow \downarrow }}) \cdot \frac{{\sec ({\theta _{\rm{v}}})}}{{\sec ({\theta _{\rm{v}}}) + \sec ({\theta _0})}}} \right]$ | (18) |
式中,θv和θ0分别为观测天顶角和太阳天顶角。训练集则应包含不同大气状态和观测几何条件下对非荧光目标的观测辐亮度,训练得到vj则同时包含太阳和地球夫琅和费暗线高频信息(Guanter 等,2015)。
2.3.2 PCA算法
PCA算法的思想与SVD算法在本质上相同,不同的是SVD利用统计的方法同时提取了太阳暗线和地球暗线的变化特征,PCA则仅利用统计的方法提取地球大气特征,即利用训练得到的主成分(PC)表达大气高频信息。将式(16)改写为
| ${L_{{\rm{TOA}}}} = \frac{{{\mu _0} \cdot {I_{{\rm{sol}}}}}}{\text{π} }{\tau _{\rm{a}}}\rho + {F_{\rm{s}}}\,{\tau _2}$ | (19) |
式中,τa为大气高频贡献,ρ为大气和地表低频贡献,τ2为大气上行高频贡献。将τa表达为大气主成分的线性叠加,ρ表达为波长的多项式,而τ2与τa存在下列关系
| ${\tau _2} = \exp \left[ {\ln ({\tau _{\rm{a}}}) \frac{{\sec ({\theta _{\rm{v}}})}}{{\sec ({\theta _{\rm{v}}}) + \sec ({\theta _0})}}} \right]$ | (20) |
代入式(19)得到
| $\begin{aligned}&{L_{{\rm{TOA}}}} = \frac{{{\mu _0} \cdot {I_{{\rm{sol}}}}}}{\text{π}} \cdot \left( {\sum\limits_{j = 1}^{{n_{{\rm{PC}}}}} {{\alpha _j}{\rm{P}}{{\rm{C}}_j}} } \right) \cdot \sum\limits_{i = 0}^{{n_p}} {{a_i}{\lambda ^i}} + \\&{F_{\rm{s}}} \cdot {h_{\rm{F}}} \cdot \exp \left[ {\ln \left( {\sum\limits_{j = 1}^{{n_{{\rm{PC}}}}} {{\alpha _j}{\rm{P}}{{\rm{C}}_j}} } \right)\frac{{\sec ({\theta _{\rm{v}}})}}{{\sec ({\theta _{\rm{v}}}) + \sec ({\theta _0})}}} \right]\end{aligned}$ | (21) |
求解Fs的过程变为非线性最小二乘求解问题。
上述PCA算法已被用于O2-A波段附近(Joiner 等,2013;Sanders 等,2016)和O2-B波段附近(Joiner 等,2016)的SIF反演,所用数据包括GOME-2和SCIAMACHY。Köhler等人(2015b)等忽略SIF对大气上行透过率计算的影响,利用式(18)将式(19)中的τ2在辐射传输方程求解前估算得到,将(21)转化为线性形式
| ${L_{{\rm{TOA}}}} = \frac{{{\mu _0} \cdot {I_{{\rm{sol}}}}}}{\text{π} } \cdot \left( {\sum\limits_{j = 1}^{{n_{\rm{PC}}}} {{\alpha _j} \cdot {\rm{P}}{{\rm{C}}_j}} } \right) \cdot \sum\limits_{i = 0}^{{n_p}} {{a_i} \cdot \, {\lambda ^i}} + {F_{\rm{s}}} \cdot {h_{\rm{F}}} \cdot \, {T_ \uparrow }$ | (22) |
则SIF反演问题转化为对系数αj、ai和Fs的线性最小二乘求解。
2.3.3 数据驱动算法的特点
数据驱动算法是目前大多数全球SIF产品的生产算法。数据驱动算法是半经验的方法,因此算法的表现依赖于模型参数的设置与获取。影响算法表现的因素主要包括:训练集的选取、反演窗口的选择、主成分个数的选择及荧光函数hF的设置。
训练集需要包含未被荧光填充的太阳暗线和地球暗线的高频信息,在仅利用太阳暗线进行SIF反演时,选择的训练集应避免大太阳天顶角(通常<70°),降低非弹性散射带来的影响(Joiner 等,2013),且训练集的获取时间应与荧光目标光谱获取时间相距较近,降低传感器衰变、太阳辐射光谱变化带来的影响;当反演窗口包含地球暗线时,训练集应包含在不同大气状态、观测几何条件下获取的非荧光目标光谱,使训练得到的大气主成分能够表达任意观测条件下的大气特征。反演窗口的选择、训练集的个数选取和荧光函数hF对反演结果的影响与传感器光谱分辨率和信噪比有关,通常来讲较宽的反演窗口降低了反演算法对噪声的敏感性,但会加大对地表反射率和荧光光谱的不真实描述带来的反演误差,定量化描述各因素与SIF反演精度的关系可通过端对端模拟实现(Frankenberg 等,2014;Guanter 等,2015;Guanter 等,2013;Joiner 等,2016;Köhler 等,2015b)。总体来讲,数据驱动算法开辟了SIF遥感反演的新道路,综合利用了太阳暗线和地球暗线,在降低了光谱分辨率要求的同时避免了大气辐射传输方程运算,大大提高了SIF反演的效率。反演模型的参数选择会影响反演结果,参数设置需综合考虑传感器特性及选择的具体窗口。
3 数据驱动算法在GOME-2卫星数据的应用
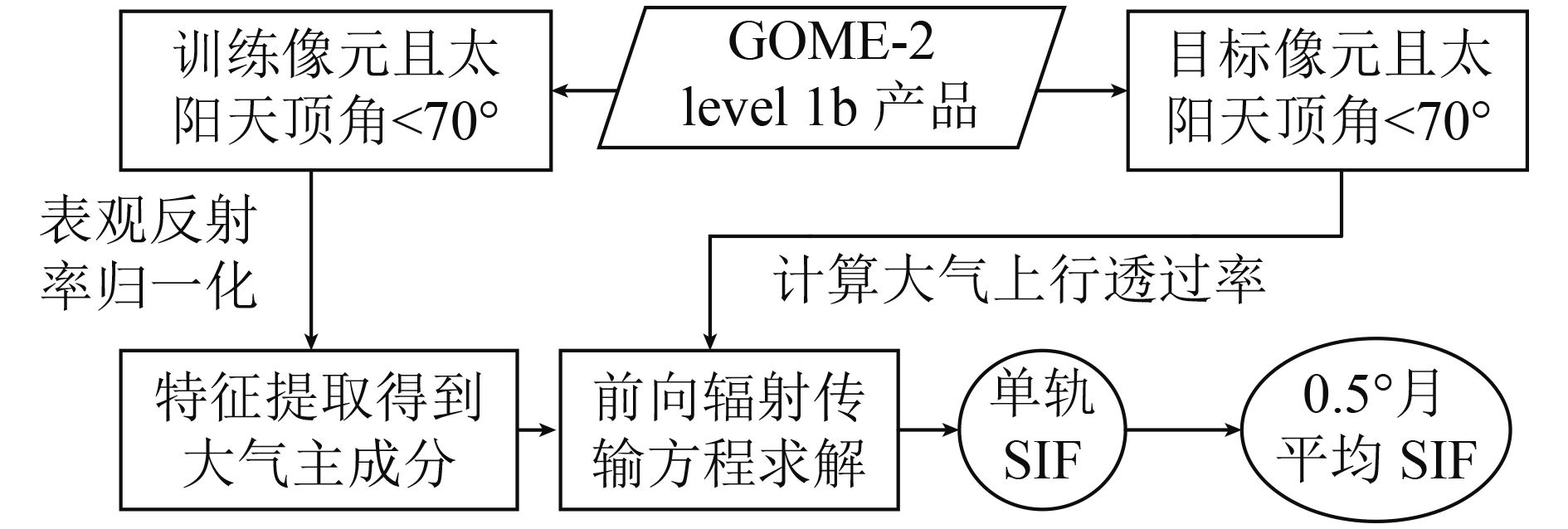
为了进一步详细展示大气层顶SIF反演的过程,本文以线性PCA算法为例,基于GOME-2 level 1b辐亮度数据进行了卫星尺度的全球SIF反演。GOME-2传感器搭载于EUMETSAT极地系统Metop系列卫星,其第4通道覆盖650—790 nm,光谱分辨率约0.5 nm,可用于SIF反演,足印大小40×80 km。GOME-2 level 1b为辐亮度产品,包含了SIF反演和制图需要的数据,包括对地观测辐亮度光谱、太阳辐照度光谱、观测时刻太阳天顶角、观测天顶角、足印经纬度和云覆盖度等信息。基于GOME-2 level 1b产品的SIF反演流程见图3,其中训练像元选取海上浓云(ρ670 nm>0.7)和沙漠像元,反演窗口选择720—758 nm。
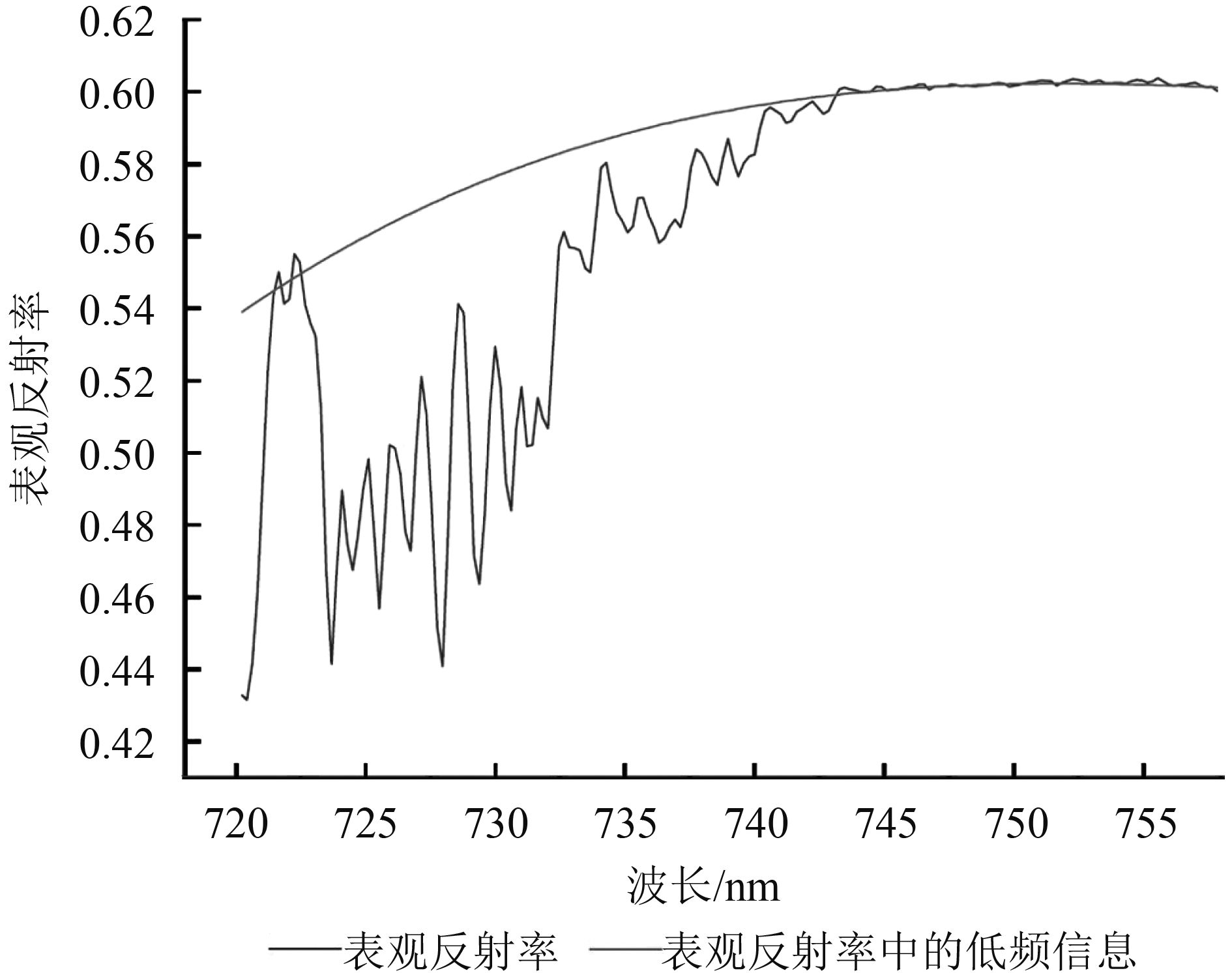
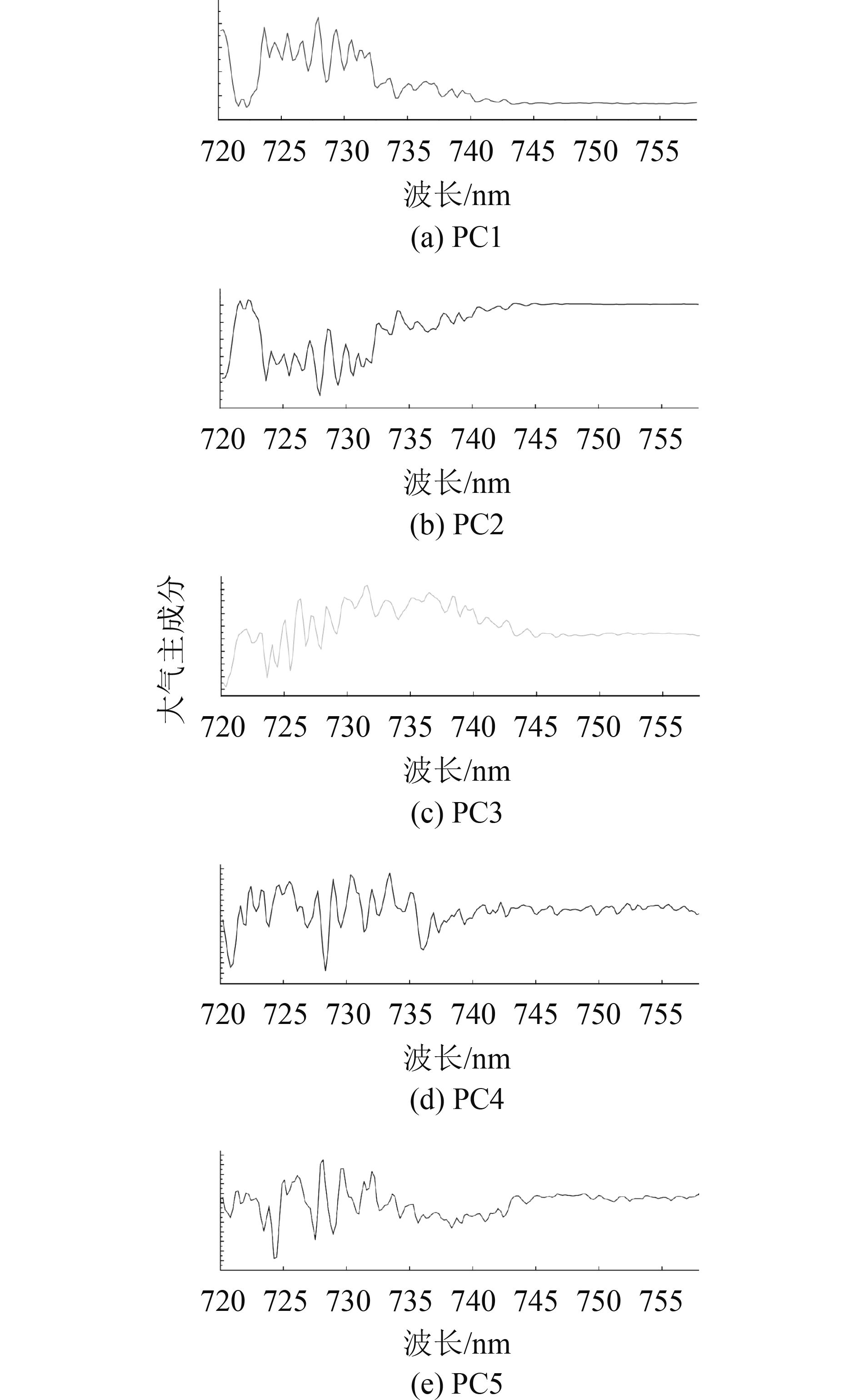
表观反射率归一化指分离表观反射率中的低频和高频信息的过程,选取大气窗口波段进行多项式拟合,得到表观反射率中的低频信息,将表观反射率用拟合得到的多项式归一化,得到表观反射率中的高频信息,将高频信息构成的集合用于大气主成分的提取。图4展示了表观反射率及表观反射率中的低频信息,图5展示了经主成分变换后提取的前5个大气主成分。值得注意的是,对于每天的SIF反演均需要重新进行训练集的选择和大气主成分的计算,目的是降低传感器信号衰减、大气模式的改变及太阳辐射光谱变化带来的影响。
训练得到主成分后,即可进行前向模型的求解。本文依据Köhler等人(2015b)的模拟结果,取前8个主成分进行拟合,取三次多项式拟合低频成分,并依照Guanter等人(2015)对前向模型做进一步简化,仅保留第一主成分的高次系数,得到
| ${L_{{\rm{TOA}}}} = \frac{{{\mu _0} \cdot {I_{{\rm{sol}}}}}}{\text{π} } \cdot \left( {{\rm{P}}{{\rm{C}}_1}\sum\limits_{i = 0}^3 {{a_i} \cdot } {\lambda ^i} + \sum\limits_{j = 2}^8 {{\alpha _j} \cdot {\rm{P}}{{\rm{C}}_j}} } \right) + {F_{\rm{s}}} \cdot {h_{\rm{F}}} \cdot {T_ \uparrow }$ | (23) |
式中,
| ${h_{\rm{F}}} = \exp \left[ {\frac{{ - {{(\lambda - {\mu _{\rm{h}}})}^2}}}{{2{\sigma _{\rm{h}}}^2}}} \right]$ | (24) |
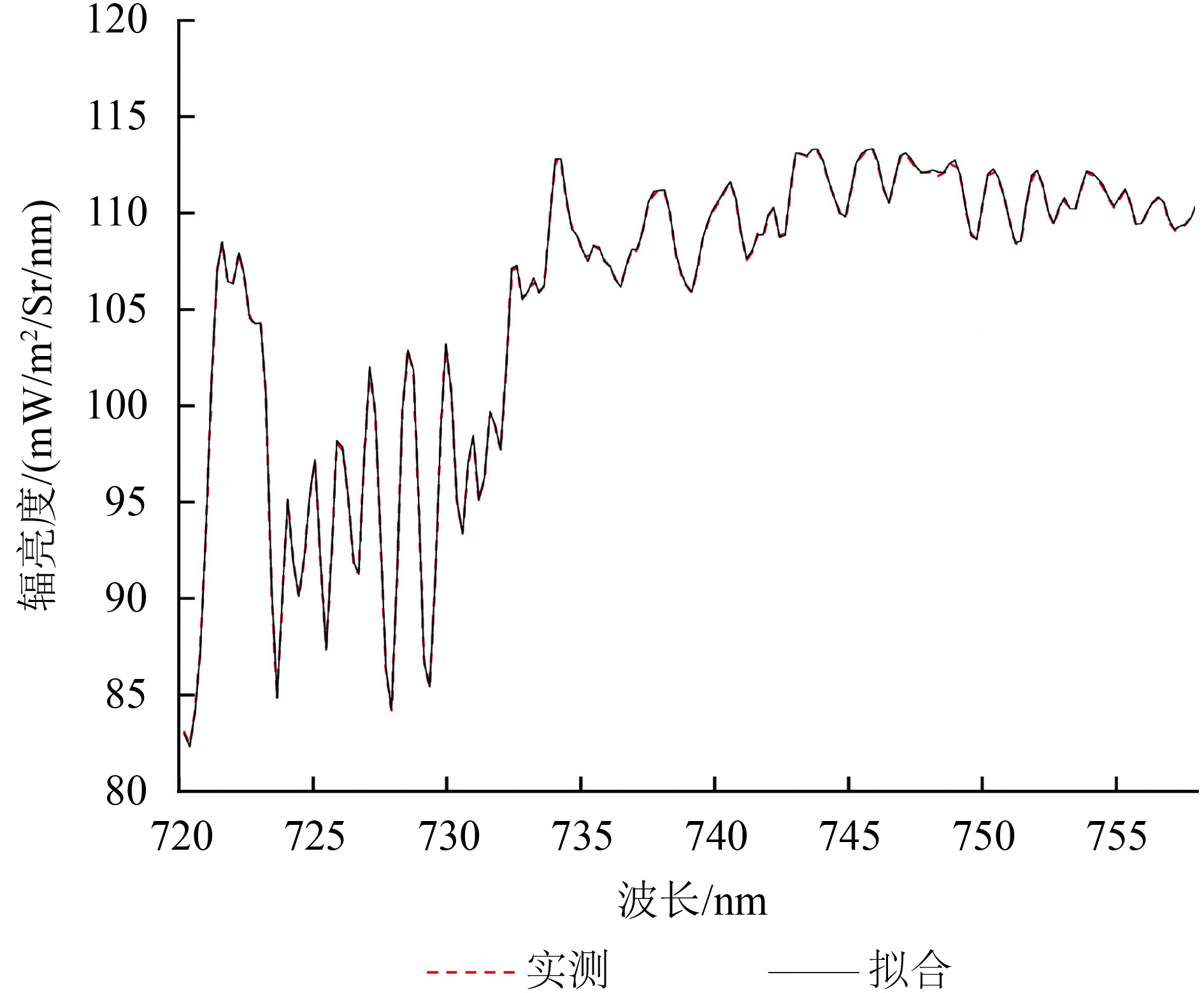
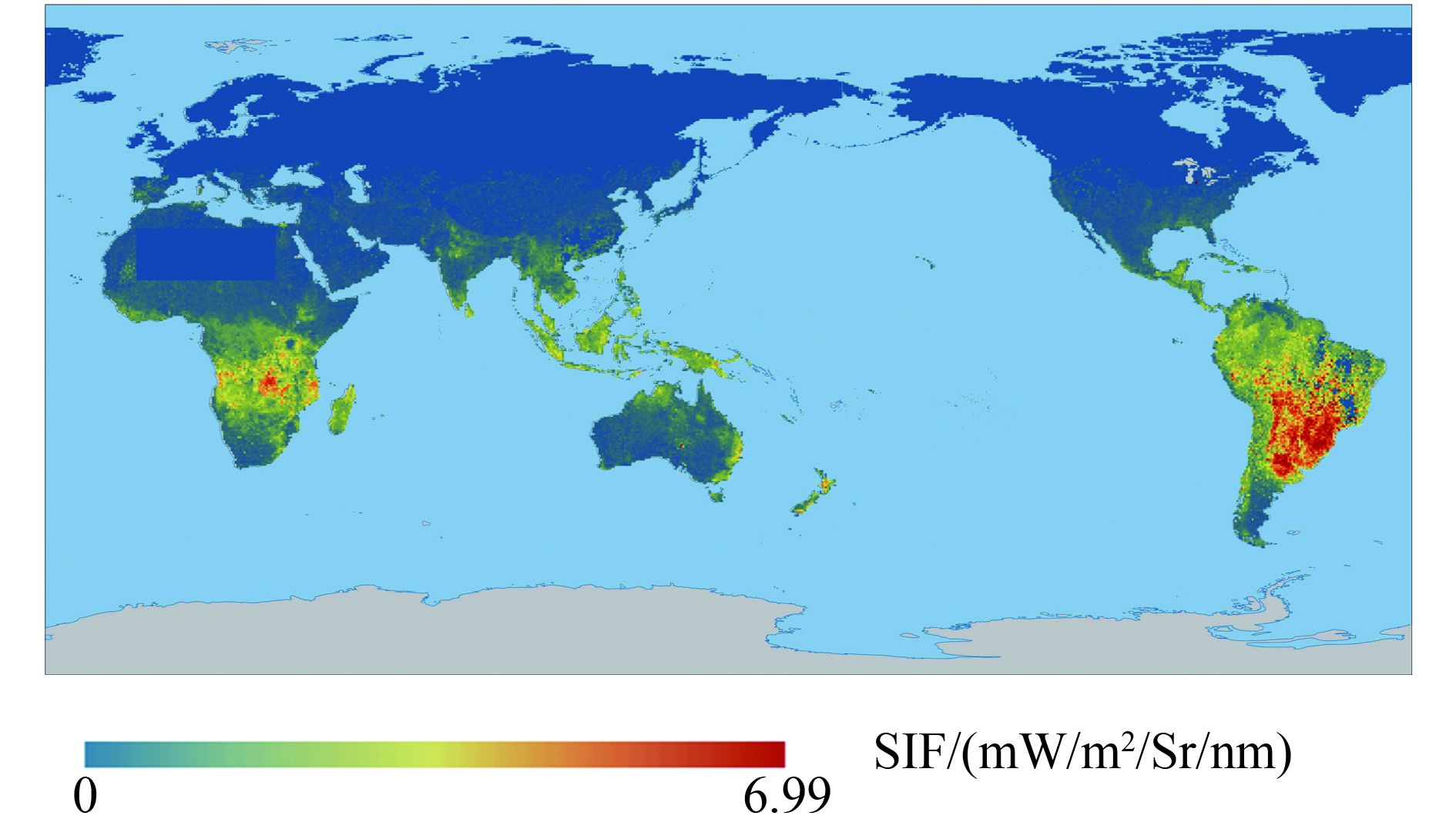
取μh=740 nm,σh=22 nm,利用线性最小二乘求解得到(23)中各系数。图6展示了某条GOME-2辐亮度光谱的拟合结果,图7展示了格网化平均得到的2016年1月全球SIF分布图。从结果看,前向模型取得了较好的拟合效果,得到的全球格网化平均SIF具有显著的空间分布特征,与已有的SIF数据集保持了较好的一致性。
4 结 语
由于与光合作用独特的联系,SIF有望成为遥感监测植被光合固碳及胁迫状态的全新手段。虽然卫星尺度探测SIF的计划很早就被提上日程(FLEX计划),但第1幅全球SIF分布图却是由温室气体监测卫星GOSAT数据反演得到的(Joiner 等,2011)。原因在于,起初科学家一直专注于O2-A、O2-B波段的SIF反演,但在大气层顶利用传统的地球大气夫琅和费暗线反演SIF的难点(精确的大气辐射传输方程计算)一直未被攻克;而GOSAT卫星超高的光谱分辨率则令利用位于大气窗口的太阳夫琅和费暗线反演SIF成为可能,Joiner等人(2011)和Frankenberg等人(2011)则基于GOSAT数据发展了简化的物理模型算法。简化的物理模型算法简单有效,但需要进行光谱卷积,且对噪声敏感。针对这些特点,Guanter等人(2012)发展了基于太阳夫琅和费暗线的数据驱动算法,Joiner等人(2013)在此基础上发展了综合利用太阳暗线和地球暗线的数据驱动算法,应用于GOME-2数据,并发布了全球0.5°格网的月平均SIF产品,该产品被广泛应用于全球GPP估算(Guanter 等,2014)、农作物估产(Guan 等,2016)、物候监测(Jeong 等,2017;Walther 等,2016)及大尺度干旱监测(Sun 等,2015;Wang 等,2016;Yoshida 等,2015)。GOME-2 SIF产品的发布极大地推动了叶绿素荧光应用的相关研究,但受时空分辨率限制,GOME-2 SIF产品几乎只能用于大尺度趋势性研究,因此,亟待发射新的具有全球荧光探测能力和更高时空分辨率的卫星。这一需求加速了FLEX计划的推进,FLEX团队开展了大量模拟和机载实验,进一步改进和完善了O2-A、O2-B波段的大气层顶SIF反演算法。
表 2 具有SIF探测能力的星载传感器的主要性能指标,包括已经在轨运行的和已列入发射日程的卫星
Table 2 Major characteristics of satellite instruments used to retrieve SIF, including currently used and scheduled to be launched
| 传感器
指标 |
GOSAT-FTS | OCO-2 | MetOp-A GOME-2 | ENVISAT-SCIAMACHY | Tan-Sat | Sentinel-5-TROPOMI | FLEX-FLORIS |
| 发射时间 | 2009 | 2014 | 2006 | 2002 | 2016.12 | 2017.07 | 2022 |
| 过境时间 | 13:00 | 13:30 | 9:30 | 10:00 | 13:30 | 13:30 | ~10:00 |
| 重访周期 | 3天 | 16天 | 1.5天 | 6天 | 16天 | 1天 | 27天(赤道) |
| 光谱范围 | 757—775 nm | 650—790 nm | 758—778 nm | 675—775 nm | 670—780 nm | ||
| 光谱分辨率 | 0.025 nm | 0.042 nm | 0.5 nm | 0.044 | 0.5 nm | ~0.3 nm | |
| 星下点 | 10.5 km | 1.3×2.25 km | 40×80 km | 30×40 km | 1×2 km | 7×7 km | 300 m |
| 分辨率 | — | — | — | — | 2×2 km | — | — |
| 幅宽 | 750 km | 10.3 km | 1920 km | 960 km | 20 km | 2600 km | 150 km |
| 空间采样方式 | 离散 | 离散 | 连续 | 连续 | 离散 | 连续 | 连续 |
| 信噪比SNR | >300 | >360 | >1000 | 3000 | >360 | 500 | >240 |
SIF的大气层顶反演与传感器的光谱分辨率密切相关,中国陆地生态系统碳卫星(预计于2020年发射)搭载的超光谱成像仪也具有空间连续荧光探测能力。SIF反演算法的选择依赖于数据的光谱分辨率,目前科学界虽然对SIF反演算法各持己见,但作者认为,综合考虑信噪比、光谱覆盖范围等因素,对数据源的需求已趋向一致,即覆盖整个红边波段和荧光光谱范围(约680—800 nm)的中高光谱分辨率数据(0.3—0.5 nm)。这一需求确定了未来针对全球SIF探测的星载传感器的指标,传感器指标的确定则决定了未来大气层顶的SIF反演算法将以基于辐射传输方程的O2-A、O2-B波段反演和基于数据驱动的各窗口反演为主。总的来说,航空数据距离地表较近,目前的成像、非成像光谱仪的光谱分辨率通常在nm级,且场景内对非荧光目标像元的观测数量可能较少,较适合应用基于辐射传输方程计算的SIF反演算法;卫星数据的获取完全位于大气层顶,且对非荧光目标在不同大气状态下的观测充足,其辐亮度光谱可构成具有足够代表性的训练集,数据驱动算法适合在卫星尺度应用;基于辐射传输方程计算的SFM算法虽然被选为FLEX计划的标准算法,但其在卫星实测数据下的表现尚未得到验证,且辐射传输方程的精确运算较为耗时,如何提高该算法的效率亦为待解决的问题。综上所述,大气层顶的SIF反演需要根据数据源的特点选择不同算法,基于大气辐射传输方程的算法表现依赖于辐射传输计算的精度,数据驱动算法的表现则依赖于训练集的代表性及经验参数的设置。
参考文献(References)
-
Cogliati S, Verhoef W, Kraft S, Sabater N, Alonso L, Vicent J, Moreno J, Drusch M and Colombo R. 2015. Retrieval of sun-induced fluorescence using advanced spectral fitting methods. Remote Sensing of Environment, 169 : 344–357. [DOI: 10.1016/j.rse.2015.08.022]
-
Damm A, Guanter L, Laurent V C E, Schaepman M E, Schickling A and Rascher U. 2014. FLD-based retrieval of sun-induced chlorophyll fluorescence from medium spectral resolution airborne spectroscopy data. Remote Sensing of Environment, 147 : 256–266. [DOI: 10.1016/j.rse.2014.03.009]
-
Frankenberg C, Butz A and Toon G C. 2011. Disentangling chlorophyll fluorescence from atmospheric scattering effects in O2A-band spectra of reflected sun-light . Geophysical Research Letters, 38 : L03801 [DOI: 10.1029/2010GL045896]
-
Frankenberg C, O’dell C, Berry J, Guanter L, Joiner J, Köhler P, Pollock R and Taylor T E. 2014. Prospects for chlorophyll fluorescence remote sensing from the Orbiting Carbon Observatory-2. Remote Sensing of Environment, 147 : 1–12. [DOI: 10.1016/j.rse.2014.02.007]
-
Guan K, Berry J A, Zhang Y, Joiner J, Guanter L, Badgley G and Lobell D B. 2016. Improving the monitoring of crop productivity using spaceborne solar-induced fluorescence. Glob Chang Biol, 22 : 716–26. [DOI: 10.1111/gcb.13136]
-
Guanter L, Aben I, Tol P, Krijger J M, Hollstein A, Köhler P, Damm A, Joiner J, Frankenberg C and Landgraf J. 2015. Potential of the TROPOspheric Monitoring Instrument (TROPOMI) onboard the Sentinel-5 Precursor for the monitoring of terrestrial chlorophyll fluorescence. Atmospheric Measurement Techniques, 8 : 1337–1352. [DOI: 10.5194/amt-8-1337-2015]
-
Guanter L, Alonso L, Gómez-Chova L, Amorós-López J, Vila J and Moreno J. 2007. Estimation of solar-induced vegetation fluorescence from space measurements. Geophysical Research Letters, 34 : L08401 [DOI: 10.1029/2007GL029289]
-
Guanter L, Alonso L, Gómez-Chova L, Meroni M, Preusker R, Fischer J and Moreno J. 2010. Developments for vegetation fluorescence retrieval from spaceborne high-resolution spectrometry in the O2-A and O2-B absorption bands. Journal of Geophysical Research, 115 : D19303 [DOI: 10.1029/2009JD013716]
-
Guanter L, Frankenberg C, Dudhia A, Lewis P E, Gómez-Dans J, Kuze A, Suto H and Grainger R G. 2012. Retrieval and global assessment of terrestrial chlorophyll fluorescence from GOSAT space measurements. Remote Sensing of Environment, 121 : 236–251. [DOI: 10.1016/j.rse.2012.02.006]
-
Guanter L, Rossini M, Colombo R, Meroni M, Frankenberg C, Lee J-E and Joiner J. 2013. Using field spectroscopy to assess the potential of statistical approaches for the retrieval of sun-induced chlorophyll fluorescence from ground and space. Remote Sensing of Environment, 133 : 52–61. [DOI: 10.1016/j.rse.2013.01.017]
-
Guanter L, Zhang Y, Jung M, Joiner J, Voigt M, Berry J A, Frankenberg C, Huete A R, Zarco-Tejada P and Lee J-E. 2014. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proceedings of the National Academy of Sciences, 111 : E1327–E1333. [DOI: 10.1073/pnas.1320008111]
-
Hu J C, Liu L Y and Liu X J. 2015. Assessing uncertainties of sun-induced chlorophyll fluorescence retrieval using FluorMOD model. Journal of Remote Sensing, 19 (4): 594–608. [DOI: 10.11834/jrs.20154053] ( 胡姣婵, 刘良云, 刘新杰. 2015. FluorMOD模拟叶绿素荧光夫琅和费暗线反演算法不确定性分析. 遥感学报, 19 (4): 594–608. [DOI: 10.11834/jrs.20154053] )
-
Jeong S-J, Schimel D, Frankenberg C, Drewry D T, Fisher J B, Verma M, Berry J A., Lee J-E and Joiner J. 2017. Application of satellite solar-induced chlorophyll fluorescence to understanding large-scale variations in vegetation phenology and function over northern high latitude forests. Remote Sensing of Environment, 190 : 178–187. [DOI: 10.1016/j.rse.2016.11.021]
-
Joiner J, Guanter L, Lindstrot R, Voigt M, Vasilkov A P, Middleton E M, Huemmrich K F, Yoshida Y and Frankenberg C. 2013. Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: methodology, simulations, and application to GOME-2. Atmospheric Measurement Techniques, 6 : 2803–2823. [DOI: 10.5194/amt-6-2803-2013]
-
Joiner J, Yoshida Y, Guanter L and Middleton E. M. 2016. New methods for retrieval of chlorophyll red fluorescence from hyper-spectral satellite instruments: simulations and application to GOME-2 and SCIAMACHY[J]. Atmospheric Measurement Techniques Discussions, 1–41 [DOI: 10.5194/amt-2015-387, 2016]
-
Joiner J, Yoshida Y, Vasilkov A P, Yoshida Y, Corp L A and Middleton E M. 2011. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences, 8 : 637–651. [DOI: 10.5194/bg-8-637-2011]
-
Köhler P, Guanter L and Frankenberg C. 2015. Simplified physically based retrieval of sun-induced chlorophyll fluorescence from GOSAT data. IEEE Geoscience and Remote Sensing Letters, 12 : 1446–1450. [DOI: 10.1109/LGRS.2015.2407051]
-
Köhler P, Guanter L and Joiner J. 2015. A linear method for the retrieval of sun-induced chlorophyll fluorescence from GOME-2 and SCIAMACHY data. Atmospheric Measurement Techniques, 8 : 2589–2608. [DOI: 10.5194/amt-8-2589-2015]
-
Liu L Y, Zhang Y J, Wang J H and Zhao C J. 2006. Detecting photosynthesis fluorescence under natural sunlight based on fraunhofer line. Journal of Remote Sensing, 10 (1): 130–137. [DOI: 10.3321/j.issn:1007-4619.2006.01.020] ( 刘良云, 张永江, 王纪华, 赵春江. 2006. 利用夫琅和费暗线探测自然光条件下的植被光合作用荧光研究. 遥感学报, 10 (1): 130–137. [DOI: 10.3321/j.issn:1007-4619.2006.01.020] )
-
Liu X and Liu L. Assessing band sensitivity to atmospheric radiation transfer for space-based retrieval of solar-induced chlorophyll fluorescence[J]. Remote Sensing. 2014. Assessing band sensitivity to atmospheric radiation transfer for space-based retrieval of solar-induced chlorophyll fluorescence. Remote Sensing, 6 (11): 10656–10675. [DOI: 10.3390/rs61110656]
-
Liu X J and Liu L Y. 2013. Retrieval of chlorophyll fluorescence from GOSAT TANSO-FTS data based on weighted least square fitting. Journal of Remote Sensing, 17 (6): 1518–1532. [DOI: 10.11834/jrs.201332356] ( 刘新杰, 刘良云. 2013. 叶绿素荧光的GOSAT卫星遥感反演. 遥感学报, 17 (6): 1518–1532. [DOI: 10.11834/jrs.201332356] )
-
Meroni M, Rossini M, Guanter L, Alonso L, Rascher U, Colombo R. and Moreno J. 2009. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sensing of Environment, 113 : 2037–2051. [DOI: 10.1016/j.rse.2009.05.003]
-
Porcar-Castell A, Tyystjarvi E, Atherton J, Van Der Tol C, Flexas J, Pfundel E E, Moreno J, Frankenberg C and Berry J A. 2014. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: mechanisms and challenges. J Exp Bot, 65 : 4065–95. [DOI: 10.1093/jxb/eru191]
-
Sanders A F, Verstraeten W W, Kooreman M L, Van Leth T C, Beringer J and Joiner J. 2016. Spaceborne Sun-Induced Vegetation Fluorescence Time Series from 2007 to 2015 Evaluated with Australian Flux Tower Measurements. Remote Sensing, 8 : 895 [DOI: 10.3390/rs8110895]
-
Sun Y, Fu R, Dickinson R, Joiner J, Frankenberg C, Gu L, Xia Y and Fernando N. 2015. Drought onset mechanisms revealed by satellite solar-induced chlorophyll fluorescence: Insights from two contrasting extreme events. Journal of Geophysical Research: Biogeosciences, 120 : 2427–2440. [DOI: 10.1002/2015JG003150]
-
Van Der Tol C Berry J A, Campbell P K E and Rascher U. 2014. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. Journal of Geophysical Research: Biogeosciences, 119 : 2312–2327. [DOI: 10.1002/2014JG002713]
-
Vasilkov A Joiner J and Spurr R. 2013. Note on rotational-Raman scattering in the O2 A- and B-bands . Atmospheric Measurement Techniques, 6 : 981–990. [DOI: 10.5194/amt-6-981-2013]
-
Vicent J, Sabater N, Tenjo C, Acarreta J R, Manzano M, Rivera J P, Jurado P, Franco R, Alonso L and Verrelst J. 2016. FLEX end-to-end mission performance simulator. IEEE Transactions on Geoscience and Remote Sensing, 54 : 4215–4223. [DOI: 10.1109/TGRS.2016.2538300]
-
Walther S, Voigt M, Thum T, Gonsamo A, Zhang Y, Kohler P, Jung M, Varlagin A and Guanter L. 2016. Satellite chlorophyll fluorescence measurements reveal large-scale decoupling of photosynthesis and greenness dynamics in boreal evergreen forests. Glob Chang Biol, 22 : 2979–96. [DOI: 10.1111/gcb.13200]
-
Wang S H, Huang C P, Zhang L F, Lin Y, Cen Y and Wu T X. 2016. Monitoring and Assessing the 2012 Drought in the Great Plains: Analyzing Satellite-Retrieved Solar-Induced Chlorophyll Fluorescence, Drought Indices, and Gross Primary Production. Remote Sensing, 8 : 61 [DOI: 10.3390/rs8020061]
-
Yoshida Y, Joiner J, Tucker C, Berry J, Lee J E, Walker G, Reichle R, Koster R, Lyapustin A and Wang Y. 2015. The 2010 Russian drought impact on satellite measurements of solar-induced chlorophyll fluorescence: Insights from modeling and comparisons with parameters derived from satellite reflectances. Remote Sensing of Environment, 166 : 163–177. [DOI: 10.1016/j.rse.2015.06.008]
-
Zhang L F, Wang S H, Huang C P, Cen Y., Zhai Y G and Tong Q X. 2017. Retrieval of sun-induced fluorescence using statistical method without synchronous irradiance data. IEEE Geoscience and Remote Sensing Letters, 14 (3): 384–388. [DOI: 10.1109/LGRS.2016.2644643]
-
Zhang Y G, Guanter Der Tol, L. X., Berry J W and J. F. 2016. Model-based analysis of the relationship between sun-induced chlorophyll fluorescence and gross primary production for remote sensing applications. Remote Sensing of Environment, 187 : 145–155. [DOI: 10.1016/j.rse.2016.10.016]