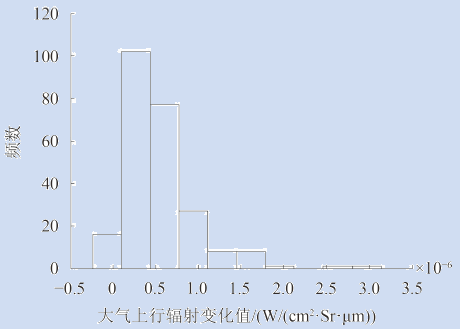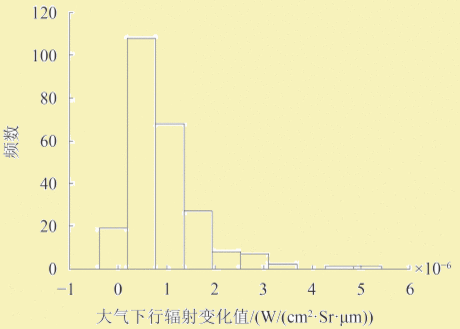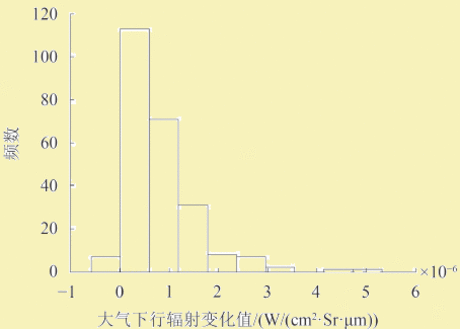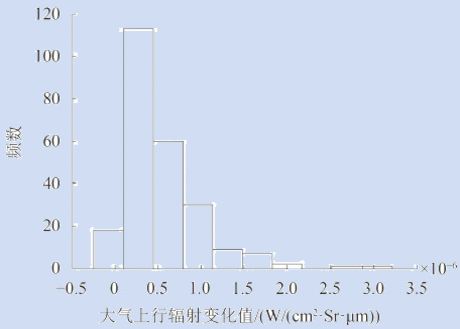|
收稿日期: 2017-02-27; 优先数字出版日期: 2018-01-01
基金项目: 国家自然科学基金(编号:41571353);资源与环境信息系统国家重点实验室自主创新项目(编号:O88RA801YA)
第一作者简介: 战川(1991— ),男,硕士研究生,研究方向为定量遥感。E-mail:zhanc.14s@igsnrr.ac.cn
通讯作者简介: 唐伯惠(1973— ),男,副研究员,研究方向为地表净辐射遥感估算、地表温度与地表发射率遥感反演与验证。E-mail:tangbh@igsnrr.ac.cn
中图分类号: TP79
文献标识码: A
|
摘要
为了减少近地表大气逆温对地表温度遥感反演精度的影响,提出在晴空的地表温度“通用劈窗算法”模型中增加一个温度改正项来实现。在建立该误差改正项时,利用正常条件下的通用劈窗算法系数和具有不同逆温强度的逆温廓线,并结合大气辐射传输模型MODTRAN计算,得到近地表大气逆温条件下的地表温度反演误差,并在分析了该误差值与相应的逆温强度的关系后,发现该温度改正项可以表示为近地表大气逆温强度的二次项函数。为了进一步提高地表温度的反演精度,将地表温度和大气水汽含量进行分组,分别针对每个分组来确定温度改正项方程的系数。模拟结果表明,在逆温强度为1.7 K/100 m时,该温度改正项可以使地表温度的反演精度提高0.44 K。利用内蒙古海拉尔试验站的实测数据对地表温度反演结果进行了验证,在近地表大气存在逆温的条件下,该方法能提高地表温度的遥感反演精度0.47 K。但是,由于本文提出的方法需要已知大气温度廓线来计算大气逆温强度,因此在实际应用中该方法受到了一定的限制。
关键词
近地表大气逆温, 逆温强度, 通用劈窗算法, 地表温度误差改正, MODIS
Abstract
Land Surface Temperature (LST), which controls the basic interactions between the Earth’s surface and the atmosphere, is significant in many aspects. By far, many algorithms have been proposed to retrieve LST from different satellite thermal infrared data. However, the influence of Air Temperature Inversion (ATI) on LST retrieval has not been considered in the development of existing algorithms. This study aims to analyze and reduce the influence of ATI on LST retrieval. Considering that the Generalized Split-Window (GSW) algorithm has been widely used, we choose this algorithm to retrieve LST in this study. Furthermore, considering that the LST retrieval error increases when ATI intensity increases, we add an error correction related to intensity to the GSW algorithm. To determine the relationship between the LST retrieval error and the ATI intensity, we manually change the normal profile in the Thermodynamic Initial Guess Retrieval (TIGR) database into the ATI profile with the intensity ranging from 1.0 K/100 m to 5.0 K/100 m and the step being 1.0 K/100 m because the intensities of the existing ATI profiles in the TIGR database are not large enough. The LST errors are calculated using the changed ATI profiles and the GSW coefficients derived from normal conditions. To improve the accuracy of the LST retrieval, we divide LST and Water Vapor Content (WVC) into different groups. After calculating the LST retrieval errors of all groups, we find that the LST retrieval error could be expressed as a quadratic function of ATI intensity. The coefficients that correspond to the correction of each group are derived by fitting the LST retrieval errors with various ATI intensities. Results show that the monomial coefficient and the constant of the quadratic function increase when the LST increases while the quadratic coefficient does not change significantly. In addition, the coefficients do not change regularly when the WVC increases. To test whether the proposed method could be used to reduce the influence of ATI on LST retrieval accuracy, we use both simulated data and in situ data. Simulation results show that the LST retrieval accuracy could be improved by 0.44 K when the ATI intensity is 1.7 K/100 m. In situ measurements at the Hailar site are also used to test this method. Results show that the proposed method could improve the LST retrieval accuracy by 0.47 K for the GSW algorithm in atmospheres with ATI. This study aims to add an error correction to the GSW algorithm to improve LST retrieval accuracy when the atmosphere shows ATI. Validation using both simulated data and in situ measurements indicates that the proposed method could effectively reduce the influence of ATI on LST retrieval. However, the application of the proposed method is restricted by the air temperature profile that it requires. A model by which the ATI could be determined from satellite data is expected to be developed in a future study.
Key words
Air Temperature Inversion (ATI), ATI intensity, Generalized Split-Window algorithm, land surface temperature error correction, MODIS
1 引 言
地表温度作为地表和大气之间物质和能量交换综合作用的结果,是研究全球和区域尺度陆地表层系统过程的关键参数,同时也是描述温室效应以及全球变暖等现象的指示性指标(Mannstein,1987;Sobrino等,1991;Becker和Li,1995;Tang 等,2006)。准确获取全球尺度地表温度信息是地球表层水热平衡、陆地生态系统物质、能量交换及全球气候变化等研究中的关键(Price,1984;Tang和Li,2008;Kalma 等,2008)。
大气逆温指的是在特殊的天气条件下,大气中会出现大气温度随海拔高度升高而升高的现象(刘增强 等,2007)。近地表大气逆温则是指海拔高度3 km以下范围内出现的逆温现象。由于现有的热红外地表温度遥感反演算法都没有考虑近地表层大气逆温的影响,所以大气存在逆温时会影响地表温度遥感反演算法的精度(Li 等,2013)。
自20世纪80年代以来,不少学者注意到了近地表大气逆温现象,并分析了由该现象引起的地表温度反演误差。Minnett(1986)对近地表大气逆温对海表温度反演精度的影响进行了分析,发现近地表大气逆温带来的额外的海表温度反演误差在0—1 K。Platt和Prata(1993)发现近地表大气逆温经常发生在晴朗无云的夜晚,并分析了大气水汽和地表发射率带来的影响。Lagouarde等人(2015)也指出大气的震荡会给地表温度的反演带来额外的误差。此外,刘增强等人(2007)利用探空观测数据对乌鲁木齐市的近地表大气逆温特征进行研究,给出逆温强度的概念,以此分析不同强度的近地表大气逆温对大气辐射的影响,发现乌鲁木齐市一年四季都存在逆温层,并且冬季是逆温特征最显著的季节,此时强度也最强,平均逆温强度为1.06 K/100 m。
在此基础上,为了减小近地表大气逆温对地表温度反演精度的影响,本文利用通用劈窗算法分析了近地表大气逆温对地表温度反演精度的影响,并结合近地表大气逆温强度,通过建立误差改正模型有效地减小了该影响。
2 近地表大气逆温对地表温度反演精度的影响
2.1 大气逆温廓线的筛选
由于利用大气辐射传输模型MODTRAN进行模拟实验时需要输入大气廓线,本文选择了TIGR2002大气廓线库中的廓线数据来进行分析 (http://ara.lmd.polytechnique.fr/htdocs-public/products/TIGR/TIGR.html[2017-02-27])。TIGR2002共包含了2311条大气廓线,这些廓线包括5类大气状况:冬天极地大气、北半球甚极地大气、寒温带与极地大气、温带大气、热带大气,其中总水汽含量从0.1—8.0 g/cm2。此外,TIGR从1013—0.05 hPa共设40个气压级,每个气压级包含大气温度、水汽、臭氧等离散采样值。由于本文讨论的都是晴空无云条件下的情况,所以挑选出了其中的946条晴空廓线(Tang和Li,2008)。
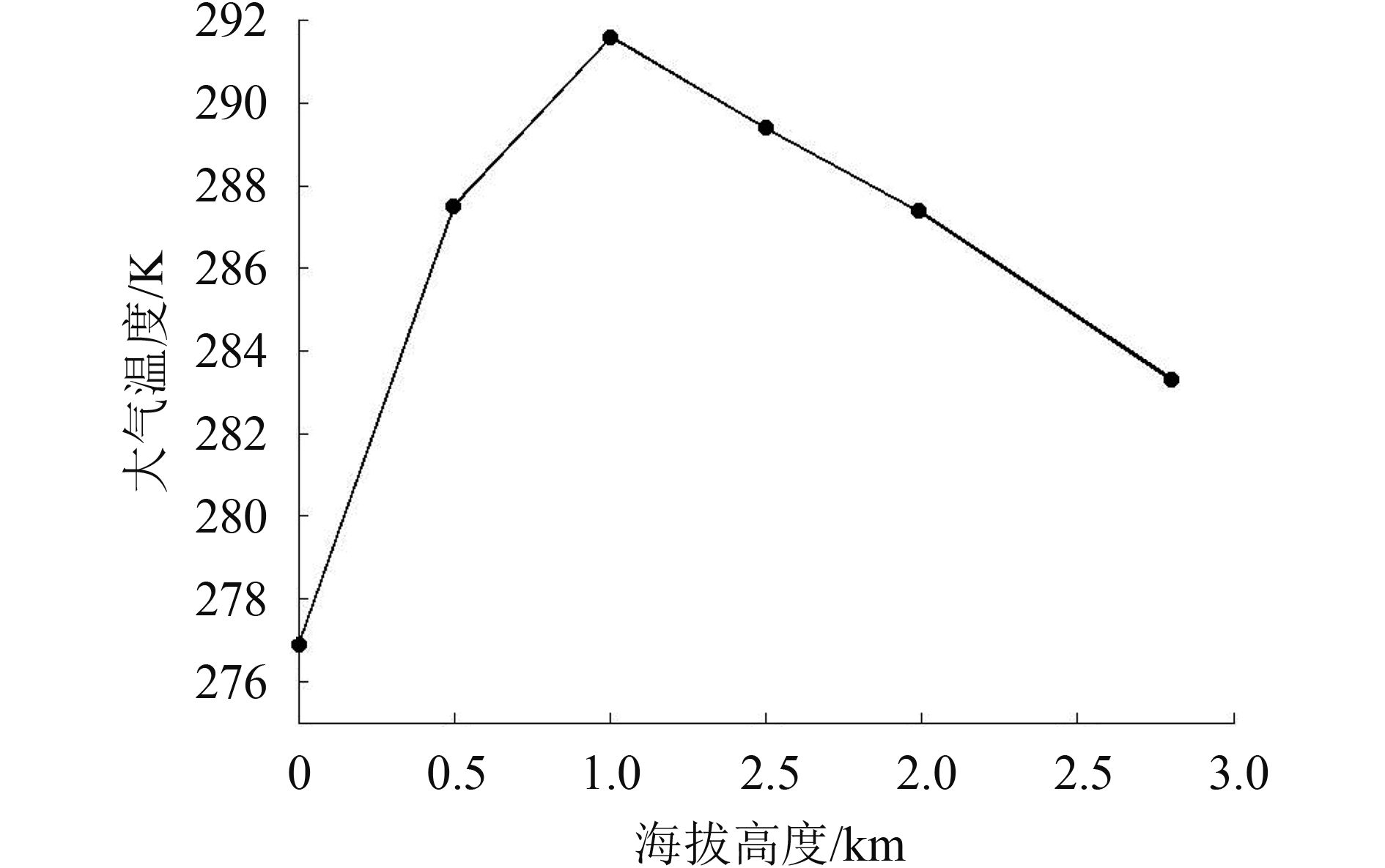
在本研究中,逆温廓线的提取主要依赖于对大气温度随高度变化图的判断。在TIGR大气廓线库中,每隔0.5 km给出一个气温值,为了排除偶然因素,本研究在筛选逆温廓线时认为只有满足在离地面3 km以内连续两次出现大气温度随海拔高度增加而增加的现象(图1),才认定该廓线为逆温廓线。
从所有946条晴空廓线中筛选出267条大气逆温廓线。为了更好地分析近地表大气逆温对地表温度反演的影响,将从TIGR大气廓线库中提取出的逆温廓线修改为了非逆温廓线。
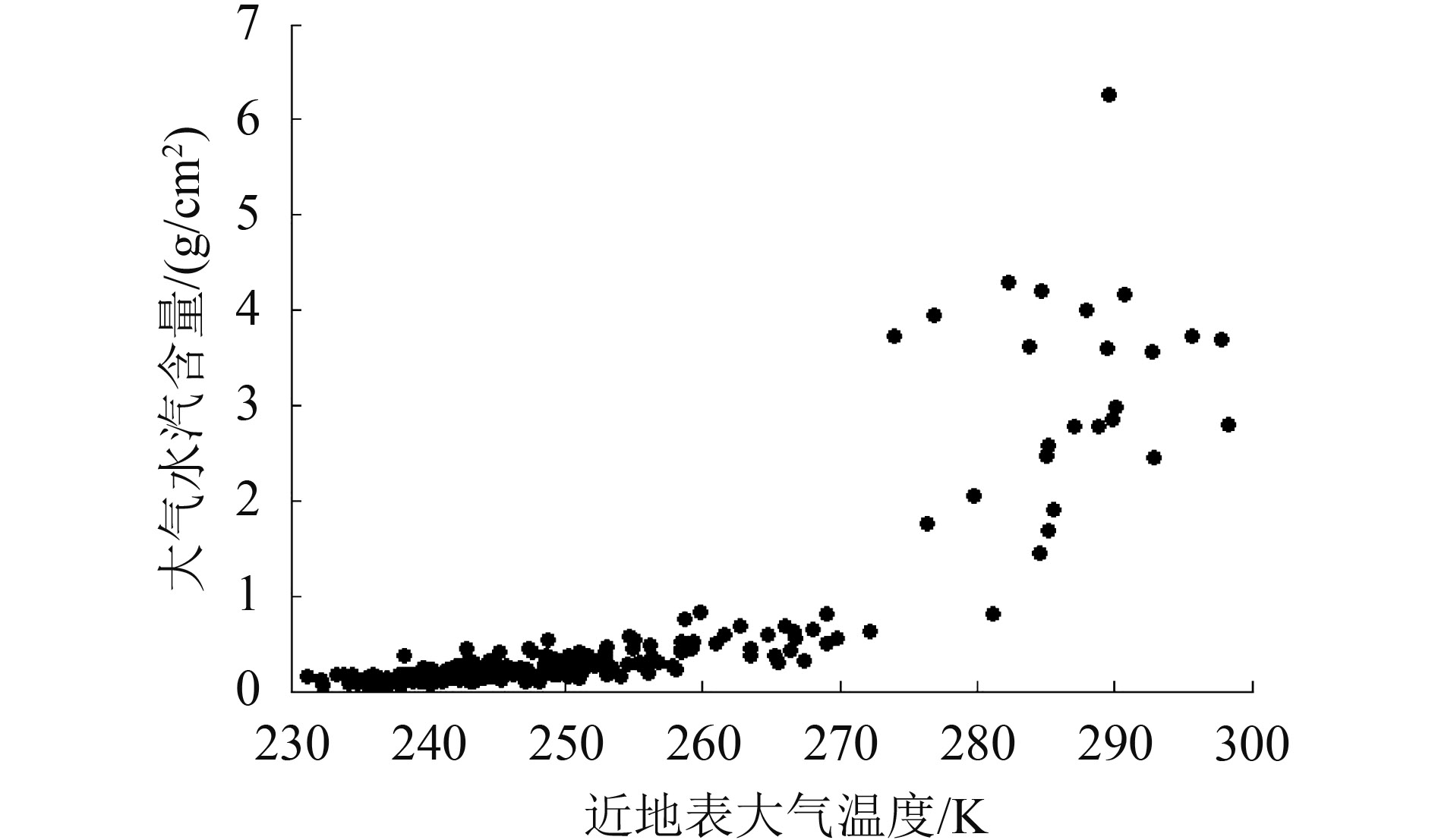
图2显示的是这267条逆温廓线对应的近地表大气温度和大气水汽含量的大小,从图2中可以看出这些逆温廓线大多是干冷的廓线,以水汽含量不超过1.0 g/cm2,近地表大气温度不超过270 K的廓线为主。
2.2 模拟数据库的建立
在晴空大气条件下,根据辐射传输原理,卫星传感器在热红外通道测量得到的大气顶部的通道辐射值
| ${B_i}({T_i}){\rm{ = }}{\varepsilon _i}{B_i}({T_{\rm{s}}}){\tau _i} + R_{{\rm{atm\_i}}}^ \uparrow + (1 - {\varepsilon _i})R_{{\rm{atm\_i}}}^ \downarrow {\tau _i}$ | (1) |
式中,Bi为普朗克函数,Ti为大气顶部的亮温值,εi为地表发射率,Ts为地表温度,τi为大气透过率,
在此基础上,McMillin(1975)提出了劈窗算法,并将其应用到海表温度反演上,取得了不错的结果。劈窗算法利用两个具有不同大气透过率的热红外窗口通道,将辐射传输方程以温度或波长作为函数进行线性化后,将地表温度表达为两个通道星上亮温的线性或非线性组合。考虑到大气水汽含量、卫星观测天顶角以及地表发射率的影响,Tang等人(2008)在原有通用劈窗算法(GSW)的基础上按照一定的步长对观测天顶角、大气水汽、地表温度以及地表发射率进行分组,将其用于基于FY-2C数据的地表温度反演。通用劈窗算法可以表示为(Wan和Dozier,1996)
| $\begin{aligned}LST = & {a_{\rm{0}}}{\rm{ + }}\left( {{a_{\rm{1}}} + {a_{\rm{2}}}\frac{{1 - \varepsilon }}{\varepsilon } + {a_{\rm{3}}}\frac{{\Delta \varepsilon }}{{{\varepsilon ^2}}}} \right)\frac{{{T_{{\rm{31}}}} + {T_{{\rm{32}}}}}}{2} + \\ &\left( {{a_{\rm{4}}} + {a_{\rm{5}}}\frac{{1 - \varepsilon }}{\varepsilon } + {a_{\rm{6}}}\frac{{\Delta \varepsilon }}{{{\varepsilon ^{\rm{2}}}}}} \right)\frac{{{T_{{\rm{31}}}} - {T_{{\rm{32}}}}}}{2}\end{aligned}$ | (2) |
式中,T31和T32为MODIS传感器31和32通道的星上亮温;ε和Δε分别为两个通道地表发射率的均值和差;
由于在实际中很难得到大量实测的地表温度以及星上亮温值,因此获得GSW系数的唯一方法是通过建立模拟数据库进行线性回归。本文通过大气辐射传输模型MODTRAN 5并结合MODIS两个热红外通道的通道响应函数来模拟大气顶部的亮温值。
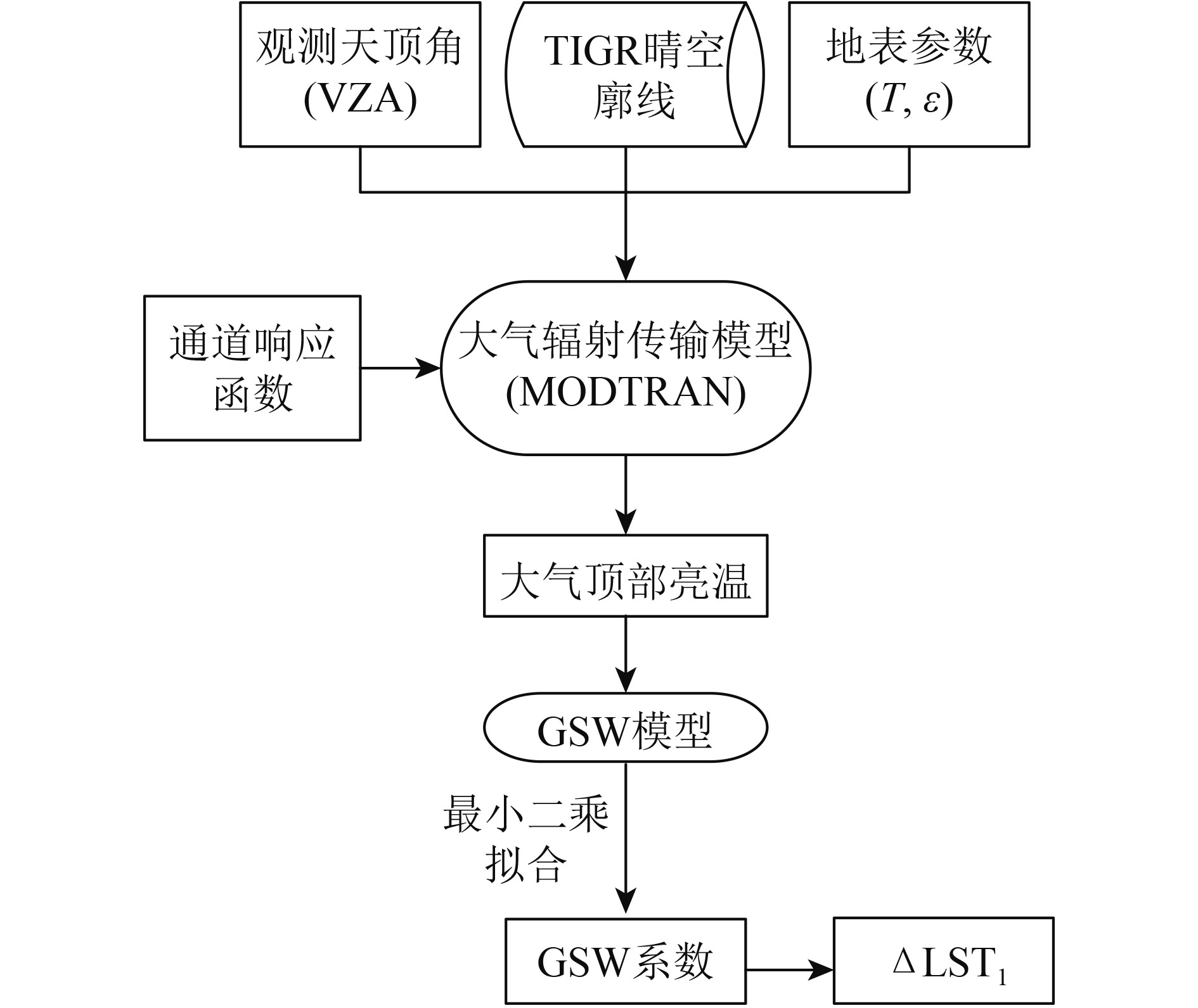
为了更好地逼近线性表达,减小误差,GSW算法采用分组的方式确定出多组系数,以达到提高精度的目的(Tang 等,2008)。观测天顶角分为6种情况:0.00°,33.56°,44.42°,51.32°,56.25°和60.00°;大气水汽含量分为11组:[0.0, 1.0],[0.5, 1.5],[1.0, 2.0],[1.5, 2.5],[2.0, 3.0],[2.5, 3.5],[3.0, 4.0],[3.5, 4.5],[4.0, 5.0],[4.5, 5.5],[5.0, 6.5];地表温度分为5组:[0, 280],[275, 295],[290, 310],[305, 325],[320, 340];地表发射率分低发射率组[0.90, 0.96]和高发射率组[0.94, 1]。在模拟计算时,地表温度的取值范围是依据大气底层的温度T0决定的,即当T0不小于290 K时,地表温度是以5 K为步长从T0–5 K增加到T0+15 K;当T0小于290 K时,地表温度是以5 K为步长从T0–5 K增加到T0+5 K。考虑到大多数地物的发射率都大于0.90,因此,发射率的均值是以0.02为步长从0.90增加到1.0,发射率的差值则是以0.005为步长从–0.025增加到0.015。本文共模拟了660(6×11×5×2)组情况,每组对应的通用劈窗系数均通过最小二乘法回归得到。图3显示的是确定GSW算法系数的流程,其中ΔLST1为利用某一分组下所有晴空廓线计算出的地表温度反演误差。
2.3 误差计算方法与结果
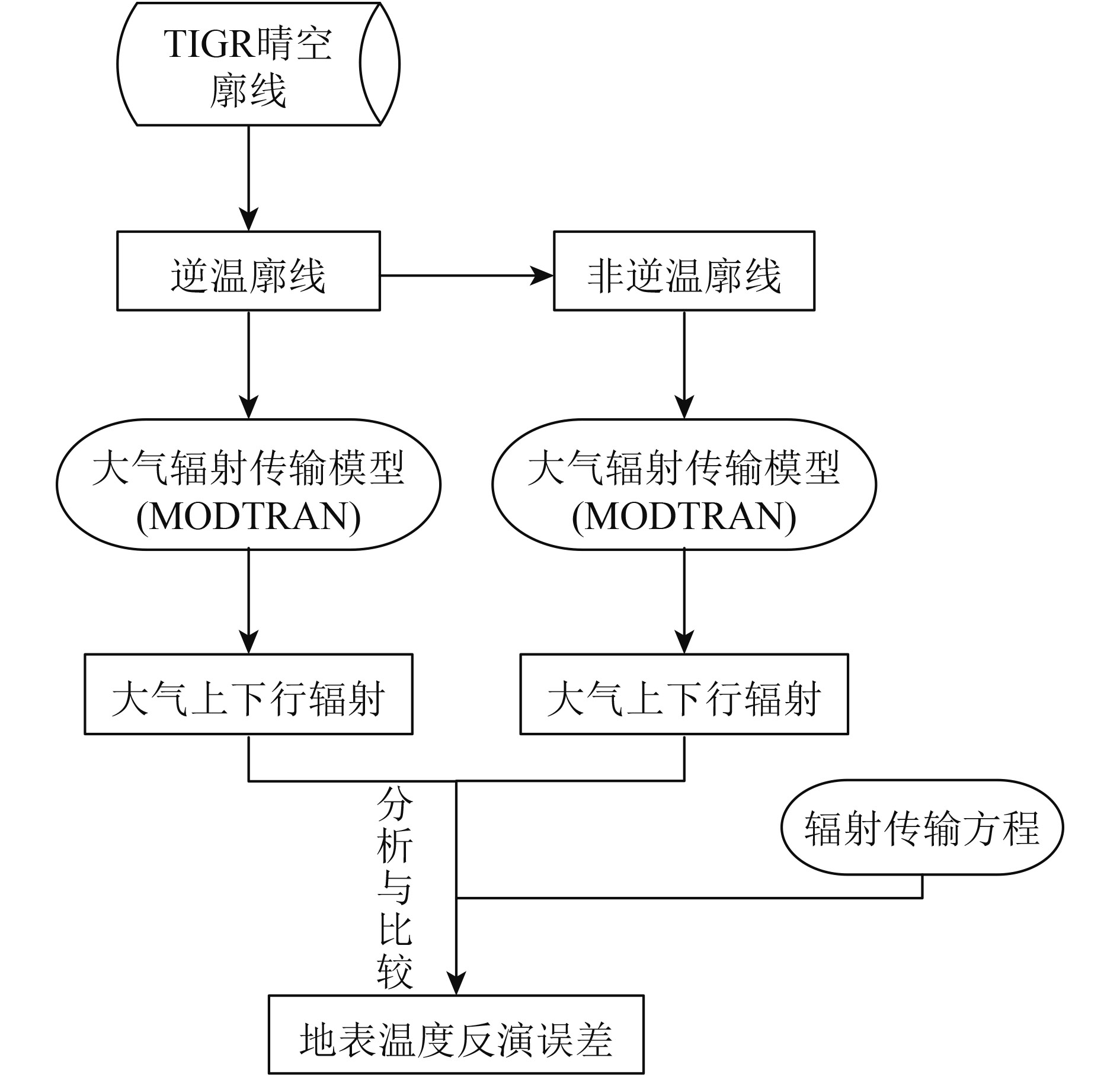
近地表大气逆温的存在会对大气上下行辐射产生影响,为了定量分析这一影响,本文通过MODTRAN模拟得到了逆温和非逆温两种情况下的大气上下行辐射值,并将两者作差,经过比较分析并结合辐射传输方程便可计算出由此引起的地表温度反演误差,流程方案如图4。
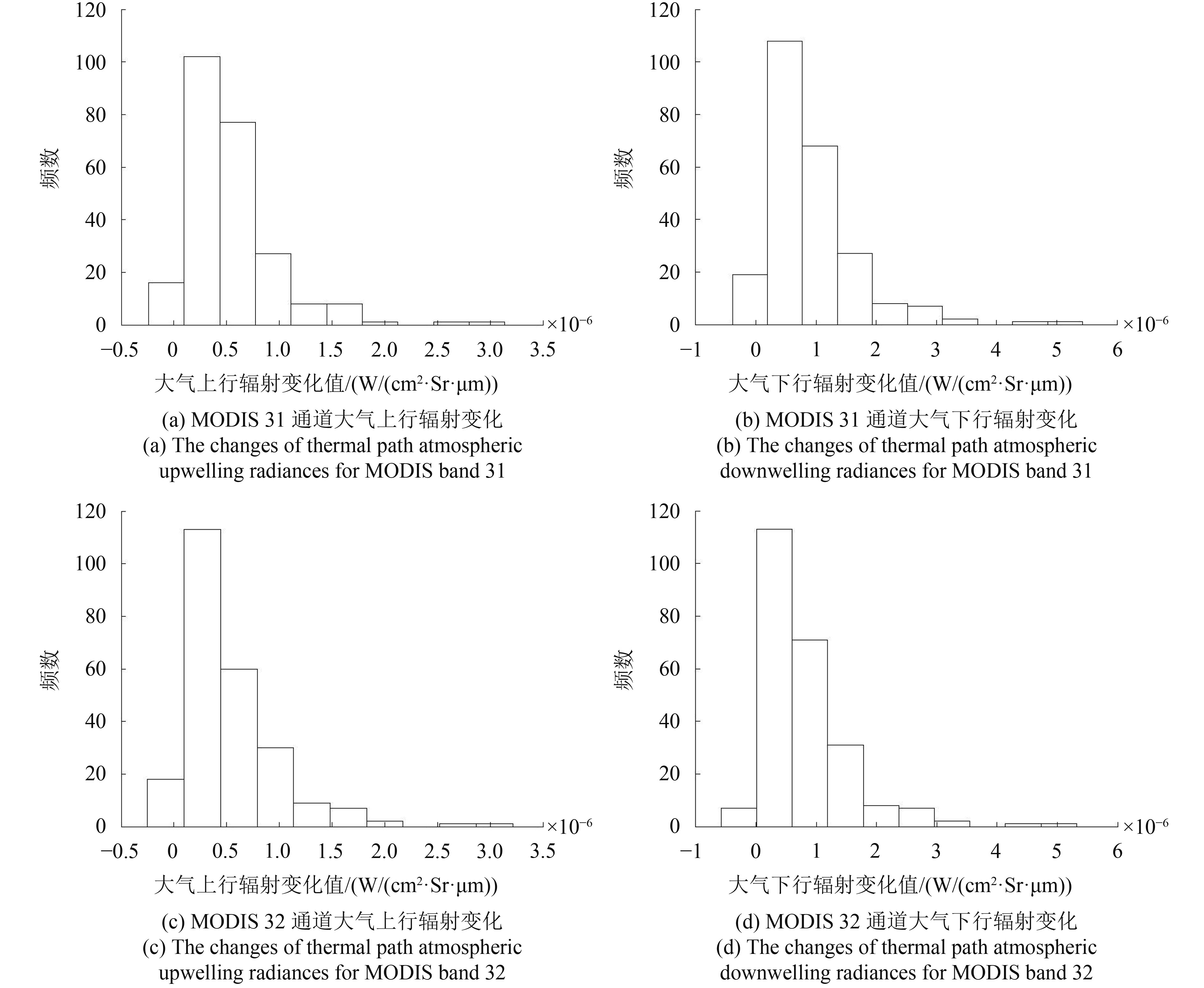
两种情况下大气上下行辐射差值的分布结果如图5。从图5中可以看出,近地表大气逆温的存在会使大气上下行辐射增大,并且大气下行辐射比大气上行辐射增加的幅度更大,由此说明近地表大气逆温对大气下行辐射的影响更大。此外,图5还说明在分析近地表大气逆温对大气上下行辐射的影响时,MODIS两热红外通道(31、32通道)的表现并没有太大差异。
为了说明近地表大气逆温对地表温度反演精度的影响,首先以TIGR廓线库中所有晴空廓线为研究对象,利用图3显示的流程得到各个分组的GSW系数。为了表明存在近地表大气逆温时GSW系数的变化,还利用逆温廓线回归出了存在大气逆温条件下的GSW系数。图6显示的分别是正常情况下和存在大气逆温条件下WVC∈[1.0 g/cm2, 2.5 g/cm2],Ts∈[290 K, 310 K]的低发射率组对应的不同观测天顶角(VZA)条件下的GSW系数。通过对比发现两种情况下回归出的系数存在较大的差别,说明在存在近地表大气逆温条件下仍采用原有的GSW算法会给地表温度反演带来较大的误差。
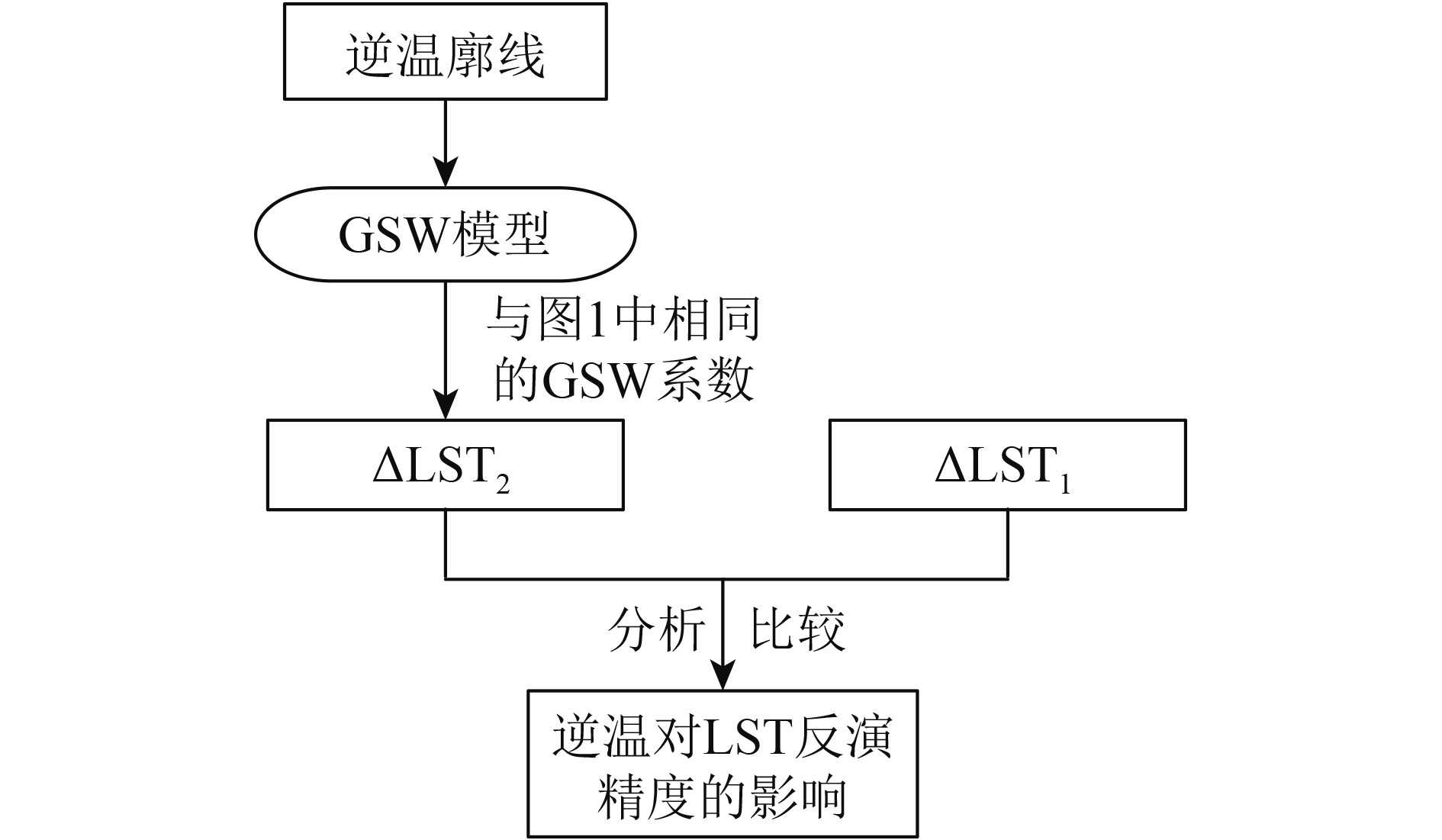
为了进一步说明该影响,依据图3的流程计算出正常情况下的GSW系数,并将此相同系数的GSW模型分别应用到所有廓线和逆温廓线上,通过对比两者产生的地表温度反演误差,即可说明大气逆温对地表温度遥感反演的影响。图8显示的是相应的流程图,其中采用的GSW模型对应的GSW系数与图3中的GSW系数相同,ΔLST2为利用相同分组下所有逆温廓线计算出的地表温度反演误差,通过比较ΔLST2与图1中的ΔLST1便可得到近地表大气逆温对地表温度反演精度的影响。
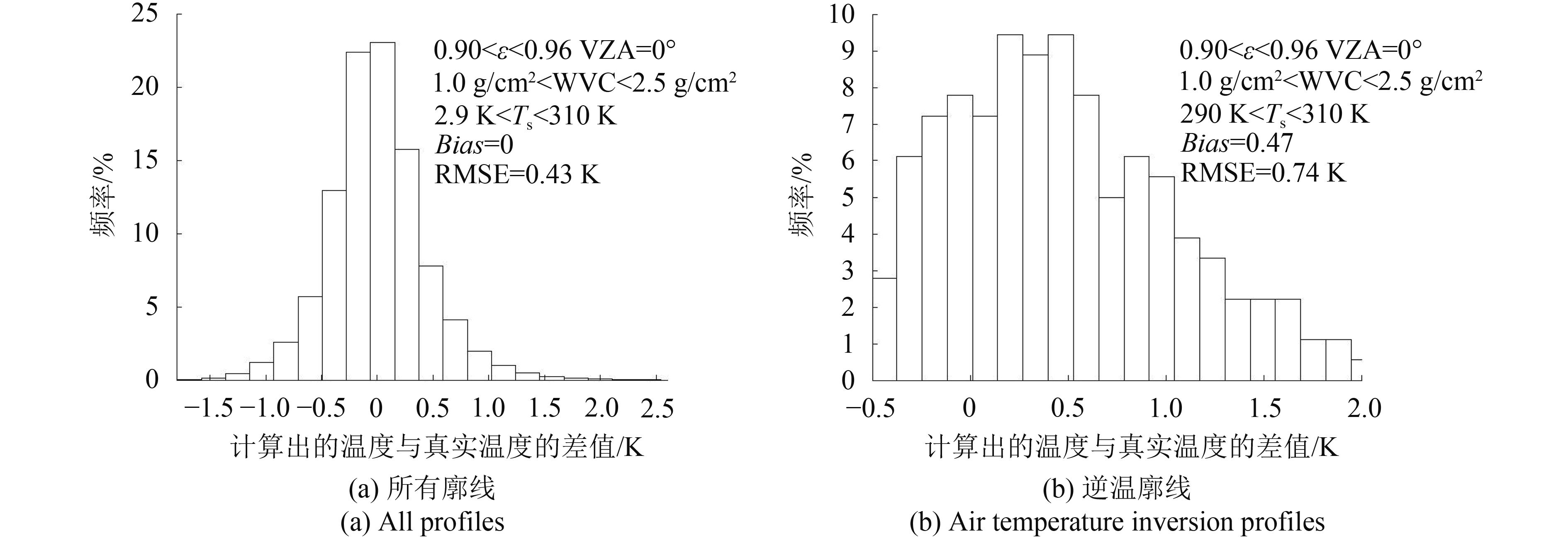
由此得到的地表温度反演误差如图7,对应分组为WVC∈[1.0 g/cm2, 2.5 g/cm2],Ts∈[290 K, 310 K]的低发射率组。图7(a)表明正常情况下该分组的地表温度反演误差为0.43 K,图7(b)表明存在大气逆温情况下相同分组的地表温度反演误差增加到0.74 K。通过比较图7(a)和7(b)可以看出,将利用所有廓线回归得到的GSW系数应用到逆温廓线上后,地表温度反演误差增加了0.31 K,表明由逆温廓线引起的地表温度反演误差达到了0.31 K,这与通过辐射传输方程计算得到的误差值是一致的,由此也说明逆温廓线的存在会影响地表温度反演的精度。
3 误差改正模型的建立
为了减小近地表大气逆温带来的额外的地表温度反演误差,本文在GSW算法的基础上建立了相应的误差改正模型。为了更好地描述近地表大气逆温现象中大气温度上升的速度,引入了逆温强度的概念(刘增强 等,2007)
| $I = \frac{{\Delta T}}{{\Delta H}} \times 100 = \frac{{{T_2} - {T_1}}}{{{H_2} - {H_1}}} \times 100$ | (3) |
式中,I为逆温强度,T1和T2分别为逆温层底部和顶部的大气温度,H1和H2分别为逆温层底部和顶部对应的海拔高度。
考虑到逆温强度越大,近地表大气逆温对地表温度反演精度的影响也越大。因此,本文猜想需要增加的改正项可能与逆温强度存在一定的关系。图9显示的是所有267条逆温廓线的逆温强度值的分布情况。从图9中可以看出,TIGR大气廓线库中逆温廓线的逆温强度偏小,逆温强度为0.2—0.6 K/100 m的廓线居多。
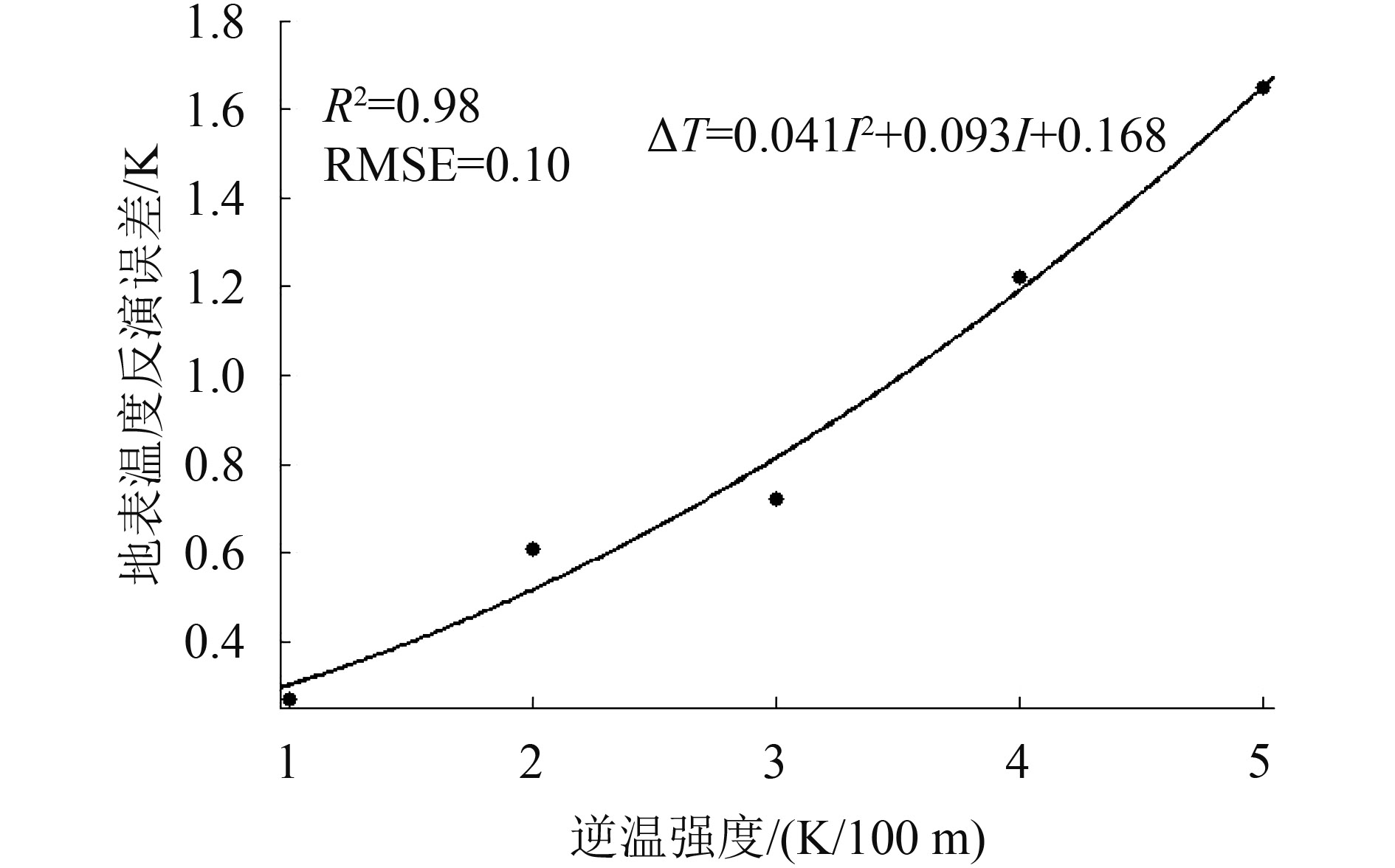
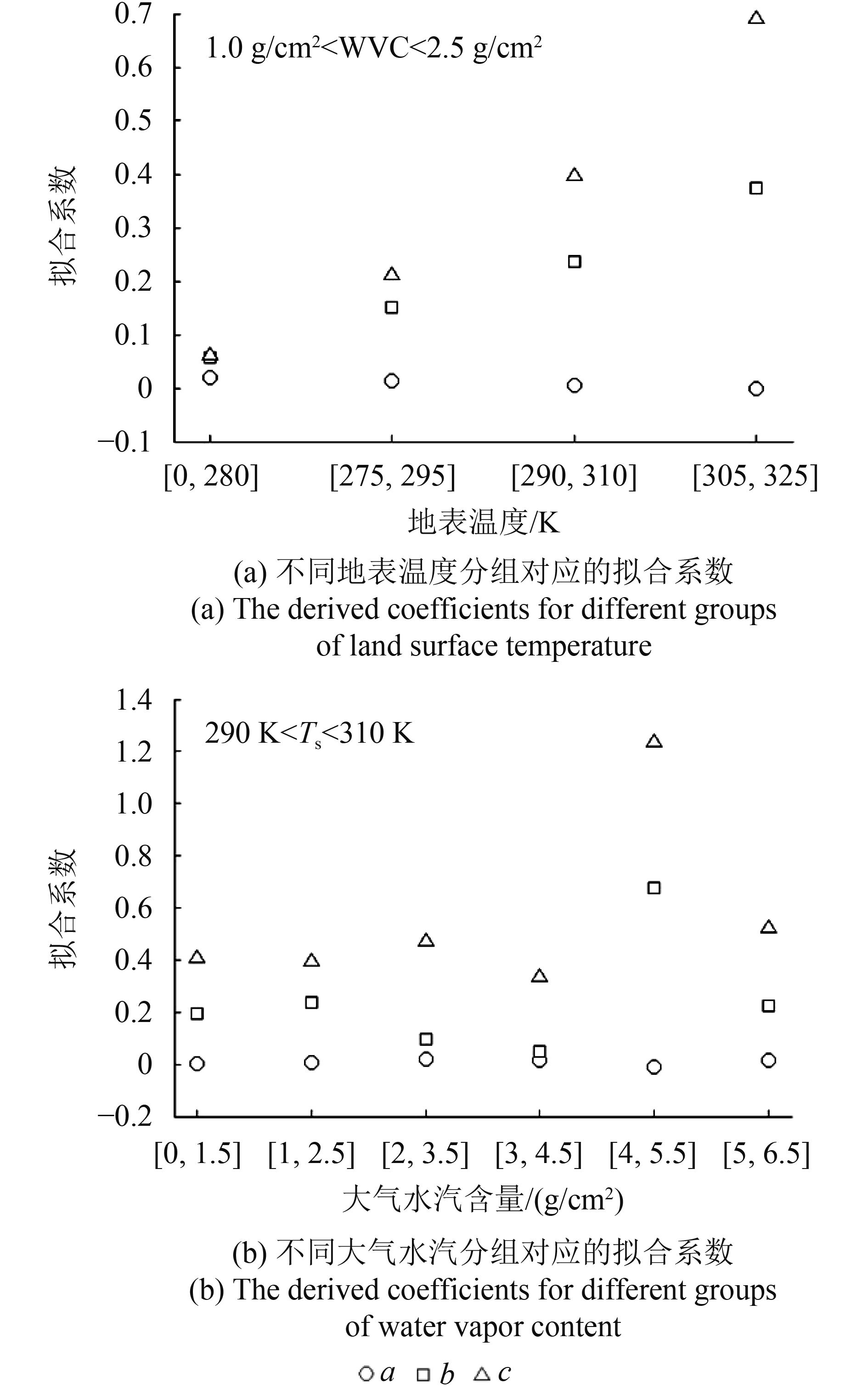
由于TIGR大气廓线库中存在的逆温廓线所对应的逆温强度过小,通过批量修改正常大气廓线来判断逆温强度的影响,选择了各个分组内多条正常的大气廓线,通过将它们的逆温强度依次修改为1.0 K/100 m到5.0 K/100 m(1.0 K/100 m为间隔)后,利用GSW算法得到了不同逆温强度的大气廓线对地表温度反演精度的额外的影响。模拟结果显示,对于WVC∈[0 g/cm2, 1.5 g/cm2],Ts∈[0 K, 280 K]这一分组,需要增加的改正项与近地表大气逆温强度存在明显的正相关关系,如图10所示。最终,由不同逆温强度对应的误差值拟合出的曲线方程为
| $\Delta T = 0.041{I^2} + 0.093I{\rm{ + }}0.168$ | (4) |
式中,ΔT为GSW算法中增加的改正项,I为逆温强度,单位为K/100 m。式(4)为对应的曲线方程。其他分组结果也可以用相同的方法得到,结果表明所有的分组条件下的需要增加的改正项都能近似表达成近地表大气逆温强度的二次函数。其他分组拟合出的系数如图11,图11中a,b,c对应的分别是各分组二次函数
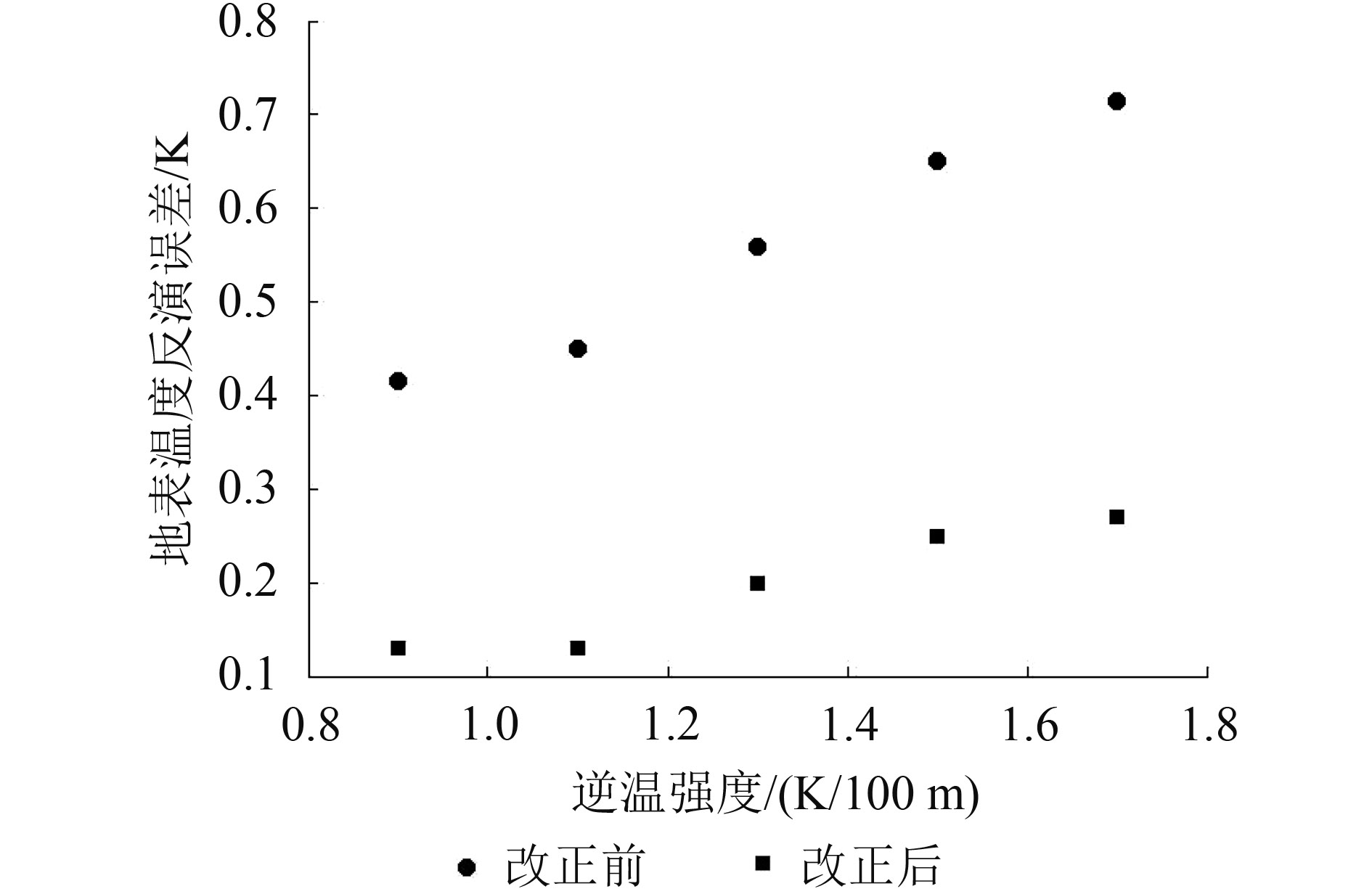
为了验证所建立的误差改正模型,本文根据TIGR大气廓线库中逆温廓线的廓线强度的分布情况从中等间距地挑选出了5条逆温廓线,逆温强度分别为0.9 K/100 m、1.1 K/100 m、1.3 K/100 m、1.5 K/100 m、1.7 K/100 m。针对这5条逆温廓线,利用改正前和改正后的GSW算法得到的地表温度反演误差如图12。从图12中可以看出,在增加改正项后,5种情况下的地表温度反演精度都得到了提高,特别是当逆温强度为1.7 K/100 m时,地表温度反演误差从0.71 K减小到了0.27 K,由此说明该误差改正模型的建立能有效提高近地表大气逆温条件下地表温度反演的精度。
4 结果验证
4.1 实验数据介绍
本文使用了5种类型的MODIS数据产品,分别是星上辐亮度产品MOD021KM/MYD021KM、几何定位产品MOD03/MYD03、地表温度和发射率产品MOD11_L2/MYD11_L2、大气水汽产品MOD05_L2/MYD05_L2以及云掩膜产品MOD35_L2/MYD35_L2(http://ladsweb.nascom.nasa.gov/data/search.html[2017-02-27])。
MOD021KM/MYD021KM产品是经过辐射校正的1级产品,分别是大气顶部的反射率和辐射亮度数据(Savtchenko 等,2004)。MOD03/MYD03是用于数据地理定位的1级产品,它给出了每个1 km分辨率像元的地理坐标等信息,包括每个像元的经度、纬度、地面高程、太阳天顶角和方位角、卫星观测天顶角和方位角以及海陆掩膜等数据(Wolfe 等,2002)。本文选择了相应的MODIS地表温度产品MOD11_L2/MYD11_L2作为对照,获取了每个1 km分辨率像元的地表温度。在利用实测数据验证时,利用MOD05_L2/MYD05_L2判断出水汽值的大小,从而确定GSW算法中对应的分组。此外,为了剔除云的影响,利用MODIS云掩膜产品MOD35_L2/MYD35_L2选出了确定无云的像元。
为了进一步验证通过在GSW算法中增加温度改正项来反演地表温度的精度,选用海拉尔试验站的地面温度实测数据进行验证。海拉尔试验站(120.12°E,49.35°N)属于寒温带半干旱大陆季风性气候,年平均气温为–2 ℃,年平均降水量350 mm。试验站的面积约为0.4 km2,全部由草地覆盖,地表类型均匀,但由于气候变化,在秋冬季节草地退化成干草,并被雪覆盖,直到春夏季节,绿草才会慢慢长出(Tang 等,2015)。
站内分散放置了4台SI-111温度传感器,对地表温度进行测量。由于红外温度传感器SI-111地面观测的辐亮度数据耦合了地表温度、地表发射率和大气下行辐射,因此需要利用下式计算出地表温度(Tang和Wang,2016)
| ${\rm{LST}} = B_{\textit{λ}} ^{ - 1}[\frac{1}{{{\varepsilon _{\textit{λ}} }}}({L_{{\rm{ground, {\textit{λ}} }}}} - (1 - {\varepsilon _{\textit{λ}} })R_{{\rm{atm, {\textit{λ}} }}}^ \downarrow)]$ | (5) |
式中,ελ表示地表发射率,
由于近地表大气逆温现象经常发生于秋冬季节,并且获得的实测数据主要包括2013与2014年的部分数据,因此本文选择了2013年11月、12月以及2014年1月的实测数据来对算法进行验证。由于校正SI-111的地表温度数据以及利用MODTRAN 5.2模拟时都需要地表发射率值,而所选择的时间段内海拉尔试验站被积雪覆盖,故本研究利用ASTER光谱库中提供的雪地的光谱曲线与SI-111光谱响应函数进行计算,得到雪地的发射率为0.988,将该发射率值与仪器接收的辐射信号代入式(5),便能得到地表真实温度数据。
此外,本文还利用美国怀俄明州大学提供的大气廓线数据选出了4个月中所有的逆温廓线。该廓线获取的时间为当地时间每天的0点和12点,为了减小时间差异造成的影响,选择了过境时间与实测数据获取时间相差不到2小时的卫星数据。该廓线数据获取的位置坐标为(119.75°E,49.21°N),与获取地面实测数据的海拉尔试验站相距约30 km。虽然本研究中大气廓线数据与地表实测数据的获取在时间和空间上存在一定的差异,但考虑到海拉尔属于平原地区并且实测数据的获取时间是在晚秋和冬季,而这一时段内大气的状况在短时间内不会发生显著的变化。因此,实测的大气廓线数据仍然可以用来反映海拉尔试验站的大气状况。考虑到相近时间点的卫星数据所对应的实测数据相同,所以对应的逆温强度相同,因此增加的改正值也相同,所以对于过境时间十分接近的卫星数据,只选择其中一景来分析说明。对于实测廓线,本文同样通过绘制大气温度随海拔高度变化图从中筛选出大气逆温廓线。
4.2 验证结果与分析
通过分析海拉尔试验站点在所选择时间段内的MOD11_L2/MYD11_L2数据和MOD05_L2/ MYD05_L2后发现,站点在该时间段内对应的地表温度值均小于280 K,大气水汽含量均小于1.5 g/cm2。因此,可以通过该站点实测数据来验证之前建立的误差改正模型。由于该误差改正模型的建立需要已知大气逆温强度,验证过程中需要通过美国怀俄明州大学提供的实测的大气温度廓线数据来计算逆温强度。
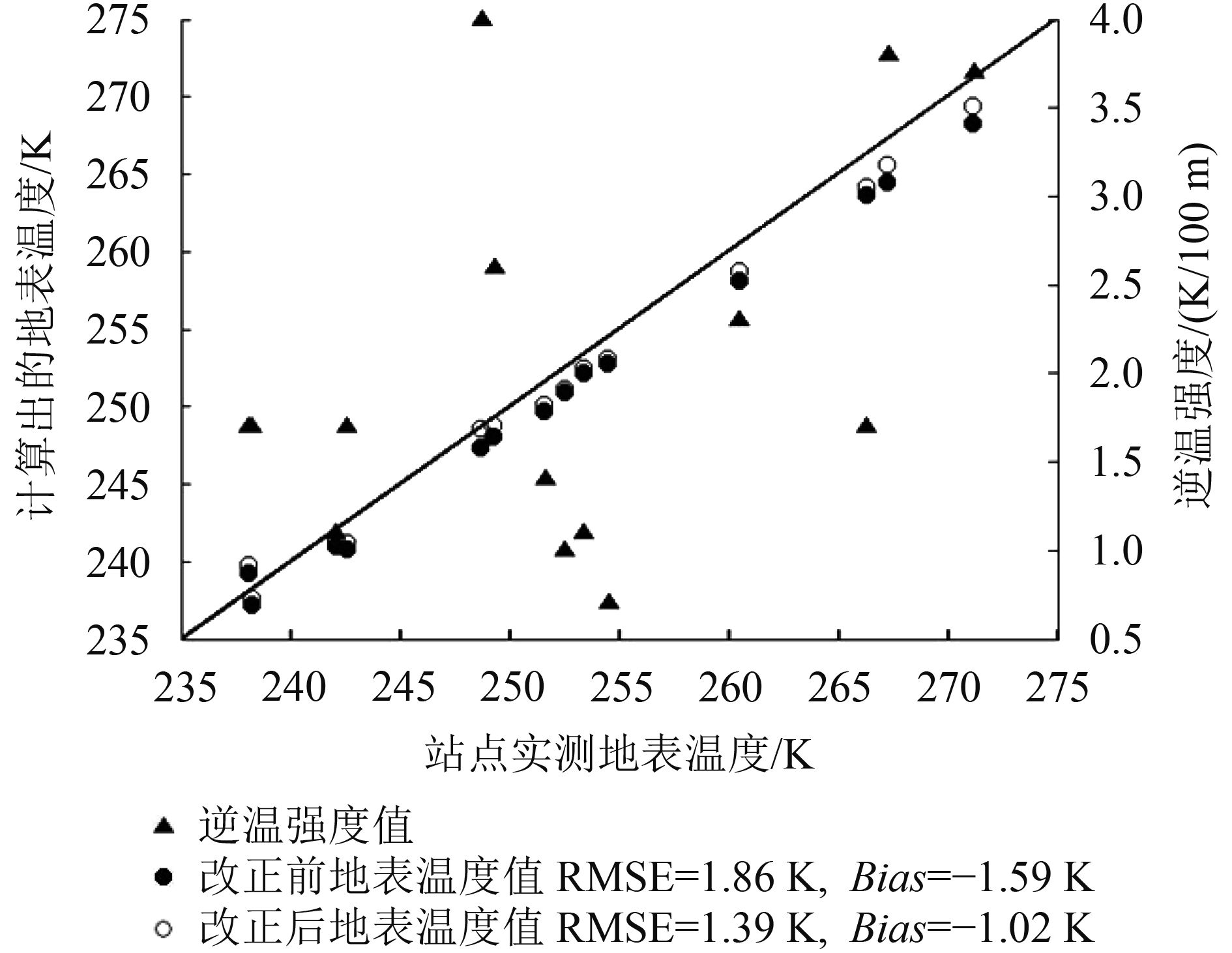
当近地表大气逆温存在时,MOD11_L2/ MYD11_L2中的地表温度值LST可利用之前计算出的ΔT按照LSTcor=LST+ΔT进行改正,则LSTcor即为改正后的地表温度值。图13为海拉尔试验站利用本文提出的方法改正前和改正后的地表温度值与逆温强度关系图。
从图13中可以看出,与TIGR大气廓线库中逆温廓线对应的逆温强度的分布相比,该实测廓线的逆温强度分布范围更广且更均匀,最大值达到了4.0 K/100 m,更适合于对本文所建立模型的验证。由于验证所选择的时间为晚秋和冬季,海拉尔站点被积雪覆盖,因此地表温度普遍较低,实测数据显示其变化范围在235—275 K。
利用实测的温度廓线计算得到了大气逆温强度,再依据之前建立的误差改正模型便可以计算出相应温度改正项的值,图13中各个实心圆点与对应空心圆点间的垂直距离表示的便是这一改正项的大小。从图13中可以看出,逆温强度越大,所增加的改正项的值也越大。特别是当逆温强度为4.0 K/100时,增加的改正项的值达到了1.20 K。由于在误差改正前,与实测数据相比,利用通用劈窗算法计算出的绝大多数地表温度值都偏低,因此温度改正项的加入明显改善了地表温度反演精度。
在将改正前后计算出的地表温度值与实测数据比较后发现,在增加温度改正项后,地表温度反演的RMSE值从改正前的1.86 K减小到了1.39 K,Bias值则是从–1.59 K变为了–1.02 K。这表明该误差改正模型的建立将原有的地表温度反演的精度提高了0.47 K,即说明了通过该方法来减少近地表大气逆温对地表温度反演精度的影响十分有效。
5 结 论
为了减小近地表大气逆温对地表温度遥感反演精度的影响,本文提出了在晴空的地表温度通用劈窗算法模型中增加温度改正项的方法。模拟结果表明,该温度改正项可以表示为近地表大气逆温强度的二次函数。为了进一步提高地表温度反演的精度,本文对地表温度和大气水汽含量进行了分组,并拟合得到了不同分组条件下二次函数对应的各项系数,以此建立误差改正模型。模拟数据验证结果表明,当逆温强度为1.7 K/100 m时,增加的温度改正项可以使地表温度反演精度提高0.44 K。为了进一步验证该误差改正模型,本文利用内蒙古海拉尔试验站的实测数据对地表温度反演结果进行了验证。结果表明,该误差改正模型的建立将原有的近地表大气逆温条件下的地表温度反演误差减小了0.47 K。这表明本文提出的误差改正方法可以有效地提高近地表大气逆温条件下的地表温度遥感反演精度。
本文利用通用劈窗算法分析了近地表大气逆温对地表温度反演精度的影响,通过计算TIGR大气廓线库中已有的逆温廓线对地表温度反演精度的影响后发现,高温高水汽含量和低温低水汽含量的条件下均可能出现近地表大气逆温,并且这种逆温现象会带来额外的0.3 K的地表温度反演误差,这与前人的研究结果是一致的。然而,虽然之前有研究分析指出近地表大气逆温对地表温度反演精度的影响,但并没有提出相关的误差改正方法,本文的创新点在于结合近地表大气逆温强度对热红外地表温度遥感反演误差的影响,构建了考虑大气逆温强度的地表温度反演误差改正模型,提高了近地表大气逆温条件下地表温度的遥感反演精度。
此外,由于利用该方法进行产品生产时需要用到大气温度廓线,因此如果实际中无法获得大气廓线,该方法便不再适用,这也是本文提出的方法所存在的局限性。因此,在未来的研究中,希望能建立一种直接根据卫星遥感数据确定大气逆温是否存在的逆温判断模型,从而使本文提出的方法能够得到更好的应用。
参考文献(References)
-
Becker F and Li Z L. 1995. Surface temperature and emissivity at various scales: definition, measurement and related problems. Remote Sensing Reviews, 12 (3/4): 225–253. [DOI: 10.1080/02757259509532286]
-
Kalma J D, McVicar T R and McCabe M F. 2008. Estimating land surface evaporation: a review of methods using remotely sensed surface temperature data. Surveys in Geophysics, 29 (4/5): 421–469. [DOI: 10.1007/s10712-008-9037-z]
-
Lagouarde J P, Irvine M and Dupont S. 2015. Atmospheric turbulence induced errors on measurements of surface temperature from space. Remote Sensing of Environment, 168 : 40–53. [DOI: 10.1016/j.rse.2015.06.018]
-
Li Z L, Petitcolin F and Zhang R H. 2000. A physically based algorithm for land surface emissivity retrieval from combined mid-infrared and thermal infrared data. Science in China Series E: Technological Sciences, 43 (S1): 23–33. [DOI: 10.1007/BF02916575]
-
Li Z L, Tang B H, Wu H, Ren H Z, Yan G J, Wan Z M, Trigo I F and Sobrino J A. 2013. Satellite-derived land surface temperature: current status and perspectives. Remote Sensing of Environment, 131 : 14–37. [DOI: 10.1016/j.rse.2012.12.008]
-
Liu Z Q, Zheng Y P, Li J L, Chen J and Yan Z J. 2007. Temperature inversion characteristics of low-air atmosphere of Urumqi City. Arid Land Geography, 30 (3): 351–356. [DOI: 10.3321/j.issn:1000-6060.2007.03.005] ( 刘增强, 郑玉萍, 李景林, 陈洁, 闫战江. 2007. 乌鲁木齐市低空大气逆温特征分析. 干旱区地理, 30 (3): 351–356. [DOI: 10.3321/j.issn:1000-6060.2007.03.005] )
-
Mannstein H. 1987. Surface energy budget, surface temperature and thermal inertia//Vaughan R A, ed. Remote Sensing Applications in Meteorology and Climatology. Dordrecht, Netherlands: Springer: 391–410 [DOI: 10.1007/978-94-009-3881-6_21]
-
McMillin L M. 1975. Estimation of sea surface temperatures from two infrared window measurements with different absorption. Journal of Geophysical Research, 80 (36): 5113–5117. [DOI: 10.1029/JC080i036p05113]
-
Minnett P J. 1986. A numerical study of the effects of anomalous North Atlantic atmospheric conditions on the infrared measurement of sea surface temperature from space. Journal of Geophysical Research, 91 (C7): 8509–8521. [DOI: 10.1029/JC091iC07p08509]
-
Platt C M R and Prata A J. 1993. Nocturnal effects in the retrieval of land surface temperatures from satellite measurements. Remote Sensing of Environment, 45 (2): 127–136. [DOI: 10.1016/0034-4257(93)90037-X]
-
Price J C. 1984. Land surface temperature measurements from the split window channels of the NOAA 7 advanced very high resolution radiometer. Journal of Geophysical Research, 89 (D5): 7231–7237. [DOI: 10.1029/JD089iD05p07231]
-
Savtchenko A, Ouzounov D, Ahmad S, Acker J, Leptoukh G, Koziana J and Nickless D. 2004. Terra and Aqua MODIS products available from NASA GES DAAC. Advances in Space Research, 34 (4): 710–714. [DOI: 10.1016/j.asr.2004.03.012]
-
Sobrino J A, Coll C and Caselles V. 1991. Atmospheric correction for land surface temperature using NOAA-11 AVHRR channels 4 and 5. Remote Sensing Environment, 38 (1): 19–34. [DOI: 10.1016/0034-4257(91)90069-I]
-
Tang B H, Bi Y Y, Li Z L and Xia J. 2008. Generalized split-window algorithm for estimate of land surface temperature from Chinese geostationary FengYun meteorological satellite (FY-2C) data. Sensors, 8 (2): 933–951. [DOI: 10.3390/s8020933]
-
Tang B H and Li Z L. 2008. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sensing of Environment, 112 (9): 3482–3492. [DOI: 10.1016/j.rse.2008.04.004]
-
Tang B H, Li Z L and Zhang R H. 2006. A direct method for estimating net surface shortwave radiation from MODIS data. Remote Sensing of Environment, 103 (1): 115–126. [DOI: 10.1016/j.rse.2006.04.008]
-
Tang B H, Shao K, Li Z L, Wu H, Nerry F and Zhou G Q. 2015. Estimation and validation of land surface temperatures from Chinese second-generation polar-orbit FY-3A VIRR data. Remote Sensing, 7 (3): 3250–3273. [DOI: 10.3390/rs70303250]
-
Tang B H and Wang J. 2016. A physics-based method to retrieve land surface temperature from MODIS daytime midinfrared data. IEEE Transactions on Geoscience and Remote Sensing, 54 (8): 4672–4679. [DOI: 10.1109/TGRS.2016.2548500]
-
Wan Z M and Dozier J. 1996. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Transactions on Geoscience and Remote Sensing, 34 (4): 892–905. [DOI: 10.1109/36.508406]
-
Wolfe R E, Nishihama M, Fleig A J, Kuyper J A, Roy D P, Storey J C and Patt F S. 2002. Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sensing of Environment, 83 (1/2): 31–49. [DOI: 10.1016/S0034-4257(02)00085-8]