出版日期: 2017-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176491
2017 | Volumn21 | Number 6
上一篇 | 下一篇

SBDART的参数化短波辐射传输模型

赵静^1,2 , 阎广建² , 焦中虎^2,3 , 陈玲⁴ , 储卿²

1. 哈尔滨工业大学深圳研究生院，深圳 518000

2. 北京师范大学地理科学学部遥感科学与工程研究院遥感科学国家重点实验室，北京 100875

3. 中国地震局地质研究所，北京 100029

4. 北京林业大学，北京 100083

收稿日期: 2017-01-12; 优先数字出版日期: 2017-11-01

基金项目: 国家自然科学基金(编号：41331171)；国家重点基础研究发展计划(973计划)(编号：2013CB733402)

第一作者简介: 赵静(1987—　)，女，博士研究生，研究方向为定量遥感。E-mail：jingzhao_rs@foxmail.com

通讯作者简介: 阎广建(1972—　)，男，教授，研究方向为多角度遥感测量、建模及参数反演。E-mail：gjyan@bnu.edu.cn

中图分类号: P41

文献标识码: A

摘要

云层对地气系统辐射能量平衡有重要的调节作用，然而传统1维大气辐射传输模型仅能考虑晴空和全云两种情况。为了更好地研究云层对地表短波辐射的影响，以大气辐射传输模型SBDART(Santa Barbara Disort Atmospheric Radiative Transfer)为基础，在短波辐射传输基本方程中引入半球天空有效云覆盖度和区域真实云覆盖度两个关键云参数，考虑太阳方向和半球天空云层覆盖情况，对模型进行几何关系的修正。结合短波辐射的影响因素和SBDART模型的内置参数，选择13个参数，使用全局定量敏感性分析软件SimLab对修正后的模型进行参数敏感性分析及应用讨论。研究结果表明：该模型能够较好地描述云层对地表短波辐射的影响；对下行短波辐射和地表短波净辐射而言，太阳天顶角和地表反照率的影响最为显著；两个云覆盖参数在很大程度上也影响了地表短波辐射分量；在模型实际应用过程中，敏感性较强的6个参数均可以通过卫星遥感数据得到，模型具有较好的应用前景。由此可见，改进的短波辐射传输模型能够更好地考虑不同云层条件下、不同太阳–云–观测几何下的短波辐射传输问题，有利于提高短波辐射参量的遥感反演精度。

关键词

地表短波辐射, 云参数, 辐射传输模型, SBDART, SimLab, 敏感性分析

Enhanced shortwave radiative transfer model based on SBDART

ZHAO Jing^1,2 , YAN Guangjian² , JIAO Zhonghu^2,3 , CHEN Ling⁴ , CHU Qing²

1.Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518000, China

2.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing Science and Engineering, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China

3.Institute of Geology, China Earthquake Administration, Beijing 100029, China

4.Beijing Forestry University, Beijing 100083, China

Abstract

Clouds, being the most abundant and variable factor in the atmosphere, are critical to the modification of Earth–atmosphere energy balance. The effects of clouds on radiation should therefore be carefully and thoroughly considered. However, traditional atmospheric radiative transfer models only consider two extreme situations, namely, all clear and overcast. To understand the influence of clouds on surface shortwave radiation and improve the accuracy of shortwave radiative components derived from remote sensing dataset, we propose a novel radiative transfer model to analyze the cloud conditions in this work. Based on the traditional one-dimensional radiative transfer model Santa Barbara DISORT Atmospheric Radiative Transfer (SBDART), this study first classifies the actual sun/cloud-viewing geometric conditions into nine subtypes, considering whether the directions of the sun and sensor are obscured by clouds. Then, the original formula of land surface downward radiative components is expanded. Two cloud fraction parameters (i.e., hemispherical effective cloud fraction and regional cloud fraction) are introduced to the formula to establish an improved shortwave radiative transfer model, namely, the SBDART-CF model. Based on the formula, the nine subtypes are summarized into two types, that is, the situations where the direction of the sun is either obscured by the cloud or not. Then, the atmospheric spherical albedo and atmospheric transmission of different cloud conditions are compared to narrow the range of cloud parameters. Other thirteen parameters, such as solar zenith angle, surface albedo, and cloud thickness, among others, are introduced to the following sensitive analysis. Finally, the effects of the above-mentioned model parameters on the surface shortwave radiative components under different circumstances are calculated and analyzed by using SimLab software, which employs a global quantitative sensitivity analysis method. The proposed shortwave radiative transfer model can efficiently describe the influence of clouds on the surface shortwave radiation by considering the cloud horizontal distribution in the sky. Solar zenith angle and surface albedo both play significant roles in the modification of downward shortwave radiation and surface net shortwave radiation. Hemispherical effective cloud fraction and regional cloud fraction also considerably affect the radiation components. Six factors that are also important to the model can be easily derived from the satellite products and therefore can contribute to the model application effectively. Water vapor, ozone, and carbon dioxide column volume exert minimal effects on the surface shortwave radiation components under all the considered conditions. The above analysis results show that the proposed SBDART-CF model can deal with shortwave radiative problems under different cloud conditions. Therefore, the model can effectively accomplish the radiative component estimation from remotely sensed datasets.

Key words

surface shortwave radiation, cloud parameter, radiative transfer model, SBDART, SimLab, sensitivity analysis

1 引　言

太阳辐射是地气系统能量和物质循环的主要驱动力，对太阳辐射在大气中的传输过程进行建模是利用遥感数据进行太阳辐射反演的基础，而研究各种大气因子对太阳辐射的影响则是辐射传输建模过程中的重要工作内容。建模过程中的难点主要体现在两个方面：(1)各种大气成分(如水汽、臭氧等)在垂直方向上呈非均匀分布，且随地域、时间等因素的不同而变化；(2)云的分布和物理性质存在较为明显的时空变化特征。云层覆盖了地球约2/3的面积，相较于大气层中水汽、二氧化碳等因子，云层的辐射强迫更为显著，是地气系统辐射能量平衡的最大调节者(Stevens和Bony，2013；Harrison 等，1990；Stull，1988)。

从考虑云层对地表辐射量影响的角度而言，现有的辐射传输模型大致可分为3大类：1维辐射传输模型、3维辐射传输模型和改进的1维辐射传输模型。1维辐射传输模型通常适用于中等空间分辨率的辐射量估算，如遥感辐射产品ISCCP(International Satellite Cloud Climatology Project)和GEWEX(Global Energy and Water Cycle Experiment)等(Zhang 等，2004；Pinker 等，2003)。3维辐射传输模型详细地考虑了云层的光学厚度、颗粒大小、3维结构等参数对辐射的影响，可精确地估算有云大气情况下地表短波辐射量(O’Hirok和Gautier，1998；Oreopoulos和Cahalan，2005)。针对现有高空间分辨率遥感辐射研究多采用传统1维模型的情况，改进型的1维辐射传输模型逐渐被提出。Chen等人(2012)基于传统1维辐射传输模型MODTRAN(MODerate resolution atmospheric TRANsmission)进行修正，将晴空和有云两种模式按照太阳和观测方向是否被云遮盖拓展为4种几何关系，给出了能够考虑像元之间云相互影响的短波辐射估算结果。

本研究以被广泛使用的大气辐射传输模型SBDART(Santa Barbara DISORT Atmospheric Radiative Transfer)为基础，对其进行太阳—云—观测几何关系的修正，使之能够更好地估算较高空间分辨率情况下的地表直射辐射、短波下行辐射、短波上行辐射和短波净辐射等短波辐射各分量。

2 SBDART模型概述

SBDART是一种基于平面平行大气假设的、能够计算晴空和有云条件下大气层和地表辐射情况的辐射传输模型，由美国加利福利亚大学圣巴巴拉分校地球系统计算学院研发的(Ricchiazzi 等，1998)。该模型集合了离散纵标辐射传输模型(DISORT)(Stamnes 等，1988)、低分辨率大气透过率模型(LOWTRAN)(Kneizys 等，1988)和米氏散射模型(Lam 等，1992)，包括紫外、可见光和红外波段辐射传输的重要过程。SBDART被广泛应用于辐射能量的相关研究中。Achad等人(2013)利用SBDART计算了不同类型的气溶胶对紫外波段辐射的贡献量(Achad等，2013)；Pinker等人(2010)通过SBDART模拟得到撒哈拉沙漠地区在无气溶胶情况下的地表短波辐射量，从而得到由于气溶胶的存在所造成的辐射强迫；Mora(2011)使用SBDART估算得到无云和全云条件下地表下行长波辐射分量，并利用台站的数据对估算结果进行了验证和分析。

3 改进的SBDART模型

3.1 模型原理

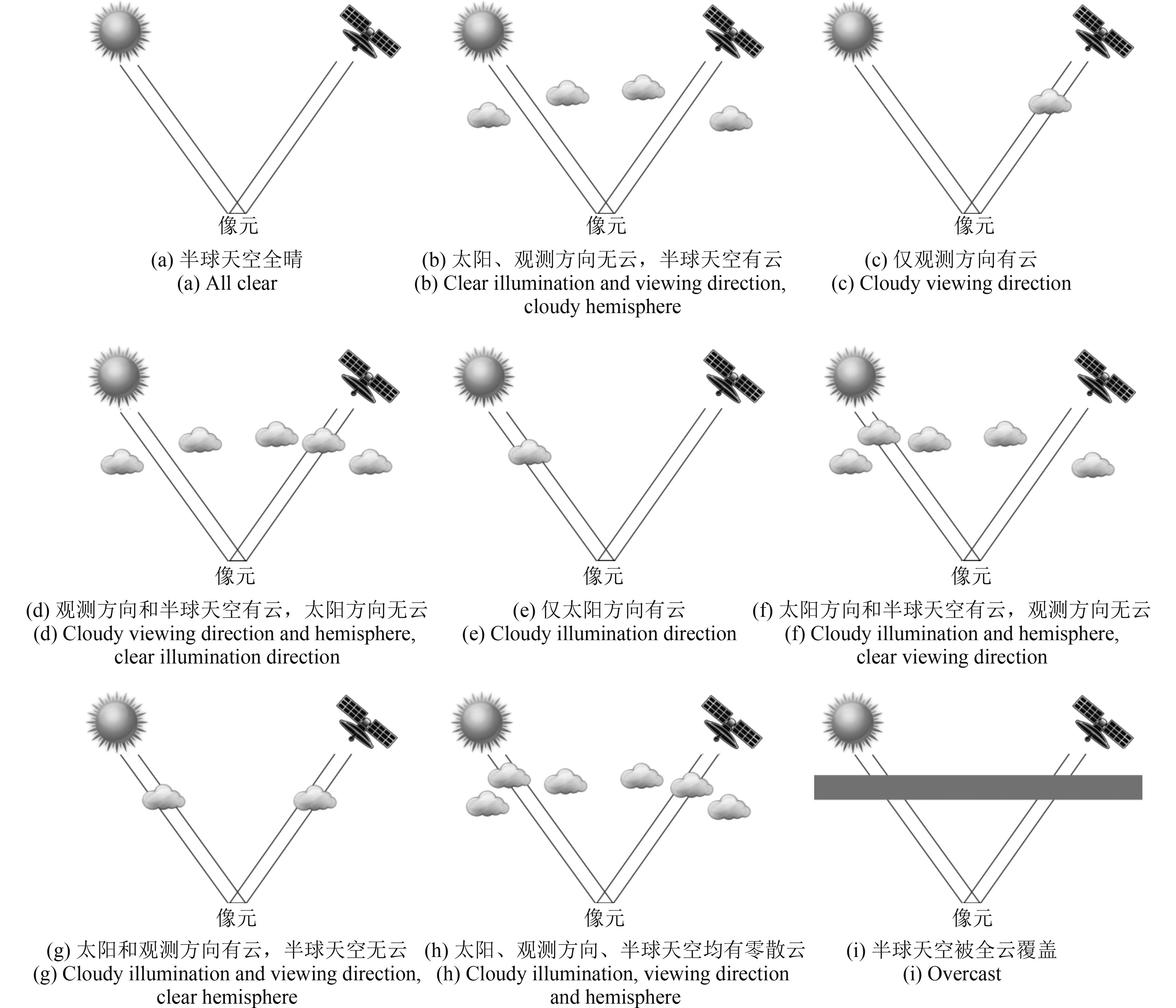
传统的1维辐射传输模型将大气层视为多层水平均质垂直异质的平面平行层，仅能考虑晴空和全云两种情况，而真实情况更多的是部分云。为了提高地表短波辐射估算精度，需要对太阳—云—观测几何做更为细致的考虑。Chen等人(2012)在MODTRAN的基础上开发出了一种改进的短波辐射传输模型MODTRAN-CF，根据观测方向和太阳方向是否有云分为4类：(1)太阳方向有云，观测方向晴空；(2)太阳方向晴空，观测方向有云；(3)太阳和观测方向均有云；(4)太阳和观测方向均无云，但半球空间可能有云。本研究为了细化真实情况的分类，使用二进制的方法将太阳方向、观测方向和半球天空是否有云的情况分为8种(图1)，并补充了一种全云的情况。由图1可知，以SBDART为代表的1维辐射传输模型仅能全晴(图1(a))和全云(图1(i))两种情况下的地表短波辐射的估算问题。因为改进的SBDART模型是基于MODTRAN-CF的思路，故将其称为SBDART-CF。虽然同为1维辐射传输模型，但是相较于MODTRAN，SBDART有着更为丰富的云参数，能够更好地描述真实情况下的云层，而且由于采用了第一顺序纠正法，对于大太阳天顶角的情况能够处理得更好(Ricchiazzi 等，1998；Dahlback和Stamnes，1991)。

图 1 太阳—观测—半球云覆盖情况分类

Fig. 1 Classification for sun-sensor-hemisphere cloud cover situation

假设地表为朗伯表面，地表下行辐射通量 $F({\mu _i})$ 的计算式为(Liang，2005)

$F\left( {{\mu _i}} \right) = {F_0}\left( {{\mu _i}} \right) + \frac{{{r_{\rm{s}}}\bar \rho }}{{1 - {r_{\rm{s}}}\bar \rho }}{\mu _i}{E_0}\gamma \left( {{\mu _i}} \right)$

(1)

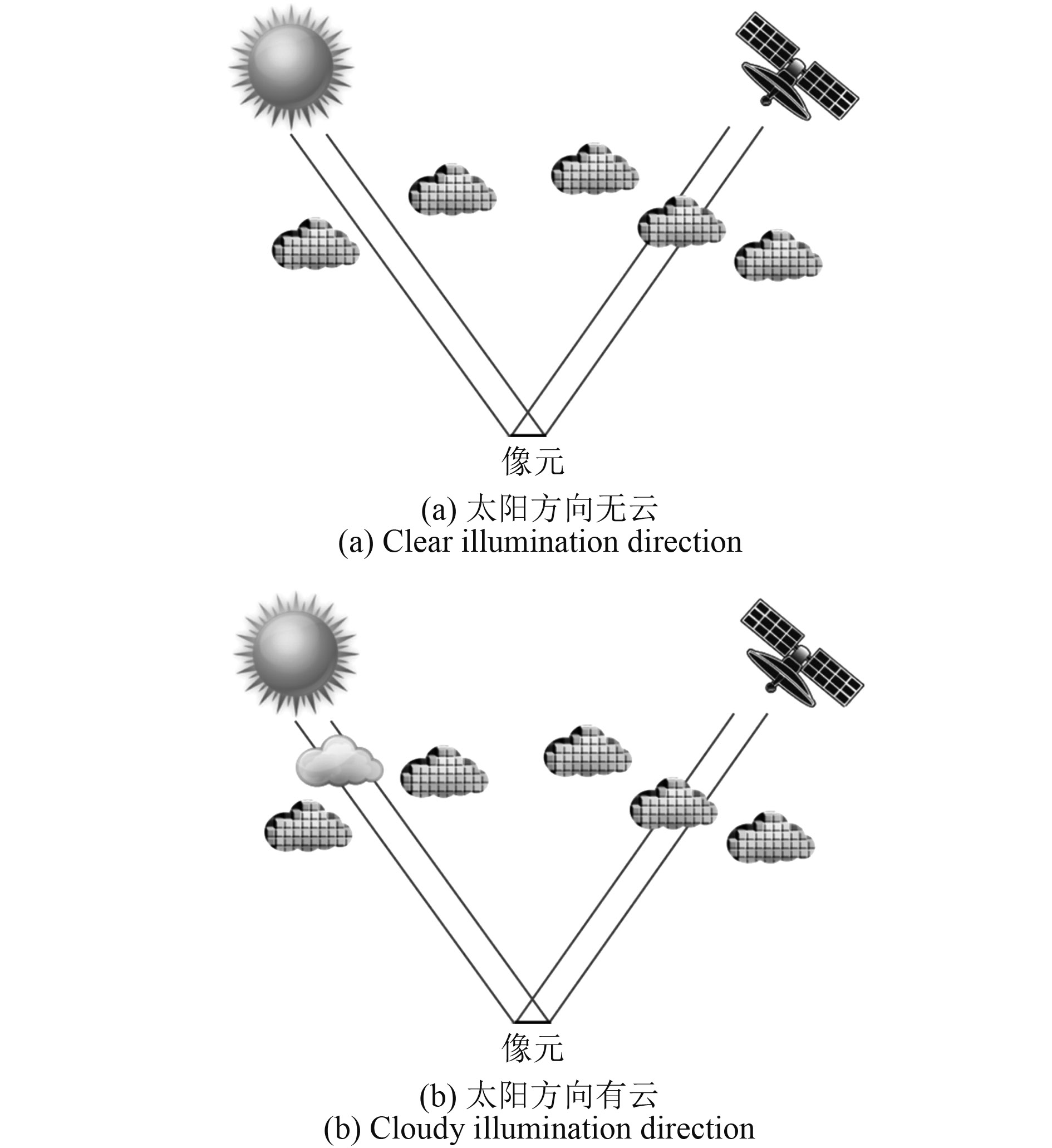
式中，所有辐射量都是波长的函数，μ_i是太阳天顶角的余弦，r_s是地表反射率，F₀(μ_i)代表无地表贡献时(即r_s为0)的地表下行辐射通量， $\bar \rho $ 是大气球面反照率，E₀是大气层顶的太阳辐照度，γ(μ_i)是太阳方向的大气总透过率(包括直射和散射透过率)，等号右边第二项即为地气之间多次散射的太阳辐射F_m(μ_i)。

无地表贡献时(即地表视为黑体，r_s设为0)的地表下行辐射通量F₀(μ_i)由直射太阳辐射Dir和散射太阳辐射Dif两部分组成，应当考虑两种情况：太阳方向无云(图1(a)—(d))和太阳方向有云(图1(e)—(i))，计算式如下(Chen 等，2012)

${F_{0\_{\rm{clr}}}} = Di{r_{{\rm{clr}}}} + Di{f_{{\rm{cld}}}} \cdot f1 + Di{f_{{\rm{clr}}}} \cdot \left( {1 - f1} \right)$

(2)

${F_{0\_{\rm{cld}}}} = Di{r_{{\rm{cld}}}} + Di{f_{{\rm{cld}}}} \cdot f1 + Di{f_{{\rm{clr}}}} \cdot \left( {1 - f1} \right)$

(3)

式中，Dir_clr和Dir_cld分别为SBDART在晴空模式和全云模式下所输出的地表直射辐射项。散射太阳辐射包括云层的散射项和半球空间中未被云层覆盖的天空中其他大气分子的散射项，Dir_clr和Dir_cld分别是SBDART在晴空模式和全云模式下输出的地表散射辐射项，半球天空有效云覆盖度f1 HECF(Hemispherical Effective Cloud Fraction)是指研究像元所对应的整个半球空间范围内被云所覆盖的比例，1—f1即半球空间范围内的晴空比例。

计算地气之间多次散射项F_m(μ_i)需要将地表视为反射率为r_s的朗伯表面，并考虑到由于云层覆盖所造成的半球天空和地表的辐射情况的改变。

$\begin{aligned}{F_{\rm{m}}} = & \left[ {{F_{0\_{\rm{clr}}}}.\left( {1 - f2} \right) + {F_{0\_{\rm{cld}}}}.f2} \right]. \\ &\frac{{{r_{\rm{s}}}.\left[ {\left( {1 - f1} \right).{\rho _{\rm{a}}} + f1.{\rho _{\rm{c}}}} \right]}}{{1 - {r_{\rm{s}}}.\left[ {\left( {1 - f2} \right).{\rho _{\rm{a}}} + f2.{\rho _{\rm{c}}}} \right]}}\end{aligned}$

(4)

式中， ${F_{0\_{\rm{clr}}}}$ 和 ${F_{0\_{\rm{cld}}}}$ 分别是将地表反射率r_s设为0时，SBDART在晴空和全云模式下输入的地表直射和散射辐射之和，即总的地表下行辐射通量，也即 ${\mu _i}{E_0}\gamma \left( {{\mu _i}} \right)$ 项；ρ_a和ρ_c分别是晴空和有云大气的球面反照率；f2是区域真实云覆盖度RCF(Regional Cloud Fraction)，用以表征云垂直投影占地表的比例。所有的辐射项都是波长和太阳天顶角的函数，地表下行短波辐射是0.3—3.0 μm光谱范围内所有短波辐射的积分。

综上所述，对于地表下行短波辐射通量而言，首先需考虑太阳方向是否为云遮挡以计算无地表贡献时的地表下行辐射，再引入云覆盖度来描述包括观测方向在内的半球天空云覆盖情况以计算地气之间多次散射(f=0即观测和半球天空全晴空，f=1即观测和半球天空全云)，最后对两者进行加和。因此，分类情况可简化为两种：太阳方向未被云遮挡(图2(a))和被云遮挡(图2(b))，其中网状云代表可能存在的云。

图 2 地表下行短波辐射计算情况分类图

Fig. 2 Classification for the calculation of surface downward shortwave radiation

3.2 模型参数

SBDART模型的云参数包括云光学厚度、云顶和云底高度、云滴有效半径、液态水路径长度等。综合考虑运算量和现有卫星数据的产品类型，本研究选择了云层高度、云光学厚度和云滴有效半径对云的性质进行刻画。

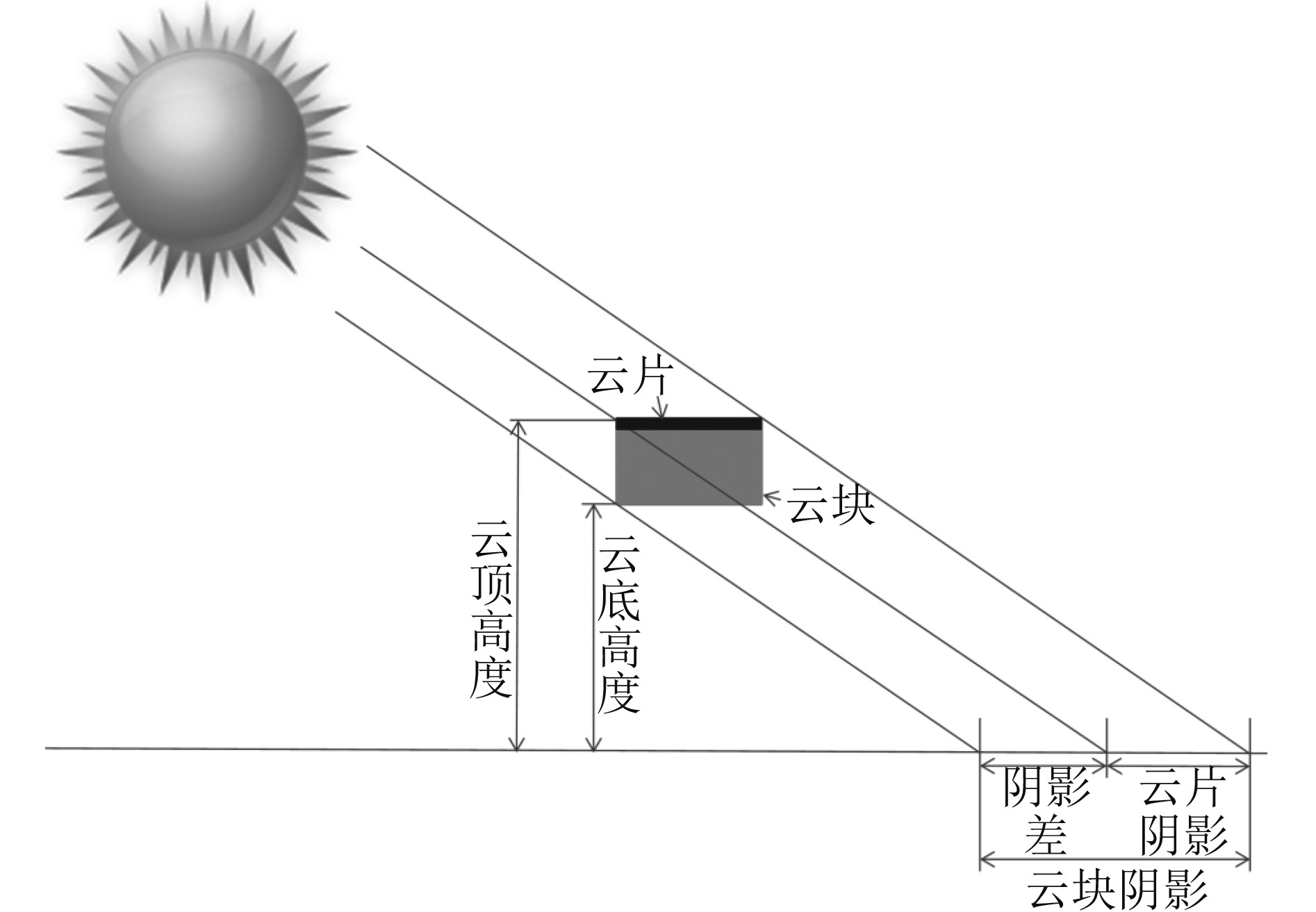
云层高度包括云顶高度和云底高度，按照云底高度通常可将云划分为低云族(2 km以下)、中云族(2—6 km)和高云族(6 km以上)3类(对于中纬度温带地区而言)。以往研究多以云顶高度来代替云的垂直高度，这是由于光学遥感无法探测云底信息。事实上云层是具有一定的物理厚度的，这样的物理厚度不仅仅会造成云光学厚度的变化，更会造成云对太阳直射光的物理遮挡，将云层考虑为没有厚度的薄片将会造成云层在地表投影范围的计算误差(如图3中阴影差项)，对于大太阳天顶角和厚云的情况，这种低估会更为显著。Suomi-NPP等新一代卫星数据能够提供更多的云层垂直方向上的信息，这为更深入地研究云层厚度对地表短波辐射的影响提供了契机，因此，有必要引入SBDART中的两个云高度参数对云层进行更为准确的表示。

图 3 云薄片和云块的阴影差异示意图

Fig. 3 The shadow difference between cloud slice and cloud solid

云光学厚度表征了光束在穿过某种介质的过程中被散射或吸收的情况，也即描述了介质的消光能力，其基本表达式为

$\tau = - \ln \frac{I}{{{I_0}}} = - \ln T$

(5)

式中，I₀为光源处的辐射强度，I为穿过介质后的辐射强度，T为介质的透过率，即当T接近0.01时，光学厚度约为5。

云滴的大小不一且空间分布不均匀，需要一个有效参数来描述其粒径分布情况。云滴有效半径就是用于表征一个区域内的云滴颗粒的加权平均半径的参数，可用于量化表达云层的微物理特性，其表达式为

$r = \frac{{{\rm{ }}\int_0^\infty {{r^3}n\left( r \right){\rm{d}}r} }}{{{\rm{ }}\int_0^\infty {{r^2}n\left( r \right){\rm{d}}r} }}$

(6)

式中，r代表颗粒半径，n(r)代表颗粒分布函数。云滴有效半径的数值与季节、纬度、人类活动等多种因素有关，而且冰云和水云的数值也存在着较大的差异，大粒径的云滴更容易形成降水。

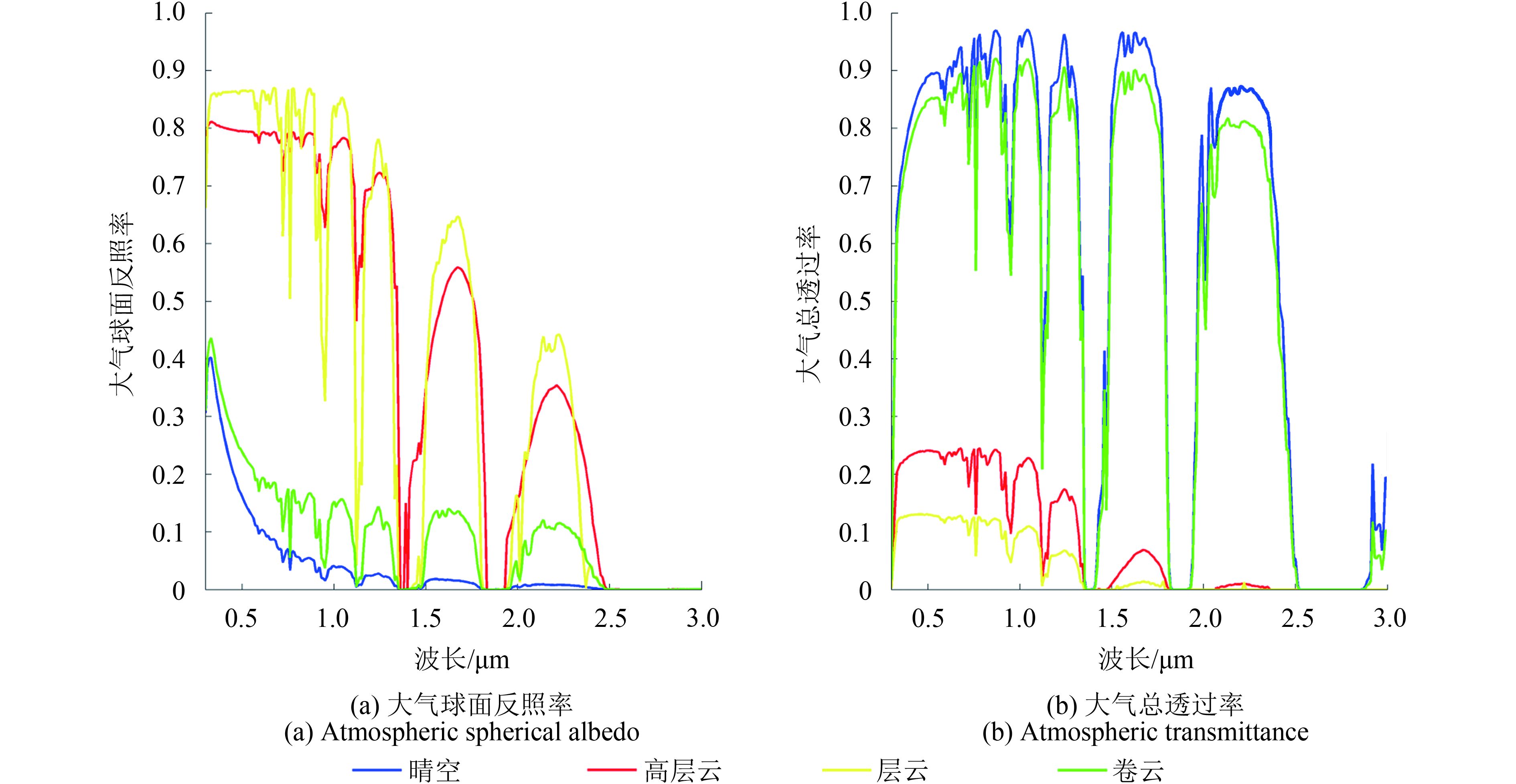
为进一步明确云参数的取值区间和缩小研究对象的范围，本研究以晴空、层云、高层云和卷云为对象，分别给出在相同的大气模拟条件下4种情况的大气球面反照率和透过率情况。模拟条件为垂直观测、太阳垂直照射、中纬度夏季大气温湿廓线、乡村型气溶胶，地表反照率为0.5，海拔高度为0 m。如图4所示，可以看出典型高云族的卷云的光学性质与晴空条件十分接近，这是由于卷云主要由冰晶组成，光学透过率较高。虽然层云和高层云的大气球面反照率和透过率在不同波段有所差异，但是都远远大于晴空和卷云的情况，这也反映了形态以水滴为主的中低云的光学消光作用。因此本文将研究的云类型限定为中低云族。

图 4 卷云、高层云、层云以及晴空的大气球面反照率与大气总透过率的比较

Fig. 4 Comparison between atmospheric spherical albedo and atmospheric transmission of different cloud conditions

4 敏感性分析

4.1 参数设置

目前，基于卫星遥感的地表短波辐射反演研究多采用混合模型法，其基础是拥有大量具有区域代表性的辐射传输模拟数据集。为了更高效地建立这样的模拟数据集，需要事先明确各个输入参数对模拟生成的辐射分量的贡献，根据它们各自的敏感度设置合理的变化步长，从而有效地缩短模拟所需的时间。

根据输入参数的变化方式，敏感性分析方法分为局部和全局两类。局部敏感性分析法通常需要一定的先验知识了解哪些参数更为重要，然后对关键参数进行分析，这种分析方法简单易用，但无法给出各个输入参数之间的贡献强弱关系。全局敏感性分析法的主要特点是能够一并给出各个输入参数占总体参数贡献的百分比，有助于理解和简化模型。近10年来，越来越多的学者使用全局定量的敏感性分析方法对模型进行分析，研究结果均显示全局敏感性分析方法具有较为明显的优势(Confalonieri，2010；Richter 等，2010；Drouet 等，2011；Confalonieri 等，2010)。

本研究采用SimLab软件进行敏感性分析，并使用内置的基于方差准确度较高的Sobol模型。结合短波辐射的影响因素和SBDART软件中的内置参数，共选择了13个参数进行敏感性分析的研究。

表 1 SBDART-CF中用于敏感性分析的参数
Table 1 Parameters for SBDART-CF sensitivity analysis

下载CSV

参数名称	含义	单位	阈值
SZA	太阳天顶角	(°)	40—90
UW	水汽柱含量	g/cm²	1.0—2.0
UO₃	臭氧柱含量	atm-cm	0.1—0.6
Albedo	地表反照率	—	0.1—0.95
VIS	水平能见距离	km	2—100
CO₂	CO₂含量	ppmv	360—390
COT	云光学厚度	—	0.1—5^a; 5—100^b
CBH	云底高度	km	0.1—2.5
CT	云物理厚度	km	0.5—4.0
NRE	云滴有效半径	micron	2—60
Alt	海拔高度	km	0—4
HECF	半球有效云覆盖度	—	0—1
RCF	区域云覆盖度	—	0—1
注：a对应光学厚云，b对应光学薄云。

4.2 结果与分析

SBDART-CF模型可以同时输出包括地表下行短波直射辐射、下行短波辐射(直射和散射)、地表短波净辐射3个短波辐射分量，下面将根据不同的模拟情况对它们分别进行敏感性分析。

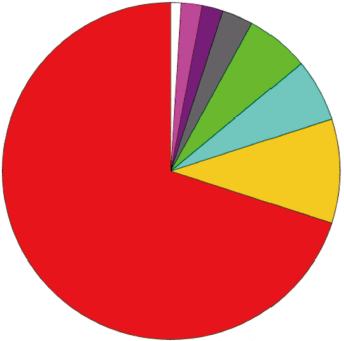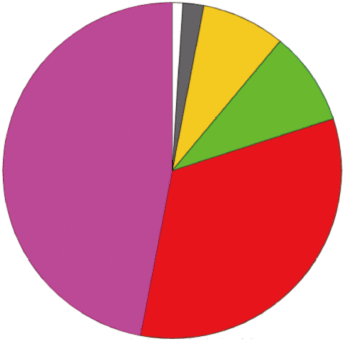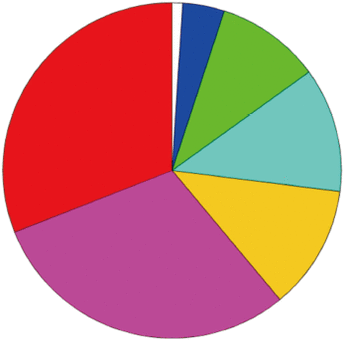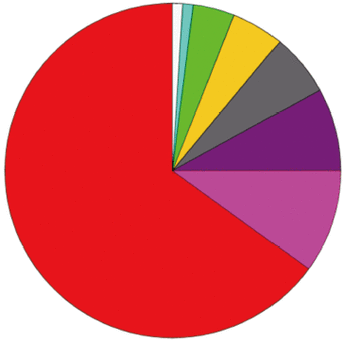
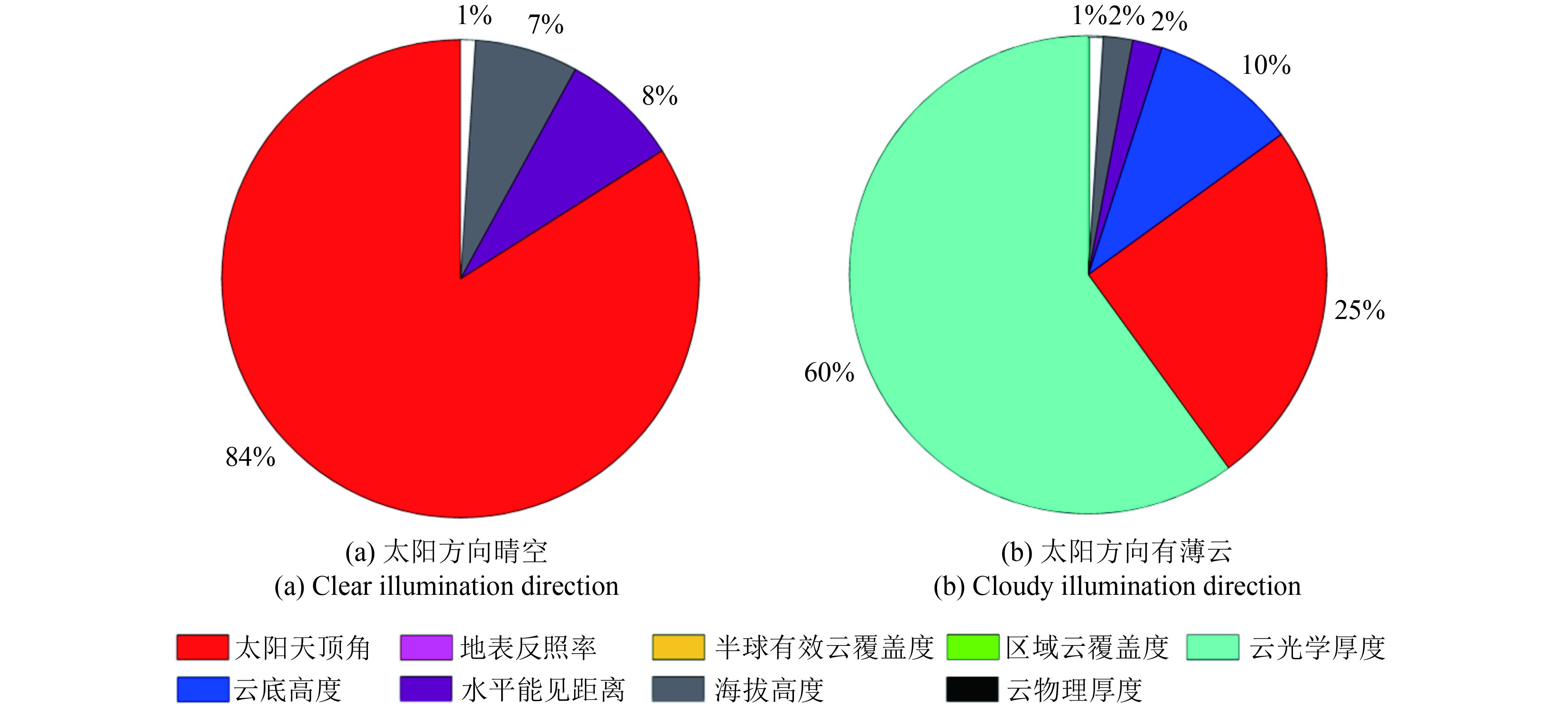
图5展示了地表下行短波直射辐射的敏感性分析结果，由图5(a)可知SZA、VIS和Alt等3个参数为主要敏感参数，其总敏感性指数加和接近100%，即其他10个参数在使用SBDART-CF模型计算太阳方向晴空条件下的地表直射辐射不敏感，均可以设为固定值。图5(b)表示的是太阳方向有薄云的情况，总敏感度高于1%的参数共有5个，分别是COT、SZA、CBH、VIS和Alt。云层光学厚度的总敏感度指数远远超过了其他因素，即在进行太阳方向有薄云情况下的地表直射辐射反演过程中，必须准确地输入云层的光学厚度信息。此外，由于光学厚云对于太阳辐射的散射和吸收作用剧烈，短波直射透过率接近于0，因此这里不对其进行计算和讨论。

图 5 太阳方向晴空或有薄云时地表直射辐射的归一化总敏感性指数

Fig. 5 Normalized total sensitivity index for direct solar flux with clear illumination direction and cloudy illumination direction obscured by optically thin clouds

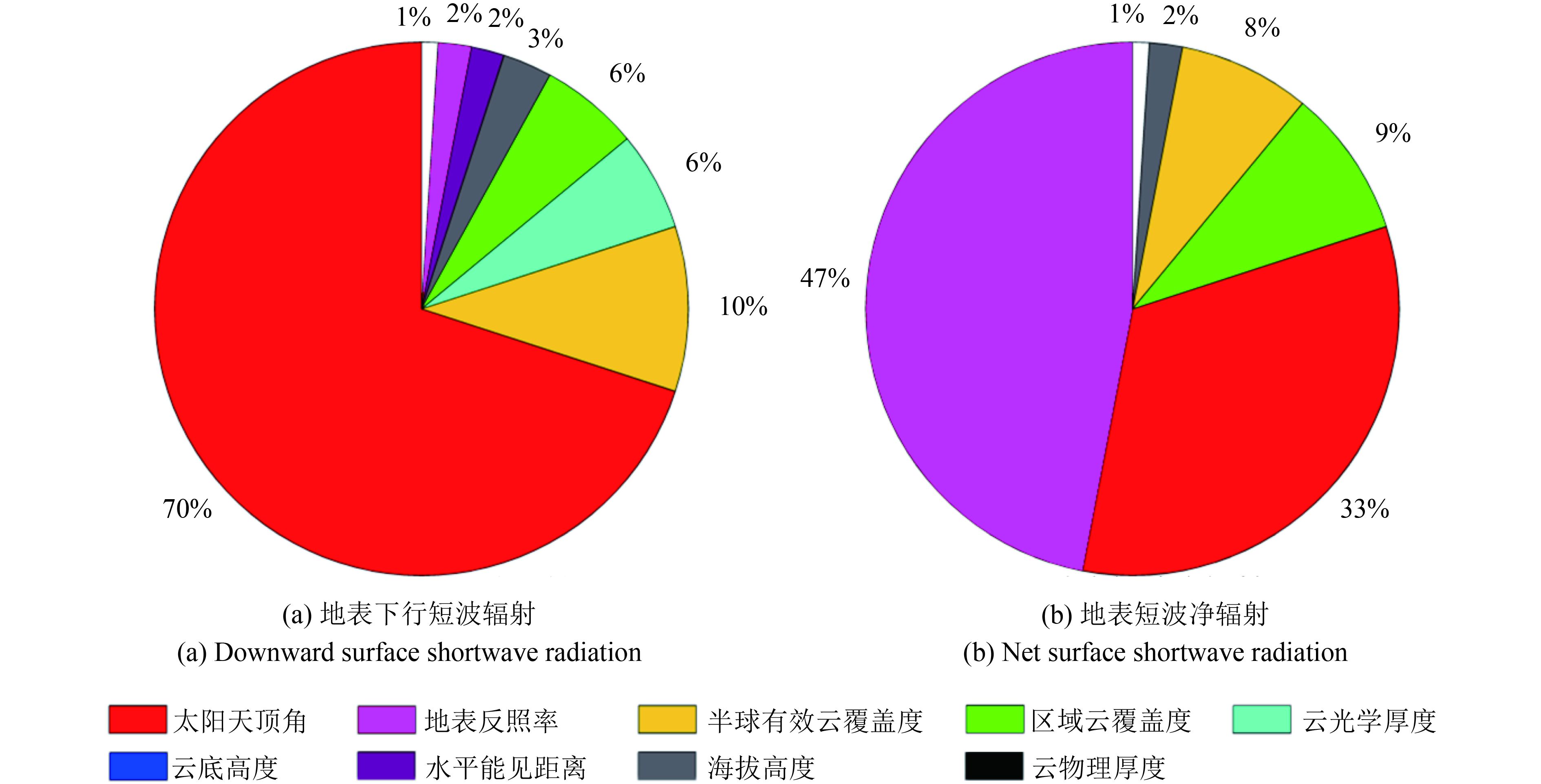
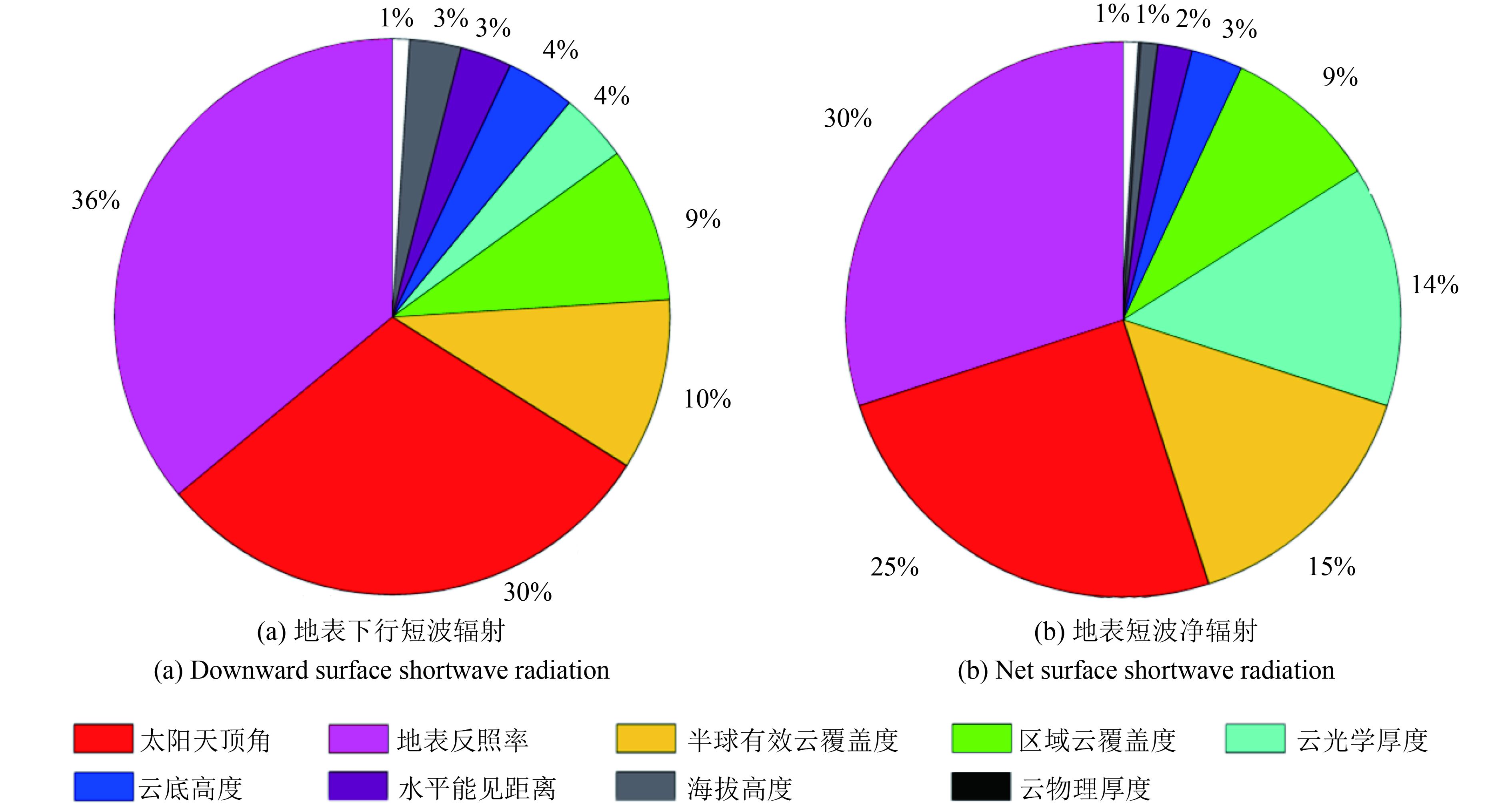
图6是太阳方向晴空、半球空间可能有薄云时的地表辐射参量的敏感性分析结果，图6(a)为地表下行短波辐射的结果，SZA是起决定因素的参数，总敏感度高达70%。此外，还有6个参数的总敏感度较高，排序依次是HECF、COT、RCF、Alt、VIS和Albedo。这是因为当太阳方向无云时，地表下行短波辐射主要组成部分为地表下行直射辐射，而直射辐射的主要影响因素为SZA(图5(a))，与地表类型无关。此外，地表下行短波辐射中的地表下行散射辐射由大气散射辐射和地气之间的多次散射有关，因此它与半球天空云层情况以及地表反照率有一定相关性。图5(b)为地表短波净辐射地表短波净辐射的结果，总敏感度占据前四位的为Albedo、SZA、HECF和RCF，此外还与Alt有关，表明地表短波辐射主要还是依赖于地表覆盖状况。

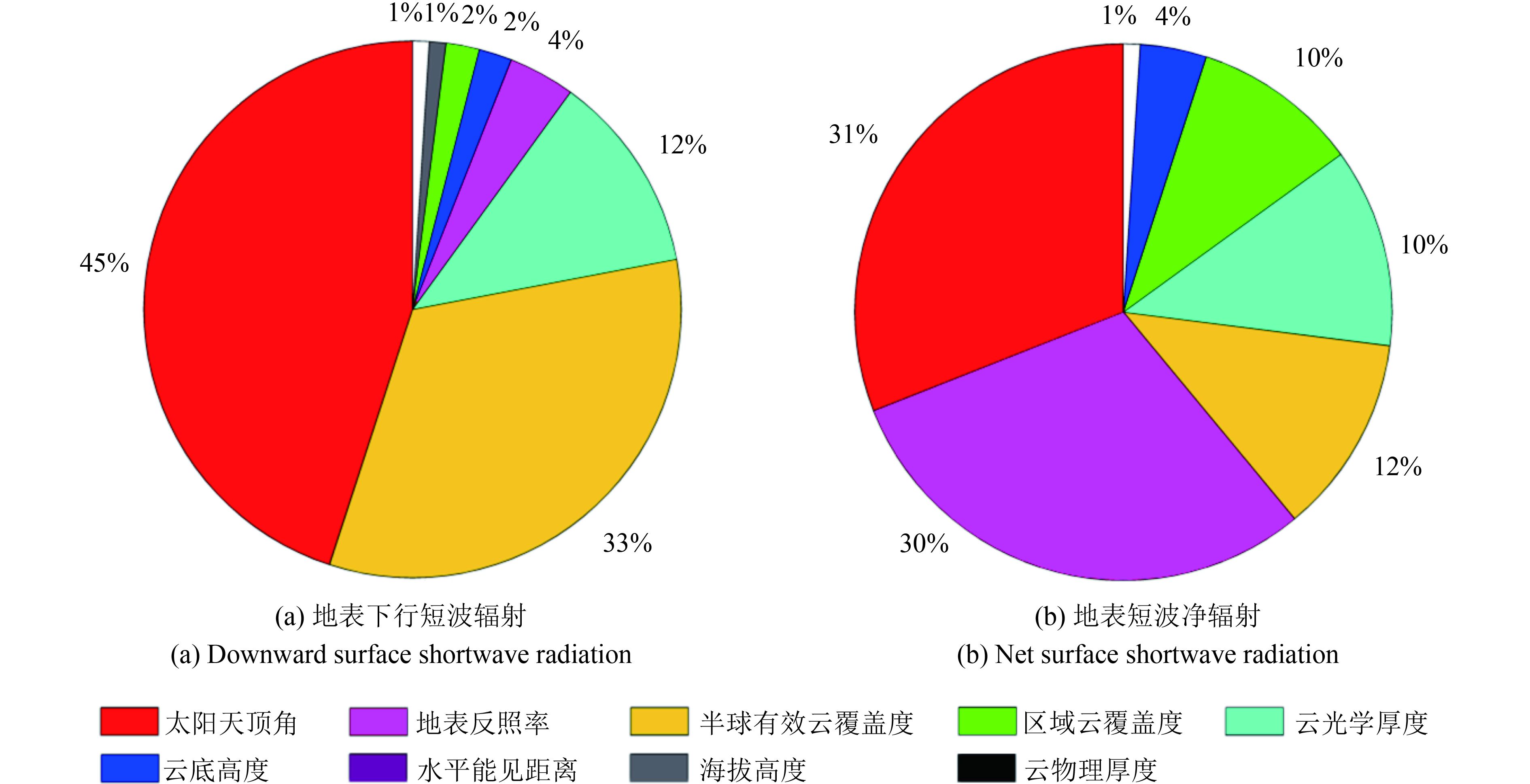
图 6 太阳方向晴空，半球空间可能有薄云的地表下行短波辐射和地表短波净辐射的归一化总敏感性指数

Fig. 6 Normalized total sensitivity index for DSSR and NSSR with clear illumination direction and optical thin clouds might exist in non-illumination hemisphere

太阳方向有薄云、半球空间可能晴空或有薄云情况下的地表短波下行辐射和短波净辐射的敏感性分析结果如图7所示。由图7(a)可知，当太阳方向被光学薄云遮挡时，由于云的消光作用造成下行直射光的减少，这与图5(b)一致。此外，半球空间的薄云还会造成到达地表的散射辐射量的变化，与地表反照率共同控制着地气之间多次散射造成的辐射量的变化。图7(b)是地表短波净辐射的情况，SZA、Albedo、HECF、COT、RCF和CBH为总敏感度较强的参数，与太阳方向晴空条件所不同的是，云顶高度的影响作用突出，这与太阳方向存在薄云情况下的直射光的受影响因素相对应。

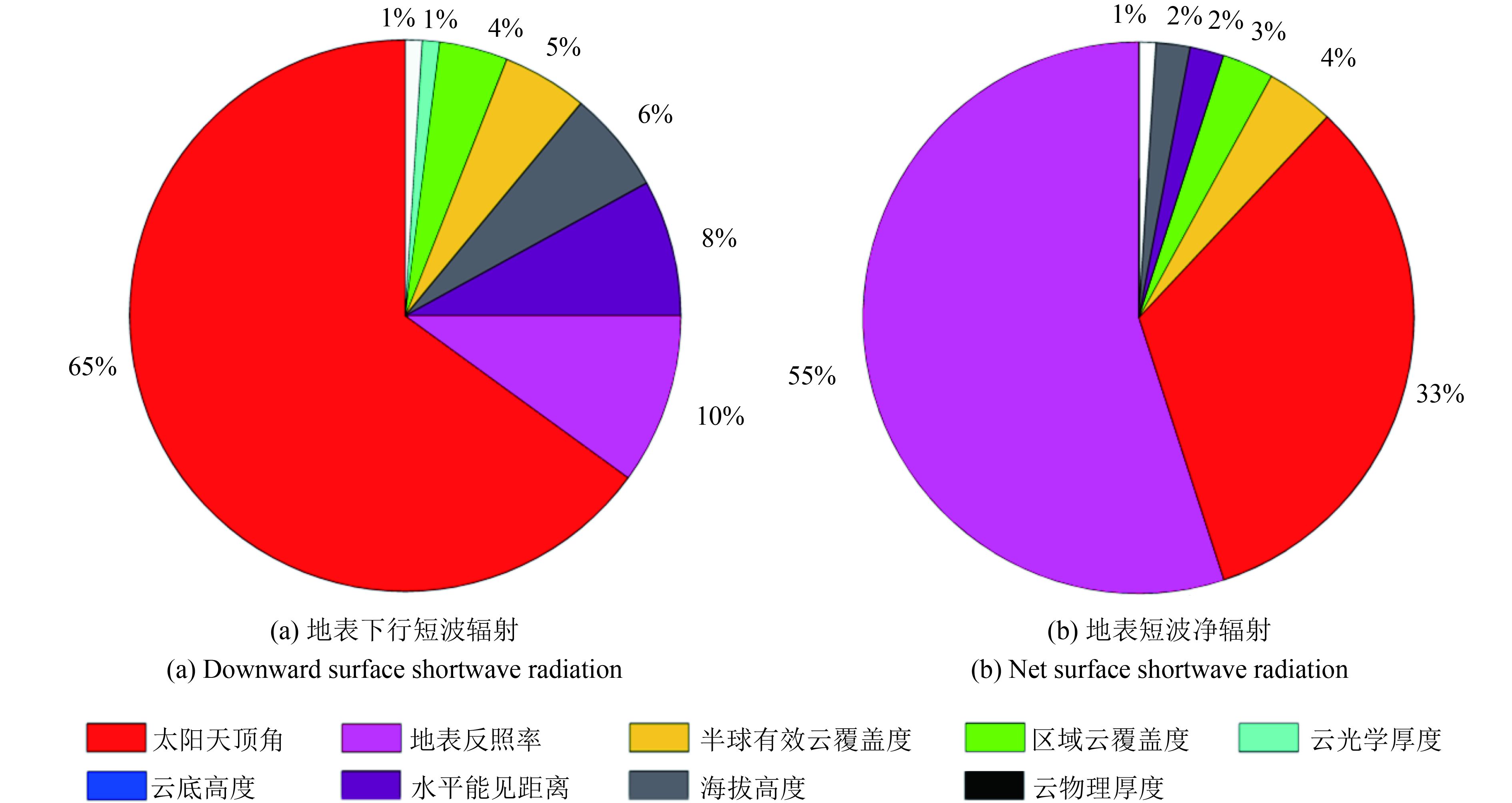
图 7 太阳方向有薄云的地表下行短波辐射和地表短波净辐射的归一化总敏感性指数

Fig. 7 Normalized total sensitivity index for DSSR and NSSR with cloudy illumination direction obscured by optically thin clouds

图8为太阳方向晴空、半球天空可能无云或有厚云情况下的地表下行短波辐射和短波净辐射的敏感性分析结果。由图8(a)可以看出，当半球天空有厚云时，由于地气之间多次散射的存在，整个下行短波辐射对地表反照率的依赖性有所增加，达到10%，比半球天空是薄云的情况的总敏感度高2%。此外，多次散射项还与RCF和云光学厚度(此处COT范围为10—50)呈现出一定的相关性。图8(b)的地表短波净辐射与太阳方向晴空、半球空间可能有薄云情况的敏感性分析结果十分相似，主要影响因素是SZA、Albedo、HECF和RCF，这表明在太阳方向晴空条件下，云层的影响因素与云层物理性质相关性较小。

图 8 太阳方向晴空，半球空间可能有厚云的地表下行短波辐射和地表短波净辐射的归一化总敏感性指数

Fig. 8 Normalized total sensitivity index for DSSR and NSSR with clear illumination direction and optical thick clouds might exist in non-illumination hemisphere

太阳方向为厚云所遮挡、半球天空可能无云或有厚云情况下的地表下行短波辐射和地表短波净辐射敏感性分析结果如图9所示。当太阳方向有厚云时，地表无法接收到太阳直射光，整个下行短波辐射由散射辐射组成，对比图7太阳方向薄云的情况，可以看出地表反照率的总敏感度由4%上升至30%，这是由于散射辐射在很大程度上取决于地表的反射情况，反照率越高，地气间的多次散射次数越多，被地表所能吸收到的辐射量也相应增加。如前文所述，大气散射辐射与HECF有关，地气间多次散射与RCF和COT相关，因此，这种情况下3者的总敏感度都较高。图9(a)地表短波净辐射的情况与图7的地表短波净辐射有一定的相似性，主要影响因素仍然是Albedo、SZA、HECF、RCF以及CBH，其总敏感度之和高达95%。

图 9 太阳方向有厚云的地表下行短波辐射和地表短波净辐射的归一化总敏感性指数

Fig. 9 Normalized total sensitivity index for DSSR and NSSR with cloudy illumination direction obscured by optically thick clouds

5 结　论

云层对地气系统辐射能量平衡有重要的调节作用，然而传统的1维大气辐射传输模型建立在平面平行大气假设上，只能考虑晴空和全云两种极端情况，但真实条件下半球天空部分云的情况占据绝大多数。鉴于此，本文在1维大气辐射传输模型SBDART的基础上，引入了两个云覆盖度并考虑太阳方向和半球天空云层覆盖状况，建立了改进的短波辐射传输模型SBDART-CF。

为了更好地理解模型各个参数之间的相互关系和对模型输出参数(地表直射辐射、短波下行辐射、短波上行辐射和短波净辐射等短波辐射各分量)的影响，利用SimLab对模型进行了不同情况下的敏感性分析，结果表明：13个模型参数中的UW、UO₃和CO₂等3个参数对于上述所有情况下的各个地表短波辐射分量的影响作用都微乎其微。对下行短波辐射和地表短波净辐射而言，SZA和Albedo都起着较为重要的作用，因此需要采用小步长最大程度的描述这两个因子的变化对地表各辐射分量的影响。在实际应用中，这两个参数都可以较容易获取，其中SZA可通过目标地点的经纬度、时间等进行计算，而Albedo可以采用卫星遥感反演产品得到。另外两个重要的参数是VIS和Alt，VIS可以通过气溶胶光学厚度的方式获取，Alt则可以更为方便的从地表数字高程模型得到。

HECF和RCF两个云覆盖度参数也在很大程度上影响下行短波辐射和地表短波净辐射，而且两者的总敏感度都较高，因此需要准确的获取。在基于遥感数据的短波辐射估算过程中，需要引入云顶和云底高度，以求得到更高精度的云覆盖度。对于大太阳天顶角情况下，云底高度CBH的影响作用显著，传统的光学遥感无法穿透云层，仅能得到云顶高度，而如Suomi-NPP云产品之类的新一代卫星数据产品能够提供云底高度，可以为地表短波辐射参量的准确估算提供良好的数据保障。

以上的敏感性分析结果是基于SimLab的Monte Carlo模型进行参数的随机组合，参数阈值、分布方式、步长、组合的方法和模拟次数等因素均会在一定程度上影响敏感性分析的结果。因此，本研究的敏感性分析结果不具有普适性，仅能说明在上述一系列设置条件下的分析结果。如需将其用于其他地区，还需依照类似的方法进行合理的设置和模拟分析。此外，需要说明的是本文的核心在于物理模型的创建及其参数的敏感性分析，物理模型的合理性确实应该进行验证，但由于单点物理模型对于实地测量数据本身的要求非常高，如采样频率、参数完备性等，而且也是相对验证，因为数据测量时刻的大气参数无法全部获取，只能通过设定基准值来实现，通常验证结果的好坏会较强的依赖于基准值的设定，从而不能很好的反映模型本身的性质。因此，可以采用混合模型法对于短波辐射传输模型进行验证，即结合改进的短波辐射传输模型和经验统计(如人工神经网络等)的方法，结合遥感数据产品进行相关分量的估算，之后再利用所选取的研究区域的地面实测辐射数据进行验证，这样的验证结果能够更好地反映模型的适用性和合理性。

志谢感谢北京师范大学地理学与遥感科学学院穆西晗老师、谢东辉老师为本文模型构建和完善所提出的意见和建议！

参考文献(References)

Achad M, López M L, Palancar G G and Toselli B M. 2013. Retrieving the relative contribution of aerosol types from single particle analysis and radiation measurements and calculations: a comparison of two independent approaches. Journal of Aerosol Science, 64 : 11–23. [DOI: 10.1016/j.jaerosci.2013.05.008]

Chen L, Yan G J, Wang T X, Ren H Z, Calbó J, Zhao J and McKenzie R. 2012. Estimation of surface shortwave radiation components under all sky conditions: modeling and sensitivity analysis. Remote Sensing of Environment, 123 : 457–469. [DOI: 10.1016/j.rse.2012.04.006]

Confalonieri R, Bellocchi G, Tarantola S, Acutis M, Donatelli M and Genovese G. 2010. Sensitivity analysis of the rice model WARM in Europe: exploring the effects of different locations, climates and methods of analysis on model sensitivity to crop parameters. Environmental Modeling and Software, 25 (4): 479–488. [DOI: 10.1016/j.envsoft.2009.10.005]

Confalonieri R. 2010. Monte Carlo based sensitivity analysis of two crop simulators and considerations on model balance. European Journal of Agronomy, 33 (2): 89–93. [DOI: 10.1016/j.eja.2010.03.004]

Dahlback A and Stamnes K. 1991. A new spherical model for computing the radiation field available for photolysis and heating at twilight. Planetary and Space Science, 39 (5): 671–683. [DOI: 10.1016/0032-0633(91)90061-E]

Drouet J L, Capian N, Fiorelli J L, Blanfort V, Capitaine M, Duretz S, Gabrielle B, Martin R, Lardy R, Cellier P and Soussana J F. 2011. Sensitivity analysis for models of greenhouse gas emissions at farm level. Case study of N₂O emissions simulated by the CERES-EGC model. Environmental Pollution , 159 (11): 3156–3161. [DOI: 10.1016/j.envpol.2011.01.019]

Harrison E F, Minnis P, Barkstrom B R, Ramanathan V, Cess R D and Gibson G G. 1990. Seasonal variation of cloud radiative forcing derived from the Earth radiation budget experiment. Journal of Geophysical Research: Atmospheres, 95 (D11): 18687–18703. [DOI: 10.1029/JD095iD11p18687]

Kneizys F X, Shettle E P, Abreu L W, Chetwynd J H and Anderson G P. 1988. User guide to LOWTRAN7. Hanscom, MA: Air Force Geophysics Laboratory: 1–4

Lam C C, Leung P T and Young K. 1992. Explicit asymptotic formulas for the positions, widths, and strengths of resonances in Mie scattering. Journal of the Optical Society of America B, 9 (9): 1585–1592. [DOI: 10.1364/JOSAB.9.001585]

Liang S L. 2005. Quantitative Remote Sensing of Land Surfaces. New York: John Wiley and Sons: 140

O’Hirok W and Gautier C. 1998. A three-dimensional radiative transfer model to investigate the solar radiation within a cloudy atmosphere. Part II: spectral effects. Journal of the Atmospheric Sciences, 55 (19): 3065–3076. [DOI: 10.1175/1520-0469(1998)055<3065:ATDRTM>2.0.CO;2]

Oreopoulos L and Cahalan R F. 2005. Cloud inhomogeneity from MODIS. Journal of Climate, 18 (23): 5110–5124. [DOI: 10.1175/JCLI3591.1]

Pinker R T, Liu H, Osborne S R and Akoshile C. 2010. Radiative effects of aerosols in sub-Sahel Africa: dust and biomass burning. Journal of Geophysical Research: Atmospheres, 115 (D15): D15205 [DOI: 10.1029/2009JD013335]

Pinker R T, Ttarpley J D, Laszlo I, Mitchell K E, Houser P R, Wood E F, Schaake J C, Robock A, Lohmann D, Cosgrove B A, Sheffield J, Duan Q Y, Luo L F and Higgins R W. 2003. Surface radiation budgets in support of the GEWEX Continental-Scale International Project (GCIP) and the GEWEX Americas Prediction Project (GAPP), including the North American Land Data Assimilation System (NLDAS) project. Journal of Geophysical Research: Atmospheres, 108 (D22): 8844 [DOI: 10.1029/2002JD003301]

Ricchiazzi P, Yang S, Gautier C and Sowle D. 1998. SBDART: a research and teaching software tool for plane-parallel radiative transfer in the earth’s atmosphere. Bulletin of the American Meteorological Society, 79 (10): 2101–2114. [DOI: 10.1175/1520-0477(1998)079<2101:SARATS>2.0.CO;2]

Richter G M, Acutis M, Trevisiol P, Latiri K and Confalonieri R. 2010. Sensitivity analysis for a complex crop model applied to Durum wheat in the Mediterranean. European Journal of Agronomy, 32 (2): 127–136. [DOI: 10.1016/j.eja.2009.09.002]

Stamnes K, Tsay S C, Wiscombe W and Jayaweera K. 1988. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Applied Optics, 27 (12): 2502–2509. [DOI: 10.1364/AO.27.002502]

Stevens B and Bony S. 2013. Climate change. What are climate models missing. Science, 340 (6136): 1053–1054. [DOI: 10.1126/science.1237554]

Stull R B. 1988. An Introduction to Boundary Layer Meteorology. Netherlands: Springer: 545–558

Viúdez-Mora A. 2011. Atmospheric Downwelling Longwave Radiation at the Surface During Cloudless and Overcast Conditions. Measurements and Modeling. Catalonia: Universitat de Girona: 10–15

Zhang Y, Rossow W B, Lacis A A, Oinas V and Mishchenko M. 2004. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. Journal of Geophysics Research, 109 (19): 2156–2202.

摘要

关键词