出版日期: 2017-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20176405
2017 | Volumn21 | Number 6
上一篇 | 下一篇

3维成像微波高度计风速反演

鲍青柳^1,2 , 林明森¹ , 张有广¹ , 贾永君¹ , 郎姝燕¹

1. 国家卫星海洋应用中心国家海洋局空间海洋遥感与应用研究重点实验室，北京 100081

2. 清华大学地球科学中心，北京 100084

收稿日期: 2016-11-03; 优先数字出版日期: 2017-11-01

基金项目: 国家青年科学基金(编号：41406207，41606202)；国家海洋局空间海洋遥感与应用研究重点实验室开放基金(编号：201601001)

第一作者简介: 鲍青柳(1986—　)，男，博士后，研究方向为海洋遥感、遥感数据处理等。E-mail：baoqingliu2000@163.com

中图分类号: TP79

文献标识码: A

摘要

随着航天技术的发展和新型微波载荷的发射(如3维成像高度计)，越来越多的小入射角海洋观测雷达将投入运行，如何有效地利用这些小入射角的后向散射数据成为研究的热点课题。利用TRMM (Tropical Rainfall Measuring Mission)的PR (Precipitation Radar)后向散射系数NRCS (Normalized Radar Cross Section)数据对小入射角情况下的海面风速反演方法和风速反演精度进行研究，并对风速反演性能进行统计分析。基于无雨条件下的PR海面后向散射数据，建立小入射角情况下的风速反演算法和经验的GMF模型。风速反演结果分别与浮标、ASCAT进行交叉比对。结果表明：反演风速的偏差小于0.28 m/s，标准差小于1.51 m/s；在中等风速条件下，反演风速的偏差和标准差均小于低风速条件和高风速条件；0°—8°入射角范围内的风速反演精度明显优于8°—12°入射角范围的风速反演精度。

关键词

TRMM PR, 风速反演, 小入射角, 反演精度

Wind speed inversion for imaging microwave altimeter

BAO Qingliu^1,2 , LIN Mingsen¹ , ZHANG Youguang¹ , JIA Yongjun¹ , LANG Shuyan¹

1.Key Laboratory of Space Ocean Remote Sensing and Application, National Satellite Ocean Application Service, Beijing 100081, China

2.Center for Earth System Science, Tsinghua University, Beijing 100084, China

Abstract

As the development of space technology and the launch of new type microwave payloads, such as imaging microwave altimeter, more and more radars that observe the ocean at low incident will be in orbit, such as the Precipitation Radar (PR) (incident angle: 0°—18°) on Tropical Rainfall Measuring Mission (TRMM) satellite, the Imaging ALTimeter (IALT) (incident angle: 1°—7°) on the TG-2 space station which is lunched on September 15, 2016, and the Surface Ware Investigation and Monitoring (SWIM) (incident angle: 0°—10°) on China France Oceanography Satellite which is scheduled to launch in 2018. How to make use of the Normalized Radar Cross Section (NRCS) at low incident angle effectively is a very hot topic. Can the NRCS at low incident angle be used for wind speed inversion? This is also the motivation of our research. This paper uses the PR data on TRMM to research the sea surface wind speed inversion method and analyze the inversion accuracy. In this paper, the empirical Geophysical Model Function (GMF) model is established by crossing the PRNRCS with the QuikScat wind speed, and the GMF Table is given out in section 2. The Maximum Likelihood Estimation (MLE) method is used for PR wind speed inversion, and the objective function of MLE is provided in section 3. At last, the retrieved wind speeds are compared with the buoy and advanced scatterometer (ASCAT) wind speed. The performance of MLE method and the wind speed inversion accuracy are analyzed. By the performance analysis, we find that the bias and standard deviation of retrieved wind speed is smaller than 0.28 m/s and 1.51 m/s respectively. Moreover, the wind speed retrieval performances versus wind speed and incident angle are analyzed. The wind speed retrieval performance at medium wind speed is better than that at low and high wind speed. The inversion accuracy with 0°—8° incident angles is better than that with 8°—12° incident angles. From the results of this paper we can concluded that the NRCS at low incident angle can be used for wind speed retrieval. And the wind speed retrieval accuracy is even higher than that of scatterometer (typically 2 m/s). Thus, for the radars that operate near nadir, such as the IALT and the SWIM on China France Oceanography Satellite, we can offer the product of wind speed.

Key words

TRMM PR, wind speed inversion, low incident angle, inversion accuracy

1 引　言

海面风场、浪高、海流、温度是海洋动力学中的几个重要参数。海洋动力学参数的准确获取对于海洋环境监测、海洋权益维护、海洋灾害的预警预报具有重要意义，尤其是海洋动力参数的同步获取对于全面分析和掌握海况条件及海洋动态至关重要。卫星遥感是获得全球海洋动力环境参数的最有效手段，其中微波遥感可以进行全天时和全天候的持续观测。目前有多种在轨运行的微波遥感载荷，包括雷达高度计、微波散射计、微波辐射计等。不同的有效载荷主要针对不同的海洋动力学参数，其中雷达高度计是应用范围最广的有效载荷之一，可以进行高精度的距离测量。

3维成像微波高度计(IALT)是新一代雷达高度计系统，在传统高度计的基础上，结合偏离天底点观测技术、高度计跟踪测量技术、合成孔径技术和干涉测量技术发展起来的新型雷达高度计(张云华等，1999；Zhang 等，2007)。3维成像微波高度计已于2016年9月15日随天宫二号空间实验室发射升空，目前处于在轨测试阶段，具有刈幅宽度宽、空间分辨率高等特点。

20世纪90年代，国际上一些学者就对海面的准镜面散射特性进行了研究和建模(Brown，1990；Apel，1994)。俄勒冈州立大学的Freilich等人(2003)利用1999年8月到2000年7月内的TRMM(Tropical Rainfall Measuring Mission) PR(Precipitation Radar)后向散射系数NRCS (Normalized Radar Cross Section)数据以及TRMM TMI的风速产品，对海面风速、表面粗糙度与小入射角下雷达后向散射系数之间的关系进行研究，建立了入射角范围为0°—18°的后向散射系数经验模型，并通过最小二乘拟合的方法得到有效天底点反射系数及有效均方斜率。2004年JPL(Jet Propulsion Laboratory)的Li等人(2004)给出了一种基于最大似然估计(MLE)的区域风速反演算法，并将TRMM PR的风速反演结果与TMI、QuikSCAT以及浮标测量的风速进行对比，反演结果具有较好的一致性。该方法借鉴单视SAR的高分辨率风速反演算法，有效地缓解了小入射角情况下海面后向散射系数对风速不敏感的问题。

热带降雨观测任务(TRMM)主要目的是测量热带降雨及其变化。轨道高度350 km，轨道倾角35°。搭载的降雨雷达(PR)为主动微波遥感器，工作频率为13.8 GHz。PR采用近天底观测，入射角范围为0°—17°，入射角分辨率为0.75°，观测刈幅220 km (Kuroiwa 等，1996)。3维成像微波高度计同样采用近天底点观测，工作频率同样为13.8 GHz，入射角范围约为2°—8°，观测体制与TRMM PR基本一致。本文基于TRMM PR的小入射角海面后向散射系数数据，开展了3维成像高度计的海面风速反演技术研究，建立小入射角情况下的海面风速反演算法，对风速反演精度进行交叉比对，并对不同入射角和不同风速情况下的反演性能进行了统计分析。

2 小入射角GMF模型

2.1 理论模型

对于小入射角观测的雷达系统，海面后向散射以准镜面反射为主。后向散射系数的大小与垂直入射方向的小面元的概率密度成正比。如果 ${p_{\rm{s}}}({\xi _x},{\xi _y})$ 表示两个正交水平方向海面斜率的联合概率密度分布，那么 ${p_{\rm{s}}}( - \tan \theta ,0)$ 对应垂直于雷达视向的小面元概率。小入射角情况下的海面归一化后向散射系数可表示为(Freilich和Vanhoff，2003)

${\sigma _0}(\theta ) = {\text{π}}{\left| {R(0)} \right|^2}{\sec ^4}\theta {p_{\rm{s}}}( - {\rm{tan}}\theta ,0)$

(1)

式中，θ为本地入射角， ${\left| {R(0)} \right|^2}$ 为有效的天底点反射系数(菲涅尔系数)。一般认为，当本地入射角小于15°时，式(1)表示的海面后向散射系数是准确的(Barrick，1974；Valenzuela，1978)。

当海面斜率满足高度分布和各向同性的假设时，式(1)可表示为

${\sigma _0}(u,\theta ) = \frac{{{{\left| {R(0)} \right|}^2}}}{{s(u)}}{\sec ^4}\theta \exp \left[ { - \frac{{{{\tan }^2}\theta }}{{s(u)}}} \right]$

(2)

式中，s(u)为有效的均方斜率。尽管海面斜率满足各向同性和高斯分布的假设并不十分准确，但是研究表明，在小入射角情况下各向异性和非高斯分布的影响可以忽略(Wentz 等，1984；Jackson 等，1992)。

Cox和Munk(1954)利用经典的光学散射数据得到了海面均方斜率与海面风速的线性关系。随后，Wu等人(1972，1990)对Cox和Munk(1954)的结果进行再分析，认为海面均方斜率和海面风速可近似为对数关系。Freilich等人(2003)通过对TRMM PR数据的分析认为：海面均方斜率和海面风速的对数模型比线性模型在高风速和低风速情况下更接近于测量结果。海面均方斜率和海面风速的对数模型可表示为

$s(u) = {\textit{W}_0} + {\textit{W}_1}\lg u$

(3)

式中，W₀和W₁为经验确定的常数。通过对PR数据的拟合，W₀和W₁可分段表示为

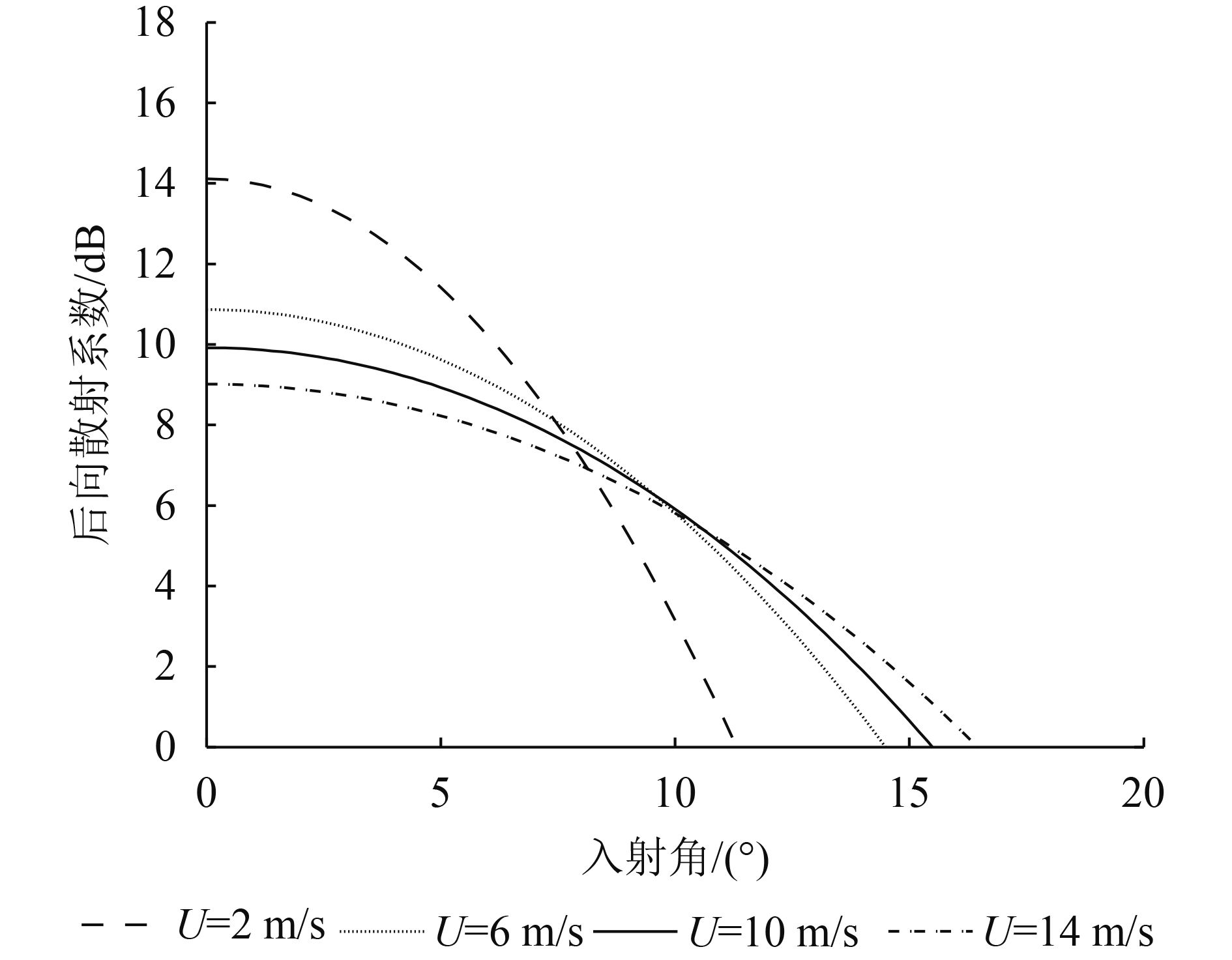
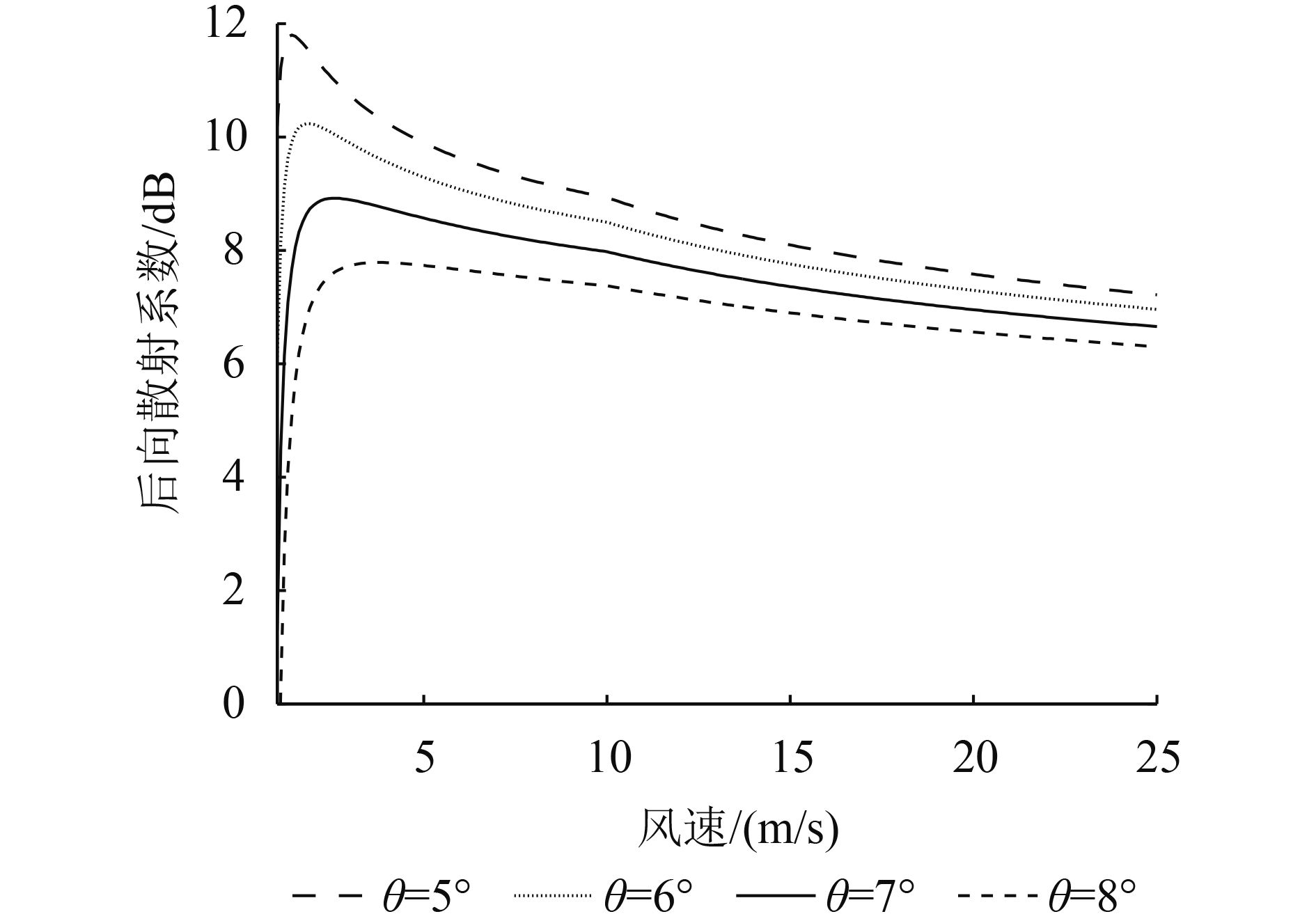
{\begin{cases} \begin{matrix} W_{0} = 0.0036 \\ W_{1} = 0.028 \end{matrix} 1 \leq u \leq 10 m / s （ 4 ） \\ \begin{matrix} W_{0} = - 0.0184 \\ W_{1} = 0.05 \end{matrix} u > 10 m / s ​ （ 5 ） \end{cases}

式(2)和式(3)确定了小入射角海面后向散射系数的半经验模型。图1为不同风速(U)条件下，后向散射系数随入射角的变化。图2为不同入射角(θ)情况下，后向散射系数随风速的变化。

图 1 不同风速条件下后向散射系数随入射角的变化

Fig. 1 The NRCS versus incident angle under different wind speed

图 2 不同入射角条件下后向散射系数随风速的变化

Fig. 2 The NRCS versus wind speed under different incident angles

2.2 经验模型

基于最大似然估计的海面风速反演需要GMF模型作为输入，其中GMF模型的准确度直接决定海面风速的反演精度(详见第3节)。由Freilich和Vanhoff (2003)的研究结果可以看出，在入射角大于15°时，理论的准镜面散射模型明显低于实测结果。为了实现高精度的海面风速反演，首先需要建立准确的经验GMF模型。

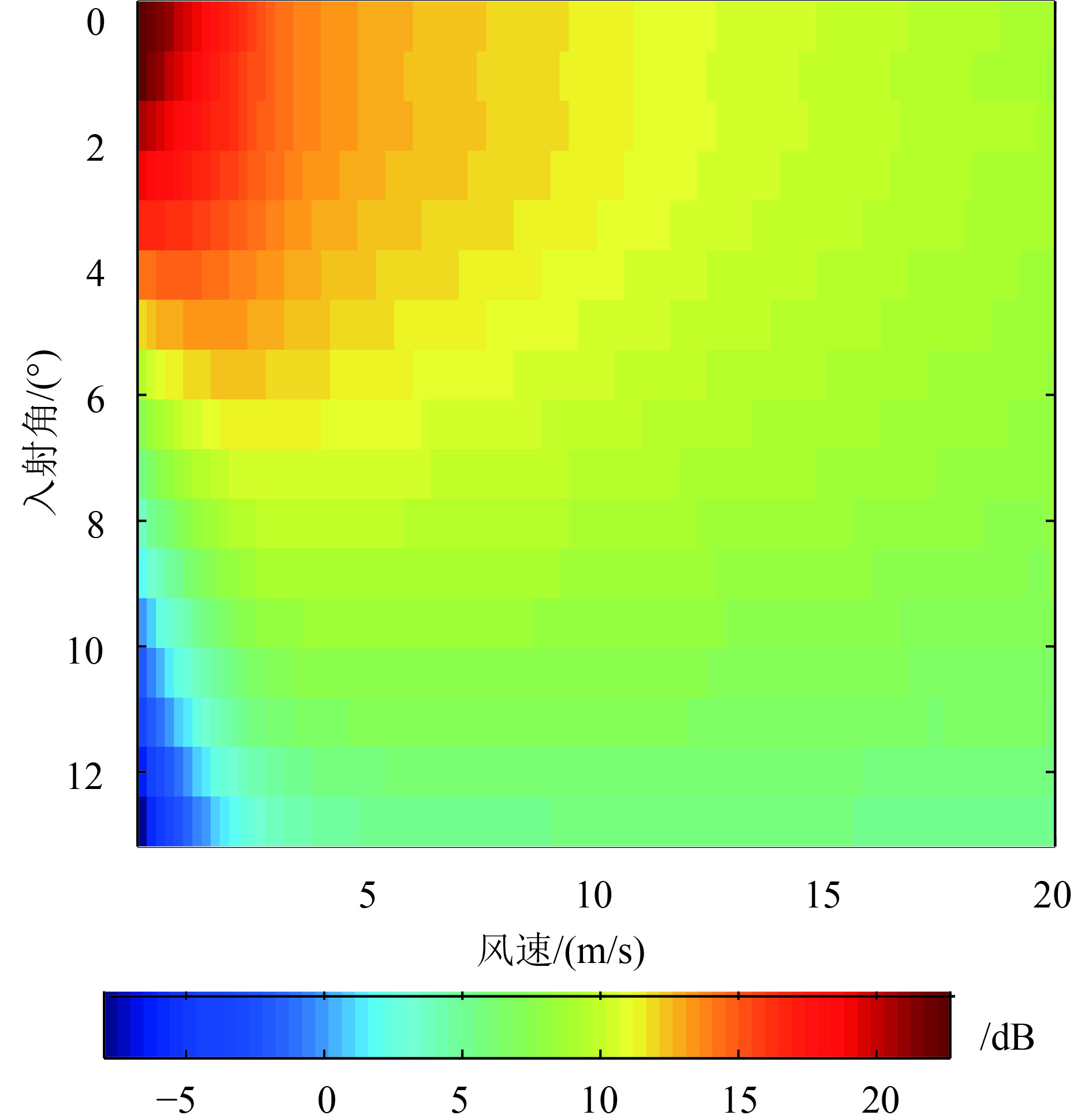
经验GMF模型的建立可以通过将TRMM PR后向散射系数与参考风速进行匹配来实现，其中参考风速可以为ECMWF/NCEP再分析风速、散射计风速或者浮标风速等。本文选择QuikScat数据作为风速参考并与PR数据进行交叉，时间窗口和空间窗口分别选择为±10 min和25 km×25 km。通过对匹配数据统计分析，建立后向散射系数与入射角和风速之间的对应关系。交叉点的风速分布曲线和2维经验GMF模型分别如图3和图4所示。

由图3可以看出，交叉点的风速主要分布在中等风速(7 m/s左右)附近，高风速和低风速的数据点相对较少。风速小于2 m/s和大于12 m/s的数据点不足15%，风速在4—10 m/s范围内的数据点大于70%。图4给出了入射角小于12°，风速小于20 m/s的经验GMF模型查找表，单位为dB。其中，入射角间隔为0.8°，风速间隔为0.2 m/s。

图 3 交叉点的风速分布

Fig. 3 Wind speed distribution of crossover point

图 4 2维经验GMF模型

Fig. 4 Two dimensional empirical GMF model

3 海面风速反演算法

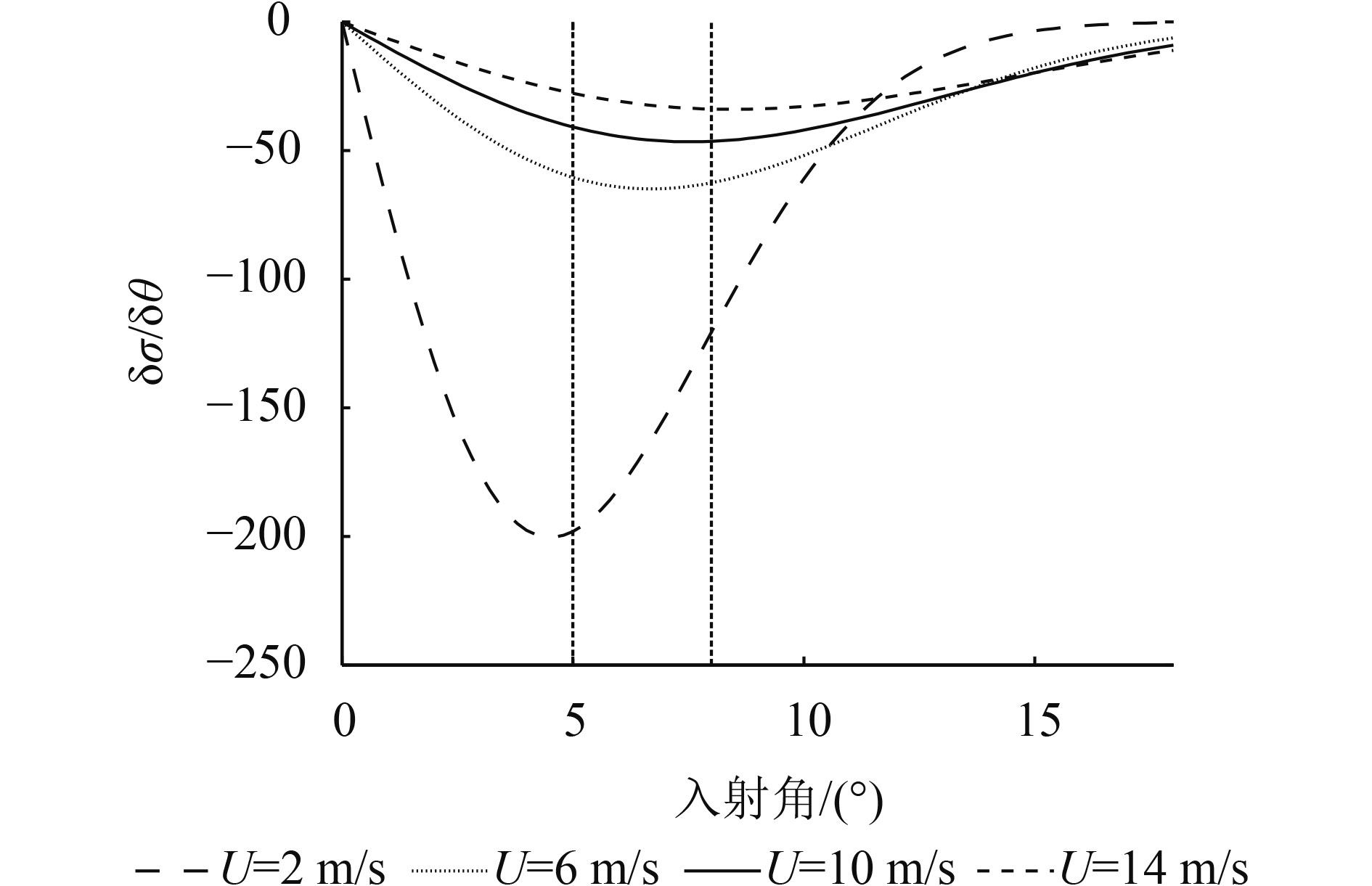
在近天底方向，后向散射以准镜面反射为主，后向散射系数随着风速的增加而降低。在中等入射角情况下，Bragg散射起主要作用，后向散射系数随风速的增加而增大。在10°入射角附近，不同风速的后向散射系数相交，详见图1。因此，在小入射角情况下，雷达后向散射系数相对于海面风速不敏感，尤其是在10°入射角附近(Hesany 等，2000)。然而，在小入射角情况下，不同风速的后向散射系数随入射角的变化率却有明显的差别(图5)。因此，可利用后向散射系数的多入射角信息进行小入射角海面风速的反演。

图 5 不同风速条件下后向散射系数对入射角的导数

Fig. 5 NRCS derivative of the incident angle under different wind speed

针对小入射角后向散射系数的特点，本文基于多入射角的最大似然估计，建立小入射角的风速反演算法。基于多入射角最大似然估计的目标函数可表示为

$\quad\quad J\left( {{U_{\rm{r}}}} \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {{\sigma _{\rm{m}}}\left( {{\theta _i}} \right) - {\sigma _{{\rm{GMF}}}}\left( {{\theta _i},{U_{\rm{r}}}} \right)} \right]}^2}} \quad\quad\quad\quad(6)$

式中，U_r为反演的风速，N为入射角个数，σ_m为测量的后向散射系数，θ_i为入射角，σ_GMF为模型后向散射系数。最大似然估计要通过循环迭代算法进行风速优化，使得目标函数达到最小值。

4 风速反演结果分析

利用第2节给出的小入射角经验GMF模型以及第3节介绍的最大似然估计风速反演算法，对无雨条件下的TRMM PR雷达后向散射系数进行风速反演。由于风速反演的后向散射系数入射角范围为0°—12°，风单元大小选为25 km×50 km(距离向×方位向)。分别对2007年和2008年的PR后向散射系数进行风速反演，并与浮标风速和ASCAT风速分别进行交叉比对，对小入射角后向散射系数的风速反演精度和反演性能进行分析。

4.1 风速反演精度

4.1.1 与浮标风速对比

浮标可以实现海面风场的高精度实时测量，浮标数据常被用于遥感设备标定的参考源。用于风速交叉对比的浮标包括Tao浮标和NDBC浮标。值得注意的是对于不同的浮标类型，风速计安装在不同的高度。为了便于交叉比对，将浮标测量的风速统一到海面以上10 m处(Mears 等，2001)。

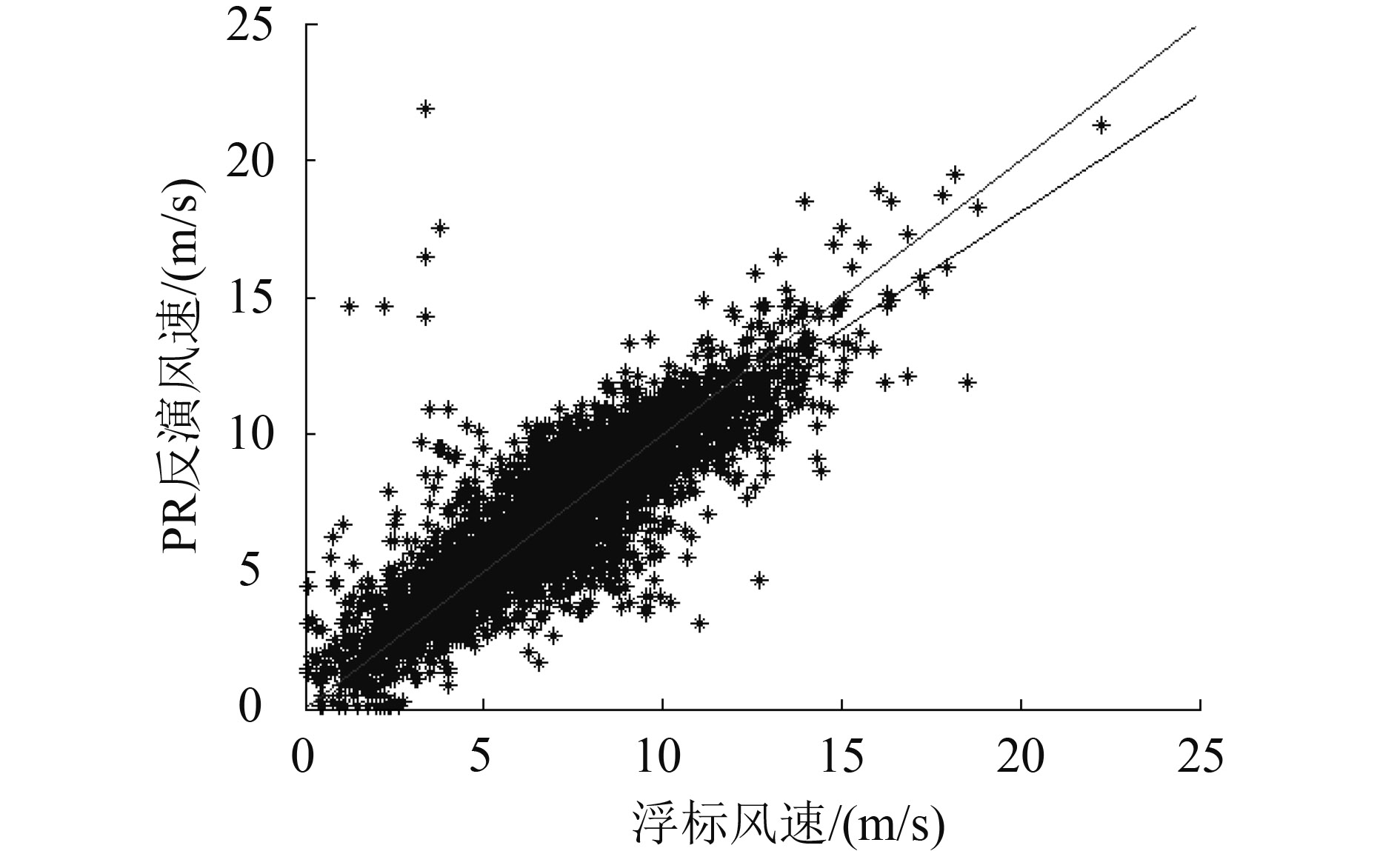
利用TRMM PR小入射角后向散射系数反演的海面风速与浮标风速进行交叉，数据匹配的时间窗口为10 min，空间窗口为25 km。对交叉点的风速数据进行统计，浮标风速和反演风速的散点图如图6所示。由图6可以看出，TRMM PR反演的风速与浮标风速基本一致。与浮标风速相比，风速反演偏差约为0 m/s，风速反演标准差为1.51 m/s。

图 6 浮标风速和反演风速的散点图

Fig. 6 The scatter plot of buoy and retrieved wind speed

4.1.2 与ASCAT风速对比

ASCAT是一个C波段固定扇形波束雷达散射计，工作频率为5.255 GHz，搭载在Metop系列卫星上。ASCAT的主要任务是进行全球风速和风向的测量，可以提供自2007年以来的全球风场数据，且风场测量具有很高的精度。与浮标和QuikScat相比，ASCAT风速反演的平均偏差接近于0 m/s，标准差小于1 m/s，是十分可靠的全球风场数据源。

PR反演的海面风速与ASCAT风速进行交叉比对，数据匹配的时间窗口和空间窗口分别选为30 min和25 km。ASCAT风速与反演风速的散点图(图7)。与ASCAT风速相比，PR反演风速的偏差约为0.28 m/s，标准差为1.08 m/s。反演风速与ASCAT风速的相关系数达0.94。

图 7 ASCAT风速和反演风速的散点图

Fig. 7 The scatter plot of ASCAT and retrieved wind speed

4.2 风速反演性能

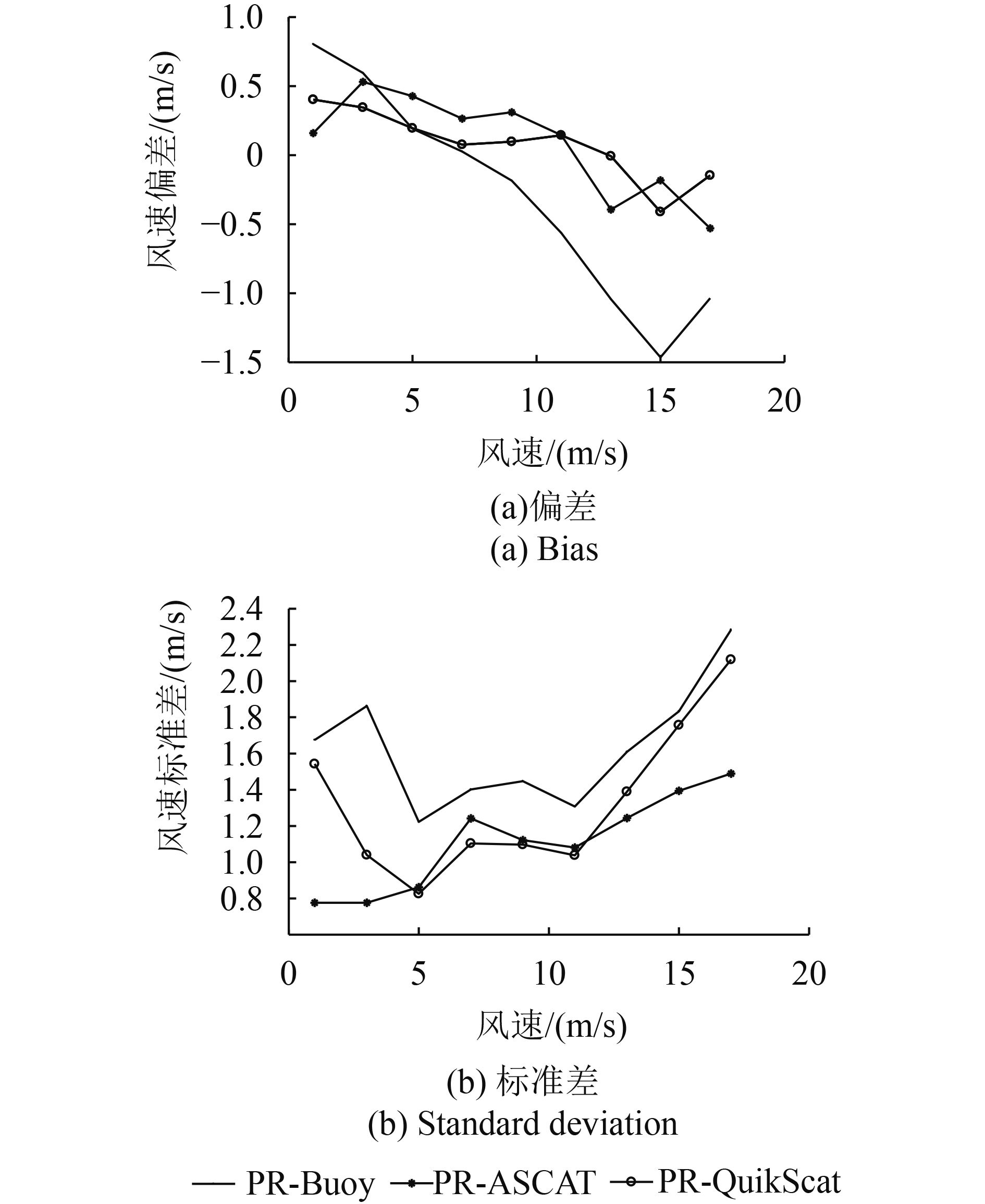
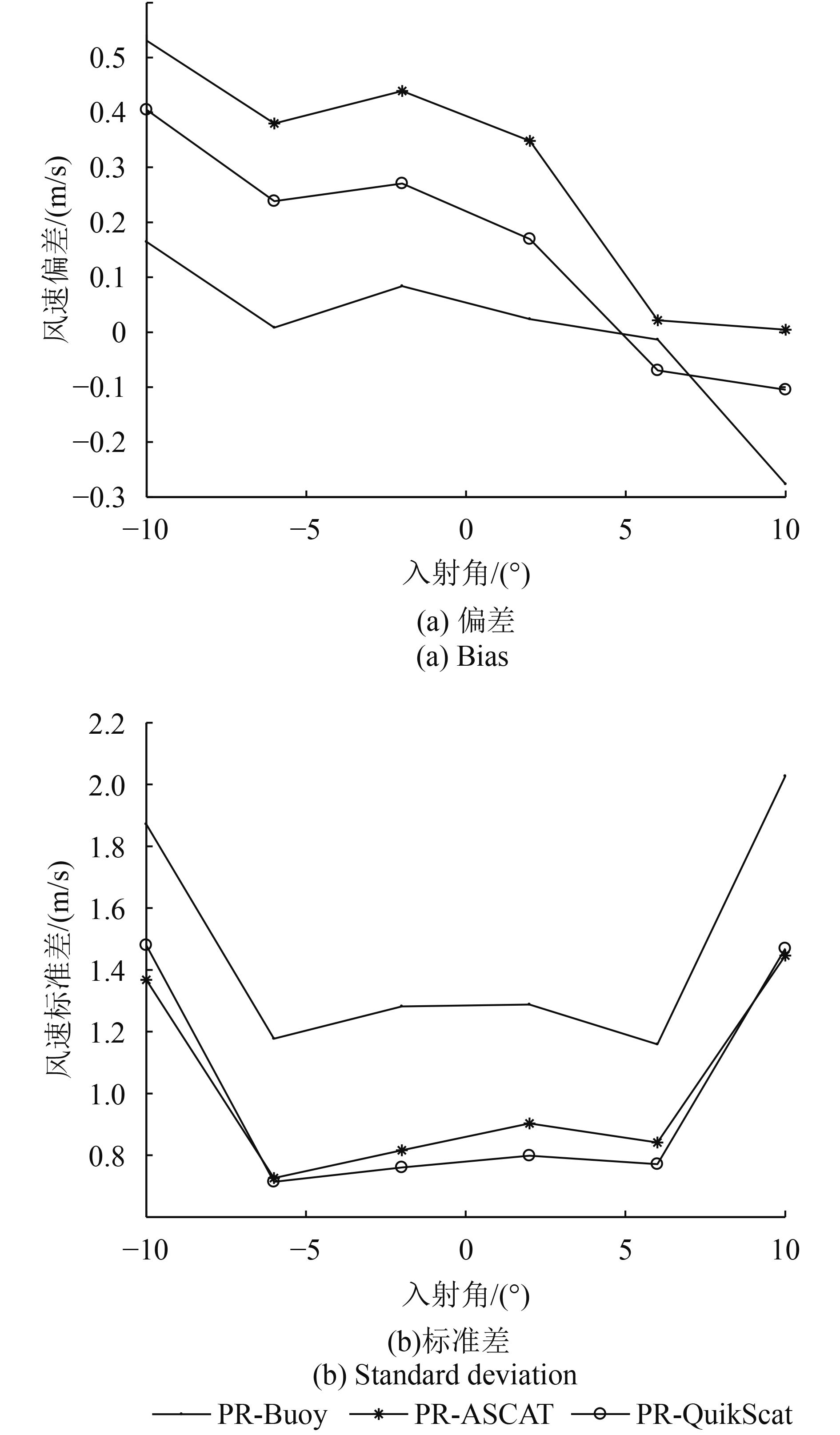
为了进一步分析小入射角海面风速反演的性能，对不同风速和不同风单元(距离向)的反演精度进行统计，得到不同风速和不同入射角情况下的风速反演偏差和标准差，其中风速间隔为2 m/s，风单元入射角范围约为4°。不同风单元对应的入射角范围见表1。图8为不同风速情况下的风速反演偏差和标准差。图9为不同入射角范围的风速反演偏差和标准差。

表 1 不同风单元对应的入射角范围
Table 1 The local incident angle of wind speed cell

下载CSV

风单元编号	本地入射角范围
风单元编号	TRMM轨道调整前(2001-08-07前)	TRMM轨道调整后(2001-08-24后)
6号风单元(刈幅左侧)	–12.7°—8.5°	–11.1°—7.4°
5号风单元(刈幅左侧)	–8.5°—4.3°	–7.4°—3.7°
4号风单元(刈幅左侧)	–4.3°—0°	–3.7°—0°
3号风单元(刈幅右侧)	0°—4.3°	0°—3.7°
2号风单元(刈幅右侧)	4.3°—8.5°	3.7°—7.4°
1号风单元(刈幅右侧)	8.5°—12.7°	7.4°—11.1°

图 8 不同风速情况下的反演精度偏差和标准差

Fig. 8 Inversion accuracy bias and standard deviation under different wind speed

图 9 不同入射角范围的反演精度偏差和标准差

Fig. 9 Inversion accuracy bias and standard deviation under different incident angle

由图8(a)可以看出，在低风速条件下，PR反演的风速偏高，而在高风速条件下，PR反演的风速偏低。同时由图8(a)和图8(b)可知，在中等风速条件下，风速反演的偏差和标准差均优于低风速和高风速条件。由图9(a)可以看出，在刈幅远端，风速反演的偏差较大，且刈幅左侧为正偏差，刈幅右侧为负偏差。经过初步分析，该误差主要是由卫星姿态带来的本地入射角差异而引起的。由图9(b)可知，2—5号风单元的风速反演标准差明显低于1号和6号风单元，即0°—8°入射角范围的风速反演精度明显优于8°—12°。

图9中8°—12°单元风速反演标准差明显高于0°—4°和4°—8°风单元的原因主要有两个：首先，由图5可以看出，在0°—8°范围内不同风速情况下的δσ/δθ变化率最大，而在8°—12°入射角范围内不同风速情况下的δσ/δθ变化并不十分明显，即风速相对于δσ/δθ的敏感性有所降低；其次，随着入射角的增大，风向引起的后向散射系数各向异性逐渐增大，而该各向异性将成为风速反演的误差，因此风速反演标准差也会随着入射角逐渐增加。

5 结　论

通过对TRMM PR的小入射角后向散射系数对3维成像微波高度计的风速反演方法进行研究，对小入射角情况下的风速反演精度进行统计分析。结果表明：小入射角(0°—12°)的后向散射系数可以有效地进行海面风速反演，风速反演的偏差小于0.28 m/s，标准差小于1.51 m/s。同时，中等风速条件下的风速反演精度优于低风速和高风速条件，且0°—8°入射角的风速反演精度明显优于8°—12°入射角范围。由此，3维成像微波高度计(入射角：1°—7°)的后向散射数据适合于进行海面风速的反演，且可以实现较高的风速反演精度。

由于高风速数据较少，因此风速反演结果相对较差，高风速情况下的经验GMF模型仍须进一步改善。

参考文献(References)

Apel J R. 1994. An improved model of the ocean surface wave vector spectrum and its effects on radar backscatter. Journal of Geophysical Research: Atmospheres, 99 (C8): 16269–16291. [DOI: 10.1029/94JC00846]

Barrick D. 1974. Wind dependence of quasi-specular microwave sea scatter. IEEE Transactions on Antennas and Propagation, 22 (1): 135–136. [DOI: 10.1109/TAP.1974.1140736]

Brown G S. 1990. Quasi-specular scattering from the air-sea interface//Geernaert G L and Plant W L, eds. Surface Waves and Fluxes: Volume II—Remote Sensing. Dordrecht, Netherlands: Springer: 1–39 [DOI: 10.1007/978-94-009-0627-3_1]

Cox C S and Munk W H. 1954. Statistics of the sea surface derived from sun glitter. Journal of Marine Research, 13 : 198–227.

Freilich M H and Vanhoff B A. 2003. The relationship between winds, surface roughness, and radar backscatter at low incidence angles from TRMM Precipitation Radar measurements. Journal of Atmospheric and Oceanic Technology, 20 (4): 549–562. [DOI: 10.1175/1520-0426(2003)20<549:TRBWSR>2.0.CO;2]

Hesany V, Plant W J and Keller W C. 2000. The normalized radar cross section of the sea at 10° incidence. IEEE Transactions on Geoscience and Remote Sensing, 38 (1): 64–72. [DOI: 10.1109/36.823902]

Jackson F C, Walton W T, Hines D E, Walter B A and Peng C Y. 1992. Sea surface mean square slope from K_u-band backscatter data . Journal of Geophysical Research: Oceans, 97 (C7): 11411–11427. [DOI: 10.1029/92JC00766]

Kuroiwa H, Kawanishi T, Kojima M, Oikawa K and Kozu T. 1996. Precipitation radar onboard TRMM satellite//Proceedings of the IEEE International Symposium on Phased Array Systems and Technology. Boston, MA: IEEE: 249–254 [DOI: 10.1109/PAST.1996.566094]

Li L, Im E, Connor L N and Chang P S. 2004. Retrieving ocean surface wind speed from the TRMM Precipitation Radar measurements. IEEE Transactions on Geoscience and Remote Sensing, 42 (6): 1271–1282. [DOI: 10.1109/TGRS.2004.828924]

Mears C A, Smith D K and Wentz F J. 2001. Comparison of special sensor microwave imager and buoy-measured wind speeds from 1987 to 1997. Journal of Geophysical Research: Oceans, 106 (C6): 11719–11729. [DOI: 10.1029/1999JC000097]

Valenzuela G R. 1978. Theories for the interaction of electromagnetic and oceanic waves—a review. Boundary-Layer Meteorology, 13 (1/4): 61–85. [DOI: 10.1007/BF00913863]

Wentz F J, Peteherych S and Thomas L A. 1984. A model function for ocean radar cross sections at 14. 6 GHz. Journal of Geophysical Research: Atmospheres, 89 (C3): 3689–3704. [DOI: 10.1029/JC089iC03p03689]

Wu J. 1972. Sea-surface slope and equilibrium wind-wave spectra. Physics of Fluids, 15 (5): 741–747. [DOI: 10.1063/1.1693978]

Wu J. 1990. Mean square slopes of the wind-disturbed water surface, their magnitude, directionality, and composition. Radio Science, 25 (1): 37–48. [DOI: 10.1029/RS025i001p00037]

Zhang Y H, Xu K, Li M T, Li J, Liu H G and Wang X Z. 1999. Study on spaceborne topography mapping altimeter. Remote Sensing Technology and Application, 14 (1): 11–14. [DOI: 10.3969/j.issn.1004-0323.1999.01.003] ( 张云华, 许可, 李茂堂, 李靖, 刘和光, 王新中. 1999. 星载三维成像雷达高度计研究. 遥感技术与应用, 14 (1): 11–14. [DOI: 10.3969/j.issn.1004-0323.1999.01.003] )

Zhang Y H, Zhang X K, Meng X, Luo W, Zhou Z X and Jiang J S. 2007. An interferometric imaging altimeter applied for both ocean and land observation//Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Barcelona: IEEE: 3821–3824 [DOI: 10.1109/IGARSS.2007.4423676]

摘要

关键词