|
收稿日期: 2016-09-23; 优先数字出版日期: 2017-09-01
基金项目: 国家自然科学基金(编号:91337218);公益性行业(气象)科研专项(编号:GYHY201406008)
第一作者简介: 周泽华(1992— ),男,硕士研究生,研究方向为卫星资料质量控制。E-mail:zehuazhou@foxmail.com
通讯作者简介: 邹晓蕾(1960— ),女,教授,研究方向为资料同化。E-mail:xzou@nuist.edu.cn
中图分类号: P414.4
文献标识码: A
|
摘要
由于卫星微波成像仪频率的非保护性,微波成像仪资料受到相近频率的无线电信号干扰影响,主要干扰源于洋面反射的静止电视卫星信号。为提高微波成像仪资料的准确性,尤其是洋面资料的可用性,对电视卫星信号干扰的检测和特征分析尤为重要。中国风云3号C星(FY-3C)上搭载了微波成像仪。本文使用标准化主成分分析法来识别FY-3C微波成像仪的电视卫星干扰信号,并分析电视卫星信号干扰的主要空间特征。研究表明,FY-3C微波成像仪中心频率为10.65 GHz和18.7 GHz的4个低频通道受到卫星信号干扰。10.65 GHz通道在欧洲海域英吉利海峡和地中海西部希腊沿岸地区受到电视卫星信号干扰,并且干扰信号位置和强度与FY-3C卫星和欧洲静止电视卫星相对空间位置有关;18.7 GHz通道主要受到美国电视卫星的干扰,在北美东、西沿岸海域都存在干扰信号。FY-3C微波成像仪在中国海域不受电信号干扰影响,主要因为中国静止电视卫星频率与微波成像仪各通道频率不一样。
关键词
风云3号C星(FY-3C), 微波成像仪, 海洋, 电视信号干扰, 识别
Abstract
Observations of a satellite Microwave Radiation Imager (MWRI) are easily interfered by signals of active remote sensing because of their similar frequency. The primary source of interference over oceans is the reflected signal of geostationary television (TV) satellites by the ocean surface. The accurate detection of such interferences is largely important for the effective use of MWRI observations and an essential preprocessing step of the MWRI data onboard the FY-3C satellite. A Normalized Principal Component Analysis Method (NPCA) is used to detect the TV Frequency Interference (TFI) signals over oceans. High correlations exist among the different MWRI channels, but the RFI signal eliminates these correlations. Hence, NPCA can detect the TFI signal by employing this aspect. The TFI signals of the MWRI at 10.65 GHz horizontal polarization over oceans are distributed widely near the coastal areas of Europe, especially the English Channel and western parts of the Mediterranean Sea. The TFI signal definitively originates from the hot bird, and its intensity is related to the angle between the MWRI incidence and geostationary satellite TV signals reflection. The threshold of the TFI signals is defined to quantify the TFI intensity. The TFI signals at 18.7 GHz are observed over the offshore marine areas of North America. As expected, no RFI signal is detected near the coastal areas of China because the geostationary satellite TV frequency over China is different from those of MWRI channels. The NPCA method can detect TFI signals over oceans. The distribution of TFI signals are in Europe at 10.65 GHz and North America at 18.7 GHz. The intensity of the TFI signals is completely related to the Glint angle. TFI signals evidently affect the result of the retrieval production. Correcting and eliminating TFI signals will be pursued in future studies. Clear brightness temperature data will also be adopted in retrieval production and data assimilation.
Key words
FY-3C, Microwave Radiation Imager (MWRI), ocean, television frequency interference, detection
1 引 言
自1960年第1颗气象卫星发射以来,经过50多年的发展,极轨气象卫星已经发展到了第5代。搭载在极轨气象卫星上的微波成像仪也在不断发展,1987年美国国防气象系列卫星DMSP (Defense Meteorological Satellite Program)上首次搭载了微波辐射计特别传感器SSM/I(Special Sensor Microwave/Imager)(Hollinger 等,1990);1997年发射的热带降雨测量卫星TRMM(Tropical Rainfall Measuring Mission)也搭载了微波成像仪TMI(TRMM Microwave Imager)(Kummerow 等,1998);2002年,美国地球观测系统EOS(Earth Observation System)Aqua卫星上搭载了先进微波扫描辐射计AMSR-E(Advanced Microwave Scanning Radiometer-Earth Observation System)(Kawanishi 等,2003);2003年美国国防部发射的Coriolis卫星上搭载了全球化微波辐射计(Wind Sat Polarimetric Radiometer)(Gaiser 等,2004),之后又在2012年发射了第一期全球水循环变化观测卫星GCOM-W1(Global Change Observation Mission)上搭载了先进微波扫描辐射计AMSR-2(Advanced Microwave Scanning Radiometer2)(Oki 等,2010)。近年来,中国的风云系列卫星也逐步发射升空。风云3号卫星(FY-3C)是中国的第2代极轨气象卫星,分别发射了FY-3A/B/C 3颗系列卫星,其中B星和C星上都搭载了微波成像仪MWRI(Microwave Radiation Imager)(Dong 等,2009)。
由于微波具有较强的“穿透”能力,微波图像能够反映物体的温度和介电特性等信息。如对海洋表面温度的监测,利用微波仪器可以获取白天和夜间的洋面温度信息,且这些信息的获取不易受天气的影响,即使在非降水云覆盖的情况下,也可以获取洋面温度信息。随着卫星微波遥感技术的发展,微波成像仪在反演陆地和洋面气象要素,如:地表温度、土壤水分、雪深雪水当量、海表温度、海面风速、海冰、晴空大气可降水量等具有重要的作用(王振占,2003),并且还可用于检测台风等气象灾害天气过程。
但是,在微波成像仪不断发展的同时,人类对各类主动遥感设备的使用也在逐步增加。如:静止电视、通讯卫星、军用、民用雷达、全球定位系统、空中交通管制等,这些主动遥感仪器发射的信号与微波成像仪接收的微波信号频率非常接近,所以微波成像仪在接收地球的热辐射时,会同时接收主动遥感设备发射的信号,对微波成像仪的观测数据造成一定程度的干扰,这种干扰被称之为无线电信号干扰RFI(Radio Frequency Interference)(邹晓蕾,2012)。
已有研究表明(Li 等,2004,2006;Njoku 等,2005;Adams 等,2010),在目前广泛使用的微波成像仪中,如美国的Aqua卫星上搭载的先进微波辐射计(AMSR-E),以及后续的AMSR-2仪器、国防卫星上WindSat辐射计、中国的风云卫星上搭载的微波成像仪(MWRI),它们的低频通道均受到不同程度的无线电信号干扰的影响。为正确的识别和剔除这些干扰信号的影响,已有不少气象学家对干扰信号识别方法进行研究。Li等人(2004)提出使用相邻频率通道之间的亮温差值来量化RFI的强度和范围,即谱差法。同等情况下,微波成像仪探测到的亮温数据值会随着通道频率的增加而增大,即高频通道的亮温值高于低频通道。但当低频通道中存在有无线电干扰信号时,会增加低频通道的亮温值,使得亮温随频率递增的变化趋势发生改变,将低频通道减去高频通道的差值大小代表了无线电干扰信号的强弱。2006年,Li等人(2006)进一步提出将主成分分析PCA(Principal Component Analysis)方法应用于陆地地区的RFI分析中,但是该方法严重受到下垫面的影响,所以只能应用于夏季的RFI检测。Zou等人(2012)扩展了PCA方法,运用标准化PCA方法NPCA(Normalized Principal Component Analysis)对WindSat上C波段和X波段的陆地各个季无线电信号干扰进行识别,成功剔除了雪盖造成的虚假信号。针对常年冰雪覆盖区域,近期Zhao 等人(2013)进一步提出了DPCA(Double Principal Component Analysis)方法,剔除了冰雪下垫面的强反射信号造成的识别困难,从而有效地进行格陵兰岛等长期冰雪覆盖区域的RFI检测,最终实现了全球陆地的RFI信号的有效检测。
虽然陆地RFI检测问题得到解决,但是海洋上的RFI检测还有待进一步研究。在海洋上,由于海洋本身的辐射特性,海洋上的干扰信号识别要比陆地上更困难。洋面的微波发射率低于陆地,并且海表的状况和天气现象,如云和降水,会导致低频通道的亮温显著增加,这与受到干扰信号影响的亮温增长结果类似,会造成虚假的干扰信号,并且洋面上的远洋航运、客轮等移动主动微波遥感设备的存在,使得海洋上的干扰信号识别更加困难。
Adams等人(2010)研究发现海表反射的静止电视卫星信号是海洋上干扰信号的主要来源,并提出用基于WindSat反演地球物理参数的卡方概率(Chi-Square Probability Method)对洋面反射的无线电干扰信号做出识别。Zou等人(2014)对海洋无线电干扰信号研究时发现AMSR-E的10.65 GHz和18.7 GHz通道上欧洲和北美海域降轨资料受到了严重的电视信号干扰TFI(Television Frequency Interference)。使用标准化主成分分析法NPCA识别干扰信号之后,发现干扰信号与电视卫星和极轨卫星的法向夹角有着密切的关系。官莉等人(2015)对AMSR-E的18.7 GHz通道海洋上的电视信号干扰运用双主成分分析法进行识别,进一步明确了闪烁角较小时卫星观测易受到污染。
中国近年来发射的风云系列卫星逐步开始业务使用,随着研究和业务应用的不断深入,对卫星资料的质量要求也越来越高。无线电信号干扰是微波成像仪资料的主要误差来源,所以无线电干扰信号的识别研究尤为重要。目前已有研究人员针对风云系列卫星在陆地上所受的干扰信号特征进行了研究(冯呈呈和赵虹,2015),并发现在低频通道上也存在干扰信号,但是对风云卫星微波成像仪资料在海洋上的电视信号干扰识别研究还有待开展,另外由于中国、美国和欧洲地区的电视信号频率不同,微波成像仪资料在不同区域所受的电视信号干扰的空间特征也有待进一步分析。为适应业务应用以及科研的需要,本文对风云卫星微波成像仪资料在海洋上的干扰信号进行检测研究。本文将使用标准化主成分分析法对FY-3C上搭载的微波成像仪资料(MWRI)在洋面上的电视干扰信号进行识别研究,并分析在不同洋面上的电视干扰信号差异,探究其空间分布特征及其原因,从而为提高微波成像仪资料的准确性和资料的更广泛应用建立基础。
2 微波成像仪仪器与通道特征
微波成像仪MWRI搭载于FY-3A星、B星、C星上,该仪器有5个频率(10.65 GHz,18.7 GHz,23.8 GHz,36.5 GHz和89 GHz),每个频率都有两个极化模式:垂直极化(V)和水平极化(H)。微波成像仪以圆锥形扫描方式对地向前扫描,扫描角度为45°,扫描宽度为1400 km,每次扫描可获得254个扫描点数据。从低频到高频各通道的地面分辨率为51×85 km、30×50 km、27×45 km、18×30 km、9×15 km、7.5×12 km。仪器的具体数据和各通道特征如表1。
表 1 微波成像仪仪器数据和通道特征
Table 1 MWRI instrument data and the channel characteristics
| 通道特征 | 频率/GHz | ||||
| 10.65 | 18.7 | 23.8 | 36.5 | 89 | |
| 极化 | V, H | V, H | V, H | V, H | V, H |
| 带宽/MHz | 180 | 200 | 400 | 900 | 2×2300 |
| 灵敏度/k | 0.5 | 0.5 | 0.8 | 0.5 | 1.0 |
| 定标精度/k | 1.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| 动态范围/k | 3—340 | ||||
| 采样点数 | 240 | ||||
| 量化等级 | 12比特 | ||||
| 主波束效率 | ≥90% | ||||
| 地面分辨率≤/(km×km) | 51×85 | 30×50 | 27×45 | 18×30 | 9×15 |
| 通道间配准 | 波束指向误差<0.1° | ||||
| 扫描方式 | 圆锥扫描 | ||||
| 幅宽/km | 1400 | ||||
| 天线视角/(°) | 45±0.1 | ||||
| 扫描周期/s | 1.7±0.1 | ||||
| 扫描周期误差/ms | 0.34 ms(相邻扫描线)1 ms(连续30 min内) | ||||
| 注:http://satellite.nsmc.org.cn/PortalSite/StaticContent/DeviceIntro_FY3_MWRI.aspx [2016-7-10]。 | |||||
由于微波成像仪向前扫描的特点,而静止电视卫星位于赤道上空不断向下发射信号,在北半球,只有在降轨观测时,洋面反射的下行信号才有可能进入微波成像仪观测天线中,从而导致观测亮温受到干扰。南半球则相反,在升轨观测中才会存在TFI干扰信号。所以本文选用2014年7月MWRI的降轨观测资料,选取中国、欧洲和北美大陆这3个主要干扰源区作为研究区域进行分析。
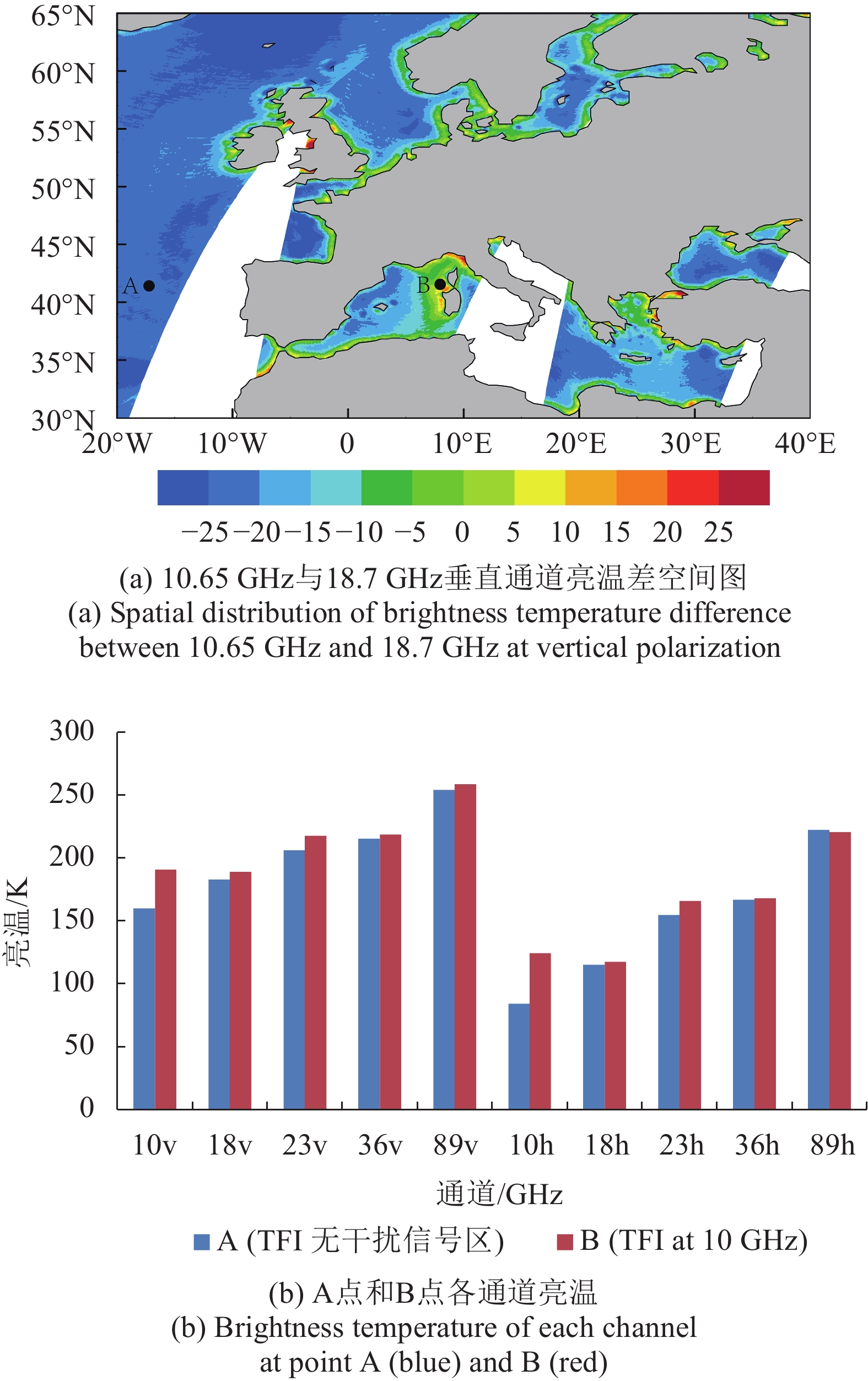
在晴空区大部分陆地和海洋上,若没有干扰信号,微波成像仪亮温值则会随着频率的增大而增大,但是如果存在干扰信号,就会导致该通道接收的辐射增多,亮温增大,使得原本亮温值随着频率增大而增大的变化趋势发生变化,导致相邻频率的亮温差值变小,甚至有低频通道亮温值高于高频通道亮温值情况的发生。图1(a)是10.65 GHz与18.7 GHz垂直通道亮温差值图,发现海面上的差值正值区很少,主要存在于撒丁岛附近,为比较不同通道间的亮温变化,选择图1(a)中的两个点A点(41°N,18°W)和B点(41°N,7°E),其中A点没有干扰信号,B点可能存在干扰信号。在图1(b)中是两个点各个通道亮温的柱状图,可以看到除了10.65 GHz通道上,所有通道的亮温值相差不大,并且均随着频率的增大而增大,同时垂直通道的亮温值要大于水平极化通道,而在10.65 GHz通道上,B点的亮温值无论是在垂直极化通道还是水平极化通道上都要远远大于A点,说明在B点撒丁岛可能存在干扰信号使得该处的10.65 GHz通道亮温值异常偏高。
3 标准化主成分识别方法
由于大气中云和降水的散射效应能大幅度地降低高频通道的亮温值,因而海洋上反符号的谱差也可能与云和降水有关,导致谱差法无法准确的识别电视干扰信号,同时因为微波成像仪是被动接收自然辐射,所以各个通道之间的相关性往往很高,而干扰信号的存在破坏了通道间的相关性。主成分分析法正好可以利用通道间的相关性被破坏这个特点来识别干扰信号,所以这里选用NPCA方法(Zou 等,2014)对MWRI资料进行检测试验。下面首先简单介绍NPCA方法的主要步骤:
(1) 对所有通道的亮温值进行标准化处理
|
${{V}_i} = {\left( {\begin{array}{*{20}{c}}{\frac{{TB_{10{\rm{H}}}^{\rm{o}} - \mu }}{\sigma }}\\[5pt]{\frac{{TB_{10{\rm{V}}}^{\rm{o}} - \mu }}{\sigma }}\\[5pt] \vdots \\[5pt]{\frac{{TB_{89.0{\rm{H}}}^{\rm{o}} - \mu }}{\sigma }}\\[5pt]{\frac{{TB_{89.0{\rm{V}}}^{\rm{o}} - \mu }}{\sigma }}\end{array}} \right)_j} = {\left( {\begin{array}{*{20}{c}}{TB_{10{\rm{H}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{10{\rm{V}}}^{\left( {\rm{n}} \right)}}\\[5pt] \vdots \\[5pt]{TB_{89.0{\rm{H}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{89.0{\rm{V}}}^{\left( {\rm{n}} \right)}}\end{array}} \right)_j}$
|
(1) |
式中,
|
$\mu = \frac{1}{m}\mathop \sum \limits_{j = 1}^m TB_j^{\rm{o}}$
|
(2) |
|
$\sigma = \sqrt {\frac{1}{m}\mathop \sum \limits_{j = 1}^m {{\left( {TB_j^{\rm{o}} - \mu } \right)}^2}} $
|
(3) |
式中,μ和σ分别是观测点各个通道亮温值的平均值和标准差,m是通道数。
(2) 利用标准化后的数据构造一个包括5个成分的干扰指数,用来检测电视信号干扰(TFI),通过主成分分析法将干扰指数线性的转化为一组不相关的主成分分量,从而将TFI信号从自然辐射中分离出来,这里以10.65 GHz垂直极化通道为例,构建干扰指数向量。
|
${{R}_i} = {\left( {\begin{array}{*{20}{c}}{TB_{10{\rm{V}}}^{\left( {\rm{n}} \right)} - TB_{18{\rm{V}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{18{\rm{H}}}^{\left( {\rm{n}} \right)} - TB_{23{\rm{H}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{18{\rm{V}}}^{\left( {\rm{n}} \right)} - TB_{23{\rm{V}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{23{\rm{H}}}^{\left( {\rm{n}} \right)} - TB_{36{\rm{H}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{23{\rm{V}}}^{\left( {\rm{n}} \right)} - TB_{36{\rm{V}}}^{\left( {\rm{n}} \right)}}\end{array}} \right)_j} = {\left( {\begin{array}{*{20}{c}}{{N_{10{\rm{V}} - 18{\rm{V}}}}}\\[5pt]{{N_{18{\rm{H}} - 23{\rm{H}}}}}\\[5pt]{{N_{18{\rm{H}} - 23{\rm{H}}}}}\\[5pt]{{N_{23{\rm{H}} - 36{\rm{H}}}}}\\[5pt]{{N_{23{\rm{V}} - 36{\rm{V}}}}}\end{array}} \right)_j},j = 1,2,3, \cdots ,k$
|
(4) |
式中,k是一个观测轨道的总观测数。
根据前人的研究,无线电频率干扰只存在于低频通道,在较高频的通道上不存在干扰信号或干扰信号可以忽略不计,所以在选定干扰指数向量时,后4个成分不存在干扰信号,通道间相关性保持的相对较好,用来作为通道间高相关性的依据,第1个成分
用于识别10.65 GHz垂直通道上的无线电干扰信号的原始数据矩阵如下
|
${{A}_{5 \times n}} = \left[ {\begin{array}{*{20}{l}}{{{\left( {{N_{10{\rm{V}} - 18{\rm{V}}}}} \right)}_1}} & {{{\left( {{N_{10{\rm{V}} - 18{\rm{V}}}}} \right)}_2}} & \cdots & {{{\left( {{N_{10{\rm{V}} - 18{\rm{V}}}}} \right)}_k}}\\[5pt]{{{\left( {{N_{18{\rm{H}} - 23{\rm{H}}}}} \right)}_1}} & {{{\left( {{N_{18{\rm{H}} - 23{\rm{H}}}}} \right)}_2}} & \cdots & {{{\left( {{N_{18{\rm{H}} - 23{\rm{H}}}}} \right)}_k}}\\[5pt]{{{\left( {{N_{18{\rm{V}} - 23{\rm{V}}}}} \right)}_1}} & {{{\left( {{N_{18{\rm{V}} - 23{\rm{V}}}}} \right)}_2}} & \cdots & {{{\left( {{N_{18{\rm{V}} - 23{\rm{V}}}}} \right)}_k}}\\[5pt]{{{\left( {{N_{23{\rm{H}} - 36{\rm{H}}}}} \right)}_1}} & {{{\left( {{N_{23{\rm{H}} - 36{\rm{H}}}}} \right)}_2}} & \cdots & {{{\left( {{N_{23{\rm{H}} - 36{\rm{H}}}}} \right)}_k}}\\[5pt]{{{\left( {{N_{23{\rm{V}} - 36{\rm{V}}}}} \right)}_1}} & {{{\left( {{N_{23{\rm{V}} - 36{\rm{V}}}}} \right)}_2}} & \cdots & {{{\left( {{N_{23{\rm{V}} - 36{\rm{V}}}}} \right)}_k}}\end{array}} \right]$
|
(5) |
(3) 构造协方差矩阵
|
${S}{{e}_i} = {\lambda _i}{{e}_i}\left( {i = 1,2,3,4,5} \right)$
|
(6) |
式中,i表示第i个主成分模态,ei是第i个主成分模态,λi表示第i个主成分模态对总方差的贡献。
(4) 将数据矩阵投影到由
|
${{U}_{5 \times N}} = {\left[ {\begin{array}{*{20}{c}}{{{e}_{1,i}}} & {{{e}_{2,i}}} & {{{e}_{3,i}}} & {{{e}_{4,i}}} & {{{e}_{5,i}}}\end{array}} \right]^{\rm{T}}}{A} = \left( {\begin{array}{*{20}{c}}{{{u}_1}}\\{{{u}_2}}\\{{{u}_3}}\\{{{u}_4}}\\{{{u}_5}}\end{array}} \right)$
|
(7) |
数据矩阵A也可由以下5个主成分来进行重构
|
${A} = {eU} = \mathop \sum \limits_{i = 1}^5 {{e}_i}{{u}_i}$
|
(8) |
式中,
类似的,18.7 GHz垂直通道的干扰指数向量为
|
${{R}_i} = {\left( {\begin{array}{*{20}{l}}{TB_{18{\rm{V}}}^{\left( {\rm{n}} \right)} - TB_{23{\rm{V}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{23{\rm{H}}}^{\left( {\rm{n}} \right)} - TB_{36{\rm{H}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{23{\rm{V}}}^{\left( {\rm{n}} \right)} - TB_{36{\rm{V}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{36{\rm{H}}}^{\left( {\rm{n}} \right)} - TB_{89{\rm{H}}}^{\left( {\rm{n}} \right)}}\\[5pt]{TB_{36{\rm{V}}}^{\left( {\rm{n}} \right)} - TB_{89{\rm{V}}}^{\left( {\rm{n}} \right)}}\end{array}} \right)_i}$
|
(9) |
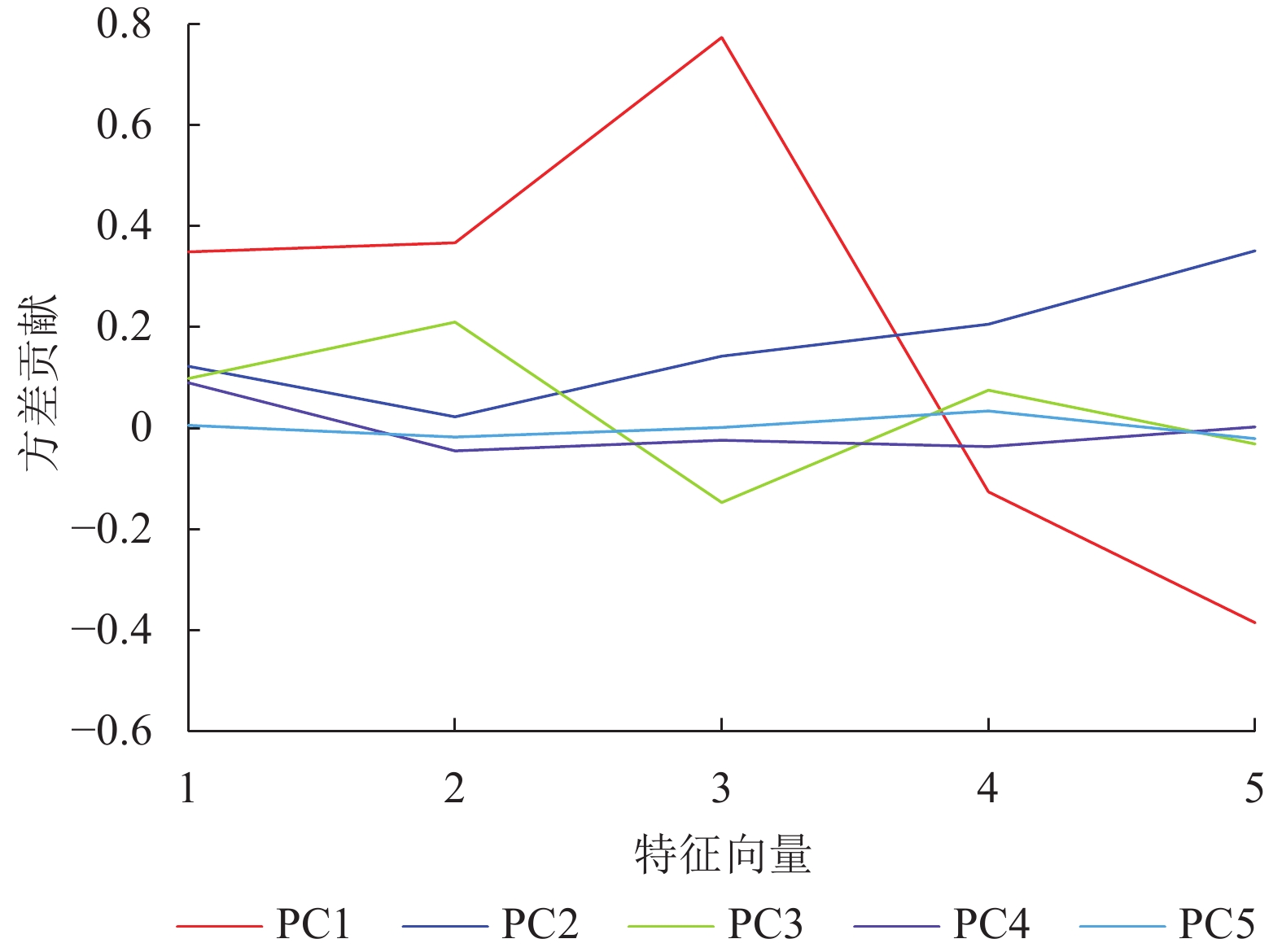
图2为2014年7月1日欧洲海域扫描轨道经过标准化主成分分析法计算得到的各个成分向量的特征向量。从图2中可以看到第一个成分
4 电视干扰信号检测结果验证
4.1 闪烁角定义
海洋上干扰信号的主要来源是静止通讯卫星和静止电视卫星,静止卫星在赤道上空固定点持续不断地向地面固定区域发射无线电信号,这些信号大部分发射向陆地,为人类提供电视、通讯服务,但是这些信号同时还会发射到海岸线附近的海域上。由于海面存在反射的特性,这些电视信号会被反射向太空,从而被极轨气象卫星的微波成像仪接收到,产生电视信号干扰。假定海洋表面是镜面反射,电视信号干扰的存在依赖于静止电视、通讯卫星下行信号经由洋面进行反射后的方向角和风云卫星的观测入射角之间相对位置,所以定义静止卫星下行反射信号方向和气象卫星入射方向的向量夹角为闪烁角(Zou 等,2014)。图3为闪烁角的示意图,以观测点作为局地坐标原点,X轴沿观测点纬圈切线方向,Y轴沿观测点经线切线方向,Z轴穿过观测点和地心,垂直于地面。闪烁角θ的计算公式为
|
$\cos \theta = \frac{{ - {\alpha } \cdot {\beta }}}{{\left| { - {\alpha }} \right| \cdot \left| {\beta } \right|}}$
|
(10) |
式中,α是静止电视卫星的入射方向,–α是经由洋面反射的出射方向,β是MWRI的观测入射方向,
干扰信号只能影响与其频率相近的通道。表2为目前使用的静止电视、通讯卫星的中心频率和覆盖区域,这些静止卫星的中心频率均与部分微波成像仪低频通道频率接近,如Telstar系列卫星、Anik系列卫星以及Hotbird卫星与10.65 GHz通道频率相近,DirecTV系列卫星和SpacewayF1卫星与18.7 GHz通道频率接近。
表 2 部分静止电视、通讯卫星
Table 2 List of some geostationary TV satellite
| 卫星 | 星下点 | 覆盖区域 | 中心频率/GHz | 辐射功率/dBW |
| Telstar18 | 138°E | 中国, 澳大利亚 | 12.5 | 41、50 |
| Telstar12 | 15°W | 欧洲, 北美东部 | 11.5 | 50 |
| Telstar11 | 37.5°W | 欧洲, 北美东部 | 11.7 | 51 |
| Hotbird | 13°E | 欧洲 | 11.6 | 53 |
| Telstar14R | 63°W | 北美, 南美 | 12.2 | 59 |
| AnikF1R | 107.3°W | 北美 | 12.2(V) | 53 |
| AnikF2 | 111.1°W | 北美 | 12.2 | 52 |
| AnikF3 | 118.7°W | 北美 | 11.7(H) | 52 |
| DirecTV10 | 103°W | 美国 | 19.1 | – |
| DirecTV11 | 99°W | 美国 | 18.5 | – |
| SpacewayF1 | 102.8°W | 北美 | 18.3—19.8 | – |
图4是欧洲Hotbird卫星的下行信号辐射范围及功率变化图(http://www. eutelsat.com/en/satellites/the-fleet/EUTELSAT-HB13B-downlink-coverage.html [2016-12-14])。Hotbird静止卫星的主要下行信号区域在欧洲,并且其中心辐射功率在西欧,德国、法国、西班牙、意大利附近,逐渐向外减弱。但是当闪烁角很小时,静止卫星反射信号和极轨卫星入射信号就会接近重合,从而导致信号干扰。
4.2 欧洲近海海域MWRI资料的干扰信号的空间分布特征
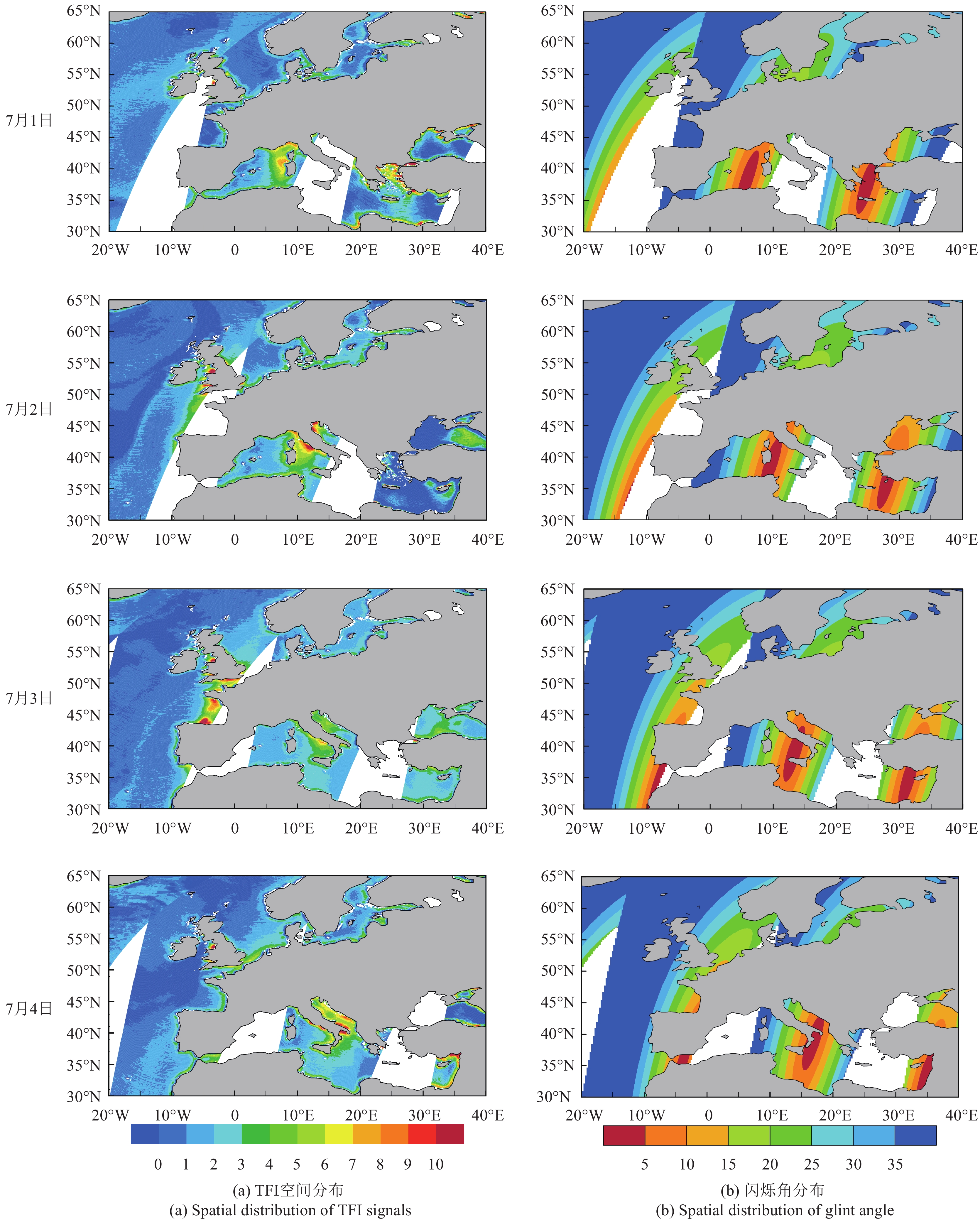
图5是7月1日—4日欧洲海域的NPCA方法检测的10.65 GHz通道上无线电信号和闪烁角空间分布图,灰色是陆地,白色是卫星观测的空白区域,干扰信号分布图中量值越大代表干扰信号的强度越大,闪烁角分布图则是颜色越深代表闪烁角越小。比较图5(a)和图5(b)可以看出干扰信号的强度和位置与闪烁角的大小呈现了紧密的联系,闪烁角小的区域存在干扰信号的可能性和强度就越大,如图5中意大利、法国附近海域,对于静止通讯、电视卫星干扰信号而言,闪烁角较小应该是必要条件,但闪烁角小的地区不一定存在强的干扰信号,如图5中土耳其、希腊等附近海域,结合图4中给出的静止卫星下行信号辐射功率空间分布特征,可以发现当辐射功率较小时,即使有反射信号,也不会对MWRI观测产生明显的影响。图5中,受到信号干扰的地区都是闪烁角θ较小的地区,基本都小于20°,而且θ角越接近于0°,干扰指数的值就越大。在每日的干扰信号分布情况看,在13°E西面的扫描轨道的干扰信号都存在于扫描轨道的偏东部分,而在13°E东面的扫描轨道的干扰信号均存在于扫描轨道的偏西部分,这也证明干扰信号的来源主要是由于Hotbird卫星(位于13°E)下行信号经由洋面反射所造成的。
图6是7月1日—15日欧洲海域的半月平均无线电信号干扰分布图,分辨率是0.25°×0.25°的格点,从图上可以看到无线电干扰信号主要分布在地中海西北部地区、英吉利海峡以及法国沿海和西班牙北部海域。
虽然NPCA方法能够很好的识别TFI的空间位置,但是NPCA方法的识别结果还多是用于干扰信号的定性研究,客观的给出NPCA方法的识别阈值是该方法全面应用的必要条件。从上述分析结果中我们可以看到,TFI与NPCA的识别结果和闪烁角两者都有紧密关系,而且识别结果和闪烁角又是相对独立的数据,这就形成一个数学上的超定问题。利用两种识别方法的对应关系,就可确定NPCA方法判别干扰信号的客观阈值。
首先定义变量R
|
$R = \frac{{u \geqslant x{\text{且}}\theta \leqslant y{\text{时格点数}}}}{{u \geqslant x{\text{时的所有格点数}}}}$
|
(11) |
式中,u值是式(8)中的u3,x是X轴上干扰指数,y是左边Y轴闪烁角θ的值。
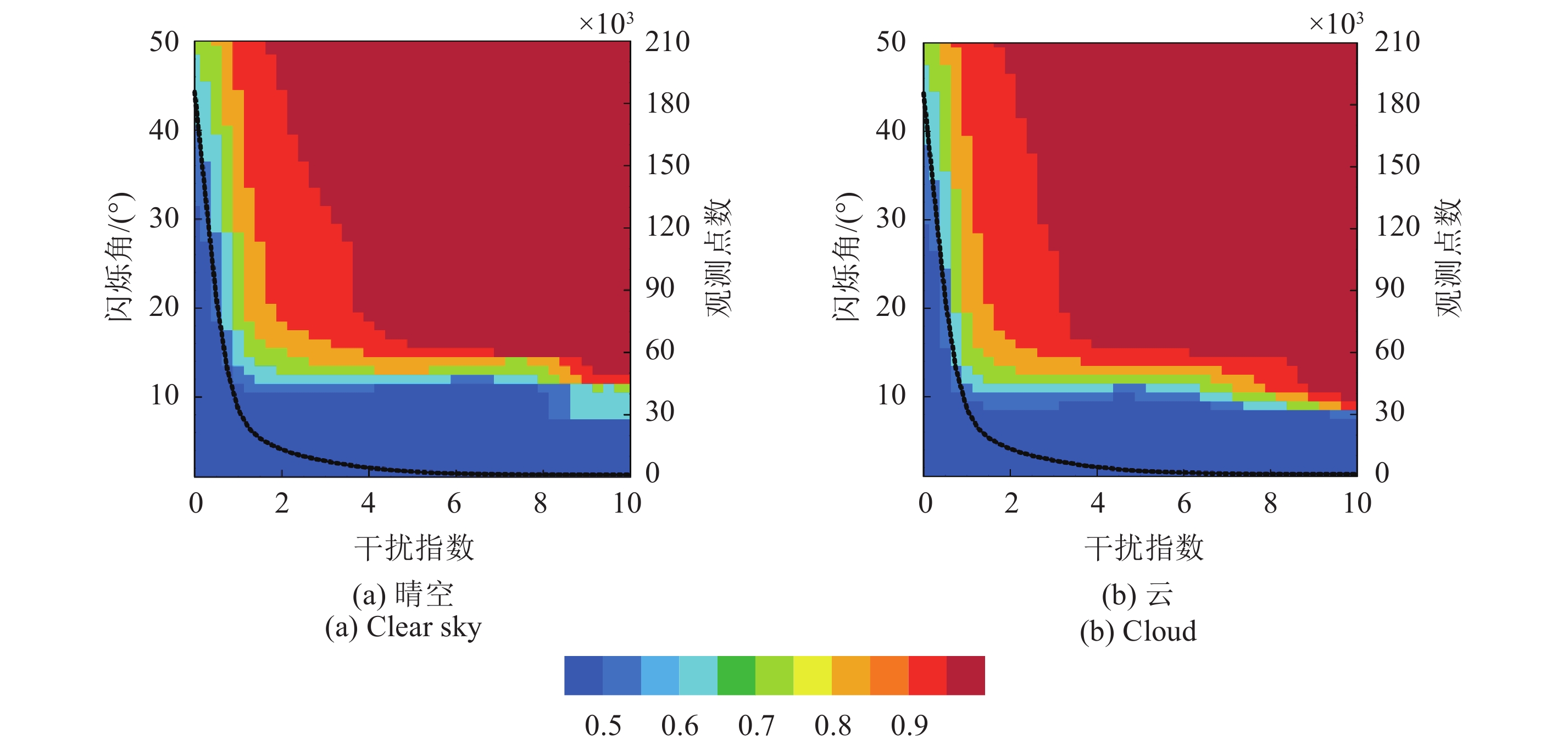
图7为R值随着闪烁角和识别信号的分布图,虚线对应的是右边Y轴格点数值,是当u≥x时的所有格点数。闪烁角和识别信号存在紧密的关系,闪烁角小并且干扰指数大的地区存在干扰信号,闪烁角大的地区不存在干扰信号,当满足干扰指数大,并且闪烁角较小这两个条件,且能找到最多的干扰信号时,认为该处的条件时可以作为干扰信号的判定阈值。
图7(a)是夏季欧洲海域观测区域晴空时选取5天数据统计的分布图,这里选取的观测区是地中海海域(30°N—50°N,0°E—25°E),通过FY-3C中分辨率光谱成像仪(MERSI)对观测区域的晴空和云区进行分类,观测区无云时为晴空,观测区有大量云存在时为云区。可以看到,当干扰指数≥6,闪烁角≤25°时,满足条件的地区占的比例达到90%以上,并且随着闪烁角的增大,其比例增长速度非常缓慢,认为当干扰指数≥6时的格点所处的位置均在闪烁角的小值区域。从整体格点变化规律(图中黑色虚线)来看,随着干扰指数的增长,当格点数迅速减少的时候,不存在干扰信号的格点正在被大量的去除,在干扰指数≤4之前变化率非常大,说明在干扰指数≤4时有大量的非RFI格点,而在干扰指数≥6之后的格点变化趋势较小,图7(b)是夏季欧洲海域观测区域有云情况下5天数据统计的干扰指数闪烁角比例图和对应u≥x虚线分布图,与晴空相比,两张图趋势基本一致,所以可以定义干扰指数阈值为干扰指数≥6,该方法定义的干扰指数可以应用于欧洲海域并且可剔除天气因素的影响。
远海地区可能会存在由于航道、游轮、航空等主动遥感发射装置导致的干扰信号,这种信号的位置和强度不明确。同时,由于静止电视卫星的下行信号主要存在于大陆地区,仅有小部分信号会辐射到靠近大陆的洋面上如图4,但是图4没有给出具体的电视信号的辐射范围。由于静止电视卫星下行信号导致的信号干扰仅存在于近大陆的洋面上,所以对干扰信号的离岸距离判定也是必要的。图8是干扰地区格点数随着离岸距离变化的折线图,当干扰地区格点数不增长或者增长缓慢时,认为在这个距离外,没有干扰信号的存在。从图8中可以看到,在离岸100 km以内的格点数增长迅速,离岸150 km以后,格点数增长非常缓慢,即在离岸150 km以外,没有干扰信号的存在。
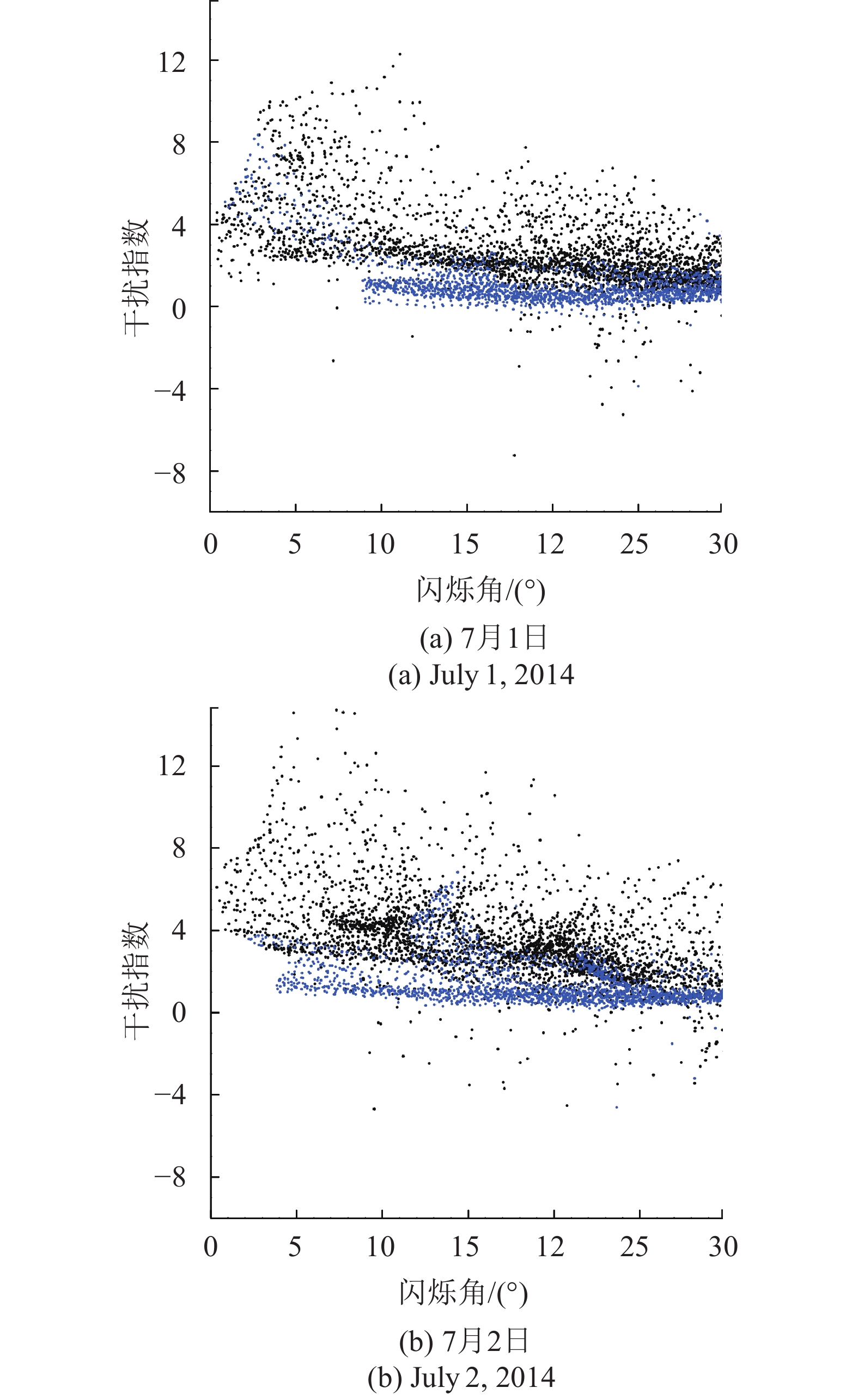
为进一步验证干扰指数和闪烁角以及离岸距离的关系,图9给出了7月1日和2日欧洲海域干扰指数和闪烁角的散点分布图。图9中黑色点是离岸150 km以内的点,蓝色点是离岸150 km以外的点。蓝色点几乎都集中在干扰指数0值附近,并且干扰指数不随着闪烁角的增长而变化,再次说明在远岸地区不存在干扰信号。黑色点的干扰指数高值区集中在闪烁角≤25°的范围内。
综上所述,将第3主成分u3≥6且离岸距离≤150 km作为是否受到静止卫星信号干扰的阈值判据。
4.3 北美近海海域MWRI资料的干扰信号的空间分布特征
在北美海域上,主要的静止电视卫星为Direct TV10和DirectTV11,其主要频率位于18.5 GHz— 19.1 GHz,所以MWRI受干扰的主要是18.7 GHz通道。同样对北美海域上亮温资料使用NPCA方法来进行TFI信号识别。图10是北美海域半月7月1日至16日干扰信号的分布图,从图10可看出干扰信号主要在分布美国的东西海岸,西海岸南起下加利福尼亚,北至华盛顿州海岸线沿岸均有干扰信号分布,东海岸则是马萨诸塞州一路南至佛罗里达州沿海,在华盛顿附近干扰强度很大,而在弗罗里达往西的部分南海岸附近也有干扰信号分布。
图11为北美区域的干扰指数阈值分析图,北美区域观测区选取北美东海岸(20°N—60°N,85°W—60°W),资料选取了2015年2月。图11中变量与图7一致,可以发现与夏季欧洲海域相比,无论晴空还是云区,四张图趋势基本一致,但干扰指数的大值区更加明显地集中在闪烁角的小值区域中,以至于在干扰指数≥4的观测点几乎完全集中在闪烁角≤25°的区域,这可能是由于北美海域主要是大范围海域,TFI的检测效果更加优秀所造成的。可以定义干扰阈值为干扰指数≥4,并且能够剔除天气因素的影响。
4.5 海表反演变量检验
为了检验TFI信号识别的正确性和必要性,这里还对海表温度(SST)和海表风速(SSW)进行反演试验,反演方法选用的是扈培信等人(2011)建立的反演方程,利用NCEP再分析资料中的海面风、海表温度资料和对应的AMSR-2资料,扈培信等人构造了SST和SSW的反演方程,反演公式为
|
$S\!S\!T\left( {S\!S\!W} \right) = {A_0} + \mathop \sum \limits_i A\left( i \right)T\left( i \right)$
|
(12) |
式中,T(i)是各通道亮温,A(i)是拟合系数,SST和SSW对应的系数值如表3。
表 3 MWRI全通道反演SST、SSW匹配系数列表
Table 3 Coefficients for the retrieval of SST and SSW based on MWRI observations
| A0 | 10.6V | 10.6H | 18.7V | 18.7H | 23.8V | 23.8H | 36.5V | 36.5H | 89V | 89H | |
| SST | 4.96 | 0.33 | –0.4 | –0.1 | 0.45 | 0.09 | 0.32 | –0.5 | –0.1 | 0.21 | 0.01 |
| SSW | 131 | 0.63 | –0.4 | –0.3 | –0.5 | –0.1 | 0.35 | –1.2 | 0.82 | –0.02 | 0.05 |
反演结果如图13,在欧洲海域TFI识别区域,对应区域反演的SST值要偏小,但对SSW的反演没有造成影响,而在北美海域TFI识别区域中,7月7日与7月23日是一个观测周期,其干扰信号位置大致相同,强度分布也基本一致,所反演的SST值均相对偏高,SSW值均相对偏低。说明TFI信号的存在对于海表气象要素的反演有一定的影响,也证明了TFI信号识别的正确性。同时由于经历了1个周期,两天的信号分布可见天气原因并不能对识别干扰信号造成影响。
5 结 论
微波成像仪低频通道海洋上的电视信号干扰识别对后续的卫星资料处理以及应用有重要的作用。本研究针对中国FY-3C卫星的微波成像仪资料,利用标准化主成分分析法对美国、欧洲和中国附近洋面的静止电视卫星干扰信号进行识别,并分析干扰来源以及空间分布特征,客观的给了NPCA方法干扰信号的识别阈值,从而为NPCA方法的全面应用提供了参考基础。结果表明:
(1) 标准化主成分分析法能够识别微波成像仪低频通道上由于静止电视、通讯卫星下行信号经由洋面反射所造成的无线电干扰,以第3主成分系数μ3≥6和离岸距离≤150 km,作为欧洲是否受到静止电视卫星下行信号的干扰的阈值,对北美而言,则使用干扰指数μ3≥4作为阈值。
(2) 欧洲海域降轨观测受到10.65 GHz通道上的干扰,干扰信号存在位置与闪烁角大小呈现密切的关系,干扰信号呈现周期性分布,闪烁角小的地区存在干扰信号的可能性就越大,具体静止卫星下行信号强度达到多少存在干扰信号仍有待研究,干扰信号来源主要来源于Hotbird静止卫星,欧洲海域英吉利海峡和地中海西部希腊沿岸地区有较强的信号分布。
(3) NPCA方法能够运用于全球海域的电视信号干扰的识别。10.65 GHz通道干扰信号主要存在于欧洲海域,18.7 GHz通道干扰信号存在于北美海域,但是由于电视卫星频率与MWRI各通道频率相差较大,中国海域在MWRI的所有通道均未受到电视信号的干扰。
(4) 在后续的研究中,将对干扰信号进行订正和剔除,并将微波成像仪数据应用到反演和同化研究应用中。
参考文献(References)
-
Adams I S, Bettenhausen M H, Gaiser P W and Johnston W. 2010. Identification of ocean-reflected radio-frequency interference using WindSat retrieval chi-square probability. IEEEGeoscience and Remote Sensing Letters, 7 (2): 406–410. [DOI: 10.1109/LGRS.2009.2037446]
-
Dong C H, Yang J, Yang Z D, Lu N M, Shi J M, Zhang P, Liu Y J, Cai B and Zhang W J. 2009. An overview of a new Chinese weather satellite FY-3A. Bulletin of the American Meteorological Society, 90 (10): 1531–1544. [DOI: 10.1175/2009BAMS2798.1]
-
Feng C C and Zhao H. 2015. Identification of radio-frequency interference signal from FY-3B microwave radiation imager over ocean. Journal of Remote Sensing, 19 (3): 465–475. [DOI: 10.11834/jrs.20154056] ( 冯呈呈, 赵虹. 2015. FY-3B微波成像仪海洋数据无线电干扰识别. 遥感学报, 19 (3): 465–475. [DOI: 10.11834/jrs.20154056] )
-
Gaiser P W, St.Germain KM, Twarog EM, Poe GA, Purdy W, Richardson D, Grossman W, Jones WL, Spencer D, Golba G, Cleveland J, Choy L, Bevilacqua RM and Chang PS. 2004. The WindSatspacebornePolarimetric microwave radiometer: sensor description and early orbit performance. IEEE Transactions on Geoscience and Remote Sensing, 42 (11): 2347–2361. [DOI: 10.1109/TGRS.2004.836867]
-
Guan L, Xia S C and Zhang S B. 2015. Identifying the interference of spaceborne microwave radiometer over large water area. Journal of Applied Meteorological Science, 26 (1): 22–31. [DOI: 10.11898/1001-7313.20150103] ( 官莉, 夏仕昌, 张思勃. 2015. 大面积水体上空星载微波辐射计的干扰识别. 应用气象学报, 26 (1): 22–31. [DOI: 10.11898/1001-7313.20150103] )
-
Hollinger J P, Peirce J L and Poe G A. 1990. SSM/I instrument evaluation. IEEE Transactions on Geoscience and Remote Sensing, 28 (5): 781–790. [DOI: 10.1109/36.58964]
-
Hu P X. 2011. Evaluation and Retrival of FY-3B Micro Wave Radiation Imager Brightness Temperature. Qingdao: Ocean University of China (扈培信. 2011. FY-3B微波成像仪数据质量评价与参数反演. 青岛: 中国海洋大学)
-
Kawanishi T, Sezai T, Ito Y, Imaoka K, Takeshima T, Ishido Y, Shibata A, Miura M, Inahata H and Spencer RW. 2003. The advanced microwave scanning radiometer for the earth observing system (AMSR-E), NASDA's contribution to the EOS for global energy and water cycle studies. IEEE Transactions on Geoscience and Remote Sensing, 41 (2): 184–194. [DOI: 10.1109/TGRS.2002.808331]
-
Kummerow C, Barnes W, Kozu T and ShiueJ andSimpson J. 1998. The tropical rainfall measuring mission (TRMM) sensor package. Journal of Atmospheric and Oceanic Technology, 15 (3): 809–817. [DOI: 10.1175/1520-0426(1998)015<0809:TTRMMT>2.0.CO;2]
-
Li L, Njoku E G, Im E, Chang P S and St. Germain K. 2004. A preliminary survey of radio-frequency interference over the U.S. in aqua AMSR-E data.IEEE Transactions on Geoscience and Remote Sensing, 42(2): 380–390 [DOI: 10.1109/TGRS. 2003.817195]
-
Li L, Gaiser P W, Bettenhausen M H and Johnston W. 2006. WindSat radio-frequency interference signature and its identification over land and ocean. IEEE Transactions onGeoscience and Remote Sensing, 44 (3): 530–539. [DOI: 10.1109/TGRS.2005.862503]
-
Njoku E G, Ashcroft P, Chan TK and Li L. 2005. Global survey and statistics of radio-frequency interference in AMSR-E land observations. IEEE Transactions on Geoscience and Remote Sensing, 43 (5): 938–947. [DOI: 10.1109/TGRS.2004.837507]
-
Oki T, Imaoka KandKachi M. 2010. AMSR instruments on GCOM-W1/2: concepts and applications//Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium. Honolulu, HI:IEEE: 1363–1366 [DOI: 10.1109/IGARSS.2010.5650001]
-
Wang Z Z. 2003. A Model for inversing sea surface wind speeds by using SSM/I 19.35 GHZ vertical and horizontal brightness temperatures. Ocean Technology, 22 (2): 1–6. [DOI: 10.3969/j.issn.1003-2029.2003.02.001] ( 王振占. 2003. 用19.35 GHz星载微波辐射计(SSM/I)亮温反演海面风速. 海洋技术学报, 22 (2): 1–6. [DOI: 10.3969/j.issn.1003-2029.2003.02.001] )
-
Zhao J, Zou X L and Weng F Z. 2013. WindSat radio-frequency interference signature and its identification over greenland and antarctic. IEEE Transactions on Geoscience and Remote Sensing, 51 (9): 4830–4839. [DOI: 10.1109/TGRS.2012.2230634]
-
Zou X L. 2012. Serial of applications of satellite observations Introduction to microwave imager radiance observations from polar-orbiting meteorological satellites. Advances in Meteorological Science and Technology, 2 (3): 45–50. [DOI: 10.3969/j.issn.2095-1973.2012.03.007] ( 邹晓蕾. 2012. 极轨气象卫星微波成像仪资料. 气象科技进展, 2 (3): 45–50. [DOI: 10.3969/j.issn.2095-1973.2012.03.007] )
-
Zou X L, Zhao J, Weng F Z and Qin Z K. 2012. Detection of radio-frequency interference signal over land from FY-3B Microwave Radiation Imager (MWRI). IEEE Transactions onGeoscience and Remote Sensing, 50 (12): 4994–5003. [DOI: 10.1109/TGRS.2012.2191792]
-
Zou X L, Tian X X and Weng F Z. 2014. Detection of television frequency interference with satellite microwave imager observations over oceans. Journal of Atmospheric and Oceanic Technology, 31 (12): 2759–2776. [DOI: 10.1175/JTECH-D-14-00086.1]