Print

出版日期: 2016-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20165288
2016 | Volumn20 | Number 6





                              上一篇|





下一篇
技术方法
ECM算法的多视SAR影像分割
expand article info 张英海1 , 李玉1 , 赵雪梅1 , 赵泉华1
辽宁工程技术大学 测绘与地理科学学院 遥感科学与应用研究所，辽宁 阜新 123000
收稿日期: 2015-11-23; 优先数字出版日期: 2016-11-25
基金项目: 国家自然科学基金(编号：41301479,41271435)；辽宁省自然科学基金(编号：2015020190)
第一作者简介: 张英海(1990—)，男，硕士研究生，研究方向为ECM算法及其在遥感数据处理中的应用。E-mail： 763979646@qq.com
中图分类号: TP701
文献标识码: A

摘要

多视SAR影像像素强度通常建模为Gamma分布，其形状参数为常数(视数)。实验表明，多视SAR影像分割时，设Gamma分布的形状参数为变量可取得更好的分割结果。由于Gamma分布中形状参数以Gamma函数的形式出现，利用EM算法求解时无法获得形状参数的解析解。为此，本文提出了一种基于Expectation/Conditional Maximization(ECM)算法的多视SAR影像分割方法。利用ECM算法估计最大化后验概率条件下的Gamma分布参数及表征最优多视SAR影像分割的标号场实现。采用模拟和真实多视SAR影像验证提出算法。实验结果表明，Gamma分布的形状和尺度参数均能快速收敛到稳态值，且以此得到各同质区域的Gamma分布曲线可以很好地拟合其直方图。通过对分割结果的定性和定量分析，可知提出算法具有有效性和可行性，且优于EM算法。

关键词

多视SAR影像 , ECM算法 , 影像分割 , 直方图拟合

ECM-based segmentation for multi-look SAR image
expand article info ZHANG Yinghai1 , LI Yu1 , ZHAO Xuemei1 , ZHAO Quanhua1
Institute for Remote Sensing Science and Application, School of Geomatics, Liaoning Technical University, Fuxin 123000, China

Abstract

The intensities of pixels in images of multi-look Synthetic Aperture Radar (SAR) are usually modeled by gamma distribution. To obtain a segmentation result, the parameters that indicate the distributions should be estimated. However, traditional expectation maximization (EM) algorithm cannot approach the shape parameter through taking partial derivation of the likelihood probability. Thus, to solve this problem, the shape parameter should be made equal to the number of looks, and only the scale parameter should be estimated. Nevertheless, the conclusion is obtained under the assumption that a pixel is constructed by infinite scattering units, which is impossible especially in high-resolution SAR images. Apparently, that assumption is unreasonable and will lead to inaccurate estimation of the corresponding parameters. Moreover, gamma distribution with fixed-shape parameter cannot completely describe the characteristics of intensity distribution in multi-look SAR images. Thus, this paper proposes a scheme for solving the parameter based on Expectation/Conditional Maximization (ECM) algorithm and develops a new segmentation algorithm for multi-look SAR images. First, the neighborhood system on the label field is considered, and Markov random field model is employed to define prior distribution. Then, intensities in each homogeneous region of a multi-look SAR image are modeled by gamma distribution, in which both shape and scale parameters are considered as variables. Finally, the gamma distribution along with the prior distribution constructs the posterior distribution, on which purpose it should be maximized. In this paper, Metropolis-Hastings algorithm is used as a random sampling method in estimating the marginal posterior probability model and changing the labels of each pixel. However, the estimation of the shape parameter remains a problem because it cannot be solved through partial derivation. ECM algorithm introduces the Newton iterative method to approach the real value of parameters, which cannot be directly solved from an equation. Therefore, shape parameter is evaluated by ECM algorithm, and all variables are obtained ultimately. The proposed algorithm is applied to simulated and real multi-look SAR images. Experimental results show that the proposed method can accurately estimate shape and scale parameters of gamma distribution. The proposed algorithm′s user, product, and total accuracies, and kappa coefficient are all higher than those of the EM algorithm′s, and the estimated values of the algorithm are much closer to the real values. The proposed algorithm can estimate the parameters of gamma distribution and the corresponding reality of the label field under the circumstance of maximized posteriori probability. Experiments on simulated and real multi-look SAR image verify the effectiveness and feasibility of the proposed algorithm, and the shape and scale parameters of gamma distribution can quickly converge to their stable state in a considerably short time. The ECM algorithm introduced in this paper can estimate the value of the shape parameter in gamma distribution, which is treated as the number of looks in the traditional EM algorithm. Thus, the connections between different looks are included in the distribution, and the corresponding segmentation results are improved.

Key words

multi-look SAR images , ECM algorithm , image segmentation , histogram fitting

1 引 言

合成孔径雷达(SAR)是一种高分辨率的雷达成像技术，具有覆盖范围广，能全天时、全天候工作( Zeng 等，2012)。在遥感技术的不断发展中，实现了SAR从低分辨率的单一工作模式到高分辨率的多工作模式，其应用范围非常广泛，特别是在对地观测中，如：地形测绘、地图绘制、土地覆盖及利用、农业、林业、生态科学、水文科学、海洋科学、灾害监测和应急响应等领域中发挥着越来越重要的作用。同时，在国民经济和军事应用领域也起着十分重要的作用( 常霞 等，2010)。虽然SAR技术有着众多的优点，但是在其成像的过程中会产生不可避免的斑点噪声，降低SAR影像的判读性。抑制斑点噪声的最有效方法是多视处理( 王隽 等，2008)，多视处理技术通常采用非相干叠加的方法使斑点噪声得到平滑，在一定程度抑制了斑点噪声，但难以完全消除斑点噪声。获得的多视SAR影像，由于其噪声的特性，使得传统基于区域和基于灰度等分割方法难以抑制噪声，从而不适用于SAR影像分割。近年来，基于Markov Random Field(MRF)模型( Li 等，2009; 宋晓峰 等，2010; 贾亚飞 等，2011; 倪维平 等，2011)的分割方法引起诸多学者的关注。MRF模型( 杨学志和沈晶，2009; 陈华杰和吴香伟，2010)不但考虑像素自身强度对分割结果的影响，还引入邻域像素作用，并结合其空间特性，有效地抑制了斑点噪声。

在影像分割中，为了获取模型参数，减少误分类现象，研究人员通常采用最大后验概率(MAP)算法( 李海生和贺新毅，2012)优化分割结果。多数情况下，MAP算法在计算上是难以实现的，并且在分割过程中，MAP算法需要给出模型参数的先验概率分布( 赵泉华 等，2013)。为了解决上述问题， Comer和Delp(2000)提出了Expectation Maximization/Maximization of the Posterior Marginal(EM/MPM)算法，该方法利用Gaussian分布建模，并结合EM/MPM算法对纹理影像进行分割。

对于SAR影像，传统EM算法均利用Gaussian分布建模SAR影像，然而 Goodman(1975)证明SAR影像服从Gamma分布( Deng和Clausi，2005)，用Gaussian分布建模会导致分割结果及参数估计出现一定的偏差。因此， 赵泉华等人(2013)提出了基于Voronoi几何划分和EM/MPM算法的多视SAR影像分割方法。该方法建立了Gamma分布SAR影像区域特征模型，为了解决Gamma分布中形状参数 α无法通过偏导求解的问题，将该参数看作多视SAR影像视数，避免了对Gamma分布中 Γ( α)求导的难题。但，满足形状参数 α等于其视数这一条件的前提是各视之间必须相互独立。事实上，在实际分割中各视之间并不相互独立，并且各参数之间存在着相关性。所以，在建模和分析过程中忽视了变化的形状参数和尺度参数之间的相互影响，这样分割出的结果，不可避免地存在着一些误差。为了解决这一问题，实现多视SAR影像分割，并同时准确地估计出其变化的形状参数 α和尺度参数 β，本文提出了一种基于ECM算法的多视SAR影像分割方法。为了实现优化分割的结果，本文采用Metropolis-Hastings(M-H)算法设计随机采样器，改变标号场操作。

2 算法描述

设 Z = { Z i = Z( x i ， y i );( x i ， y i )∈ D ， i=1， $ \cdots $ ， n}是影像域 D 上的离散随机场，其中， i为像素点索引；( x i ， y i )为第 i个像素点的位置； Z i 为表征第 i个像素点强度的随机变量，即定义在 D 上的连续随机函数 Z在( x i ， y i )点的采样； n为像素的总个数。给定影像 z = { z i : i=1， $ \cdots $ ， n}可以看作离散随机场 Z 的一个实现。 Z 所有可能实现构成的空间记为Ω Z 。

为了实现影像域的划分，首先，假设某个像素隶属于某一个目标类且每个像素之间相互独立；其次，为每一个像素 i分配一个标号变量 L i ∈{1， $ \cdots $ ， k}，以表征其隶属的目标类，其中 k为待分割影像的目标类总数。显然，对所有像素的标号集合 L = { L i : i=1， $ \cdots $ ， n}形成了一个随机标号场，而该随机标号场的每一个实现对应影像 z 的一个分割结果。同样，标号场的所有可能实现构成的空间记为Ω L 。

2.1 影像模型

为了建立影像特征场 Z 的统计分割模型，假设同一类标号像素满足同一独立的Gamma分布，分布参数 θ ={ θ l =( α l ， β l )； l∈(1， $ \cdots $ ， k)}， α为形状参数， β为尺度参数。每一个像素只与其在标号场内对应的标号有关，则

$p({ Z}\left| { L};{{\theta}} \right.)=\prod\limits_{i=1}^{n}{p({{Z}_{i}}\left| {{L}_{i}};{{\theta }_{{{L}_{i}}}} \right.)}$ (1)
$p({{Z}_{i}}\left| {{L}_{i}};{{\theta }_{{{L}_{i}}}} \right.)=\frac{1}{{{\varGamma}} ({{\alpha }_{{{L}_{i}}}})}\frac{Z_{i}^{{{\alpha }_{{{L}_{i}}}}-1}}{\beta _{{{L}_{i}}}^{{{\alpha }_{{{L}_{i}}}}}}\exp \left( -\frac{{{Z}_{i}}}{{{\beta }_{{{L}_{i}}}}} \right)$ (2)

像素的随机变量 Z i ( x i ， y i )∈ D 服从同一独立的Gamma分布，假设所有像素是相互独立，则影像模型可以表示如下：

$ \begin{aligned} & p({ Z}\left| { L};{{\theta}} \right.)=\prod\limits_{i=1}^{n}{p({{Z}_{i}}\left| {{L}_{i}};{{\alpha }_{{{L}_{i}}}},{{\beta }_{{{L}_{i}}}} \right.)}= \\ & \prod\limits_{i=1}^{n}{\frac{1}{\varGamma ({{\alpha }_{{{L}_{i}}}})}}\frac{Z_{i}^{{{\alpha }_{{{L}_{i}}}}-1}}{\beta _{{{L}_{i}}}^{{{\alpha }_{{{L}_{i}}}}}}\exp \left( -\frac{{{Z}_{i}}}{{{\beta }_{{{L}_{i}}}}} \right) \end{aligned}$ (3)

式中， Γ(·)为Gamma函数。

2.2 标号场模型

对像素 i，其标号 L i 的分布函数与其邻域像素标号有关为

$p({{L}_{i}}\left| {{L}_{i'}},i'\in {{N}_{i}} \right.)=\frac{1}{A}\exp \left\{ -2\eta \sum\limits_{i'\in {{N}_{i}}}{t({{L}_{i}},{{L}_{i'}})} \right\}$ (4)

式中， L i′ 是 L i 的邻域像素， N i 是像素 i的邻域像素集合。 A为归一化常数，由式(4)分子中所有可能的标号值求和得到， η是邻域像素间的空间作用参数，本文中为已知， t( L i ， L i′ )为指示函数

$t({{L}_{i}},{{L}_{i'}})=\left\{ \begin{align} & 1\ \ \ \ \ \ \ \ \ {{L}_{i}}\ne {{L}_{i'}} \\ & 0\ \ \ \ \ \ \ \ {{L}_{i}}={{L}_{i'}} \\ \end{align} \right.$ (5)

为了实现影像分割，需求得已知影像 Z 和参数 θ 条件下的标号场 L 的条件概率密度函数。根据贝叶斯定理，由上述条件概率密度函数可得

$\begin{equation} \begin{array}{l} p({{L}}\left| {{Z}} \right.;\theta ) \propto p({{Z}}\left| {{{L}};{{\theta}} } \right.) \! \times \! p(L) \! = \! \displaystyle\prod\limits_{i = 1}^n {\left( {\frac{1}{{{{\varGamma}} ({\alpha _{{L_i}}})}}\frac{{Z_i^{{\alpha _{{L_i}}} - 1}}}{{\beta _{{L_i}}^{{\alpha _{{L_i}}}}}} \! \times \! } \right.} \\ {\exp \left( { - \frac{{{Z_i}}}{{{\beta _{{L_i}}}}}} \right)} \Biggr) \! \times \displaystyle\prod\limits_{i = 1}^n {\frac{1}{{{A}}}} \exp \left\{ { - 2\eta \sum\limits_{i' \in {N_i}} {t({L_i},{L_{i'}})} } \right\} \end{array} \end{equation}$ (6)

为了实现影像分割，对标号场 L 进行估计，需要为每一个像素找到一个标号 l值，使如下函数最大：

$\tilde{ L}={\rm arg} \underset{{\tilde{ L}}}{\mathop{\rm max}}\, p({ L}\left| { Z};{ {\theta}} \right.)$ (7)

由于精确计算边缘概率是不可能的， Marroquin等人(1987)提出了边缘概率近似估计法，本文采用该算法近似估计边缘概率。设计随机采样器，根据式(6)的概率密度函数生成离散时间马尔可夫链 L ( t)={ L i ( t): i=1， $ \cdots $ ， n}，而 L ( t)收敛于标号场 L ，即对任意给定标号场的初始实现 l(0)，则

$\underset{t\to \infty }{\mathop{\lim }}\,p({ L}(t)=l\left( t \right)\left| { Z}=z,{ L}(0)=l(0) \right.)=p(l\left| z,\theta \right.)$ (8)

采样时只改变标号场的某一个标号 L i ，因此，定义在马尔可夫链上，则

${{a}_{i,l}}(t)=\left\{ \begin{align} & 1\ \ \ \ \ \ \ \ \ {{L}_{i}}\left( t \right)=l \\ & 0\ \ \ \ \ \ \ \ {{L}_{i}}\left( t \right)\ne l \\ \end{align} \right.$ (9)

给定影像下的标号场内某一标号的概率为

$p({{L}_{i}}=l\left| {{Z}_{i}}={{z}_{i}};{{\theta }_{l}} \right.)=\frac{1}{T}\sum\limits_{t=1}^{T}{{{a}_{i,l}}(t)}$ (10)

式中， T为随机采样的总次数，式(10)即为标号场 L 的估计，代替边缘概率进行参数估计。

采用M-H算法设计随机采样器，为了完备地采样，设计如下，对每次迭代采样都改变当前标号场操作。对于当前标号场 L ={ L i : i=1， $ \cdots $ ， n}以等概率(1/ n)在{1， $ \cdots $ ， n}中抽取任意值(如 i)，本次迭代只改变 L i 而其他标号保持不变，候选标号 L i *以等概率(1/ k)在{1， $ \cdots $ ， k}中抽取并满足： L i ≠ L i 。改变 L i 的接受概率可计算为

$\begin{equation*} {{a}_{L}}({{L}_{i}},L_{i}^{*})=\min \left\{ 1,R \right\} \end{equation*}$

式中，

$R=\!\frac{\prod\limits_{i=1}^{n}{\frac{1}{{{\varGamma}} ({{\alpha }_{L_{i}^{*}}})}}\!\times\! \frac{Z_{i}^{{{\alpha }_{L_{i}^{*}}}-1}}{\beta _{L_{i}^{*}}^{{{\alpha }_{L_{i}^{*}}}}}\!\times\! \exp \left( -\frac{{{Z}_{i}}}{{{\beta }_{L_{i}^{*}}}} \right)\!\times\! \exp \left\{ -2\eta \sum\limits_{i'\in {{ N}_{i}}}{t(L_{i}^{*},L_{i'}^{{}})} \right\}}{\prod\limits_{i=1}^{n}{\frac{1}{{{\varGamma}} ({{\alpha }_{{{L}_{i}}}})}}\!\times\! \frac{Z_{i}^{{{\alpha }_{{{L}_{i}}}}-1}}{\beta _{{{L}_{i}}}^{{{\alpha }_{{{L}_{i}}}}}}\!\times\! \exp \left( -\frac{{{Z}_{i}}}{{{\beta }_{{{L}_{i}}}}} \right)\!\times\! \exp \left\{ -2\eta \sum\limits_{i'\in {{ N}_{i}}}{t(L_{i}^{{}},{{L}_{i'}}}) \right\}}$ (11)

2.3 ECM算法参数估计

ECM算法可分为E-type和CM-type( Liu和Donald，1994； Wang和Lin，2013)，其中E-type与EM算法中E-type相同，CM-type是将EM算法中的M-type分解为 k次条件最大化。对上述条件概率密度求期望，可得到参数期望(E-type)( 罗季，2008； 卢洁 等，2011)

$ \begin{aligned} Q({{ {\theta}}^{(t+1)}}\left| { {\theta}} \right.,{ Z})=E[\log p({ Z},{ L};{{ {\theta}}^{(t+1)}})]= \\ E[\log p({ Z}\left| { L} \right.;{{ {\theta}}^{(t)}})]+E[\log p({ L};{{ {\theta}}^{(t)}})] \end{aligned} $ (12)

由于标号场 L 的概率密度函数与 θ 无关，式(12)右边第二项在计算时可忽略，参数 θ ( t+1) 是通过最大化期望函数 Q ( θ ( t) | θ ， Z )得到的，满足条件为

$ Q({{ {\theta}}^{(t+1)}}\left| { {\theta}} \right.,{ Z})\geqslant { Q}({{ {\theta}}^{(t)}}\left| { {\theta}} \right.,{ Z})$ (13)

求期望函数的参数估计值，可通过对期望函数求导，得出 α l ( t) ， β l ( t) 的通式为

$\alpha _{l}^{(t)}={{\varphi }^{-1}}\left( \frac{\sum\limits_{i=1}^{n}{(\ln {{Z}_{i}}-\ln \beta _{l}^{(t)}})\times p({{L}_{i}}^{(t)}=l)}{\sum\limits_{i=1}^{n}{p({{L}_{i}}^{(t)}=l)}} \right)$ (14)
$\beta _{l}^{(t)}=\frac{\sum\limits_{i=1}^{n}{\left\{ {{Z}_{i}}\times p({{L}_{i}}^{(t)}=l) \right\}}}{\alpha _{l}^{(t-1)}\times \sum\limits_{i=1}^{n}{p({{L}_{i}}^{(t)}=l)}}$ (15)

式(14)为对形状参数 α求导公式， φ( α)是Digamma函数， φ( α)= Γ( α)′/ Γ( α)， φ -1是Digamma函数的反函数。显然，利用EM算法无法通过求导计算 α的值。本文采用Newton-Raphson( Jensen 等，1991； Meng和Donald，1993； 凤尔银 等，2001； 温艳清 等，2009)方法可得到 α的近似公式

$\alpha _{l}^{(t)}=\alpha _{l}^{(t-1)}+\frac{\overline{y}-\varphi \left( \alpha _{l}^{(t-1)} \right)}{\varphi '\left( \alpha _{l}^{(t-1)} \right)+{{\left\{ \overline{y}-\varphi \left( \alpha _{l}^{(t-1)} \right) \right\}}^{2}}}$ (16)

式中，

$\overline{y}=\frac{\sum\limits_{i=1}^{n}{(\ln {{Z}_{i}}-\ln \beta _{l}^{(t)}})\times p({{L}_{i}}^{(t)}=l)}{\sum\limits_{i=1}^{n}{p({{L}_{i}}^{(t)}=l)}}$ (17)

对于多维参数 θ ={ θ l =( α l ， β l )； l∈(1， $ \cdots $ ， k)}，ECM算法中的CM-type将EM算法中的M-type分解为 k次条件最大化。在第 t+1次迭代中，记 θ l ( t) =( α l ( t) ， β l ( t) )， l∈(1， $ \cdots $ ， k)，得到期望函数 Q ( θ ( t) | θ ， Z )后。首先，在采样得到标号场 L 的估计 p( L i ( t) = l)后，利用 α l ( t) ，代入式(15)，得到 β l ( t+1) ，再根据Newton-Raphson方法，利用式(16)便可得到 α l ( t+1) ，经过 k次最大化，可得到一个最大化的 θ ( t+1) 。同样的方法进行下一次迭代，直至收敛或达到迭代的次数停止。

2.4 ECM算法估计，实现步骤如下：

(1) 设初始值 θ (0)=( α l (0)， β l (0))， l∈(1， $ \cdots $ ， k)；

(2) 执行 T次采样，利用式(10)可以得到标号场 L 的估计；

(3) 利用初始值及步骤(2)中得到的标号场 L 估计，代入式(15)(16)估计参数的估计值；

(4) 返回步骤(2)，直到达到总的循环次数或参数收敛稳定。

3 实验结果与讨论

3.1 模拟多视SAR影像实验分割

首先对模拟的多视SAR影像进行分割，验证本文算法的有效性和可行性。 图 1(a)为模拟影像模板，像素大小为128×128，其编号Ⅰ—Ⅴ代表不同的同质区域， 图 1(b)类别数为5，像素大小为128×128模拟生成的多视SAR影像。各同质区域像素服从同一独立的Gamma分布， 表 1列出各同质区域所对应模拟影像的形状参数 α和尺度参数 β。

表 1 模拟SAR影像Gamma分布参数
Table 1 Parameter value of Gamma distributions for simulated SAR image

下载CSV 
参数 区域
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ
α 3 4 5 6 7
β 5 10 20 25 30


图 1 模拟影像
Fig. 1 Simulated images

图 2是采用本文算法和EM算法对模拟的多视SAR影像进行分割结果图。本次实验是在Intel Core i7-4790 3.6 GHz/4 G内存/Matlab2010b环境下进行了100000次采样，800次迭代，本文算法和EM算法分别用时为23831.79 s和42253.07 s，可以说明本文算法较EM算法具有更好的收敛性。


图 2 分割结果
Fig. 2 Segmentation results

显然，与EM算法相比，本文算法明显优于EM算法。虽然本文算法在边界分割上还存在着一些缺陷，有少量的噪声，这在影像处理中是不可避免的。本文算法边界的分割优于EM算法，且噪声少。本文算法不仅能得到很好的分割结果，还得到了较为准确的分布参数估计值，而EM算法的估计的分布参数值，误差相对较大，如 表 2。

表 2 模拟影像各同质区域的形状参数和尺度参数估计值和真实值
Table 2 Estimated and real values of the shape and scale parameters for the homogeneous regions of the simulated image

下载CSV 
算法 参数 Ⅰ(估计值 /真实值) Ⅱ(估计值 /真实值) Ⅲ(估计值 /真实值) Ⅳ(估计值 /真实值) Ⅴ(估计值 /真实值)
ECM α 5.2/5.3 6.7/6.7 5.2/3.9 3.0/2.9 11.6/10.5
β 19.2/19.1 22.3/22.4 9.7/10.3 5.1/5.3 16.7/18.5
ECM算法参数误差比 α误差比/% 1.9 0 33.3 3.4 10.5
β误差比/% 0.5 0.4 5.8 3.8 9.7
EM α 4/10.4 4/5.4 4/4.4 4/3.2 4/6.7
β 48.3/18.5 25.1/18.5 9.9/8.9 3.6/4.6 37.5/22.3
EM算法参数误差比 α误差比/% 61.5 25.9 9.1 25 40.3
β误差比/% 161.1 35.7 11.2 21.7 68.2
注：误差比=(|估计值-真实值|)/真实值×100%。

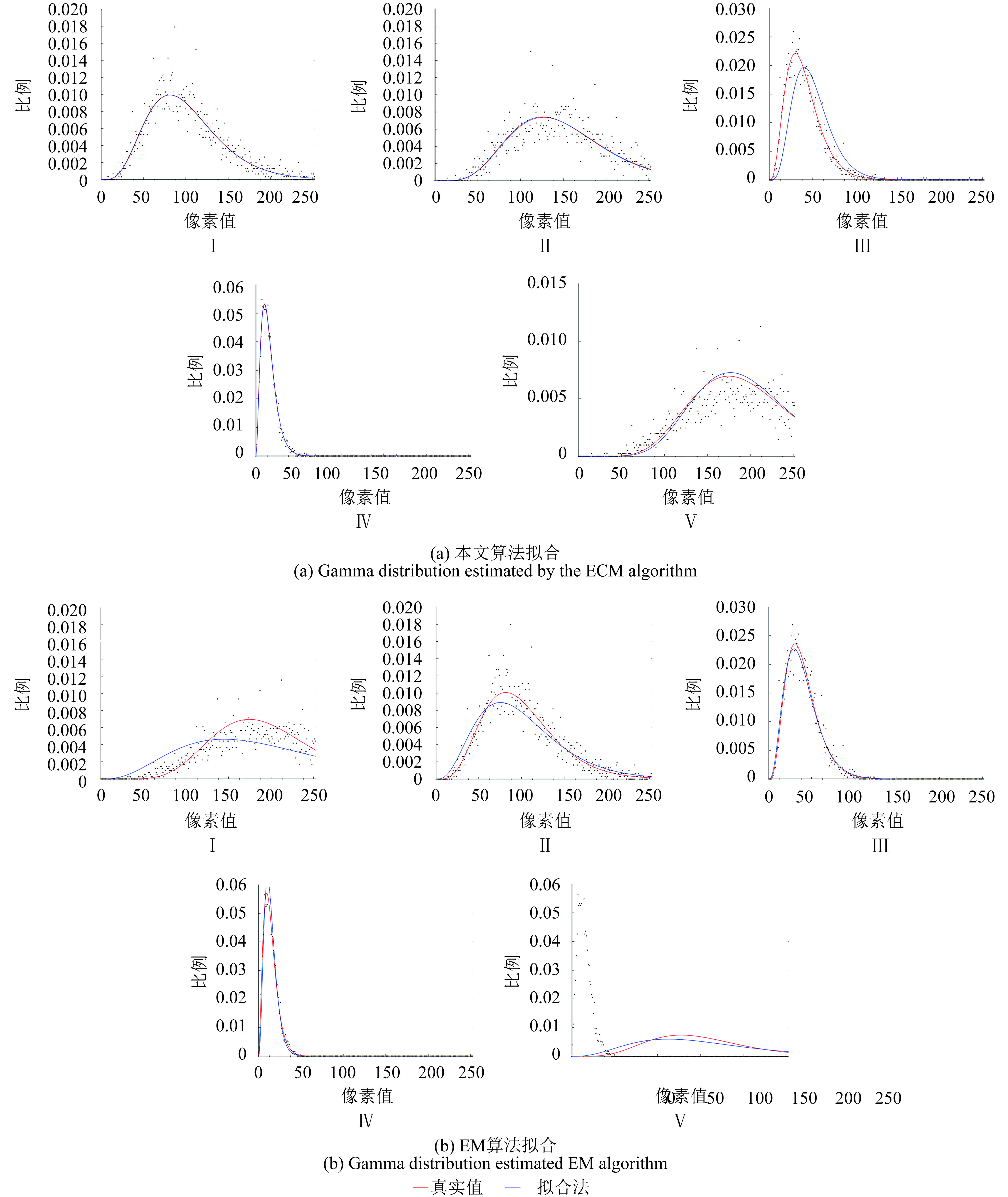
表 2中各同质区域参数的真实(Real)值是由分割结果所得到的标号集来求出各同质区域的各个参数值。本文算法得出的参数误差比在很小的范围内浮动，虽然同质区域Ⅲ、Ⅴ的参数误差比大于10%，主要是因为同质区域Ⅲ、Ⅴ在边界上的误分现象和噪声的影响，而EM算法的参数误差比浮动较大，是因为误分和噪声产生的。对各同质区域参数的真实值和估计值进行直方图拟合( 图 3)。


图 3 直方图拟合
Fig. 3 Fitting estimated Gamma distribution and the histogram for each homogeneous regions in simulated SAR multi-look

图 3(a) (b)为采用本文算法和EM算法对模拟影像分割得出的5个同质区域参数的直方图拟合曲线图。由模拟影像的各同质区域的直方图，分割结果得出的标号集求出每个同质区域的参数及本文算法估计出的参数，三者很好的拟合在一起。虽然 图 3(a)Ⅲ在拟合上出现偏差，由 表 2可以看出，出现的偏差是由于第3个(Ⅲ)同质区域 α误差比过大，主要是同质区域Ⅲ、Ⅴ在分割时在边界上产生的误差，第5类有一部分被分割到了第3类。而采用EM算法分割得出的参数拟合，出现较大的误差，其主要忽视了参数之间地相互影响，从而产生大量噪声。同时也证明了各参数之间存在着相关性，在一定程度上，其形状参数 α影响分割结果以及分割结果的精度。

本文模拟的多视SAR影像，其形状参数和尺度参数各不相同。尽管模拟的多视SAR影像各区域之间的参数相差不大，但本文算法很好地将其区分开，说明本文算法有很好地区分性。以模拟多视SAR影像的模板作为标准分割数据，求其混淆矩阵，计算其用户精度、产品精度、总精度和Kappa系数，对分割结果进行定量评价。( 表 3)

表 3 用户精度、产品精度、总精度和Kappa系数
Table 3 User accuracy，product accuracy，total accuracy and Kappa coefficient

下载CSV 
算法 同质区域 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ
ECM 用户精度/% 99.87 99.24 99.42 98.56 99.31
产品精度/% 99.97 98.80 99.61 99.00 99.14
Kappa系数 — — 0.9909 — —
总精度/% — — 99.27 — —
EM 用户精度/% 97.69 95.72 95.81 95.13 95.88
产品精度/% 98.14 96.38 96.40 93.89 95.26
Kappa系数 — — 0.9501 — —
总精度/% — — 96.03 — —

由 表 3可知，本文算法用户精度都大于98%，产品精度都大于98%，其Kappa系数为0.9909，且本文算法各种精度都优于EM算法。一般认为，Kappa系数达到0.8以上的分割算法具有有效性。因此，可以说明本文算法有一定的有效性和可行性。

3.2 真实多视SAR影像分割

图 4为真实待分割多视SAR影像，像素大小均为128×128，显然，由影像可目视判别出各影像的类别数， 图 4(a) (b) (c)类别数分别为3、4、5。首先，为尺度参数和形状参数设定随机值，随机采样次数设为 T=50000，迭代循环次数设为200。 图 5为采用本文算法和EM算法得到的分割结果图， 图 6、 图 7为采用本文算法和EM算法对其各同质区域直方图拟合曲线图， 表 4为采用本文算法和EM算法对真实多视SAR影像分割后的估计参数值。

表 4 真实SAR影像的参数估计值与真实值
Table 4 Real and estimated values of the Gamma distribution parameters for real SAR images

下载CSV 
影像 算法 参数 Ⅰ(估计值/真实值) Ⅱ(估计值/真实值) Ⅲ(估计值/真实值) Ⅳ(估计值/真实值) Ⅴ(估计值/真实值)
示例1 ECM α 29.3/28.2 14.3/15.1 18.4/18.1 — —
β 6.6/6.8 3.1/2.9 6.6/6.6 — —
EM α 4/12.2 4/14.2 4/26.9 — —
β 32.8/10.8 10.9/3.1 48.1/7.2 — —
示例2 ECM α 31.3/31.7 17.4/17.3 19.6/19.6 17.8/18.4 —
β 6.7/6.6 6.6/6.6 2.4/2.4 1.7/1.6 —
EM α 4/14.1 4/17.4 4/24.6 4/12.4 —
β 7.6/2.1 11.7/2.7 51.9/8.4 27.8/8.9 —
示例3 ECM α 22.6/22.9 16.2/16.4 5.6/5.8 21.9/21.9 55.5/55.7
β 8.0/7.9 2.3/2.2 2.3/2.2 5.1/5.2 4.0/4.0
EM α 4/16.7 4/12.8 4/29.9 4/17.8 4/6.9
β 29.2/7.0 9.0/2.8 53.6/7.2 44.7/10.0 2.7/1.5


图 4 真实SAR影像
Fig. 4 Real SAR images

对比 图 5(a)本文算法较EM算法而言更好地减少了噪声；对比 图 5(b)本文算法更好地减少了噪声及误分现象；对比 图 5(c)本文算法减少了错分和误分，类别数也更加清晰。从视觉角度分析，本文算法明显优于EM算法，主要是由于本文算法在分割过程中考虑了变化的形状参数对分割结果的影响，因此得到的分割结果优于EM算法。本文算法和EM算法对多视SAR影像分割的同时都会得到分割后的参数估计值，如 表 4，可以看出本文算法估计出的参数值更接近多视SAR影像的真实分布参数值，而采用EM算法估计的参数值与真实值相差较大。对其各同质区域参数进行直方图拟合( 图 6、 图 7)。显然，本文算法可更好地与直方图拟合，而EM算法在拟合直方图时相差太大。EM算法直方图拟合产生较大误差主要是由于没有考虑各参数之间的相关性，形状参数 α被限定为4，对唯一的变量 β求导并进行最大化。此种方法的前提是各视之间相互独立，但是，在实际中，各视之间并不相互独立，并且SAR影像在成像过程中产生噪声具有随机性和复杂性，诸多因素都会影响SAR影像的成像，同样这些因素也会影响分割结果的精度。本文算法既考虑了各视之间地相关性，也着重强调各参数之间的相互影响，借用Newton-Raphson公式对 α， β进行迭代最大化。对本文算法的分割结果进行定量分析证明了本文算法行之有效，且分割的结果和参数估计值都优于EM算法。


图 5 分割结果比较
Fig. 5 Comparison of segmentation results

4 结 论

本文针对Gamma分布的多视SAR影像利用EM算法无法对其形状参数求导并进行估计的问题，提出了ECM算法。利用ECM算法不仅实现了对Gamma分布的多视SAR影像分割，而且又能对其形状参数和尺度参数进行同步估计。与EM算法相比，本文算法同时考虑变化的形状参数和尺度参数得到了较好的分割结果，进而证明了Gamma分布的多视SAR影像其形状参数和尺度参数之间具有相关性。在得到标号场的基础上，计算出各同质区域内真实参数，并且与本文算法估计出的参数在直方图拟合时也较为吻合。本文算法既有EM方法的收敛性，又能很好地实现影像分割以及参数估计。由 表 4可知，EM算法估计的参数值与实际的参数值相差较大，主要是EM算法忽视了参数之间的相关性。本文算法着重考虑变化的形状参数对分割结果及参数值的影响，实现了影像分割，并得到了较为准确的参数估计值，本文算法估计出的参数值完全可以应用于与之相关的工作中，如：地物反演。在以后的工作中将本文算法应用到多维参数的估计中以及可变类的多视SAR影像分割中。

参考文献(References)

数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献