|
收稿日期: 2016-01-08; 优先数字出版日期: 2016-11-25
基金项目: 国家自然科学基金(编号: 41271435,41301479)
第一作者简介: 王玉(1990—),女,博士研究生,研究方向为遥感图像处理。E-mail:
1009059221@qq.com
中图分类号: TP751
文献标识码: A
|
摘要
确定图像类别数是图像分割中的重要任务,在大多数分割算法中需由用户预先指定类别数。受地物目标及其分布的多样性、复杂性和未知性等因素的限制、对彩色遥感图像而言,人为确定其类别数非常困难。为此,提出了一种基于区域和统计的可变类分割方法,融合规则划分技术和RJMCMC算法,利用规则划分将图像域划分成若干个规则子块,并假设每个规则子块内的像素服从同一独立的多值Gaussian分布;在此基础上由贝叶斯定理构建图像分割模型;利用Reversible Jump Markov Chain Monte Carlo(RJMCMC)算法模拟该模型,实现图像类别数的自动确定及图像粗分割;为了进一步提高图像分割精度,设计精细化操作,对Worldview-2合成及彩色遥感图像和多光谱IKONOS图像进行可变类分割,实验结果表明,提出方法不仅能自动确定图像类别数,还可以较好地实现区域分割。本文方法较好地实现彩色遥感图像的可变类分割。
关键词
可变类分割 , 彩色遥感图像 , 规则划分 , RJMCMC算法 , 贝叶斯定理
Abstract
Image segmentation has been a hot topic in image processing. It involves two tasks: determining the number of homogeneous regions and segmenting them. Most image segmentation algorithms mainly focus on the latter and determine a priori the number. Artificially determining the number of classes is difficult for certain reasons. Consequently, the number should be automatically determined.A statistical and region-based segmentation approach for color remote-sensing images is introduced in this paper. First, the image domain is partitioned into groups of regular sub-regions (or blocks) by regular tessellation. Second, the image is modeled on the assumption that the intensities of its pixels in each homogeneous region follow an identical and independent multivariate Gaussian distribution. The Bayesian paradigm is applied to establish the image segmentation model. Third, a reversible-jump Markov chain Monte Carlo (RJMCMC) scheme is designed to simulate the segmentation model, which determines the number of classes and roughly segments the image. A refined operation is performed to improve the accuracy of the image segmentation results further.Real and synthetic color remote-sensing images from Worldview-II and multispectral IKONOS images are tested. Qualitative and quantitative evaluation results are obtained to verify the feasibility and effectiveness of the proposed method. The proposed method exhibits advantages over two other segmentation methods, namely, the ISODATA method and the segmentation method combining Voronoi tessellation with EM/MPM algorithm.An image segmentation approach based on regular tessellation and RJMCMC algorithm is proposed in this study. The proposed approach can not only automatically determine the number of classes but also segment homogenous regions better. Furthermore, the test results also show that the approach demonstrates high performance and high efficiency. In future studies, other tessellation methods can be used to partition the image domain.
Key words
segmentation of unknown number of classes , multispectral remote sensing image , regular tessellation , RJMCMC algorithm , Bayesian paradigm
1 引 言
图像分割是图像处理中的重点问题之一,它包括两个基本任务:确定图像类别数及分割同质区域。目前,灰度图像的分割算法相对成熟,主要分为阈值分割( 李积英 等,2014; 尹奎英 等,2011; 吴一全 等,2012)、聚类分割( 卢洁 等,2011; 田小林 等,2008; 于波 等,2013)和统计分割( 倪维平 等,2011; 杨学志 等,2014; 郑玮 等,2008)等。随着传感器技术的不断发展,人们可以获取越来越多的彩色遥感图像,由此,其分割技术的开发引起广泛的重视。对彩色遥感图像而言,受地物目标及其分布的多样性、复杂性和未知性等因素的限制,人为确定其类别数非常困难。因此,实现彩色遥感图像的可变类分割是相当必要的,同时也是十分困难的工作。
研究表明,针对回归变量选择、目标识别、图像分割等诸多可变类问题,基于统计的处理方法是最为有效的方法(Green,1995; Richardson和Green,1997; Kato,2008)。为了解决上述可变类问题,Green (1995)提出RJMCMC(Reversible Jump Markov Chain Monte Carlo)算法。该算法通过构建马尔可夫随机场链,使其状态能够在不同维度的参数空间跳变,最终实现目标概率密度函数的模拟。在Green(1995)工作基础上,Richardson和Green(1997)利用RJMCMC算法模拟贝叶斯混合模型,实现混合模型中组分数及各组分概率分布参数估计。但该研究只适用于小数据量混合模型。Kato(2008)将高斯混合模型与RJMCMC算法相结合,以完成可变类彩色图像分割。该方法虽能实现彩色图像分割,但图像分割细节模糊。
以上方法均为基于像素的图像分割,但基于像素的方法很难解决高分辨率遥感图像分割问题,分割精度较低,为此,研究者试图在图像建模过程中引入区域处理的思想,即,对图像域进行几何划分,并建立基于区域的图像模型。常用的几何划分方法有:规则划分(Askari 等,2013)、Voronoi划分(Lucarini 等,2009; 赵泉华 等,2013)和泊松划分(Schneider,2009,2010)等。由于规则划分在划分图像域时原理简单、操作方便,可快速地实现图像域的划分。
本文提出了一种融合规则划分和RJMCMC算法的彩色遥感图像可变类分割方法。首先,利用规则划分将图像域划分成若干个相同大小的规则子块,并建立基于区域的图像分割模型。然后,利用RJMCMC算法自动确定图像类别数,并实现粗分割。为了提高图像精度,提取分割图像同质区域的边界线,并以这些边界线为中心生成缓冲区,再利用邻域准则对缓冲区的每个像素重新分类,生成新的分割区域边界线。在RJMCMC算法中,设计的移动操作类型包括:分裂或合并实类、改变参数矢量、改变标号及生成或删除空类。为了验证提出的方法,分别对合成及彩色遥感图像进行可变类分割实验,定性和定量的评价结果表明提出方法的可行性及有效性。
2 算法描述
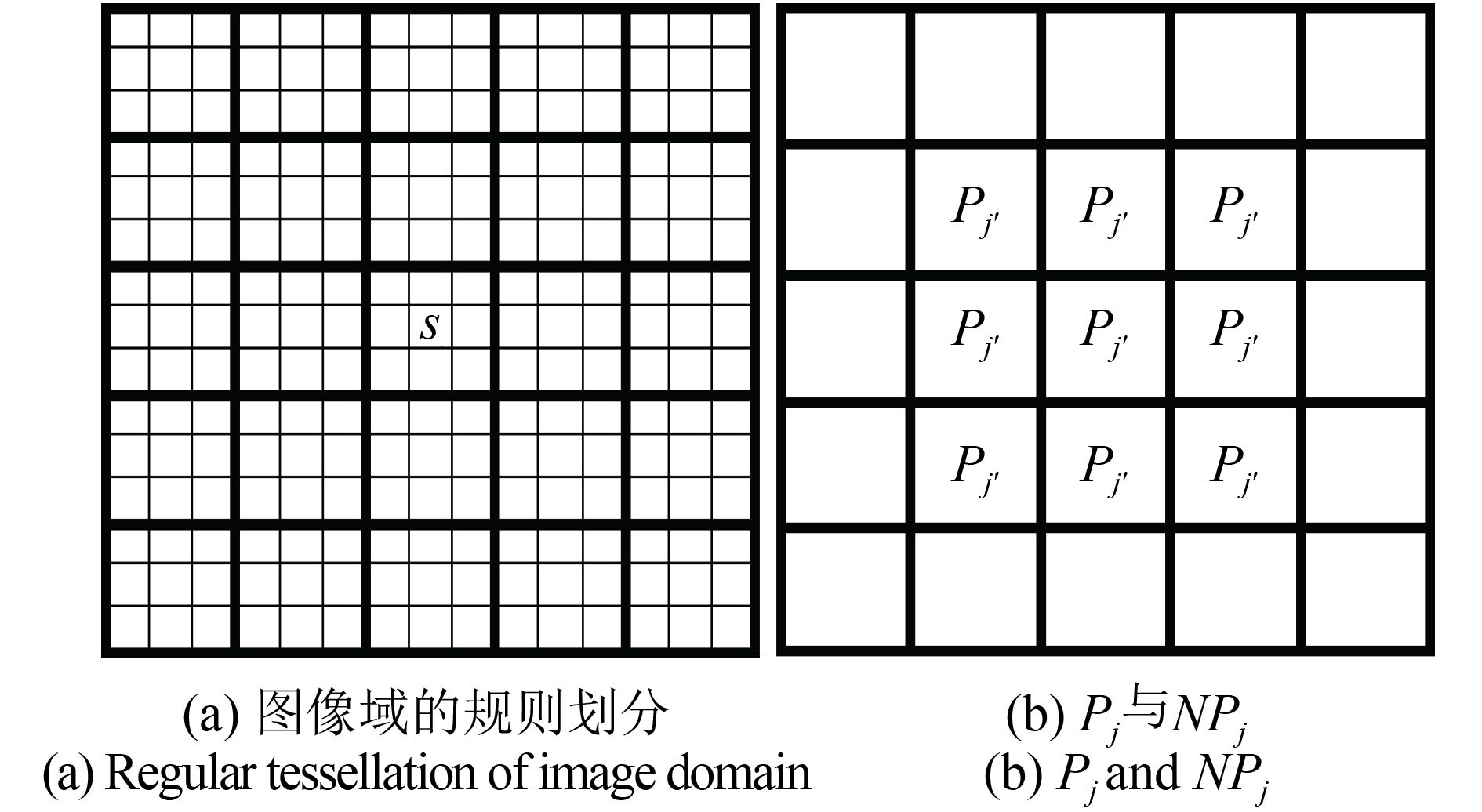
2.1 图像分割模型
彩色遥感图像
z
={
z
s
,
s ∈
S
}可以看作定义在图像域
S
上的离散随机场
Z
={
Z
s
,
s ∈
S
}的一个实现,其中,
Z
s
={
Z
sd
,
d=1,
为了建模遥感图像,首先利用规则划分将
S
划分成
J 个含
m ×
m 个像素规则子块,
S
={
P
j
,
j=1,
为每个规则子块
P
j
分配一个标号变量
X
j
∈{1,
为了表达邻域子块标号的相关性,在规则划分的图像域上建立MRF模型,并采用改进的静态Potts模型定义其邻域关系(
Besag,1986;
Strauss,1975)。假设
X
j
(
j=1,
| $\begin{aligned} & p({\textbf{\emph{X}}}|k)=\prod\limits_{j=1}^{J}{p({{X}_{j}}|{{X}_{{{j}^{'}}}},{{P}_{j'}}\in {{N}}{{{P}}_{j}})}= \\ & \text{ }\prod\limits_{j=1}^{J}{\frac{\exp \left\{ -\eta \sum\limits_{{{P}_{j'}}\in {{N}}{{{P}}_{j}}}{t({{X}_{j}},{{X}_{j'}})} \right\}}{\sum\limits_{{{l}^{'}}=1}^{k}{\exp \left\{ -\eta \sum\limits_{{{P}_{j'}}\in {{N}}{{{P}}_{j}}}{t({{l}^{'}},{{X}_{j'}})} \right\}}}} \\ \end{aligned}$ | (1) |
式中, η 为邻域子块的空间作用参数; NP j 为规则子块 P j 的八邻域子块的集合(如 图 1(b)), t 为指示函数,若 X j ≠ X j' , t ( X j , X j' )=1;否则为0。
假设,同一个规则子块 P j 中具有标号 X j = l 的随机变量 Z j ={ Z s , s ∈ P j }服从独立的多值Gaussian分布,其概率密度函数具体如下
式中,
Φ
l
=(
μ
l
,
Σ
l
),
μ
l
=(
u
l
1,
进一步假设,所有规则子块相互独立,则 Z ={ Z j , j=1,…, J}的概率密度函数为
| $ \begin{aligned} p({\textbf{\emph{Z}}}|{\textbf{\emph{X}}},{{{\varPhi }}},k)=\prod\limits_{j=1}^{J}{p({{{\textbf{\emph{Z}}}}_{j}}|{{X}_{j}}=l,{{{{\varPhi}}}_{l}})} \end{aligned} $ | (3) |
假设类别数 k 为随机变量,服从均值为 λ 的泊松分布,则其概率密度函数为
| $ \begin{aligned} p(k)=\frac{{{\lambda}^{k}}}{k!}\exp (-\lambda) \end{aligned} $ | (4) |
多值Gaussian分布的均值(协方差)参数 μ l ( Σ l )的各分量,服从均值 μ μ ( μ Σ )、标准差 σ μ ( σ Σ )的正态分布且相互独立( Yong 等,2006),则其概率密度函数可分别写为
| $\eqalign{ & p(\mu ) = \prod\limits_{l = 1}^k {\prod\limits_{i \in \{ 1, \cdots ,r\} } {p({\mu _{li}})} } \cr & = \prod\limits_{l = 1}^k {{\prod _{i \in \{ \{ 1, \cdots ,r\} }}{1 \over {\sqrt {2\pi } {\sigma _\mu }}}\exp \left\{ { - {{{{({\mu _{li}} - {\mu _\mu })}^2}} \over {2\sigma _\mu ^2}}} \right\}} \cr} $ | (5) |
| $\eqalign{ & p(\sum ) = \prod\limits_{l = 1}^k {\prod\limits_{i \in \{ 1, \cdots ,r\} } {\prod\limits_{i' \in \{ 1, \cdots ,r\} } {p({\sum _{lii'}})} } } \cr & = \prod\limits_{l = 1}^k {\prod\limits_{i \in \{ 1, \cdots ,r\} } {\prod\limits_{i' \in \{ 1, \cdots ,r\} } {{1 \over {\sqrt {2\pi } {\sigma _\sum }}}\exp \left\{ { - {{{{({\sum _{lii'}} - {\mu _\sum })}^2}} \over {2\sigma _\sum ^2}}} \right\}} } } \cr} $ | (6) |
多值Gaussian分布的参数矢量 Φ =( μ , Σ ),假设 μ 和 Σ 相互独立,且根据贝叶斯定理得到联合后验概率密度函数 p ( k, X , Φ | Z ),即
| $\begin{aligned} & p(k,{\textbf{\emph{X}}},{{{\varPhi }}}|{\textbf{\emph{Z}}})\propto p({\textbf{\emph{Z}}}|{{{\varPhi}}}{\textbf{\emph{X}}},{\textbf{\emph{X}}},k)p({\textbf{\emph{X}}}|k)p({{{\varPhi}}}|k)p(k) \\ &=p({\textbf{\emph{Z}}}|{{{\varPhi}}},{\textbf{\emph{X}}},k)p({\textbf{\emph{X}}}|k)p(k)p({{{\mu}}}|k)p({\textbf{\emph{∑}}}|k) \\ \end{aligned}$ | (7) |
2.2 RJMCMC算法
2.2.1 基本原理
假设总参数矢量
| $a(\varphi ,{{\varphi }^{*}})=\min \left\{ 1,\frac{p({{\varphi }^{*}}|Z)q({{\varphi }^{*}},\varphi )}{p(\varphi |Z)q(\varphi ,{{\varphi }^{*}})} \right\}$ | (8) |
当参数空间维度不变时,式(8)可简化为( Green,1995)
| $a({{\varphi }_{l}},\varphi _{l}^{*})=\min \left\{ 1,\frac{p(Z|\varphi _{l}^{*})p(\varphi _{l}^{*})}{p(Z|{{\varphi }_{l}})p({{\varphi }_{l}})} \right\}$ | (9) |
式中,
当参数空间维数改变时,其接受率表示为
| $a(\varphi ,{{\varphi }^{*}})=\min \left\{ 1,\text{ }\frac{p({{\varphi }^{*}}|Z){{q}_{m}}({{\varphi }^{*}},\varphi )}{p(\varphi |Z){{q}_{m}}(\varphi ,{{\varphi }^{*}})} \right\}$ | (10) |
式中,
m 移动操作的转换概率
q
m
(
2.2.2 移动操作类型及其接受率
在RJMCMC算法中,设计了如下的移动操作。对每次迭代需遍历所有的移动操作;在每次迭代中,每个移动操作的初始状态为上一个操作的结果状态;而前一次迭代参数结果是后一次迭代的初始参数。
(1) 分裂或合并实类
在图像域中有对应的规则子块隶属该类别,则该类别为实类,
k
r
表示其实类别数。分裂操作就是将一组同标号的规则子块集合分解为两组标号不同的规则子块集合。在当前状态下,假设
S
={
S
1,
| $ \begin{aligned} {{a}_{{{s}_{r}}}}({\varphi} ,{{\varphi}^{*}})=\min \left\{ 1,\text{ }{{R}_{{{s}_{r}}}} \right\} \end{aligned} $ | (11) |
式中,
| $$ | (12) |
| $\begin{align} & {{R}_{{{s}_{r}}}}=\frac{p(Z_{l}^{*}|\Phi _{l}^{*},X_{l}^{*},k+1)p(Z_{k+1}^{*}|{{\Phi }_{k+1}},{{X}_{k+1}},k+1)}{p({{Z}_{l}}|{{\Phi }_{l}},{{X}_{l}},k)}\times \\ & \frac{p(X_{l}^{*}|k+1)p(X_{k+1}^{*}|k+1)}{p({{X}_{l}}|k)}\times \frac{{{r}_{{{m}_{k+1}}}}}{{{r}_{{{f}_{k}}}}}\times \frac{p(k+1)}{p(k)}\times \\ & \frac{p({{\mathbf{\mu }}_{k+1}})p({{\sum }_{k+1}})}{q(u)}\times \left| \frac{\partial {{\varphi }_{k+1}}}{\partial ({{\varphi }_{k}},u)} \right| \\ \end{align}$ | (12) |
式中,
r
f
k
=
f
k
/{
k
r
(2
B
-2)},其中选择分裂操作的概率为
f
k
,
B 为分裂前标号为
l 的所有规则子块的总个数;
合并实类操作是分裂实类操作的对偶操作,即在现有实类中随机选择两个实类,将其合并成一个新的实类。因此,其接受率为
| $ \begin{aligned} {{a}_{{{m}_{r}}}}({\varphi},{{\varphi}^{*}})=\min \left\{ 1,\text{ }1/{{R}_{{{s}_{r}}}} \right\} \end{aligned} $ | (13) |
(2) 改变参数矢量 Φ
等概率(1/
k)的从{1,
首先判断 l 是空类还是实类,若是空类,则对应的接受率为
| ${{a}_{{{\varPhi }}}}({{{{\varPhi}}}_{l}},{{{\varPhi}}}_{l}^{*})=\min \left\{ 1,\text{ }\frac{p({{{\varPhi}}}_{l}^{*}|k)}{p({{{{\varPhi}}}_{l}}|k)} \right\}$ | (14) |
若 l 是实类,则其接受率为
| ${{a}_{\Phi }}({{\Phi }_{l}},\Phi _{l}^{*})=\min \left\{ 1,\frac{\prod\limits_{{{P}_{j}}\in {{S}_{l}}}{p({{Z}_{j}}|{{X}_{j}}=l,\Phi _{l}^{*})p(\Phi _{l}^{*}|k)}}{\prod\limits_{{{P}_{j}}\in {{S}_{l}}}{p({{Z}_{j}}|{{X}_{j}}=l,{{\Phi }_{l}})p({{\Phi }_{l}}|k)}} \right\}$ | (15) |
(3) 改变标号场
等概率(1/
J)从图像域
S
={
P
j
,
j=1,
| ${{a}_{X}}({{X}_{j}}=l,{{X}_{j}}={{l}^{*}})=\min \left\{ 1,\frac{p({{Z}_{j}}|{{X}_{j}}=l,{{\Phi }_{{{l}^{*}}}})p({{X}_{j}}={{l}^{*}}|k)}{p({{Z}_{j}}|{{X}_{j}}=l,{{\Phi }_{l}})p({{X}_{j}}=l|k)} \right\}$ | (16) |
(4) 生成或删除空类
如果一类别数在图像域中没有对应的规则子块集合,那么这个类别数为空类,
k
e
表示其空类数。移动操作过程为生成一空类,设其标号为
k+1;由于该操作仅改变参数矢量
Φ
和标号场
X
,故令候选总参数矢量
| ${{a}_{{{b}_{e}}}}({\varphi},{{\varphi}^{*}})=\min \{1,{{R}_{{{b}_{e}}}}\}$ | (17) |
式中,
| $\begin{align} & {{R}_{{{b}_{e}}}}=\frac{p({{\varphi }^{*}}){{r}_{{{d}_{k+1}}}}({{\varphi }^{*}})}{p(\varphi ){{r}_{{{b}_{k}}}}(\varphi )q(u)}\left| \frac{\partial {{\Phi }^{*}}}{\partial (\Phi ,u)} \right|= \\ & \frac{p({{\Phi }^{*}}|k+1)p({{X}^{*}}|k+1)p(k+1)}{p(\Phi |k)p(X|k)p(k)}\times \frac{{{r}_{{{d}_{k+1}}}}({{\varphi }^{*}})}{{{r}_{{{b}_{k}}}}(\varphi )q(u)}\left| \frac{\partial {{\Phi }^{*}}}{\partial (\Phi ,u)} \right| \\ \end{align}$ | (18) |
式中,
r
d
k+1
=
d
k
+1/(
k
e
+1)和
r
bk
=
b
k
,其中
d
k
+1、
b
k
分别为选择其对应操作的概率。设
u
=(
综上所述,式(18)可简化为
| $\begin{align} & {{R}_{{{b}_{e}}}}=\frac{{{d}_{k+1}}p({{X}^{*}}|k+1)p(k+1)}{{{b}_{k}}({{k}_{0}}+1)p(X|k)p(k)}= \\ & \frac{{{d}_{k+1}}\underset{{{P}_{j}}\in S}{\mathop{\prod }}\,\sum\limits_{l'=1}^{k}{\exp \left\{ -\eta \sum\limits_{{j}'\in N{{P}_{j}}}{t(l',{{X}_{{{j}'}}})} \right\}}\lambda }{{{b}_{k}}({{k}_{e}}+1)\underset{{{P}_{j}}\in S}{\mathop{\prod }}\,\sum\limits_{l'=1}^{k+1}{\left\{ -\eta \sum\limits_{{j}'\in N{{P}_{j}}}{t(l',{{X}_{{{j}'}}})} \right\}\left( k+1 \right)}} \\ \end{align}$ | (19) |
删除空类操作是生成空类操作的对偶操作,即在现有的空类中随机选择一个空类,将其删除。因此其接受率为
| $ \begin{aligned} {{a}_{{{d}_{e}}}}({\varphi},{{\varphi}^{*}})=\min \{1,\text{}1/{{R}_{{{b}_{e}}}}\} \end{aligned} $ | (20) |
3 实验结果与讨论
3.1 合成彩色遥感图像分割
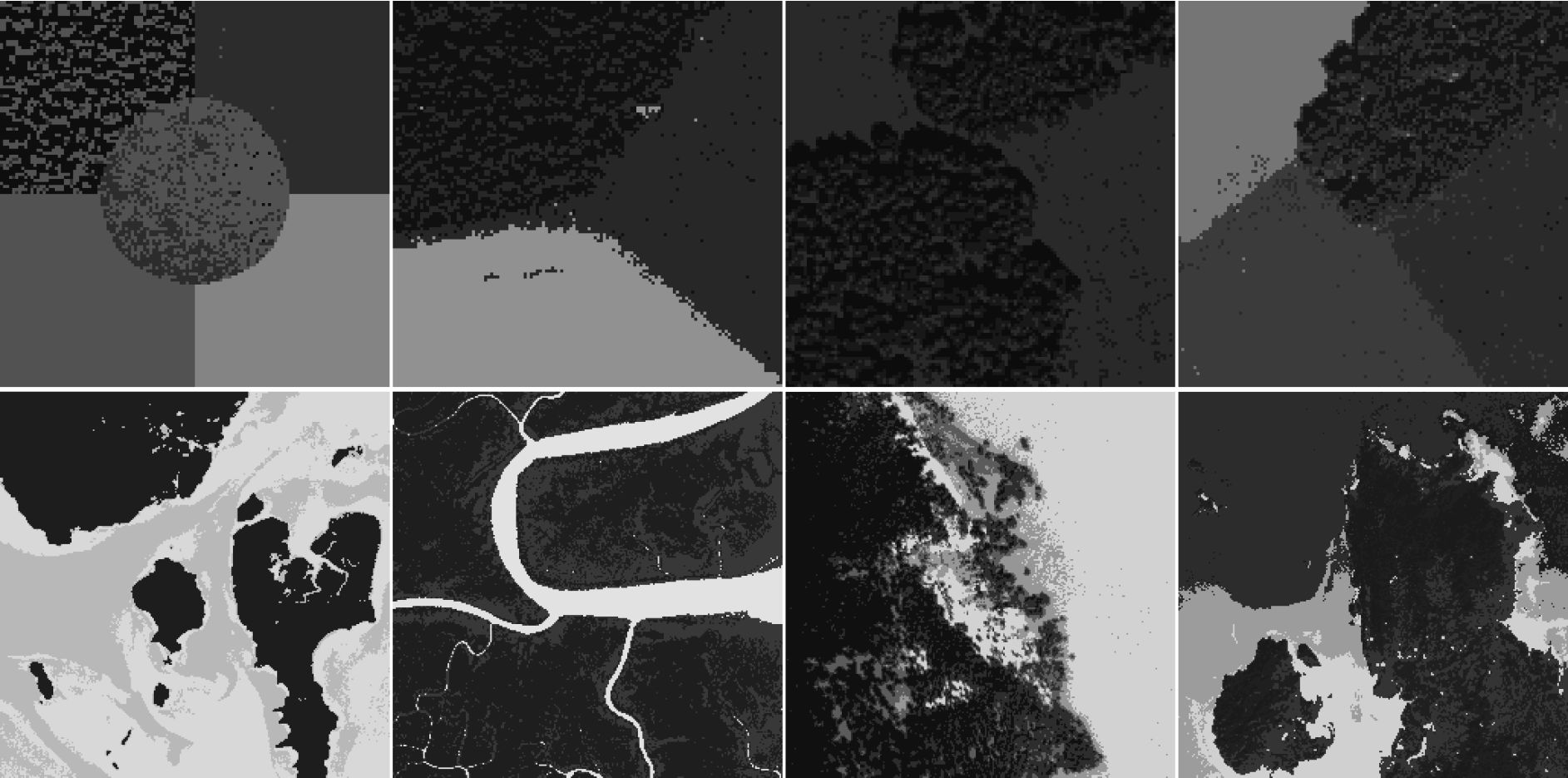
图 2(b)为由Worldview-2上截取不同地物填充在 图 2(a)(模板)的、包含红、绿和蓝3个波段的合成遥感图像,其类别数为5,尺度为128×128像素。
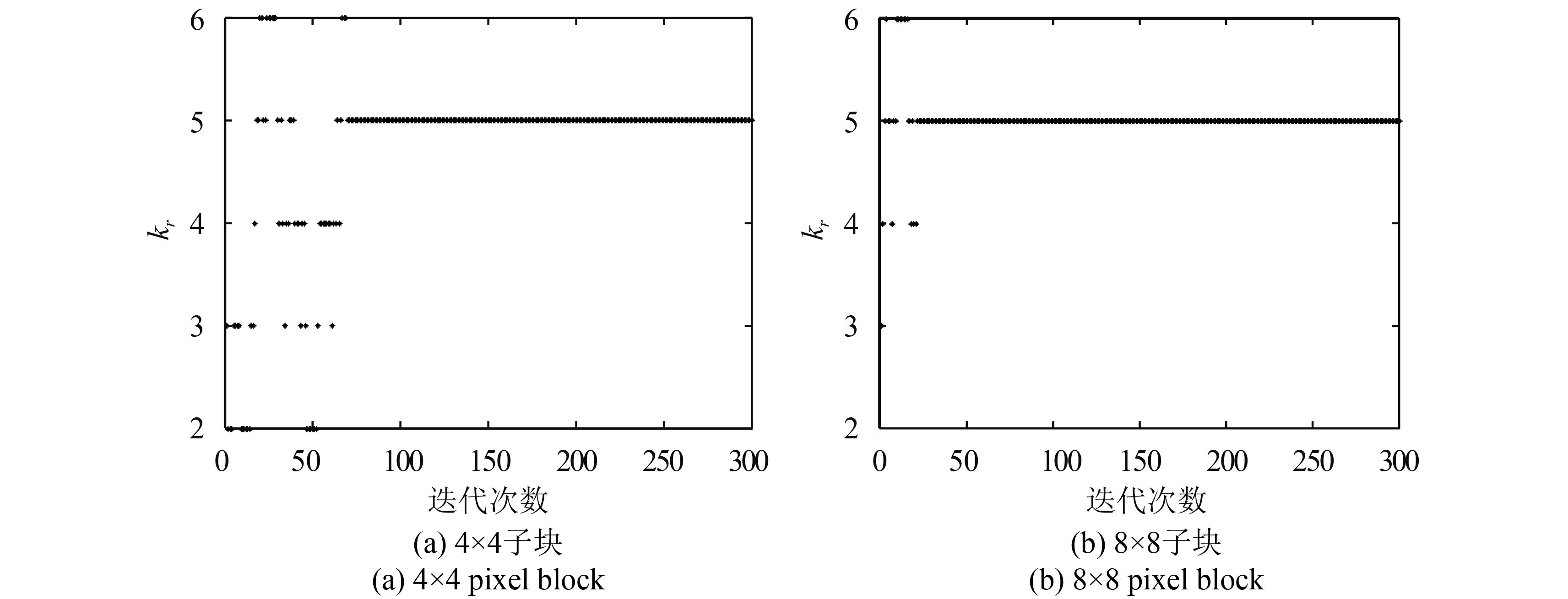
为了合理划分图像域,采用规则划分,分别将图像域划分成若干个4×4和8×8的规则子块,并在此基础上,在Intel Core2 2.53Ghz/1G内存/Matlab7.0环境下,验证提出的方法,然后通过比较其结果,选择合适的规则子块尺寸。在实验中,进行了20000次迭代, 图 3为截取前300次迭代对应的图像实类别数 k r 的变化。 图 3(a) (b)分别为在迭代过程中采用4×4和8×8子块规则划分对应的 k r 变化。
实验表明:(1)在 k r 稳定前,其值在[2, k max] 之间跳变;通过 图 3(a) (b)可以看出,对应4×4和8×8子块的规则划分,分别在70和25次迭代后 k r 达到稳态,即, k r =5;(2)在跳变期间,没有任何一个类别数保持连续20次不变;因此,为稳健起见,假设在迭代过程中,如果一类别数连续50次不变,则认为 k r 达到稳态,并设该数为图像实类别数;(3)8×8子块规则划分对应 k r 的收敛速度要比4×4子块规则划分快,因为划分的规则子块尺寸越大,同一幅图像划分的规则子块数越少,其对应类别数收敛的也就越快。
图 4为分别采用4×4和8×8规则子块划分的粗分割结果,其中 图 4 (a)分别为 k r 初收敛在5时的初分割结果; 图 4 (b)分别为在20000次迭代的粗分割结果,用它们的彩色均值表示其同质区域; 图 4 (c)分别为粗分割轮廓线与原图的叠加。
为了提高图像分割精度,设计了精细化操作。首先,以提取出的粗分割轮廓线为中心,生成宽为2个规则子块的缓冲区;然后采用邻域准则,即利用静态Potts模型定义像素间的邻域关系( Besag,1986),对缓冲区内每个像素重新分类,形成新的边界。 图 5(a)分别为4×4和8×8子块规则划分的粗分割轮廓线(白色)与缓冲区轮廓线(黑色)的叠加; 图 5(b)分别为其细化结果,各分割区域用该区域像素彩色均值表示; 图 5(c)分别为对应的细分割轮廓线与原图叠加。从视觉效果来看,4×4子块规则划分提取的细分割轮廓线与实际轮廓线更加吻合。从 图 3、 图 4和图 5可以看出,提出的方法不仅能自动确定图像类别数,而且可以很好的实现图像分割。
为了对提出方法进行定量评价,将合成彩色遥感图像的模板( 图 2(a))作为标准分割数据,求其混淆矩阵,并据此分别计算用户精度、产品精度、总精度及Kappa值,见 表 1。从 表 1可以看出,4×4子块规则划分对应的产品精度、用户精度及总精度均大于等于99%,而Kappa值高达0.996;而8×8子块规则划分对应的第3个用户精度低达94.8%,而其Kappa值为0.981。综上所述,采用4×4子块规则划分图像域更为适合。
表 1 定量评价
Table 1 Quantitative evaluation
| 尺寸 | 4×4 | 8×8 | |
| 产品精度/% | C 1 | 99.9 | 98.4 |
| C 2 | 99.6 | 96.1 | |
| C 3 | 99.8 | 99.8 | |
| C 4 | 99.9 | 100 | |
| C 5 | 99.0 | 98.4 | |
| 用户精度/% | C 1 | 99.6 | 99.5 |
| C 2 | 99.9 | 99.8 | |
| C 3 | 100 | 100 | |
| C 4 | 99.6 | 94.8 | |
| C 5 | 99.1 | 99.2 | |
| 总精度/% | 99.7 | 98.5 | |
| Kappa值 | 0.996 | 0.981 | |
3.2 多光谱遥感图像分割
图 6为3幅分辨率为1.8 m的、包含Worldview-2红、绿和蓝3个波段的真彩色遥感图像,尺度128×128像素,人为判读其类别数分别为3,3,4。在Intel Core2 2.53Ghz/1G内存/Matlab7.0环境下,利用提出方法对 图 6进行分割实验, 图 7为图像的分割结果,其中 图 7(a)为其对应的粗分割结果,而 图 7(b)为精细化后的分割结果。通过 图 7可以看出,提出的方法不仅能自动确定图像类别数,还能实现图像分割。
为了验证提出方法的分割精度,分别对其分割结果进行了视觉评价,图 8为3幅真彩色遥感图像对应的粗轮廓线(白色)、细轮廓线(黑色)与原图叠加结果。通过图 8可以看出,3幅图像的粗轮廓线与实际边界的吻合不甚理想,而细分割轮廓线能很好的与实际边界吻合,因此,设计的精细化操作有效地提高了图像分割精度,且提出方法的分割精度很高。
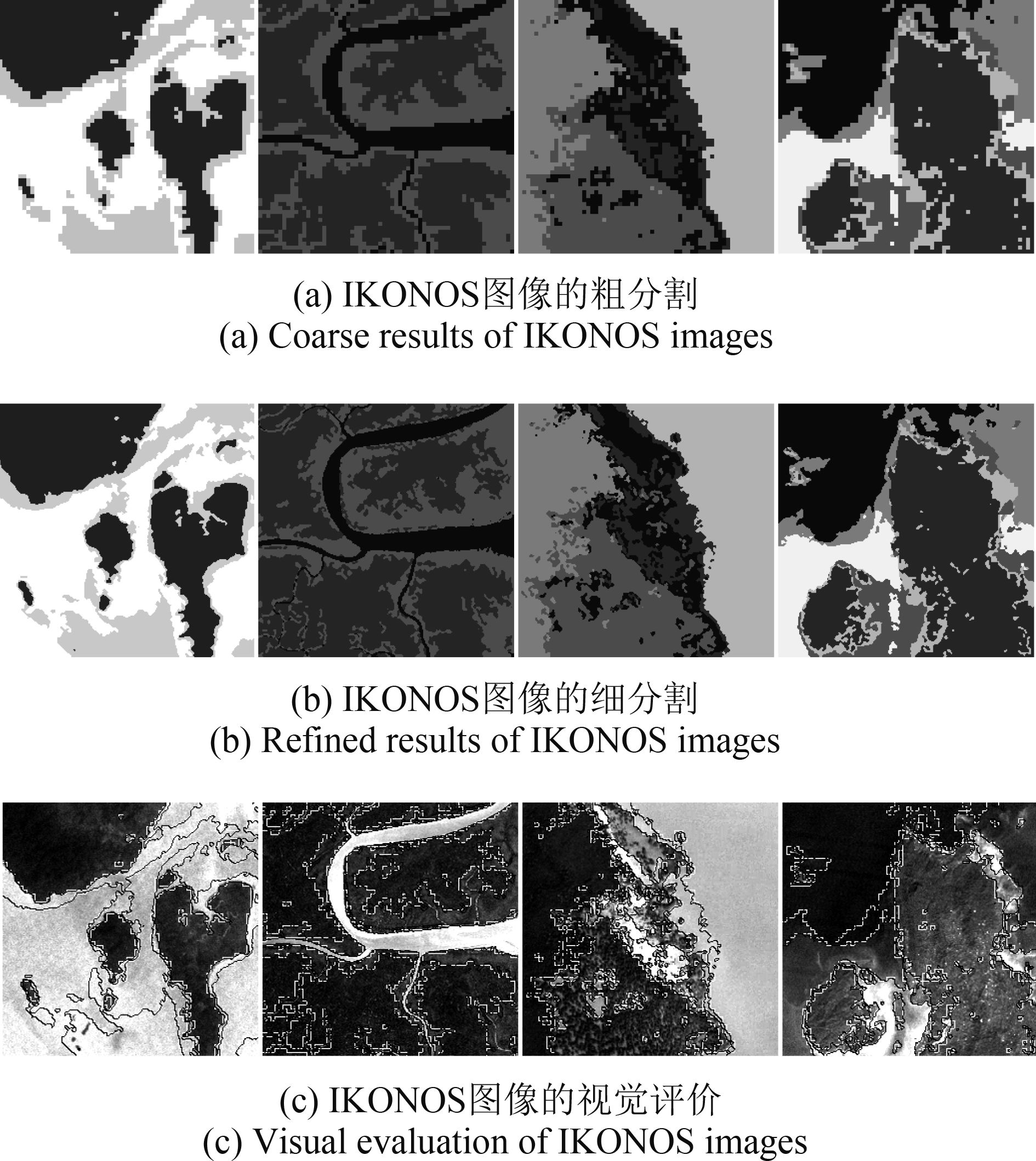
图 9为4幅4波段IKONOS的整景图像,分辨率为10 m,尺度为256×256像素,人为判别其类别数为3、3、5和6,其中图 9(a)包含红、绿和蓝3个波段的真彩色图像,图 9(b)为近红外波段的灰度图像。在Intel Core2 2.53Ghz/1G内存/Matlab7.0环境下,利用提出方法对其进行可变类分割,图 10(a)为其对应的粗分割结果,而图 10(b)为精细化结果。为了验证提出方法的分割精度,分别对提取分割结果的粗轮廓线(白色)和细轮廓线(黑色),并将其轮廓线叠加到原图中,见图 10(c)。通过图 10可以看出,提出方法对多波段图像的可行性及有效性。
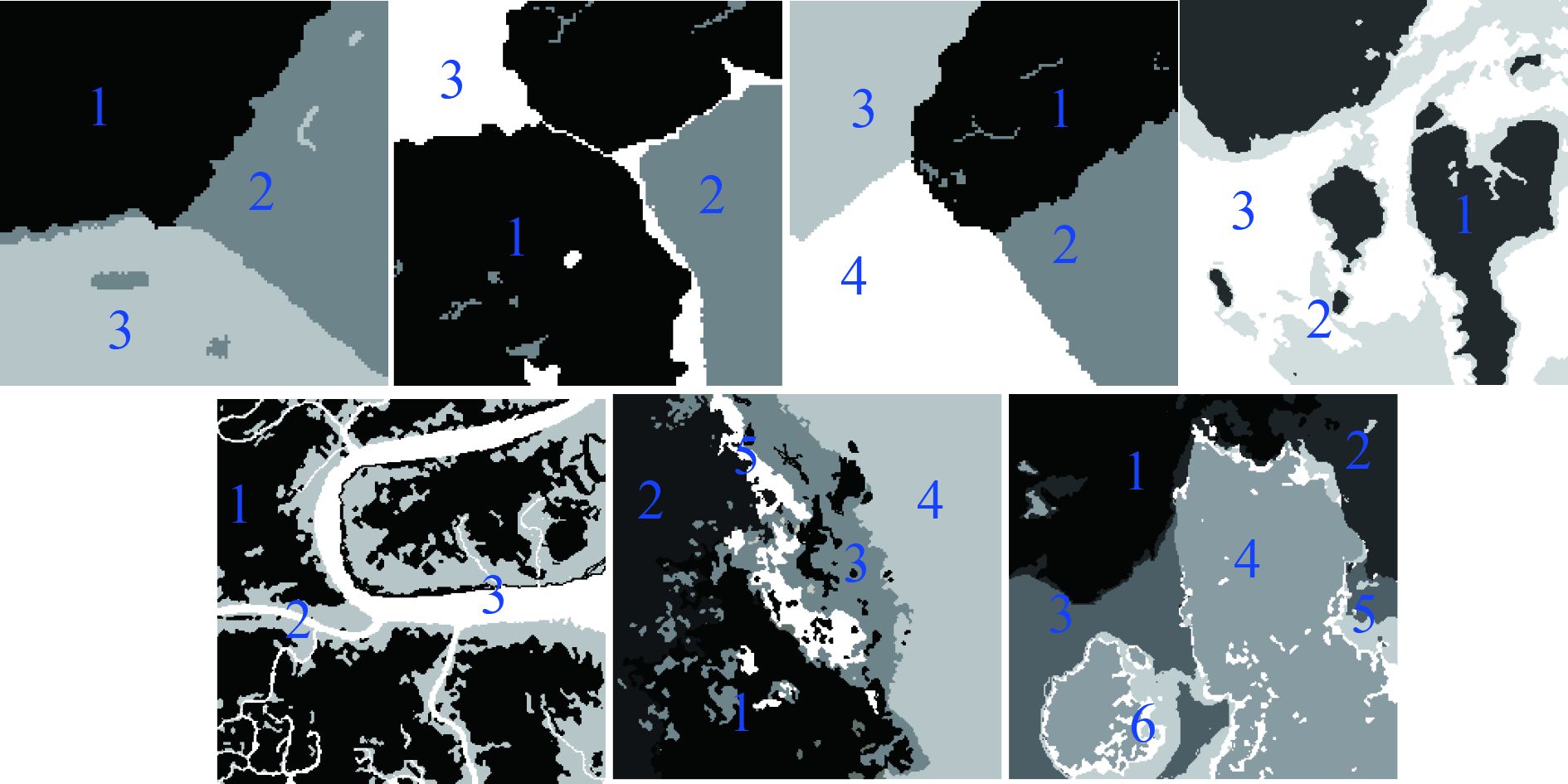
为了对提出方法进行定量评价,以 图 6和 图 9中的遥感图像的手动标记模板 图 11为标为标准分割数据,分别求其对应最终分割结果的混淆矩阵,并依次计算其对应的产品精度、用户精度、总精度及kappa值(见 表 2)。由 表 2计算得,平均产品精度为92.9%,平均用户精度为91.1%,平均总精度为94.2%,平均Kappa值为0.911。通过这些参数值,验证了提出方法的可行性及有效性。
表 2 彩色遥感图像的定量评价
Table 2 Quantitative evaluation of color remote sensing images
| 图像 | 产品精度/% | 用户精度/% | 总精度/% | Kappa | |||||||||||
| C 1 | C 2 | C 3 | C 4 | C 5 | C 6 | C 1 | C 2 | C 3 | C 4 | C 5 | C 6 | ||||
| a | 96.9 | 95.4 | 98.9 | 99.9 | 95.4 | 95.4 | 97.1 | 0.954 | |||||||
| b | 96.4 | 91.4 | 93.7 | 97.4 | 99.5 | 81.3 | 94.9 | 0.905 | |||||||
| c | 95.4 | 97.0 | 98.0 | 99.9 | 97.1 | 94.8 | 99.9 | 98.7 | 97.1 | 0.948 | |||||
| d | 98.6 | 95.7 | 84.4 | 97.7 | 91.4 | 92.2 | 93.8 | 0.905 | |||||||
| e | 94.9 | 96.4 | 82.2 | 98.0 | 86.2 | 91.2 | 93.4 | 0.886 | |||||||
| f | 88.5 | 99.1 | 72.4 | 97.8 | 78.8 | 94.4 | 98.8 | 79.5 | 99.9 | 48.4 | 90.5 | 0.876 | |||
| g | 99.3 | 91.7 | 76.0 | 94.4 | 97.1 | 99.0 | 99.5 | 80.8 | 98.8 | 100 | 74.6 | 69.6 | 92.7 | 0.904 | |
4 算法比较
4.1 ISODATA算法
利用ENVI软件中的ISODATA算法对Worldview-2合成及彩色遥感图像和多光谱IKONOS图像进行可变类分割, 图 12为对应的分割结果。通过视觉评价可以看出,ISODATA算法在某些情况下虽然能正确确定图像类别数,但分割结果精度不高,甚至有的分割结果与实际情况不符。而提出方法不仅能正确确定图像类别数,且能很好地实现图像分割。因此,相对而言,本文方法更具有优越性。
4.2 基于Voronoi划分和EM/MPM的分割算法
利用 赵泉华等人(2013)提出的基于Voronoi划分和EM/MPM的分割算法分别对Worldview-2合成及彩色遥感图像和多光谱IKONOS图像进行不变类分割, 图 13为对应的分割结果。通过视觉评价可以看出,该方法虽然有效地提高区域分割精度,但由于某些Voronoi多边形跨越边界,导致区域边界分割精度降低。而提出方法不仅能自动确定类别数,还可以很好地实现分割。另外,从时间上角度看,文献算法实现分割的平均运行速度为45 min,而提出方法实现分割的平均运行速度为40 min,因此提出方法更有效率。
5 结 论
提出了一种基于规则划分和RJMCMC算法的可变类遥感图像分割方法,该方法不仅能自动确定图像类别数,还可以精确地实现同质区域分割。为了提高图像分割精度,利用规则划分将图像域划分成规则子块,并在此基础上建立统计模型,但是分割结果边界与实际边界的拟合不甚理想,为此,设计了精细化操作。利用提出方法、ISODATA算法和基于Voronoi划分和EM/MPM的分割算法分别对Worldview-2合成及彩色遥感图像和多光谱IKONOS图像进行分割实验,通过提出方法的分割结果,验证了该方法的可行性及有效性;通过对比实验,验证了提出算法的优越性。在今后的工作中,将采用其他几何划分方法划分图像域。
参考文献(References)
-
Askari G, Xu A G, Li Y, Alavipanah S K.2013.Automatic determination of number of homogenous regions in SAR images utilizing splitting and merging based on a Reversible Jump MCMC Algorithm. Journal of the Indian Society of Remote Sensing, 41 : 509–521. DOI: 10.1007/s12524-013-0269-0.
-
Besag J E.1986.On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society, Series B (Methodological), 48 : 259–302.
-
Green P J.1995.Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika, 82 : 711–732. DOI: 10.1093/biomet/82.4.711.
-
Kato Z.2008.Segmentation of color images via reversible jump MCMC sampling. Image and Vision Computing, 26 : 361–371. DOI: 10.1016/j.imavis.2006.12.004.
-
Li J Y, Dang J W, Wang Y P.2014.Medical image segmentation algorithm based on quantum clonal evolution and two-dimensional Tsallis entropy. Journal of Computer-Aided Design & Computer Graphics, 26 : 465–471. ( 李积英, 党建武, 王阳萍. 2014. 融合量子克隆进化与二维Tsallis熵的医学图像分割算法. 计算机辅助设计与图形学学报, 26 : 465–471. )
-
Lu J, Yang X Z, Lang W H, Zuo M X, Xu Y.2011.SAR image segmentation with region-based GMM. Journal of Image and Graphics, 16 : 2088–2094. ( 卢洁, 杨学志, 郎文辉, 左美霞, 徐勇. 2011. 区域GMM聚类的SAR图像分割. 中国图象图形学报, 16 : 2088–2094. )
-
Lucarini V.2009.Symmetry-break in Voronoi tessellations. Symmetry, 1 : 21–54. DOI: 10.3390/sym1010021.
-
Ni W P, Yan W D, Bian H, Wu J Z, Lu Y, Wang P Z.2011.SAR image segmentation based on MRF model and morphological operation. Electronics Optics & Control, 18 : 32–36. ( 倪维平, 严卫东, 边辉, 吴俊政, 芦颖, 王培忠. 2011. 基于MRF模型和形态学运算的SAR图像分割. 电光与控制, 18 : 32–36. )
-
Richardson S, Green P J.1997.On Bayesian analysis of mixtures with an unknown number of components (with discussion). Journal of the Royal Statistical Society, Series B (Statistical Methodology), 59 : 731–792. DOI: 10.1111/1467-9868.00095.
-
Schneider R.2009.Weighted faces of Poisson hyperplane tessellations. Advances in Applied Probability, 41 : 682–694. DOI: 10.1239/aap/1253281060.
-
Schneider R.2010.Vertex numbers of weighted faces in Poisson hyperplane mosaics weighted faces. Discrete and Computational Geometry, 44 : 599–607. DOI: 10.1007/s00454-010-9260-5.
-
Strauss D J.1975.A model for clustering. Biometrika, 62 : 467–475. DOI: 10.1093/biomet/62.2.467.
-
Tian X L, Jiao L C, Gou S P.2008.SAR image segmentation based on spatially constrained FCM optimized by particle swarm optimization. Acta Electronica Sinica, 36 : 453–457. ( 田小林, 焦李成, 缑水平. 2008. 基于PSO优化空间约束聚类的SAR图像分割. 电子学报, 36 : 453–457. )
-
Wu Y Q, Ji Y, Shen Y, Zhang Y F.2012.Marine spill oil SAR image segmentation based on Tsallis entropy and improved Chan Vese model. Journal of Remote Sensing, 16 : 678–690. DOI: 10.11834/jrs.20121192. ( 吴一全, 吉玚, 沈毅, 张宇飞. 2012. Tsallis熵和改进CV模型的海面溢油SAR图像分割. 遥感学报, 16 : 678–690. DOI: 10.11834/jrs.20121192. )
-
Yang X Z, Liu C J, Wu K W, Lang W H.2014.SAR sea ice image segmentation using SRRG-MRF. Journal of Remote Sensing, 18 : 1247–1257. DOI: 10.11834/jrs.20143266. ( 杨学志, 刘灿俊, 吴克伟, 郎文辉. 2014. SRRG-MRF的SAR海冰图像分割算法. 遥感学报, 18 : 1247–1257. DOI: 10.11834/jrs.20143266. )
-
Yin K Y, Liu H W, Jin L.2011.Fast SAR image segmentation method based on Otsu adaptive double threshold. Journal of Jilin University (Engineering and Technology Edition), 41 : 1761–1765. ( 尹奎英, 刘宏伟, 金林. 2011. 快速的Otsu双阈值SAR图像分割法. 吉林大学学报(工学版), 41 : 1761–1765. )
-
Yong Y, Sun H, He C.2006.Supervised SAR image MPM segmentation based on Region-Based Hierarchical model. IEEE Geoscience and Remote Sensing Letters, 3 : 517–521. DOI: 10.1109/LGRS.2006.879105.
-
Yu B, Meng J M, Zhang X, Ji Y G.2013.Segmentation method for agglomerative hierarchical-based sea ice types using polarimetric SAR data. Journal of Remote Sensing, 17 : 887–904. DOI: 10.11834/jrs.20132091. ( 于波, 孟俊敏, 张晰, 纪永刚. 2013. 结合凝聚层次聚类的极化SAR海冰分割. 遥感学报, 17 : 887–904. DOI: 10.11834/jrs.20132091. )
-
Zhao Q H, Li Y, He X J, Song W D.2013.Multi-look SAR image segmentation based on Voronoi tessellation technique and EM/MPM algorithm. Journal of Remote Sensing, 17 : 841–854. DOI: 10.11834/jrs.20132239. ( 赵泉华, 李玉, 何晓军, 宋伟东. 2013. 基于Voronoi几何划分和EM/MPM算法的多视SAR图像分割. 遥感学报, 17 : 841–854. DOI: 10.11834/jrs.20132239. )
-
Zheng W, Kang G W, Chen W F, Li X W.2008.Unsupervised segmentation of remote sensing images based on Fuzzy Markov Random Field model. Journal of Remote Sensing, 12 : 246–252. DOI: 10.11834/jrs.20080232. ( 郑玮, 康戈文, 陈武凡, 李小文. 2008. 基于模糊马尔可夫随机场的无监督遥感图像分割算法. 遥感学报, 12 : 246–252. DOI: 10.11834/jrs.20080232. )