出版日期: 2016-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20165279
2016 | Volumn20 | Number 6

国产卫星

FY-3B微波成像仪资料的地理定位误差与订正

唐飞¹ , 董慧杰¹ , 李南² , 刘彩虹¹

1. 南京信息工程大学大气科学学院资料同化研究与应用中心，江苏南京 210044

2. 南京信息工程大学大气物理学院，江苏南京 210044

收稿日期: 2016-01-20; 优先数字出版日期: 2016-11-25

基金项目: 国家自然科学基金(编号：91337218, 41305031)；公益性行业(气象)科研专项经费资助(编号：GYHY201406008, GYHY201306078)

第一作者简介: 唐飞(1984年—)，男，博士研究生，研究方向为气象卫星微波成像仪资料质量控制及应用。E-mail： tangfei@nuist.edu.cn

中图分类号: P414.4

文献标识码: A

摘要

风云3号B星(FY-3B)上的微波成像仪(MWRI)通过10.65 GHz，18.7 GHz，23.8 GHz，36.5 GHz和89.0 GHz 5个频率的双极化通道对地球表面进行监测。自卫星发射至今，MWRI资料的地理定位误差还未进行深入研究。为了提高FY-3B MWRI L1级数据地理定位精度，基于海、陆响应的升、降轨亮温差理论NDM(Node Differential Method)，通过卫星位置和速度矢量建立卫星姿态模型、采用非线性最优化方法估计卫星姿态偏差，进而对MWRI 89 GHz通道的地理定位误差进行分析与订正。结果表明，2015年1—9月份俯仰、滚动和偏航角度的平均偏差分别为-0.220°，0.068°和0.062°，对应沿轨误差大约3—4 km，跨轨误差小于1 km。定位误差订正后，地中海、澳大利亚区域海岸线附近的升降轨亮温差明显减小；观测亮温在红海和南美洲东南部区域的分布和海岸线更加吻合，定位精度得到明显提高。

关键词

微波成像仪 , 定位误差 , 升降轨亮温差 , 圆锥扫描 , 卫星姿态 , 非线性最优化

Geolocation errors and correction of FY-3B microwave
radiation imager measurements

TANG Fei¹ , DONG Huijie¹ , LI Nan² , LIU Caihong¹

1.Center of Data Assimilation for Research and Application, College of Atmospheric Science, Nanjing 210044, China

2.College of Atmospheric Physics, Nanjing University of Information Science and Technology, Nanjing 210044, China

Abstract

The geolocation accuracy of meteorological satellites is a key factor in remote-sensing applications. The microwave radiation imager (MWRI) onboard the FengYun (FY)-3B satellite provides measurements of the Earth’s atmosphere and surface at 10.65 GHz, 18.7 GHz, 23.8 GHz, 36.5 GHz, and 89.0 GHz with dual polarization. Although FY-3 MWRI data have been widely distributed to the user community, their geolocation accuracy must be corrected to render the MWRI data useful for quantitative remote sensing. To improve the geolocation accuracy of FY-3B MWRI measurements, a method based on the brightness temperature difference between the ascending and descending orbits is used in the conical scanning MWRI at the 89 GHz channel and called Node Differential Method (NDM). The core principle of the geolocation error correction algorithm is minimizing the number of pixels along the coastlines, where the node difference in brightness temperature is greater than the threshold (20 K) and the distance from the coastlines near the Mediterranean Sea is less than 100 km. In this study, a satellite attitude model (satellite coordinate system) is established based on the vectors of the satellite position and velocity to estimate the satellite attitude angles, and a nonlinear optimization algorithm is used to minimize the objective function. This algorithm can avoid the effect of the tuning order of pitch, roll, and yaw in the traditional method. The satellite attitude offset (i.e., pitch, roll, and yaw) can be derived and further utilized to adjust the satellite attitude. After the satellite attitude angle correction, the geolocation errors in the MWRI at the89 GHz channel are corrected. Results show that the FY-3B MWRI at the 89 GHz channel has the mean offset of the satellite attitude, with the pitch, roll, and yaw angles from January to September of 2015 being -0.220°, 0.068°, and 0.062°, respectively. The mean geolocation error in the along-track direction is approximately 3—4 km, and that in the cross-track direction is less than 1 km at 89 GHz. The geolocation errors are stable during this period. They exist in the Mediterranean Sea, Australia, Red Sea, and Southeast of South America in the MWRI L1 data. The geolocation errors are detected from the high absolute values of brightness temperature difference between the ascending and descending orbits near the coastal regions and from the maps of brightness temperature compared with the coastlines. After geolocation error correction, the MWRI geolocation accuracy is improved at the 89 GHz channel. In this study, the geolocation error correction algorithm is applied to the selected coastal regions from the middle and high latitudes of the north and south hemispheres of Earth. This algorithm can be extended to global measurement correction. The attitudes normally explain the status and stability of the satellite. Although the geolocation error can be corrected by adjusting satellite attitude offset, other factors, such as sensor mounting, uncertainty in the ephemeris data, or timing error, must be considered in future studies to improve geolocation accuracy.

Key words

microwave radiation imager , geolocation error , node differential method , conical scanning , satellite attitude , nonlinear optimization

1 引言

中国风云系列极轨气象卫星自20世纪90年代发射至今得到了快速发展，不仅为气候和环境的研究提供了丰富的资料，而且在微波和红外波段的观测资料进入同化系统，为数值天气预报模式提供最优初始场，明显提高了数值预报精度。如今，FY-3B和FY-3C卫星同时在轨运行，组成晨昏轨道可以提供一天4次的全球观测( Tang 等，2016)。风云三号气象卫星上携带的微波成像仪MWRI(Microwave Radiation Imager)，有10.65 GHz，18.7 GHz，23.8 GHz，36.5 GHz和89 GHz共5个探测频率，每个频率均有水平和垂直两种极化模式，能够反映出如海面风速、海表温度以及降水等大气物理信息。目前，中国气象局国家卫星气象中心网站可以为用户公开提供MWRI L1级数据。分析显示仪器性能稳定( 乔木等，2012)，其数据资料同化对数值预报具有重要的业务应用价值。

气象卫星资料的地理定位误差影响其定量化应用。造成卫星仪器定位误差的因素很多，例如天线扫描角精度、探测器、天线和仪器的安装偏差、卫星仪器的系统误差等都会造成定位误差，这些误差不随时间变化，可以通过地面处理减小或消除( Wolfe 等，2002)。而卫星姿态测量精度和卫星位置测量精度随时间变化，其变化行为很难模拟( 关敏和杨忠东，2009)，需要通过在轨实时分析。国内、外已有很多针对卫星微波辐射计地理定位误差分析与订正的研究。对美国空军防御气象卫星计划F-8上的SSM/I仪器定位误差， Poe和Conway(1990)用1组卫星姿态角度订正，使得定位误差减小7 km左右。 Atkinson和McLellan(1998)最初利用AMSU-A通道15和AMSU-B通道1之间的互相关性，对NOAA-15地理定位精度进行评估，发现两个通道之间不重合度很小。 Purdy等人(2006)利用海岸线匹配方法和扫描误差分析，发现了WindSat定位有5 km的不确定性。Poe等人(2008)对SSM/I数据使用偏微分的方法估计地理定位精度，并将定位精度提高4—5 km。

针对微波辐射计的定位误差订正一般有两种方法：拐点法CCM(Coastline Crossing Method)和升、降轨亮温差法NDM(Node Differential Method)。拐点法是利用晴空条件下扫描线扫过海岸线时，以亮温梯度变化最大处(拐点)作为海岸线位置，并将拐点到高精度海岸线最近的距离认为是定位误差。拐点法首先用于美国NOAA-9卫星以及地球辐射收支卫星ERBS上的地球辐射收支实验扫描仪ERBE( Hoffman 等，1987)，之后广泛应用于国外其他一些卫星上的辐射扫描仪( Smith 等，2009； Gregorich和Aumann，2003； Currey，2002)。升、降轨亮温差法是通过调整卫星姿态误差，直到海岸线附近的亮温差大于给定阈值的像素点数达到最小。国外的卫星所携带的微波成像仪如SSM/I和AMSR-E，都曾使用升降轨亮温差的原理对地理定位误差进行分析和订正( Berg 等，2013； Wiebe 等，2008)。 Moradi等人(2013)采用升、降轨观测亮温差方法，针对跨轨仪器扫描特征，按照俯仰、滚动和偏航的顺序依次计算出3个姿态角度的偏差值，给出了NOAA-15等卫星上携带的AMSU仪器不同通道姿态角度偏差随时间的变化趋势。 Tang等人(2016)使用拐点法估计了FY-3C卫星MWRI仪器存在俯仰、滚动和偏航偏差分别平均为-0.59°、-0.09°和0.21°，并使用升、降轨亮温差方法作为对比( Moradi 等，2013)，得到俯仰、滚动和偏航偏差分别平均为-0.52°、-0.05°和0.27°，两种方法结果基本一致。

拐点法虽然简单、直接，但是由于海岸线的不规则分布，拐点到海岸线的距离并不是实际的定位误差( Wang 等，2013)。升降轨亮温差法中，对于跨轨扫描仪器求解卫星姿态误差的过程是，先假定滚动和偏航角度偏差分别为零，对俯仰角度增加或减小一个很小的值来不断调整卫星姿态、重新计算地理经、纬度，直到升降轨亮温差超过给定阈值的像素点数达到最小，再重复这一过程分别求滚动和偏航偏差，其结果与求解俯仰、滚动和偏航角的次序有关( Moradi 等，2013； Tang 等，2016)，且计算时间长；而圆锥扫描仪器的滚动偏差和偏航偏差产生的定位偏移特征相似，很难区分跨轨误差(扫描方向的误差)是来源于滚动偏差还是偏航偏差，因此不能按照计算跨轨扫描仪器卫星姿态误差的方法估计圆锥扫描仪器的卫星姿态误差。

FY-3B作为中国第二代极轨气象卫星，自2010年11月发射以来，其上携带的MWRI不间断地对全球提供大气及地表物理参数，成为了中国进一步改善数值预报质量的重要基础。但是，对FY-3B MWRI地理定位误差的评估与订正研究工作相对较少，直接影响了该资料在数值预报资料同化中的有效应用。本文在前人研究的基础上，结合圆锥扫描仪器的定位偏移特征，采用非线性最优化方法，求解满足升、降轨亮温差大于给定阈值的像素点数达到最小时的一组卫星姿态角度偏差，称为最优解，并对FY-3B MWRI资料进行定位误差分析与订正。

2 MWRI仪器与地理定位坐标系

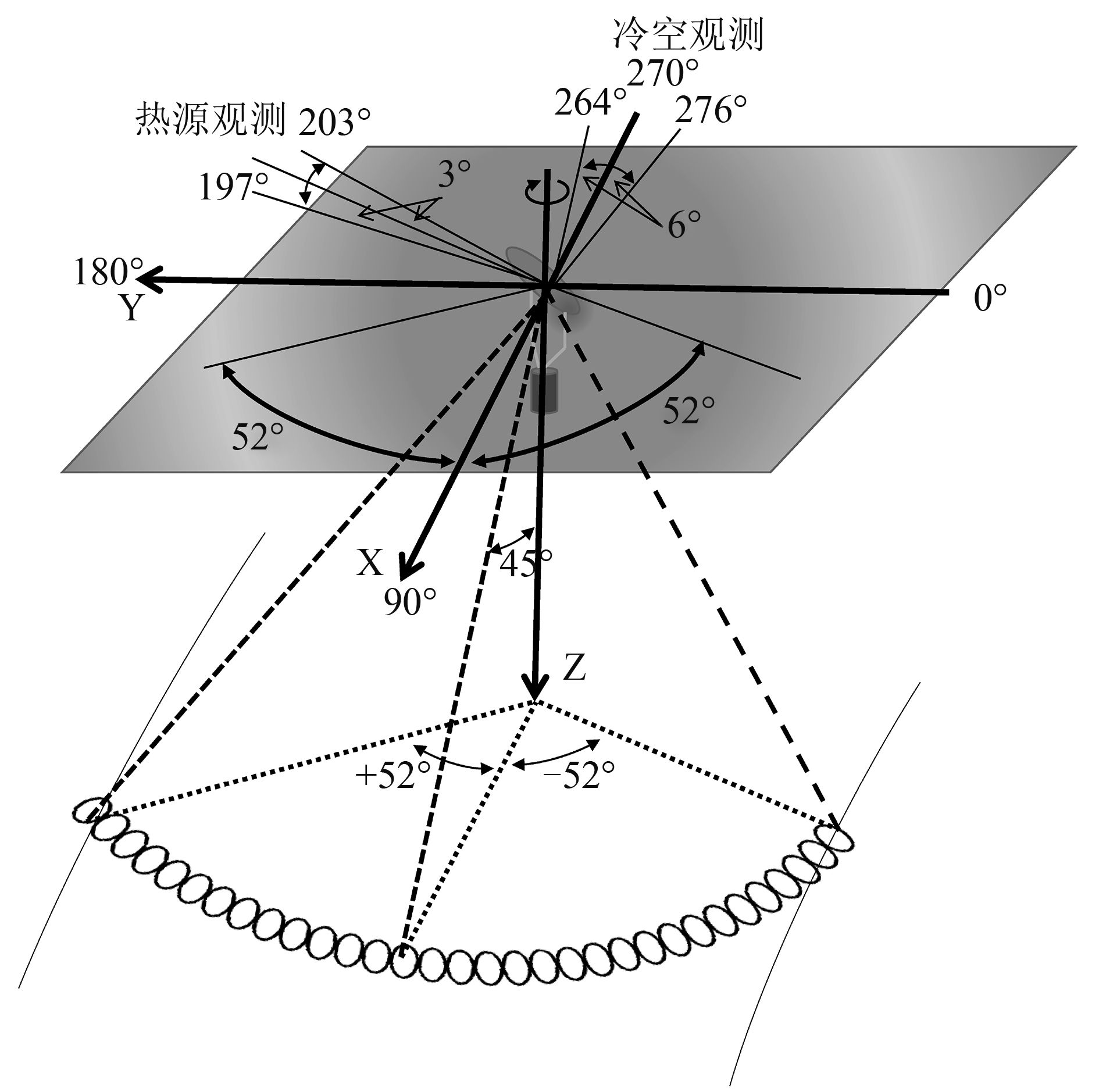
MWRI通过天线的绕轴旋转形成圆锥扫描，天线波束视角为45°，对地扫描范围为±52°，扫描幅宽1400 km。扫描周期为1.8 s，每帧采样为254点。扫描几何如图1。MWRI的接收机共有5个频率，空间分辨率从89 GHz通道的9 km×15 km到10.65 GHz通道的51 km×85 km。89 GHz馈源喇叭的相位中心位于天线反射器抛物面的焦点处。在进行遥感数据地理定位计算时使用89 GHz通道的采样时间( 关敏和杨忠东，2009)。

图 1 微波成像仪扫描几何( Tang 等，2016)

Fig. 1 A schematic illustration of MWRI scan geometry ( Tang et al., 2016)

MWRI定位算法涉及7个坐标系( Tang 等，2016)，分别是天线坐标系、仪器坐标系、卫星本体坐标系、轨道坐标系、地心惯性坐标系(ECI)( Liu，1992)、地心旋转坐标系(ECR)和大地测量坐标系( Liu，2003)。

3 定位误差估计与订正方法

在水平均匀的晴空大气条件下，大气窗区通道的大气透过率接近于1，大气中的散射辐射和反射辐射可以忽略，根据微波辐射传输方程( Lipton 等，2009； Kroodsma 等，2012)，卫星仪器的观测亮温可以近似表示为地表(海洋、陆地)发射率 ε _s 和地表温度 T _s 的乘积( 陈渭民，2005)，即 Tb≈ ε _s T _s 。 Moradi等人(2013)认为，在微波波段海洋表面的平均发射率在0.5左右，而陆地上的平均发射率为0.9，海、陆亮温差可能大于100 K。在微波辐射计地理定位准确的情况下，海岸线附近的升、降轨亮温差绝对值相对很小。如果卫星姿态不稳定，沿着卫星轨道方向或天线扫描方向会产生遥感图像偏移，且升、降轨扫描点的偏移方向相反，会导致在海岸线附近洋面上的扫描点偏向陆地、陆面的扫描点偏向海洋，造成沿着海岸线附近分布的升、降轨亮温差绝对值较大(超过20 K)。因此，可以通过调整卫星姿态对地理定位误差进行订正。

3.1 建立卫星姿态模型

由某一时刻的卫星位置(卫星的瞬时位置由星上全球定位系统GPS接收机提供或者通过轨道根数计算外推获得)，其在地球上的经、纬度分别是 λ _s 和 φ _s ，卫星速度矢量 $\vec { v}$ ，建立卫星本体坐标系( Tang 等，2016)。图2 给出了地心旋转坐标系、卫星本体坐标系以及卫星姿态示意图。卫星本体坐标系的 Z轴(偏航轴)定义为从卫星指向星下点

图 2 坐标系示意图

Fig. 2 Illustration of coordinate systems

$ \vec { z} = {\left[ {\begin{array}{*{20}{c}} { - {\rm{cos}}{\varphi _s}{\rm{cos}}{\lambda _s}} & { - {\rm{cos}}{\varphi _s}{\rm{sin}}{\lambda _s}} & { - {\rm{sin}}{\varphi _s}} \end{array}} \right]^{\rm{T}}} $

(1)

Y轴(俯仰轴)指向卫星速度方向但不完全与速度方向重合，定义为Z轴和速度矢量的外积

$ \vec { y} = \frac{{\vec { z} \times \vec { v}}}{{\left| {\vec { z} \times \vec { v}} \right|}} $

(2)

X轴(滚动轴)定义为Y轴和Z轴的外积

$ \vec { x} = \vec { y} \times \vec { z} $

(3)

则天线观测波束视向量从地心旋转坐标系到卫星本体坐标系的转换矩阵为

$ {{ R}_{E/S}} = {\left[ {\begin{array}{*{20}{c}} {\overrightarrow { x} } & {\overrightarrow { y} } & {\overrightarrow { z} } \end{array}} \right]^{\rm{T}}} $

(4)

卫星姿态的旋转矩阵按照Z，X和Y轴的旋转矩阵乘积的顺序来表示( 吴荣华等，2012)

$\[{{R}_{zxy}}=\text{ }\left[ \begin{matrix} \cos {{\xi }_{y}}\cos {{\xi }_{p}}-\sin {{\xi }_{y}}\sin {{\xi }_{r}}\sin {{\xi }_{p}} \\ \sin {{\xi }_{y}}\cos {{\xi }_{p}}+\cos {{\xi }_{y}}\sin {{\xi }_{r}}\sin {{\xi }_{p}} \\ -\cos {{\xi }_{y}}\sin {{\xi }_{p}} \\ \end{matrix} \right.\begin{matrix} -\sin {{\xi }_{y}}\cos {{\xi }_{r}} \\ \cos {{\xi }_{y}}\cos {{\xi }_{r}} \\ \cos {{\xi }_{y}}\cos {{\xi }_{r}} \\ \end{matrix}\left. \begin{matrix} \cos {{\xi }_{y}}\sin {{\xi }_{p}}+\sin {{\xi }_{y}}\sin {{\xi }_{r}}\cos {{\xi }_{p}} \\ \sin {{\xi }_{y}}\sin {{\xi }_{p}}-\cos {{\xi }_{y}}\sin {{\xi }_{r}}\cos {{\xi }_{p}} \\ \cos {{\xi }_{r}}\cos {{\xi }_{p}} \\ \end{matrix} \right]\text{ }\]$

(5)

式中， ξ _r ， ξ _p 和 ξ _y 分别为滚动、俯仰和偏航角度。在卫星本体坐标系下，卫星姿态调整前、后的波束视向量 ${\vec { b}_S}$ 、 ${\vec { b'}_S}$ (从卫星天线指向地球观测点)可以表示为

$ {\vec { b'}_S} = {{ R}_{zxy}} \times {\vec { b}_S} $

(6)

3.2 估计卫星姿态误差

在 Moradi等人(2013)的研究基础上，建立估计MWRI卫星姿态偏差的方案，主要步骤如下：

(1) 选择海岸线分布方向复杂多样、且海、陆亮温差异很大的地中海区域(12°W—40°E，25°N—50°N)，将俯仰、滚动和偏航角度分别设为零，根据卫星位置和速度矢量建立的卫星姿态模型(卫星本体坐标系)，计算一天中经过该区域的每个扫描位置的经、纬度( λ _i ， φ _i )( i表示第 i个扫描点)。

(2) 将一天中经过地中海区域的升轨和降轨的观测资料分别进行0.1°×0.1°格点化，然后计算升轨和降轨之间的亮温差，并统计海岸线附近100 km范围内、亮温差大于20 K的像素点数 N _p。如果 N _p=0，不需要对该资料进行定位误差订正，则对下一天的资料进行计算。否则，进入第(3)步。

(3) 以俯仰( ξ _p )、滚动( ξ _r )和偏航( ξ _y )角度为自变量，以像素点数 N _p为因变量，构造三元目标函数 N _p= f( ξ _r ， ξ _p ， ξ _y )，使用“Nelder-Mead单纯形直接搜索法”( Lagarias 等，1998；谢政等，2010)求该目标函数的极小值。该方法的基本思想是：从一个基本可行解出发，求出使目标函数值下降的另一个基本可行解；通过不断改进基本可行解，力图找出使目标函数达到最小的基本可行解。以初始卫星姿态( ξ _r ， ξ _p ， ξ _y )=0进行搜索，当结果达到精度10 ^-6时，满足搜索终止条件，得到目标函数达到极小值 N _p ^min=min f( ξ _r ， ξ _p ， ξ _y )时的一组卫星姿态角度( ξ _r ^min， ξ _p ^min， ξ _y ^min)，即为所求的卫星姿态误差。

3.3 定位误差订正方法

在地心旋转坐标系下，对于给定的某时刻卫星所在位置向量(从地心指向卫星) $\vec { s}$ 和存在定位误差的观测向量 $\vec { r}$ (由地心指向地面的观测点( λ _i ， φ _i )， i表示第 i个扫描点)，则从卫星仪器指向地球观测点的波束视向量 ${\vec { b}_E}$ ( 图2)可以表示为

$ {\vec { b}_E} = \vec { r} - \vec { s} $

(7)

由式(4)、式(5)和式(6)，通过卫星姿态角偏差( ξ _r ^min， ξ _p ^min， ξ _y ^min)订正后的波束视向量 ${\vec { b'}_E}$ 在地心旋转坐标系下表示为

$ {\vec { b'}_E} = {{ R}_{S/E}} \cdot {{ R}_{zxy}} \cdot {{ R}_{E/S}} \cdot {\vec { b}_E} $

(8)

式中， ${{ R}_{S/E}} = { R}_{E/S}^{ - 1}$ 是卫星本体坐标系到地心旋转坐标系的转换矩阵。由式(7)、(8)得到通过调整卫星姿态订正后的观测向量为

$ \vec { r'} = {\vec { b'}_E} + \vec { s} $

(9)

最后将 $\vec { r'}$ 在地心旋转坐标系下的坐标转换成订正后的地理经、纬度 $({\lambda _i}^\prime ,{\varphi _i}^\prime )$ 。

沿海岸线分布的升、降轨亮温差绝对值越小说明定位误差订正效果越好。而升、降轨亮温差不仅受到地理定位误差的影响，其他因素如升轨和降轨观测同一地点的时间差异，其观测的地表温度也不同，或者天气因素尤其是高频通道对云很敏感，都会对升、降轨亮温差产生影响，从而影响定位误差订正结果。另外，卫星位置和速度的测量误差能够带来10 m量级的定位误差( 关敏和杨忠东，2009)。由于微波成像仪89 GHz通道空间分辨率(9 km×15 km)相对较低，地形对其地理定位造成的误差相对较小，本文在定位误差估计及订正过程中没有考虑地形的影响。在今后的研究中，会进一步考虑各种因素对定位误差的影响，改进订正方法以提高定位精度。

4 定位误差及订正结果分析

4.1 卫星姿态对定位结果的影响分析

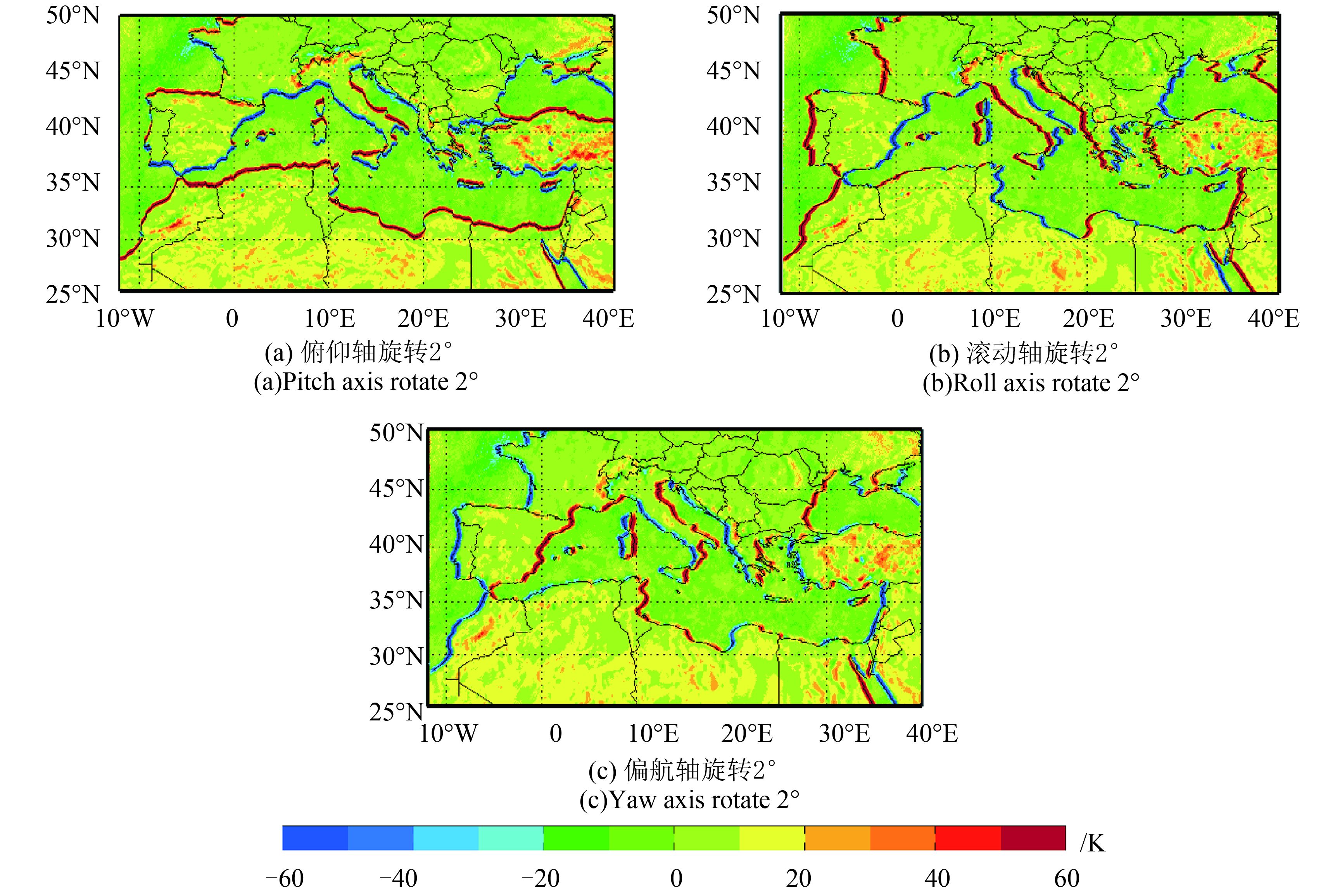
图3是模拟卫星坐标系分别绕 X、 Y和 Z轴正向旋转2°时，MWRI所产生的地理定位结果，图中蓝色和红色曲线分别表示卫星姿态变化前、后的扫描轨迹。可以看出，圆锥扫描方式下，俯仰和滚动轴的旋转分别在地理定位扫描点产生沿轨和垂轨方向的偏移( 图3(a)，图3(b))，且相互之间基本没有影响。而偏航轴旋转后扫描点偏移情况相对复杂，扫描线沿着扫描轨迹偏移，从整个扫描轨迹看，扫描轨迹往垂轨方向偏移，偏移方向与滚动轴旋转的定位偏移结果相反( 图3(c))。因此，沿轨误差主要由俯仰偏差造成，而对于跨轨误差，很难区分是由于滚动偏差还是偏航偏差造成的。

图 3 模拟FY-3B MWRI卫星姿态变化对定位结果的影响

Fig. 3 Simulated effects of satellite attitude offset on FY-3B MWRI geolocation results

针对上述模拟产生的定位结果特征，图4给出了在地中海区域与图3对应的卫星坐标系坐标轴正向旋转2°情况下，89 GHz水平极化通道在2015年1月份升轨和降轨之间亮温差的月平均分布。可以看出，卫星姿态变化对海岸线附近的升降轨亮温差造成明显的不均匀分布特征。俯仰轴旋转主要对垂轨方向(东西走向)的海岸线附近的亮温差产生明显影响，对接近沿轨方向(南北走向)的海岸线附近亮温差影响较小( 图4(a))，并且地中海北岸主要是负偏差，南岸主要是正偏差。滚动轴的旋转主要对沿轨方向的海岸线附近的升降轨亮温差产生影响( 图4(b))，其中西岸为负偏差，东岸为正偏差。偏航轴旋转结果和滚动轴类似，但沿海岸线的亮温差正、负值分布相反( 图4(c))。

图 4 模拟FY-3B MWRI卫星姿态偏差对升、降轨亮温差分布的影响

Fig. 4 Simulated effects of satellite attitude offset on FY-3B MWRI brightness temperature differences between ascending and descending orbit

4.2 FY-3B MWRI定位误差

圆锥扫描不同于跨轨扫描方式，二者由于卫星姿态变化产生的定位结果偏移特征不尽相同。基于海、陆响应的升降轨亮温差理论，本文采用非线性最优化方法，对FY-3B MWRI 89 GHz通道2015年1月份到9月份、经过地中海区域的L1级数据，寻找满足升、降轨亮温差大于给定阈值(20 K)的像素点数最小时的最优解，即卫星姿态偏差，其变化曲线如图5所示。可以看出，从1月份到9月份，卫星姿态虽然有微小变化，但总体上比较稳定。俯仰误差在-0.22°上下波动，方差为0.06。滚动和偏航误差平均值(方差)分别是0.068(0.04)和0.062(0.03)。MWRI俯仰角度的偏差造成的定位误差大于滚动和偏航误差。根据Moradi等人(2013)的研究理论，俯仰偏差为-0.22°时，导致MWRI的遥感图像在地面上的沿轨误差大约3—4 km，而跨轨误差相对较小，大约在1 km以内。

图 5 FY-3B MWRI 89 GHz通道2015年1月至9月份卫星姿态的时间变化曲线

Fig. 5 Temporal variation of FY-3B MWRI attitude at 89 GHz channel from January to September, 2015

4.3 定位误差订正结果

4.3.1 订正前、后的升降轨亮温差

根据卫星姿态偏差，利用卫星姿态旋转矩阵，对2015年2月份地中海区域和8月份澳大利亚区域的MWRI 89 GHz水平极化通道的观测数据逐日进行定位误差订正。图6是订正前后升降轨亮温差的月平均分布。可以看出，远离海岸线的亮温差分布比较均匀，均在20 K以下，而沿海岸线附近分布的亮温差绝对值超过30 K( 图6(a))。同时发现，亮温差绝对值超过20 K的位置主要沿着垂直轨道方向(东西向)的海岸线分布，尤其在红海北部的地中海海岸线、澳大利亚北部海岸线附近( 图6(c))比较明显。这种特征与图4(a)的升降轨亮温差分布特征符合，也进一步验证了图5中卫星姿态以俯仰偏差为主的结论。根据上述对图4(a)的分析，造成东、西走向的海岸线附近升降轨亮温差较大的主要原因是，卫星姿态的俯仰轴旋转导致扫描点沿着轨道在升轨阶段向北偏移，降轨阶段向南偏移。因此在地中海南岸的海岸线附近升降轨亮温差超过20 K、北岸的海岸线附近小于-30 K。定位误差订正后，沿着地中海区域和澳大利亚区域海岸线分布的亮温差绝对值较大的现象均得到明显消除(减小到20 K以下)( 图6(b)，图6(d))。由于订正澳大利亚区域的定位误差使用的卫星姿态误差，是利用地中海区域的资料所求得，说明区域的选择对所求的卫星姿态误差以及订正结果基本没有影响。

图 6 FY-3B MWR资料定位误差订正前、后升降轨亮温差月平均分布

Fig. 6 Monthly averaged brightness temperature difference maps of FY-3B MWRI before and after geolocation error correction

4.3.2 订正前、后的亮温分布特征

通过升、降轨亮温差能体现出FY-3B MWRI的定位误差订正效果。本节直接从海陆亮温的分布来分析定位误差订正前、后的特征。由于红海海岸线附近的海、陆亮温在晴空条件下差异明显，其沿着海岸线的分布特征适合用于检验地理定位误差。图7是FY-3B MWRI在89 GHz水平极化通道2015-02-03 11:16(UTC)升轨和23:57(UTC)降轨经过红海区域的的观测亮温在地理定位误差订正前、后的分布。卫星仪器扫描经过该区域时为晴空观测，海、陆亮温对比明显。定位误差订正前的海、陆亮温分布明显偏离海岸线的位置，特别是在北纬28°N和30°N之间的海岸线附近，且升轨和降轨偏移的方向相反( 图7(a)， 7(c))，在升轨观测时，亮温值分布向西北方向偏移，降轨观测时向东南方向偏移。定位误差订正之后，升轨和降轨的海、陆亮温分布特征均与海岸线位置十分吻合( 图7(b)和 7(d))，说明定位误差订正方法有效。图8是FY-3B MWRI在89 GHz水平极化通道2015-04-13 19:48(UTC)经过南美洲东南部海岸的时候，地理定位误差订正前、后的观测亮温分布。通过对比可以看出，订正后的地理定位结果有所改善。南美洲南部区域所处纬度(51°S—45°S)较高，说明本文的订正方法具有较大地理范围的适用性，可以用于全球范围的定位误差订正，提高定位精度。

图 7 红海区域FY-3B MWRI定位误差订正前、后观测亮温分布(黑色曲线表示实际海岸线位置)

Fig. 7 FY-3B MWRI brightness temperature distributions over Red Sea before and after geolocation error corrections (Black curve indicates the real coastline)

图 8 南美洲东南海岸区域升轨观测FY-3B MWRI定位误差订正前、后观测亮温分布(黑色曲线表示实际海岸线位置)

Fig. 8 FY-3B MWRI brightness temperature distributions over coastal regions of Southeast of South America in ascending orbit before and after geolocation error corrections

5 结论

气象卫星地理定位精度是影响其遥感数据定量化应用的重要因素。因此，在MWRI资料反演大气及地表物理参数之前，对MWRI资料定位误差的分析与订正是十分必要的。本文使用升、降轨亮温差法(NDM)，通过对卫星姿态的调整对MWRI地理定位误差进行了分析与订正，构建了一种适用于FY-3B MWRI资料的定位误差估计与订正方法。主要结论如下：

(1) 通过建立卫星姿态模型，分析了圆锥扫描仪器的定位误差偏移特征。由于滚动偏差和偏航偏差造成的偏移特征相似，本文采用了非线性最优化算法估计卫星姿态偏差，避免了以往的求解过程中依次调整俯仰、滚动和偏航角度时造成的相互影响，该最优化求解方法适用于圆锥扫描方式的卫星姿态偏差估计。

(2) 对FY-3B MWRI 2015年1月到9月份的L1级观测资料定位误差分析显示，定位误差相对稳定，沿轨误差为3 km，跨轨误差在1 km以内，表明本文对误差的求解结果稳定，方法可行。

(3) 从所选取的地中海区域、红海区域、澳大利亚区域和南美洲东南部区域的亮温以及升、降轨亮温差的分布上，可以看出地理定位误差的存在。订正后的以上区域在FY-3B MWRI 89 GHz通道的定位精度均得到明显提高。因此，可以将本文的方法用于FY-3B MWRI全球资料的定位误差估计与订正。

利用升、降轨亮温差法(NDM)一定程度上改善了FY-3B MWRI地理定位效果，提高了地理定位精度。但导致MWRI地理定位误差的因素有很多，如仪器自身的安装精度、星历时间的误差等，以及天气因素对海、陆亮温差的影响，本文并没有进行全面分析。在今后的研究中，会细致考虑各种因素分别带来的定量化定位误差，进行综合订正。

参考文献(References)

(Atkinson N C and McLellan S. 1998. Initial evaluation of AMSU-B in-orbit data // Proc. SPIE, 3503, Microwave Remote Sensing of the Atmosphere and Environment. Beijing, China: SPIE: 276-287 [DOI: 10.1117/12.319506]) http://cn.bing.com/academic/profile?id=2146509061&encoded=0&v=paper_preview&mkt=zh-cn

Berg W, Sapiano M R P, Horsman J, Kummerow C.2013.Improved geolocation and earth incidence angle information for a fundamental climate data record of the SSM/I sensors. IEEE Transactions on Geoscience and Remote Sensing, 51 : 1504–1513. DOI: 10.1109/TGRS2012.2199761.

Chen W M. Satellite Meteorology. 气象出版社: Beijing 2005 . ( 陈渭民. 2005. 卫星气象学c. 气象出版社: 北京 . )

(Currey J C. 2002. Geolocation Assessment Algorithm for CALIPSO Using Coastline Detection. NASA Technical Paper Rep. NASA/TP-2002-211956, NASA Langley Research Center, Hampton, Virginia.)

Gregorich D T, Aumann H H.2003.Verification of AIRS boresight accuracy using coastline detection. IEEE Transactions on Geoscience and Remote Sensing, 41 : 298–302. DOI: 10.1109/TGRS.2002.808311.

Guan M, Yang Z D.2009.Geolocation method for FY-3 MWRI’s remote sensing image. Journal of Remote Sensing, 13 : 463–474. ( 关敏, 杨忠东. 2009. FY-3微波成像仪遥感图像地理定位方法研究. 遥感学报, 13 : 463–474. )

(Hoffman L H, Weaver W L and Kibler J F. 1987. Calculation and accuracy of ERBE scanner measurement locations. NASA Technical Paper Rep. NASA/TP-2670. NASA Langley Research Center, Hampton, Virginia.)

Kroodsma R A, McKague D S, Ruf C S.2012.Inter-calibration of microwave radiometers using the vicarious cold calibration double difference method. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5 : 1006–1013. DOI: 10.1109/JSTARS.2012.2195773.

Lagarias J C, Reeds J A, Wright M H, Wright P E.1998.Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM Journal on Optimization, 9 : 112–147. DOI: 10.1137/S1052623496303470.

Lipton A E, Moncet J L, Boukabara S A, Uymin G, Quinn K J.2009.Fast and accurate radiative transfer in the microwave with optimum spectral sampling. IEEE Transactions on Geoscience and Remote Sensing, 47 : 1909–1917. DOI: 10.1109/TGRS.2008.2010933.

Liu J Y. Principles and Methods of GPS Satellite Navigation and Positioning. 科学出版社: Beijing 2003 . ( 刘基余. 2003. GPS卫星导航定位原理与方法. 科学出版社: 北京 . )

Liu L. Mechanics of Man-mad Satellite Orbit. 高等教育出版社: Beijing 1992 . ( 刘林. 1992. 人造地球卫星轨道力学. 高等教育出版社: 北京 . )

Moradi I, Meng H, Ferraro R R, Bilanow S.2013.Correcting geolocation errors for microwave instruments aboard NOAA satellites. IEEE Transactions on Geoscience and Remote Sensing, 51 : 3625–3637. DOI: 10.1109/TGRS.2012.2225840.

Poe G A, Conway R W.1990.A study of the geolocation errors of the Special Sensor Microwave/Imager (SSM/I). IEEE Transactions on Geoscience and Remote Sensing, 28 : 791–799. DOI: 10.1109/36.58965.

Poe G A, Uliana E A, Gardiner B A, von Rentzell T E, Kunkee D B.2008.Geolocation error analysis of the Special Sensor Microwave Imager/Sounder. IEEE Transactions on Geoscience and Remote Sensing, 46 : 913–922. DOI: 10.1109/TGRS.2008.917981.

Purdy W E, Gaiser P W, Poe G A, Uliana E A, Meissner T, Wentz F J.2006.Geolocation and pointing accuracy analysis for the WindSat sensor. IEEE Transactions on Geoscience and Remote Sensing, 44 : 496–505. DOI: 10.1109/TGRS.2005.858415.

Qiao M, Yang H, He J K, Lv L Q.2012.On-orbit performance stability analysis of microwave radiometer imager onboard FY-3 Satellite. Journal of Remote Sensing, 16 : 1246–1261. ( 乔木, 杨虎, 何嘉恺, 吕丽清. 2012. 风云三号卫星微波成像仪在轨性能稳定性分析. 遥感学报, 16 : 1246–1261. )

Smith G L, Priestley K J, Hess P C, Currey C, Spence P.2009.Validation of geolocation of measurements of the Clouds and the Earth’s Radiant Energy System (CERES) scanning radiometers aboard three spacecraft. J. Atmos. Oceanic Technol., 26 : 2379–2391. DOI: 10.1175/2009JTECHA1207.1.

Tang F, Zou X L, Yang H, Weng F Z.2016.Estimation and correction of geolocation errors in FengYun-3C microwave radiation imager data. IEEE Transactions on Geoscience and Remote Sensing, 54 : 407–420. DOI: 10.1109/TGRS.2015.2458851.

Wang L K, Tremblay D A, Han Y, Esplin M, Hagan D E, Predina J, Suwinski L, Jin X, Chen Y.2013.Geolocation assessment for CrIS sensor data records. Journal of Geophysical Research, 118 : 12690–12704. DOI: 10.1002/2013JD020376.

Wiebe H, Heygster G, Meyer-Lerbs L.2008.Geolocation of AMSR-E Data. IEEE Transactions on Geoscience and Remote Sensing, 46 : 3098–3103. DOI: 10.1109/TGRS.2008.919272.

Wolfe R E, Nishihama M, Fleig A J, Kuyper J A, Roy D P, Storey J C, Patt F S.2002.Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sensing of Environment, 83 : 31–49. DOI: 10.1016/S0034-4257(02)00085-8.

Wu R H, Yang Z D, Guan M, Li X X.2012.Improved FY-3B/MERSI geolocation accuracy using installation matrix. Journal of Image and Graphics, 17 : 1327–1332. ( 吴荣华, 杨忠东, 关敏, 李翔翔. 2012. 修正安装矩阵提高FY-3B/MERSI的地理定位精度. 中国图像图形学, 17 : 1327–1332. )

Xie Z, Li J P, Chen Z. Nonlinear Optimization Theory and Methods. 高等教育出版社: Beijing 2010 . ( 谢政, 李建平, 陈挚. 2010. 非线性最优化理论与方法. 高等教育出版社: 北京 . )

摘要

关键词