|
收稿日期: 2016-01-06; 优先数字出版日期: 2016-11-25
基金项目: 国家自然科学基金(编号:61378078)
第一作者简介: 史潇天(1987—),博士研究生,研究方向为机载LiDAR数据处理理论研究与计算机视觉。E-mail:
xiaotians1987@163.com
通讯作者简介: 马洪超(1969—),教授,博士生导师,研究方向为机载LiDAR点云数据理论研究。E-mail:
hchma@whu.edu.cn
中图分类号: P237
文献标识码: A
|
摘要
现有密集匹配点云数据已实现了地表3维信息的精细化表达,然而由于误匹配,此类点云往往包含一定数量粗差点并影响后续应用的处理效果。针对此类数据中误匹配所产生粗差点的剔除问题,将变差函数引入移动最小二乘(MLS)粗差剔除算法。变差函数对MLS拟合区域内点对间的相关性进行估算,以此为依据设置权值对最小二乘的结果进行优化;然后利用MLS局部、分区域地对点云进行曲面拟合;最终根据拟合结果剔除粗差。利用A3数字测图系统生成的城区、山区密集点云数据进行实验,并将处理结果、等权MLS处理结果与人工剔除结果进行对比。实验结果表明该算法可有效对点云中的粗差进行剔除,相较于等权MLS粗差剔除算法,该算法在城区、山区的误判率分别降低了5.16%和1.31%。
关键词
匹配点云 , 粗差剔除 , 移动最小二乘 , 权重 , 变差函数
Abstract
With the development of digital mapping cameras and image-matching techniques, highly dense point clouds can be automatically obtained by stereo image matching. These point clouds can be applied to 3D building reconstruction and DEM/DSM generation. However, owing to certain factors, such as textural differences, geometric distortions, and shadows, point clouds sustain gross errors. To address this problem, a semivariogram-based weight moving least square (SWMLS) method is proposed for gross error detection in point clouds obtained by stereo image matching.The SWMLS method is an iterative process. For each iteration, a semivariogram is used to estimate in advance the covariance between points in different distances and aspects. The weight can be calculated based on the estimated covariance and applied to approximate the least square and terrain surface separately. The distance between each point and the surface is calculated with the approximated local parametric surface, and the distance-constrained histogram method is used to detect the gross errors. Ingross error detection, the least square approximation move through the entire region of the point cloud by the same steps in the x-axis and y-axis. In this paper, we focus on discussing the adaptability of semivariogram to the digital elevation model and its variation across different terrains.The A3 system-generated point clouds of two datasets of urban and mountainous area ares used in the experiments. The point cloud for the urban area contains a 4.00% gross error, whereas the point cloud for the mountainous area contains 0.19% gross error. To test the efficiency and advantages of our method, the results of our method and those of the equal weight based MLS (EWMLS) method are compared manually to the detected results. Experimental results show that both SWMLS and EWMLS have removed all the gross errors in the point cloud. However, the results of a further quantitative analysis suggest that SWMLS is more accurate than EWMLS. For the urban area, the misclassification by S WMLS is 2.07%, whereas that by EWMLS is 7.72%. For the mountainous area, EWMLS has committed 2.56% misclassification, whereas our proposed method generated a reduced misclassification (0.76%).We may draw the conclusion as below. (1) As a regionalized method, semivariogram is efficient in weight estimation in MLS. (2)Both SWMLS and EWMLS are effective in detecting gross errors in point clouds generated from stereo images. However, both methods may commit few misclassifications for urban and mountainous areas. (3)Compared with EWMLS, SWMLS generated less misclassification in both datasets, suggesting that SWMLS demonstrates a better performance in the gross error detection in stereo-matched point clouds.
Key words
stereo-images-matched point cloud , gross error detection , moving least square , weight , semi-variogram
1 引 言
随着航空航天摄影测量以及相关匹配技术的发展,通过立体像对获取密集点云成为一种可能。为将此类点云与机载激光雷达(LiDAR)点云数据进行区分,这里将其称为匹配点云。相较于LiDAR点云数据,匹配点云数据同样可以精细地表达3维空间信息,因而将这种点云的应用从4D产品生产拓展到3维建模、建筑物变化检测等领域( Nebiker 等,2014; Furukawa 等,2010)。但此类点云数据受到误匹配的影响,不可避免地包含一些粗差点,为消除粗差对后续应用的影响,在相关应用前需自动对点云中的粗差点进行剔除。
目前直接针对密集匹配点云的粗差剔除算法较少,结合机载LiDAR点云数据中粗差点(outlier)的剔除算法和较稀疏数字高程模型(DEM)数据中粗差的剔除算法,粗差剔除算法分为以下几种:基于频谱分析的粗差剔除算法( Reddy 等,2009)、基于密度的粗差剔除算法( Tian 等,2012; Sotoodeh,2006)、基于坡度的粗差剔除算法( Hannah,1981)以及基于局部邻近点拟合的粗差剔除算法( Brovelli 等,2002; 周晓明,2011)。其中,基于频谱分析的粗差剔除算法主要针对LiDAR数据中的粗差剔除问题,该算法通过分析LiDAR点云生成前的波形信号对粗差点进行剔除( Zhou,2013),不能推广到匹配点云中;基于密度的粗差剔除算法针对离散分布的粗差点,该算法统计局部小空间内点云的数量以及分布情况对粗差点进行剔除( 蒋晶珏 等,2007), Sotoodeh(2006)介绍了对此算法中的几种常见的空间密度表达算子并利用LOF(Local Outlier Factor)算子对机载LiDAR点云数据进行粗差剔除。此类算法根据局部空间内点云的分布密度对粗差点进行判断,因此无法有效识别簇集分布的粗差点;基于坡度的粗差剔除算法主要根据局部区域的坡度信息对高程数据中的粗差进行剔除, Hannah(1981)就将此类算法用于格网化的DTM(Digital Terrain Model)中并取得了较好的效果;基于局部邻近点拟合的粗差剔除算法,利用局部点云数据的曲面拟合结果对粗差进行剔除( 杨晓云 等,2005),此类算法所利用的局部空间远大于基于密度的剔除算法中的局部空间大小且拟合范围内粗差点占总点数的比例较小,此类算法可以在局部区域内较好地拟合曲面,杨晓云( 杨晓云 等,2005)将此类算法用于较为稀疏点云数据中的粗差剔除中,通过点与不同窗口下拟合曲面的残差值对其是否为粗差点进行判断。
在基于局部邻近点拟合的粗差剔除算法中,MLS算法由于其较好的适应性,被广泛地应用于不同领域( 杨晓云 等,2005; Qiu 等,2011)。该算法设定阈值并利用最小二乘对数据进行局部、分区域地曲面拟合,在拟合后根据拟合结果与阈值的对比结果对局部区域内的粗差进行剔除。然而此类算法的粗差剔除效果受拟合精度影响( Zhang 等,2010)。在MLS的相关处理中,需根据对象的不同,选择合适的权重函数以达到较好的拟合效果( Lancaster和Salkauskas,1981; Gois和Buscaglia,2010; Felter 等,2014)。因此,在利用MLS进行密集匹配点云的粗差剔除中应考虑权值设置问题。
就此问题,本文提出了一种基于变差函数的权值估算方法,针对密集匹配点云的去噪问题进行优化。为验证算法,将A3数字测图系统生成的城区、山区密集点云数据用于实验分析。实验表明相较于等权MLS粗差剔除算法,本文算法可以在保证粗差剔除的同时,大幅降低误判率,取得较好的剔除效果。
2 匹配点云中粗差的分布特点
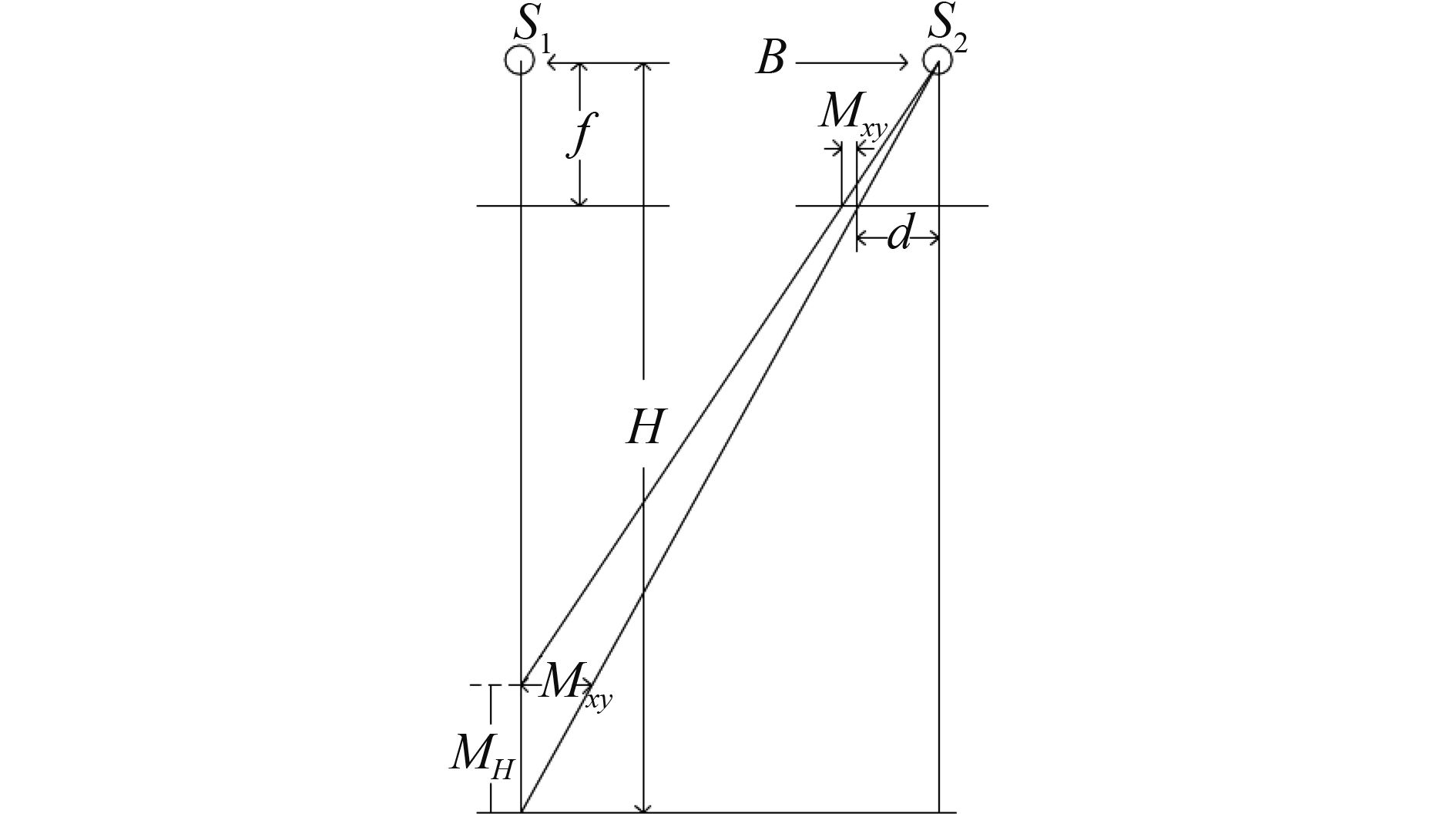
通过立体成像获得的密集匹配点云中,不可避免地包含一些由误匹配产生的粗差,粗差分布原理如 图1所示,假设 S 1、 S 2分别为一对立体相对的投影中心, B为基线, f为焦距, d为像方摄影基线, H为航高,则由误匹配所导致的粗差相较于正确匹配计算的点云在平面和高程上具有一定的偏移即 M XY 和 M H 。根据立体成像的基本几何原理误匹配所导致的粗差在水平和高程上的偏移量可有下式表达
| $ {M_{XY}} = \frac{{{M_{xy}} \times H}}{f} $ | (1) |
| $ {M_H} = \frac{{{M_{xy}} \times H}}{B} $ | (2) |
点云数据中此类粗差点会受 M XY 、 M H 影响,分布情况将有异于其他有效点,其分布形式如 图2(a)、 图2(b)所示。其中粗差点在平面和高程都存在一定偏移,常以簇集和孤立两种形式远离地表随机分布。
考虑到误匹配所导致的粗差点总是远离地表并随机分布,可以拟合地表曲面,并对粗差点进行剔除。为适应不同地形下地表的曲面拟合,本文提出了一种变差函数权值估算下的移动最小二乘粗差剔除算法。
3 基于移动最小二乘的粗差剔除算法
在密集匹配的点云数据中,点云的分布并不均匀。而在最小二乘进行参数求解中,需要足够数量、分布均匀的点云数据。因此,在进行曲面拟合之前,首先对局部范围内点云数量及分布进行分析。当点云数量过少或者出现较大空洞时,扩大拟合范围以便增加点云数量并降低局部区域内点云分布不均匀所造成的影响。选定范围后,利用最小二乘算法对曲面拟合的参数进行求解,这里使用的拟合函数为
| $ f\left( {x,y} \right) = {a_0} + {a_1}x + {a_2}y + {a_3}{x^2} + {a_4}xy + {a_5}{y^2} $ | (3) |
式中,ai为曲面拟合参数;x、y为点云数据的平面坐标,f(x,y)可理解为点(x,y)所对应的高程值。误差方程可由下式进行表达
| $ V = AX - L,W(h) $ | (4) |
获取局部区域的拟合曲面后,通过比较阈值和点云与拟合曲面的关系识别粗差点。考虑到粗差对地表拟合的影响以及不同地物对应点云到拟合曲面距离上的差异性,提出带有分布密度约束的距离阈值判断方法。该方法首先对点云到拟合曲面的距离进行直方图统计,然后根据该直方图中每组所包含的点数以及该组到拟合曲面的距离进行剔除。该算法的具体参数设置和本文算法的总体流程将在第5节进行详细介绍。
就MLS地表拟合而言,局部区域的拟合精度受拟合范围地表起伏的复杂程度制约。若拟合范围内地表变化较为复杂,即含有多个高程剧烈变化,则点对间的相关性较弱。拟合过程中需增大不同距离h下W(h)的差异,降低拟合曲面光滑度,提高拟合区域中心的拟合精度。针对这一问题,本文提出了一种基于变差函数的权值估算算法。
4 基于变差函数的权值估算
4.1 变差函数及其在不同地形的适用性分析
变差函数首次提出于20世纪60年代( Clark,1979),该算子可对空间中呈现出一定结构性和随机性的区域化变量进行分析。该方法认为当区域化变量满足准本征条件时即:
(1) 在有限区域范围内对于$\forall$p存在期望E[Z(p)]且E[Z(p)]为常数;
(2) 增量E[Z(p)-Z(p+h)]的方差函数存在且不依赖于p;
可以通过计算特定距离下,区域化变量间的增量方差来反映区域化变量间的相关性( Webster和Oliver,2007)。其中,特定距离下的变差函数可以通过下式表达
| $ \gamma \left( h \right) = \frac{1}{{2m\left( h \right)}}\sum\limits_{i = 1}^{m\left( h \right)} {{{\left[ {z\left( {{p_i}} \right) - z\left( {{p_i} + h} \right)} \right]}^2}} $ | (5) |
式中, γ(h)是距离为h的变差函数值;m(h)是距离为h的区域化变量对的数量;z(p i)为点p i所对应的区域化变量。
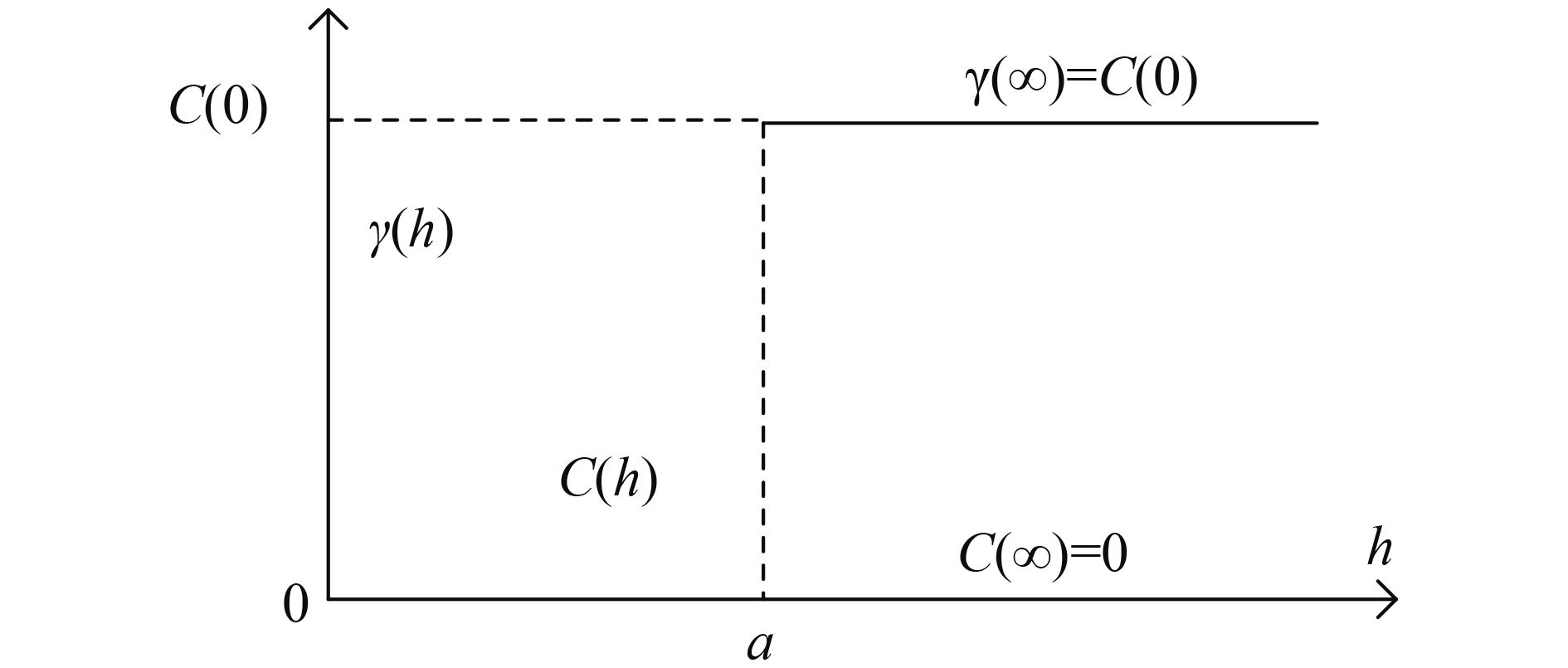
在此条件下变差函数值和协方差函数值如图3所示。
图3中,γ(∞)=C(0)为局域变量的方差,C(h)为距离h下两点间的协方差,当统计区域满足准本征条件时,则存在C(h)=γ(∞)-γ(h),其中变差函数值γ(h)会随着距离的增加不断递增并在距离为a处达到一个峰值即γ(∞)。这是C(0)为0之后变量间将不具备相关性。
而若统计范围内存在漂移现象,即统计对象在一定范围内存在较为明确的变化走势,则需在统计前对其趋势进行模拟,然后对残剩余的随机项进行变差函数统计。
| $ Z\left( p \right) = m\left( p \right) + R\left( p \right) $ | (6) |
式中,Z(p)为区域化变量,m(p)称为趋势项,R(p)称为随机项。
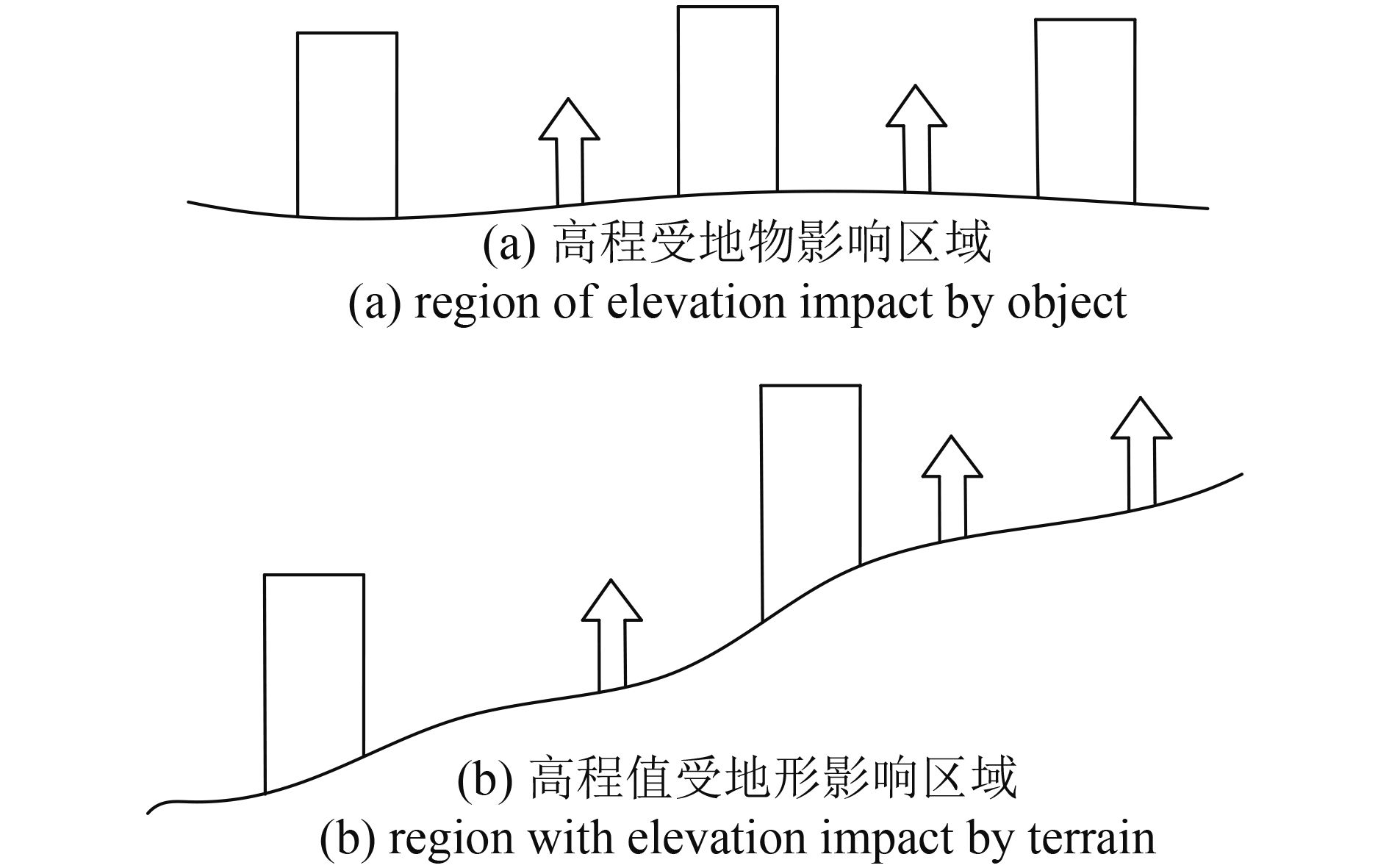
在对不同区域进行高程值相关性分析中,同样存在不同的情况,如图4所示。
其中城区地表高程值主要受地物影响如 图4(a) 所示,在一定范围内,地物随机均匀分布,可满足准本征条件的基本假设;山区地表高程主要受地形影响如 图4(b) 所示,随着山体的连续变化,在相关性分析时需先对变化的趋势项拟合后再进行统计。
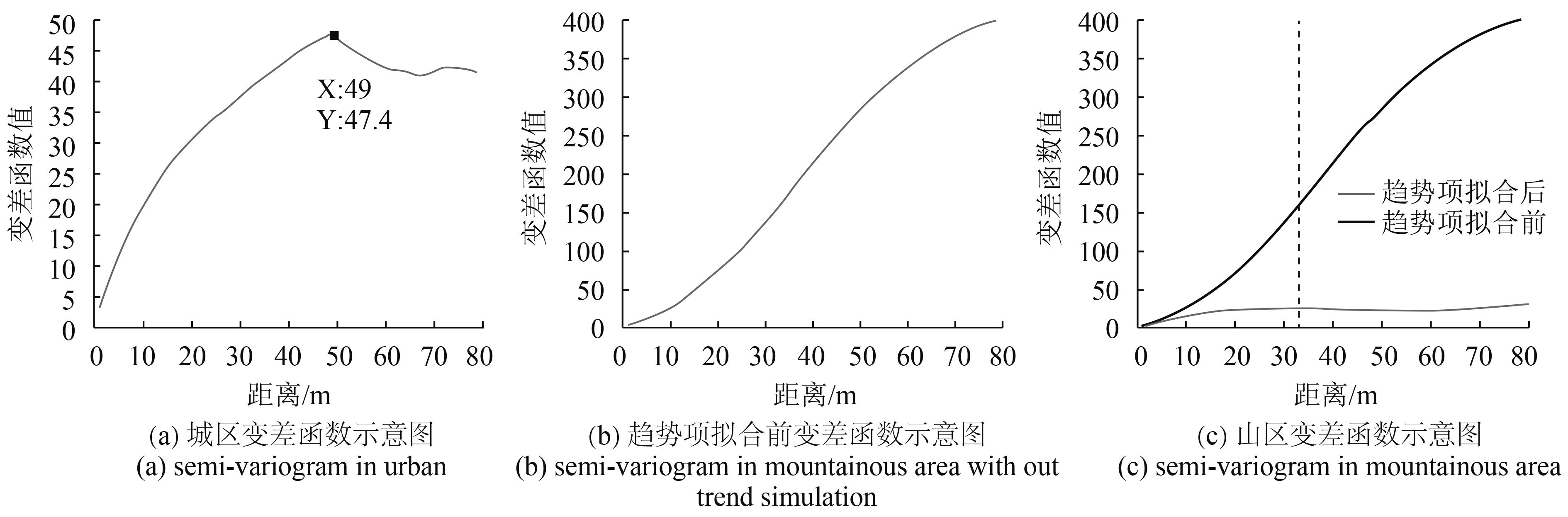
如 图5所示, 图5(a)中为城区的变差函数统计结果,其结果较好地反映出变差函数在满足准本征条件时应有的特征,点对间失相关的距离为49 m; 图5(b)为山区在趋势项拟合前的变差函数曲线,这里利用多项式进行趋势项分析后( Lloyd和Atkinson,2006),其结果具有满足本征条件下变差函数的基本特征。 图5(c)中浅色曲线为山区趋势项拟合后的变差函数图,深色为趋势项拟合前变差函数图,虚线为趋势项拟合后点对间失相关的距离即33 m。
该算法利用变差函数对局部区域内高程值的相关性进行描述,以此为依据设置最小二乘拟合中的权值。若区域内高程值存在高程突变则相关性较低,根据变差函数结果设置权重可使拟合中心区域获得较大的权值,降低曲面拟合光滑度,提高局部拟合精度和粗差剔除效果。但变差函数只能对1维统计空间内点对间的相关性进行描述,而在MLS中点对间的距离属于2维空间;同时,变差函数在不同地形下差异较大(城区不需要趋势项拟合、山区需要趋势项拟合),不同地形失相关距离存在差异。而在使用中希望通过一种通用的方式对权值进行估算,如何对其进行简化,简化会产生什么影响。下文就将对这两个问题进行分析。
4.2 基于变差函数的MLS权值估算
变差函数是1维数据的统计算法,因此无法对2维空间内点对间的相关性进行完整的描述。参考( Tesfamichael 等,2009)中变差函数在高程数据中的处理方法,对变差函数在2维高程空间内的统计方式进行优化,将统计区域分为4个方向,即0°、45°、90°、135°,并以45°作为缓冲区对不同方向分别进行统计。通过设置统计方向,增加了变差函数在2维空间内的适应性,提高其在权值估算中的可靠性。
根据变差函数与协方差函数的关系,可通过下式对一定距离的权值进行估算
| $ W\left( h \right) = \frac{{\gamma \left( \infty \right) - \gamma \left( h \right)}}{{\gamma \left( \infty \right)}} $ | (7) |
图3中距离 a即统计区域内样本间失相关时所对应的变差函数值。
在权值估算中,希望通过统一的权值函数是不同地形的权值进行计算,因此需要分析不同因素对权值计算的影响,选择性的对权值计算方法进行简化。
在MLS曲面拟合中,不同距离 h下导致的 W( h)差异增加的简化方式是可以接受的,这种简化方式增加了算法拟合中心权值,减小了在较远点的权值。对MLS拟合而言,这种做法将减少拟合曲面光滑度,对粗差剔除结果影响较小。
在对不同地形的权值计算中,需要对两个因素进行分析:(1)趋势项分析前后的权值计算差异;(2)较小变差函数值 γ( h)对 γ(∞)的替代问题。
由 图5c可以发现,相较于趋势项拟合后的变差函数值,趋势项拟合前的变差函数值变化更剧烈,由式(7)可知,直接使用趋势项拟合前的变差函数将会增加不同距离 h下 W( h)的差异性,在 γ( h)不变的情况下,降低 γ(∞)同样可以达到类似的效果。在应用中直接使用求得的最大变差函数值 γ max对 γ(∞)进行替代。
变差函数是离散的相关性计算方法,为将其更加便利的应用于权值估算,需对其进行拟合。考虑到 图5(a)和 图5(c)中可能同时存在变差函数梯度 γ′存在变大、变小等不同情况,这里选择变差函数拟合中常用的通用线性模型( Clark,1979)对其进行拟合。通用线性模型公式如下所示
| $ \gamma^*\left( h \right) = {C_0} + p{h^\alpha } $ | (8) |
式中, W( h)最终经过归一化后,MLS拟合中的任意点的权值可由下式进行表达
| $ \left\{ {\begin{array}{*{20}{l}} {W\left( h \right) = \frac{{{\gamma _{\max }} - \gamma^*{{\left( h \right)}_{dir}}}}{{{\gamma _{\max }}}} \quad h < b}\\ {W\left( h \right) = 0 \quad h \geqslant b} \end{array}} \right. $ | (9) |
式中, h为该点到曲面拟合中心的平面距离; $ {\gamma ^*}{(h)_{dir}} $为该点在其特定方向上所对应的变差函数值; γ max为区域内4个方向上变差函数的最大值; b为拟合的MLS曲面拟合的范围。
5 算法总体流程
综上所述,算法总体流程包括以下几步:
(1) 以5 m为步长以20 m为基本窗口大小对点云数据进行分块处理,若20 m窗口内点云数量过于稀疏则增加窗口大小。其中,步长与拟合中精度较高的拟合中心区域范围相关;基本窗口大小受变差函数中失相关范围。 图1(a)和图1(b)中变差函数分别在45 m和33 m处开始失相关,这里将拟合窗口设为20 m可满足失相关范围要求。
(2) 以拟合曲面中心为中心,以100 m为半径划分区域,利用式(5)对区域内的高程值进行变差函数统计,并根据式(9)计算权重函数。
(3) 将该权值带入到MLS函数中进行拟合计算,计算各点到平面的距离。根据点到平面的距离以0.5 m为间隔进行分组。由于测试数据点云密度大致为0.5 pts/m 2,这里将点数阈值设为5;为降低局部区域内剧烈高程变化导致的拟合精度误差这里将距离阈值设为10 m。最终根据结果对判断结果对粗差点进行剔除。
6 实验与分析
6.1 实验数据
为了验证本文算法在密集匹配点云中的粗差剔除效果,这里使用两组A3数字测图系统生成的点云数据进行分析,其中山区范围约为1000×1000 m,点云为0.58 pts/m 2;城区范围约为400×400 m,点云密度为0.49 pts/m 2。为更好地对算法效果进行定量分析,本文通过人工分类的方式对点云中的粗差点进行分类。人工分类中,根据误匹配所产生粗差点的特征,将远离地表或地物的点作为粗差点进行剔除,最终剔除结果如 图6所示,其中浅色点为粗差点。
对人工粗差剔除结果进行统计,统计结果如 表1所示,由 表1可知两块区域点数存在一定差异,城区点云数量小于山区;两块区域均包含一定数量的粗差点,其中城区由于误匹配所产生的粗差点为4%,山区由于误匹配所产生的粗差点为0.19%,城区数据受粗差点影响更大。
表 1 点云信息
Table 1 Information of point clouds
| 参数 | Site1 | Site2 |
| 匹配点总数 | 119486 | 224205 |
| 粗差点数 | 4.00% | 0.19% |
6.2 粗差去除实验
为分析比较该算法在不同地形条件下的效果,利用基于变差函数的MLS粗差剔除算法和等权MLS粗差剔除算法,分别对含有粗差的点云数据进行处理,并与人工提取结果进行比较。
如 图7所示,通过对两种地形下实验结果进行可视化比较,发现基于MLS的粗差剔除算法在不同地形下,均可在保持地物完整性的同时较好地对粗差进行剔除。在剔除中,对簇集形式的粗差或空间分布较为复杂的粗差群均具备较强的识别效果。对粗差达到了100%的识别。
将两种算法结果与人工剔除结果进行对比和定量分析,结果如 表3所示。通过 表3可以发现MLS粗差剔除算法的误判率会随着地形突变的增多而增多。等权MLS粗差剔除算法对两块区域进行处理,较小的误判率出现在山区,只有2.07%,而在城区则高达7.72%。通过算法优化,将变差函数引入到MLS中的权值估算可以在不同程度上降低粗差剔除过程中的误判率。通过对比我们发现,本文算法和等权MLS粗差剔除算法相比,其误判率在城区的降低了5.16%、在山区降低了1.31%。考虑到山区粗差剔除的误判率较小,只有2.07%,可以认为基于变差函数权值计算的MLS粗差剔除算法相较于基于等权MLS等权粗差剔除算法在山区和城区均能很好的降低粗差的误判率。
表 2 粗差结果对比
Table 2 Gross error number of different method
| 参数 | Site1 | Site2 |
| 等权MLS粗差提取点数 | 13595 | 5493 |
| 基于变差函数的MLS粗差提取点数 | 7431 | 2546 |
表 3 两种算法的误判率评估
Table 3 Errors in the two gross error detecting method
| 参数 | Site1 | Site2 |
| 等权MLS粗差剔除效果 | 7.72% | 2.07% |
| 基于变差函数MLS粗差剔除效果 | 2.56% | 0.76% |
| 误判率降低比例 | 5.16% | 1.31% |
7 结 论
针对不同地形下,密集匹配点云数据的粗差剔除问题提出了一种基于变差函数权重估算的MLS粗差剔除算法。该算法利用变差函数对MLS中的权重进行优化并最终达到提高粗差剔除效果的目的。通过实验,可以得出以下结论:(1)MLS算法可以有效地对密集匹配点云中的粗差进行剔除,但这种方法可能会产生一定数量的误判,导致一部分有效点被判定为粗差;(2)利用变差函数统计相关性,并应用于MLS的权重估算中可以有效降低粗差剔除结果中的误判率,提高粗差剔除效果。进一步分析可以发现,城区粗差剔除后误判了高于山区。因此,今后将针对城区的粗差剔除展开研究。研究分析城区复杂地物的拟合问题进行优化问题。
参考文献(References)
-
(Brovelli M A, Cannata M and Longoni U M. 2002. Managing and processing LIDAR data within GRASS // Proceedings of the Open Source GIS-GRASS Users Conference 2002. Trento, Italy.) http://cn.bing.com/academic/profile?id=2131048615&encoded=0&v=paper_preview&mkt=zh-cn
-
Clark I. Practical Geostatistics. Applied Science Publishers: London 1979 .
-
Felter C L, Walther J H, Henriksen C.2014.Moving least squares simulation of free surface flows. Computers & Fluids, 91 : 47–56. DOI: 10.1016/j.compfluid.2013.12.006.
-
(Furukawa Y, Curless B, Seitz S M and Szeliski R. 2010. Towards internet-scale multi-view stereo // 2010 IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, CA: IEEE: 1434-1441 [DOI: 10.1109/CVPR.2010.5539802])
-
Gois J P, Buscaglia G C.2010.Resampling strategies for deforming MLS surfaces. Computer Graphics Forum, 29 : 1969–1980. DOI: 10.1111/j.1467-8659.2010.01663.x.
-
Hannah M J.1981.Error detection and correction in digital terrain models. Photogrammetric Engineering and Remote Sensing, 47 : 63–69.
-
Jiang J J, Zhang Z X, Ming Y.2007.Filtering of lidar point clouds for complex cityscapes. Geomatics and Information Science of Wuhan University, 32 : 402–405. ( 蒋晶珏, 张祖勋, 明英. 2007. 复杂城市环境的机载Lidar点云滤波. 武汉大学学报(信息科学版), 32 : 402–405. )
-
Lancaster P, Salkauskas K.1981.Surfaces generated by moving least squares methods. Mathematics of Computation, 37 : 141–158. DOI: 10.1090/S0025-5718-1981-0616367-1.
-
Lloyd C D, Atkinson P M.2006.Deriving ground surface digital elevation models from LiDAR data with geostatistics. International Journal of Geographical Information Science, 20 : 535–563. DOI: 10.1080/13658810600607337.
-
Nebiker S, Lack N, Deuber M.2014.Building change detection from historical aerial photographs using dense image matching and object-based image analysis. Remote Sensing, 6 : 8310–8336. DOI: 10.3390/rs6098310.
-
Qiu Y J, Zhou X H, Yang P H, Qian X P.2011.Curvature estimation of point set data based on the moving-least square surface. Journal of Shanghai Jiaotong University (Science), 16 : 402–411. DOI: 10.1007/s12204-011-1168-6.
-
Reddy T S, Reddy G R, Varadajan S, Reddy K Y.2009.Noise reduction in LIDAR signal using wavelets. International Journal of Engineering and Technology, 2 : 21–28.
-
Sotoodeh S.2006.Outlier detection in laser scanner point clouds. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 36 : 297–302.
-
Tesfamichael S G, Ahmed F, Van Aardt J A N, Blakeway F.2009.A semi-variogram approach for estimating stems per hectare in Eucalyptus grandis plantations using discrete-return lidar height data . Forest Ecology and Management, 258 : 1188–1199. DOI: 10.1016/j.foreco.2009.06.016.
-
(Tian X R, Xu L J, Li X L, Jing L L and Zhao Y. 2012. A kernel-density-estimation-based outlier detection for airborne LiDAR point clouds // 2012 IEEE International Conference on Imaging Systems and Techniques Proceedings. Manchester: IEEE: 263-266 [DOI: 10.1109/IST.2012.6295546])
-
Webster R, Oliver M A. Geostatistics for Environmental Scientists. John Wiley & Sons: Chichester, UK 2007 .
-
Yang X Y, Gu L Y, Cen M Y, Li Z L.2005.A method based fitting of moving quadric surface with variable windows for detecting gross errors in irregular DEM. Acta Geodaetica Et Cartographica Sinica, 34 : 148–153. DOI: 10.3321/j.issn:1001-1595.2005.02.011. ( 杨晓云, 顾利亚, 岑敏仪, 李志林. 2005. 基于不同大小窗口的移动曲面拟合法探测不规则DEM粗差的一种方法. 测绘学报, 34 : 148–153. DOI: 10.3321/j.issn:1001-1595.2005.02.011. )
-
Zhang L, Liu L G, Gotsman C, Huang H.2010.Mesh reconstruction by meshless denoising and parameterization. Computers & Graphics, 34 : 198–208. DOI: 10.1016/j.cag.2010.03.006.
-
(Zhou X M. 2011. Research and Application of Airborne LIDAR Point Cloud Data Filters. Zhengzhou: The PLA Information Engineering University: 40-52周晓明. 2011. 机载激光雷达点云数据滤波算法的研究与应用. 郑州: 解放军信息工程大学: 40-52)
-
Zhou Z R, Hua D X, Wang Y F, Yan Q, Li S C, Li Y, Wang H W.2013.Improvement of the signal to noise ratio of Lidar echo signal based on wavelet de-noising technique. Optics and Lasers in Engineering, 51 : 961–966. DOI: 10.1016/j.optlaseng.2013.02.011.