Print

出版日期: 2016-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20165234
2016 | Volumn20 | Number 6





                              上一篇|





下一篇
遥感应用
热红外与可见光数据的云边缘高度匹配
expand article info 李彬1,2 , 辛晓洲2 , 张海龙2 , 胡继超1
1. 南京信息工程大学 应用气象学院，南京 210044
2. 中国科学院遥感与数字地球研究所遥感科学国家重点实验室，北京 100101
收稿日期: 2016-01-22; 修改日期: 2016-05-18; 优先数字出版日期: 2016-11-25
基金项目: 中国科学院重点部署项目(编号: KZZD-EW-TZ-18)；国家自然科学基金(编号: 41371360)
第一作者简介: 李彬(1989—)，男，硕士研究生，研究方向为地表辐射平衡。E-mail： 983229508@qq.com
通讯作者简介: 辛晓洲(1976—)，男，副研究员，研究方向为地表辐射与能量平衡遥感估算理论与方法。E-mail： xin_xzh@163.com
中图分类号: TP79
文献标识码: A

摘要

高分辨率数据中云高度的差异性突显，特别是边缘处高度在云阴影识别和地表辐射估算等方面成为需要考虑的重要因素。热红外数据获取云高度分辨率较低、缺乏细部差异性特征，为解决这一问题，首先将对应的热红外和可见光数据进行特征点配准，再将基于热红外数据计算的云高度重采样至高分辨率，然后以基于欧式距离变换的围线搜索方法及距离加权将热红外云边缘高度匹配至对应的可见光图像，最后根据云阴影的相似度匹配方法确定真实云高度。结果表明，算法在遵循热红外云高信息分布变化规律的同时，可以得到较准确的高分辨率云边缘高度，一定程度上解决了热红外技术获取云高在分辨率上的局限，扩展了其在云高反演方面的作用。

关键词

云边缘高度 , 欧氏距离变换 , 围线搜索 , 云阴影

Cloud edge heights matching between thermal infrared and visible data
expand article info LI Bin1,2 , XIN Xiaozhou2 , ZHANG Hailong2 , HU Jichao1
1.School of Applied Meteorology, Nanjing University of Information Science & Technology, Nanjing 210044, China
2.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China

Abstract

Differences in cloud height are obvious in high-resolution data, especially because cloud edge heights have become an important factor in cloud shadow identification and estimation of surface solar radiation. However, the resolution of cloud heights calculated by thermal infrared data is low and lacks detailed characteristics. Cloud edges of visible and thermal infrared bands differ considerably both in shape and geometric features. The edge of high-resolution image has rich characteristics, whereas that of thermal infrared cloud height data is single and fuzzy in geometric characteristics, so they cannot match exactly. Although some feature points of clouds can be obtained by some feature point matching methods such as Scale-Invariant Feature Transform (SIFT) and Harris, the difference between two data on geometric features made available by feature points was less. This result cannot satisfy the need to match the information of thermal infrared cloud heights and high-resolution cloud edge data, and obtain a result with abundant diversity. To solve this problem, an algorithm was presented in this study. First, SIFT algorithm was utilized in this method to extract feature points for further image registration and correction. Then, cloud edge heights were calculated by thermal infrared data and re-sampled to a high resolution. Next, Euclidean distance transform was performed for each cloud edge pixel of high-resolution data to all thermal infrared cloud edge pixels, which could obtain spatial relationships between the two types of data. As the two types of data differed considerably in edge characteristics, directly determining the optimal matching point was difficult. Thus, a hierarchical searching method was used here. While the searched objects had different significance to matching points, the weight was given by distance to determine the final matching height. Finally, real cloud heights were determined according to the matching method of cloud shadow similarity. We used five images of HJ-1B CCD and IRS data in the Heihe area on June 8, 2012. From all the matched results, the corresponding regions of the matched results had high cloud heights where thermal infrared data also had high cloud heights. At the same time, resolution and details were improved. To evaluate the accuracy of the calculated heights, we selected 10 highly recognizable feature shadow points in each image and marked their coordinates in the image. We set the actual shadow points as reference and calculated the offset of the same feature shadow point, in which we could obtain the error of each cloud height. We found that the errors between 0.1 km to 0.3 km were 70% among all 50 points, 12% were less than 0.1 km, and 0.25 km was the average error of all points. Compared with other studies, cloud height accuracy was higher in our study. Also, we chose SIFT algorithm to match cloud heights by using two types of data and compared the matched results of some feature points with our method. The height accuracy obtained by SIFT was lower than that of our algorithm. In addition, unlike some feature point matching methods, our method can complete full-information matching. A cloud edge height matching method based on Euclidean distance transform by hierarchical searching is proposed in our paper. The method can match the cloud height information of low-resolution thermal infrared to corresponding cloud edge of high-resolution image. Experimental results showed that the matched results followed the distribution and variation law of thermal infrared cloud heights, as well as the cloud edge heights with high accuracy and detailed characteristics. To a certain extent, our study solved the resolution problem in obtaining cloud height by thermal infrared data. In addition, compared with some matching methods of feature points, our method could complete full-information matching and had a higher accuracy. However, the accuracy of matched results would be influenced by many factors, such as accuracy of cloud detection, surface in homogeneity, and image registration. The method in our paper is only for cloud edge height. Thus, matching for other parts of cloud still needs further research.

Key words

cloud edge heights , Euclidean distance transform (EDT) , contour scanning , cloud shadows

1 引 言

云高的获取方法有多种，如利用地基激光云高仪、毫米波雷达和热红外测云仪等。但实测手段较为费时费力，无法在较大范围内实时的获取云高，具有一定的局限性。随着卫星遥感技术的不断成熟，利用遥感数据反演地表、大气和云的各种参数，可以大范围实时的获取云高度信息。如利用遥感数据获取云顶亮温与晴空时的参考温度的差值，以垂直减温率来估算云高；除此之外还有分裂窗法和二氧化碳分层法等( 刘诚 等，2007； Hasler，1981)。应用几何的方法获取，如 Inomata等人(2002)利用遥感数据，采取傅里叶变换找到云和云阴影的对应点，并利用几何关系来计算云高；Zhu和Woodcock(2012)利用几何学方法计算云阴影，并根据计算阴影与遥感数据实际检测阴影之间的相似度来获取最后的云高度。此外，还有单星多角度、双星观测的几何反演方法，但使用时会受到较多限制。以上方法获取的云高度大多是比较单一的云顶或云底高度，没有考虑了云体内部、边缘或者不同云块高度的差异性，而这种差异性在高分辨率数据中更加突出。

虽然热红外数据能够较为方便的获得具有差异性的云高，但数据分辨率较低，在应用时受到限制( Genkova 等，2007)。基于HJ-1B的热红外数据，通过垂直减温率计算云高度，从计算结果可以发现云的高度存在差异，边缘处的高度比中心区域的要低，并且边缘处的云高之间也具有明显差异。

将同一区域可见光与热红外云边缘进行比较发现，两者在云的形状和几何特征上存在较大差异，高分辨率图像具有丰富的边缘特征，而热红外云高数据的边缘几何特征相比之下单一且模糊，两者不能完全匹配；云边缘各部分的对应关系也不明确，较难直接确定。因此如何将低分辨率的云高信息匹配到对应的高分辨率云边缘，并保持丰富的细节差异性特征成为需要解决的问题。虽然一些点特征匹配方法(如SIFT、Harris等)能够获取一些特征点，但两种数据在几何特征上的差异使可获取的特征点有限，不能满足热红外云高信息与高分辨率云边缘数据整体匹配的需要，无法得到具有丰富差异性信息的结果( 钟涛 等，2015； 甘玲和马艳春，2010)。

在现有技术中，距离变换是有效计算并标识空间点对目标点距离的方法，作为一种图像处理技术，广泛应用于图像配准等领域。原始图像经过二值化和距离变换后所得距离图像包含着一定的几何信息，是实现图像间匹配的基础，而欧氏距离作为重要的相似度测度准则常用于特征信息的匹配。另外，搜索算法也常被用于图像的配准( 徐建斌 等，2005)。当公式或模拟方法无法获得解时，需要根据一些条件，在问题的所有或部分可能解中用某种方式找出合适的解，即搜索法或搜索技术( 欧阳圣和胡望宇，2011)。首先组成一些候选解，依据某些适应性条件测算这些候选解的适应度。根据适应度保留某些候选解，放弃其他候选解，对保留的候选解进行某些操作，生成新的候选解。如围线搜索的方法，即以一定的像素宽为搜索半径形成围线区，由近及远逐步扩大搜索范围，搜索最邻近或次邻近欧氏距离范围内的点作为匹配点( 任勇勇 等，2011)。

为了能够基于低分辨率热红外数据获取高分辨率的云边缘高度，以满足云阴影计算、云参数获取及地表辐射平衡等方面的需要，本文以上述研究为参考，提出了一种基于欧氏距离的围线搜索云边缘高度匹配方法。

2 基于欧氏距离的围线搜索云边缘高度匹配方法

2.1 匹配方法框架

由于卫星热红外数据与可见光数据在分辨率、灰度和边缘特征等方面差异较大，图像间像元的位置可能存在偏移和旋转等问题，因此需要进行图像配准。对于不同分辨率、不同传感器的遥感影像，尺度不变特征算法因其对于不同尺度、灰度以及视角变化等保持不变的特性常被用于配准。由于实验影像均来自HJ-1B的同时同地的可见光和热红外数据，视角差异小，因此本文首先根据可见光图像的地理坐标信息确定对应热红外数据的大致配准区域作为待配准影像。参考倪希亮等人对HJ星可见光和红外影像配准的方法，先将基准影像与待配准影像分块处理，在相对应的影像块内利用尺度不变特征变换(SIFT)算法提取特征点进一步配准及校正( 倪希亮 等，2012)。下一步将高分辨率云边缘中每个像素对热红外云边缘像素进行欧氏距离变换，获得两种数据间的空间关系。但两种数据云边缘各部分的对应关系并不十分明确，难以根据欧氏距离直接确定(如 图1所示)，于是考虑利用搜索算法搜索距离关系密切的点作为待匹配点。


图 1 可见光与热红外云边缘叠加图
Fig. 1 Cloud edge stacking chart of visible and thermal infrared band

为了完成搜索需对云高数据先重采样至与可见光数据相同分辨率，使高分辨率的云边缘各部分，特别是一些细节丰富的部分与云高数据的距离关系更加明确；同时如果不进行重采样，两种数据存在严重的信息不对称，无法进行有效搜索。利用热红外数据计算得到云高度，使用三次样条的方法将高度图重采样到30 m分辨率，可以得到相对平滑的边缘。该方法设[ a，b]上有插值节点， a= x 1＜ x 2＜ ， $\cdot\! \cdot \! \cdot $， ＜ x n = b，对应函数值为 y 1 ，y 2， … ， y n 。函数 S( x)满足 S( x i )= y i ( i=1，2， $\cdot \! \cdot \! \cdot $ ， n)， S( x)在[ x i ， x i+1 ]( i=1，2， …， n-1)上都是不高于三次的多项式。 S( x)在[ a，b]具有二阶连续导数，边界条件为非节点边界条件( 许小勇和钟太勇，2006)。由于重采样过程中不对云与地表进行区分，会致使边缘处的云高产生较大变异，因此将非云区设为某一云高度值进行“填充”(一般取该区域的云高最小值)后重采样。

两种数据边缘特征差异大，最优匹配点难以直接确定，欧氏距离最小的点高度并不能代表目标点的高度，但可以根据距离先进行一定的聚类，获取相近程度高的一些对象( 宋宇辰 等，2007)。这里使用了围线搜索的方法，但搜索到的这些对象相对待匹配点的重要性是不同的，于是通过距离加权赋予对象不同权重来确定最后的匹配高度。 图2为匹配算法的技术流程图，文中将高分辨率的云边缘像素作为要匹配的目标像素集合，称为目标图像；将热红外的云边缘像素(代表云高度)作为背景像素集合，称为背景图像。


图 2 基于欧氏距离变换的围线搜索云边缘高度匹配技术流程图
Fig. 2 Technology flow chart of cloud heights matching method based on Euclidean distance transform by hierarchical searching way

2.2 针对背景图像的距离变换

一幅二值图像中包含目标和背景两种像素，目标像素集合值为1，背景像素集合值为0。距离变换的结果是一幅灰度级图像，即距离图像，欧氏距离变换图中每个像素的灰度值为该像素与背景像素间的最短距离( 刘湘滨 等，2006)。逐一选取目标图中的边缘像素点 p( x p，y p )对背景图中的所有像素点 i( x i，y i )( i=1， $\cdot \! \cdot \! \cdot $， n)计算欧氏距离，得到距离变换的结果，定义为

$d_p \left[({{x}_{p}}\text{，}\!\!{{y}_{p}})\text{，}({{x}_{i}}\text{，}\!\!{{y}_{i}})\right]={{\left[ {{\left({{x}_{p}}-{{x}_{i}} \right)}^{2}}+{{\left({{y}_{p}}-{{y}_{i}} \right)}^{2}} \right]}^{{}^{1}\!\!\diagup\!\!{}_{2}\;}}$ (1)

图3为某一目标像素点对背景图中的像素集合进行欧氏距离变换后的效果图。


图 3 某目标像素点对背景像素集的距离变换效果图
Fig. 3 The rendering ofdistance transformationof a target pixel to all background pixels

2.3 围线搜索与距离加权确定匹配点云高

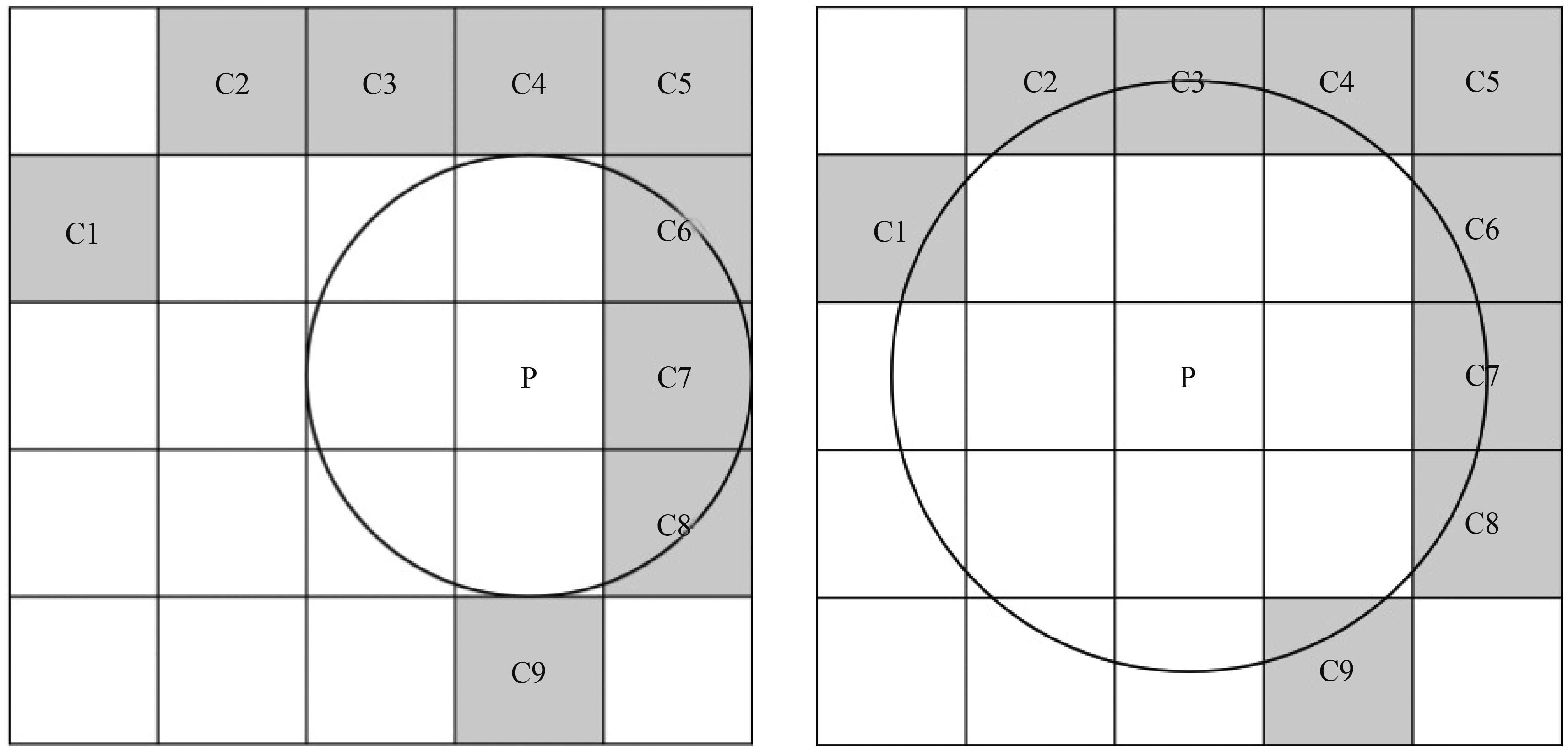
如 图4所示， P为目标像素点，C1—C9为背景像素，围线半径 r分别为1.5和2个像素宽。如 r=1.5围线区域内的元素，他们距离目标像素 p的欧氏距离关系为： d c7 < d c6 = d c8 。根据其距目标像素的距离将其高度值加权赋给目标像素点。不同搜索半径所搜索的候选点具有差异性，过多的候选解可能导致过度平均化，过少则会被一两点代表，因此需要做一定的数量控制，过少或过多的目标点会被暂时跳过。对于在初始搜索范围内未完成匹配的目标点，考虑其距离背景像素较远，匹配结果的代表性相对较小，因此将以周围已匹配的目标点为基础进行下一步匹配。对于超出搜索范围较多的一些细碎云块则赋值背景图云高的平均值。


图 4 分段围线搜索方法
Fig. 4 The hierarchical searching way

算法步骤如下：

步骤 1 将尺寸相同的目标图像和背景图像置于同一坐标系中，构成一幅二值图像矩阵 B =[ b i，j ]。以目标像素集 P =[ p( x p ， y p )]( p=1， $\cdot \! \cdot \! \cdot $， m)上一点 p( x p，y p )为目标点，利用式1对图中的背景像素集 I =[ i( x i，y i )]( i=1， $\cdot \! \cdot \! \cdot $， n)进行欧氏距离变换，输出距离变换结果存放于图像矩阵 D =[ dp xi，yi ]中。

步骤 2 首先将 d min=min{ dp xi，yi }大于20的一些目标像素赋值背景图云高的平均高度 H a 。

步骤 3 以目标像素点 p( x p，y p )为中心设定搜索半径形成围线区，分段扫描图像 D 。

(1) 初始围线半径 r设定为1.5个像素宽，将围线区内的像素集合作为候选点集 C =[ c k ]( k=1， $\cdot \! \cdot \! \cdot $， q)，若集合内候选点数量 q大于2且小于8时，则将每个候选点距目标点的距离 d k 求和得 Sd p ，并求每个候选点相对目标点的距离权值 w k ，最后将高度 h k 加权计算并赋值给目标点，得到距离加权后的高度值 H p 。

$S{d_p} = \sum\limits_{k = 1}^q {{d_k}} $ (2)
${{w}_{k}}={{{d}_{k}}}/{S{{d}_{p}}}\;$ (3)
${H_p} = \sum\limits_{k = 1}^q {{w_k} \times {h_k}} $ (4)

(2) 若集合内候选点数量 q小于2或大于8时，则跳过，继续扩大 r。至7.5个像素宽之前，以0.5为步长由内向外逐步扩大围线区范围，8到12以1个像素宽为步长，直至满足条件。重复步骤(1)中的计算过程。

(3) 逐一选取目标像素集 P 中的点完成上述步骤。若某点的 r>12仍未满足条件，则终止扫描，跳至下一个目标点。

步骤 4 在步骤3所得结果的基础上，以未匹配的像素组成新的目标像素集合，以目标图中已匹配的像素集合为新的背景像素集合 I ′=[ i′( x i′ ， y i′ )]( i′=1， $\cdot \! \cdot \! \cdot $， n′)。继续步骤3的过程，但这一步将的搜索半径 r固定为6个像素宽，直到完成剩余目标像素点的匹配。

步骤 5 输出结果。输出匹配高度结果于图像矩阵 H =[ H xp，yp ]中。

2.4 迭代法确定真实云高度

采取上述方法得到的是高分辨率下具有差异性的下限云高度，而真实云高则根据云和云阴影的相似度匹配方法来进一步确定。该方法不会对匹配结果的差异性特征产生影响，且可以获得更为准确的云高度。对于标准大气，干绝热减温率为-9.8 K/km，湿绝热减温率为-6.5 K/km；而对于薄云而言其亮温受到下部较暖地表的影响较大，所以可取湿绝热减温率为-1 K/km( Zhu和Woodcock，2012)。由于云的高度一般在200 —12000 m，因此一般可以确定一个云高范围：

$\begin{align} & {{H}_{\min }}=\max \left(0.2\text{，}{{{T}_{surface}}-{{T}_{cloud}}}/{9.8}\; \right)\\ & {{H}_{\max }}=\min \left(12\text{，}{{{T}_{surface}}-{{T}_{cloud}}}/{1}\; \right)\\ \end{align}$ (5)

根据云和云投射到地面的阴影在形状上具有相似性的特点，利用计算得到的阴影，通过迭代不同的云高增量，计算可能的云阴影与计算的云阴影之间的相似度来判断真实的云高。相似度是以计算云阴影和阈值检测云阴影的重叠部分与计算的云阴影的比率来表示的。由于云阴影会被云部分遮挡，因此在计算时只考虑未被遮挡的部分。迭代不同云高直到匹配相似度达到一定阈值的95%—98%，这一阈值一般可设置在0.3—0.5之间( Zhu 等，2015)。本文通过试验将阈值设为0.415—0.495。

3 结果及分析

3.1 匹配结果分析

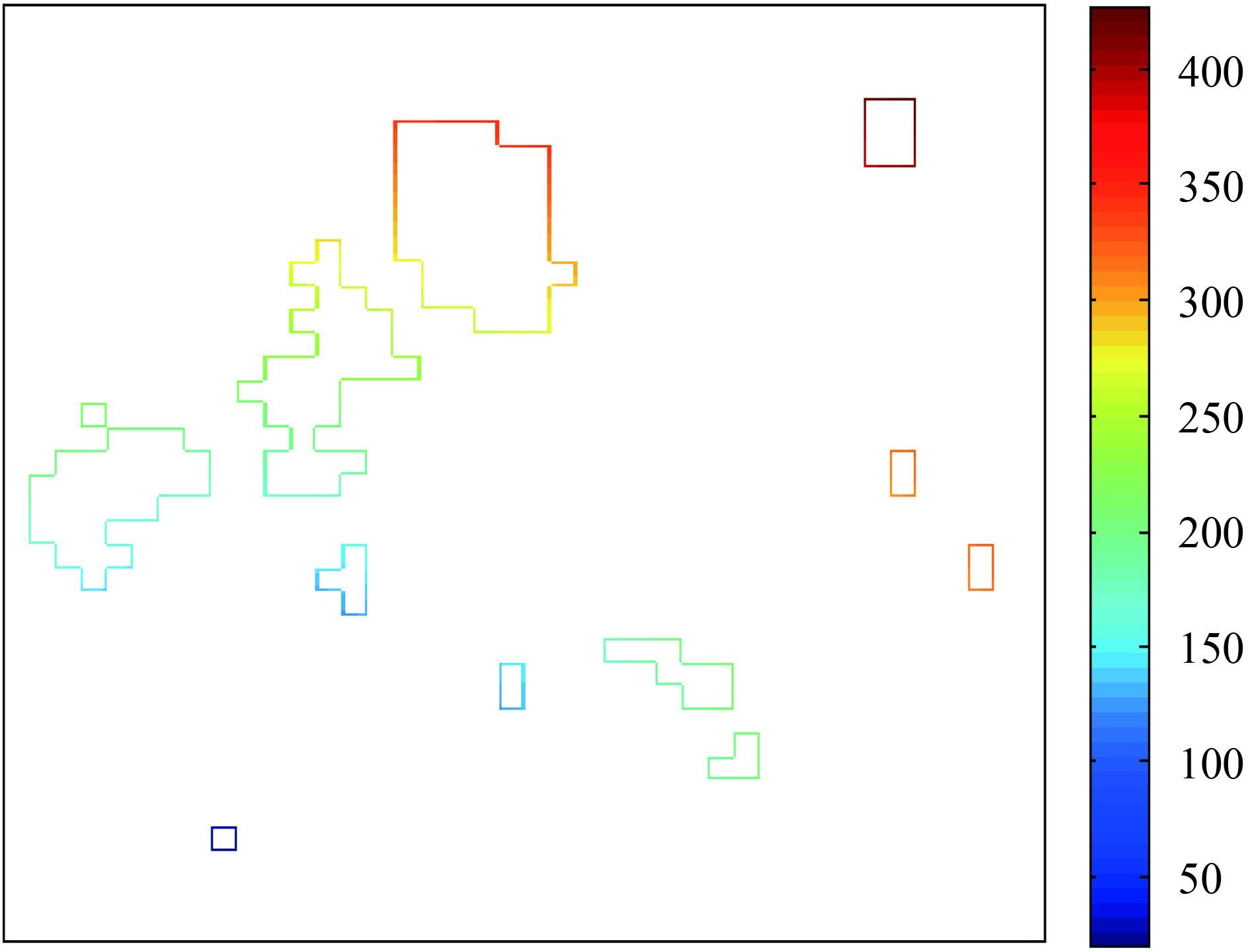
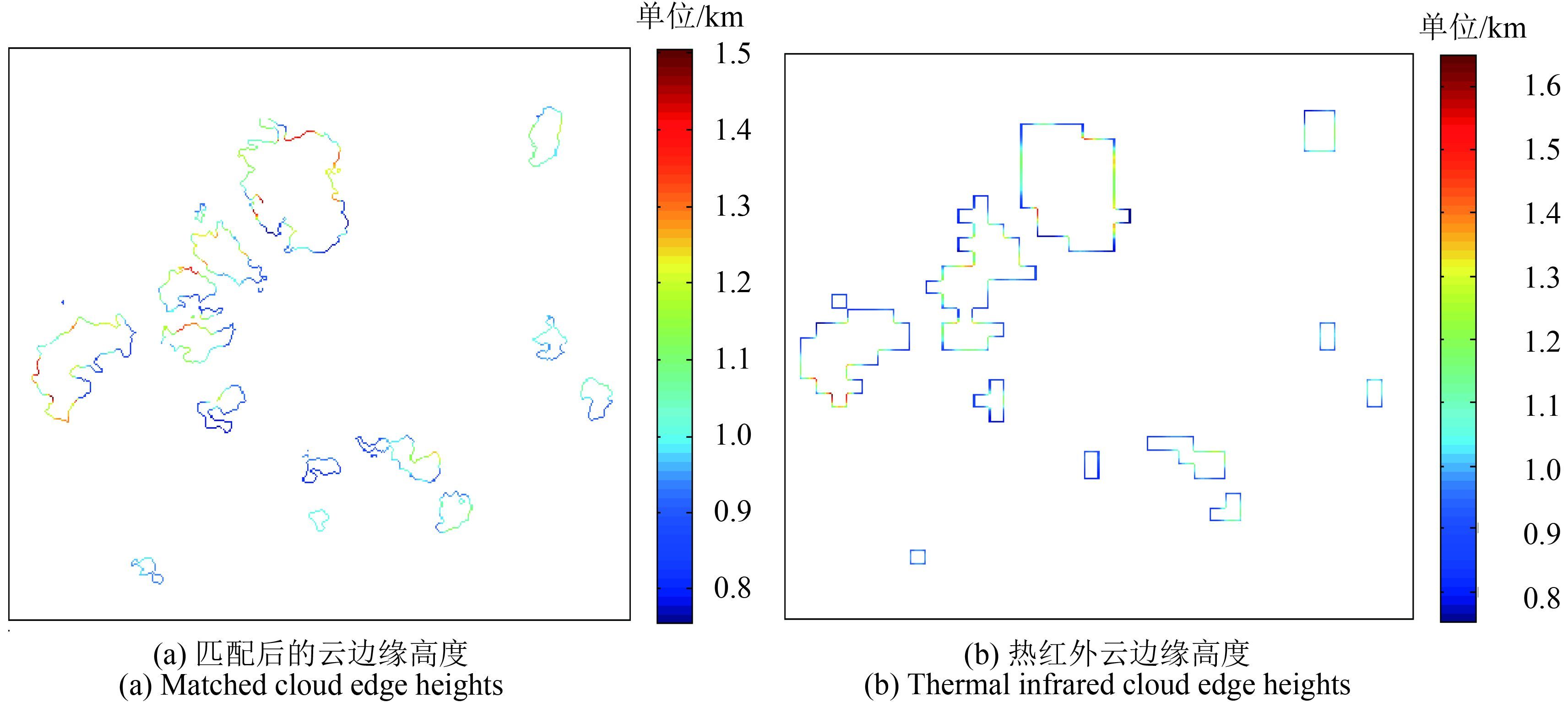
实验过程使用了HJ-1B 2012-06-08日黑河地区的CCD和IRS图像共5幅，其分辨率分别为30 m和300 m。 图5为其中1幅匹配后的结果与热红外云边缘高度。从总体的匹配结果来看，热红外数据中高度较高的区域，匹配结果的对应区域也得到了较高的云高分布，分辨率得到了提高，细节得到了丰富。


图 5 匹配后的云边缘高度及热红外云边缘高度
Fig. 5 Matched cloud edge heights and thermal infrared cloud edge heights

为了更好地对匹配前后的云高进行分析，将每幅400×400像素的实验图像分为16个100×100像素大小的分区，再将两幅图中对应分区进行对比，如 图6。由于云在研究区内的分布无规律，有的分区内无云，因此，们将分区中有云分布的分区定义为有效分区加以讨论，5幅图中共有64个有效分区。下面主要分析了云高分布和邻域平均差值的变化。


图 6 网格分区
Fig. 6 Grid partition

3.1.1 云高分布的变化

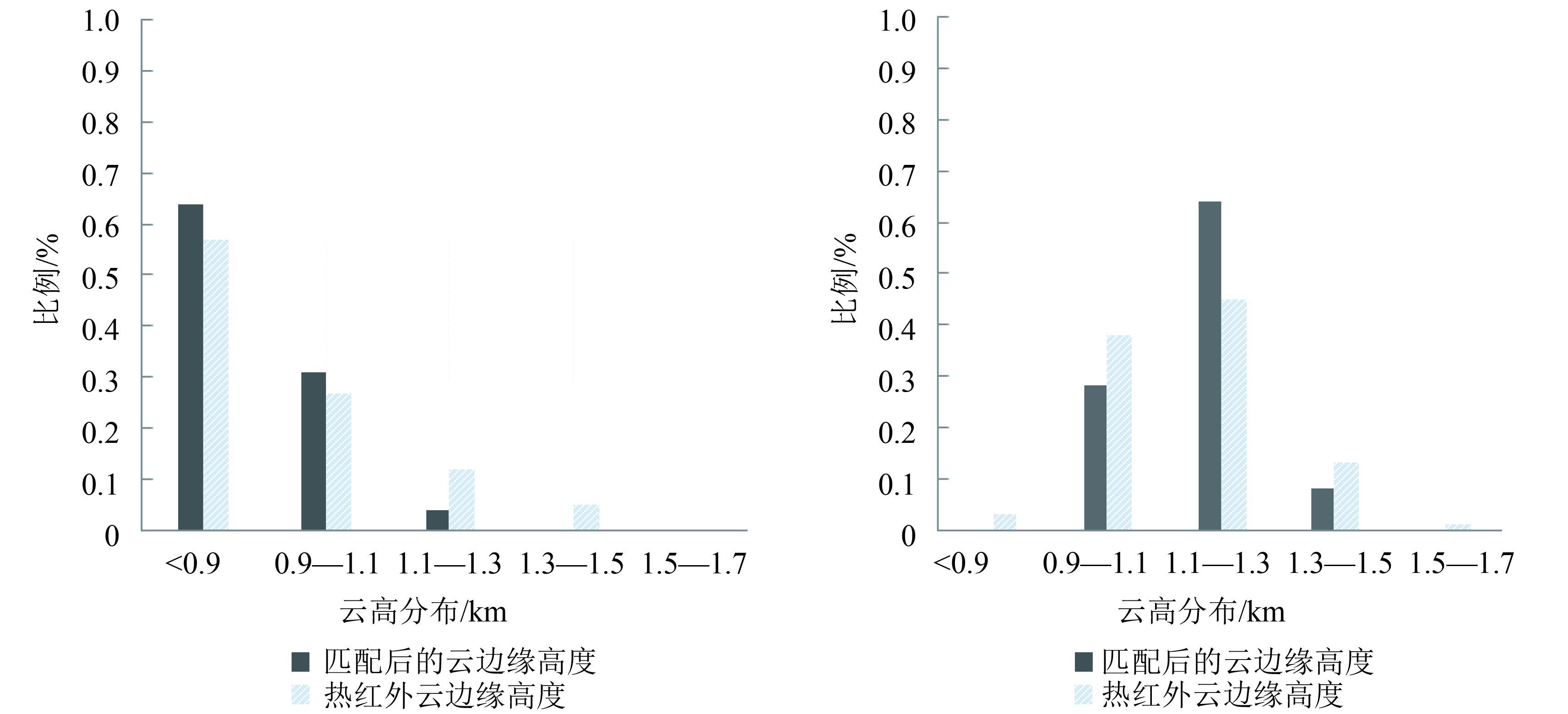
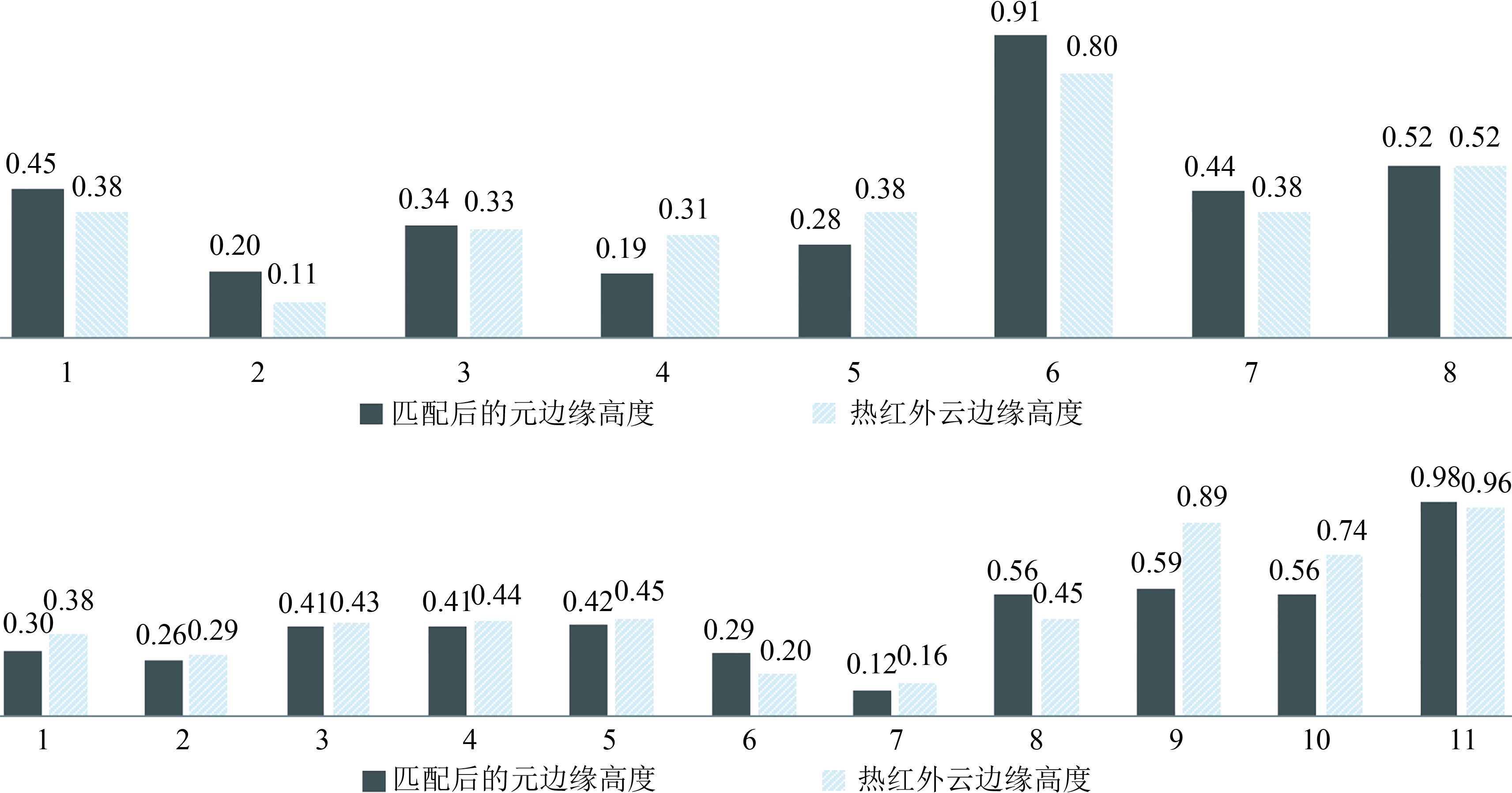
以0.2 km为间隔对热红外云高与对应匹配结果的高度分布情况进行统计。 图7为1幅影像中2个分区的云高分布比例柱状图，每幅图像的热红外云高与对应匹配结果的云高分布比例具有一定的差异；但在热红外云高中分布比例较高的云高度，在对应匹配结果中的比例也较高，两者在比例变化上具有一致性。


图 7 1幅影像中两个分区云高分布比例柱状图
Fig. 7 A distribution histogram of cloud heights proportion from two partitions of one image

图8为两幅影像各有效分区中热红外云高与对应匹配结果的对比图，图中所示为0.9—1.1 km云高所占比例。可以看出匹配前后该范围云高所占比例呈现出较大的一致性，但在某些区域，也出现较大的差异。一方面，比例的变化主要取决于云高范围内像元数的增幅和两者像元数在分区内的差异，同时，分区内可见光云边缘都要比热红外更复杂，这种复杂性也是引起比例差异的重要因素；另一方面，较为优势的云高范围会在高分辨率图像中占据更多的像元，比例增加，而较为劣势的云高范围的像元数则会相对少一些，导致其比例较小。这些变化使得匹配后云高分布产生了一定的差异，计算发现变化幅度在6%—15%之间。


图 8 2幅影像中各分区0.9—1.1 km云高范围的比例柱状图
Fig. 8 Distribution histogram of cloud heights proportion among 0.9—1.1 km from various partitions of two images

3.1.2 邻域平均差值的变化

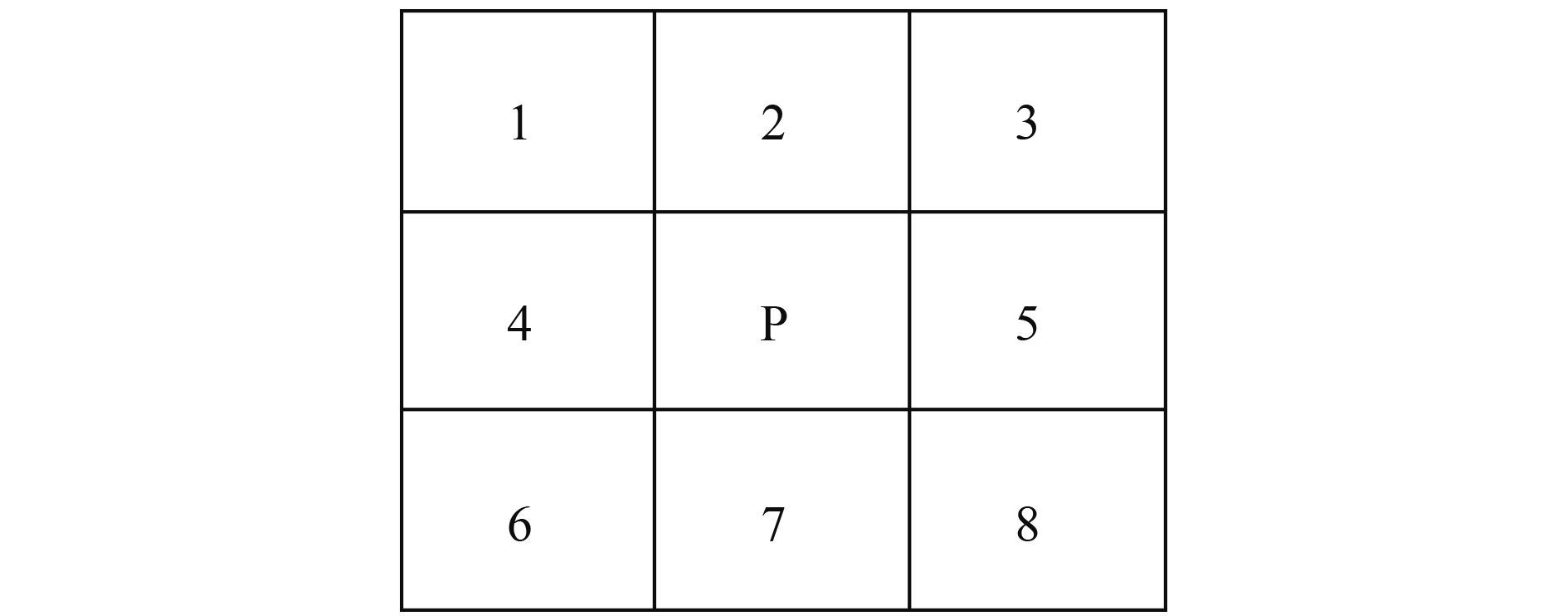
云高度的差异性以往较少有研究涉及，因此对于如何评价没有合适的标准。为了能够量化评价云高之间的差异性，本文提出了邻域平均差值的概念。由于讨论某一点云高度与其他距离较远点的差异不具意义，只有分析与其相邻区域云高的差异才能较好地反映出云高的细部差异性特征，因此选用3×3的邻域；另一方面，也可以最大限度地避免将邻近的其他云或距离较近但不相连的云纳入邻域范围。如 图9所示，首先选取一个中心点P，计算其云高度与其3×3邻域内其余各点云高度的差值的绝对值并计算平均值，得到邻域平均差值。


图 9 以P为中心点的3×3邻域
Fig. 9 The 3×3 contour region around P

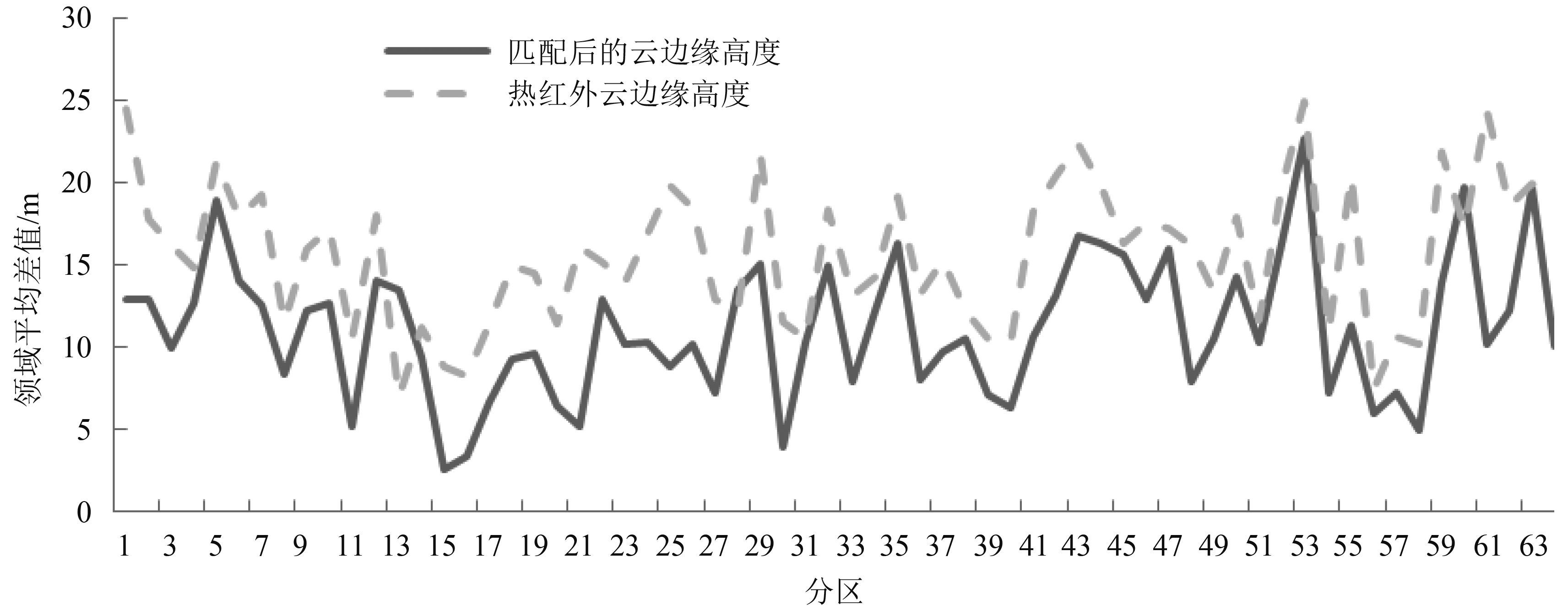
图10为64个分区的热红外云高与对应匹配结果的邻域平均差值的对比图。可以看出，热红外云高邻域平均差值大的分区，匹配结果也较大，反之亦然。两者邻域平均差值的相关系数为0.69，具有显著的相关性。另外，可见光云边缘形状和细节都比热红外复杂，相同范围内一般有更多像元，像元间的高度差异会有所减小，即邻域平均差值小，说明匹配后的结果相比低分辨率数据细节高度信息得到一定程度的丰富。


图 10 64个分区邻域平均差值
Fig. 10 Neighborhood average difference of 64 partitions

3.2 云高的准确性评价

由于目前不同云高测量仪器之间的测量结果仍有较大差异(最大可达0.3—0.5 km)，易受天气条件影响，且云高度的地基观测数据十分缺乏，使反演云高度的准确性评价具有一定困难( 黄兴友 等，2013； 李思腾 等，2015)。另外，本文所研究的边缘高度更加难以进行准确测量和对应，因此参考前人的研究，通过云影的对应关系来判断高度的准确性( Luo 等，2008； Inomata 等，2002)。考虑到所选实验区地势平坦，云阴影较为明显清晰，在太阳角度确定的情况下，云与阴影的对应关系与其高度直接相关，可以通过比较特征阴影点位置的方法来估计算法所得云高的准确性。运用本文算法选取5幅HJ-1B CCD图像分别计算相应的阴影区， 图11为其中一幅图像的计算结果。


图 11 真彩色图像与计算的云阴影结果(云为白色，阴影为灰色)
Fig. 11 True color image and computed cloud shadows(the cloud is white，the shadow is grey)

为了尽量避免云检测不够准确而可能造成的偏差，在每幅图像中各选取了10个辨识度高的特征阴影点。分别标记他们在图像中的坐标位置，以挑选的实际阴影点为参照，计算同一特征阴影点的偏移量，据此利用几何学方法获取云高度的误差值。如 表1所示，表中列出了其中两幅图像相应特征阴影点的位置和高度误差。可以看出高度误差约在0.1—0.3 km，第1幅平均为0.25 km，第2幅平均为0.15 km。50个点中有70%误差在0.1—0.3 km之间，12%误差小于0.1 km，所有点的平均误差为0.25 km。 林琳等人(2006)利用MODIS数据反演云高，认为误差约为0.3 km； 张亚琳等人(2013)反演ASTER云高，认为模型的反演精度在±0.5 km； Naud等人(2006)将反演的ATSR2云高与地基雷达结果进行比较，两者误差为0.35 km左右。从上述研究结果来看，本文所得云高度的准确性较高。

表 1 特征阴影点云高度误差
Table 1 Error of cloud heights of feature cloud shadow points

下载CSV 
特征点编号图像1图像2
计算阴影坐标实际阴影坐标高度误差/m计算阴影坐标实际阴影坐标高度误差/m
1(254，91)(251，89)217(145，90)(142，94)300
2(260,101)(257,101)180(145，85)(142，89)300
3(226,236)(224234)170(162，64)(161，63)85
4(241,225)(238,221)300(167，64)(167，63)60
5(191,340)(188,339)190(188，65)(186，62)217
6(115,256)(112,254)217(215，63)(214，62)85
7(115,267)(112,270)256(305,281)(303,283)170
8(42,334)(37,333)307(310,280)(311,280)60
9(376，48)(371，43)427(47,114)(45,116)170
10-306215-302214249(170,255)(169,254)85

另外，为了对比本方法与其他方法的不同，还选用了SIFT算法对两种数据做了云高度匹配，并将一些特征点匹配后的云高与本文算法所得结果进行比较， 表2中列出了实验对比结果。从表中可以看出，本文算法所得结果与直接采用SIFT算法所得结果有较大差异，均超出上面分析的误差范围，因此直接匹配所得高度的精度相比本文算法较低。另外，相比一些依据特征点进行匹配的方法，本文算法可以完成完整高度信息的匹配，而不局限于点。单纯使用特征匹配无法进行之后的阴影计算与云高迭代过程来获取更加准确的云高度，不能够满足与本文类似研究的需要。

表 2 云高度匹配结果对比
Table 2 Comparison for matched cloud heights

下载CSV 
/km
算法特征点云高
图像1图像2
特征点1234512345
SIFT1.71.82.31.62.32.62.12.12.21.9
本文算法2.62.62.92.52.84.143.93.84.3

4 结 论

为了能够依据低分辨率热红外数据获取高分辨具有细部特征的云高度，以满足高分辨率异质性条件下云阴影识别、云高参数获取及地表辐射估算等方面的应用，本文提出一种基于欧氏距离的围线搜索云边缘高度匹配方法。该方法可以将低分辨率热红外云高信息匹配到对应的高分辨率云边缘。实验结果表明，算法在遵循热红外云高信息分布变化规律的同时，得到了较准确的云边缘高度，一定程度解决了热红外技术获取云高在分辨率上的局限，利用高分辨率图像和热红外图像的互补性进行云高计算，扩展了其在云高反演方面的作用。另外，相比单纯依据特征点进行匹配的方法，获得的高度信息更完整、准确性更高。

但结果的真实性也会受到许多因素的影响。首先热红外云检测的结果会对最后的结果的准确性评价产生影响，一些细碎云块在低分辨下难以检出，某些边缘部分存在漏检和误检的可能。在一些形状较复杂、细节复杂度较高的区域，热红外背景信息难以与其进行较为准确合理的匹配，这对匹配的结果也会造成影响。在一些云块分布较密集的情况可能会搜索到邻近云块而产生一定的偏差，但由于邻近区域的大气稳定度等状况较为接近，对结果的影响较小。此外图像配准的准确度也会对结果产生影响，地表温度的不均匀性对初始的云高度的计算也会造成一定偏差。

本文只针对边缘高度进行了匹配，其他部分云高的匹配仍需进一步研究。云高度的差异性是遥感科学空间异质性的一个方面，对于这种异质性的考虑是十分必要的，且越来越成为一个重要的研究方向。随着遥感数据空间分辨率的不断提高，云高度异质性的研究也将成为下一步努力的方向。

参考文献(References)

数据专区
  • 目录 目录
  • 文章信息 文章信息
  • 引用格式 引用格式
  • 地图 地图
  • 评论 评论
  • 图 图
  • 表 表
  • 二维码 二维码
  • 参考文献 参考文献