出版日期: 2016-11-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20166020
2016 | Volumn20 | Number 6

遥感应用

线性/非线性光谱混合模型估算白刺灌丛植被覆盖度

姬翠翠^1,2 , 贾永红¹ , 李晓松² , 王金英²

1. 武汉大学遥感信息工程学院，湖北武汉 430079

2. 中国科学院遥感与数字地球研究所数字地球重点实验室，北京 100101

收稿日期: 2016-02-01; 优先数字出版日期: 2016-11-25

基金项目: 国家自然科学基金(编号：41571421)；国家科技重大专项(编号：21-Y30B05-9001-13/15)

第一作者简介: 姬翠翠(1984—)，女，博士研究生，研究方向为高光谱遥感应用研究。E-mail： cuicuiji@whu.edu.cn

通讯作者简介: 李晓松(1981—)，男，博士，副研究员，研究方向为生态遥感研究。E-mail： lixs@radi.ac.cn

中图分类号: TP79

文献标识码: A

摘要

及时监测干旱与半干旱区光合/非光合植被覆盖度时空变化，可以为指导荒漠化防治工程及植被衰退机制研究提供重要信息。本文以甘肃民勤典型植被白刺灌丛为研究对象，通过地面控制性光谱实验获取混合光谱、端元光谱与丰度信息，开展线性与非线性光谱混合模型(包括核函数非线性和双线性混合模型)估算光合和非光合植被覆盖度的对比研究，采用全限制最小二乘法进行模型解混，分别获取各样本数据中各类端元丰度及其精度信息，通过模型分解的均方根误差(RMSE)与地面验证精度确定用于光合和非光合植被覆盖度估算的最佳光谱混合模型，其中参考端元丰度采用神经网络(NNC)分类算法对数字影像进行分类获取。结果表明：(1)引入阴影端元的四端元模型相对于传统的三端元模型(光合/非光合植被与裸土)能有效提高光谱解混的精度，并提高光合和非光合植被覆盖度估算精度；(2)对白刺灌丛来说，光合植被、非光合植被、裸土及阴影间多重散射混合效应存在，但混合效应不够显著；考虑非线性参数的核函数非线性光谱混合模型表现略低于线性光谱混合模型，因此非线性光谱混合模型在估算白刺灌丛光合和非光合植被覆盖度时相对于线性光谱混合模型没有明显优势；(3)基于光合/非光合植被、裸土与阴影四端元的线性光谱混合模型可以实现白刺灌丛光合和非光合植被覆盖度的准确估算，光合植被覆盖度估算RMSE为0.1177，非光合植被覆盖度估算RMSE为0.0835。

关键词

高光谱 , 光合/非光合植被 , 线性/非线性光谱混合模型 , 干旱与半干旱区 , 多重散射

Research on linear and nonlinear spectral mixture models for estimating vegetation fractional cover of nitraria bushes

JI Cuicui^1,2 , JIA Yonghong¹ , LI Xiaosong² , WANG Jinying²

1.School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China

2.Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China

Abstract

Sand invasion is intensified by the serious degradation and disappearance of Nitraria bushes, which has a serious effect on the oasis ecological security of deserts. Quantitative analysis of different multiple scattering factors in mixed spectral contribution for the ecological environment on deserts is particularly important. Timely monitoring of spatial and temporal variations in photosynthetic/non-photosynthetic vegetation(PV/NPV) fraction cover provides essential information for guiding management practices on land desertification and research on vegetation recession mechanism. In this paper, taking the typical vegetation of Nitraria bushes in Minqin County of Gansu Province as an example, mixed and endmember spectra, and fraction information were acquired by ground-controlling spectroscopy experiment. Then, the fractional cover of PV( f _pv) and that of NPV ( f _npv) were estimated by linear and nonlinear spectral mixture models (NSMM) (including Kernel NSMM (KNSMM) and bilinear spectral mixture model (BSMM)), respectively. Fully constrained least square method was adopted to mix the models, and the fraction of every endmember and the accuracy information of all the samples were calculated. The performances of the models were compared based on root mean square error (RMSE) of the unmixing model and accuracy of field validation, and the endmember fraction of field validation is based on the abundance of digital image classification by the neural network classification algorithm. Results show that (1) compared with the traditional three-endmember model (PV, NPV, and bare soil (BS)), the four-endmember model, which incorporates an additional shadow endmember, can effectively improve both the accuracy of spectral mixture model(RMSE decreased from 0.0429 to 0.0052 and improved 16% in accuracy) and the estimation precision of f _pv and f _npv(increased by 44% and 83%, respectively). (2)Moreover, the precision of the unmixing of model could be improved by BSMM considering the multiple scattering between NPV and BS endmembers. However, the improved precision was insignificant. Also, considering the nonlinear parameters, the performance of KNSMM was slightly lower than that of the LSMM model. (3) The validation RMSE of f _pv was 0.1177( R ²=0.7049), and that of f _npvwas 0.0835 ( R ²=0.4896) with LSMM based on PV/NPV, BS, and shadow endmembers. Process monitoring describes the multiple photon-scattering effect among PV/NPV, BS, and shadows in Nitrariabushes.The selection and application of the types of NSMMs should be confirmed according to specific research object and the required precision. Shadows cannot be ignored in estimating vegetation fractional cover, especially in improving f _npv accuracy. This finding illustrates that the types and number of endmembers chosen are significant in improving the accuracy of fraction estimation. The conclusion also shows that LSMM is suitable to estimate f _pv and f _npv of Nitraria bushes accurately based on PV/NPV, BS, and shadow endmembers.

Key words

hyperspectral data , photosynthetic/non-photosynthetic vegetation , linear/non-linear mixture model , arid and semi-arid area , multiple photon scattering

1 引言

白刺灌丛耐风沙、抗盐碱，防风固沙功能显著，是中国西北干旱区绿洲的天然生态屏障( 贾晓红和李新荣，2008)。由于地下水的过度利用及过度放牧等其他人类不合理利用等原因，甘肃民勤绿洲边缘的天然白刺群落退化和消亡严重，导致风沙侵入加剧，严重影响了绿洲的生态安全( 赵长明等，2005)。及时、准确掌握白刺灌丛覆盖信息，特别是进一步区分开光合与非光合植被覆盖度，对定量评估白刺灌丛的时空动态、进而开展科学荒漠化评估、荒漠化治理效益评价具有重要的意义( Jiapaer 等，2011)。

针对于光合植被PV(Photosynthetic Vegetation)和非光合植被NPV(Non-photosynthetic Vegetation)覆盖度的测算方法已有一些研究，但大部分的研究精力集中于前者。一些光谱指数，如亮度指数(BI)、归一化作物茬指数(NDRI)、土壤调整作物茬指数(SACRI)、木质素-纤维素吸收指数(LCA)等，能够较好地估算非光合植被覆盖度，但这些指数都基于仅有非光合植被与裸土(Bare Soil，BS)两种成分，是否适用于光合植被，非光合植被和裸土三者共存的情况有待研究( 李涛等，2015)。线性光谱混合模型(LSMM)以其物理意义明确、计算方便的优势已经开始用于光合、非光合植被和裸土信息的估算( Asner 等，2002； Guerschman 等，2015)，但影像尺度上线性光谱混合模型的应用无法有效顾及端元反射率内部差异(Ustin 等，1998；Johnson 等，1992)，也假定端元间多重散射可以被忽略。然而，Ray与Murray(1996)就证明了沙漠植被的非线性光谱混合特性，指出非线性光谱混合模型(NSMM)效果更好。但是，因为非线性光谱混合模型实现起来困难，大多数研究仍采用线性光谱混合模型，而把非线性光谱混合的影响简单归到误差里。

考虑到白刺灌丛为典型的沙漠植被，其开放性的冠层结构也更易导致多重散射，开展服务于光合/非光合植被覆盖度估算的白刺灌丛最佳光谱混合模型研究，并定量分析不同多重散射因素在光谱混合中贡献则显得特别重要。为此，针对甘肃民勤绿洲边缘的白刺灌丛，本研究基于地面控制性光谱实验获取混合光谱、端元光谱与丰度信息，通过选择不同端元组合，分别利用不同线性光谱混合模型和非线性光谱混合模型进行光合和非光合植被覆盖度估算，以期了解白刺灌丛的植被—土壤的光谱混合过程，定量评估线性与非线性光谱混合模型的差异，确定适合白刺灌丛光合和非光合植被覆盖度估算的光谱混合模型，进而为大范围光合和非光合植被覆盖度估算提供理论指导。

2 研究区概况

选取试验区位于甘肃省民勤县西部的绿洲—荒漠过渡带(38°37′42.60′′N，102°55′11.25′′E)，地处石羊河下游，属温带大陆性干旱气候区，自然植被主要是荒漠植被，组成种类少、片层结构简单、生产力低，白刺灌丛是最为主要的天然植被类型。因位于腾格里与巴丹吉林两大沙漠前缘交汇区处，民勤绿洲土地荒漠化问题十分严重，各类荒漠化土地面积152万 ha，占总面积的94.9%(戴晟懋等，2008)。

3 数据与方法

3.1 光谱数据获取

本研究基于地面控制性实验获得的端元光谱及其混合光谱信息，可以获取每个样地特定的PV/NPV/BS/Shadow(光合植被/非光合植被/裸土/阴影)端元光谱，最大程度去除端元光谱差异的影响(Ray和Murray，1996)。光谱数据获取选择晴朗无云、风力较小、太阳光照充足并稳定的时段(10:00—14:00)，测量不同端元组合的冠层混合像元光谱信息。光谱采集时间分别为2014年8月25日，仪器采用ASD(analytical spectral devices)Field Spec Pro光谱仪，光谱采集范围为350—2500 nm。选择20个地面覆盖丰度不同的白刺样地，测量其混合光谱及其各纯净端元光谱，如图1所示，采集冠层混合光谱数据是采用拉钢尺正交方式，确定样地中心，各样地选择直径1 m圆形区域确定样地范围，将探头(视场角25°)置于地物中心上方2.3 m处垂直向下采集，图1(a)，获取样地混合光谱数据，而各纯端元光谱数据获取是在各样地内分别将探头置于各典型地物类型(如白刺、枯枝、流沙、阴影等)上方贴近其表面0.1—0.2 m处向下采集，图1(b)。

图 1 样地各纯端元及冠层混合光谱获取过程

Fig. 1 Processing of each endmember and mixed canopy spectral data collection in situ

3.2 参考端元丰度获取

在研究区域内，采用数码相机拍照，每个样地重复拍照两次，获取每组混合光谱数据对应像片上地面覆盖度信息( 图2)。图2(a)中两个交叉的卷尺用来标志ABS传感器在数字图像中视场角(FOV)，对获取RGB照片，采集训练样本，采用ENVI 5.3中监督分类中的神经网络(NNC)分类算法对数字影像进行分类( Mishra和Crews，2014)，分出PV-NPV-BS(3EM)端元( 图2(b))，图2(c)中将阴影考虑在内，PV-NPV-BS-Shadow(4EM)不同端元给出不同的颜色(绿色为PV，蓝色为Shadows，红色为BS，黄色为NPV)，对分类结果经过目视解译，判定分类结果精度，通过不同地类的像元数量统计出各地类的丰度，每一样地两次获取端元丰度取平均值作为该样地各端元最终丰度。

图 2 基于神经网络的三端元和四端元分类

Fig. 2 NNC classification for 3EM and 4EM

4 光谱混合模型

4.1 线性光谱混合模型

从理论上讲，线性光谱混合模型是假设一个地球表面的组分只产生唯一一次反射，收集的反射光谱进入传感器之前不混合(即不产生多向散射)( Adams 等，1993； Settle 等，1993)。基于线性混合原理( Vikhamar和Solberg，2003； Chen和Vierling，2006； Theseira 等，2002； Wu和Murray，2003)构建线性光谱混合模型(linear spectral mixture model，LSMM)(式(1))。在LSMM中，混合光谱被看成是样地内端元光谱与其丰度的线性组合。

$\begin{aligned} & {{R}_{i}}=\sum\limits_{j=1}^{m}{({{f}_{j}}{{W}_{i,j}})}+{{\varepsilon }_{i}} \\ & 0 \leqslant {{f}_{j}} \leqslant 1\text{且}\sum\limits_{j=1}^{m}{{{f}_{j}}}=1 \\ \end{aligned}$

(1)

式中， R _i 为在 i波段混合光谱， f _j 为 j端元丰度， W _i，j 为 i波段对应 j端元实测光谱。已知混合实测光谱向量 R 及端元实测光谱向量 W ，利用式(1)，通过全受限最小二乘法(FCLS)( Heinz和Chang，2001)即可反解出端元对应的丰度 f _j

$ \begin{aligned} \sum\limits_i^n {{\varepsilon _i}} = \sum\limits_{i = 1}^n {{{(\sum\limits_{j = 1}^m {({f_j}{W_{i,j}})} - {R_i})}^2}} \end{aligned} $

(2)

式中， n为有效光谱波段数量， m为端元数量， ε _i 为光谱模型残差。

4.2 非线性光谱混合模型

利用光谱混合方法开展 f _pv和 f _npv估算研究中以LSMM的应用最为普便，植被与土壤之间的多重散射通常被当作噪声或误差来处理。然而，荒漠植被与土壤之间复杂的非线性光谱效应早已得到认知( Somers 等，2009a， 2014)，但其对 f _pv和 f _npv定量估算的影响还没有相关研究。因此，引入NSMM定量评估光合/非光合植被及其他端元间多重散射对混合光谱的影响，并验证NSMM相对于LSMM在估算 f _pv和 f _npv时精度是否有明显提升特别重要。根据不同NSMM的特点( Bioucas-Dias 等，2012)，本研究引入相对简单、物理意义明确的双线性光谱混合模型及核函数非线性光谱混合模型开展对比研究。

4.2.1 双线性光谱混合模型

双线性光谱混合模型指通过构建虚拟多重散射项模拟端元之间多重散射( Somers 等，2009b)，进而实现非线性模型的线性化表达的光谱混合模型。常用的双线性光谱混合模型有Fan模型FM(Fan Model)( Fan 等，2009)、广义双线性模型GBM(Generalized Bilinear Model)( Halimi 等，2011)、Nascimento模型( Nascimento和Bioucas-Dias，2009)等。考虑到本研究中白刺灌丛结构特点，本研究采用Nascimento双线性光谱混合模型(式(3))，不考虑高次多重散射，仅考虑各端元间的二次散射以及PV/NPV自身二次散射。考虑不同类型多重散射的双线性光谱混合模型的表现通过分解均方根误差(RMSE)来比较。

$ \begin{aligned} {{R}_{i}}=\sum\limits_{j=1}^{m}{({{f}_{j}}{{W}_{i,j}})}+\sum\limits_{j=1}^{m}{\sum\limits_{t=1}^{m}{({{f}_{j,t}}{{W}_{i,j}}{{W}_{i,t}})}}+{{\varepsilon }_{i}} \end{aligned} $

(3)

式中， R _i 为在 i波段混合光谱， f _j 为 j端元丰度， f _j，t 为 j端元与 t端元间混合散射项丰度， W _i，j 为 i波段对应 j端元实测光谱， W _i，jW _i，t 表示端元间多重散射影响下的非线性组合， ε _i 为光谱模型残差。式(3)中虚拟多重散射项作为额外端元，其丰度 f _j，t 与 f _j 无关，其作为单独端元存在，在混合模型中加入ASC和ANC约束，当 $\forall $ j$\geqslant$t 时 f _j，t =0， $\forall $ j< t时 f _j，t $\geqslant$0，同时

$ \begin{aligned} {{f}_{j}}\geqslant 0\text{且}\sum\limits_{j=1}^{m}{{{f}_{j}}}+\sum\limits_{j=1}^{m-1}{\sum\limits_{t=j+1}^{m}{{{f}_{j,t}}}}=1 \end{aligned} $

(4)

虚拟多重散射项的丰度 f _j，t 归化到对应的端元线性项中( Somers 等，2009b)，采用式(5)

${{f}_{j}}=f_{j}^{(1)}/\left( 1-\sum\limits_{t=1}^{n}{f_{j,t}^{(2)}} \right)$

(5)

式中， f _j 为加入多重散射影响后的端元丰度。 $f_{j}^{(1)}$ 为单次散射丰度， $f_{j,t}^{(2)}$ 为 j端元和 t端元二次混合散射对 j端元造成影响的丰度， m为端元种类数量。

4.2.2 核函数非线性光谱混合模型

核函数非线性光谱混合模型KNSMM(Kernel NSMM)的原理在于将数据从输入空间 R ⁿ 映射到特征空间 C ^N ，通过非线性映射，把数据间的非线性关系转化为高维空间的线性关系( 厉小润等，2011； Li 等2014；唐晓燕等，2013； Chen 等，2013)。理论上讲，任何满足Mercer定理或正定性的函数都可以作为核函数。根据研究区地表植被结构简单特点，本研究采用两种常用核函数，高斯径向基核函数RBF Kernel(Radial Basis Function Kernel) $k({x},{z})=\exp (-\frac{{{\left\| {x}-{z} \right\|}^{2}}}{2{{\sigma }^{2}}})$ ，其中， σ为核参数；与多项式核函数PKF(Polynomial Kernel Function)， $k\left( {{x},{z}} \right) = {\left( {a{{x}^{\rm T}}z + c} \right)^b}$ ，其中 a、 b、 c为核参数。RBF中的 σ参数确定采用梯度下降法确定( Chapelle 等，2002)，4EM的核参数 σ=45，3EM的核参数 σ=15。PKF中参数采用互检验方法确定( 张良培等，2014)，实验中确定多项式阶数 b=2，等于利用了光谱数据的4阶统计性质， a=1/ n， n为端元数， c=1。核函数映射后的解混采用全受限的最小二乘法(KFCLS)( Broadwater 等，2007)。

4.3 精度评估模型

光谱混合模型精度主要通过光谱混合模型分解误差、PV/NPV/BS/Shadow地面验证的RMSE( Heinz和Chang，2001)(式(6)和偏差率( Q _f )(式7)( 焦有权，2015； Fan 等，2009)来确定。光谱混合模型RMSE主要针对模型本身，主要反映模型分解精度。验证RMSE则反映分解结果与地面实测端元丰度的接近性。

$ \begin{aligned} {\rm{RMSE = }}{\left( {\sum\limits_{i = 1}^n {{{\left( {{{\hat f}_i} - {f_i}} \right)}^2}/N} } \right)^{1/2}} \end{aligned} $

(6)

$ \begin{aligned} {Q_f} = \left( {\sum\limits_{i = 1}^n {\left( {\left| {{{\hat f}_i} - {f_i}} \right|/{f_i}} \right)/N} } \right) \times 100\% \end{aligned} $

(7)

式中，RMSE为均方根误差， Q _f 为偏差率， ${{\hat{f}}_{i}}$ 为模型估测值， f _i 为获取影像中实测丰度值或实测光谱值， N为样地数或波段数。

5 结果

5.1 端元光谱特征

为实现 f _pv和 f _npv的估算，本研究通过地面光谱观测的方法获取了每一个样地的混合光谱及PV/NPV/BS/Shadow端元光谱。考虑到端元的适用性及代表性，去掉受大气影响严重波段和水汽吸收波段，保留350—1350 nm、1450—1750 nm、2000—2350 nm波谱范围( 郑国雄等，2016)；为了去除端元变化影响，实验中对每类端元获取5组光谱值，取其平均光谱作为PV/NPV/BS/Shadow的最终端元光谱。

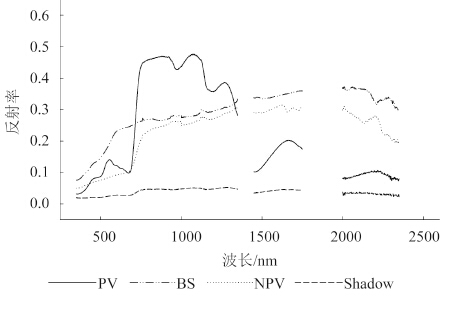
图3为一个典型样地的端元光谱曲线。通过整个光谱曲线可知，PV在红波段与近红外波段反射率差异明显，而NPV与BS反射率则不具有这一特征，因此PV相对NPV与BS相对容易区分。然而，NPV与BS光谱则非常相近，其区分则相对较为困难。从光谱特征来讲，500—900 nm、2100 nm附近两个窄范围区域，NPV与BS光谱有所差异，其中BS在500—900 nm光谱范围存在一个明显的弓形突起区( 高志海等，2011)，NPV在2100 nm附近有一个受纤维素等非结构组分引起的吸收特征( 李涛等，2015)。因此，从光谱特征来讲，高光谱数据具备有效区分PV、NPV与BS的能力。阴影反射率较低，且在全谱段范围内差异不大，与其他3类端元光谱特征存在明显差异。

图 3 各端元类光谱图

Fig. 3 The spectra line of each endmember

5.2 线性光谱解混

基于三端元与四端元、利用式(1)(2)的混合光谱分解及其验证结果如表1所示。从表1可以看出，传统所用PV-NPV-BS的三端元LSMM模型误差最大，当引入阴影端元时，四端元LSMM的精度要明显好于任何三端元LSMM，模型分解RMSE从0.0429下降到0.0052，模型偏差率均值从18.29%下降到2.15%，同时PV-NPV-BS各端元的验证RMSE均明显减少，精度分别提高44%、83%和63%。从绘制散点图4(a) (b)来看，与基于三端元 f _pv和 f _npv估算精度散点分布图比较，明显四端元的LSMM估算光谱结果与实测光谱相关性更强，且其散点分布更贴近于1 : 1等值线。可见，将阴影端元引入覆盖度估算模型，明显提高了植被覆盖度估算精度，端元的正确选取对提高植被覆盖度估算精度是不可忽略的。

表 1 基于LSMM和NSMM的光谱混合分解估算的RMSE
Table 1 RMSE of LSMM and NSMM extracted and reference sub-pixel fractions

下载CSV

模型		模型 RMSE	Q _f/ %	RMSE
模型		模型 RMSE	Q _f/ %	PV	NPV	BS	Shadow
PV-NPV-BS mixtures
LSMM		0.0429	18.29	0.2078	0.4785	0.5117	—
NSMM
KNSMM	KNSMM_RBF	0.0429	18.35	0.1905	0.4744	0.5159	—
KNSMM	KNSMM_PKF	0.0429	18.25	0.1970	0.4778	0.5158	—
BSMM	3EM+P ²	0.0126	5.31	0.1588	0.0982	0.1750	—
	3EM+P*B	0.0080	3.67	0.1673	0.0969	0.1909	—
	3EM+P ²+P*B	0.0080	3.66	0.1640	0.0969	0.1764	—
	3EM+P ²+N ²+PN+BN+P*B	0.0072	3.4	0.1768	0.1300	0.1619	—
PV-NPV-BS-Shadows mixtures		—	—	—	—	—	—
LSMM		0.0052	2.15	0.1177	0.0835	0.1875	0.1398
NSMM		—	—	—	—	—	—
KNSMM	KNSMM_RBF	0.0059	2.5	0.1184	0.0805	0.1941	0.1355
KNSMM	KNSMM_PKF	0.0067	2.8	0.1183	0.0839	0.1999	0.1398
BSMM	4EM+P ²	0.0049	2.07	0.1173	0.0819	0.1870	0.1384
	4EM+B*N	0.0048	2.05	0.1164	0.0850	0.1857	0.1350
	4EM+P ²+B*N	0.0051	2.13	0.1187	0.0872	0.1861	0.1348
	4EM+N ²+BS+NS	0.0052	2.18	0.1215	0.1115	0.2100	0.1352
注：P代表PV，B代表BS，N代表NPV，S代表(Shadow)；加黑部分为RMSE精度最高。

图 4 采用线性和非线性光谱混合模型，基于三端元和四端元 f _pv和 f _npv估算与实测结果散点分布图及其拟合线

Fig. 4 Scatterplot and best fit line of the LSMM and NSMM modeled and observed f _pvand f _npv based on 3EM and 4EM

5.3 双线性光谱解混

根据研究区植被结构特点，考虑不同端元间多重散射，根据各端元间的二次散射以及PV/NPV此类立体目标地物的自身二次迭代散射，例如PV与BS间散射或NPV分别与Shadow和BS交叉散射等，设计288类包括不同虚拟多重散射的BSMM模型，其中基于三端元的31个，四端元的255个。然后，通过式(3)(4)(5)分别求取样本数据中各端元丰度，并验证其精度。根据模型分解误差及其精度结果，分别选择三端元与四端元模型中精度较高的4种模型，将其结果列于表1。从表1中可以看出，(1)考虑多重散射项并不是越多越好，分解误差较低模型中不超过3个多重散射项。考虑自身高次散射的效果也不明显，考虑PV与NPV自身二次散射的模型分解精度并没有提高；(2)基于四端元的BSMM模型分解精度高于基于三端元模型分解精度，尤其基于四端元考虑BS与NPV间散射情况下，模型分解精度提高明显，模型分解RMSE从0.008下降至0.0048，偏差率下降1.35%。从各端元丰度估算结果验证精度来看( 图4(c)和 4(d))，与基于3EM的BSMM估算结果比较，加入阴影端元的4EM模型 f _pv估算精度提高较大，ΔRMSE _3EM-4EM=0.0424，精度提高26.7%， f _npv和 f _BS估算精度分别提高16.6%和20.9%，且三端元模型中的高估现象在四端元模型中得到了一定缓解。另外，当端元丰度较小时，BSMM易导致其估算丰度结果为零。

5.4 核函数非线性光谱解混

从表1中展示的核函数非线性光谱解混结果来看，无论采用RBF还是PKF核函数，明显引入阴影端元4EM模型分解优于3EM，模型分解RMSE分别提高86.2%和84.4%，偏差率分别提高15.85%和15.45%。从各端元估算丰度验证精度结果( 图4(e) (f) (g) (h))比较发现，以RBF和PKF为核函数情况下，基于4EM的KNSMM比基于3EM的KNSMM f _npv估算精度提高明显，分别提高83%和82.4%，其次 f _BS估算精度提高较大，分别提高62.4%和61.2%， f _pv估算精度分别提高37.8%和39.9%，且基于4EM模型各端元实测值与估算值的相关性更强，尤其 f _npv相关性提高较大，植被覆盖(PV+NPV)丰度估算RMSE分别减少0.5295和0.5350，精度分别提高79.6%和79.3%。基于以上分析可见，基于4EM的KNSMM比基于3EM的KNSMM估算本研究区内各端元丰度上更优，精度提高明显，阴影端元的选择对提高光谱分解精度是不可忽略的。无论采用描述空间复杂性更强的RBF核函数和还是描述空间物理意义及波段间高阶统计性质更好的PKF核函数，其模型分解精度和丰度估算精度相差不大。

5.5 不同光谱混合模型比较分析

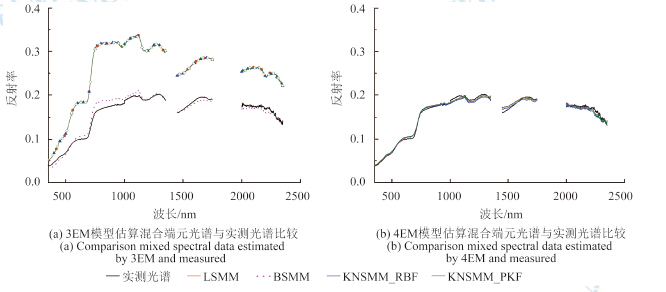
从表1中可以看出，无论是LSMM还是KNSMM，基于PV-NPV-BS-Shadow四端元模型的分解精度与验证精度都要好于基于PV-NPV-BS三端元的模型。图5为典型样地基于三端元与四端元的不同模型模拟光谱与实测光谱对比，同样可发现，基于四端元的模拟光谱与实测光谱更接近，曲线特征一致，而基于三端元的模拟光谱与实测光谱差异相对明显，尤其采用LSMM和KNSMM结果与实测光谱误差较大。因此，考虑了阴影的四端元模型对于白刺灌丛 f _pv和 f _npv的估算更为适合。

图 5 模型估算混合端元光谱与实测光谱比较

Fig. 5 Comparison mixed spectral data estimated and measured

基于四端元的模型中，LSMM、BSMM和KNSMM光谱分解精度差异不大，总体来说，BSMM最好，LSMM次之，最后为考虑了非线性参数的KNSMM。考虑NPV与BS间及PV自身之间多重散射的BSMM分解RMSE相对于LSMM有所降低，这表明四端元之间多重散射对混合光谱的影响确实存在，但其影响不是很大。

6 讨论及结论

6.1 讨论

6.1.1 非线性光谱混合模型潜力

本研究基于白刺灌丛地面光谱试验，通过对比线性与非线性光谱混合模型估算 f _pv和 f _npv发现，考虑了非线性参数的KNSMM效果不及LSMM，考虑了端元间多重散射的简单的BSMM效果相对LSMM有提升，但并不明显。然而，早前一些研究结果表明KNSMM要比LSMM计算的结果好( 厉小润等，2011； Li 等，2014；唐晓燕等，2013； Zhang 等，2007)；也有其他研究结果( Somers 等，2009b， 2011， 2014)表明BSMM可以很好反映地表各端元间散射过程及端元光谱混合机理。导致这一差异的原因主要有以下两方面：(1)应用对象不同，相对于上述研究中面向的复杂对象(生态系统、矿物成分等)，白刺灌丛结构性特征不明显，非线性混合贡献较小。从图5中可以看出，基于四端元的LSMM的模拟光谱已经与实测光谱较为接近，NSMM体现不出明显的优势。然而，该结论只适用于单株白刺灌丛尺度，对于像元尺度上或更为复杂的混合类型其适用性需进一步验证；(2)端元假设，端元数量及光谱的确定是光谱混合模型成功的关键。为服务于荒漠植被 f _pv和 f _npv的估算，本研究根据白刺灌丛的分布特征，提出了三端元与四端元两种端元组合模型。然而，实际测量中发现，同一样地、同一类型端元内部光谱还是有差异的，本研究采取了计算平均值的方式来处理这一问题。与其他NSMM研究相比，本研究所用的端元数量非常精简，因此一部分非线性混合效应可能在计算端元光谱平均值时被淹没。如果能通过混合光谱自动提取更为详尽的端元，有可能会提高光谱分解精度，但其中如何将解混结果转化为光合/非光合植被覆盖度面临较大难度。因此，针对不同研究对象，NSMM的适用性及其潜力需要科学评估，选择LSMM还是NSMM取决于对计算复杂性的考虑与对精度的具体需求。

6.1.2 阴影端元

在光谱混合模型分析中，传统理论认为阴影暗度一致情况下阴影散射影响仅占0—1%，可以忽略不计( Somers 等，2009b； Lelong 等，1998)，有些学者( Fitzgerald 等，2005)认为阴影是生物冠层特性研究重要决定因素，在混合像元反射率中是不可忽略的。在本文研究中将阴影端元引入覆盖度估算模型，明显提高了植被覆盖度估算精度，这证实了 Fitzgerald等人(2005)的结论。当前，已有的利用LSMM基于卫星遥感数据估算 f _pv和 f _npv的研究中( Asner 等，2002； Mishra和Crews，2014)，均未考虑阴影这一端元，这一尺度差异是否存在及其影响需要后续深入研究。同时，与其他端元类型选择一样，本研究未考虑存在不同种类的阴影端元问题，例如叶子上阴影和裸地阴影不同以及植被冠层阴影光谱时空变化。在未来基于卫星数据的大区域应用时，如何更好选择端元种类及端元数量仍然是一个重点研究方向( Somers 等，2011)。

6.2 结论

本文采用线性与非线性高光谱解混模型对白刺灌丛的光合/非光合植被覆盖度进行了估算研究，得出主要结论如下：

(1) 阴影对植被覆盖度估算的影响是不能忽略的，尤其对提高 f _npv估算的鲁棒性。引入阴影端元的四端元模型相对于传统的三端元模型能有效提高模型分解精度，模型分解RMSE从0.0429下降到0.0052，精度提高约16%， f _pv和 f _npv估算精度分别提高44%和83%。

(2) 对白刺灌丛来说，光合植被、非光合植被、裸土及阴影间多重散射混合效应存在，尤其加入非光合植被与裸土多重散射项的BSMM可以提高模型分解精度，模型分解RMSE从0.0052下降到0.0048，偏差率提高0.1%，但精度提升不显著；考虑非线性参数的KNSMM表现略低于LSMM，因此NSMM在白刺灌丛 f _pv和 f _npv的准确估算上相对于LSMM不具有明显优势。

(3) 基于PV/NPV/BS/Shadow四端元的LSMM可以实现白刺灌丛 f _pv和 f _npv的准确估算， f _pv估算RMSE为0.1177( R ²=0.7049)， f _npv估算RMSE为0.0835( R ²=0.4896)。

参考文献(References)

(Adams J B, Smith M O and Gillespie A R. 1993. Imaging spectroscopy: interpretation based on spectral mixture analysis//Pieters C M and Englert P A J, eds. Remote Geochemical Analysis: Elemental and Mineralogical Composition. UK: Cambridge University Press: 145-166)

Asner G P, Heidebrecht K B.2002.Spectral unmixing of vegetation, soil and dry carbon cover in arid regions: comparing multispectral and hyperspectral observations. International Journal of Remote Sensing, 23 : 3939–3958. DOI: 10.1080/01431160110115960.

Bioucas-Dias J M, Plaza A, Dobigeon N, Parente M, Du Q, Gader P, Chanussot J.2012.Hyperspectral unmixing overview: geometrical, statistical, and sparse regression-based approaches. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5 : 354–379. DOI: 10.1109/JSTARS.2012.2194696.

(Broadwater J, Chellappa R, Banerjee A and Burlina P. 2007. Kernel fully constrained least squares abundance estimates//Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium. Barcelona: IEEE: 4041-4044 [DOI: 10.1109/IGARSS.2007.4423736])

Chapelle O, Vapnik V, Bousquet O, Mukherjee S.2002.Choosing multiple parameters for support vector machines. Machine Learning, 46 : 131–159. DOI: 10.1023/A:1012450327387.

Chen J, Richard C, Honeine P.2013.Nonlinear unmixing of hyperspectral data based on a linear-mixture/nonlinear-fluctuation model. IEEE Transactions on Signal Processing, 61 : 480–492. DOI: 10.1109/TSP.2012.2222390.

Chen X X, Vierling L.2006.Spectral mixture analyses of hyperspectral data acquired using a tethered balloon. Remote Sensing of Environment, 103 : 338–350. DOI: 10.1016/j.rse.2005.05.023.

Dai S M, Qiu G Y, Zhao M.2008.Study on land desertification and its prevention and control measures in the Minqin oasis in Gansu Province. Arid Zone Research, 25 : 319–324. DOI: 10.13866/j.azr.2008.03.018. ( 戴晟懋, 邱国玉, 赵明. 2008. 甘肃民勤绿洲荒漠化防治研究. 干旱区研究, 25 : 319–324. DOI: 10.13866/j.azr.2008.03.018. )

Fan W Y, Hu B X, Miller J, Li M Z.2009.Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated-forest hyperspectral data. International Journal of Remote Sensing, 30 : 2951–2962. DOI: 10.1080/01431160802558659.

Fitzgerald G J, Pinter P J Jr, Hunsaker D J, Clarke T R.2005.Multiple shadow fractions in spectral mixture analysis of a cotton canopy. Remote Sensing of Environment, 97 : 526–539. DOI: 10.1016/j.rse.2005.05.020.

Gao Z H, Bai L N, Wang B Y, Li Z Y, Li X S, Wang Y K.2011.Estimation of soil organic matter content in desertified lands using measured soil spectral data. Scientia Silvae Sinicae, 47 : 9–16. ( 高志海, 白黎娜, 王琫瑜, 李增元, 李晓松, 王玉魁. 2011. 荒漠化土地土壤有机质含量的实测光谱估测. 林业科学, 47 : 9–16. )

Guerschman J P, Scarth P F, McVicar T R, Renzullo L J, Malthus T J, Stewart J B, Rickards J E, Trevithick R.2015.Assessing the effects of site heterogeneity and soil properties when unmixing photosynthetic vegetation, non-photosynthetic vegetation and bare soil fractions from Landsat and MODIS data. Remote Sensing of Environment, 161 : 12–26. DOI: 10.1016/j.rse.2015.01.021.

Halimi A, Altmann Y, Dobigeon N, Tourneret J Y.2011.Nonlinear unmixing of hyperspectral images using a generalized bilinear model. IEEE Transactions on Geoscience and Remote Sensing, 49 : 4153–4162. DOI: 10.1109/TGRS.2010.2098414.

Heinz D C, Chang C I.2001.Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 39 : 529–545. DOI: 10.1109/36.911111.

Jia X H, Li X R.2008.Spatial pattern of sand-mound of Nitraria in different habitat at the southeastern fringe of the Tengger desert. Environmental Science, 29 : 2046–2053. ( 贾晓红, 李新荣. 2008. 腾格里沙漠东南缘不同生境白刺(Nitraria)灌丛沙堆的空间分布格局. 环境科学, 29 : 2046–2053. )

(Jiao Y Q. 2015. Study on the Spatial Variability and Suitability of Forest Vegetation habitat factors. Beijing: Beijing Forestry University: 70-72焦有权. 2015. 森林植被生境因子空间变异及生境适宜性研究. 北京: 北京林业大学: 70-72)

Jiapaer G, Chen X, Bao A M.2011.A comparison of methods for estimating fractional vegetation cover in arid regions. Agricultural and Forest Meteorology, 151 : 1698–1710. DOI: 10.1016/j.agrformet.2011.07.004.

Johnson P E, Smith M O, Adams J B.1992.Simple algorithms for remote determination of mineral abundances and particle sizes from reflectance spectra. Journal of Geophysical Research: Planets (1991-2012), 97 : 2649–2657. DOI: 10.1029/91JE02504.

Lelong C C D, Pinet P C, Poilvé H.1998.Hyperspectral imaging and stress mapping in agriculture: a case study on wheat in Beauce (France). Remote Sensing of Environment, 66 : 179–191. DOI: 10.1016/S0034-4257(98)00049-2.

Li T, Li X S, Li F.2015.Estimating fractional cover of photosynthetic vegetation and non-photosynthetic vegetation in the Xilingol steppe region with EO-1 hyperion data. Acta Ecologica Sinica, 35 : 3643–3652. DOI: 10.5846/stxb201308142075. ( 李涛, 李晓松, 李飞. 2015. 基于Hyperion的锡林郭勒草原光合植被、非光合植被覆盖度估算. 生态学报, 35 : 3643–3652. DOI: 10.5846/stxb201308142075. )

Li X R, Cui J T, Zhao L Y.2014.Blind nonlinear hyperspectral unmixing based on constrained kernel nonnegative matrix factorization. Signal, Image and Video Processing, 8 : 1555–1567. DOI: 10.1007/s11760-012-0392-3.

Li X R, Wu X M, Zhao L Y.2011.Unsupervised nonlinear decomposing method of hyperspectral imagery. Journal of Zhejiang University(Engineering Science), 45 : 607–613. DOI: 10.3785/j.issn.1008-973X.2011.04.004. ( 厉小润, 伍小明, 赵辽英. 2011. 非监督的高光谱混合像元非线性分解方法. 浙江大学学报(工学版), 45 : 607–613. DOI: 10.3785/j.issn.1008-973X.2011.04.004. )

Mishra N B, Crews K A.2014.Estimating fractional land cover in semi-arid central Kalahari: the impact of mapping method (spectral unmixing vs. object-based image analysis) and vegetation morphology. Geocarto International, 29 : 860–877. DOI: 10.1080/10106049.2013.868041.

(Nascimento J M P and Bioucas-Dias J M. 2009. Nonlinear mixture model for hyperspectral unmixing//Proceedings of the SPIE 7477, Image and Signal Processing for Remote Sensing XV. Berlin, Germany: SPIE [DOI: 10.1117/12.830492]) http://cn.bing.com/academic/profile?id=1977824599&encoded=0&v=paper_preview&mkt=zh-cn

Ray T W, Murray B C.1996.Nonlinear spectral mixing in desert vegetation. Remote Sensing of Environment, 55 : 59–64. DOI: 10.1016/0034-4257(95)00171-9.

Settle J J, Drake N A.1993.Linear mixing and the estimation of ground cover proportions. International Journal of Remote Sensing, 14 : 1159–1177. DOI: 10.1080/01431169308904402.

Somers B, Asner G P, Tits L, Coppin P.2011.Endmember variability in spectral mixture analysis: a review. Remote Sensing of Environment, 115 : 1603–1616. DOI: 10.1016/j.rse.2011.03.003.

Somers B, Cools K, Delalieux S, Stuckens J, van der Zande D, Verstraeten W W, Coppin P.2009a.Nonlinear hyperspectral mixture analysis for tree cover estimates in orchards. Remote Sensing of Environment, 113 : 1183–1193. DOI: 10.1016/j.rse.2009.02.003.

Somers B, Delalieux S, Stuckens J, Verstraeten W W, Coppin P.2009b.A weighted linear spectral mixture analysis approach to address endmember variability in agricultural production systems. International Journal of Remote Sensing, 30 : 139–147. DOI: 10.1080/01431160802304625.

Somers B, Tits L, Coppin P.2014.Quantifying nonlinear spectral mixing in vegetated areas: computer simulation model validation and first results. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 : 1956–1965. DOI: 10.1109/JSTARS.2013.2289989.

Tang X Y, Gao K, Ni G Q.2013.Advances in nonlinear spectral unmixing of hyperspectral images. Remote Sensing Technology and Application, 28 : 731–738. ( 唐晓燕, 高昆, 倪国强. 2013. 高光谱图像非线性解混方法的研究进展. 遥感技术与应用, 28 : 731–738. )

Theseira M A, Thomas G, Sannier C A D.2002.An evaluation of spectral mixture modelling applied to a semi-arid environment. International Journal of Remote Sensing, 23 : 687–700. DOI: 10.1080/01431160010019652.

Ustin S L, Roberts D A, Pinzón J, Jacquemoud S, Gardner M, Scheer G, Castañeda C M, Palacios-Orueta A.1998.Estimating canopy water content of chaparral shrubs using optical methods. Remote Sensing of Environment, 65 : 280–291. DOI: 10.1016/S0034-4257(98)00038-8.

Vikhamar D, Solberg R.2003.Snow-cover mapping in forests by constrained linear spectral unmixing of MODIS data. Remote Sensing of Environment, 88 : 309–323. DOI: 10.1016/j.rse.2003.06.004.

Wu C S, Murray A T.2003.Estimating impervious surface distribution by spectral mixture analysis. Remote sensing of Environment, 84 : 493–505. DOI: 10.1016/S0034-4257(02)00136-0.

Zhang L P, Du B, Zhang L F.2014.Hyperspectral Remote Sensing Image Processing. Beijing: Science Press : 78–84. ( 张良培, 杜博, 张乐飞. 2014. 高光谱遥感影像处理. 北京: 科学出版社 : 78–84. )

Zhang L P, Wu B, Huang B, Li P.2007.Nonlinear estimation of subpixel proportion via kernel least square regression. International Journal of Remote Sensing, 28 : 4157–4172. DOI: 10.1080/01431160600993454.

Zhao C M, Wei X P, Yu Q S, Deng J M, Cheng D L, Wang G X.2005.Photosynthetic characteristics of Nitraria tangutorum and Haloxylon ammoden-dron in the ecotone between oasis and desert in Minqin, Region, Country. Acta Ecologica Sinica, 25 : 1908–1913. ( 赵长明, 魏小平, 尉秋实, 邓建明, 程栋梁, 王根轩. 2005. 民勤绿洲荒漠过渡带植物白刺和梭梭光合特性. 生态学报, 25 : 1908–1913. )

Zheng G X, Li X S, Zhang K X, Wang J Y.2016.Spectral mixing mechanism analysis of photosynthetic/non-photosynthetic vegetation and bared soil mixture in the Hunshandake (Otindag) sandy land. Spectroscopy and Spectral Analysis, 36 : 1063–1068. ( 郑国雄, 李晓松, 张凯选, 王金英. 2016. 浑善达克沙地光合/非光合植被及裸土光谱混合机理分析. 光谱学与光谱分析, 36 : 1063–1068. )

摘要

关键词