|
收稿日期: 2016-03-03; 优先数字出版日期: 2016-11-25
基金项目: 国家科技重大专项项目(编号:03-Y20A04-9001-15/16, 30-Y20A29-9003-15/17)
第一作者简介: 耿君(1988—),男,博士研究生,研究方向为植被定量遥感研究。E-mail:
gaoyugengjun@163.com
通讯作者简介: 田庆久(1964—),男,教授,研究方向为高光谱遥感、定量遥感研究。E-mail:
tianqj@nju.edu.cn
中图分类号: TP79
文献标识码: A
|
摘要
冠层间隙率和叶片聚集度指数对植被拦截光和冠层辐射传输过程有重要影响。叶片往往以树冠的形式聚集在森林中,而树冠在诸多森林冠层几何光学模型中有重要作用。之前的研究主要集中于树冠的形状(例如圆柱、圆锥、椭球、圆锥+圆柱等)特征对冠层间隙率和叶片聚集度的影响。然而,树冠的结构特征除了包括形状特征外,还包括尺寸特征。事实上,树冠的尺寸特征是植被在长期进化过程中与自然环境相互作用的结果,且比树冠形状特征具有更明显的地理空间特征。本文首先修改了前人常用的用于描述树冠分布的泊松分布模型,其次,利用超几何模型更为真实地、定量地描述树冠之间的排斥效应和树冠的分布情况;最后,以椭球树冠为例,设定了从“瘦高”型到“矮胖”型等7种尺寸的树冠,分别通过固定树冠半径和树冠体积两种途径探讨了树冠尺寸特征对冠层间隙率和叶片聚集度的影响。结果表明:(1)无论固定树冠半径,还是固定树冠体积,树冠尺寸特征对冠层间隙率和叶片聚集度指数的影响,均比树冠形状特征对间隙率和叶片聚集度指数的影响明显;(2)树冠的尺寸对冠层间隙率和叶片聚集度的影响非常显著,且具有明显的规律性。树冠在观测方向的投影面积越大,冠层间隙率越小,叶片聚集指数度越大,冠层内叶片越趋于泊松分布。
关键词
树冠尺寸 , 间隙率 , 聚集度指数 , 超几何分布 , 树冠形状
Abstract
Gap fraction and foliage clumping index play key roles in plant light interception; therefore, they have strong influences on plant growth and canopy radiative transfer processes. Leaves always aggregate in crowns, which are important objects innumerous geometric-optical models of forests. Researchers have mainly focused on the influences of crown shape (e.g., cylinder, cone, ellipsoid, and cone + cylinder) on gap fraction and foliage clumping index. However, size is also an important characteristic of tree crowns. Crown sizes result from the interactions between plants and environments during the long-term evolution process of the plants. In fact, crown size characteristics have more obvious geographical spatial features than crown shape. Therefore, crown size should be given considerable attention when studying plant light interception and canopy radiative transfer processes in the fields of phytogeography, remote sensing and global change. The main objective of this study is to exhibit how crown size characteristics influence the gap fraction and foliage clumping index of forest canopies. First, a simple and general distance factor, which is defined as the relative allowable shortest distance between centers of any two crowns divided by the mean diameter of tree crowns, is proposed to quantitatively describe the degree of repulsion effect among trees in forest canopies. Second, the Poisson distribution model of trees is completely replaced by the hypergeometric model, which is more suitable for quantitatively describing the repulsion effect and spatial relationship among trees in forest stands. Finally, seven sizes of ellipsoids (from prolate ellipsoids to oblate ellipsoids) are selected for the tree crowns, and the influences of crown size on gap fraction and foliage clumping index are exhibited by means of fixing the radius and the volume of the tree crowns, respectively. Results show that the following: (1) the influences of crown size characteristics are significantly greater than the effects of crown shape on gap fraction and foliage clumping index, regardless if the radius or volume of tree crowns are fixed. (2) From prolate ellipsoids to oblate ellipsoids, crown size characteristics show significant and regular effects on both gap fraction and foliage clumping index. In extreme cases, when θ=60°, the canopy gap fraction when ellipsoid height ( H b) is 16 m is 92.8% lower than that when H b=0.25 m, and the foliage clumping index when H b=16 m is 261.8% greater than that when H b=0.25 m when the crown radius is fixed. At θ=0°, the canopy gap fraction when H b=16 m is 414.1% greater than that when H b=0.25 m, and the foliage clumping index when H b=0.25 m is 11397.2% greater than that when H b=16 m when the volume of crown is fixed. The larger the projected area of the crown in the observed direction, the lower value of the gap fraction and the higher value of the foliage clumping index, indicating that leaves tend to distribute randomly in forest canopies.
Key words
crown size , gap fraction , clumping index , hypergeometric model , crown shape
1 引 言
植被冠层结构对冠层辐射传输有至关重要的作用( Stenberg 等,2001)。对于森林冠层,树冠结构不仅仅影响乔木层植被的能量交换,而且还影响林下植被和土壤环境等诸多生理和环境因素( Rautiainen 等,2011)。在遥感领域,冠层的结构特征可以用间隙率和聚集度指数来表示。其中,间隙率又称为孔隙率,是指光子穿越冠层直接到达地面的概率(Li和Strahler,1988)。间隙率可以用Lambert-Beer公式计算得到
| $ P(\theta ) = \exp \left[ { - k*L/\cos \theta } \right] $ | (1) |
式中, P(θ)表示观测天顶角 θ下的间隙率,k表示叶片的消光系数,与叶倾角有直接关系,L表示叶面积指数,定义为单位水平地面上冠层内所有叶面积的一半(Chen和Black,1992)。
然而,Lambert-Beer公式是基于叶片随机分布在冠层内的假设前提。在森林冠层内,这种假设往往不成立(Li和Strahler,1986)。Nilson基于马尔可夫过程在上一公式中引入一个调节系数来描述叶片在空间中的分布(Nilson,1971)。Lambert-Beer公式被修订为
| $ P(\theta ) = \exp \left[ { - k*L*\varOmega /\cos \theta } \right] $ | (2) |
式中, Ω表示叶片聚集度指数,定义为有效叶面积指数(假设冠层内叶片泊松分布下光学仪器(如LAI-2000)所观测到的叶面积指数 Le)除以真实叶面积指数。根据定义,当叶片聚集分布时, Ω<1;当叶片规则分布时, Ω>1;当叶片满足泊松随机分布时, Ω=1,此时式(2)等同于式(1)( Chen和Cihlar,1995; Chen 等,2005)。聚集度指数是一个非常重要的植被结构参数,它影响了叶片的拦截光量,进而影响冠层内的辐射传输过程( Chen和Leblanc,1997)。在遥感领域,聚集度指数可以用于真实叶面积指数的反演( Deng 等,2006);同时,它也可以用于区分冠层中的光照叶片和阴影叶片的面积比例( Chen 等,1999)。因此,冠层聚集度指数对于诸多植被生理过程以及植被参数反演都有着重要的科学意义。
在过去40年中,间隙率和聚集度指数得到了广泛的研究( He 等,2012; Nilson,1971)。树冠的形状在冠层间隙率、聚集度指数和辐射传输的研究中有着重要意义。例如, Chen和Leblanc(1997)假设树冠为圆锥+圆柱,基于Neyman-A分布开发的四尺度几何光学模型可以得到较为准确的双向反射因子(Bi-directional Reflectance Factor)曲线; Kucharik等(1999)通过数值试验发现聚集指数与树冠形状有关; Rautiainen等人(2004)用FRT模型分析发现树冠形状会影响冠层的BRF,但椭球型和圆锥+圆柱型树冠的BRF近似相同; 尹高飞等人(2014)研究了包括椭球、圆锥、圆锥+圆柱等常见冠型随着高度的不同对间隙率和聚集度指数以及叶面积指数估算的影响。
上述学者很好地揭示了树冠形状结构对冠层间隙率和聚集度指数的影响,并有力地推动了间隙率和聚集度指数的研究。然而,上述学者往往集中于小尺度范围(例如同一个纬度带或气候带)内树冠形状之间的差异(例如圆柱、椭球、圆锥、圆锥+圆柱等),研究树冠形状与冠层间隙率和聚集度指数的关系。事实上,树冠的结构特征不仅包括形状特征,同时包括尺寸特征。 Jahnke和Lawrence(1965)就指出,在大尺度范围内(例如全球或夸纬度带尺度),树冠的尺寸具有明显的地理空间分布特征。 Kuuluvainen(1992)也做过类似的工作,并得到树冠尺寸与纬度有直接的关系。例如,高纬度地区的树冠尺寸普遍呈“瘦高”型,而赤道等低纬度的树冠尺寸多呈“矮胖”型。树冠的这种尺寸特征是树种对自然环境长期适应的结果:在高纬度地区,太阳天顶角较大,“瘦高”型树冠(树冠高度(本文定义为树的总高度减去枝下树干高度,即树冠内叶片所在范围的垂直高度)大于幅宽)相对比“矮胖”型树冠(树冠高度小于幅宽)能够拦截和吸收更多的太阳直射,进行更多的光合作用;反之,低纬地区“矮胖”型树冠能够拦截更多的太阳辐射。树冠的这种尺寸特征是植被在长期进化过程中与自然环境相互作用的结果。然而,树冠的尺寸特征与间隙率和聚集度指数的关系在之前的研究中并未得到很好地反应和揭示。在全球气候变化背景下,基于遥感技术大尺度的植被监测以及植被参数反演对于准确估算全球物质循环和能量平衡等研究尤为重要( Wu和Chen,2012);而冠层间隙率和叶片聚集度指数对森林冠层辐射传输过程和诸多参数反演模型中有着至关重要的影响( Chen 等,2005; He 等,2012)。因此,在遥感领域,研究树冠尺寸对间隙率和聚集度指数的影响具有非常重要的科学意义。
2 理论与方法
2.1 林分内树冠的分布模式
在遥感领域,基于自然资源(例如土壤养分、水分、地形等因素)分布的随机性特点,在天然林中树冠往往假设为满足泊松分布( Li和Strahler,1985, 1992; Li 等,1995),即假设林分内树冠完全随机分布。泊松分布假设树冠为随机分布的点,树冠之间无任何影响。然而,现实中树冠是3维的几何体,由于树与树之间的竞争结果,使得地上部分的树冠与树冠之间很难完全重叠;同样,地下部分的树根也很难完全重叠。而泊松随机分布中树冠之间会发生不同程度的重叠,尤其当林分内树冠数量较多时,树冠之间会发生严重的重叠。因此,利用泊松分布来描述林分内树冠的分布过于简单。
本文假设林分内树冠的分布仍然具有一定的随机性,然而每个树冠在林分内独自占有一定的空间。例如,当第1棵树冠随机放入林地后,第2棵树可以放置到除了第1棵树占有的空间以外的其他任意空间;以此类推,第 n棵树可以放置到除了前面 n-1棵树占有的所有空间以外的其他任意空间。上述随机过程类似于有条件的随机抽样过程,而泊松分布却表达的是无条件的完全随机抽样过程,即前面的抽样对后面的抽样没有任何影响。显然有条件的随机抽样在真实林地中更为真实。这种分布模式可以表达为超几何分布。
本文首先定义林分内树冠中心位置之间的相对最小水平距离除以树冠平均直径为 RASD。RASD可以定量地描述树冠的独占空间或者“保护壳”的大小。当RASD越大,表示树冠间的排斥距离越大,树冠的独占空间或“保护壳”越大,林分内树冠分布相对越规则;反之,RASD越小,树冠间的排斥距离越小,树冠的独占空间或“保护壳”越小,林分内树冠分布越随机。当RASD=0时,表示树冠间无任何排斥效应,树冠呈泊松分布。因此,泊松分布是本文定义的超几何分布的一个特例。超几何分布即保留了树冠分布的随机性特征,同时也考虑了树冠间明显的排斥距离;林分内并非像泊松分布一样可以放置无穷多棵树,而是有限的株数。因此,相对于泊松分布,超几何分布能够更真实地、更准确地描述林分内树冠的分布模式。
2.2 冠层间隙率
为方便起见,本文用椭球树冠。事实上,椭球树冠可以通过变换得到很多其他冠型( Norman和Welles,1983)。
首先假设树冠为不透光且不能重叠的钢体。在天底下(θ=0°),当在林分内放置第1棵树时,冠层间隙率为(S-t c)/S,其中S为林分的面积,tc为单个树冠在垂直于θ平面上的投影面积,天底下时tc可以表达为(r2*π);其中r表示树冠半径;当放置第2棵树时,冠层间隙率为(S-2tc)/(S-tc)。以此类推,当放置Nc棵树后,冠层间隙率可以表达为
| $ \frac{{S - {t_{\rm{c}}}}}{S} \! * \! \frac{{S - 2 {t_{\rm{c}}}}}{{S - {t_{\rm{c}}}}}*\frac{{S - 3 {t_{\rm{c}}}}}{{S - 2 {t_{\rm{c}}}}} \! * \! \ldots \! * \! \frac{{S - {N_{\rm{c}}}{t_{\rm{c}}}}}{{S - ({N_{\rm{c}}} - 1{\rm{)}}{t_{\rm{c}}}}} = \frac{{S - {N_{\rm{c}}}{t_{\rm{c}}}}}{S} $ | (3) |
需要注意的是,在林分内每放置一个树冠,式(3)中等号左边每一项的分母都要减掉一个值。因此,相对于泊松分布和Neyman-A随机分布,超几何分布的冠层间隙率会随着树冠数目的增大迅速减小。
其次,考虑到树冠内部的间隙率以及树冠可以发生重叠。假设样地中树冠数量为 N c,则超几何分布下森林冠层的间隙率可以表达为
| $ \begin{aligned} & {P_{{\rm{Ht}}}}(\theta ) = \\ & \prod\limits_{j = 1}^{{N_{\rm{c}}}} {\Bigg[1 - \frac{{{t_{\rm{c}}}(\theta )*(1 - {P_{\rm{c}}}(\theta ))}}{{S*\cos (\theta ) - {S_{{\rm{rej\_c}}}}(\theta )*(1 - {P_{\rm{c}}}(\theta ))*(j - 1)}}\Bigg]} \end{aligned} $ | (4) |
式中, S rej_c表示树冠的排斥面积,可以表达为
| $ \begin{aligned} & {S_{{\rm{rej\_c}}}}(\theta ) = \\ & \left\{ \begin{array}{l} {\!\!\! S_{{\rm{crust\_c}}}}(\theta )\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_{{\rm{ASD}}}} \leqslant 1\\ {\!\!\! S_{{\rm{crust\_c}}}}(\theta ) - {S_{{\rm{pse\_c}}}}(\theta )\;\;\;\;{R_{{\rm{ASD}}}} > 1;\;{R_{{\rm{ASD}}}}r\rm cos(\theta ) \leqslant {t_h}(\theta ) \\ {\!\!\! t_{\rm{c}}}(\theta )\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_{{\rm{ASD}}}} > 1;\;{R_{{\rm{ASD}}}}r\rm cos(\theta ) > {t_h}(\theta ) \end{array} \right. \end{aligned} $ | (5) |
式中,Scrust_c(θ)表示θ方向单个树冠“保护壳”的面积,可以表达为
| $ {t_{\rm{c}}}(\theta ) = \left\{ \begin{array}{l} r*{\rm{\pi }}* \displaystyle \frac{{\sqrt {{k_{\rm{s}}}^2{r^2} + {{({H_{\rm{b}}}/2)}^2}} }}{{\sqrt {{k_{\rm{s}}}^2 + 1} }}\;\;\;\;\theta \ne 0^\circ\\ {r^2}*{\rm{\pi }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\theta = 0^\circ \end{array} \right. $ | (6) |
式中,
r表示树冠的半径,
H
b表示树冠高度;
式(4)中, P c( θ)表示光子在 θ方向上穿过单个树冠而不被拦截的概率(可以理解为单个树冠的透明度)。它跟视线方向累计叶面积指数有关,可以表达为( Fan 等,2014)
| $ {P_{\rm{c}}}(\theta ) = \exp \left[ { - G(\theta )*{L_0}*{\varOmega _{\rm{c}}}/{\gamma _{\rm{e}}}} \right] $ | (7) |
式中, G( θ)类似于式(1)中的 k,表示垂直于 θ方向的平面上叶片的投影面积与叶片面积的比例,与叶倾角有关。本文假设冠层内叶倾角满足球型分布, G( θ)=0.5; γ e表示针簇比,对于阔叶林而言, γ e=1; Ω c是单个树冠内叶片的聚集度指数,本文假设叶片在树冠内部满足泊松随机分布,因此 Ω c=1; L 0为视线方向累计叶面积指数。它与树冠的叶面积指数( L)体积( V)和光子在树冠中的穿过路径( s 0 )有直接关系:
| $ {L_0} = {s_{_0}}*L*S/(V*{N_{\rm{c}}}) $ | (8) |
结合上述两式可以得到:
| ${{P}_{\text{c}}}(\theta )=\exp \left[ -G(\theta )*L*S*09000{{\Omega }_{c}}/({{N}_{\text{c}}}*{{t}_{\text{c}}}(\theta )*{{\gamma }_{\text{e}}}) \right]$ | (9) |
2.3 冠层叶片聚集度指数
冠层叶片聚集度指数通常表示叶片在冠层中的分布偏离泊松分布的程度。可以表示为
| $ \varOmega (\theta ) = \frac{{\log ({P_{{\rm{Ht}}}}(\theta ))}}{{\log \left( {{P_{{\rm{Poisson}}}}(\theta )} \right)}} $ | (10) |
式中, P Poisson( θ)表示当叶片随机分布在冠层时的冠层间隙率,可以用式(1)计算得到( Chen和Leblanc,1997)。森林冠层中的叶片往往聚集在树冠内,从而导致 P Ht( θ)> P Poisson( θ), Ω( θ)<1。
然而,上述公式中聚集度指数随着 θ的变化而变化。在遥感反演叶面积指数时,有些时候需要冠层聚集度指数在观测天顶角0-π/2(半球)空间内的积分期望值。根据聚集度指数的定义可得( Chen和Leblanc,1997)
| $ \varOmega (\theta ) = \frac{{{L_{\rm{e}}}}}{L} $ | (11) |
式中, L e是冠层有效叶面积指数,也是地面光学仪器(如LAI-2000)间接实测得到的叶面积指数。根据Miller公式可知( Miller,1964)
| $ Le = - 2\int_0^{\pi /2} {\ln \left[ {P(\theta )} \right]\cos \theta \sin \theta {\rm{d}}\theta } $ | (12) |
式中, P( θ)是冠层间隙率,可以用式(4)计算得到。合并式(10)和式(11)可以求算半球空间内叶片聚集度指数的期望值,而不依赖于具体的观测天顶角( Chen 等,2005)。
3 结果与讨论
3.1 相同树冠半径下,不同树冠高度对冠层间隙率和叶片聚集度指数的影响
首先统一树冠半径,改变树冠高度,根据式(4)计算出冠层间隙率;根据式(10)和式(11)分别计算出不同天顶角下的冠层内叶片聚集度指数和叶片聚集度指数在半球内的期望值。具体的冠层参数如 表1所示。需要指出的是,本文假设其他结构参数均一致,在实际应用中并不成立;然而,这种做法能够很好地揭示树冠尺寸对冠层间隙率和叶片聚集度指数的影响。
表 1 冠层结构参数
Table 1 Canopy structural parameters
| 参数 | 值 |
| 林分面积/m 2 | 100×100 |
| 树冠数目 | 2000 |
| 叶面积指数 | 4 |
| 树干高度/m | 0.5 |
| 树冠半径/m | 1 |
| 树冠高度/m | 0.25; 0.5; 1; 2; 4; 8; 16 |
| G( θ) | 0.5 |
| Ω c | 1 |
| γ e | 1 |
| R ASD | 1 |
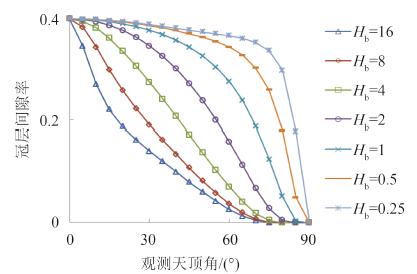
由 图2可知,当观测天顶角 θ=0°时,所有树冠尺寸下的冠层间隙率的值均相等,这是由于天底下观测到的所有冠层结构参数均一致。随着天顶角的增加,所有树冠尺寸下的冠层间隙率都呈现出递减趋势,直至为0。
然而,不同树冠尺寸下的冠层间隙率随着 θ变化的程度却有显著的差异,并且呈现出明显的规律:随着 θ的增加,“瘦高”型树冠下的冠层间隙率首先迅速减小;当 θ增大到一定角度(例如, θ=70°)时,其冠层间隙率减小速率相对平缓。反之,随着 θ的增加,“瘦高”型树冠下的冠层间隙率呈现出先缓慢减小,后迅速减小的趋势。这种现象是由于:根据式(5),冠层的间隙率与单个树冠在视线方向上的间隙率( P c( θ))呈正比关系,与单个树冠在视线方向上的投影面积( t c( θ))呈反比。当其他结构参数不变,相同观测天顶角下, t c会随着树冠高度的增加而增加。因此导致“瘦高”型树冠下的冠层间隙率比“矮胖”型树冠下的间隙率要普遍偏低。
在不同观测天顶角下,不同尺寸树冠下的冠层间隙率差异明显,例如当 θ=30°,树冠高度( H b)=16 m树冠下的冠层间隙率比 H b=0.25 m下的值低63.6%;而当 θ=60°, H b=16 m树冠下的冠层间隙率比 H b=0.25 m下的值低92.8%。值得注意的是,之前研究的不同冠型(如圆锥、椭球和圆锥+圆柱体)下冠层间隙率的差异,远远低于不同尺寸树冠下的冠层间隙率差异。例如,前者的差异平均小于10%,极端情况下的差异约40%( 尹高飞 等,2014)。
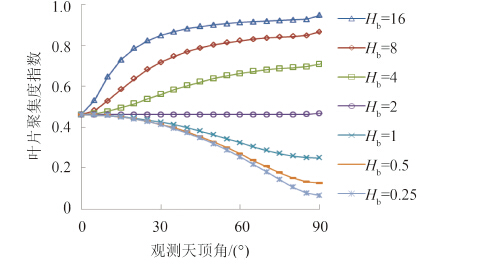
图3揭示了不同树冠尺寸下叶片聚集度指数随着观测天顶角变化的差异。根据式(2),由于聚集度指数与冠层间隙率呈反比,因此间隙率较大的冠层对应较小的叶片聚集度,表明冠层中叶片的聚集程度越大。
然而,与冠层间隙率不同,聚集度指数随着观测天顶角的变化并非有一致的变化趋势:球型树冠的聚集度指数在任何天顶角下均不变(约0.3)。球型树冠的聚集度相当于一个边界线:所有“瘦高”型树冠下的聚集度均随着天顶角增大而增大。这说明此类树冠下的叶片越来越趋于泊松随机分布。反之,“矮胖”型树冠下的聚集度随着天顶角增大,叶片聚集效应越来越明显。
与冠层间隙率类似,在不同观测天顶角下,不同尺寸树冠下的叶片聚集度差异明显。例如当 θ=30°, H b=16 m下的叶片聚集度比 H b=0.25 m下的值高106.5%;而当 θ=60°, H b=16 m树冠下的叶片聚集度比 H b=0.25 m下的值高261.8%。
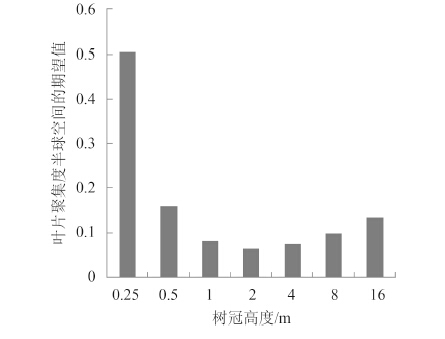
根据式(11)得到冠层内叶片聚集度指数在观测天顶角0-π/2空间内的期望值。 图4显示了不同尺寸树冠下,半球空间内冠层内叶片聚集度指数期望值具有明显的差异和规律性变化。随着树冠高度的增加,叶片聚集度指数逐渐增加,这意味这冠层内叶片越趋于泊松随机分布。极端情况下, H b=16 m下的值高于 H b=0.25 m下的值250.8%。
总体而言,树冠尺寸对冠层间隙率和叶片聚集度的影响要远远大于树冠形状对二者的影响。由于统一树冠半径、叶面积指数等冠层参数,树冠越高对应的树冠体积越大。因此,树冠越高对应的冠层间隙率越小,叶片聚集度越大,意味着冠层内叶片越趋于泊松分布。
3.2 相同树冠体积下,不同树冠尺寸对冠层间隙率和叶片聚集度指数的影响
3.1节中揭示了不同树冠尺寸下的冠层间隙率和叶片聚集度指数因树冠体积的不同表现出有规律的变化。本节通过固定单个树冠体积,同时调节树冠高度和树冠半径,讨论不同树冠尺寸对冠层间隙率和聚集度指数的影响。为防止当 R ASD=1时“矮胖型”树冠溢出林分边界,设定林分内树冠株数为360;树冠尺寸参数如 表2所示,其他参数参照 表1。
表 2 相同树冠体积下的不同树冠尺寸参数
Table 2 Crown sizes with same
V
| 树冠半径/m | 树冠高度/m |
| 2.83 | 0.25 |
| 2 | 0.5 |
| 1.41 | 1 |
| 1 | 2 |
| 0.71 | 4 |
| 0.5 | 8 |
| 0.35 | 16 |
图5与 图2类似,所有树冠尺寸下的冠层间隙率都随着观测天顶角的增大而减小,当天顶角为90°时,所有间隙率均趋于0。
然而,与 图1不同,当观测天顶角 θ=0时,所有树冠尺寸下的冠层间隙率的值并不相等。这是由于天底方向下,虽然单个树冠内的间隙率的差异不大,但“瘦高”型树冠的 t c( θ)要小于“矮胖型”树冠的值。根据式(3),冠层间隙率与 t c( θ呈反比,因此,“瘦高”型树冠下的冠层间隙率高于“矮胖型”树冠下的值。值得注意的是,在几乎所有观测天顶角下,不同尺寸树冠之间的间隙率差异都非常明显:例如,当 θ=0°, H b=16 m下的冠层间隙率高于 H b=0.25 m下的值404.6%;当 θ=30°, H b=16 m下的冠层间隙率高于 H b=0.25 m下的值391.4%;当 θ=30°, H b=16 m下的冠层间隙率高于 H b=0.25 m下的值414.1%。
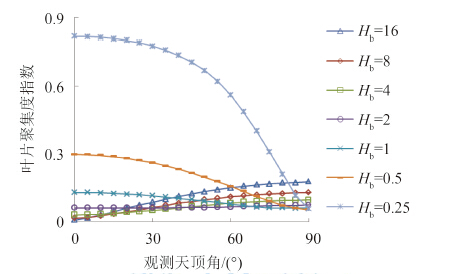
图6显示了相同体积下7种树冠下叶片聚集度指数的比较。相比较3.1节, 图6与 图3有一定的相似性,例如:球型树冠下的叶片聚集度指数不随观测天顶角变化而变化(始终为0.06);球型树冠的值相对于其它尺寸树冠下的间隙率仍然相当于一条边界线:随着观测天顶角的增加,“瘦高”型树冠的叶片聚集度逐渐增加,而“矮胖”型树冠的叶片聚集度逐渐减小。
在天底方向,与间隙率相反,“矮胖”型树冠的叶片聚集度远远高于“瘦高”型树冠的值。例如,天底下, H b=0.25 m下的叶片聚集度高于 H b=16 m下的值11397.2%。
观测天顶角约60°时,7种树冠尺寸下叶片聚集度差异最小。然而,即便在此角度下,7种树冠下叶片聚集度也存在较为明显的差异:例如, H b=0.25 m下的值高于 H b=2 m下的值约274.1%。
图7揭示了相同树冠体积下的观测天顶角在0-π/2空间内聚集度指数期望值的变化。与 图4不同,在7种树冠尺寸下,球型树冠的叶片聚集度指数期望值最低,说明该类树冠下的叶片聚集效应最明显,聚集程度最高。随着树冠的尺寸越偏离球型,叶片聚集度指数期望值越高,说明冠层内叶片越趋于泊松随机分布。7种树冠尺寸下球型树冠的叶片聚集度指数期望值的差异比较明显, H b=0.25 m下的叶片聚集度期望值高于 H b=2 m下的值677.3%。
总体而言,在相同树冠体积条件下,树冠尺寸对冠层间隙率和叶片聚集度的影响要远远大于树冠形状对二者的影响。不同尺寸树冠下的冠层间隙率和叶片聚集度差异非常明显。单个树冠在 θ方向上的投影面积 t c( θ)不同。球体树冠的 t c( θ)最小,树冠尺寸与球体的差异越大, t c( θ)越大,对应的冠层间隙率越小,叶片聚集度指数越大。
4 结 论
树冠的冠型特征不仅包括形状特征,同时包括尺寸特征。在大尺度范围内(例如全球、跨纬度带尺度),树冠的尺寸特征往往比树冠的形状特征更具有显著的地理空间特征。之前的学者主要集中研究了树冠形状特征对冠层间隙率和叶片聚集度指数的影响。本文首先将林分内树冠泊松分布模式修改为更为真实的超几何分布模式,通过设定不同树冠尺寸参数,揭示了冠层间隙率和叶片聚集度与树冠尺寸存在非常显著的规律性,不同树冠尺寸下的冠层间隙率和叶片聚集度差异非常明显。主要结论如下:
(1) 揭示了树冠尺寸特征对冠层间隙率和叶片聚集度指数的影响比树冠形状特征对间隙率和叶片聚集度指数的影响更为明显,在大范围研究中更值得关注。
(2) 相同树冠半径下,不同树冠高度对冠层间隙率和叶片聚集度的影响显著,且具有明显的规律性:树冠越高对应的冠层间隙率越小,叶片聚集度越大,冠层内叶片越趋于泊松分布。例如,当 θ=60°, H b=16 m树冠下的冠层间隙率比 H b=0.25 m下的值低92.8%;当 θ=60°, H b=16 m树冠下的叶片聚集度比 H b=0.25 m下的值高261.8%; H b=16 m下的叶片聚集度指数期望值高于 H b=0.25 m下的值约250.8%。
(3) 相同树冠体积下,不同树冠尺寸对冠层间隙率和叶片聚集度的影响非常显著,且具有非常明显的规律性。球体树冠的叶片聚集度最小;树冠尺寸与球体的差异越大,叶片聚集度越大。例如, θ=0°时, H b=16 m下的冠层间隙率高于 H b=0.25 m下的值414.1%; H b=0.25 m下的叶片聚集度高于 H b=16 m下的值11397.2%; H b=16 m下的叶片聚集度期望值高于 H b=2 m下的值677.3%。
近10年中,在小尺度范围内,利用机载和车载等平台下激光雷达等技术已经得到较为精准的树冠尺寸参数( 吴迪和范文义,2014; 庞勇 等,2008);在全国乃至全球尺度,目前只有树冠高度产品,还没有可靠的树冠半径或者冠幅产品( Simard 等,2011)。然而,随着星载高空间分辨率和多角度光学遥感以及激光雷达遥感技术的发展,全国乃至全球尺度的树冠半径或者冠幅等参数产品势必将陆续生产。本文从理论出发,讨论了不同树冠尺寸对冠层间隙率和聚集度指数的影响。下一步研究将从实际应用出发,利用目前已经发布的树冠尺寸数据,研究区域乃至全国范围的树冠尺寸的分布格局,深入分析实际的树冠尺寸参数对冠层间隙率和叶片聚集度指数的影响。
参考文献(References)
-
Chen J M, Black T A.1992.Defining leaf area index for non-flat leaves. Plant, Cell & Environment, 15 : 421–429. DOI: 10.1111/j.1365-3040.1992.tb00992.x.
-
Chen J M, Cihlar J.1995.Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Applied Optics, 34 : 6211–6222. DOI: 10.1364/AO.34.006211.
-
Chen J M, Leblanc S G.1997.A four-scale bidirectional reflectance model based on canopy architecture. IEEE Transactions on Geoscience and Remote Sensing, 35 : 1316–1337. DOI: 10.1109/36.628798.
-
Chen J M, Liu J, Cihlar J, Goulden M L.1999.Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecological Modelling, 124 : 99–119. DOI: 10.1016/S0304-3800(99)00156-8.
-
Chen J M, Menges C H, Leblanc S G.2005.Global mapping of foliage clumping index using multi-angular satellite data. Remote Sensing of Environment, 97 : 447–457. DOI: 10.1016/j.rse.2005.05.003.
-
Deng F, Chen J M, Plummer S, Chen M Z, Pisek J.2006.Algorithm for global leaf area index retrieval using satellite imagery. IEEE Transactions on Geoscience and Remote Sensing, 44 : 2219–2229. DOI: 10.1109/TGRS.2006.872100.
-
Fan W L, Chen J M, Ju W M, Zhu G L.2014.Gost: a geometric-optical model for sloping terrains. IEEE Transactions on Geoscience and Remote Sensing, 52 : 5469–5482. DOI: 10.1109/TGRS.2013.2289852.
-
He L M, Chen J M, Pisek J, Schaaf C B, Strahler A H.2012.Global clumping index map derived from the MODIS BRDF product. Remote Sensing of Environment, 119 : 118–130. DOI: 10.1016/j.rse.2011.12.008.
-
Jahnke L S, Lawrence D B.1965.Influence of photosynthetic crown structure on potential productivity of vegetation, based primarily on mathematical models. Ecology, 46 : 319–326. DOI: 10.2307/1936335.
-
Kucharik C J, Norman J M, Gower S T.1999.Characterization of radiation regimes in nonrandom forest canopies: theory, measurements, and a simplified modeling approach. Tree Physiology, 19 : 695–706. DOI: 10.1093/treephys/19.11.695.
-
Kuuluvainen T.1992.Tree architectures adapted to efficient light utilization: is there a basis for latitudinal gradients?. Oikos, 65 : 275–284. DOI: 10.2307/3545019.
-
Li X W, Strahler A H.1985.Geometric-optical modeling of a conifer forest canopy. IEEE Transactions on Geoscience and Remote Sensing, GE-23 : 705–721. DOI: 10.1109/TGRS.1985.289389.
-
Li X W, Strahler A H.1986.Geometric-optical bidirectional reflectance modeling of a conifer forest canopy. IEEE Transactions on Geoscience and Remote Sensing, GE-24 : 906–919. DOI: 10.1109/TGRS.1986.289706.
-
Li X W, Strahler A H.1988.Modeling the gap probability of a discontinuous vegetation canopy. IEEE Transactions on Geoscience and Remote Sensing, 26 : 161–170. DOI: 10.1109/36.3017.
-
Li X W, Strahler A H.1992.Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: effect of crown shape and mutual shadowing. IEEE Transactions on Geoscience and Remote Sensing, 30 : 276–292. DOI: 10.1109/36.134078.
-
Li X W, Strahler A H, Woodcock C E.1995.A hybrid geometric optical-radiative transfer approach for modeling albedo and directional reflectance of discontinuous canopies. IEEE Transactions on Geoscience and Remote Sensing, 33 : 466–480. DOI: 10.1109/36.377947.
-
Miller J B.1964.An integral equation from phytology. Journal of the Australian Mathematical Society, 4 : 397–402. DOI: 10.1017/S1446788700025210.
-
Nilson T.1971.A theoretical analysis of the frequency of gaps in plant stands. Agricultural Meteorology, 8 : 25–38. DOI: 10.1016/0002-1571(71)90092-6.
-
Norman J M, Welles J M.1983.Radiative transfer in an array of canopies. Agronomy Journal, 75 : 481–488. DOI: 10.2134/agronj1983.00021962007500030016x.
-
Pang Y, Zhao F, Li Z Y, Zhou S F, Deng G, Liu Q W, Chen E X.2008.Forest height inversion using airborne Lidar technology. Journal of Remote Sensing, 12 : 152–158. ( 庞勇, 赵峰, 李增元, 周淑芳, 邓广, 刘清旺, 陈尔学. 2008. 机载激光雷达平均树高提取研究. 遥感学报, 12 : 152–158. )
-
Rautiainen M, Stenberg P, Nison T, Kuusk A.2004.The effect of crown shape on the reflectance of coniferous stands. Remote Sensing of Environment, 89 : 41–52. DOI: 10.1016/j.rse.2003.10.001.
-
Rautiainen M, Mõttus M, Heiskanen J, Akujärvi A, Majasalmi T, Stenberg P.2011.Seasonal reflectance dynamics of common understory types in a northern European boreal forest. Remote Sensing of Environment, 115 : 3020–3028. DOI: 10.1016/j.rse.2011.06.005.
-
Simard M, Pinto N, Fisher J B, Baccini A.2011.Mapping forest canopy height globally with spaceborne lidar. Journal of Geophysical Research, 116 : G04021 DOI: 10.1029/2011JG001708.
-
Stenberg P, Palmroth S, Bond B J, Sprugel D G, Smolander H.2001.Shoot structure and photosynthetic efficiency along the light gradient in a scots pine canopy. Tree Physiology, 21 : 805–814. DOI: 10.1093/treephys/21.12-13.805.
-
Wu C, Chen J M.2012.The use of precipitation intensity in estimating gross primary production in four northern grasslands. Journal of Arid Environments, 82 : 11–18. DOI: 10.1016/j.jaridenv.2012.02.014.
-
Wu D, Fan W Y.2014.Forest canopy height estimation using Lidar and optical multi-angler data. Journal of Beijing Forestry University, 36 : 8–15. ( 吴迪, 范文义. 2014. 激光雷达协同多角度光学遥感数据反演树高. 北京林业大学学报, 36 : 8–15. )
-
Yin G F, Liu Q H, Li J, Zeng Y L, Xu B D.2014.Effect of crown shape on the estimation of gap probability and leaf area index. Journal of Remote Sensing, 18 : 752–759. ( 尹高飞, 柳钦火, 李静, 曾也鲁, 徐保东. 2014. 树冠形状对孔隙率及叶面积指数估算的影响分析. 遥感学报, 18 : 752–759. )
-
Zheng G, Moskal L M, Kim S H.2013.Retrieval of effective leaf area index in heterogeneous forests with terrestrial laser scanning. IEEE Transactions on Geoscience and Remote Sensing, 51 : 777–786. DOI: 10.1109/TGRS.2012.2205003.