合成孔径雷达SAR(Synthetic Aperture Radar)是一种高分辨率成像雷达，具有全天时、全天候和透视性等特点，已广泛用于军事侦察、地图测绘、资源勘探等方面(Cumming和Wong，2005)。地面动目标显示GMTI(Ground Moving Target Indication)技术可以检测和跟踪地面运动目标，将SAR与GMTI相结合即SAR-GMTI，已成为战略情报侦察和战场监视系统的重要组成部分( Sjögren 等，2014； 张焕胜，2006)。SAR-GMTI技术的广泛应用和快速发展，严重削弱了地面军事运动目标的战场生存能力和作战效能，使侦察方能够快速洞悉地面运动目标(如坦克、装甲车等)的军事意图，因此，SAR-GMTI干扰技术研究已成为电子对抗领域的热点问题( 孙光才 等，2010； 吴晓芳 等，2012a； Huang 等，2015)。

SAR-GMTI系统通常采用多个通道对杂波和干扰进行抑制和对消，传统的SAR干扰样式很容易被多通道SAR-GMTI所抑制( Zhang 等，2015； 贾鑫 等，2014； 黄龙 等，2014； 张静克 等，2015)，干扰效果不尽意。目前，针对SAR-GMTI的干扰技术研究相对较少，主要集中在利用固定干扰站对SAR产生虚假动目标欺骗干扰( 李伟 等，2006； 吴晓芳 等，2012b)，干扰信号产生需要时频域变换和复杂调制，干扰的实时性差，对侦察依赖度高，通常需要多部干扰机协同工作才能实现逼真的欺骗干扰效果，且没有深入讨论对多通道SAR-GMTI系统的干扰效果和对抗性能。 唐波(2008， 2009)先后研究了运动干扰站对SAR和InSAR双通道抑制的影响，指出干扰站的运动可以有效降低双通道对干扰信号的抑制性能； 田贤峰和万广有(2010)提出基于运动干扰站的SAR随队欺骗干扰方法，有效降低了欺骗干扰的难度，但只能在方位向较小范围内形成良好的聚焦图像； 祝俊等人(2013)则提出基于运动干扰站的SAR移频压制干扰，该方法可对SAR产生面状的压制干扰，但由于移频量的限制，只能在距离向较小范围内形成压制干扰，同时也未对多通道SAR-GMTI的干扰效果进行研究。针对上述问题，本文提出基于运动干扰站的SAR-GMTI余弦调相转发干扰方法，首先对运动干扰站转发式干扰的成像特性进行分析，并利用该特性实现干扰目标的方位向扩展，然后利用余弦调相信号的频谱复制、搬移特性实现距离向扩展；理论推导了该方法对SAR的干扰成像输出结果，并以三通道干涉对消技术为例，着重分析了其对多通道SAR-GMTI的干扰效果和对抗性能。本文方法对SAR和SAR-GMTI均能够产生2维条带状或面状遮盖干扰效果，可随队保护地面运动或静止的分布式目标，为多通道SAR-GMTI干扰提供了有效途径。

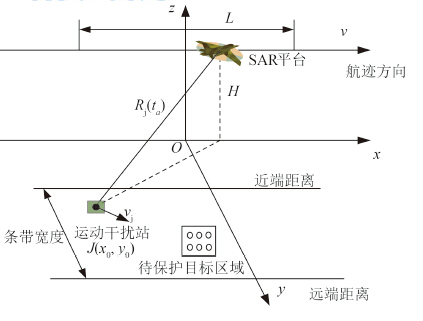
设SAR平台飞行速度为 v，合成孔径长度为 L，以SAR航迹方向为 X轴正方向建立坐标系， 图1为基本的干扰原理几何示意图。图中运动干扰站 J和待保护目标均处于成像条带范围内，运动干扰站由干扰机和干扰车组成，运动干扰站通过实时侦收雷达信号，经过调制后对SAR进行转发式干扰，从而对运动或静止目标提供随队干扰保护。

如 图1所示，设地面干扰站初始坐标为( x ₀， y ₀，0)，以速度为 v _j=( v _x， v _y)做匀速运动，干扰站到SAR平台的初始斜距 ${{R}_{\text{j}0}}=\sqrt{x_{0}^{2}+y_{0}^{2}+{{H}^{2}}}$ ，则瞬时斜距按麦克劳林公式展开可得

$ \begin{aligned} & {R_{\rm{j}}}({t_{\rm{a}}}) = \sqrt {{{({x_0} + {v_x}{t_{\rm{a}}} - v{t_{\rm{a}}})}^2} + {{({y_0} + {v_y}{t_{\rm{a}}})}^2} + {H^2}} \\& \approx {R_{{\rm{j0}}}} + \frac{{{x_0}\left( {{v_x} - v} \right) + {y_0}{v_y}}}{{{R_{{\rm{j0}}}}}}{t_{\rm{a}}} + \frac{{{{\left( {{v_x} - v} \right)}^2} + {v_y}^2}}{{2{R_{{\rm{j0}}}}}}{t_{\rm{a}}}^2 \end{aligned} $

(1)

设SAR发射线性调频信号为

$ s\left( {{t}_{\text{r}}},{{t}_{\text{a}}} \right)=\text{rect}\left( {{{t}_{\rm r}}}/{{{T}_{\text{p}}}}\; \right)\exp \left[ j2\text{ }\!\!\pi\!\!\text{ }\left( {{f}_{0}}t+{{{u}_{\rm r}}t_{\rm r}^{2}}/{2}\; \right) \right] $

(2)

式中，rect(·)为矩形窗函数， t _r为距离向快时间， t _a为方位向慢时间，全时间 t= t _r+ t _a， T _p为脉冲宽度， f ₀为载频， u _r为调频斜率。运动干扰站接收到雷达信号后直接转发，忽略干扰机转发延时，则SAR接收到的基频干扰信号为

$ \begin{aligned} & {{s}_{\text{j}}}({{t}_{\text{r}}},{{t}_{\text{a}}})=\text{rect}(\frac{{{t}_{\text{r}}}-{{\tau }_{\text{r}}}}{{{T}_{\text{p}}}})\text{rect}(\frac{{{t}_{\text{a}}}}{{{T}_{\text{L}}}}) \exp \left[ \text{j}\pi\text{}{{u}_{\text{r}}}{{({{t}_{\text{r}}}-{{\tau }_{\text{r}}})}^{2}} \right]\cdot \\ & \ \ \ \ \ \ \ \ \ \exp (-\text{j}\frac{4\text{ }\!\!\pi\!\!\text{ }}{\lambda }{{R}_{\text{j}}}({{t}_{\text{a}}})) \\ \end{aligned} $

(3)

式中， ${{\tau }_{\text{r}}}=2{{R}_{\text{j}}}({{t}_{\text{a}}})/c$ 为干扰信号的传播时延， T _L为合成孔径时间。采用经典RD(Range Doppler)算法对干扰信号成像结果进行分析，SAR距离向匹配滤波函数 ${{h}_{\text{r}}}({{t}_{\text{r}}})=\text{rect}({{t}_{\text{r}}}/{{T}_{\text{p}}})\exp (-\text{j}\pi\text{}{{u}_{\text{r}}}t_{\text{r}}^{2})$ ，则对干扰信号进行距离向匹配滤波和距离徙动校正可得(忽略与成像无关的幅度和相位项影响，下同)

$ \begin{aligned} & {{s}_{\text{jr}}}({{t}_{\text{r}}},{{t}_{\text{a}}})=\left( 1-\frac{\left| t_{\text{r}}^{*} \right|}{{{T}_{\text{p}}}} \right)\cdot \text{sinc}\left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{r}}}t_{\text{r}}^{*}({{T}_{\text{p}}}-\left| t_{\text{r}}^{*} \right|) \right)\cdot \\ & \ \ \ \ \ \ \ \ \exp (-\text{j}\frac{4\text{ }\!\!\pi\!\!\text{ }}{\lambda }{{R}_{\text{j}}}({{t}_{\text{a}}})) \\ \end{aligned} $

(4)

式中， t _r ^*是对 t _r- τ _r经过距离徙动校正后与方位向慢时间无关的回波到达时间，由于干扰站速度远小于信号传播速度，可忽略干扰站运动对SAR距离向成像的影响( 吴晓芳 等，2012a)。由式(4)可得干扰信号的方位向慢时间相位 $\phi =-4\text{ }\!\!\pi\!\!\text{ }{{R}_{\text{j}}}({{t}_{\text{a}}})/\lambda $ ，从而可求得干扰信号的多普勒中心频率 f _c1和调频率 u _a1分别为

$ \left\{ \begin{aligned} & {{f}_{\text{c1}}}={{f}_{\text{c}}}-\frac{2({{x}_{0}}{{v}_{\text{x}}}+{{y}_{0}}{{v}_{\text{y}}})}{\lambda {{R}_{\text{j0}}}} \\ & {{u}_{\text{a1}}}={{u}_{\text{a}}}-\frac{2(v_{\text{x}}^{2}+v_{\text{y}}^{2}-2{{v}_{\text{x}}}v)}{\lambda {{R}_{\text{j0}}}} \\ \end{aligned} \right. $

(5)

式中， ${{f}_{\text{c}}}=2{{x}_{0}}v/\lambda {{R}_{\text{j0}}}$ 、 ${{u}_{\text{a}}}=-2{{v}^{2}}/\lambda {{R}_{\text{j0}}}$ 分别为固定干扰站的SAR匹配滤波器的多普勒中心频率和调频率，可见，匀速运动干扰站方位向慢时间信号仍具有线性调频信号特性，但运动干扰站的多普勒参数与匹配滤波器存在匹配失配，其中，多普勒中心频率失配导致目标方位向位置的偏移，多普勒调频率失配将导致方位向的展宽。在Fresnel近似条件下，回波干扰信号经距离徙动校正后在距离向和方位向可分离处理，SAR方位向匹配滤波函数 ${{h}_{\text{a}}}({{t}_{\text{a}}})=\text{rect}({{t}_{\text{a}}}/{{T}_{\text{L}}})\exp (-\text{j }\!\!\pi\!\!\text{ }{{u}_{\text{a}}}t_{\text{a}}^{2})$ ，则式(4)方位向匹配滤波的时域表达式为

$ \begin{aligned} & {{s}_{\text{ja}}}({{t}_{\text{r}}},{{t}_{\text{a}}})={{s}_{\text{jr}}}({{t}_{\text{r}}},{{t}_{\text{a}}})\otimes {{h}_{\text{a}}}({{t}_{\text{a}}}) \\ & \ \ \ \ \ \ \ \ \ \ \ \ =\int\limits_{-\infty }^{+\infty }{{{s}_{\text{jr}}}({{t}_{\text{r}}},\tau )}\cdot {{h}_{\text{a}}}({{t}_{\text{a}}}-\tau )\text{d}\tau \\ \end{aligned} $

(6)

式中，“ $\otimes $ ”表示卷积。由于方位向慢时间干扰信号分量仍可视为线性调频信号，且具有较大的时宽带宽积，故可采用驻定相位原理进行近似求解( Cumming和Wong，2005)，则式(6)关于慢时间的待积分相位项为

$ \begin{aligned} & \varphi (\tau )=\text{-}4\text{ }\!\!\pi\!\!\text{ }{{R}_{\text{j}}}(\tau )/\lambda -\text{ }\!\!\pi\!\!\text{ }{{u}_{\text{a}}}{{({{t}_{\text{a}}}-\tau )}^{2}} \\ & \ \ \ \ \ \ \ =2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{c1}}}\tau +\text{ }\!\!\pi\!\!\text{ }{{u}_{\text{a1}}}{{\tau }^{2}}-\text{ }\!\!\pi\!\!\text{ }{{u}_{\text{a}}}{{({{t}_{\text{a}}}-\tau )}^{2}} \\ \end{aligned} $

(7)

对式(7)关于 τ求导，并令 ${{\varphi }^{'}}(\tau )\left| _{\tau ={{\tau }^{*}}}=0 \right.$ ，可得驻定相位点 τ ^*处对应的方位向时刻 t _am为

$ \begin{aligned} & {{t}_{\text{am}}}=-\frac{{{f}_{\text{c1}}}}{{{u}_{\text{a}}}}+\frac{{{u}_{\text{a}}}-{{u}_{\text{a1}}}}{{{u}_{\text{a}}}}{{\tau }^{*}} \\ & \ \ \ \ \ =\frac{{{x}_{0}}}{v}-\frac{{{x}_{0}}{{v}_{\text{x}}}+{{y}_{0}}{{v}_{\text{y}}}}{{{v}^{2}}}-\frac{v_{\text{x}}^{2}+v_{\text{y}}^{2}-2{{v}_{\text{x}}}v}{{{v}^{2}}}{{\tau }^{*}} \\ \end{aligned} $

(8)

则干扰信号方位向匹配滤波输出包络为

$ \begin{aligned} {{s}_{\text{ja}}}({{t}_{\text{r}}},{{t}_{\text{a}}})= & \left( 1-\frac{\left| t_{\text{r}}^{*} \right|}{{{T}_{\text{p}}}} \right)\cdot \left( 1-\frac{\left| t_{\rm a}^{*} \right|}{{{T}_{\rm L}}} \right)\cdot \text{sinc}\left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{r}}}t_{\text{r}}^{*}({{T}_{\text{p}}}-\left| t_{\text{r}}^{*} \right|) \right)\cdot \\ & \text{sinc}\left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{a}}}t_{\text{a}}^{*}({{T}_{\text{L}}}-\left| t_{\text{a}}^{*} \right|) \right) \\ \end{aligned} $

(9)

式中， t _a ^*= t _a- t _am，当 t _a= t _am时匹配滤波后干扰信号方位向取得峰值，其中 t _am关于 τ ^*的常数项表示干扰目标方位向的中心位置， t _am关于 τ ^*的一次项表示干扰目标方位向峰值时刻随 τ ^*线性变化，使得方位向成像沿中心位置产生均匀展宽，则由式(8)可得干扰目标方位向中心位置和展宽量为

$ \left\{ \begin{aligned} & x={{x}_{0}}-\frac{{{x}_{0}}{{v}_{\text{x}}}+{{y}_{0}}{{v}_{\text{y}}}}{v} \\ & \delta x=-\frac{v_{\text{x}}^{2}+v_{\text{y}}^{2}-2{{v}_{\text{x}}}v}{v}{{T}_{\text{L}}} \\ \end{aligned} \right. $

(10)

干扰目标相对静止干扰站的方位向中心位置偏移量 $\Delta x=-({{x}_{0}}{{v}_{\text{x}}}+{{y}_{0}}{{v}_{\text{y}}})/v$ ，且由于 ${x_0} \ll {y_0}$、干扰站运动速度通常远小于SAR载机速度，故可认为方位向偏移量主要由干扰站距离向速度 v _y产生，展宽量主要由干扰站方位向速度 v _x产生。通过上述分析可知，匀速运动干扰站主要对干扰信号方位向成像产生影响，使得干扰信号回波多普勒参数与匹配滤波器失配的同时，导致干扰目标方位向中心位置偏移、主瓣展宽、峰值下降等成像特性。

运动干扰站转发式干扰方位向的成像特性，在降低SAR欺骗性干扰成像质量的同时，为SAR压制性干扰提供了有效途径。利用运动干扰站方位向成像特性，通过对干扰站速度的灵活控制，即可形成方位向位置和展宽长度灵活可控的条带状干扰目标，当产生的干扰条带位于 图1所示的待保护目标区域时，可对真实运动或静止目标提供遮盖性干扰，且干扰站产生的是具有运动特性的干扰信号，所以对SAR和SAR-GMTI均具有干扰效果。

运动干扰站仅能够产生方位向位置和展宽长度灵活可控的条带状干扰目标，若要产生2维条带状的干扰目标，则需要对干扰信号进行距离向扩展。余弦调相可使干扰信号频谱产生多次复制、搬移，且能够保证干扰信号与SAR信号的相干性，因此，运动干扰站可对干扰信号进行距离向余弦调相，从而实现干扰目标的距离向扩展。

余弦调相信号的数学模型可表示为

$ p(t)=A\cos \left[ 2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{c}}}t+{{\beta }_{\text{m}}}\cos (2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{m}}}t) \right] $

(11)

式中， β _m为调制指数， f _m为调制频率，对式(11)进行级数展开可得

$ p(t)=A\sum\limits_{n=-\infty }^{+\infty }{{{J}_{\text{\emph n}}}({{\beta }_{\text{m}}})}\cos \left[ 2\text{ }\!\!\pi\!\!\text{ }({{f}_{\rm c}}+n{{f}_{\text{m}}})t+\frac{n\text{ }\!\!\pi\!\!\text{ }}{2} \right] $

(12)

式中， J _n ( β _m)为第一类 n阶贝塞尔函数，对上式进行傅里叶变换可得

$ \begin{aligned} & P(f)=\text{ }\!\!\pi\!\!\text{ }A\sum\limits_{n=-\infty }^{+\infty }{{{J}_{n}}({{\beta }_{\text{m}}})}\cdot \\ & \left\{ {{\text{e}}^{-\text{j}\frac{n\text{ }\!\!\pi\!\!\text{ }}{2}}}\delta \left[ 2\text{ }\!\!\pi\!\!\text{ }(f+{{f}_{\text{c}}}+n{{f}_{\text{m}}}) \right]+{{\text{e}}^{\text{j}\frac{n\text{ }\!\!\pi\!\!\text{ }}{2}}}\delta \left[ 2\text{ }\!\!\pi\!\!\text{ }(f-{{f}_{\text{c}}}-n{{f}_{\text{m}}}) \right] \right\} \\ \end{aligned} $

(13)

由式(13)可知，余弦调相信号频谱由无穷多个边频分量组成，各边频分量的幅度正比于相应阶数的贝塞尔函数 J _n ( β _m)，并以调制频率 f _m等间隔分布。从频谱形状来看，余弦调相信号频谱是通过第一类贝塞尔函数进行幅度加权而形成的“梳状”谱，且忽略幅度较小高阶边频分量，单边边频分量通常只取到( β _m+1)次( 陈思伟 等，2009)。

设距离向基频余弦调相信号为

$ p({{t}_{\rm r}})={{A}_{\rm r}}\cdot \exp \left[ \text{j}{{\beta }_{\text{r}}}\cos (2\text{ }\!\!\pi\!\!\text{ }{{f}_{\text{r}}}{{t}_{\text{r}}}) \right] $

(14)

式中， A _r为余弦调相信号的幅度， f _r为调制频率， β _r为调制指数。运动干扰站对接收到的SAR信号进行距离向余弦调相处理并转发(忽略干扰机转发延时)，则SAR接收到的余弦调相干扰信号为

$ j({{t}_{\text{r}}},{{t}_{\text{a}}})={{s}_{\text{j}}}({{t}_{\text{r}}},{{t}_{\text{a}}})\cdot p({{t}_{\text{r}}}) $

(15)

结合式(12)和(13)，对式(15)进行距离向傅里叶变换可得干扰信号频谱为

$ J(f,{{t}_{\text{a}}})=2\text{ }\!\!\pi\!\!\text{ }{{A}_{\rm r}}\sum\limits_{n=-\infty }^{+\infty }{{{J}_{n}}\text{(}{{\beta }_{\text{r}}}\text{)}}{{S}_{\text{j}}}(f+n{{f}_{\text{r}}},{{t}_{\text{a}}}) $

(16)

式中， S _j( f， t _a)为 s _j( t _r， t _a)的距离向频谱。干扰信号经过距离向和方位向2维解藕后，运动干扰站距离向快时间余弦调相分量与方位向慢时间多普勒相位分量可分离处理，仍采用RD成像算法，对余弦调相干扰信号进行距离向匹配滤波可得

$ \begin{aligned} & {j_{\rm{r}}}({t_{\rm{r}}},{t_{\rm{a}}}) = {A_{\rm{r}}}\sum\limits_{n = - \infty }^{ + \infty } {{J_n}({\beta _{\rm{r}}})} \left( {1 - \frac{{\left| {t_{\rm{r}}^*} \right|}}{{{T_{\rm{p}}}}}} \right) \cdot \\ & {\mathop{\rm sinc}\nolimits} \left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{r}}}(t_{\text{r}}^{*}+\frac{n{{f}_{\text{r}}}}{{{u}_{\text{r}}}})({{T}_{\text{p}}}-\left| t_{\text{r}}^{*} \right|) \right)\cdot \exp \left[ \text{-j}\frac{4\text{ }\!\!\pi\!\!\text{ }}{\lambda }{{R}_{\text{j}}}({{t}_{\text{a}}}) \right] \\ \end{aligned} $

(17)

对比式(4)、(16)、(17)可知，余弦调相干扰信号频谱是原干扰信号频谱的多次复制、搬移，频谱复制次数约为2( β _r+1)(向下取整)，各频谱分量间隔为 f _r，幅度正比于相应阶数的贝塞尔函数 J _n ( β _r)；同时，原干扰信号回波距离向峰值时刻为 t _r ^*，余弦调相干扰信号回波距离向峰值时刻为 t _r ^*=- nf _r/ u _r，可见，干扰信号在距离向快时间域会产生多个峰值时刻，将在SAR距离向产生多阶干扰目标，各干扰目标距离间隔为 cf _r/(2 u _r)。

结合式(9)，可得干扰信号方位向匹配滤波输出包络为

$ \begin{aligned} & {{y}_{\text{j}}}({{t}_{\text{r}}},{{t}_{\text{a}}})={{A}_{\text{r}}}\sum\limits_{n=-\infty }^{+\infty }{{{J}_{n}}({{\beta }_{\text{r}}})}\left( 1-\frac{\left| t_{\rm r}^{*} \right|}{{{T}_{\text{p}}}} \right)\cdot \left( 1-\frac{\left| t_{\rm a}^{*} \right|}{{{T}_{\text{L}}}} \right)\cdot \\ & {\mathop{\rm sinc}\nolimits} \left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{r}}}(t_{\text{r}}^{*}+\frac{n{{f}_{\text{r}}}}{{{u}_{\text{r}}}})({{T}_{\text{p}}}-\left| t_{\text{r}}^{*} \right|) \right)\cdot {\mathop{\rm sinc}\nolimits} \left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{a}}}t_{\text{a}}^{*}({{T}_{\text{L}}}-\left| t_{\text{a}}^{*} \right|) \right) \\ \end{aligned} $

(18)

由式(18)可知，本文方法兼具余弦调相干扰和运动干扰站直接转发干扰的特性，可沿SAR距离向产生多阶条带状干扰目标，各阶干扰目标方位向中心位置和展宽量相同，距离向间隔为∆ R= cf _r/(2 u _r)，各阶干扰目标距离向和方位向中心位置为

$ \left\{ \begin{aligned} & {{R}_{n}}={{R}_{\text{j0}}}-\frac{cn{{f}_{\text{r}}}}{2{{u}_{\text{r}}}} \\ & x={{x}_{0}}-\frac{{{x}_{0}}{{v}_{\text{x}}}+{{y}_{0}}{{v}_{\text{y}}}}{v} \\ \end{aligned} \right. $

(19)

余弦调相干扰分量使得原干扰信号频谱在距离向进行了2( β _r+1)次复制、搬移，共可形成(2 β _r+3)个条带状干扰目标。设SAR距离向分辨率为 δR，当干扰条带间距∆ R> δR时，各干扰条带等间距平行排列；当干扰条带间距∆ R≤ δR时，SAR成像时相邻干扰条带相互重叠，将对SAR形成面状的遮盖干扰效果，且遮盖面积为

$ S=(2{{\beta }_{\text{r}}}+3)\Delta R\cdot \delta x $

(20)

对干扰信号进行2维匹配滤波时，干扰站运动导致多普勒参数与方位向滤波器失配，余弦调相导致各干扰目标部分频谱落在距离向匹配滤波器带宽之外，两者共同作用将使得干扰目标匹配输出的主瓣展宽、峰值下降，距离向第 n阶干扰条带输出的峰值幅度为

$ G(n)={{A}_{\text{r}}}{{J}_{\text{\emph n}}}({{\beta }_{\text{r}}})(1-\left| \frac{n{{f}_{\text{r}}}}{{{B}_{\text{r}}}} \right|)(1-\left| \frac{{{t}_{\text{am}}}}{{{T}_{\text{L}}}} \right|) $

(21)

由式(20)、(21)可知，遮盖面积与余弦调相信号的调制指数 β _r和调制频率 f _r以及干扰站运动产生的展宽量 δx成正比；干扰目标的峰值幅度与调制指数 β _r、调制频率 f _r以及干扰站运动速度成反比，根据能量守恒定律，遮盖面积越大，则干扰目标幅度越小，因此，实际干扰中可对干扰站运动速度以及余弦调相参数进行灵活控制，从而对遮盖面积和干扰强度进行折中或择优。

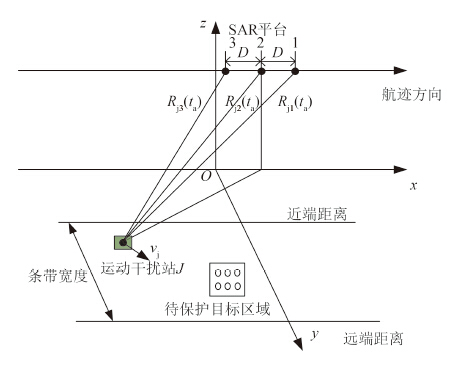
基于运动干扰站的余弦调相转发干扰可对SAR形成2维条带状或面状遮盖干扰效果，但对于SAR-GMTI而言，通过对杂波和干扰的抑制、对消来实现动目标检测和成像，本文方法对SAR-GMTI是否具有干扰效果，具体的干扰效果和对抗性能如何是亟待研究的问题。GMTI按实现方式的不同可分为两类，一是单通道GMTI，该方式对硬件的需求较低，实现简单，运算量小，但是对慢速目标和弱目标的检测性能较差；二是多通道GMTI，该方式通过增加SAR系统的空间维信息对杂波和干扰进行抑制和对消，可在较低信噪比条件下对慢速目标和弱目标实施快速检测，主要包括DPCA、ATI、STAP等，这里以典型的三通道干涉对消技术为例分析本文方法对SAR-GMTI系统的干扰效果和对抗性能( 张焕胜，2006)，其几何模型如 图2所示。

3个通道的子孔径天线以等间隔 D沿航迹排列，采用一发三收工作模式，即孔径2发射SAR信号，3个孔径同时接收回波信号。忽略干扰机转发延迟影响，由图2可知，干扰信号到3个通道的距离传播路程分别为 ${{R}_{J1}}({{t}_{\text{a}}})=({{R}_{\text{j2}}}({{t}_{\text{a}}})+{{R}_{\text{j1}}}({{t}_{\text{a}}}))$ 、 ${{R}_{J2}}({{t}_{\text{a}}})=2{{R}_{\text{j2}}}({{t}_{\text{a}}})$ ， ${{R}_{J3}}({{t}_{\text{a}}})=({{R}_{\text{j2}}}({{t}_{\text{a}}})+{{R}_{\text{j3}}}({{t}_{\text{a}}}))$ ，则对3个通道的干扰信号进行距离向匹配滤波可得

$ \left\{ \begin{aligned} & {{j}_{\text{r}1}}({{t}_{\text{r}}},{{t}_{\text{a}}})\approx {{j}_{\text{r}2}}({{t}_{\text{r}}},{{t}_{\text{a}}})\cdot \exp \left[ - j \frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }(\frac{{{D}^{2}}-2D{{x}_{0}}}{2{{R}_{\text{j}0}}}+\frac{Dv{{t}_{\text{a}}}}{{{R}_{\text{j}0}}}) \right] \\ & {{j}_{\text{r}2}}({{t}_{\text{r}}},{{t}_{\text{a}}})={{A}_{\text{r}}}\sum\limits_{n=-\infty }^{+\infty }{{{J}_{n}}({{\beta }_{r}})}\left( 1-\frac{\left| t_{\text{r}2}^{*} \right|}{{{T}_{\text{p}}}} \right)\cdot \\ & \ \ \ {\mathop{\rm sinc}\nolimits} \left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{r}}}(t_{\text{r}2}^{*}+\frac{n{{f}_{\text{r}}}}{{{u}_{\text{r}}}})({{T}_{\text{p}}}-\left| t_{\text{r}2}^{*} \right|) \right)\cdot \exp \left[ - \text{j}\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }{{R}_{J2}}({{t}_{\text{a}}}) \right] \\ & {{j}_{\text{r}3}}({{t}_{\text{r}}},{{t}_{\text{a}}})\approx {{j}_{\text{r}2}}({{t}_{\text{r}}},{{t}_{\text{a}}})\cdot \exp \left[ \text{-j}\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }(\frac{{{D}^{2}}+2D{{x}_{\text{t}}}}{2{{R}_{\text{t}0}}}-\frac{Dv{{t}_{\text{a}}}}{{{R}_{\text{t}0}}}) \right] \\ \end{aligned} \right. $

(22)

由于 R _J1≈ R _J2≈ R _J3，可忽略接收通道位置差异对距离向成像的影响，故认为距离徙动矫正后回波到达时间 t _r1 ^*≈ t _r2 ^*≈ t _r3 ^*≈ t _r ^*。在进行匹配方位向滤波之前，以通道2为参考，对通道1和3进行多普勒中心频率偏差补偿，可得方位向匹配滤波的输出包络为

$ \left\{ \begin{aligned} & {{y}_{\text{j}1}}({{t}_{\text{r}}},{{t}_{\text{a}}})={{y}_{\text{j}2}}\cdot \exp \left[- \text{j}\frac{2\text{ }\!\!\pi\!\!\text{ }}{\lambda }(\frac{{{D}^{2}}-2D{{x}_{0}}}{2{{R}_{\rm j0}}}) \right] \\ & {{y}_{\text{j}2}}({{t}_{\text{r}}},{{t}_{\text{a}}})={{A}_{\text{r}}}\sum\limits_{n=-\infty }^{+\infty }{{{J}_{n}}({{\beta }_{\text{r}}})}\left( 1-\frac{\left| t_{\text{r}}^{*} \right|}{{{T}_{\text{p}}}} \right)\cdot \left( 1-\frac{\left| t_{\text{a}}^{*} \right|}{{{T}_{\text{L}}}} \right)\cdot \\ & {\mathop{\rm sinc}\nolimits} \left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{r}}}(t_{\text{r}}^{*}+\frac{n{{f}_{\text{r}}}}{{{u}_{\text{r}}}})({{T}_{\text{p}}}-\left| t_{\text{r}}^{*} \right|) \right)\cdot {\mathop{\rm sinc}\nolimits} \left( \text{ }\!\!\pi\!\!\text{ }{{u}_{\text{a}}}t_{\text{a}}^{*}({{T}_{\text{L}}}-\left| t_{\text{a}}^{*} \right|) \right) \\ & {{y}_{\text{j}3}}({{t}_{\text{r}}},{{t}_{\text{a}}})={{y}_{\text{j}2}}\cdot \exp \left[- \text{j}\frac{\text{ }\!\!\pi\!\!\text{ }}{\lambda }(\frac{{{D}^{2}}+2D{{x}_{0}}}{{{R}_{\text{j}0}}}) \right] \\ \end{aligned} \right. $

(23)

由式(23)可知，通道2的匹配滤波结果与式(18)一致，但由于各接收通道存在沿航迹方向的位置偏差，在进行杂波对消之前，必须补偿由位置偏差引起的相位偏差，相应的补偿函数为

$ \left\{ \begin{array}{l} {C_{12}}({t_{\rm{a}}}) = \exp \left[ {{\rm{j\pi }}D(D - 2v{t_{\rm{a}}})/\lambda {R_{{\rm{j}}0}}} \right]\\ {C_{23}}({t_{\rm{a}}}) = \exp \left[ {{\rm{j\pi }}D(D + 2v{t_{\rm{a}}})/\lambda {R_{{\rm{j}}0}}} \right] \end{array} \right. $

(24)

利用式(24)进行相位误差补偿，并进行杂波对消可得

$ \left\{ \begin{array}{l} {y_{_{12}}}({t_{\rm{r}}},{t_{\rm{a}}}) = {y_{{\rm{j}}1}}({t_{\rm{r}}},{t_{\rm{a}}}){C_{12}} - {y_{{\rm{j}}2}}({t_{\rm{r}}},{t_{\rm{a}}}){\kern 1pt} \\ {\kern 1pt} \;\;\;\;\;\;\;\;\;\;\;\; = {y_{{\rm{j}}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \cdot \left[ {\exp \left( {{\rm{j}}\frac{{2{\pi}{D_{\rm{a}}}v}}{{\lambda {R_{{\rm{j}}0}}}}(\frac{{{x_0}}}{v} - {t_{\rm{a}}})} \right) - 1} \right]\\ {y_{_{23}}}({t_{\rm{r}}},{t_{\rm{a}}}) = {y_{{\rm{j}}2}}({t_{\rm{r}}},{t_{\rm{a}}}) - {y_{{\rm{j}}3}}({t_{\rm{r}}},{t_{\rm{a}}}){C_{23}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {y_{{\rm{j}}2}}({t_{\rm{r}}},{t_{\rm{a}}}) \cdot \left[ {1 - \exp \left( {{\rm{j}}\frac{{2{\pi}{D_{\rm{a}}}v}}{{\lambda {R_{\rm j0}}}}({t_{\rm{a}}} - \frac{{{x_0}}}{v})} \right)} \right] \end{array} \right. $

(25)

对上式取模可得

$ \begin{aligned} \left| {{y_{_{12}}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| = & \left| {{y_{_{23}}}({t_{\rm{r}}},{t_{\rm{a}}})} \right|{\kern 1pt} {\kern 1pt} {\kern 1pt} \\ = & 2\left| {{y_{{\rm{j}}2}}({t_{\rm{r}}},{t_{\rm{a}}})} \right| \cdot \left| {\sin \left( {\frac{{{\pi}Dv}}{{\lambda {R_{{\rm{j}}0}}}}({t_{\rm{a}}} - \frac{{{x_0}}}{v})} \right){\kern 1pt} {\kern 1pt} } \right|{\kern 1pt} {\kern 1pt} \end{aligned} $

(26)

对比式(18)、(26)可知，SAR-GMTI杂波对消后干扰信号输出幅度是对原来SAR干扰信号输出幅度的正弦调制，调制系数 $\rho = \left| {2\sin \left( {{\pi}Dv({t_{\rm{a}}} - {x_0}/v)/\lambda {R_{{\rm{j}}0}}} \right)} \right|{\kern 1pt} $ ，当方位向取得峰值即 t _a ^*=0时，对于静止杂波或固定干扰站而言 t _a= t _am= x ₀/ v，此时正弦调制系数 ρ=0，成像输出为零，可见三通道SAR-GMTI对杂波或固定干扰具有良好的对消性能。对于运动干扰站转发的余弦调相干扰信号而言，当方位向取得峰值时 t _a= t _am，由式(8)可得正弦调制系数为 $\rho = \left| {2\sin \left( {\pi D} \right.} \right.$ $\left. {\left. {({x_0}{v_{\rm{x}}} + {y_0}{v_{\rm{y}}} + (v_{\rm{x}}^2 + v_{\rm{y}}^2 - 2{v_{\rm{x}}}v){\tau ^*})/v\lambda {R_{{\rm{j}}0}}} \right)} \right|$ ，可见，对消后干扰目标能量与干扰站运动速度有关，通常情况下关于 τ ^*的一次项对能量的影响较小，且 x ₀· y ₀，故可认为对消后干扰目标能量主要取决于v_y。若ρ<1，干扰信号能量被削弱，且当ρ≈0，即${v_{\rm{y}}} \approx kv\lambda {R_{{\rm{j}}0}}/D{y_0}{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} (k \in Z)$ 时，对消后干扰目标幅度约为零；若 ρ>1，干扰信号能量得到增强，且当 ρ≈2，即 ${v_{\rm{y}}} \approx (k + 1/2)v\lambda {R_{{\rm{j}}0}}/D{y_0}{\kern 1pt} {\kern 1pt} $ 时，对消后干扰目标幅度最大增强为原来的两倍。综合以上分析可知，本文干扰方法对SAR和SAR-GMTI均能够形成2维条带状或面状干扰效果，干扰目标位置、距离向间隔、方位向展宽等干扰指标基本相同，两者的干扰效果主要区别在于假目标能量的对消情况，由于SAR-GMTI对干扰信号的对消处理，干扰目标幅度受正弦调制系数影响将出现增强或削弱。

三通道SAR-GMTI及干扰参数如表1所示，SAR成像场景距离向范围为[9800，10200](单位/m)，方位向范围为[-150，150]，场景中心坐标为[10000，0](斜距-方位坐标)，运动干扰站初始位置位于场景中心。

图3为不同速度情况下运动干扰站转发式干扰在通道2的成像结果， 图3(a)干扰站运动速度 v _x =5 m/s、 v _y =1 m/s，运动干扰站相对静止干扰站可沿SAR方位向形成条带状干扰目标，干扰目标方位向中心位置偏移量约为-43 m，展宽量约为15 m； 图3(a)干扰站运动速度 v _x =10 m/s、 v _y =-1.5 m/s，此时条带状干扰目标方位向中心位置偏移量约为65 m，展宽量约为30 m，两种情况下运动干扰站成像特性均与理论分析一致。

采用余弦调相对干扰条带进行距离向扩展，干扰站运动速度与 图3(b)相同，图4为不同余弦调相参数情况下运动干扰站的干扰成像结果， 图4(a)余弦调相参数 β_r=2、f_r=0.3 MHz，依据余弦调相信号性质，干扰信号在SAR距离向共形成7个干扰条带，各干扰条带距离向间隔为9 m，方位向中心位置和展宽量与 图3(b)相同，但干扰强度受贝塞尔函数和频谱失配的调制，导致各干扰条带的亮度和长度有所不同；图4(b)余弦调相参数 β_r=2、f_r=0.1 MHz，各干扰条带距离向间隔为3 m，且由于条带间隔与SAR分辨率相近，导致相邻干扰条带相互重叠，将形成面状的遮盖干扰效果，遮盖面积约为600 m²。

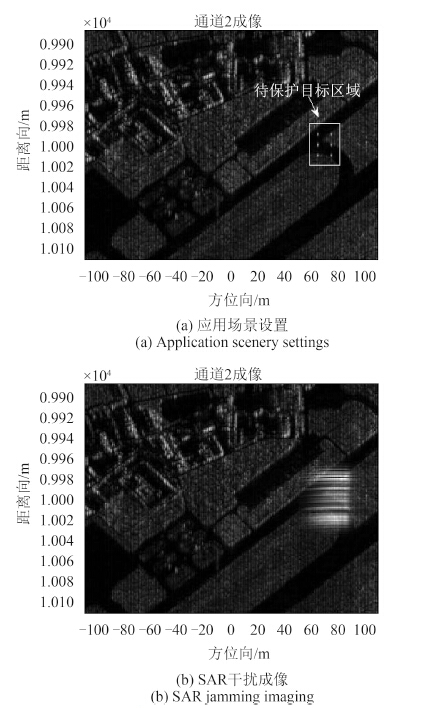
SAR成像场景如 图5(a)所示，矩形框为待保护的目标区域，包含6个强散射目标(如坦克、装甲车等)，通过运动干扰站对目标区域中静止或运动目标提供干扰保护。假设干扰站初始位置仍位于场景中心，待保护区域面积大小以及相对干扰机的位置是已知的，干扰站接收到雷达信号并侦测到SAR平台速度、分辨率等信息，则依据式(10)、(20)估算出干扰站所需速度v_x=15 m/s、v_y= -1.7 m/s，余弦调相参数β_r=8、 f_r=0.1 MHz。运动干扰站接收到SAR信号后进行余弦调相转发，图5(b)为相应的SAR干扰成像结果。在干扰过程中，干扰站的持续运动将导致所形成的干扰区域位置相对待保护区域不断发生运动，为避免干扰区域偏离出待保护区域，必须依据干扰站的运动特性对其运动速度进行控制，以确保干扰区域始终遮盖在被保护区域之上，其中，方位向速度主要对干扰目标展宽量产生影响，由待保护区域的宽度决定，无需进行实时改变；距离向速度决定了干扰目标方位向位置，图5(b)中干扰站的运动将导致干扰区域位置在单位时间内方位向偏移15 m，距离向偏移1.7 m，此时距离向偏移量相对干扰区域可忽略，因而主要通过控制干扰站距离向速度对干扰区域方位向位置偏移进行补偿，忽略微小加速度对运动干扰站成像特性的影响(吴晓芳 等，2012b)，可得干扰站距离向平均加速度为0.35 m/s²，从而可保证待保护区域始终在干扰区域范围内。可见，本文方法可对待保护区域提供有效遮盖性干扰，且通过灵活控制干扰站速度和余弦调相参数，可对SAR产生位置和面积可控的遮盖性干扰。

需要指出的是，当待保护区域内的目标编队运动时，运动干扰站应配置在编队中对目标进行随队保护，此时干扰站应与被保护目标保持一致的速度和运动轨迹，从而保证干扰站和运动目标具有相同运动特性，此时所形成的干扰区域能够对运动目标成像区域进行有效遮盖，且可通过多部运动干扰站的协同工作有效扩大干扰区域的范围和强度。

依据三通道SAR-GMTI干涉对消原理对 图5(b)干扰成像进行对消处理， 图6(a)为通道1和2的SAR-GMTI对消成像结果(通道2和3的对消结果相同)，从对消结果可以看出，三通道SAR-GMTI对背景杂波具有良好的对消性能，而干扰信号未能对消，依据式(26)可得对消后干扰目标幅度的正弦调制系数ρ≈1.5，因而SAR-GMTI对消后的干扰信号强度相对SAR有所增强。为验证三通道SAR-GMTI对干扰信号的对消特性，干扰站距离向速度变为v_y= -0.5 m/s，其他干扰参数不变，此时正弦调制系数ρ≈0.4，对消后干扰目标强度被削弱，图(6)为两种情况下干扰对消后的对比结果，因而实际干扰中，应合理控制干扰站距离向速度，以避免对消后干扰目标强度被严重削弱。以上仿真只考虑了干扰目标方位向中心位置偏移的情况，当干扰站相对保护区域中心位置在方位向和距离向都存在偏移时，可通过干扰站转发延时或移频干扰实现距离向中心位置偏移。

通过上述分析可知，本文干扰方法对SAR以及多通道SAR-GMTI均具有干扰效果，可对保护区域内静止或运动目标同时提供遮盖性干扰，且干扰效果取决于干扰站运动速度以及余弦调相参数，其中，干扰站距离向速度决定了干扰目标方位向中心位置的偏移以及GMTI对消后的干扰目标强度，方位向速度、余弦调相指数、以及调制频率共同影响遮盖面积大小。

SAR-GMTI干扰技术研究是电子对抗领域的热点和难点问题，运动干扰站转发式干扰可产生方位向位置和展宽长度灵活可控的条带状干扰目标，距离向余弦调相可对干扰信号频谱进行多次复制、搬移，本文将两者巧妙结合，针对多通道SAR-GMTI提出基于运动干扰站的余弦调相转发干扰，研究结果表明：该方法对SAR和SAR-GMTI均可产生灵活可控的2维条带状或面状干扰目标，但由于多通道GMTI对干扰的抑制和对消，干扰目标幅度受正弦调制系数影响将出现增强或削弱。本文干扰方法实现简单、灵活可控，与欺骗式干扰相比对侦察的依赖度较低，与传统压制干扰相比，干扰信号能够获得部分2维相干处理增益，因而对干扰功率的要求较低，既能够保护地面静止目标，又能够对运动目标提供实时的随队干扰，具有重要的军事应用价值。