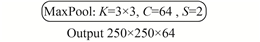| 深度神经网络条件随机场高分辨率遥感图像建筑物分割 |
收稿日期: 2018-03-27
2. Field Scientific Observation and Research Base of Ministry of Land and Resources, Henan Polytechnic University, Jiaozuo 454000, China
3. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China
4. School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China
5. School of Computer Science, Shenyang Aerospace University, Shenyang 110136, China
高分辨率遥感图像是重要的国土信息资源。对高分辨率遥感图像中的建筑物实现自动识别和分割,在土地资源勘查、土地利用规划、地质灾害监控,以及国防安全等方面具有重要意义。
遥感图像目标分割的实质是建立图像到分割目标之间的映射模型。通常,该过程包含特征提取和建模两个部分。其中,特征提取是从输入图像中选出有效的特征,构成特征空间;而建模过程则是在特征空间的基础上,通过人工或者机器学习的方法建立图像到分割目标之间的映射模型。因此,如何构建分割模型的特征空间,进而采用有效的方法建立分割模型,是实现遥感图像目标高精度分割的关键。
传统的遥感图像分割方法,以灰度值、梯度、纹理信息等图像特征为基础,采用人工或机器学习建立从特征空间到分割目标之间的映射模型。如主动轮廓模型ACM(Active Contour Model)所需的图像特征是区域灰度值或信息熵(王宇 等,2018);统计区域融合SRM(Statistical Region Merging)的图像特征来自于区域的同质性信息(张建龙和王斌,2017);分水岭算法则采用区域内的像素灰度值建立集水盆函数(陈杰 等,2011)。上述几类图像分割方法从特征提取到模型建立都是通过人工完成。为此,神经网络(周东国 等,2014)、支持向量机(王玉 等,2018)等机器学习方法被用来建立特征空间到分割目标之间的映射模型。这类方法以手动提取的特征为基础,通过样本训练自动建立特征与分割目标之间的映射关系。
由于地物的种类和分布状态十分复杂,从图像到分割目标的真实映射模型常常表现为高维、强耦合、强非线性,如果特征空间的维度较低,则无法有效描述高分辨率遥感图像中目标的特性。传统的遥感图像分割方法无法获得有效的高维特征变量。人工方法和早期的机器学习方法建立的模型,难以精确逼近真实映射模型的强耦合性和强非线性,从而导致算法的泛化能力不强,目标分割精度不高,甚至分割失效。
近年来,深度神经网络因为能自动提取特征,并通过大量样本的训练,建立从输入到输出的高维强非线性模型,实现了端对端(End-to-End)的分类或预测,在图像分割领域取得了丰硕的成果(Chen 等,2014)。
2015年,Long Jonathan首次提出全卷积神经网络图像语义分割架构(Shelhamer 等,2017),该架构采用VGG(Simonyan和Zisserman,2014)作为基础网络,通过FCN(Fully Convolutional Netwoks)和反卷积Deconvolution实现图像的语义分割。同样,(Badrinarayanan 等,2017)采用VGG作为基础网络,但在目标特征提取和分割复原时采用了Encoder-Decoder架构。除了VGG以外,常用的基础网络还包括ResNet网络(He 等,2015)、Inception网络(Glorot 等,2011;Xu 等,2016)等。语义分割的框架还包括U-net结构(Ronneberger 等,2015)和DeconvNet结构(Noh 等,2015)。
在遥感图像分割领域,深度神经网络的研究和应用也越来越广泛。Wang等(2017)将全卷积神经网络应用于高分三号遥感图像和H-A-α极化分解,完成了水域、植被和建筑物的分类识别。Alshehhi等(2017)提出一种single patch-based卷积神经网络结构,可从遥感图像中提取道路和建筑物的特征,从而实现对两者的分割。Lin等(2017)将全卷积神经网络应用于近海岸线的舰船检测。Jiao等(2017)针对高光谱遥感图像分割问题,提出一种深度全卷积神经网络的多尺度空间—频谱特征提取方法,实现了特征的自动提取和目标分割。
在图像的语义分割中,深度神经网络所提取的特征信息主要来自于当前像素点及其邻域。然而,在遥感图像中,往往存在多个建筑物,且可能随机分布在图像上的任意位置。理论上,这些建筑物对应的像素点应该具有相同的映射关系。因此,在建立分割模型时,仅考虑邻域内的信息并不完整。如果将深度神经网络提取特征的范围扩展至非邻域建筑物所对应的图像区域,则有可能提升建筑物的分割精度。
条件随机场CRF(Conditional Random Field)表示在给定一组输入随机变量的条件下,另一组输出随机变量的条件概率分布(Liu 等,2005;Chatzis 等,2013)。将条件随机场应用于图像语义分割时,当前像素点的分类概率由一元势函数和成对势函数两个部分决定。其中,一元势函数通过当前像素点自身的信息决定其分类的概率;成对势函数则是通过当前像素点与其他像素点之间的关联关系,来决定其分类的概率。
将条件随机场引入深度神经网络中,通过条件随机场的成对势函数将当前像素点的非邻域图像信息纳入到目标特征提取的范围,是提高目标分割精度的有效途径。Krähenbühl和Koltun(2012)和Chen等(2017)将深度神经网络的分割结果作为条件随机场的一元势函数的值,实现了深度神经网络和条件随机场的有效结合,提高了分割精度。Zheng等(2015)将条件随机场转换为RNN(Recurrent Neural Networks),使条件随机场和神经网络有机融合,并实现了参数的同步训练。
深度神经网络是人工智能中连接主义Connectionism的一种(沈家煊,2004)。如果从概率模型出发,图像的语义分割可看作是条件随机场意义下的概率分布模型。受到Krähenbühl和Koltun(2012)和Zheng等(2015)的启发,为进一步提升高分辨率遥感图像中建筑物的分割精度,本文将条件随机场与深度残差网络(ResNet)有机结合,构建Encoder-Decoder遥感图像建筑物特征提取与分割复原的架构,以逼近遥感图像中建筑物的真实分割模型,实现建筑物的精确分割。
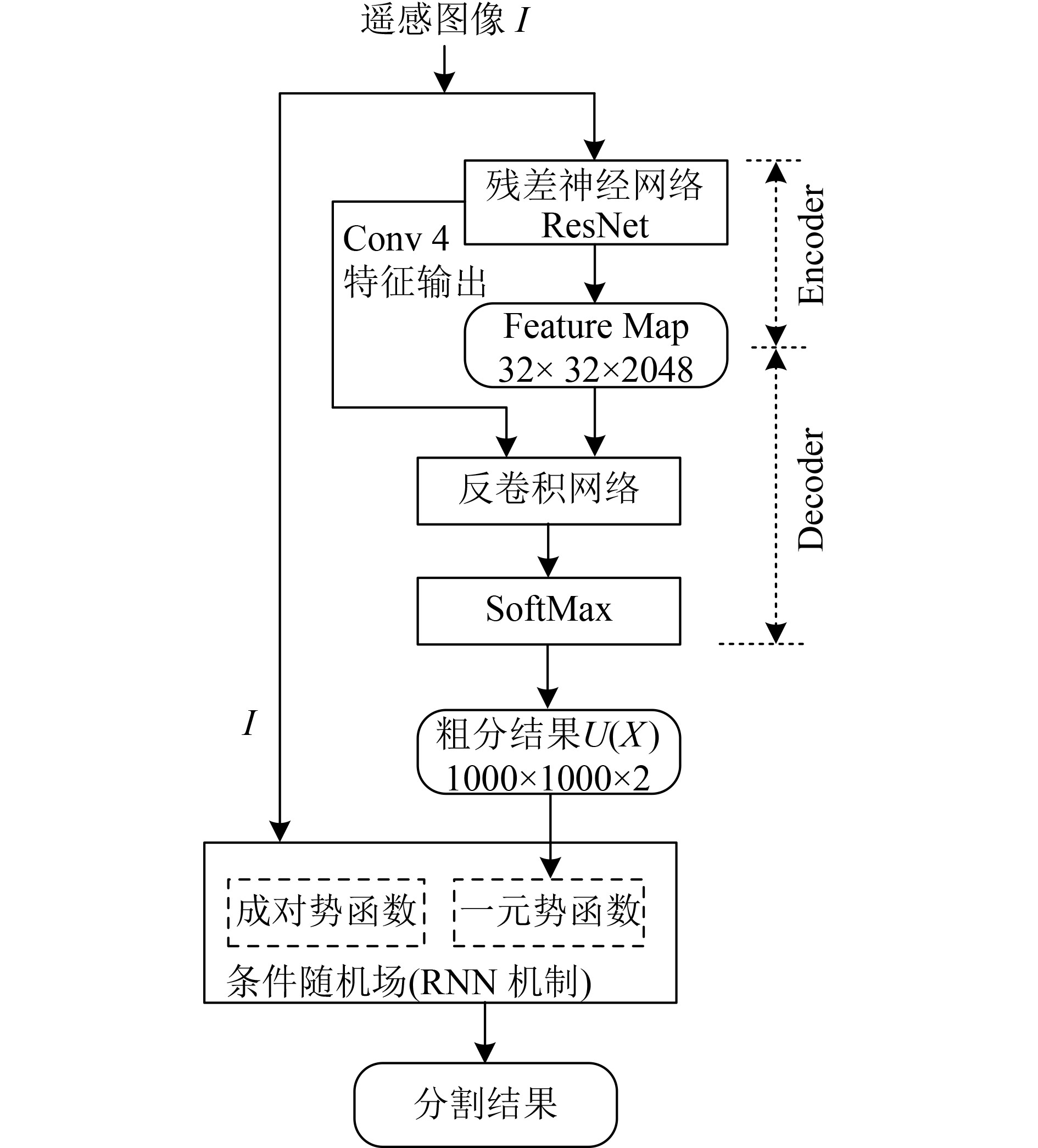
2、ResNet网络Encoder-Decoder图像分割框架本文提出的高分辨率遥感图像建筑物分割算法的整体架构如图1所示。遥感图像I首先通过深度残差网络自动提取建筑物的特征图(Feature Map),从而实现Encoder的编码功能。然后通过反卷积网络,实现对特征图的上采样,完成Decoder的解码功能;同时将输出结果的尺寸还原到原始图像大小,得到粗分割结果
|
| 图 1 遥感图像建筑物分割算法整体架构 Figure 1 Framework of building segmentation in remote sensing image |
在遥感图像建筑物分割中,Encoder的主要作用是通过建立输入图像和输出特征之间的映射关系
|
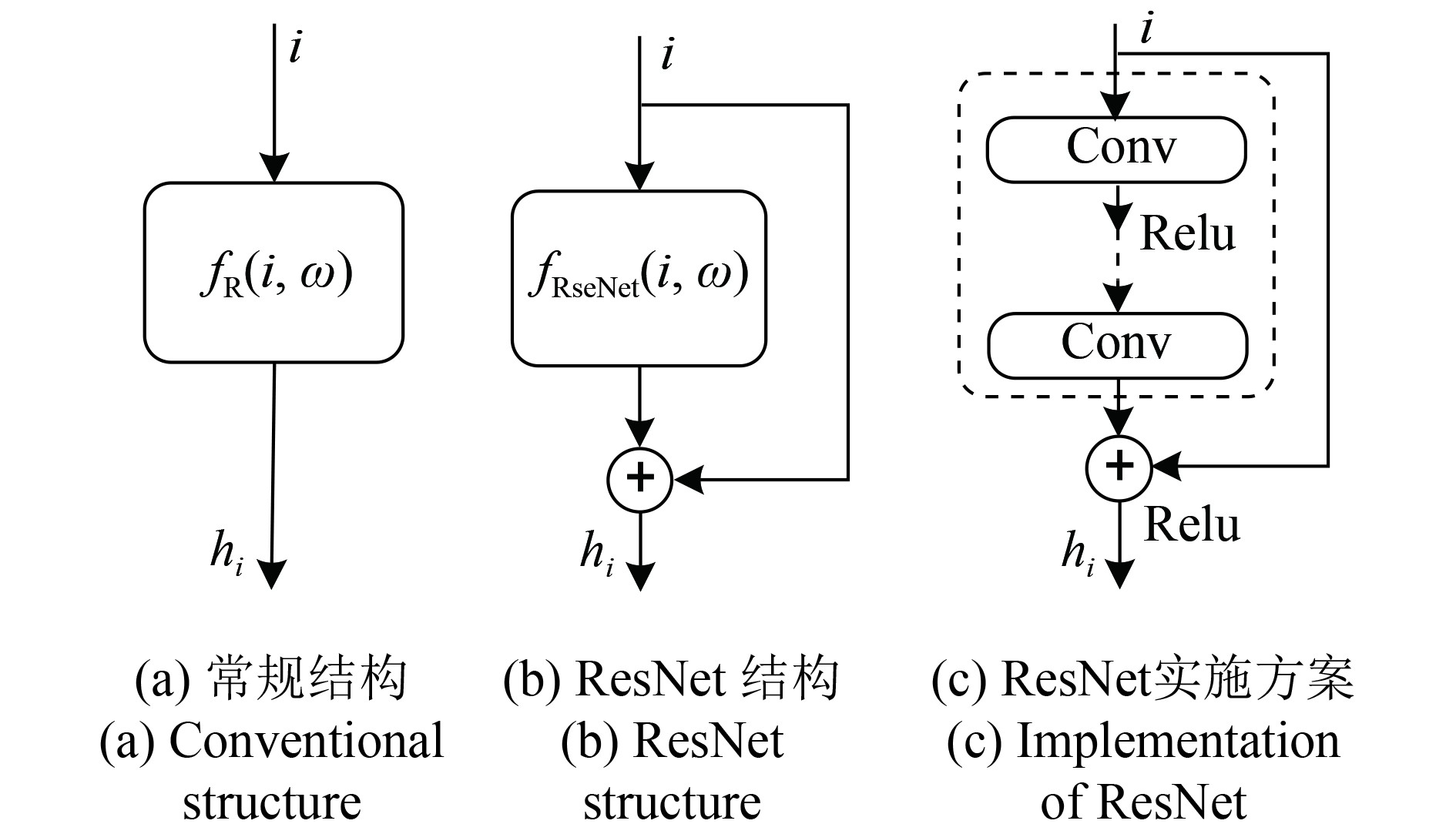
| 图 2 ResNet结构 Figure 2 ResNet structure |
在图2(a)所示的常规结构中,神经网络实现的是从输入i到输出hi的映射关系
Encoder在算法中的逻辑关系如图1所示,实施方案如表1所示。其中,K表示卷积核的尺寸、C表示卷积核的通道数量、S表示步长、BN表示批量规范化操作、Relu表示Relu激活操作、MaxPool表示最大池化操作、AveragePool表示平均池化操作(Glorot 等,2011)。
|
|
表 1 ResNet的Encoder结构 Table 1 Encoder structure by ResNet |
在Encoder结构中,共分为5类卷积和2类池化。其中,Conv2至Conv5的每一个子层都包含3个卷积层和1个前馈通道。Conv1、Conv3、Conv4和Conv5这4个子层中都包含一个步长S=2的卷积操作,再加上Pool 1中的步长S=2,这使得输出特征图的尺寸缩小为输入图像的1/32。Pool 2是均值池化操作。
(1)ResNet的卷积层数及前馈通道实现方法。ResNet的前馈通道中所包含的卷积层数可以根据需要设置。本文采用经典的设置值,在前馈通道中包含2个卷积层,卷积核大小都为3×3。为了降低计算量,将这两个卷积层转换成卷积核大小分别为1×1、3×3和1×1的3个卷积层,同时通过增加卷积核的数量来确保精度(He 等,2015)。
ResNet的前馈通道通过卷积核为1×1的卷积操作来实现;同时通过设置卷积核的数量,来匹配输入和输出的通道数量。
(2)批量规范化(Batch normalization)。数据在神经网络中逐层传递,通过卷积操作不断提取数据的特征值。然而,卷积操作必然使得输入和输出的数据分布发生变化,且这种变化随着卷积层数的增加而加大。这不断加剧了深度神经网络训练过程中的梯度竞争,从而导致网络训练更加困难。为此,本文采用Ioffe和Szegedy(2015)提出的批量规范化技术,在每个卷积层输入前,将数据都转化成为均值为0、方差为1的规范形式,从而使得每次权重值的更新步调保持一致,大幅降低了深度神经网络的训练难度。
(3)单步均值池化。本文实验中所采用的遥感图像为1000×1000×3,其中1000×1000表示像素点,3表示通道数量。Encoder获取较为稠密的输出特征图,为后续Decoder提供更多的可选特征,是建筑物语义分割的关键点之一。
在分割算法实验过程中,通过参数设置,先后选取了8×8×1024、16×16×1024、32×32×1024、32×32×2048等一系列特征图的输出规格,实验对分割结果的影响。实验发现在32×32×2048特征图上采用反卷积,可以对样本库中的各类建筑物实现分割。
Pool2是均值池化操作,其步长直接影响特征图输出的规格。在上述实验基础上,本文采用2×2的均值池化,并设置步长S=1,构成单步均值池化操作,该操作的实质是2×2的均值滤波。单步均值池化操作不降低Conv5提取的32×32×2048特征图的稠密度,可以为后续的Decoder提供更多的可选特征。此外,均值滤波有可能消除特征图中噪点的影响。
(2.2) Decoder实现Decoder的主要功能是对Encoder提取的特征进行解码,并输出建筑物的初步分割结果。
Badrinarayanan等(2017)提出的Encoder-Decoder结构,是在特征提取过程中记录每次池化的输出结果,并在Decoder中顺次引入,取得了较好的分割效果。根据该思想,针对本文的Encoder结构特点,可以在提取特征时存储每个子层的输出数据,并将其顺次引入到Decoder中,用于特征图解码。然而,这必然大幅增加存储量和计算量。当输入图像为1000×1000×3,且每次只输入一个训练样本,若以float数据类型存储Cov1至Conv5的输出结果,则需要额外增加280 MB左右的存储开销。此外,每一个子层的特征数据都是通过1×1的卷积操作引入Decoder的,这必然会有新的权重需要存储和训练。以引入Conv3的输出到Decoder为例,卷积核的规格为[1,1,512,2],则会增加1024个权重需要存储和训练。
若按照Badrinarayanan等(2017)的Decoder构建方式,将Encoder中所有卷积层和池化层的输出结果引入到Decoder中,对于提升建筑物的分割精度会有帮助。但是受到实验平台的硬件限制,为了降低存储量和计算量,本文中Decoder的信息只选用了Encoder的输出特征和Conv4的输出结果,并通过两次反卷积对特征图进行解码,完成建筑物的分割。
卷积操作本质上是对输入图像
Decoder在算法中的逻辑关系如图1所示,其具体的实施方案如图3所示。

|
| 图 3 Decoder的反卷积实现过程 Figure 3 Deconvolution for Decoder |
首先对Encoder输出的特征图进行反卷积,其输出通道数量为2,对应于分割的种类;输出的尺寸与Conv4的输出尺寸相同,以便与Conv4的信息相融合。Conv4的输出特征通过卷积操作引入到Decoder中,其卷积核的规格为[1,1,1024,2]。融合两次操作的结果,进行第二次反卷积操作,其输出尺寸与输入图像的尺寸相同,输出通道数量保持为2。最后通过SoftMax计算,得到建筑物分割的概率值。
3、全连接条件随机场 (3.1) 遥感图像建筑物分割的条件随机场表示形式将遥感图像
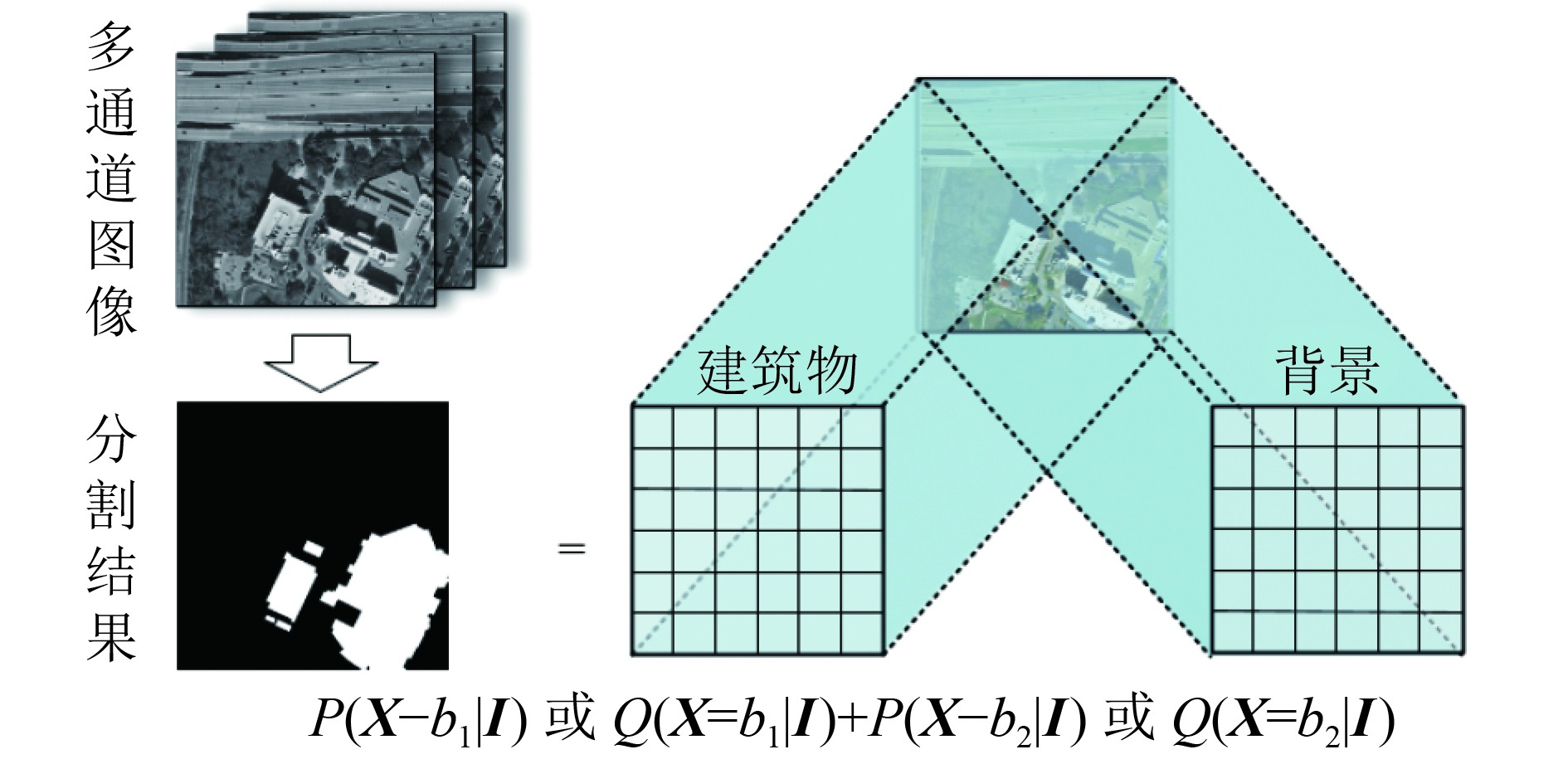
|
| 图 4 条件随机场建筑物分割示意图 Figure 4 Building segmentation by conditional random field |
根据Hammersly-Clifford定理(李航,2012),
| $P\left({{{X}}\left| {{I}} \right.} \right) = \frac{1}{{Z\left({{I}} \right)}}\prod\limits_\varOmega {{\psi _\varOmega }\left({{{{X}}_\varOmega }\left| {{I}} \right.} \right)} $ | (1) |
式中,
| $P\left({{{X}}\left| {{I}} \right.} \right) = \frac{1}{{Z\left({{I}} \right)}}\exp \left( { - {\rm{E}}\left({{{X}}\left| {{I}} \right.} \right)} \right)$ | (2) |
式中,
通常情况下,可将深度神经网络的粗分结果作为一元势函数
| ${\phi _2}\left({{x_i},{x_j}} \right) = \textit{λ} \left({{x_i},{x_j}} \right)\left({{\omega ^{\left(1 \right)}}f_{{\rm{pair}}}^{(1)}\left({{x_i},{x_j}} \right) + {\omega ^{\left(2 \right)}}f_{{\rm{pair}}}^{(2)}\left({{x_i},{x_j}} \right)} \right)$ | (3) |
式中,
要注意的是,式(3)中的权重
由于遥感图像的像素较多,而成对势函数需要计算所有像素对之间的关系,因此计算量巨大。根据Krähenbühl和Koltun(2012)和Zheng等(2015),可采用均值场(Mean field)
设一元势函数的估计值为
|
|
表 2 均值场算法 Table 2 Mean fields algorithm |
需要注意的是,在均值场算法中分类结果的相容性参数
分析均值场算法可知,
| $\begin{aligned} {{{\tilde{ Q}}}^{\left(m \right)}}\left({{b_{k'}}} \right) =& \displaystyle\sum\limits_j {f_{{\rm{pair}}}^{(m)}\left({{x_i},{x_j}} \right)} {{Q}}\left({{x_j} = {b_{k'}}\left| {{I}} \right.} \right) - {{Q}}\left({{x_i} = {b_{k'}}\left| {{I}} \right.} \right) \\ =& \displaystyle\sum\limits_j {f_{{\rm{pair}}}^{(1)}\left({{x_i},{x_j}} \right)} {{Q}}\left({{x_j} = {b_{k'}}\left| {{I}} \right.} \right) + \\ &\displaystyle\sum\limits_j {f_{{\rm{pair}}}^{(2)}\left({{x_i},{x_j}} \right)} {{Q}}\left({{x_j} = {b_{k'}}\left| {{I}} \right.} \right) - {{Q}}\left({{x_i} = {b_{k'}}\left| {{I}} \right.} \right) \\ = &{F_{\rm{1}}}{{*Q}}\left({{{X}} = {b_{k'}}\left| {{I}} \right.} \right) + {F_2}{{*Q}}\left({{{X}} = {b_{k'}}\left| {{I}} \right.} \right) - {{Q}}\\& \left({{x_i} = {b_{k'}}\left| {{I}} \right.} \right) \\ \end{aligned} $ | (4) |
式中,
均值场算法是通过迭代的方式求解
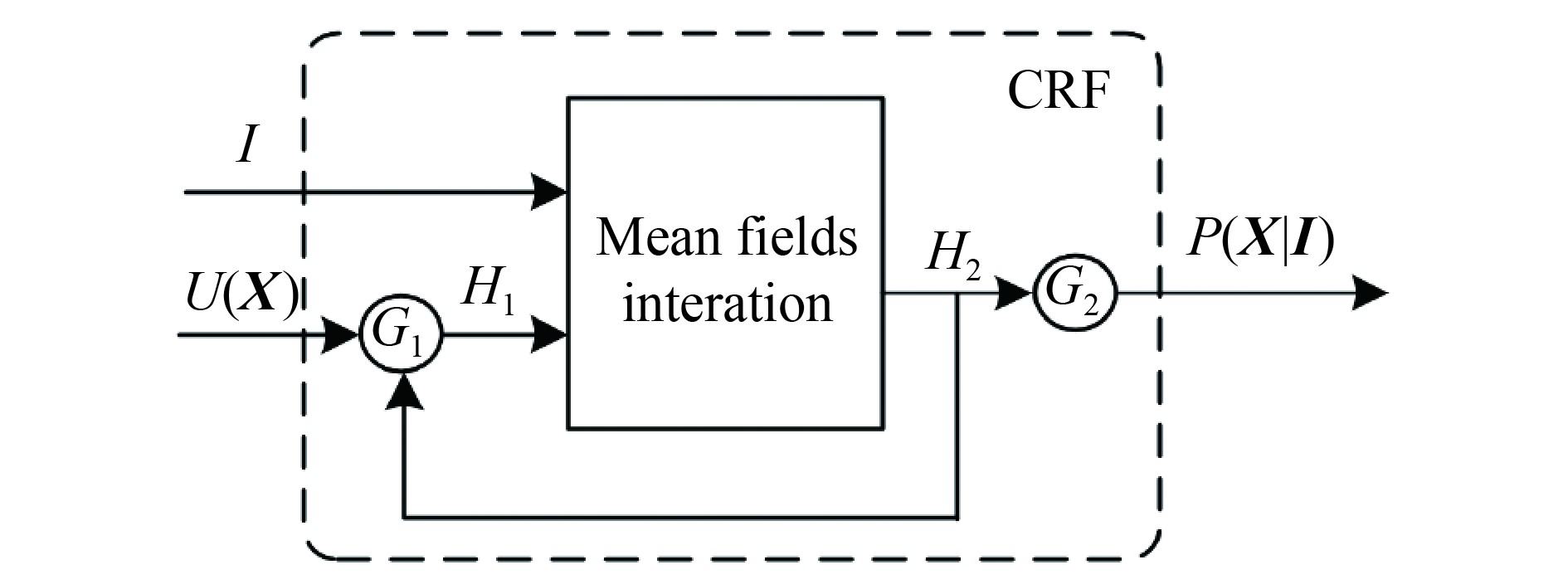
|
| 图 5 条件随机场的RNN实现机制 Figure 5 RNN mechanism of CRF |
图5中,
| ${H_1} = \left\{ {\begin{array}{*{20}{l}} {U\left( {{X}} \right),}&{{n_i} = 0}\\ {{H_{\rm{2}}}\left( {{n_i} - 1} \right),}&{{\rm{0 }}< {n_i} \leqslant MaxNum} \end{array}} \right.$ | (5) |
| $P\left( {{{X}}\left| {{I}} \right.} \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{{\rm{0 }} <{n_i} \leqslant MaxNum}\\ {{H_{\rm{2}}}\left( {{n_i}} \right),}&{{n_i} = MaxNum} \end{array}} \right.$ | (6) |
式中,
根据图5所示的RNN实现机制,条件随机场可以作为深度神经网络的一层,实现与Encoder-Decoder的有机融合,且参数
为了验证本文提出的建筑物分割算法的有效性,在IAILD(Inria Aerial Image Labeling Dataset)遥感图像数据库上展开实验研究。IAILD数据库包含810 km2的遥感图像,分辨率为0.3 m,其中405 km2已经对建筑物做过精确标记,包括美国的奥斯汀(Austin)、芝加哥(Chicago)和基特萨普(Kitsap),奥地利的蒂罗尔西部(Western Tyrol)和维也纳(Vienna)等5个地区,其建筑风格差异较大。原始数据中单个样本为5000×5000像素,共计180个(IAILD, 2016)。由于受实验平台GPU存储单元的限制,本文将每个样本裁剪成1000×1000像素大小,共计样本4500个;并将其中4480个作为训练样本,20个作为测试样本。此外,本文对未标注的奥地利蒂罗尔东部(Eastern Tyrol)、美国贝灵汉(Bellingham)、旧金山(San Francisco)和布鲁明顿(Bloomington)的部分遥感图像做了建筑物标注,用于测试算法的有效性。
实验平台采用Intel-i7-7700K四核CPU处理器、32G内存、ASUS STRIX-GTX1080TI-11G显卡(GPU处理单元);采用Google公司的Tensorflow1.2.1深度学习框架、Nvidia公司的CUDA8.0(Compute Unified Device Architecture)GPU运算平台以及cuDNN6.0深度学习GPU加速库。
(4.2) 分割性能评价指标为了量化评价建筑物的分割结果,采用召回率(Recall Rate)、精确率(Precision Rate)和F值(F-measure)来评价分割结果,其计算方法如下所示
| $\begin{split} & \displaystyle Recall = \frac{{{B_{{\rm{seg}}}}}}{{{B_{{\rm{seg}}}} + {I_{{\rm{unseg}}}}}} \\ & \displaystyle Precision = \frac{{{B_{{\rm{seg}}}}}}{{{B_{{\rm{seg}}}} + {I_{{\rm{wseg}}}}}} \\ & \displaystyle F - measure = \frac{{{\rm{2}}Recall \times Precision}}{{Recall{\rm{ + }}Precision}} \end{split} $ | (7) |
式中,
召回率表示被分割为建筑物的像素点与真实建筑物像素点的比率。表征在不考虑遥感图像背景的情况下,建筑物分割的准确度。
精确率表示被正确分割为建筑物的像素点与所有分割为建筑物的像素点的比率。精确率高表示能够将建筑物提取出来。
F值是综合召回率和精确率这两项指标的评估指标,是用于综合反映整体的指标。
(4.3) 对比实验结果分析针对IAILD数据库的不同城市,本文对几种应用于遥感图像目标分割的典型深度神经网络展开对比实验。采用的深度神经网络包括:VGG全卷积神经网络、ResNet Encoder-Decoder结构(Audebert 等,2018;Zhong 等,2018)全卷积神经网络、VGG条件随机场(Bittner 等,2017;Liu 等,2017),以及本文提出的ResNet条件随机场。4种网络结构的设置如下:
(1) VGG全卷积神经网络采用经典的结构(Shelhamer 等,2017),但其全卷积层F6、F7、F8的卷积核分别设置为[16,16,512,1024]、[1,1,1024,2048]、[1,1,2048,2],最后融合多层反卷积结果实现建筑物分割结果的输出。其中,前13层卷积核直接调用已经训练好的权重值。
(2) ResNet Encode-Decoder是以ResNet为基础网络构建的Encoder-Decoder结构,即为本文第2节所构建的深度神经网络结构。
(3) VGG条件随机场(VGGCRF)采用VGG全卷积神经网络与本文的第3节构建的条件随机场相结合,其中条件随机场参数设置为
(4) ResNet条件随机场(ResNetCRF)为本文第2节和第3节构建的神经网络结构的集成。CRF的参数设置主要是像素点的色彩信息和位置信息。通过实验,将条件随机场的参数设置为
在神经网络的参数训练过程中,优化目标设定为神经网络的输出与建筑物标签之间的交叉熵,被训参数的更新算法为随机梯度下降法。训练过程中4种神经网络交叉熵的均值变化过程如图6所示,4种深度神经网络的交叉熵均能逐渐收敛。

|
| 图 6 神经网络训练过程中交叉熵均值变化过程 Figure 6 Dynamic process of cross entropy mean during the neural network training |
由于本文的模型训练所采用的数据样本为美国的奥斯汀、芝加哥、基特萨普,奥地利的蒂罗尔西部、维也纳等5个地区,分割对比实验分为两步:(1)奥斯汀地区未参与训练的样本测试实验;(2)奥地利蒂罗尔东部、美国贝灵汉、旧金山测试样本实验。上述测试样本的像素值均为1000×1000。
由于奥斯汀地区的样本参与了深度神经网络的训练,可以认为其测试样本与训练样本满足同源性。而蒂罗尔东部、贝灵汉、旧金山地区的样本没有参与深度神经网络的训练,3个城市的建筑风格与训练样本中的城市不同,且成像时的纬度、光照条件差异较大,更能检验建筑物分割模型的有效性。
(1)奥斯汀地区测试样本分割实验。奥斯汀地区总共有20个测试样本,图7和图8是两种典型布局的建筑物分割结果。对应的建筑物分割性能指标如表3所示。

|
| 图 7 奥斯汀地区建筑物分割实验结果1 Figure 7 Building segmentation result 1 of Austin |

|
| 图 8 奥斯汀地区建筑物分割实验结果2 Figure 8 Building segmentation result 2 of Austin |
|
|
表 3 奥斯汀地区遥感图像建筑物分割性能指标 Table 3 Performance indexes of buildings segmentation in RSI of Austin |
实验结果表明,由于建筑物的顶部结构简单,受阴影的影响较小。VGG网络能较为准确地指示出建筑物的具体位置和大致轮廓,VGGCRF、ResNet、ResNetCRF都能较为精确地实现建筑物的分割。而VGGCRF和ResNetCRF引入了条件随机场,两者对图7中立交桥的抗干扰能力更强。但是分析图8中较小的建筑物分割细节可知,ResNetCRF对较小的建筑物分割效果有待提高,这也是导致表2中ResNetCRF的召回率不高的主要原因。
(2)蒂罗尔东部、贝灵汉、旧金山测试样本分割实验。选取的蒂罗尔东部地区的遥感图像分割结果如图9所示。遥感图像中林地较多,建筑物分布相对较少。选取的贝灵汉地区的遥感图像分割结果如图10所示。该区域位于海边,存在码头和大型船舶的干扰。选取的旧金山地区的遥感图像分割结果如图11所示,该区域的建筑物密度很高,且建筑物楼顶颜色和形状均有较大差异,不少建筑物存在复杂的错层,且阴影的影响十分明显。3个地区的建筑物分割性能指标如表4所示。

|
| 图 9 蒂罗尔东部地区建筑物分割实验结果 Figure 9 Building segmentation result of Eastern Tyrol |

|
| 图 10 贝灵汉地区建筑物分割实验结果 Figure 10 Building segmentation result of Bellingham |
|
|
表 4 遥感图像建筑物分割性能指标 Table 4 Performance indexes of buildings segmentation in RSI |

|
| 图 11 旧金山地区建筑物分割实验结果 Figure 11 Building segmentation result of San Francisco |
分析图9蒂罗尔东部地区建筑物的分割结果可知,VGG、ResNet和ResNetCRF的分割结果均能有效覆盖建筑物。但是VGG、ResNet将较多的背景误分为建筑物,而VGGCRF却对建筑物的召回率较低。比较四种深度神经网络,ResNetCRF对建筑物的召回率和精确度都较高,因此获得最高的F值。
图10所示贝灵汉地区建筑物的分割结果中,4种深度神经网络都存在将船舶误分为建筑物的现象,但是VGG和ResNet两种网络的误分更为严重;而VGGCRF对建筑物的召回能力不足。相对其他3种网络结构,ResNetCRF结构对船舶的误分较低,同时对建筑物的召回率、精确度和F值均相对较高。
分析图11所示的旧金山地区高密度复杂建筑物分割性能指标可知,VGGCRF和ResNet两种网络对建筑物的召回率较低;VGG和ResNetCRF对建筑物的召回率相对较高,且具有较高的F值;但对比VGG和ResNet两种网络对建筑的分割结果明显可见ResNetCRF能对成块建筑物进行提取,分割结果更符合建筑物的特征。
(4.4) 复杂建筑物分割对比实验本文选用4种深度神经网络对3幅不同来源的遥感图像中建筑物的楼顶错层及阴影对建筑物分割的影响进行了对比实验。其中,图12的遥感图像来源于训练样本中的芝加哥地区,该遥感图像参与了模型的训练;图13的遥感图像来源于奥斯汀地区未参与模型训练的样本。由于奥斯汀地区的部分样本参与了模型训练,可以认为图13的遥感图像与部分训练样本具有同源性;图14的遥感图像来源于布鲁明顿地区,该地区的样本没有参与模型训练。3幅遥感图像中的建筑物颜色不同,错层结构较为复杂,光照角度各异。分割性能指标如表5所示。

|
| 图 12 芝加哥地区复杂建筑物分割实验结果 Figure 12 Complex building segmentation result of Chicago |

|
| 图 13 奥斯汀地区复杂建筑物分割实验结果 Figure 13 Complex building segmentation result of Austin |

|
| 图 14 布鲁明顿地区复杂建筑物分割实验结果 Figure 14 Complex building segmentation result of Bloomington |
|
|
表 5 复杂建筑物分割性能指标 Table 5 Performance indexes of complex buildings segmentation |
由于图12所示的芝加哥地区的遥感图像参与了模型训练,其建筑物分割结果可以反映模型的训练程度。由分割结果可知,4种深度神经网络均未能完全实现对建筑物的精确分割,说明训练的模型与真实分割模型之间仍然存在差距。相比而言,ResNetCRF所建立的分割模型与实际模型之间的差异最小,其分割性能指标最高。
由图13所示,奥斯汀地区遥感图像建筑物分割实验结果可知,VGG和ResNet对阴影的抗干扰能力不强,均出现了较大面积的误分;VGGCRF对建筑物的召回能力相对较弱;只有ResNetCRF能较好的克服阴影的影响。此外,ResNetCRF能完全克服道路的影响,实现了建筑物的精确分割,因此其召回率、精确率和F值等综合分割性能指标均达到最好。
由图14所示的布鲁明顿地区建筑物分割结果可知,VGG网络对建筑物有一定的指示作用,但对阴影、错层的抗干扰能力较差;VGGCRF网络对建筑物的召回率最低,获取的建筑物像素点最少;ResNet网络对较大面积的连续性较好的建筑物能较好的分割,但对错层和阴影的抗干扰能力仍然较差;ResNetCRF能较为准确的对建筑物进行分割,相比其他3种网络结构,对建筑物错层和阴影的抗干扰能力最强,也获得了最好的分割性能指标。
4种深度神经网络的分割细节如图15所示。通过分割细节分析,可知本文提出的ResNetCRF建筑物分割算法具有以下特点:

|
| 图 15 分割细节 Figure 15 Detail of segmentation result |
(1) ResNetCRF对建筑物的边缘提取更为准确,特别是对于直线型边缘提取的准确度较高。但是边缘部分存在散点,如图15所示的分割结果。
(2) ResNetCRF能较好的克服建筑物阴影的影响,如图15(a)所示的分割结果。
(3) ResNetCRF对于面积较大的建筑物分割准确度较高,但是对于面积较小的建筑物容易出现漏分,如图15(g)所示的分割结果。
(4.5) 多分辨率遥感图像分割实验本文采用的IAILD遥感图像数据库分辨率为0.3 m。为了检测遥感图像分辨率对本文算法的影响,采用双三次插值法对原始遥感图像进行压缩,以减小图像的分辨率。压缩比例分别设置为R=0.2、0.5和0.8,对应的分辨率分别近似为1.5 m、0.6 m和0.375 m。同时,遥感图像对应的建筑物标签也做同样的压缩。
实验中,输入图像的规格均为1000×1000×3,实验结果如图16所示。其中,图16(d)的图像为图16(a)中白色方框标识的内部图像;图16(h)的图像则为图16(d)中白色方框标识的内部图像。分割性能指标如图17所示。由分割结果可知,当图像的分辨率变化不大时(R=0.8),本文提出的算法仍然能较为精确的完成建筑物的分割,即使遥感图像的分辨率降低了一半(R=0.5),其分割性能指标的下降也并不十分明显。但是当遥感图像的压缩比达到0.2时,分割性能明显下降,即说明ResNetCRF对小目标的分割精度有待于进一步加强。

|
| 图 16 多分辨率遥感图像分割实验结果 Figure 16 Segmentation result of RSI with multi resolution |

|
| 图 17 ResNetCRF多分辨率遥感图像分割性能指标 Figure 17 ResNetCRF segmentation performance indexes of multi resolution RSI |
本文针对高分辨率遥感图像中建筑物的精确分割问题,提出了一种以Encoder-Decoder为框架、ResNet为基础网络,并结合全连接条件随机场的深度神经网络分割算法ResNetCRF。该算法通过RNN机制,将条件随机场与Encoder-Decoder有机融合,实现了深度神经网络与条件随机场参数的同步训练。在IAILD遥感图像数据库上开展实验,实验结果表明,ResNetCRF能有效克服建筑物的错层结构、阴影以及道路的影响,可精确提取建筑的边缘信息,其分割性能指标提升较为明显。同时,在多分辨率遥感图像建筑物分割实验中,在一定分辨率范围内,ResNetCRF具有较好的泛化能力。
但是,ResNetCRF对于颜色信息与背景相似,且边缘信息不明显的建筑物存在漏分,导致精确率不高。同时,ResNetCRF对于较小的建筑物基本无法识别,容易出现漏分。在后续研究中,将进一步改进条件随机场深度神经网络的结构,消除建筑物的漏分现象。
此外,由于计算机存储资源和计算资源的限制,遥感图像往往需要进行分块处理后再进行融合,然而采用分块后的样本进行深度神经网络训练,势必会造成遥感图像整体特征的损失。如何在不增加计算机资源压力的基础上,提取并应用大幅面遥感图像的整体特征,可能会进一步提升深度神经网络对建筑物的分割精度,且该方法可能会为处理大幅面遥感图像难题提供新的思路。在后续的研究过程中,将进一步开展该研究工作。
| [1] | Adams A, Baek J and Davis M A. Fast high‐dimensional filtering using the permutohedral lattice[J]. Computer Graphics Forum, 2010, 29 (2) : 753 –762. DOI: 10.1111/j.1467-8659.2009.01645.x |
| [2] | Alshehhi R, Marpu P R, Woon W L and Mura M D. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 130 : 139 –149. DOI: 10.1016/j.isprsjprs.2017.05.002 |
| [3] | Audebert N, Le Saux B and Lefèvre S. Beyond RGB: very high resolution urban remote sensing with multimodal deep networks[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 140 : 20 –32. DOI: 10.1016/j.isprsjprs.2017.11.011 |
| [4] | Badrinarayanan V, Kendall A and Cipolla R. SegNet: a deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39 (12) : 2481 –2495. DOI: 10.1109/TPAMI.2016.2644615 |
| [5] | Bittner K, Cui S Y and Reinartz P. 2017. Building extraction from remote sensing data using fully convolutional Networks//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Hannover, Germany: ISPR: 481–486 |
| [6] | Chatzis S P, Kosmopoulos D I and Doliotis P. A conditional random field-based model for joint sequence segmentation and classification[J]. Pattern Recognition, 2013, 46 (6) : 1569 –1578. DOI: 10.1016/j.patcog.2012.11.028 |
| [7] | 陈杰, 邓敏, 肖鹏峰, 杨敏华, 梅小明, 刘慧敏. 利用小波变换的高分辨率多光谱遥感图像多尺度分水岭分割[J]. 遥感学报, 2011, 15 (5) : 908 –926. Chen J, Deng M, Xiao P F, Yang M H, Mei X M and Liu H M. Multi-scale watershed segmentation of high-resolution multi-spectral remote sensing image using wavelet transform[J]. Journal of Remote Sensing, 2011, 15 (5) : 908 –926. DOI: 10.11834/jrs.20110280 |
| [8] | Chen L C, Papandreou G, Kokkinos I, Murphy K and Yuille A L. 2014. Semantic image segmentation with deep convolutional nets and fully connected CRFs. arVix preprint arXiv: 1412.7062(2014) |
| [9] | Chen L C, Papandreou G, Kokkinos I, Murphy K and Yuille A L. DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 40 (4) : 834 –848. DOI: 10.1109/TPAMI.2017.2699184 |
| [10] | Dumoulin V and Visin F. 2016. A guide to convolution arithmetic for deep learning. arXiv preprint arXiv: 1603.07285(2016) |
| [11] | Glorot X, Bordes A and Bengio Y. 2011. Deep sparse rectifier neural networks//Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, FL, USA: [s.n.] |
| [12] | He K M, Zhang X Y, Ren S Q and Sun J. 2015. Deep residual learning for image recognition. arXiv preprint arXiv: 1512.03385(2015) |
| [13] | Ioffe S and Szegedy C. 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv: 1502.03167(2015) |
| [14] | Jiao L C, Liang M M, Chen H, Yang S Y, Liu H Y and Cao X H. Deep fully convolutional network-based spatial distribution prediction for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55 (10) : 5585 –5599. DOI: 10.1109/TGRS.2017.2710079 |
| [15] | Krähenbühl P and Koltun V. 2012. Efficient inference in fully connected CRFs with gaussian edge potentials. arXiv preprint arXiv: 1210.5644(2012) |
| [16] | 李航. 2012. 统计学习方法. 北京: 清华大学出版社 Li H. 2012. Statistical Learning Method. Beijing: Tsinghua University Press |
| [17] | Lin H N, Shi Z W and Zou Z X. Fully convolutional network with task partitioning for inshore ship detection in optical remote sensing images[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14 (10) : 1665 –1669. DOI: 10.1109/LGRS.2017.2727515 |
| [18] | Liu Y, Carbonell J, Weigele P and Gopalakrishnan V. 2005. Segmentation conditional random fields (SCRFs): a new approach for protein fold recognition//Proceedings of the 9th Annual International Conference on Research in Computational Molecular Biology. Cambridge, MA, USA: Springer: 408–422 |
| [19] | Liu Y S, Piramanayagam S, Monteiro S T and Saber E. 2017. Dense semantic labeling of very-high-resolution aerial imagery and LiDAR with fully-convolutional neural networks and higher-order CRFs//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, HI, USA: IEEE: 1561–1570 |
| [20] | Noh H, Hong S and Han B. 2015. Learning deconvolution network for semantic segmentation//Proceedings of 2015 IEEE International Conference on Computer Vision (ICCV). Santiago, Chile: IEEE: 1520–1528 |
| [21] | Ronneberger O, Fischer P and Brox T. 2015. U-Net: convolutional networks for biomedical image segmentation//Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich, Germany: Springer |
| [22] | Shelhamer E, Long J and Darrell T. Fully convolutional networks for semantic segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39 (4) : 640 –651. DOI: 10.1109/TPAMI.2016.2572683 |
| [23] | 沈家煊. 人工智能中的" 联结主义”和语法理论[J]. 外国语, 2004 (3) : 2 –10. Shen J X. Connectionism in AI and grammatical theories[J]. Journal of Foreign Languages, 2004 (3) : 2 –10. DOI: 10.3969/j.issn.1004-5139.2004.03.001 |
| [24] | Simonyan K and Zisserman A. 2014. Visual geometry group[EB/OL]. http://www.robots.ox.ac.uk/~vgg/research/very_deep/ (2014) |
| [25] | 王玉, 李玉, 赵泉华. 基于区域的多尺度全色遥感图像分割[J]. 控制与决策, 2018, 33 (3) : 535 –541. Wang Y, Li Y and Zhao Q H. A region-based multiscale segmentation of panchromatic remote sensing image[J]. Control and Decision, 2018, 33 (3) : 535 –541. DOI: 10.13195/jk.kzzyyjcjc.2.2001177.0.001177 |
| [26] | 王宇, 王宝山, 王田, 杨艺. 面向遥感图像水域分割的图像熵主动轮廓模型[J]. 光学精密工程, 2018, 26 (3) : 698 –707. Wang Y, Wang B S, Wang T and Yang Y. Image entropy active contour models towards water area segmentation in remote sensing image[J]. Optics and Precision Engineering, 2018, 26 (3) : 698 –707. DOI: 10.3788/OPE.20182603.0698 |
| [27] | Wang Y Y, Wang C and Zhang H. 2017. Integrating H-A-α with fully convolutional networks for fully PolSAR classification//Proceedings of 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP). Shanghai, China: IEEE: 1-4 |
| [28] | Xu L L, Shafiee M J, Wong A and Clausi D A. Fully connected continuous conditional random field with stochastic cliques for dark-spot detection in SAR imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9 (7) : 2882 –2890. DOI: 10.1109/JSTARS.2016.2531985 |
| [29] | 张建龙, 王斌. DSSRM级联分割的SAR图像变化检测[J]. 遥感学报, 2017, 21 (4) : 614 –621. Zhang J L and Wang B. SAR image change detection method of DSSRM based on cascade segmentation[J]. Journal of Remote Sensing, 2017, 21 (4) : 614 –621. DOI: 10.11834/jrs.20176330 |
| [30] | Zheng S, Jayasumana S, Romera-Paredes B, Vineet V, Su Z Z, Du D L, Huang C and Torr P H S. 2015. Conditional random fields as recurrent neural networks//Proceedings of 2015 IEEE International Conference on Computer Vision (ICCV). Santiago, Chile: IEEE: 1529–1537 |
| [31] | Zhong Y F, Han X B and Zhang L P. Multi-class geospatial object detection based on a position-sensitive balancing framework for high spatial resolution remote sensing imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 138 : 281 –294. DOI: 10.1016/j.isprsjprs.2018.02.014 |
| [32] | 周东国, 高潮, 郭永彩. 一种参数自适应的简化PCNN图像分割方法[J]. 自动化学报, 2014, 40 (6) : 1191 –1197. Zhou D G, Gao C and Guo Y C. Adaptive simplified PCNN parameter setting for image segmentation[J]. Acta Automatica Sinica, 2014, 40 (6) : 1191 –1197. DOI: 10.3724/SP.J.1004.2014.01191 |