| 云下地表温度与辐射变化关系的定量分析 |
收稿日期: 2018-03-20
2. Institute of Agro-Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing 100081, China
目前国内外对热红外遥感的研究,主要集中在热红外遥感机理、地表温度遥感定量反演及其参数确定、热红外遥感应用等方面,对热红外影像中云下覆盖像元的地表温度估算,研究得还较少,相关的论文发表也不多。国内常用的热红外遥感有云像元表温度的估算方法主要是空间插值方法和植被指数关系法。周义等(2012)、张军等(2011)和涂丽丽等(2011)分别从不同角度探讨并评价了空间插值法在云遮挡像元地表温度估计中的可用性。刘梅等(2011)和苏洁等(2013)研究了植被指数—地表温度关系法,进而估算云遮挡像元的可用性和精度问题。周义等(2013)总结了目前国内热红外遥感图像中有云像元地表温度估算研究的进展。
国外对云覆盖像元地表温度的估算虽然较早,但相关论文也不多,主要也是利用时空插值法、气温关系法和地表热平衡模拟等方法来进行云覆盖像元地表温度估算。早在20世纪80年代中期,Minnis和Harrison(1984)利用地表温度日循环变化规律,通过时空插值法,对静止气象卫星数据中云覆盖像元的地表温度进行估算。但由于地表异质性较大,时空插值法精度较差,在实际中应用极少。虽然Aires等(2004)也用相同的时空插值法来分析研究全球地表温度的变化,但他们主要是为了获得更多时间序列的全球地表温度而进行时空插值估算,而不是针对云覆盖像元的地表温度估算。为了估算云覆盖像元的地表温度,Jin和Dickinson (2000)根据地表热平衡原理,提出了一个通用的云像元地表温度估算方法,利用邻近无云像元的同质性特征,通过地表热平衡模型估算云覆盖像元的地表温度。但该方法没有充分考虑临近像元的空间异质性。Lu等(2011)把邻近像元法思想应用到静止卫星MSG/SEVIRI的云覆盖像元地表温度估算上,并从空间邻近、时相邻近和综合邻近等3个方面比较了邻近像元法的估算精度,发现时相邻近的估算精度相对较高。Gallo等(2011)则利用地表温度与气温之间的局地相关关系,提出了利用气象观测数据中的气温来估算云覆盖像元的地表温度,但需要每个云覆盖像元的气温为已知,从而限制了其通用性。
从地表温度变化机理上分析,地表温度发生变化主要是地表能量交换过程中,入射能量和发射能量之间的能量差引起的。当入射能量高于地表的发射能量时,地表温度就会不断升高,当入射能量低于地表的发射能量时,地表温度就会不断下降。大气中云层的出现,往往会打破其影响的下垫面地表能量交换过程。云层导致的辐射变化与地表温度的定量关系的分析,可以为热红外遥感图像中有云像元的地表温度估算方法研究提供基础。
2、方法和实验为了探索云下地表温度与辐射变化的定量关系,本文采取野外观测实验和地表能量平衡模型模拟的方法同时进行,并对模型模拟结果和实际观测结果进行对比验证。
(2.1) 云下地表温度野外观测实验在进行野外实验观测时,每个观测地点利用两套自动记录的气象观测站和两套地表温度连续观测记录仪(Raytek MI3热红外探头和数据记录仪)进行为期一周的野外观测实验。由于土壤温度传感器和土壤湿度传感器需要挖土埋设到不同深度,因此每个观测地点分别在植被和裸地上设立一套观测站,人工建筑区域采用热辐射仪(Raytek ST60 XB)定时进行采样。观测数据主要包括近地表气象数据、地表温度数据和土壤温湿度数据(表1)。
|
|
表 1 野外观测实验具体观测项目 Table 1 Terms of observation in different study sites |
地表温度的估算需要我们建立典型地表类型的地表能量平衡模型。近年来,针对不同气象、遥感应用领域(Allen 等(2007)的METRIC模型,Bastiaanssen 等(1998)的SEBAL模型)的地表能量平衡模型得到了越来越多研究人员的重视。Best(1998)指出这些模型多基于Penman-Monteith公式,针对不同的应用领域,进一步提高不同的参数估算精度,从而获得更加符合实际的模拟结果。
在准确性得到一定保障前提下,可以将能量界面当作为一张大叶,从而得到一种简单而有效的近似模拟,地表能量平衡模型一般可以表达为
| ${R_{\rm{n}}} - H - {\textit{λ}} E - G = 0$ | (1) |
式中,地表净辐射Rn,地表显热通量H,地表潜热通量λE和土壤热通量G都与地表温度有着直接的关系,因此该式也成为我们预测地表温度的关键,其中,地表净辐射,地表显热通量,地表潜热通量和土壤热通量的估算参数较多,这里不一一展开详述,具体参数的估算可以参考Qin等(2002)的文献。不同地表类型由于下垫面所含物质组成成分不同,如土壤的含水量、有机质含量和土壤的结构性质等,都会对下垫面的热力学性质产生影响,根据杨世铭和陶文铨(1998)及Best(1998)等的研究,选取不同地表类型地表能量平衡模型的参数典型值如表2所示。
|
|
表 2 地表能量平衡模型的参数典型值(30 ℃) Table 2 Typical value of different parameters in surface energy balance model at 30 ℃ |
在云下地表温度与辐射变化关系统计指标的选取上,云覆盖前地表温度的初始值(Tsini)、云覆盖后地表温度变化量(ΔT)、云覆盖时间(t)和云覆盖导致的云下辐射变化量4个参数(ΔR)作为统计主要参数,然后,可以构建单位时间内地表温度发生变化量所需的辐射变化量(ΔR/ΔT/t)与云覆盖前初始地表温度的关系。
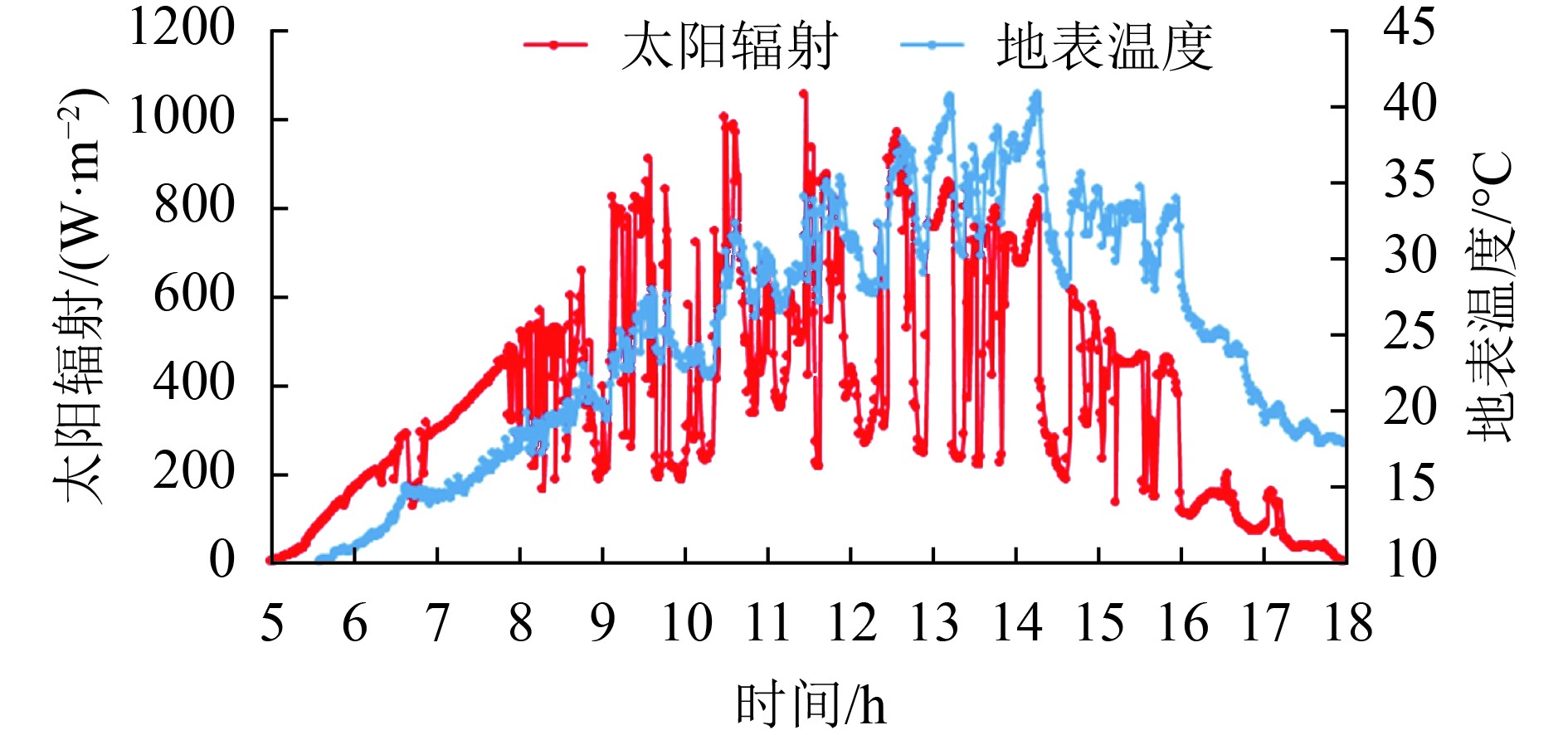
3、数据结果处理与分析 (3.1) 云下地表温度与辐射变化观测结果图1中红色曲线为2015年8月31日在内蒙古自治区锡林郭勒盟观测的草地一天内太阳辐射的变化曲线,该曲线与一般情况下观测的一天内呈正弦变化形态的太阳辐射值是有所差异的,这是因为观测地点的云层多为小块散状云,云块的边缘界限清晰,云块之间可以清晰观测到蓝色天空(图2)。这种情况下就会导致云层覆盖时太阳辐射值较低,而云层不覆盖观测地点时,到达观测地点的太阳辐射会迅速升高。观测地点当天的散云覆盖情况导致了观测地点的太阳辐射值忽高忽低,从而形成图1红色曲线分布情况。
|
| 图 1 地表温度与太阳辐射之间的变化关系 Figure 1 Relationship of LST and solar global radiation |

|
| 图 2 观测地点云覆盖情况 Figure 2 Cloud in the observation site |
随着到达地表的太阳辐射不断的波动,地表温度也发生了相应的波动,地表温度随太阳辐射值变化的情况如图1中蓝色曲线所示。对比图1中的两条曲线,可以看出,地表温度的整体变化趋势与到达地表的太阳辐射值的变化趋势基本一致,当云层导致到达地表的太阳辐射减少时,地表温度值也会相应降低,同时,在太阳辐射减少幅度差不多的情况下,地表温度在云覆盖之前的值越高,受到的影响也就会越高一点。例如,图1中上午9—10点,下午14—15点两个区间中,云层太阳辐射值都出现了由800 W·m−2降到200 W·m−2的情况,然而,对应的地表温度变化情况却不尽相同,上午9—10点区间,受云层影响的地表温度大约由31℃下降到26℃,温度降幅为5℃,而下午14—15点这个时间段内,地表温度则由40℃下降到28℃,温度降幅达到了12℃。
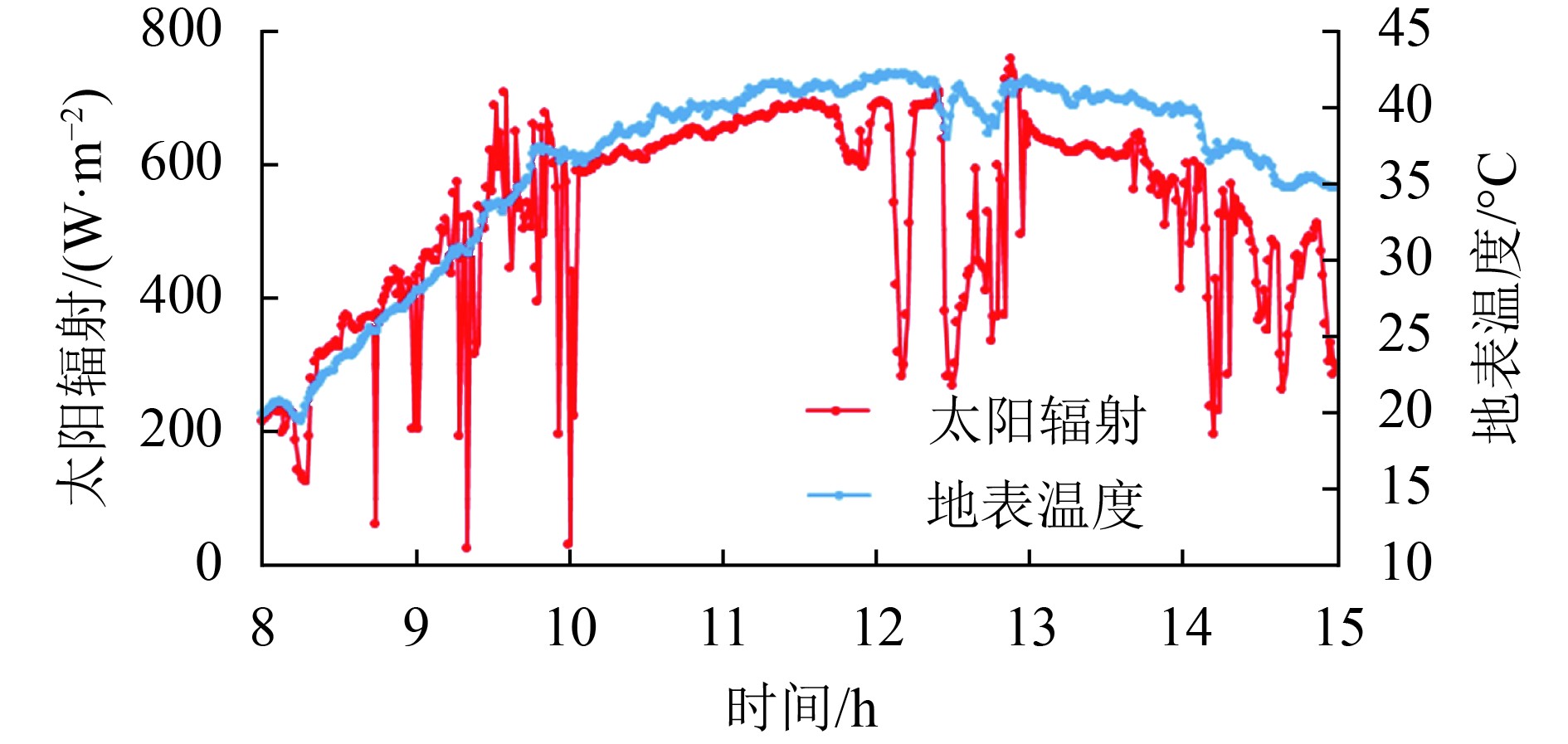
白天时段内,当太阳辐射发生变化时,同一地表类型的地表温度变化也不尽相同,不同地区、不同地表类型情况下,地表温度受云影响的情况也不尽相同。如图3所示,该图为2015年10月25日我们在湖南永州的一处水稻田的观测情况,该天中午12—13点时间段内,云层导致的太阳辐射由700 W·m−2降到300 W·m−2时,地表温度也仅从42℃降到39℃,降温幅度最大仅为3℃。同时该观测点的上午8—10点时间段内,太阳辐射出现四次突然降低的情况,但影响时间都很短,此时,地表温度并没有随着太阳辐射的剧烈变化而发生明显的变化。
|
| 图 3 地表温度与太阳辐射之间的变化规律 Figure 3 Relationship of LST and solar global radiation |
白天情况下,云对地表温度产生的直接影响就是减少到达地表的太阳辐射,进而造成地表温度不同程度的降低。到了夜晚,云对地表温度的影响过程与白天就会有所区别,晚上由于云的热力学性质,云层会减少地表向外的热辐射,对地表温度起到一定的保温作用。图4为2015年10月28日广东江门一处裸地上地表温度在晚间随云层变化的关系。由于夜晚是没有太阳辐射的,在夜晚云层的实时监测上,采取将一个热红外探头垂直于地表向上观测,这样就可以观测到大气向下辐射的等效温度。一般情况下,在空气温度在20℃左右时,在无云条件下,大气向下辐射的等效温度一般在0℃左右,在有云条件下,大气向下辐射的等效温度一般在15℃左右。

|
| 图 4 夜间地表温度与云层关系 Figure 4 The relationship between LST and cloud in the night |
从图4中可以看出,图4蓝色曲线为地表温度在夜间从19点到第二天凌晨5点期间的变化情况,浅灰色曲线为大气向下辐射等效温度的变化情况。图4中椭圆A处为晚上21—22点,在云覆盖观测地点,此时大气向下辐射等效温度为16℃左右,地表温度在该时间段内由云覆盖前的下降趋势变为稳定趋势,基本稳定在24.5℃;当椭圆A处的云层影响过后,进入图4中椭圆B处时,由于没有云层的影响,地表温度发生了明显的下降,由24.5℃下降到了23.6℃;椭圆C处也为无云处,地表温度不断下降到了21.8℃,然而,此后观测地点不断有云层覆盖,地表温度则随着云层的覆盖出现了上升后又下降的趋势,图4中椭圆D处所示。
经过对云下地表温度观测结果的初步分析,可以看出,云下地表温度不仅受透过云层到达地表的太阳辐射值大小的影响,同时还受云覆盖前地表温度值大小的影响,不同区域、不同地表类型由于热力学性质的不同,地表温度随辐射变化而变化的值也不尽相同。白天时段,云对地表温度的影响可以概括为,当地表温度处于上升阶段时(上午),云层的出现会导致地表温度上升趋势变缓或下降,当地表温度处于下降阶段时(下午),云层的出现会导致地表温度明显下降;夜晚时段,云层的出现会使地表温度的下降趋势变缓或趋于平稳,甚至出现地表温度小幅上升的情况,这也是云层晚上对地表的保温作用。云层对地表温度定性的影响我们可以简单的描述如此,但具体的云层所导致的到达地表的辐射值大小的差异和辐射导致地表温度变化的定量研究,需要进一步的建立模型,并结合观测数据进行定量的分析。
根据地表温度与辐射值之间的变化规律,不难发现,地表温度的变化值与辐射变化值有着直接的关系。本文对内蒙古自治区锡林郭勒盟观测点一天内的观测数据进行了统计,主要包括云覆盖时间,云覆盖导致的辐射变化量和地表温度变化量进行了统计,如图5所示。单位时间内,将不同地表温度变化1℃所需要的辐射值的变化量进行统计,结果可以发现,不同地表温度在单位时间内发生的温度值的单位变化量与辐射值的变化量呈线性变化的趋势,当地表温度为45℃时,地表温度在单位时间(1 min)内降到44℃所需要的辐射变化值为50 W·m−2左右,而当地表温度为25℃时,地表温度在单位时间(1 min)内降到24℃所需要的辐射变化值则达到250 W·m−2左右。该规律可以简单理解为,当地表温度值越高,地表温度值减少1℃所需的辐射值越少,或者相同的辐射变化值条件下,辐射变化前的初始地表温度值越高,地表温度值变化越剧烈。因此,可以得到以下公式
| $f(T,\Delta T/\Delta t) = a\Delta R + b$ | (2) |
式中,f(T,ΔT/Δt)为初始地表温度值T下一定时间Δt内温度变化量ΔT,ΔR为到达地表的辐射值的变化量,a和b为拟合参数。

|
| 图 5 地表温度与太阳辐射变化值的关系 Figure 5 The relationship between LST and solar global radiation variation |
式(2)表示了地表温度与太阳辐射值之间的关系,其中,参数a, b如何进一步确定,以及在不同地表类型条件下的变化规律,则需要进一步建立地表能量平衡模型,对云下地表温度的时空变化规律进行进一步的探究。
(3.2) 地表能量平衡模型的模拟结果基于地表能量平衡模型,在云覆盖情况下,分别模拟了裸地、植被、水体和人工建筑物4种典型地表类型的地表温度变化规律,以期获得云下地表温度与云覆盖时间、辐射变化量之间的变化关系。
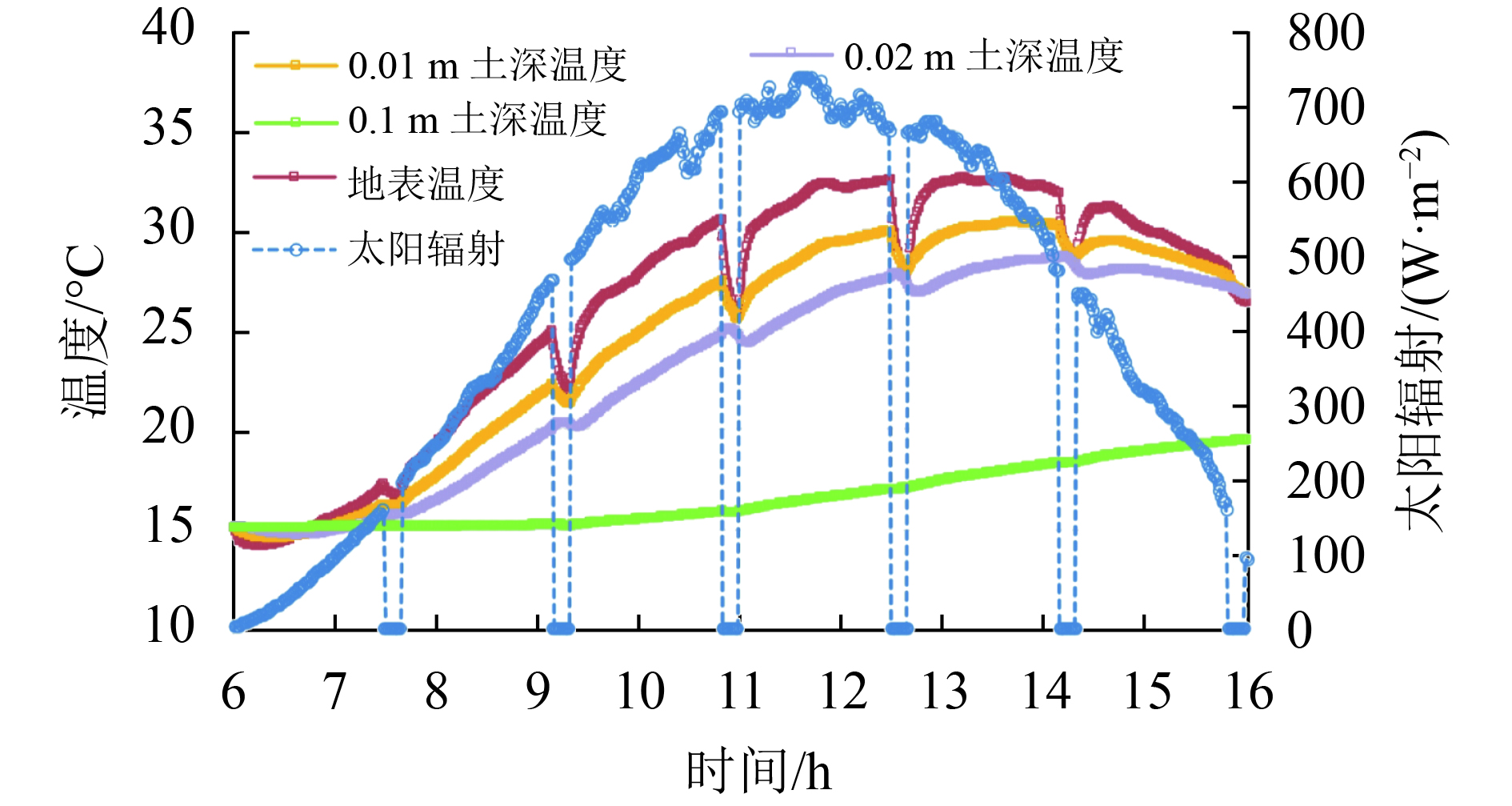
3.2.1. 裸地在云覆盖下的地表温度变化情况图6为裸土表面在云覆盖时,地表温度和不同层土壤温度随时间的变化情况。从图中可以看出,随着云层的覆盖,地表温度出现不同程度的下降,地表温度的变化程度也比土壤层的土壤温度变化更加剧烈,随着土深的不断增加,土壤温度受辐射变化的影响也不断衰减,大约在土深0.1m的深度,地表温度的变化已经在这个深度看不出影响。同时,也可以从图6中初步看出,当云覆盖前地表温度越高,云覆盖后地表温度的变化幅度就越大,下午13:00和14:00处辐射变化量基本相同,而温度变化则是下午13:00时变化更加剧烈。于是,对云覆盖处地表温度的变化幅度、变化时间和云层对辐射的影响量和影响时间进行定量的统计,试图找出地表温度与太阳辐射变化的关系。
|
| 图 6 裸地表面云覆盖后地表温度及不同层土壤温度的变化情况 Figure 6 Variations of LST and different depths soil temperature of bare soil surface covered by the cloud |
图7为不同地表温度条件下,云覆盖后,地表温度在一分钟时间内变化1℃与辐射变化值的关系,如图所示,当地表温度越高时,地表温度为单位时间内变化1℃所需的辐射量越少,这与3.1节实际观测的结果是一致的,如图7所示,当云覆盖前,地表初始温度为40℃时,地表温度降低1℃需要的辐射减少量为73 W·m−2左右,假如此时云层导致的太阳辐射较云覆盖前减少219 W·m−2,云层覆盖10 min后,则此时地表温度降低3℃,云覆盖后的地表温度为37℃,图7中表示地表温度与辐射的关系可以表达为等式3的形式,然而,当云层覆盖50 min后,地表温度应该降到25℃,此时,地表温度是否合理,需要利用模型做进一步验证分析。

|
| 图 7 裸地地表温度与太阳辐射变化值的关系 Figure 7 The relationship between LST and solar global radiation variation in the bare soil surface |
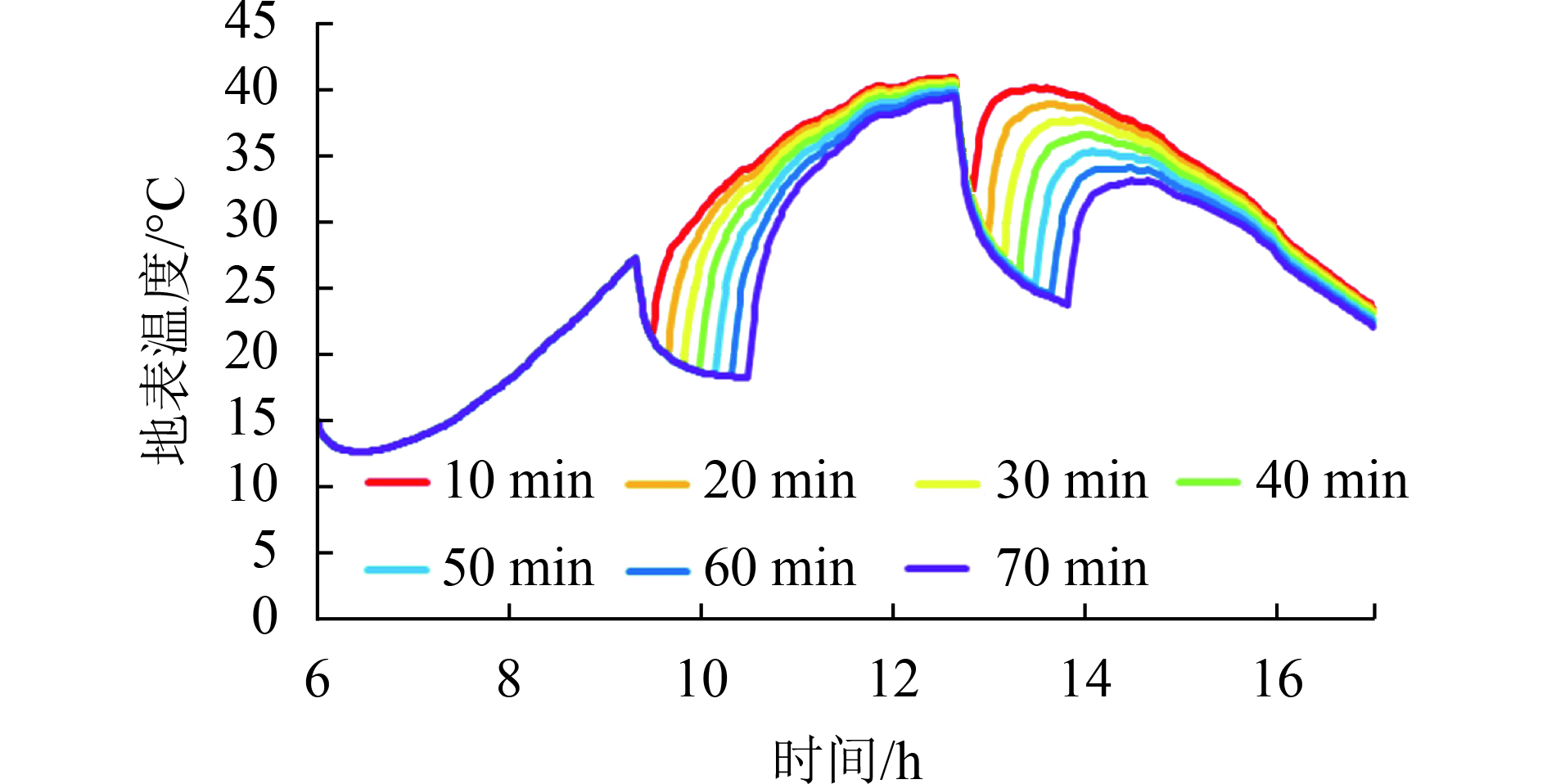
为了模拟地表温度与云覆盖时间的关系,模拟了云层分别覆盖某一区域10 min、20 min,一直到70 min,间隔10 min进行了7次地表温度的模拟,且假定云层覆盖时,到达地表的辐射值为零,分别在上午10:00左右(云覆盖前地表温度为27℃)和下午13:00左右(云覆盖前地表温度为40℃)覆盖该裸地区域,得出该裸地的地表温度变化曲线如图8所示,随着云覆盖时间的不断的增加,地表温度不断降低,然而,地表温度的下降速度随着云覆盖时间的增加而不断放缓,在上午10:00左右时,云覆盖超过40 min时,地表温度趋于平缓,当下午13:00云层覆盖时,地表温度由40℃逐渐降低到25℃,云覆盖70 min后,地表温度的下降速度也开始趋于平缓。
|
| 图 8 地表温度与云覆盖时间变化的关系 Figure 8 The relationship between LST and cloud covered time |
植被地表温度变化模型与裸地的区别在于植被表面蒸发量比较大,而土壤热通量比较小,植被地表上方主要是叶面、茎枝和空气组成,也就是植被相对与裸地,植被的热存储量较小,太阳辐射透过植被,到达植被覆盖下的土壤的辐射值一般小于太阳辐射的10%,因此,根据地表能量平衡公式,短时间内到达植被表面的地表净辐射主要以潜热和显热的形式释放到大气中。利用观测点的气象参数估算出潜热和显热传输的阻抗后,就可以计算出植被地表温度随辐射的变化情况。
图9为草地的地表温度模拟值与实际观测值之间的对比,观测的太阳辐射变化条件如图1中所示,从图9中可以看出,草地地表温度的模拟值总体变化趋势上与实际观测值非常接近,对两组曲线的差值进行统计得出,地表温度模拟值与观测值的误差均值为0.98℃,方差为2.41℃,说明植被地表能量平衡模型可以很好的模拟植被的地表温度变化情况。

|
| 图 9 植被条件下云下地表温度随辐射变化情况 Figure 9 Variations of LST on vegetation surface covered by the cloud |
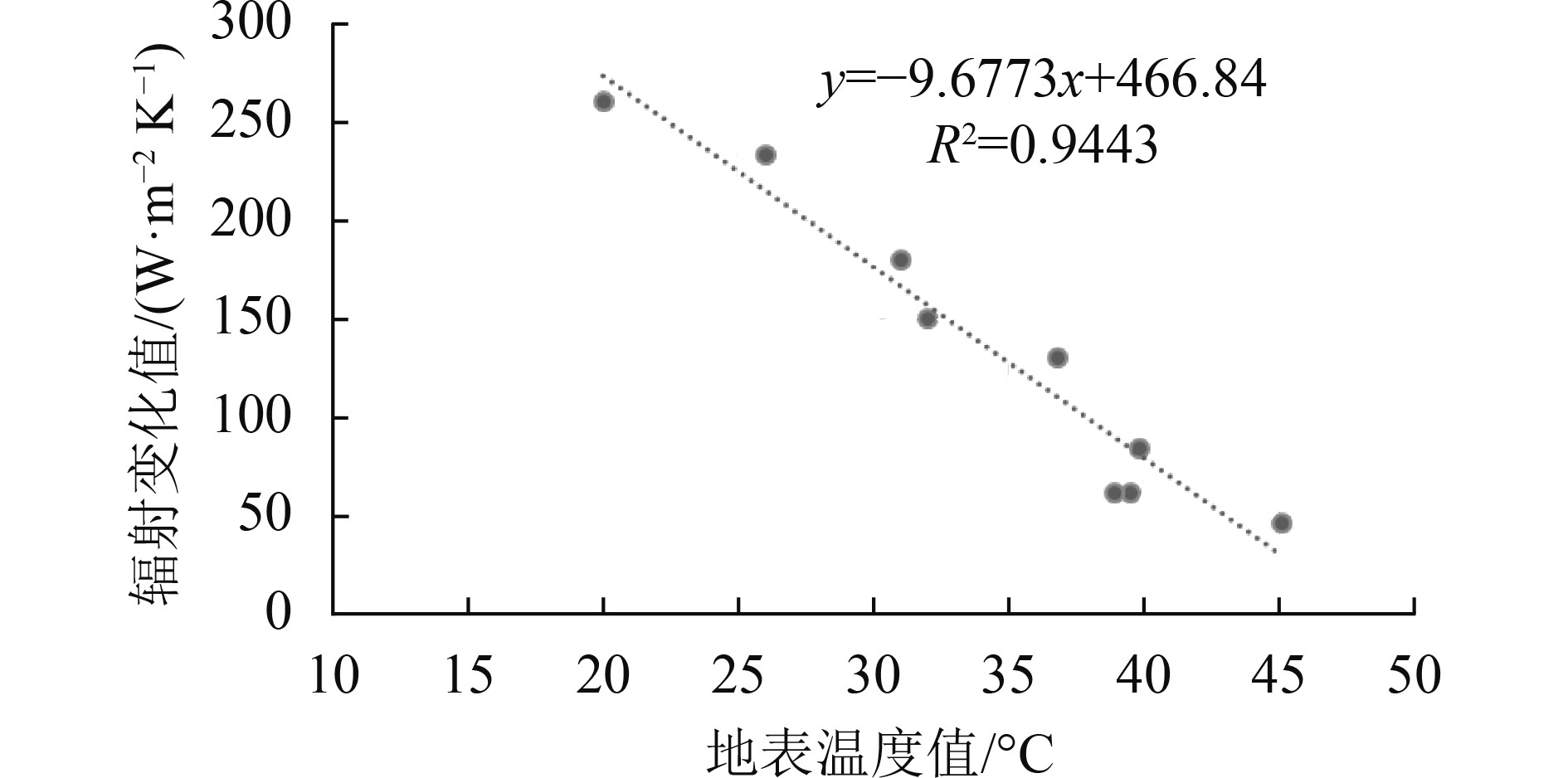
经过对裸地的模拟和观测,得出了短时间内(小于10 min),地表温度单位变化量所需的辐射变化值与地表温度的大小有一定的线性关系。那么,植被条件下,该规律是否依然存在呢,于是,模拟了不同地表温度下,地表温度变化随辐射变化量的关系,并统计了地表温度单位变化量所需的辐射变化值与地表温度的大小(图10)。从图10中可以看出,单位时间内地表温度单位变化所需的辐射变化值与地表温度的高低呈线性关系,与裸地有着相似的变化性质。
在云层长时间覆盖时,植被云下地表温度的变化情况如图11所示,从图11中可以看出,当云层导致辐射值由800 W·m−2下降到100 W·m−2左右,并覆盖植被大约50 min时,地表温度由44℃很快下降到27℃左右,并在云覆盖30 min后一致保持在27℃。这同样与裸地有着相似的变化规律。
|
| 图 10 植被条件下地表温度与太阳辐射变化值的关系 Figure 10 The relationship between LST of vegetation and solar global radiation variation |

|
| 图 11 植被条件下地表温度与云覆盖时间的关系 Figure 11 The relationship between LST of vegetation and cloud covered time |
在云层长时间覆盖时,植被云下地表温度的变化情况如图11所示,从图11中可以看出,当云层导致辐射值由800 W·m−2下降到100 W·m−2左右,并覆盖植被大约50 min时,地表温度由44℃很快下降到27℃左右,并在云覆盖30 min后一致保持在27℃。这同样与裸地有着相似的变化规律。
3.2.3. 人工建筑和水体在云覆盖下地表温度变化情况人工建筑地表相对于裸地,该地表类型的潜热通量可以忽略不计,地表能量平衡模型中,地表的净辐射值等于地表的显热通量和热通量之和。人工建筑的地表温度整体变化趋势与裸地非常相似,由于人工建筑的导热系数相对裸地更低一些(水泥:0.3 W·m−1·K−1,混凝土:0.78 W·m−1·K−1),所以人工建筑的地表温度会出现升温快,降温也快的情况。水体相对其他3种地物,由于水体时液态的,水体内部的自然对流和水体表面有足够的水分用于蒸发,使得水体的升温过程和降温过程都非常缓慢。
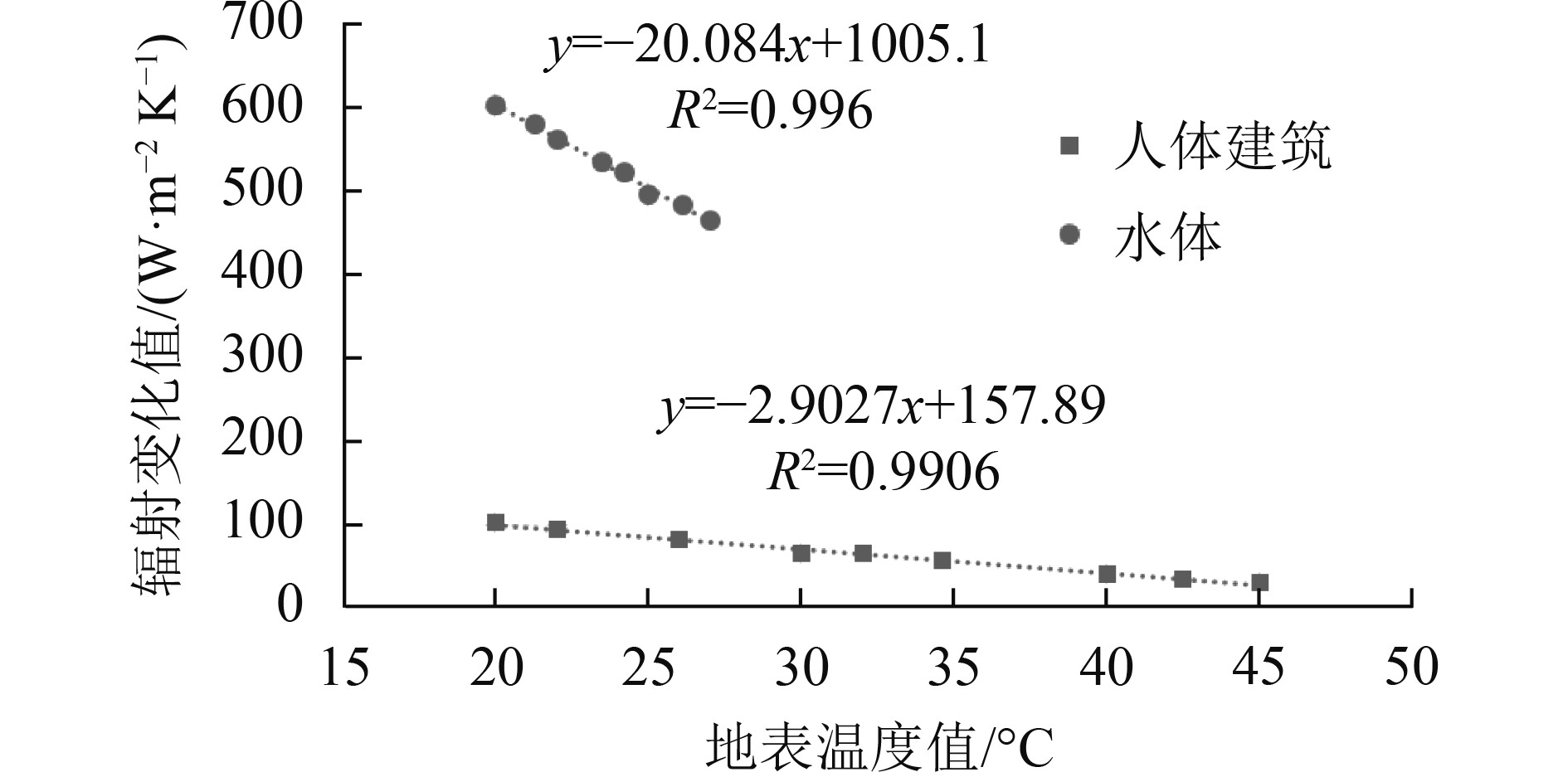
图12为水体和人工建筑地表类型条件下,云层在短时间覆盖时,地表温度在单位时间内变化单位温度值所需的辐射变化量的关系,从图12中可以看出,水体和人工建筑都呈现良好的线性关系,与植被和裸地的模拟关系相一致。对比水体和人工建筑的拟合曲线可以发现,水体变化1℃所需的辐射变化量在500—600 W·m−2,而人工建筑则仅需要不到100 W·m−2。
|
| 图 12 水体和人工建筑地表温度与辐射变化值的关系 Figure 12 Relationship between LST and solar global radiation variation respectively of water and man-made building |
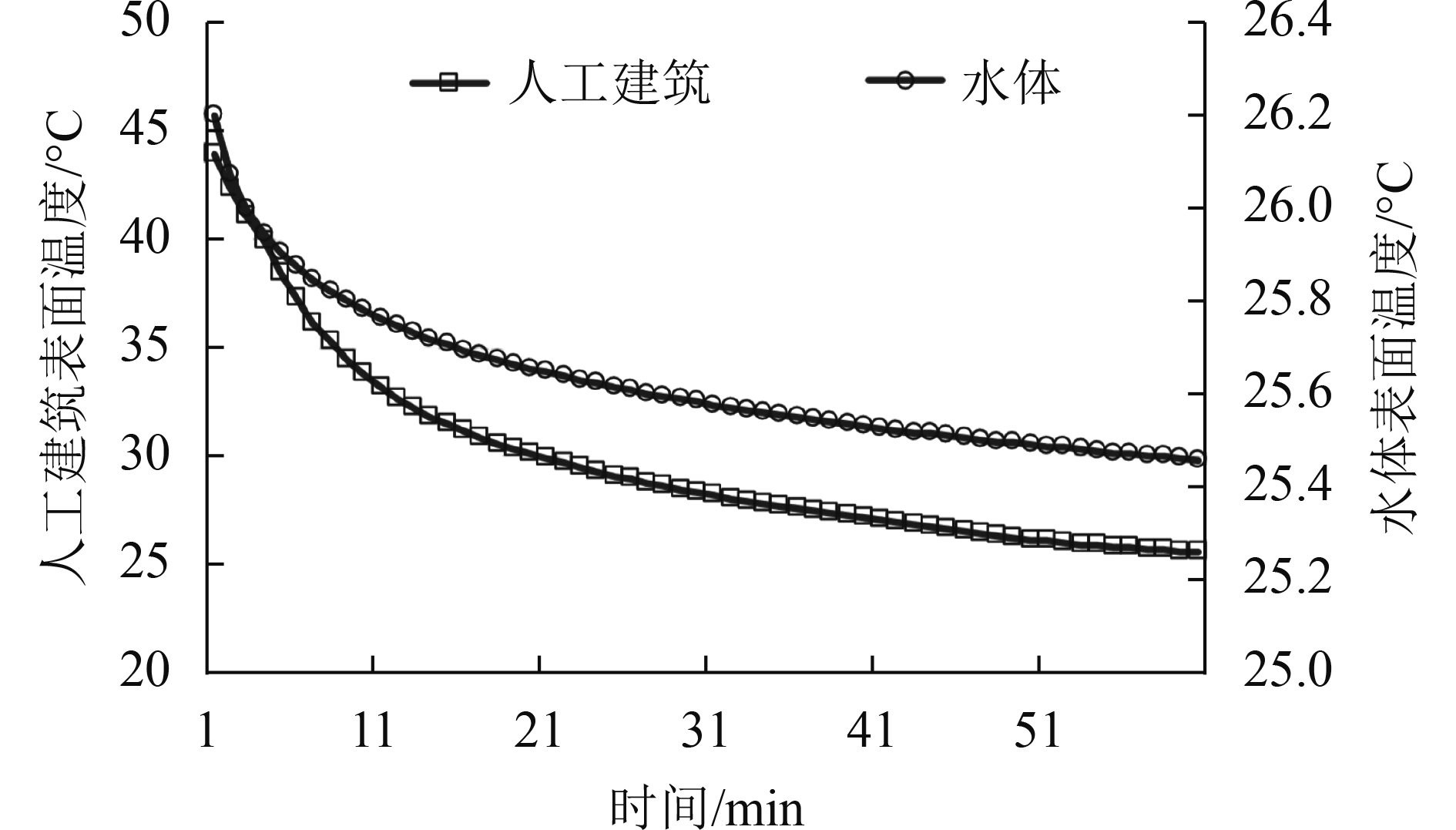
图13为水体和人工建筑地表类型在云层在长时间覆盖时,地表温度随云覆盖时间变化的情况,从图中可以看出,水体和人工建筑的地表温度总体上呈现不断下降的趋势,且下降幅度越来越小,最后趋于稳定,变化趋势与植被和裸地地表相同,不同之处在于,在相同的辐射变化量和云覆盖时间的情况下,水体的整体变化幅度非常小,水体表面温度整体由26.2℃降低到25.5℃,在近一个小时的云覆盖时间内,仅仅降温0.7℃,而人工建筑的地表温度则下降的快的多,其地表温度由45℃下降到25℃左右,降幅达到了20℃。
|
| 图 13 人工建筑和水体地表温度与云覆盖时间的关系 Figure 13 Relationship between LST and the cloud covered time respectively on water and building |
根据模拟结果和实地观测结果,可以得出,当云长时间覆盖某个地区时,该地区地表温度会趋近一个相对稳定的地表温度(TC)
| ${T_{\rm{C}}} = {T_{\rm{a}}} + ({R_{\rm{n}}} - G - \lambda E){r_{\rm{a}}}/{\rho _{\rm{a}}}{c_{\rm{a}}}$ | (3) |
当地表温度不断趋于稳定时,Idso 等(1975)及王斐(2017)指出,可以根据气象数据计算出云长时间覆盖时的地表温度值。根据表3所示,可以根据地表净辐射来估算土壤热通量,此时,地表的潜热通量也可以根据气象数据表达为地表温度和近地表气温和湿度的关系,式(3)就变成了只有一个未知数TC的方程。
|
|
表 3 典型地表类型的土壤热通量与地表净辐射的比值(G/Rn) Table 3 Typical value of the ratio between soil heat flux and surface net radiation (G/Rn) under different land surfaces |
假设一块裸地在云覆盖之前的地表温度为30℃,在空气温度分别在20—30℃,空气湿度在30%—80%时,当透过云层到达地表的净辐射为200 W·m−2时,云覆盖下裸地的地表温度变化如表2所示,当空气湿度和空气温度不断增加时,云覆盖的地表温度也不断增加;云覆盖后地表温度与空气温度相比,温度最高可以升高2.6℃。
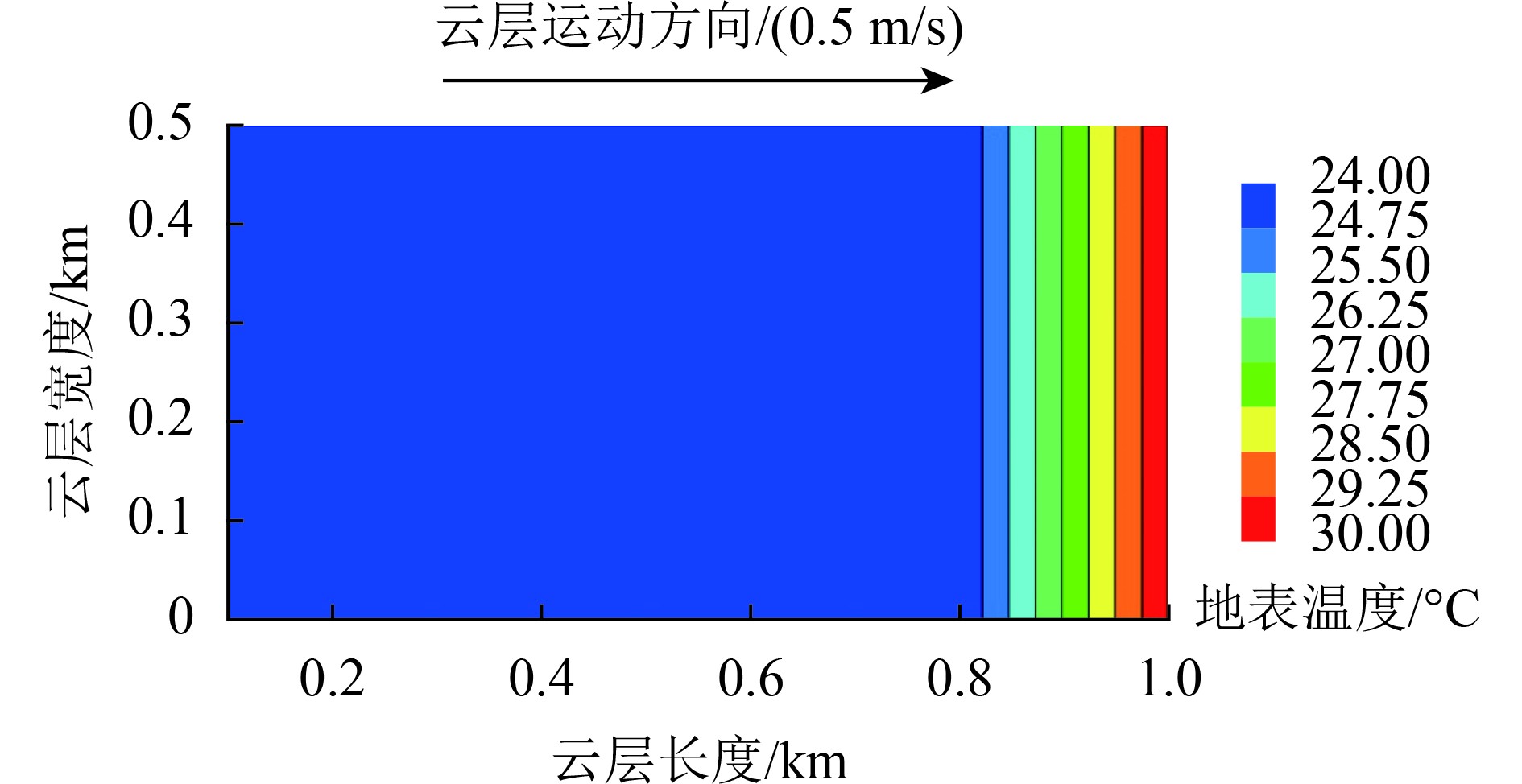
估算出云覆盖后地表温度达到稳定的时间后,根据实验观测和模型模拟,假定从云覆盖前温度降到云覆盖稳定值的变化为线性的,这样,可以根据云覆盖时间来给出云下不同位置的地表温度。例如,当有一块长1 km、宽0.5 km的云覆盖一块地表均一的裸地(表4假设情况)时,云覆盖前的地表温度为30℃,此时空气的温度为23℃,空气湿度为50%,云层以0.5 m/s的速度沿某一方向运动时,云覆盖地表温度的空间分布如图14所示,可以看出,沿着云运动方向,云头(刚覆盖)的地区地表温度最高,呈现向云尾和云中地区地表温度不断下降的趋势,云尾和云中的地表温度则会趋于稳定,地表温度约为24℃。
|
|
表 4 裸地地表温度在不同空气温湿度条件下变化表(Rn=200 W·m-2) Table 4 LST variation of the bare soil surface under different air temperature and humidity(Rn=200 W·m-2) |
|
| 图 14 理想云覆盖下地表温度空间分布 Figure 14 Distribution of LST under the hypothetical ideal cloud |
为了预测地表能量交换过程中地表温度与到达地表总辐射之间的关系,通过估算地表净辐射,地表显热通量,地表潜热通量和土壤热通量等参数,构建了地表能量平衡模型,并通过构建上述参数与地表温度之间的函数关系,实现了地表能量平衡模型的运行。
基于地表能量平衡模型,通过对裸地、植被、人工建筑物和水体在云覆盖情况下地表温度的变化模拟,我们发现,在短时间云覆盖情况下,地表温度随着云覆盖时间的增加而不断下降,当云覆盖前地表温度越高,云覆盖后地表温度的变化幅度也越大。单位时间内地表温度单位变化所需的辐射变化值与地表温度的大小呈线性关系,即当初始地表温度越高时,在云覆盖后,地表温度在一分钟时间内变化1℃,所需的辐射变化量则越小。
在长时间云覆盖情况下,地表温度的下降速度随着云覆盖时间的增加而不断放缓,最终趋于一个稳定值。当地表温度不断趋于稳定时,裸地、植被和不透水层的地表温度都随空气温度和空气湿度的增加而增加,其中,不透水层的地表温度与空气温度之间的温差是最大的,一般为3—5℃。通过估算云下地表温度由云覆盖之前的地表温度初始值,到云覆盖后地表温度稳定值之间所需要的时间,可以看出,沿着云运动方向,云头(刚覆盖)的地区地表温度最高,云尾和云中的地表温度则会趋于稳定。
论文通过特定地区野外观测实验和地表能量平衡模型模拟的方法找出了云下地表温度与辐射变化的关系,但目前观测数据量还相对较少,不同地区不同气象条件下,规律的适用性还需进一步研究探索。
| [1] | Aires F, Prigent C and Rossow W B. Temporal interpolation of global surface skin temperature diurnal cycle over land under clear and cloudy conditions[J]. Journal of Geophysical Research: Atmospheres, 2004, 109 (D4) : D04313 . DOI: 10.1029/2003jd003527 |
| [2] | Allen R G, Tasumi M and Trezza R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—model[J]. Journal of Irrigation and Drainage Engineering, 2007, 133 (4) : 380 –394. DOI: 10.1061/(asce)0733-9437(2007)133:4(380) |
| [3] | Bastiaanssen W G M, Menenti M, Feddes R A and Holtslag A A M. A remote sensing surface energy balance algorithm for land (SEBAL)[J]. 1. Formulation. Journal of Hydrology, 1998, 212-213 : 198 –212. DOI: 10.1016/s0022-1694(98)00253-4 |
| [4] | Best M J. A model to predict surface temperatures[J]. Boundary-Layer Meteorology, 1998, 88 (2) : 279 –306. DOI: 10.1023/a:1001151927113 |
| [5] | Gallo K, Hale R, Tarpley D and Yu Y Y. Evaluation of the relationship between air and land surface temperature under clear- and cloudy-sky conditions[J]. Journal of Applied Meteorology and Climatology, 2011, 50 (3) : 767 –775. DOI: 10.1175/2010jamc2460.1 |
| [6] | Idso S B, Aase J K and Jackson R D. Net radiation — soil heat flux relations as influenced by soil water content variations[J]. Boundary-Layer Meteorology, 1975, 9 (1) : 113 –122. DOI: 10.1007/bf00232257 |
| [7] | Jin M L and Dickinson R E. A generalized algorithm for retrieving cloudy sky skin temperature from satellite thermal infrared radiances[J]. Journal of Geophysical Research: Atmospheres, 2000, 105 (D22) : 27037 –27047. DOI: 10.1029/2000jd900318 |
| [8] | 刘梅, 覃志豪, 涂丽丽, 张军. 利用NDVI估算云覆盖地区的植被表面温度研究[J]. 遥感技术与应用, 2011, 26 (5) : 689 –697. Liu M, Qin Z H, Tu L L and Zhang J. Study on estimation of vegetation surface temperature in cloudy region by NDVI[J]. Remote Sensing Technology and Application, 2011, 26 (5) : 689 –697. DOI: 10.11873/j.issn.1004-0323.2011.5.689 |
| [9] | Lu L, Venus V, Skidmore A, Wang T J and Luo G P. Estimating land-surface temperature under clouds using MSG/SEVIRI observations[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13 (2) : 265 –276. DOI: 10.1016/j.jag.2010.12.007 |
| [10] | Minnis P and Harrison E F. Diurnal variability of regional cloud and clear-sky radiative parameters derived from GOES data[J]. Part I: analysis method. Journal of Climate and Applied Meteorology, 1984, 23 (7) : 993 –1011. DOI: 10.1175/1520-0450(1984)023<0993:dvorca>2.0.co;2 |
| [11] | Qin Z H, Berliner P and Karnieli A. Numerical solution of a complete surface energy balance model for simulation of heat fluxes and surface temperature under bare soil environment[J]. Applied Mathematics and Computation, 2002, 130 (1) : 171 –200. DOI: 10.1016/s0096-3003(01)00089-3 |
| [12] | 苏洁, 徐军, 刘丽强, 戴一锋. 利用NDVI估算云覆盖区的地表温度[J]. 地理空间信息, 2013, 11 (5) : 25 –28. Su J, Xu J, Liu L Q and Dai Y F. Estimation of land surface temperature in covered region of Landsat TM image based on NDVI[J]. Geospatial Information, 2013, 11 (5) : 25 –28. DOI: 10.11709/j.issn.1672-4623.2013.05.009 |
| [13] | 涂丽丽, 覃志豪, 张军, 刘梅, 耿君. 基于空间内插的云下地表温度估计及精度分析[J]. 遥感信息, 2011 (4) : 59 –63, 106. Tu L L, Qin Z H, Zhang J, Liu M and Geng J. Estimation and error analysis of land surface temperature under the cloud based on spatial interpolation[J]. Remote Sensing Information, 2011 (4) : 59 –63, 106. DOI: 10.3969/j.issn.1000-3177.2011.04.012 |
| [14] | 王斐. 2017. 热红外遥感图像中有云像元地表温度估算方法研究. 南京: 南京大学, 57-58 Wang F. 2017. An approach to estimate land surface temperature for cloud-covered pixels in thermal infrared images. Nanjing: Nanjing University, 57-58 |
| [15] | 杨世铭, 陶文铨. 1998. 传热学. 3版. 北京: 高等教育出版社: 556-560 Yang S M and Tao W Q. 1998. Heat Transfer. 3rd ed. Beijing: Higher Education Press: 556-560 |
| [16] | 张军, 覃志豪, 刘梅, 涂丽丽, 周义, 杨强. 利用空间插值法估算云覆盖像元地表温度的可行性研究[J]. 地理与地理信息科学, 2011, 27 (6) : 45 –49. Zhang J, Qin Z H, Liu M, Tu L L, Zhou Y and Yang Q. Estimating of land surface temperature under the cloud cover with spatial interpolation[J]. Geography and Geo-Information Science, 2011, 27 (6) : 45 –49. |
| [17] | 周义, 覃志豪, 包刚. GIDS空间插值法估算云下地表温度[J]. 遥感学报, 2012, 16 (3) : 492 –504. Zhou Y, Qin Z H and Bao G. Land surface temperature estimation under cloud cover with GIDS[J]. Journal of Remote Sensing, 2012, 16 (3) : 492 –504. DOI: 10.11834/jrs.20121091 |
| [18] | 周义, 覃志豪, 包刚. 热红外遥感图像中云覆盖像元地表温度估算初论[J]. 地理科学, 2013, 33 (3) : 329 –334. Zhou Y, Qin Z H and Bao G. A Preliminary view on the estimation of land surface temperature under cloud cover from thermal remote sensing data[J]. Scientia Geographica Sinica, 2013, 33 (3) : 329 –334. DOI: 10.13249/j.cnki.sgs.2013.03.012 |

