遥感影像变化检测是从不同时相获取的覆盖同一地表区域的遥感影像中，定量分析地表变化的过程(Singh 1989；Vongsy 等，2007；Wang 等，2015)。然而由于不同时相影像获取时的大气环境差异，以及不同传感器带来的辐射差异，变化检测往往无法突出人们感兴趣的变化(Theiler，2008b)。通过高光谱遥感影像所提供的丰富且详细的光谱特征和高维数据(童庆禧 等，2016)，异常变化检测能够寻找到数量稀少、与整体背景变化趋势不同的、难以发现的感兴趣的变化(Eismann 等，2008；Theiler和Matsekh 2010；彭波 等，2017)。近年来，高光谱异常变化检测技术在很多领域中得到成功应用，如边境监察、搜索营救等，因此得到有关学者的高度重视(Matteoli 等，2010)。

当前异常变化检测方法相对较少，异常变化检测方法通常先将两幅影像进行中心化，然后确定两幅影像的线性关系，将参考影像与线性变换后的测试影像做差，最后用异常探测算子计算异常变化(Pieper 等，2015b)。其中典型相关分析CCA(Canonical Correlation Analysis)方法首先将两幅影像分别采用典型相关分析进行线性变换，将变换后的影像作差后用RX算法(Reed和Yu，1990；Schweizer和Moura，2000)计算异常变化；PCA方法采用相同流程，差别在于分别对两幅影像分别提取相同数量的主成分，再检测其异常变化(Pieper 等，2015a)。异常变化检测中常用的CC(Chronochrome)方法首先采用最小二乘法将一景影像向另一景影像投影，并对投影后的两景影像进行差值异常变化检测(Theiler，2008a)；CE(Covariance Equation)方法通过对两景影像进行白化处理，消除影像之间的辐射差异后检测异常像元(Theiler和Perkins，2006；Rotman和Shalev，2017)。然而这类高光谱异常变化检测方法都是通过直接抑制背景的方式来突出异常变化，在地物较为复杂的情况下，无法有效消除辐射差异，无法保证背景的一致性，难以整体抑制背景，突出异常变化像元(Acito 等，2014)。

本文针对变化的弱信号小目标的探测模型和方法进行了研究。通过先突出异常变化再抑制背景的方式对异常变化像元进行检测，与上述直接抑制背景的异常变化检测方法相比，更加达到突出异常变化目标的效果。由于异常变化在影像中相对独立，每一个异常成分都处于一个投影空间中，因此采用独立成分分析方法将异常变化投影到独立子空间中，进而突出异常。再通过异常探测方法将投影后的影像进行背景抑制，突出变化像元，达到异常变化目标和背景的有效分离，可以有效降低虚警率，提高探测率。

基于独立成分分析的异常变化检测方法通过RX异常探测方法判定异常变化像素，选定异常变化强度最大的异常像素为初始投影方向，而后对所有像素向初始化投影方向进行正交投影，并将最异常的像素标记为第二次投影方向，直到迭代次数达到独立成分个数。原理图如图1所示。方法具体步骤如下。

图 1 异常变化检测原理图 Figure 1 The principle diagram of anomaly change detection

基于独立成分分析的原理，需首先对差分影像进行白化预处理。白化的步骤如下：将差分后的高光谱影像记为R，该高光谱数据共有L个波段，每个波段共有I个像素，m_R和 ${{{\varGamma }}_{\rm{R}}}$ 分别表示差分影像的均值向量和方差矩阵。对方差矩阵进行奇异值分解，得到 ${{{\varGamma }}_{\rm{R}}}{{ = UD}}{{{U}}^{\rm T}}$ ，式中，U是L×L大小的矩阵，且U的每个列向量代表方差矩阵的特征向量；D是L×L大小的对角矩阵，对角线上的值代表方差矩阵的特征值，对差分影像进行白化处理，如下：

式中， ${{{V}}_{{\rm{1}},I}}$ 是所有元素都为1的I维行向量。白化后的影像各波段均值为0，方差为单位阵，并用r和z分别代表原始空间和白化空间中的影像光谱。

基于独立成分分析的原理，采用投影寻踪策略寻找与最大异常变化强度对应的正交投影方向 ${{{w}}_j}$ ，利用以峭度作为非高斯度量的快速ICA方法逐次迭代计算投影方向，并设定第 $j$ 次的投影方向与前 $j$ 次的投影方向相互正交。在ICA期望计算中选择函数形式g₃(x)=x³进行迭代计算，与传统ICA不同的是，该异常变化检测方法初始化向量w需要寻找差分影像中的最大异常变化强度像元作为初始投影方向，以得到最终的异常变化检测结果。

投影方向初始化就是寻找影像中异常变化像元，其光谱就是初始化的投影方向。对于某一给定像元i，其原始假设H₀和备择假设H₁之间的广义似然比由RX异常探测算法给出式(2)

式中， ${\hat{ \varGamma }}$ 是对背景协方差矩阵 ${{\varGamma }}$ 的最大似然估计，m为背景均值向量的估计值，对于白化后的影像，其RX计算公式可表示为

在对投影方向进行初始化后，则可以用该初始化投影矩阵提取异常变化像元。异常变化强度最大的像素的索引表示如下

计算像元的投影方向如下

假设白化后影像Z的像元光谱符合标准正态分布，并且 ${{{z}}_{{i^ * }}}$ 表示异常变化像素的光谱，则 ${{{s}}_{{{{w}}^ * }}} = {{{w}}^ * }^{\rm T}{{Z}}$ 与其他投影方向投影后的向量相比峭度较高，因此正则化向量 ${{{w}}^ * }$ 可以作为初始化的投影方向。对于第 ${i^ * }$ 个像素来说，它在相应异常类别中具有最高的异常度，因此当选定 ${{{w}}^ * }$ 为初始化向量，则计算得到的投影方向 ${{w}}$ 与 ${{{w}}^ * }$ 方向相近，同时可以保证峭度最大化。

在第 $j + 1$ 次迭代中，前j次的生成的正交投影向量都保存在矩阵W中，然后将白化后的影像向与W正交的子空间投影，公式如下

生成的新影像 ${{\tilde Z}}$ 的均值为0，协方差矩阵为 ${{P}}_{{W}}^ \bot $ ，对投影后的影像利用RX异常探测算子计算异常变化强度，仍然选取异常程度最大的像元光谱作为投影方向，如此迭代循环直到达到预设的独立成分个数。

针对异常变化检测易受配准误差影响这一问题，Theiler和Wohlberg(2012)提出局部匹配策略LCRA(Local Coregistration Adjustment)进一步减小不同时相影像带来的匹配误差。由于不同时相的真实数据中常存在配准误差，异常变化检测方法与LCRA相结合，进一步降低虚警率。由于LCRA方法的计算量与窗口大小成平方倍(Theiler和Wohlberg，2012)，同时对于变化检测而言，首先都需要对影像进行粗略的几何校正，保证两景影像的偏差在一像素左右，因此窗口大小为3既可减少计算量，又可取得较高精度。图2是完整的算法流程。

图 2 算法流程图 Figure 2 Flow chart of proposed algorithm

共采用两组实验数据验证该方法的有效性，其中模拟数据为其中一幅影像加入影像中并不存在的其他地物光谱，并以一定的比例与原始像元混合，作为异常变化；真实数据即采用最新发布的公开数据集对异常变化检测方法进行评估(Rossi 等，2014)。

采用ROC曲线和ROC曲线下的面积AUC值进行精度评价。其中，ROC曲线常用来评价高光谱异常变化检测算法中对异常变化的识别能力(Vongsy 等，2009；Wohlberg和Theiler，2010)。ROC曲线的横轴为虚警率，纵轴为探测率，在相同虚警率的情况下，探测率越高，算法的检测精度越好(Wang 等，2013)。AUC值(Jin和Ling，2005)方法通过计算ROC曲线下的面积来反映算法的检测精度，数值越大，精度越好。

第1组实验高光谱数据拍摄自EO-1卫星搭载的Hyperion传感器，影像地点为中国内蒙古自治区兴安盟。如图3所示，两幅高光谱影像大小为400×400，且影像拍摄时间分别为2010年4月和2010年6月，在去除了水吸收波段和高噪声波段后，两幅影像的波段数变为155个。由于两幅原始影像获取时间相近，可以假设影像中地物并未发生变化，而影像中的像素差异均来自辐射误差和噪声。因此对原始影像植入异常像元，作为异常变化目标，异常像元的光谱为城市光谱，与周围的植被像元具有明显的光谱差异，植入的异常像元共有5×5个，每一行代表一种城市光谱，每一列代表植入异常像素所占整个像素的比例，从左到右依次为100%、80%、60%、40%、20%。

图4(a)—(h)对应下列异常变化检测方法的结果图，分别为差值RX法、基于LCRA的差值RX法、CC法、基于LCRA的CC法、方差均衡化法、基于LCRA的方差均衡化法、ICA异常变化检测法、基于LCRA的ICA异常变化检测法，结果图为ENVI中经过相同的25个异常像元ROI拉伸后的效果。

从结果中可以看出，SD方法整体要优于CC方法，而CC方法整体要优于方差均衡化异常变化检测方法(CE)，然而AICA方法与以上3种方法相比，不仅在探测率上表现优异，能够检测到最多的异常像素，而且对背景的抑制效果也是最优的。所有加入LCRA匹配策略后的结果在第1组数据实验中，并没有表现出优势，因为这两幅影像经过了很好的几何校正，因此LCRA匹配策略在两景影像对应像素发生偏移的情况下，才能起到作用。

将模拟数据中不同时相影像通过变化向量分析CVA(Change Vector Analysis)，计算得到变化强度图(图5(a))。其中，强度图中越靠近白色，表明发生变化，越靠近黑色代表没发生变化。局部放大图(图5(b))表明，模拟影像中异常变化的像素点就叠加在变化的背景地物之上；而从模拟数据的异常变化检测结果(图5(c))中看出，本文方法能够有效抑制背景变化，突出异常变化。

图 3 模拟数据和异常变化参考图 Figure 3 The simulated images and anomaly change detection reference map

图 4 基于模拟数据的异常变化检测结果 Figure 4 The anomaly change detection result based on simulated images

图 5 模拟影像变化强度分析图 Figure 5 The change magnitude analysis map of simulated images

如图6所示，在不同背景地物中共添加了50个异常变化点，分别为场景A、B、C、D，采用LCRA校正后的ICA异常变化检测方法进行异常变化检测，检测结果图表明，在场景A、B、C、D中，尽管各自的背景变化不同，都能够将异常变化探测到。

图 6 不同变化背景下的LAICA异常变化检测结果 Figure 6 The LAICA anomaly change detection result in different change background

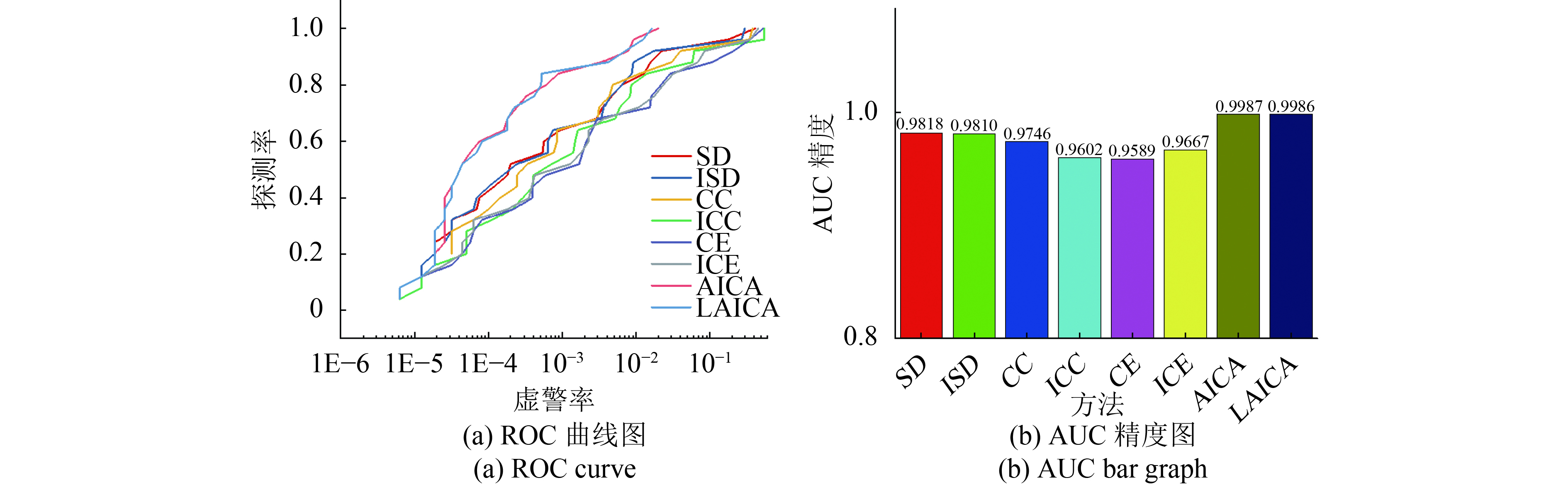
从图7的ROC曲线图和AUC精度结果中也可以得出一致的结论。图7中ROC曲线结果看出，ICA异常变化检测方法在虚警率处于1e⁻³—1e⁻²的情况下，探测率就已经达到0.9，并且在相同虚警率的情况下，探测率一直处于最高。AUC面积也同样可以看出基于投影寻踪的异常变化检测方法的总体精度最高，但是由于该原始影像已经经过精确的几何校正，因此未经过LCRA校正的投影寻踪异常变化检测方法精度更高。

图 7 基于模拟数据的精度评价结果 Figure 7 The precision evaluation of simulated images

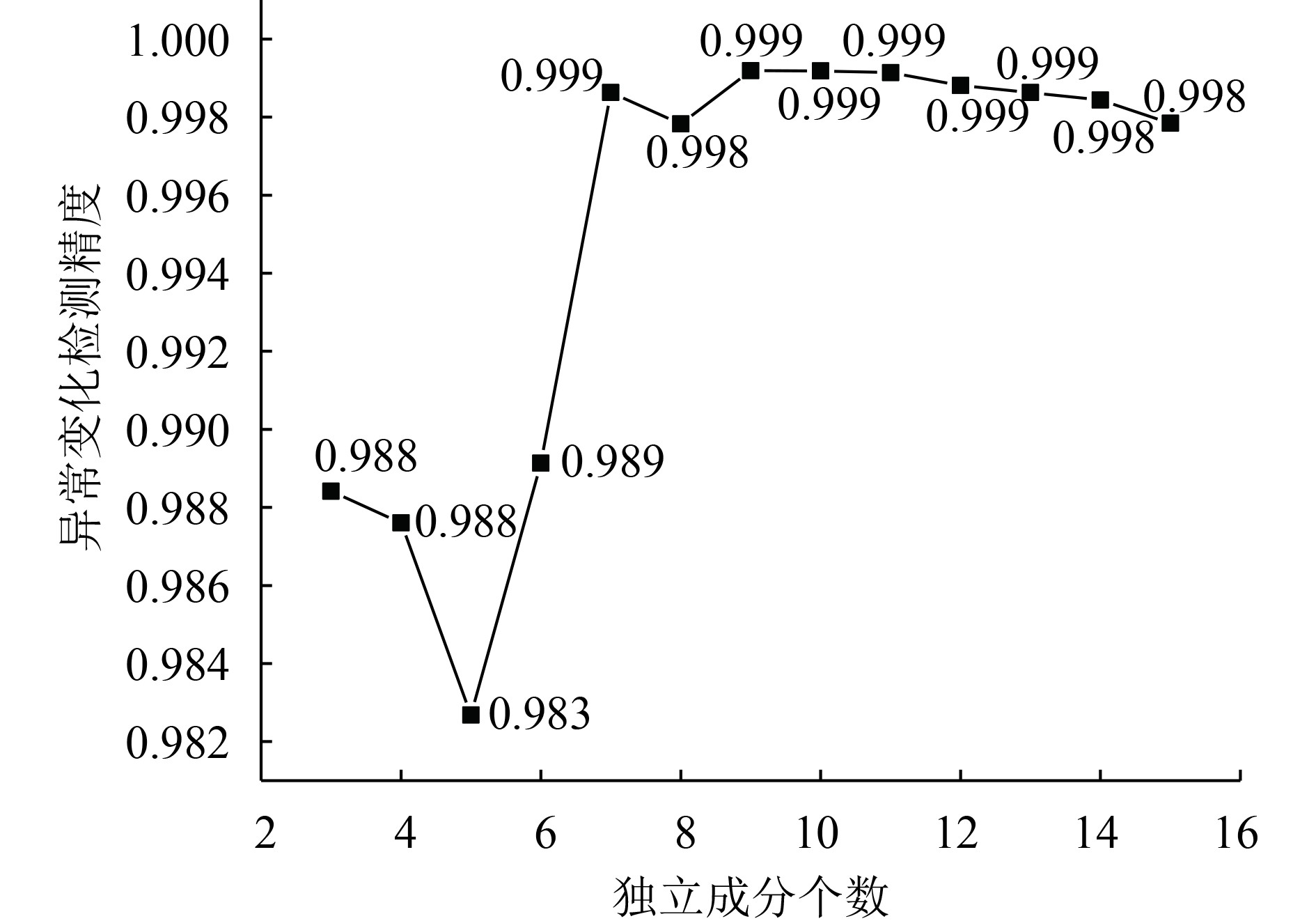
本文方法中仅存在一个参数—独立成分个数，因此图8分析了不同独立成分个数的情况下，ICA异常变化检测方法对应的结果精度，结果表明，当独立成分个数处于7—14，该方法的结果精度均处于最高，也就是说，独立成分个数对本方法的精度影响不大。即使在使用本方法过程中，独立成分个数设置不合理，过小或者过大，本文方法的精度也优于其他方法。

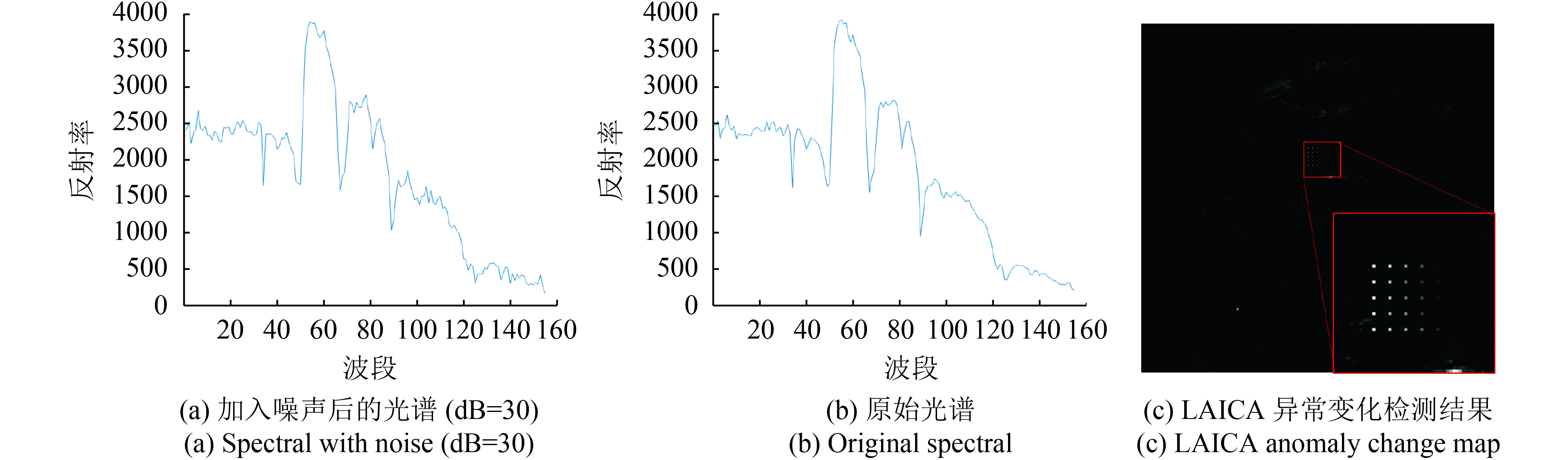
在原始的模拟影像，图3(a)中加入高斯白噪声，信噪比为30 dB，光谱差异如图9所示，采用LAICA异常变化检测方法仍然能够得到异常变化目标，本文方法的鲁棒性较好。

图 8 模拟数据参数分析 Figure 8 The parameter analysis of simulated images

图 9 LAICA算法鲁棒性分析 Figure 9 LAICA algorithm robustness analysis

该数据集采集计划由CISAM主办，并与多个大学同时合作完成，该数据集采集于2013年5月，拍摄地点在意大利的维亚雷焦市，因此数据集被命名为Viareggio 2013 trial(Rossi 等，2014)。在高光谱异常变化检测中需要有准确的参考影像对各种异常变化检测方法进行精度评价，但是目前公开的高光谱异常变化检测数据较少，因此本实验采用该数据集进行高光谱异常变化检测。

如图10中两幅影像分别拍摄于2013年5月8日和2013年5月9日，影像大小为450×375，共有128个波段。该数据集中的两幅影像经过几何校正和去除条带噪声等预处理后，影像数据中噪声为高斯白噪声。影像a(图10(a))在成像过程中受到了云的影响，而影像b(图10(b))拍摄期间晴朗无云，因而两幅影像由于天气原因产生辐射差异，造成背景像元的变化。该影像的场景为停车场，其中异常变化目标为停车场和道路上的车辆，影像c(图10(c))为参考异常变化目标。

图 10 真实数据和异常变化参考图 Figure 10 The real images and anomaly change detection reference map

从原始影像中可以看出，该高光谱影像在几何校正后影像左上角的房屋造成了较大的变形，在对两幅影像进行比对后发现，影像中房屋处仍然存在几何误差，因此本组实验中加入LCRA几何校正的异常变化检测方法均取得了较好的精度结果，同时该影像异常像元邻域内的背景像元光谱较为一致，因此采用LCRA方法可以有效抑制匹配误差从而得到更加准确的异常变化目标。图11中各异常变化检测结果所对应的方法与模拟数据的一致，局部放大结果图为ENVI中经过图10(c)中ROI拉伸后的效果。

图 11 基于真实数据的异常变化检测结果 Figure 11 The anomaly change detection result based on real images

从目视判别结果中可以看出加入LCRA后的异常变化检测结果的确有效抑制了很多的伪变化像元，CC和LCC方法的结果对比最为明显，而且从AICA和LAICA结果的对比来看，AICA红框左边检测出了很多的异常目标，然而这些目标并没有变化，而LAICA则有效抑制了这些异常目标，得到了更为准确的异常变化检测结果。与其他方法的对比来看，ICA异常变化检测方法的结果精度要明显优于其他方法，在放大的细节图中可以看出，ICA异常变化检测方法与LCC、CE、LCE方法相比，检测出了更多的异常目标，而与SD、LSD、CC方法相比，该方法有效的抑制了背景，虚警像元更少。

图12为异常变化检测的定量评价结果。从图12中可以看出，其中投影寻踪异常变化检测方法精度最高。与第1组实验不同的是，CE异常变化检测方法要好于CC法和SD异常变化检测法，原因是该数据集地物种类较少，且每种背景地物的分布较为连续，因此当进行方差均衡化操作时，背景像素可以更好地聚集在球面中。ICA异常变化检测方法仍然在较低虚警率的情况下，就能够达到很好的探测效果，且无论是否加入LCRA匹配策略，该方法都能得到最高的精度。由于真实数据存在较为明显的几何匹配误差，因此采用LCRA匹配策略后，所有方法的精度均提升了0.2左右。

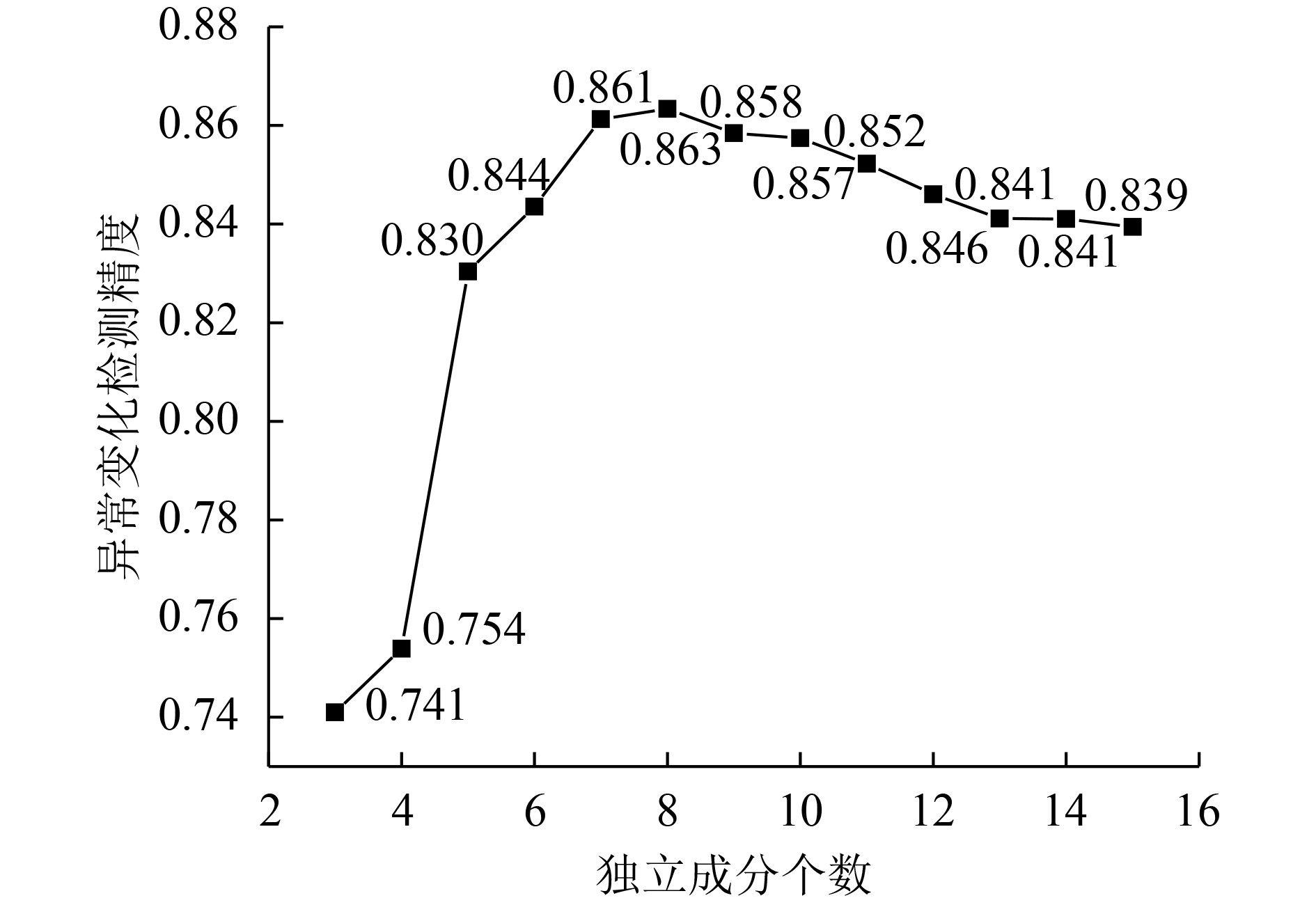
图13为分析不同独立成分个数的情况下，ICA异常变化检测方法对应的结果精度。结果表明，当独立成分个数大小适中，处于7—14之间时，该方法的结果精度均处于最高，体现了该方法的鲁棒性。只要在使用本文方法过程中参数大小设置合理，不要过小或者过大，本方法的精度都会优于其他方法。

图 12 基于真实数据的精度评价结果 Figure 12 The precision evaluation of real images

图 13 真实数据参数分析 Figure 13 The parameter analysis of real images

本文研究了针对弱信号小目标的高光谱异常探测模型和方法，通过研究，并利用模拟数据和真实数据进行比较验证，得到如下结论：

(1)传统的变化检测方法是直接抑制来发现异常变化信息，针对弱信号小目标，目标信号往往一起被抑制，造成探测精度低，虚警率高，本文方法是通过利用投影寻踪方法，将小目标信号投影到独立成分，强化小目标信号，然后再抑制背景，有效避免了弱信号小目标被抑制，从而可以提高弱信号小目标的检测精度。

(2)利用模拟数据和真实数据多探测精度进行了比较验证，得到结论为：利用模拟数据得到的检测精度为99%，利用真实数据得到的检测精度为86%，与传统异常变化检测算法相比，探测精度最高提高了9%。

(3)针对亚像元级异常变化目标，该方法与传统异常变化检测方法相比，精度提高了1%。

(4)本文研究方法仅有一个参数，且参数的选择对精度影响不大，表明该方法具有较强的鲁棒性。