| 业务化MODIS BRDF模型对冰雪BRDF/反照率的反演能力评估 |
收稿日期: 2018-01-22
2. State Key Laboratory of Remote Sensing Science, Beijing Normal University, Beijing 100875, China
地表反照率即地表总反射辐射与总入射辐射的比率(Wu 等,2010;Burakowski 等,2015),是表征地表能量收支平衡的一个重要参数,它对全球气候变化、水循环等具有重要意义。与其他自然地表类型相比,冰雪覆盖地表通常对太阳短波辐射具有较高的反射,新雪的反射率超过0.8(Stroeve 等,2005;Wu 等,2010),这使得入射的太阳辐射绝大部分被反射,只有很少部分被吸收。研究表明,积雪增加了从地球表面反射的太阳辐射的比例,与无雪表面相比产生了1.5—4.5 ℃的冷却效果(Mote,2008;Burakowski 等,2015)。冰川和积雪对气候变化极其敏感,冰雪反照率的细微变化,都会影响到地气系统的能量平衡,进而可能会影响气候变化(蒋熹,2006)。对于气候变化的研究,在全球尺度上,5—10年内地表反照率产品的误差要求为0.02—0.05(Henderson-Sellers和Wilson,1983);敏感性分析表明,区域气候模拟要求反照率的误差小于±0.02(Jacob和Olioso,2005;Qu 等,2015)。因此,冰雪反照率产品的精度对研究气候变化、冰雪水文过程等尤为重要。
地球上,冰雪主要分布在高山或极地区域,地面测量数据获取相对困难。卫星遥感技术具有多尺度、多时相、多光谱等优势,在研究冰雪动态特征变化过程中发挥了重要的作用。目前AVHRR、MODIS、GLASS以及VIIRS等都提供了全球长时间序列的地表反照率产品,对地表的研究起到了至关重要的作用。但是对于冰雪反照率的反演精度依然有待提高(Csiszar和Gutman,1999;Stroeve 等,2005, 2006;Wu 等,2010;Liu 等,2013;Wang 等,2017)。其中基于半经验、线性核驱动模型RTLSR(Rossthick- LiSparseR)生产的全球MODIS地表反照率产品使用最为广泛,该产品提供了全球每日和8天时间分辨率的反照率产品。但由于RTLSR模型是基于植被—土壤系统建立的,而植被覆盖地表和冰雪覆盖地表的反射特征存在显著的差异,如植被覆盖地表在后向散射方向存在较强的反射,而冰雪覆盖地表具有较强的前向散射特性(瞿瑛 等,2016)。因此,使用RTLSR模型反演冰雪地表类型的反照率时,其中蕴含的物理意义不明确,从而在理论上有可能影响其反演精度。Kokhanovsky等针对冰雪的反射特征,结合光线追踪的方法,提出了简化的渐进辐射传输模型ART(Asymptotic Radiative Theory)(Kokhanovsky和Breon,2012)。该模型将雪粒子作为不规则粒子,同时考虑了雪粒径和污染物,并通过实测站点数据和POLDER卫星数据验证了模型的精度(Kokhanovsky和Schreier,2009;Negi和Kokhanovsky,2011;Kokhanovsky和Breon,2012)。因此,ART模型已被广泛应用于模拟冰雪二向性反射特征,反演雪粒径、污染物和冰雪反照率等参数(潘海珠 等, 2015a,2015b;Qu 等,2016;Shi 等,2017;邵东航 等,2017)。
目前,国内外研究学者针对RTLSR模型和ART模型拟合冰雪二向反射特征和反演反照率等方面进行了较系统的研究,也取得了较大的进展。如Lyapustin等基于2008年春季ARCTAS(Arctic Research of the Composition of the Troposphere from Aircraft and Satellites)实验,详细分析了RTLS (Rossthcik-LiSparse)模型与AART (Asymptotic Analytical Radiative Transfer)模型对CAR(Cloud Absorption Radiometer)数据的拟合精度(Lyapustin 等,2010);Kokhanovsky和Breon(2012)比较了ART模型和RTLSR模型反演POLDER多角度冰雪数据的精度,结果发现,在模型缺少约束的情况下,尤其在几何光学核系数为负值时,RTLSR模型可在一定程度上拟合冰雪的反射特征(Wu 等,2011),这主要是由于几何光学核系数的负值,可能导致几何光学核形状变形,从而在一定程度上补偿冰雪的散射特征,但这种情况并不能解释冰雪散射的物理意义,且可能导致病态反照率反演(Jiao 等,2015),因此,MODIS业务化算法对RTLSR模型的核系数进行了简单约束(即反演出的核系数小于0时,取核系数为0),在RTLSR模型评估过程中本文也采取了相同的约束措施。
本文收集了2006年和2008年多角度、多光谱POLDER冰雪反射率数据,结合ART模型,系统地评估了RTLSR模型在模拟冰雪二向反射特征及反演反照率方面的能力。通过ART模型筛选了高质量的POLDER多角度冰雪反射率数据,以ART模拟结果为基准,评估了RTLSR模型对于POLDER冰雪数据的方向反射率和反照率的反演精度。本研究对于RTLSR模型的改进,冰雪BRDF模型的发展以及冰雪反照率的反演等有重要的参考意义。
2、数据与方法 (2.1) POLDER数据及预处理POLDER-3仪器主要用于测量地面大气系统散射光的方向特征和极化特征,可以长时间序列获取地面多角度、多光谱、多极化的观测数据。该仪器主要由2维CCD矩阵、滤波器和偏振器以及宽视场透镜等组成,最大视场角为114°,星下点的空间分辨率为6 km×7 km,像元大小约为6.17 km,沿着轨道方向的观测角可以达到±61°,垂直于轨道方向的观测角可以达到±50°。POLDER-3辐射计通过视场重叠的方法获取多角度观测数据,单次过境时最多可观测16个不同的角度。与POLDER-1和2相比,POLDER-3增加了1020 nm波段,共包括可见光与近红外9个波段,其中490 nm,670 nm和865 nm包含光的极化信息。法国气候与环境科学实验室将筛选出的高质量地表反射率数据,分别基于IGBP与GLC2000土地分类系统,生产了按年和按月的BRDF产品数据集。
本研究使用的数据是基于IGBP分类系统按月积累的多角度冰雪反射率数据,该数据经过地理编码、辐射定标、去云和大气校正等处理,以获取每个轨道的地表二向反射因子。POLDER多角度冰雪数据存储方式为ASCII文件,主要包括像元的经纬度、IGBP地表覆盖类型、NDVI、过境轨道个数、观测方向个数、像元均质度、观测日期、太阳天顶角、观测天顶角、相对方位角以及各波段的反射率等。每个像元每月累积的观测角可以达到300多个,基本上可以实现对地表的全方位观测。虽然POLDER BRDF数据库设置了质量控制措施,但由于ART模型主要适用纯雪覆盖区域,对于包含其他地类的混合像元,反演效果不理想(Kokhanovsky和Breon,2012)。为尽可能保证像元的均质性和质量,使ART模型高精度地拟合雪的多角度反射率数据,本文针对POLDER粗空间分辨率像元,主要采取了以下处理:首先,筛选出覆盖度为100%的多角度冰雪数据;然后,基于490 nm波段的反射率大于0.4这一约束条件(Qu 等,2014),剔除不适于本研究的数据集;最后,针对ART模型在1020 nm波段对冰雪观测数据的拟合效果,选取均方根误差(RMSE)小于0.04为阈值,分别对6个波段的多角度数据的质量进行进一步优化和约束,共筛选出284套POLDER多角度冰雪数据集,每个波段约为94000多个观测,用于RTLSR模型的评估。
(2.2) MODIS线性核驱动模型核驱动模型最初由Roujean发展而来(Roujean 等,1992),其表达式如下
| $ \begin{split} R\left({{\theta _i},{\theta _r},\varphi,{\textit{λ}} } \right) = & {f_{{\rm{iso}}}}\left({\textit{λ}} \right) + {f_{{\rm{vol}}}}\left({\textit{λ}} \right){K_{{\rm{vol}}}}\left({{\theta _i},\theta_r,\varphi } \right) +\\ & {f_{{\rm{geo}}}}\left({\textit{λ}} \right){K_{{\rm{geo}}}}\left({{\theta _i},{\theta _r},\varphi } \right) \end{split} $ | (1) |
式中,R(θi,,θr,φ,λ)表示第λ波段的二向反射分布函数,Kvol(θi,,θr,φ)为体散射核,Kgeo(θi,,θr,φ)为几何光学核,它们分别是关于太阳天顶角(θi)、观测天顶角(θr)、相对方位角(φ)的函数;fiso、fvol和 fgeo分别为各向同性散射、体散射和几何光学散射所对应的权重系数;通过确定了体散射核和几何光学核后,根据多角度反射率数据,使用最小二乘法即可反演出最优的3个权重系数 fiso、fvol和 fgeo,然后,可以根据3个权重系数前向计算任意入射方向和观测方向的反射率。
目前,MODIS业务化算法采用罗斯表层核—李氏稀疏互易核RTLSR(RossThick-LiSparseR)的组合形式。罗斯表层核(RossThick)描述了水平均匀植被的各向异性散射,李氏稀疏互易核(LiSparseR)描述了植被3维结构及其阴影作用所产生的几何光学散射,RossThick核和LiSparseR核是针对植被—土壤系统的建模,因此RossThick核和LiSparseR核的组合可以理论上较好地拟合植被—土壤系统的BRDF数据,进而较准确地估算地表反照率(Lucht 等,2000;Schaaf 等,2002;白冬妮 等,2017)。但植被的散射特征与冰雪的散射特征存在显著差异,因此采用RTLSR模型拟合冰雪BRDF数据和反演冰雪反照率有待进一步评估。RossThick核和LisparseR核计算公式如下
| ${K_{{\rm{thick}}}} = \frac{{({\text{π}} /2 - {\rm{\zeta }})\cos {\rm{\zeta }} + \sin {\rm{\zeta }}}}{{\cos {\theta _i} + \cos {\theta _r}}} - \frac{\text{π}}{4}$ | (2) |
| $\cos {\rm{\zeta }} = \cos {\theta _i}\cos {\theta _r} + \sin {\theta _i}\sin {\theta _r}\cos \varphi $ | (3) |
| $ \begin{split} {K_{{\rm{geo}}}} = & O({\theta _i},{\theta _r},\varphi) - \sec {\theta _i}' - \sec {\theta _r}' + \\ & \frac{1}{2}(1 + \cos {\rm{\zeta '}})\sec {\theta _i}'\sec {\theta _r}' \end{split} $ | (4) |
| $O = \frac{1}{\text{π}}(\arccos X - X\sqrt {1 - {X^2}})(\sec {\theta _i}' + \sec {\theta _r}')$ | (5) |
| $X = \frac{h}{b}\frac{{\sqrt {{D^2} + {{(\tan {\theta _i}'\tan {\theta _r}'\sin \varphi)}^2}} }}{{\sec {\theta _i}' + \sec {\theta _r}'}}$ | (6) |
| $D = \sqrt {{{\tan }^2}{\theta _i}'{{\tan }^2}{\theta _r}' - 2\tan {\theta _i}'\tan {\theta _r}'\cos \varphi } $ | (7) |
| $\cos {\rm{\zeta '}} = \cos {\theta _i}' \cdot \cos {\theta _r}' + \sin {\theta _i}'\sin {\theta _r}'\cos \varphi $ | (8) |
| $\theta ' = \arctan (\frac{b}{r}\tan \theta)$ | (9) |
针对MODIS业务化算法,h/b=2,b/r =1。计算反照率时,由于RossThick核和LiSparseR核的积分可以预先求出,然后将核积分以 fiso、fvol和 fgeo为权重相加,即可反演出相应的黑白天空反照率,其表达式为
| $ \begin{split} {\rho _{{\rm{bsa}}}}({\theta _i},{\textit{λ}}) = & \frac{1}{{\text{π}} }\int_0^{2{\text{π}} } {\int_0^{{\text{π}} /2} {{K_k}({\theta _i},{\theta _r},{\varphi},{\textit{λ}})} }\\ & \sin {\theta _r}\cos {\theta _r}{\rm{d}}{\theta _r}{\rm{d}}\varphi \end{split} $ | (10) |
| ${\rho _{{\rm{ws}}{\rm{a}}}}({\textit{λ}}) = 2\int_0^{{\text{π}} /2} {{\rho _{{\rm{bs}}{\rm{a}}}}({\theta _i},{\textit{λ}})\sin {\theta _i}\cos {\theta _i}{\rm{d}}{\theta _i}} $ | (11) |
式中,ρbsa为黑天空反照率,ρwsa为白天空反照率,黑天空反照率和白天空反照率均是在相对理想的条件下的定义,这两种反照率的线性加权即可得到地表真实反照率,如式(12)
| $\alpha ({\theta _i}) =(1 - S){\rho _{{\rm{bs}}{\rm{a}}}}({\theta _i},{\textit{λ}}) + S{\rho _{{\rm{wsa}}}}$ | (12) |
式中,S是天空散射光所占的比例,对于植被地表类型,该式可以较好的估算地表真实反照率。式(12)计算得到的是窄波段反照率,对于宽波段反照率,可以采用从窄波段到宽波段的反照率转换公式得到(Liang,2001;Liang 等,2003)
| $ \begin{split} \alpha = & 0.112{\alpha _1} + 0.388{\alpha _2} - 0.266{\alpha _3}+\\ & 0.668{\alpha _4} + 0.0019 \end{split} $ | (13) |
渐进辐射传输模型,又称双参数模型,该模型主要包括雪粒径和污染物两个参数,雪粒径主要影响近红外波段的吸收,污染物主要影响可见光波段的吸收(Kokhanovsky和Zege,2004)。由于ART模型简洁,参数较少,可以快速反演雪颗粒、污染物以及冰雪反照率等参数,因此被广泛使用(王杰 等,2014;潘海珠 等,2015a;Qu 等,2016;Shi 等,2017;邵东航 等,2017)。Qu等(2016)基于ART模型模拟冰雪BRDF数据库作为先验知识反演北极地区短波段的反照率;Shi等(2017)对于地表积雪类型,采用ART模型模拟积雪二向反射因子,用于MODIS多参数反演等。ART模型计算公式如下
| $ R({\theta _i},{\theta _r},\varphi) = {R_0}({\theta _i},{\theta _r},\varphi) \cdot {\rm{exp}} {\rm{(}} - \alpha {K_0}({\theta _i}){K_0}({\theta _r})/{R_0}({\theta _i},{\theta _r},\varphi){\rm{)}} $ | (14) |
| ${R_0}({\theta _i},{\theta _r},\varphi) = \frac{{(A + B({\cos\theta _i} + {\cos\theta _r})) + ({\cos\theta _i}{\cos\theta _r} + P(\zeta))}}{{4({\cos\theta _i} + {\cos\theta _r})}}$ | (15) |
| ${K_0} = \frac{3}{7}(1 + 2\cos\theta)$ | (16) |
| $ \alpha = \sqrt {4{\text{π}}L\left({\chi + M} \right)/{\textit{λ}} } $ | (17) |
式中,R0表示半无限、非吸收(semi-infinite non-absorbing)介质的反射率函数,λ表示波长(单位为m);A,B,C的值分别为1.247,1.186,5.157。χ表示冰晶体复折射指数的虚部,L是与雪粒径有关的参数,大约为13d,d表示雪粒径(单位为m);M是与污染物浓度有关的参数,θi、θr和φ分别表示太阳天顶角、观测天顶角、相对方位角,单位为弧度,ζ为散射相角(单位为度)。
ART模型的主要参数为L和M,因此想要得到完整的ART模型计算公式,首先应反演出参数L和M。Kokhanovsky等基于ART理论推导出单一波段反演雪粒径和污染物的算法,本文选择1020 nm波段进行雪颗粒反演,选择490 nm波段进行污染物反演(Kokhanovsky和Schreier,2009;王杰 等,2014),其计算公式如下
| $L = \frac{{{{\left({\dfrac{{{R_0}}}{{{K_0}}}\ln (\dfrac{{{R_0}}}{R})} \right)}^2}\times{{\textit{λ}}_{1020}}}}{{4{\text{π}}{\chi _{1020}}}}$ | (18) |
| $M = \frac{{{{\left({\dfrac{{{R_0}}}{{{K_0}}}\ln (\dfrac{{{R_0}}}{R})} \right)}^2}\times{{\textit{λ}} _{490}}}}{{4{\text{π}} L}} - {\chi _{490}}$ | (19) |
在计算L时,由于污染物对1020 nm波段吸收较弱,取M为0,λ1020为1020 nm的波长,
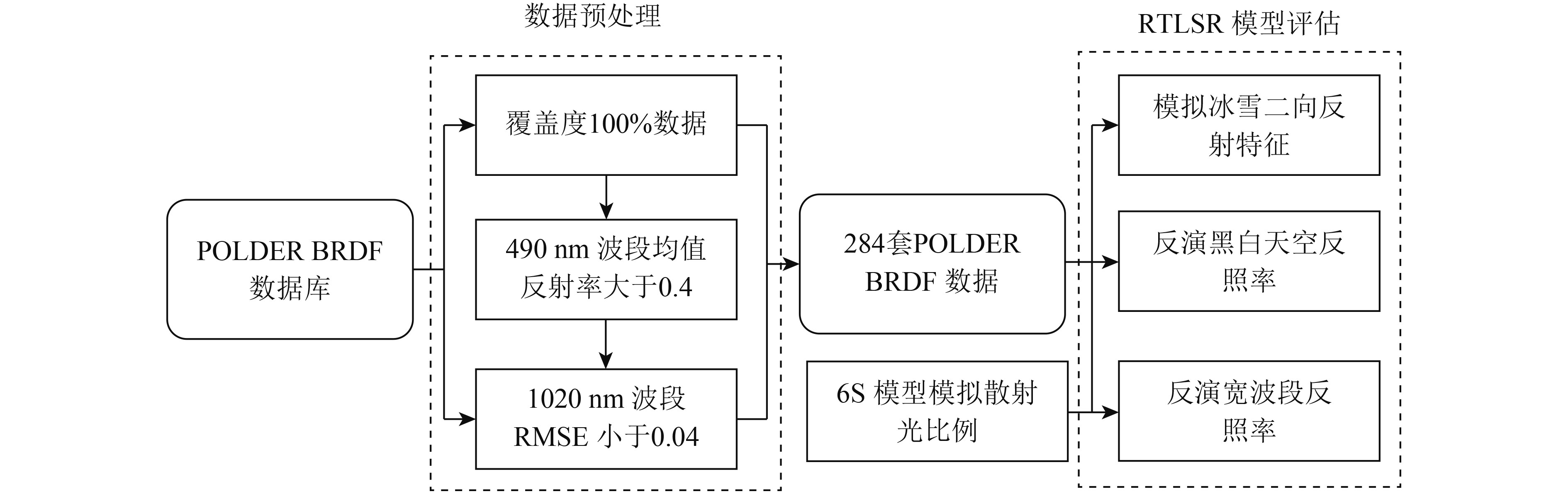
为了较为准确表征和量化POLDER数据的冰雪二向性反射和反照率,本文通过引入ART冰雪散射物理模型,以便于从POLDER数据库中筛选出高质量的冰雪反射率数据,用于表征冰雪总体的二向性反射特征,进而反演其反照率作为参考,具体评估流程如图1所示。首先对POLDER数据进行预处理,然后以ART模型筛选的高质量POLDER冰雪反射率数据作为实验数据集,最后将ART模型拟合POLDER数据的冰雪反射数据、反演黑白天空反照率和地表真实反照率等作为参考,评估RTLSR模型在拟合POLDER多角度冰雪二向反射特征与反演反照率的能力。在反演地表真实反照率方面,需计算散射光比例。6S大气校正模型已被广泛应用于模拟散射光的比例(Kimes,1983),通过该模型可以进行不同地表覆盖类型的散射光比例的模拟。通过研究发现,6S模型模拟的散射光比例与太阳天顶角和地表反射率等有关,本文为了精确计算散射的比例,建立了太阳天顶角、地表反射率和散射光比例的查找表,具体的参数设置如表1所示,进而提取出对应POLDER像元的散射光比例,用于计算地表真实反照率。
|
| 图 1 RTLSR模型评估流程图 Figure 1 The flow chart of model estimating |
|
|
表 1 6S模型输入参数 Table 1 The input parameters of the 6S model |
为了详细直观分析ART模型与RTLSR模型在模拟冰雪二向反射特征的差异,本文首先选取了一组典型的POLDER多角度冰雪反射率数据,时间为2006年4月,经纬度分别为52.1° W,78.03° N,太阳天顶角范围为63°—75°,角度分布情况如图2所示,横坐标代表主平面,纵坐标代表垂直主平面。较大的实点表示太阳入射方向,较小的实点表示观测方向,不同的颜色表示不同的太阳入射方向以及其所对应的观测方向。

|
| 图 2 POLDER数据角度分布图 Figure 2 Angle distribution of POLDER data |
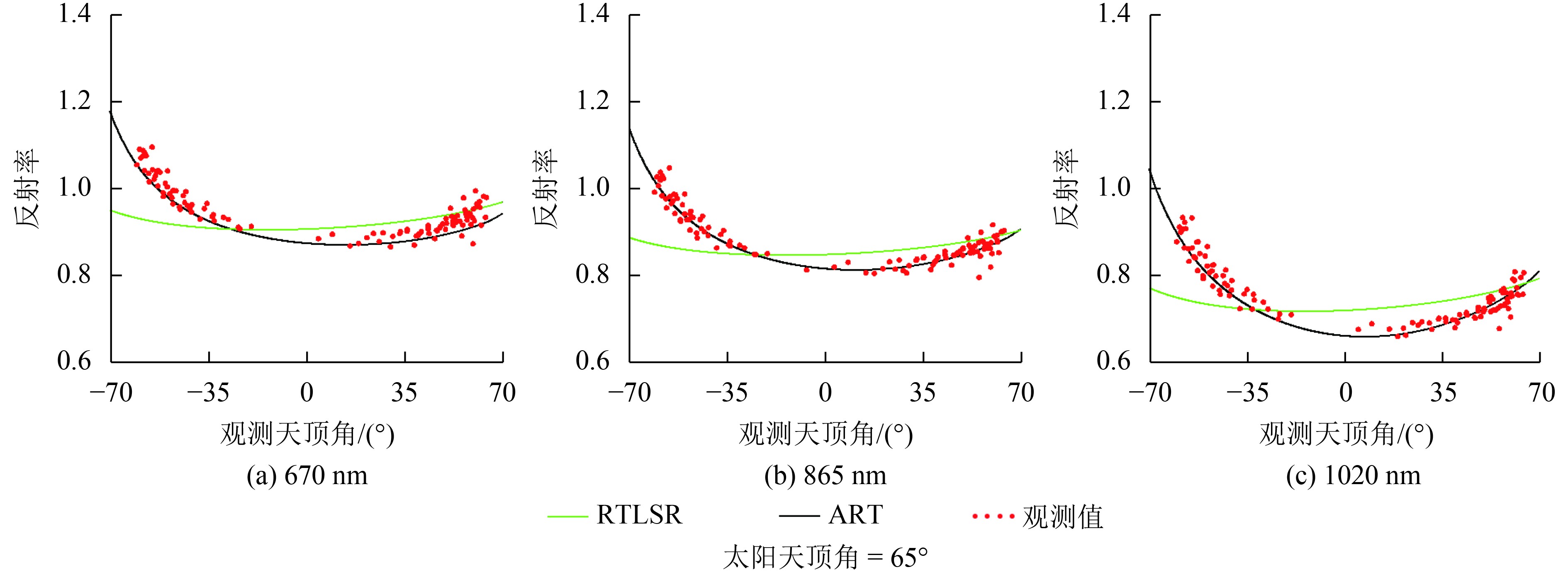
通过分别使用ART模型与RTLSR模型对该组典型数据进行拟合,绘制出两个模型在主平面的BRDF形状。65°为POLDER传感器过境时的太阳天顶角,选用3个常用波段,其中心波长分别是670 nm、865 nm和1020 nm,结果如图3所示。图3中,负坐标方向代表前向,正值代表后向。
从图3可以很明显看出,ART模型对所选择的POLDER冰雪反射率数据有很好地拟合结果,能够准确表征冰雪的二向反射特征,即冰雪前向散射高于后向散射的特点;而RTLSR模型的模拟和POLDER的冰雪观测数据有较大的差异,拟合线基本趋于直线,与冰雪的二向反射特征存在显著差异,主要特征为后向散射稍大于前向散射,这与冰雪的实际反射特征不符合。
|
| 图 3 ART模型与RTLSR模型拟合POLDER数据主平面冰雪BRDF形状 Figure 3 ART model and RTLSR model simulated POLDER data principal plane snow/ice BRDF shape |
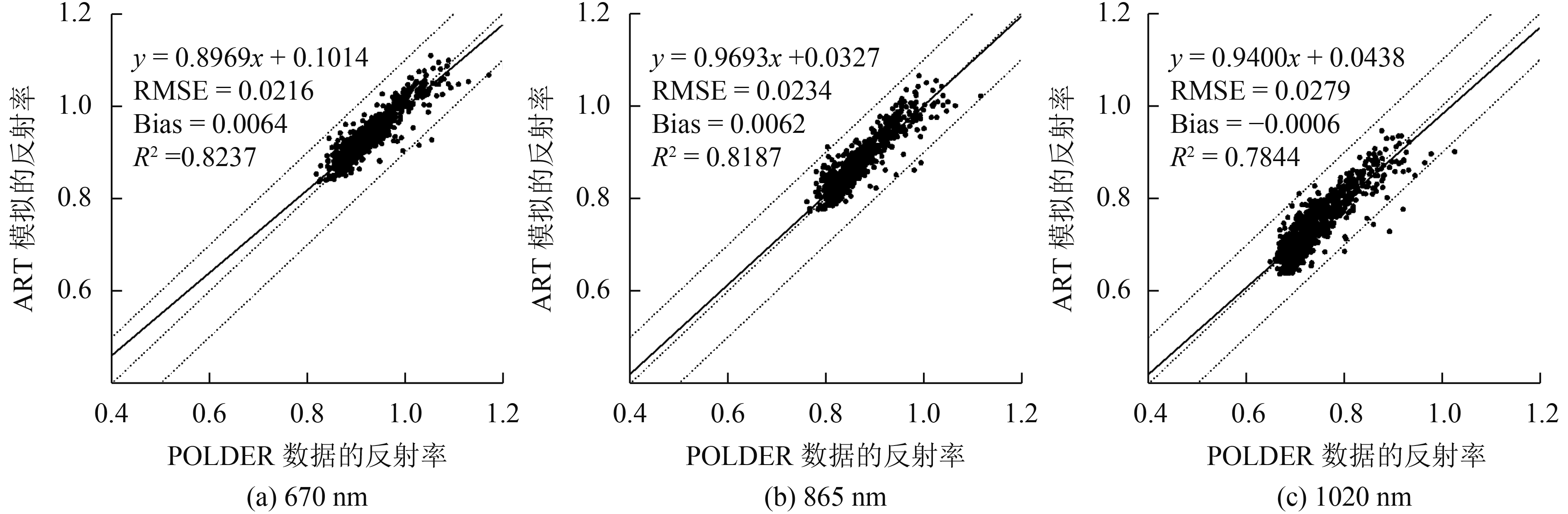
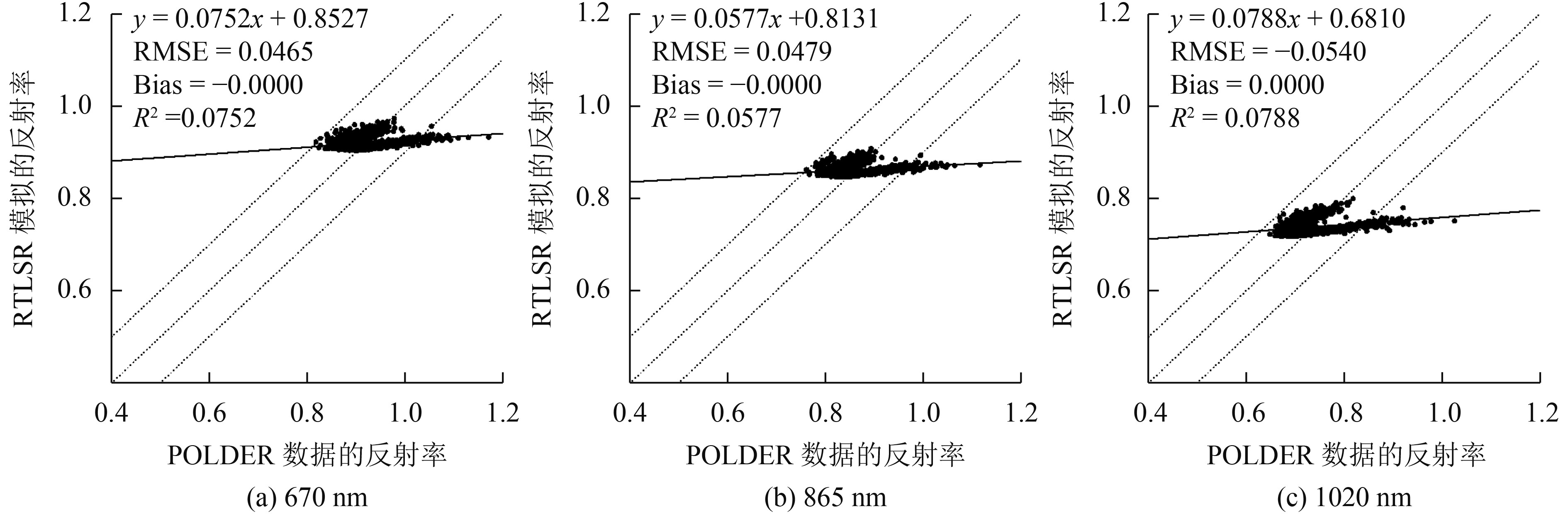
为了进一步定量分析,本文画出了ART模型与RTLSR模型拟合POLDER数据的散点图(图4、图5)。很明显,ART模型模拟结果与POLDER冰雪观测数据存在很高的相关性,其决定系数均超过0.78,RMSE均小于0.03;而RTLSR模型的模拟结果,与POLDER冰雪观测几乎不相关,其决定系数均小于0.1,RMSE整体偏高。随着波长的增加,ART模型与RTLSR模型拟合POLDER观测数据的RMSE也相应增大,但RTLSR模型拟合的RMSE结果相较于ART模型增幅更大,拟合结果也相对较差。尤其是在1020 nm波段,RTLSR模型拟合POLDER数据的RMSE高达0.054。
|
| 图 4 ART模型拟合POLDER数据散点图(L约为3.692 mm,M为0) Figure 4 ART model simulates POLDER data scatter plot |
|
| 图 5 RTLSR模型拟合POLDER数据散点图 Figure 5 RTLSR model simulates POLDER data scatter plot |
采取同样的方法,基于筛选的284套POLDER高质量多角度冰雪反射率数据,我们对RTLSR模型拟合冰雪二向反射特征的能力进行了总体评估,如图6所示。

|
| 图 6 ART模型与RTLSR模型拟合POLDER高质量数据密度图 Figure 6 ART model and RTLSR model simulate high-quality POLDER data density diagram |
从图6可知,ART模型的决定系数随着波段的增加而增加,在1020 nm波段,决定系数最高可达到0.763;均方根误差RMSE随着波段的增加先降低后增加,在865 nm波段达到最小为0.0288;而RTLSR模型的决定系数和均方根误差都随着波段的增加而增加,在1020 nm波段,其决定系数最高为0.410,均方根误差为0.0498,相对于ART模型拟合的RMSE结果增大了约53.70%。对于筛选出的高质量POLDER冰雪反射率数据而言,ART模型拟合POLDER整体数据相关性较高,RMSE较小;而RTLSR模型拟合效果相对较差。这一结果表明,将基于植被—土壤系统建立的RTLSR模型用于冰雪类型时会存在明显问题。具体而言,植被通常具有较强的后向散射,而冰雪具有较强的前向散射,因此RTLSR模型拟合冰雪反射率,致使RMSE结果整体偏高。然而,基于冰雪散射特征建立ART模型能较好的表征冰雪的散射特征。结果表明,RTLSR模型在拟合POLDER整体数据方面,短波段拟合的RMSE结果要稍优于长波段,这可能由于:一方面,由于大气瑞利散射影响,使冰雪的反射特征在短波段处更加趋于各向同性散射(Hudson 等,2006);另一方面,由于本文通过对核系数的约束,使得RTLSR模型在拟合POLDER冰雪多角度数据时,各向同性核起主导作用,体散射核次之。
(3.2) 黑白天空反照率估算精度因为反照率是方向反射率在半球空间的积分,这一过程会对BRDF的反射特征起到平滑作用,因此,即使在ART模型和RTLSR模型对冰雪方向反射特征的拟合,存在明显差异的情况下,进一步研究它们对反照率反演的差异仍具有重要意义。在此,分别使用ART模型与RTLSR模型反演POLDER多角度冰雪数据的反照率,分析比较了两个模型在反演反照率的差异。在此,假定ART模型反演的高质量POLDER多角度数据的反照率为“真值”,评估RTLSR模型反演的反照率,相对于ART模型反演结果的差别,以分析RTLSR模型反演冰雪反照率的能力。
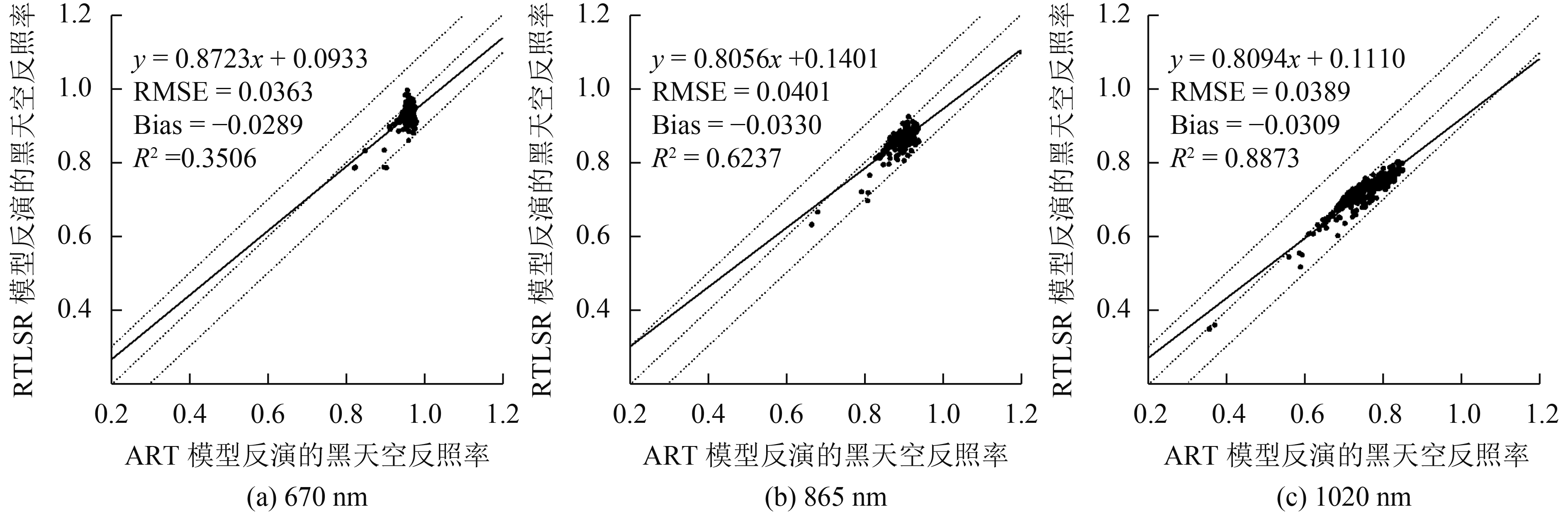
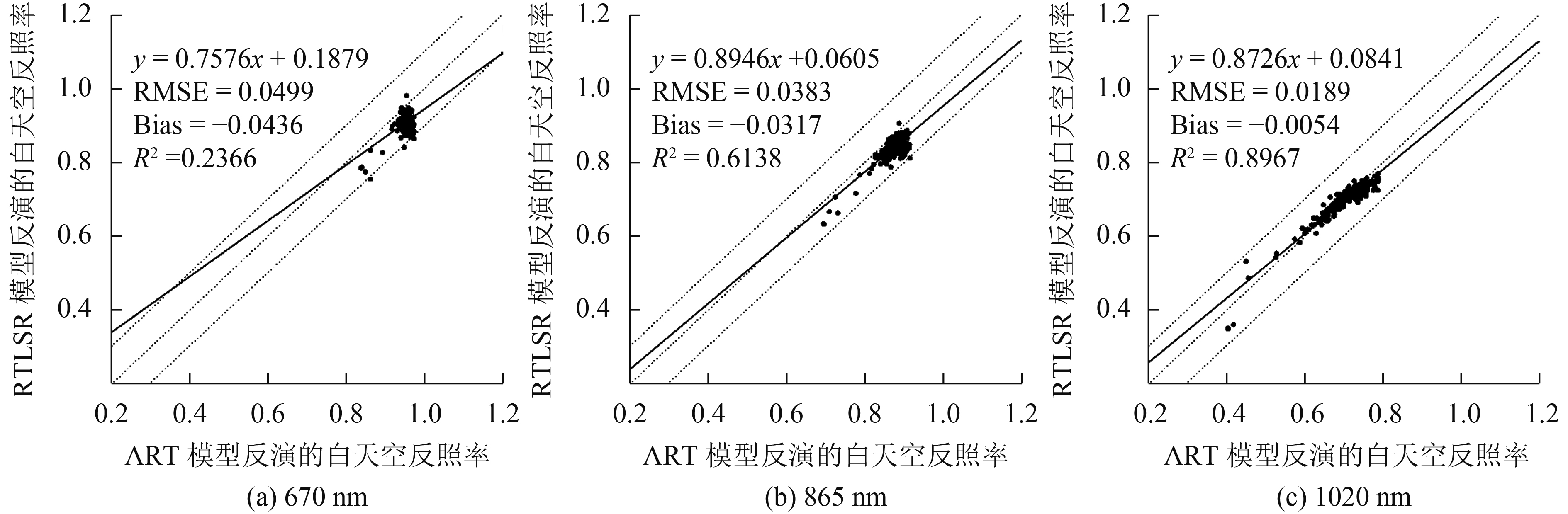
图7、图8表示了通过两模型反演地表反照率的散点图。很明显,ART模型和RTLSR模型所反演的黑白天空反照率随着波段的增加相关性也在增加,在1020 nm波段决定系数均超过0.88;而均方根误差随波段的变化而不同,从0.0189—0.0499。ART模型和RTLSR模型反演的黑天空反照率的均方根误差在670 nm取得最小值为0.0363,而白天反照率在1020 nm取得最小值为0.0189。总体上,RTSLR模型反演的黑白天空反照率相较于ART模型在不同的波段均存在不同程度的低估问题。
|
| 图 7 ART模型与RTLSR模型反演黑天空反照率散点图 Figure 7 Inversion of black sky albedo by ART model and RTLSR model scatter plot |
|
| 图 8 ART模型与RTLSR模型白天空反照率散点图 Figure 8 Inversion of white sky albedo by ART model and RTLSR model scatter plot |
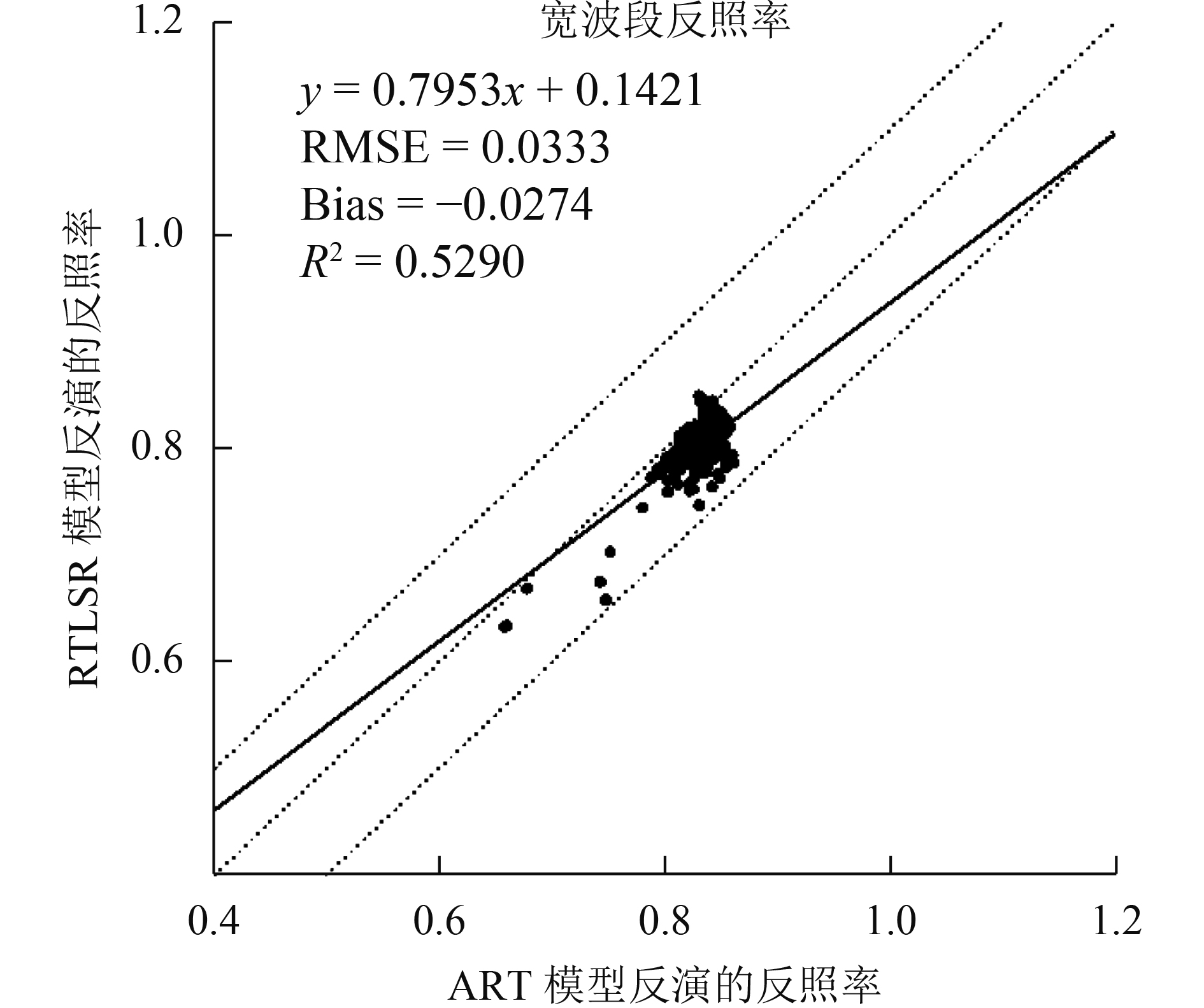
为了进一步评估两模型在反演真实反照率的差异性,本文通过6S模型模拟冰雪覆盖类型的散射光比例(Vermote 等,1997;Doyle和Dorling,2002)。进而可通过式(13)计算真实反照率,如图9所示。可知,ART模型与RTLSR模型反演的宽波段反照率决定系数为0.529,均方根误差0.0333,RTLSR模型反演的真实反照率与ART模型相比也存在明显的低估,其平均偏差可达到0.0274。
|
| 图 9 ART模型与RTLSR模型宽反照率散点图 Figure 9 Inversion of broadband albedo by ART model and RTLSR model scatter plot |
值得注意的是,虽然RTLSR模型相对于ART模型存在较为显著的低估,但是,在490 nm波段,RTLSR模型反演的黑白天空反照率均存在大于1的现象,其中,大于1的黑天空反照率,占高质量数据的21.479%,而白天空反照率占高质量数据的0.352%,从而导致在该波段存在一定比例真实反照率大于1,这显然有悖于能量守衡的基本原理。
4、结 论本文利用2006年和2008年POLDER多角度冰雪反射率数据,结合渐进辐射传输模型,分别从冰雪二向反射特征以及反照率方面全面评估了RTLSR模型表征冰雪二向性反射特征和反演反照率的能力,得出以下结论:
(1) 理论上,由于RTLSR模型建立在植被—土壤系统散射特征的基础上,其拟合POLDER多角度冰雪反射率数据方面存在不足,RMSE整体偏高。因此,RTLSR模型在拟合多角度冰雪反射率数据时,有待于进一步改进。
(2) 因为反照率为BRDF在半球空间的积分,虽然RTLSR模型拟合冰雪BRDF数据能力较差,但在反演冰雪反照率方面,RTLSR模型反演的黑白天空反照率与ART模型的差异相对较小,尤其在1020 nm波段,但RTLSR模型反演的反照率相较于ART模型整体上仍存在明显的低估。
在缺少反照率站点观测数据的情况下,本文将ART模型反演的结果作为参照,虽然对所用的POLDER冰雪BRDF数据进行了较为严格的约束,但该策略必然会由于采用了ART模型而引入模型误差。这从ART模型的模拟结果和POLDER冰雪数据的对比分析中可以看出。因此,为了使该评估更为准确,对应观测站点实时反照率的观测显得尤为必要。因此在今后的研究工作中,我们将应用观测站点数据对不同模型进行更为全面评估。
本文研究结果表明,RTLSR模型在拟合冰雪二向反射特征以及反演反照方面确实有待改进。Qu 等(2014)基于RPV模型对RTLSR模型进行了改进,增加了针对冰雪散射特征的核,从而较大程度改进了该模型对冰雪散射的拟合能力,尤其是在太阳天顶角较低的情况下。但这种改进仍需进一步考虑冰雪散射的物理特征,因此下一步工作会针对Qu等改进方法,结合冰雪散射的物理特征,进一步改进核驱动模型对冰雪二向性反射的拟合精度,这对准确表征冰雪散射和反演冰雪反照率将具有重要意义。
| [1] | 白冬妮, 焦子锑, 董亚冬, 张小宁, 李阳, 何丹丹. 双冠层反射率模型分析各向异性平整指数(AFX)对植被参数的敏感性[J]. 遥感学报, 2017, 21 (1) : 1 –11. Bai D N, Jiao Z T, Dong Y D, Zhang X N, Li Y and He D D. Analysis of the sensitivity of the anisotropic flat index to vegetation parameters based on the two-layer canopy reflectance model[J]. Journal of Remote Sensing, 2017, 21 (1) : 1 –11. DOI: 10.11834/jrs.20175335 |
| [2] | Burakowski E A, Ollinger S V, Lepine L, Schaaf C B, Wang Z S, Dibb J E, Hollinger D Y, Kim J, Erb A and Martin M. Spatial scaling of reflectance and surface albedo over a mixed-use, temperate forest landscape during snow-covered periods[J]. Remote Sensing of Environment, 2015, 158 : 465 –477. DOI: 10.1016/j.rse.2014.11.023 |
| [3] | Csiszar I and Gutman G. Mapping global land surface albedo from NOAA AVHRR[J]. Journal of Geophysical Research: Atmospheres, 1999, 104 (D6) : 6215 –6228. DOI: 10.1029/1998JD200090 |
| [4] | Doyle M and Dorling S. Visibility trends in the UK 1950-1997[J]. Atmospheric Environment, 2002, 36 (19) : 3161 –3172. DOI: 10.1016/S1352-2310(02)00248-0 |
| [5] | Henderson-Sellers A and Wilson M F. Surface albedo data for climatic modeling[J]. Reviews of Geophysics, 1983, 21 (8) : 1743 –1778. DOI: 10.1029/RG021i008p01743 |
| [6] | Hudson S R, Warren S G, Brandt R E, Grenfell T C and Six D. Spectral bidirectional reflectance of Antarctic snow: measurements and parameterization[J]. Journal of Geophysical Research: Atmospheres, 2006, 111 (D18) : D18106 . DOI: 10.1029/2006JD007290 |
| [7] | Jacob F and Olioso A. Derivation of diurnal courses of albedo and reflected solar irradiance from airborne POLDER data acquired near solar noon[J]. Journal of Geophysical Research: Atmospheres, 2005, 110 (D10) : D10104 . DOI: 10.1029/2004JD004888 |
| [8] | 蒋熹. 冰雪反照率研究进展[J]. 冰川冻土, 2006, 28 (5) : 728 –738. Jiang X. Progress in the research of snow and ice albedo[J]. Journal of Glaciology and Geocryology, 2006, 28 (5) : 728 –738. DOI: 10.3969/j.issn.1000-0240.2006.05.016 |
| [9] | Jiao Z T, Zhang H, Dong Y D, Liu Q, Xiao Q and Li X W. An algorithm for retrieval of surface albedo from small view-angle airborne observations through the use of BRDF archetypes as prior knowledge[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8 (7) : 3279 –3293. DOI: 10.1109/JSTARS.2015.2414925 |
| [10] | Kimes D S. Dynamics of directional reflectance factor distributions for vegetation canopies[J]. Applied Optics, 1983, 22 (9) : 1364 –1372. DOI: 10.1364/AO.22.001364 |
| [11] | Kokhanovsky A and Schreier M. The determination of snow specific surface area, albedo and effective grain size using AATSR space-borne measurements[J]. International Journal of Remote Sensing, 2009, 30 (4) : 919 –933. DOI: 10.1080/01431160802395250 |
| [12] | Kokhanovsky A A and Breon F M. Validation of an analytical snow BRDF model using parasol multi-angular and multispectral observations[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9 (5) : 928 –932. DOI: 10.1109/LGRS.2012.2185775 |
| [13] | Kokhanovsky A A and Zege E P. Scattering optics of snow[J]. Applied Optics, 2004, 43 (7) : 1589 –1602. DOI: 10.1364/AO.43.001589 |
| [14] | Liang S L. Narrowband to broadband conversions of land surface albedo I: algorithms[J]. Remote Sensing of Environment, 2001, 76 (2) : 213 –238. DOI: 10.1016/S0034-4257(00)00205-4 |
| [15] | Liang S L, Shuey C J, Russ A L, Fang H L, Chen M Z, Walthall C L, Daughtry C S T and Hunt R Jr. Narrowband to broadband conversions of land surface albedo: II[J]. Validation. Remote Sensing of Environment, 2003, 84 (1) : 25 –41. DOI: 10.1016/S0034-4257(02)00068-8 |
| [16] | Liu Q, Wang L Z, Qu Y, Liu N F, Liu S H, Tang H R and Liang S L. Preliminary evaluation of the long-term GLASS albedo product[J]. International Journal of Digital Earth, 2013, 6 (sup1) : 69 –95. DOI: 10.1080/17538947.2013.804601 |
| [17] | Lucht W, Schaaf C B and Strahler A H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38 (2) : 977 –998. DOI: 10.1109/36.841980 |
| [18] | Lyapustin A, Gatebe C K, Kahn R, Brandt R, Redemann J, Russell P, King M D, Pedersen C A, Gerland S, Poudyal R, Marshak A, Wang Y, Schaaf C, Hall D and Kokhanovsky A. Analysis of snow bidirectional reflectance from ARCTAS spring-2008 campaign[J]. Atmospheric Chemistry and Physics, 2010, 10 (9) : 4359 –4375. DOI: 10.5194/acp-10-4359-2010 |
| [19] | Mote T L. On the role of snow cover in depressing air temperature[J]. Journal of Applied Meteorology and Climatology, 2008, 47 (7) : 2008 –2022. DOI: 10.1175/2007JAMC1823.1 |
| [20] | Negi H S and Kokhanovsky A. Retrieval of snow grain size and albedo of western Himalayan snow cover using satellite data[J]. The Cryosphere, 2011, 5 (4) : 831 –847. DOI: 10.5194/tc-5-831-2011 |
| [21] | 潘海珠, 王建, 李弘毅. 基于ART模型的MODIS积雪反照率反演研究[J]. 遥感技术与应用, 2015a, 30 (6) : 1059 –1065. Pan H Z, Wang J and Li H Y. Retrieval snow albedo using MODIS based on the ART model[J]. Remote sensing Technology and Application, 2015a, 30 (6) : 1059 –1065. DOI: 10.11873/j.issn.1004-0323.2015.6.1059 |
| [22] | 潘海珠, 王建, 李弘毅. 祁连山区MODIS积雪反照率产品的精度验证及云下积雪反照率估算研究[J]. 冰川冻土, 2015b, 37 (1) : 49 –57. Pan H Z, Wang J and Li H Y. Accuracy validation of the MODIS snow albedo products and estimate of the snow albedo under cloud over the Qilian Mountains[J]. Journal of Glaciology and Geocryology, 2015b, 37 (1) : 49 –57. DOI: 10.7522/j.issn.1000-0240.2015.0005 |
| [23] | Qu Y, Liang S L, Liu Q, He T, Liu S H and Li X W. Mapping surface broadband albedo from satellite observations: a review of literatures on algorithms and products[J]. Remote Sensing, 2015, 7 (1) : 990 –1020. DOI: 10.3390/rs70100990 |
| [24] | Qu Y, Liang S L, Liu Q, Li X J, Feng Y B and Liu S H. Estimating Arctic sea-ice shortwave albedo from MODIS data[J]. Remote Sensing of Environment, 2016, 186 : 32 –46. DOI: 10.1016/j.rse.2016.08.015 |
| [25] | Qu Y, Liu Q, Liang S L, Wang L Z, Liu N F and Liu S H. Direct-estimation algorithm for mapping daily land-surface broadband albedo from MODIS data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52 (2) : 907 –919. DOI: 10.1109/TGRS.2013.2245670 |
| [26] | 瞿瑛, 刘强, 刘素红. 基于前向散射核函数拟合冰雪反射光谱各向异性[J]. 光谱学与光谱分析, 2016, 36 (9) : 2749 –2754. Qu Y, Liu Q and Liu S H. A forward kernel function for fitting in situ measured snow bidirectional reflectance factor[J]. Spectroscopy and Spectral Analysis, 2016, 36 (9) : 2749 –2754. DOI: 10.3964/j.issn.1000-0593(2016)09-2749-06 |
| [27] | Roujean J L, Leroy M and Deschamps P Y. A bidirectional reflectance model of the earth’s surface for the correction of remote sensing data[J]. Journal of Geophysical Research: Atmospheres, 1992, 97 (D18) : 20455 –20468. DOI: 10.1029/92JD01411 |
| [28] | Schaaf C B, Gao F, Strahler A H, Lucht W, Li X W, Tsang T, Strugnell N C, Zhang X Y, Jin Y F, Muller J P, Lewis P, Barnsley M, Hobson P, Disney M, Roberts G, Dunderdale M, Doll C, D’Entremont R P, Hu B X, Liang S L, Privette J L and Roy D. First operational BRDF, albedo nadir reflectance products from MODIS[J]. Remote Sensing of Environment, 2002, 83 (1/2) : 135 –148. DOI: 10.1016/S0034-4257(02)00091-3 |
| [29] | 邵东航, 李弘毅, 王建, 郝晓华, 王润科, 马媛. 基于多源遥感数据的积雪反照率反演研究[J]. 遥感技术与应用, 2017, 32 (1) : 71 –77, 139. Shao D H, Li H Y, Wang J, Hao X H, Wang R K and Ma Y. Retrieval of snow albedo based on multi-source remote sensing data[J]. Remote Sensing Technology and Application, 2017, 32 (1) : 71 –77, 139. DOI: 10.11873/j.issn.1004-0323.2017.1.0071 |
| [30] | Shi H Y, Xiao Z Q, Liang S L and Ma H. A method for consistent estimation of multiple land surface parameters from MODIS top-of-atmosphere time series data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55 (9) : 5158 –5173. DOI: 10.1109/TGRS.2017.2702609 |
| [31] | Stroeve J, Box J E, Gao F, Liang S L, Nolin A and Schaaf C. Accuracy assessment of the MODIS 16-day albedo product for snow: comparisons with Greenland in situ measurements[J]. Remote Sensing of Environment, 2005, 94 (1) : 46 –60. DOI: 10.1016/j.rse.2004.09.001 |
| [32] | Stroeve J C, Box J E and Haran T. Evaluation of the MODIS (MOD10A1) daily snow albedo product over the Greenland ice sheet[J]. Remote Sensing of Environment, 2006, 105 (2) : 155 –171. DOI: 10.1016/j.rse.2006.06.009 |
| [33] | Vermote E F, Tanre D, Deuze J L, Herman M and Morcette J J. Second simulation of the satellite signal in the solar spectrum, 6S: an overview[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35 (3) : 675 –686. DOI: 10.1109/36.581987 |
| [34] | Wang D D, Liang S L, Zhou Y, He T and Yu Y Y. A new method for retrieving daily land surface albedo from VIIRS data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55 (3) : 1765 –1775. DOI: 10.1109/TGRS.2016.2632624 |
| [35] | 王杰, 郝晓华, 王建. 使用多角度积雪光谱验证渐进辐射传输理论[J]. 冰川冻土, 2014, 36 (2) : 386 –393. Wang J, Hao X H and Wang J. Validation the asymptotic radiative transfer theory by using multi-angular snow spectrum[J]. Journal of Glaciology and Geocryology, 2014, 36 (2) : 386 –393. DOI: 10.7522/j.issn.1000-0240.2014.0047 |
| [36] | Wu H Y, Liang S L, Tong L and He T. 2011. Snow BRDF characteristics from MODIS and MISR data//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver, BC, Canada: IEEE: 3187-3190 [DOI: 10.1109/IGARSS.2011.6049896] |
| [37] | Wu H Y, Tong L and Li Y X. 2010. Long term validation of moderate resolution and multi-angle remote sensing snow albedo over Greenland//Proceedings of the 3rd International Congress on Image and Signal Processing. Yantai, China: IEEE: 2198-2202 [DOI: 10.1109/CISP.2010.5647453] |

