叶恺, 禹卫东, 王伟
Digital beamforming in the elevation of Spaceborne SAR assisted by DEM data
YE Kai, YU Weidong, WANG Wei
1. Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
2. University of the Chinese Academy of Sciences, Beijing 100049, China
1、引 言 星载合成孔径雷达SAR(Synthetic Aperture Radar)是一种先进的空间对地微波成像遥感设备(Cumming和Wong,2005),具有全天时、全天候的观测能力,在自然灾害监测、地形测绘、军事侦察等方面具有重要的应用价值。但是,由于传统的单通道星载SAR受到最小天线面积的约束(Freeman 等,2000),不能同时获取方位向高分辨率和距离向宽测绘带的SAR图像,这有限的成像能力越来越不能满足人们在遥感应用中对SAR图像质量的要求。随着多通道技术的发展和数字波束形成技术DBF(Digital Beam-Forming)的应用,配备多个接收天线的合成孔径雷达系统能够获得高分辨率、宽测绘带的SAR图像(Krieger 等,2008,2010,2016;Moreira 等,2015)。这种高分宽幅星载SAR系统利用方位向多通道的优势,在每个方位向采样时刻同时获取回波信号的多个空间样本,从而能够在较低的系统脉冲重复频率PRF(Pulse Repetition Frequency)条件下保证SAR图像的高方位向分辨率。而较低的系统PRF意味着SAR系统能够获取更宽的无模糊距离向测绘带,因此在发射端利用高度较小的天线产生俯仰向宽波束照射地面。但是由于天线增益随着天线尺寸的减小而降低,在SAR系统接收端需要利用较高的接收天线和数字波束形成技术(Younis 等,2003,2009)产生高增益窄波束扫描接收宽测绘带场景回波。因此,高分宽幅星载SAR系统的俯仰向DBF处理是确保SAR图像具有高信噪比和辐射分辨率的关键。
通常,高分宽幅星载SAR系统在接收端俯仰向采用SCORE(SCan-On-REceive)方法来处理回波信号(Suess 等,2001;Suess和Wiesbeck,2001)。该处理方法将接收天线分成多个俯仰向子孔径,每个俯仰向子孔径接收到的回波都各自独立地进行低噪放大、下变频和数字化等处理,然后通过DBF处理器进行时变加权合成,形成等效的高增益数字波束扫描接收整个宽测绘带场景回波。SCORE方法根据地球光滑球体模型确定目标回波时间和波达角DOA(Direction Of Arrival)的对应关系,并得出每个距离向采样时刻对应的DBF加权矢量,这使得接收波束中心能够时刻追踪指向回波信号。但是,在地形起伏较大的区域,由于地球光滑球体模型与真实地形之间存在较大的差异,使用SCORE方法形成的DBF接收波束会出现指向偏差的问题,导致回波增益下降和信噪比恶化,影响SAR系统成像质量。针对该问题,Varona(2009)提出了一种自适应数字波束形成ADBF(Adaptive Digital Beam-Forming)的处理方法,采用空间谱估计算法对回波信号的波达角进行估计(Bordoni 等,2009),然后利用波达角估计值计算DBF加权矢量来调整接收波束指向。但是由于星载SAR系统是对大面积的地面复杂场景进行二维成像,而且在卫星平台上进行的俯仰向ADBF处理需要针对每一个距离门进行DOA估计以及计算加权矢量,因此采用ADBF算法能否准确并且有效地计算每个距离门的DBF加权矢量还有待进一步深入研究。
考虑当前TerraSAR-X/Tandem-X生成的高精度数字高程数据已实现全球覆盖(Gruber 等,2012;Bueso-Bello 等,2016),本文提出了一种基于数字高程图DEM(Digital Elevation Map)的高分宽幅星载SAR俯仰向DBF处理方法。该方法首先在地面雷达站利用DEM数据、卫星轨道参数和星载SAR成像几何模型计算DBF加权矢量,确保DBF形成的接收波束指向正确,能够有效改善回波信号的接收增益;然后上传DBF加权矢量至卫星平台并在星上进行俯仰向DBF处理;最后将俯仰向DBF处理后的方位向多通道数据下传地面进行多普勒频谱重构和成像处理,从而有效实现星载SAR的高分宽幅成像。
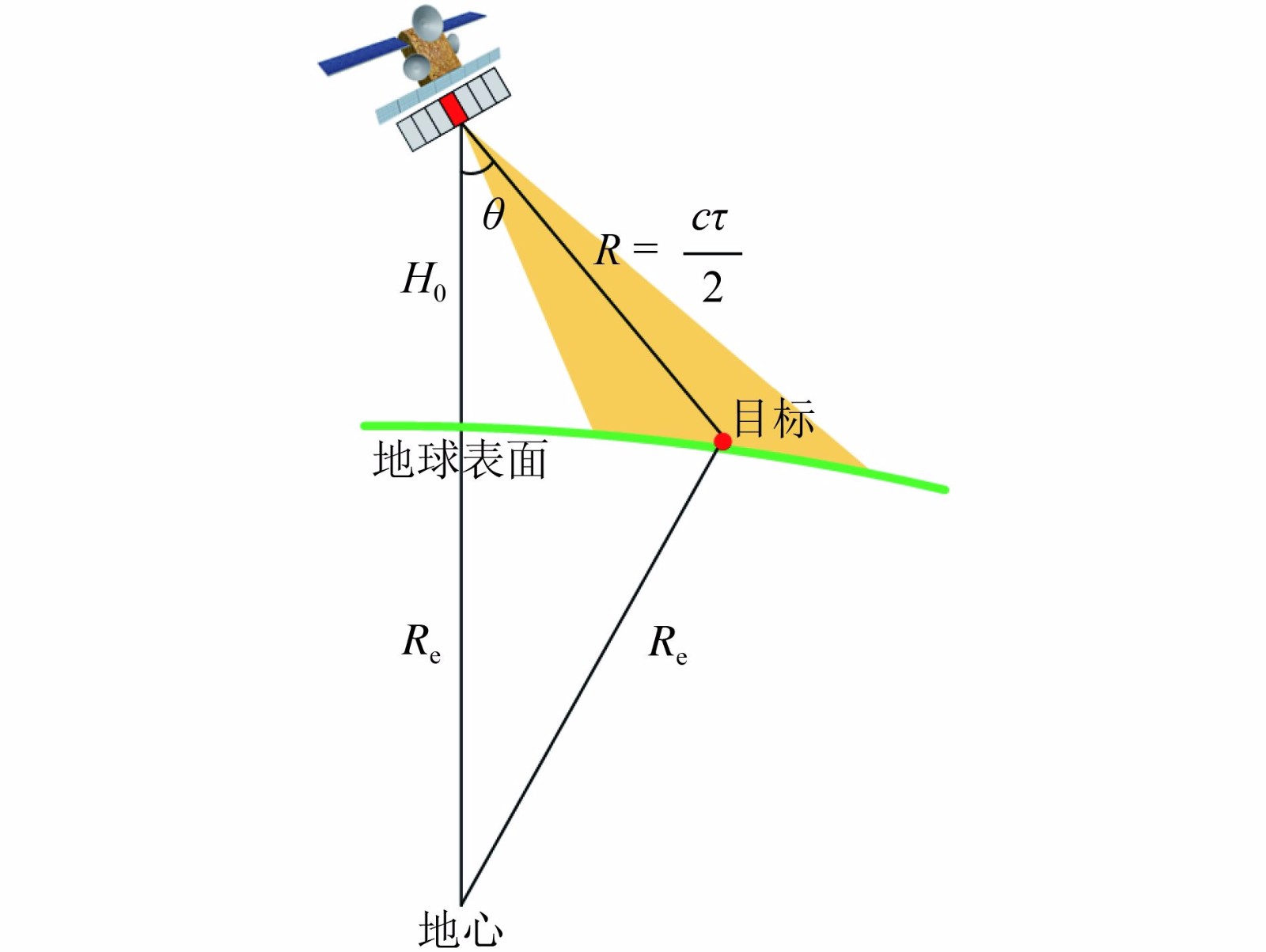
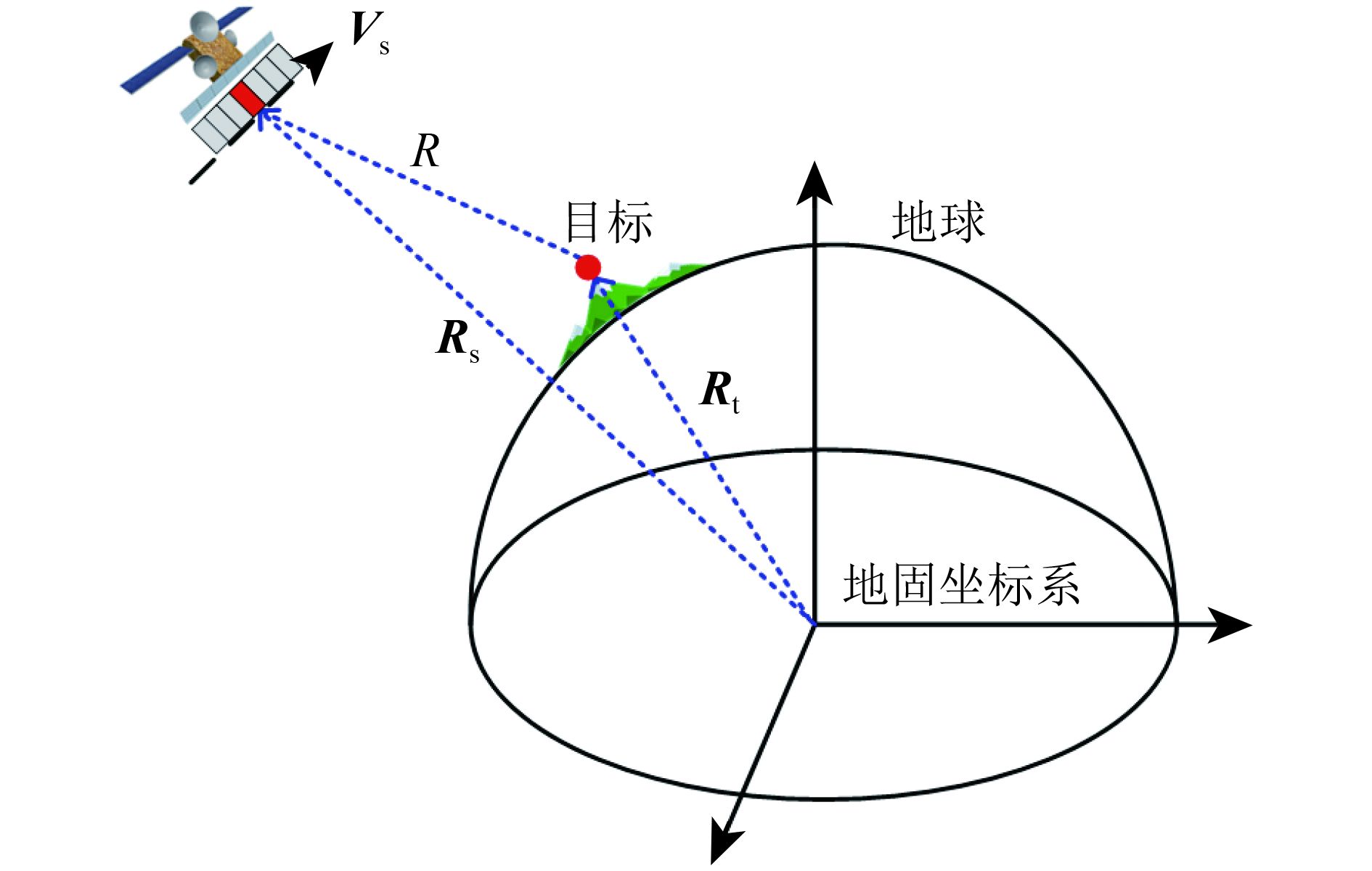
2、俯仰向DBF接收波束的扫描指向问题 通常,在遥感应用中都采用WGS 84旋转椭球体来近似地球形状,它比球体模型更接近地球的真实形状。但是,对于低轨星载合成孔径雷达(轨道高度小于1000 km),通常采用局部圆轨道和地球局部球体模型来描述“星—地”之间的运动轨迹(Cumming和Wong,2005),这主要是因为:低轨星载SAR的卫星轨道一般为近圆轨道,成像所需的合成孔径时间较短(一般为秒级)。这意味着:忽略卫星轨道偏心率和地球椭球率导致的误差对SAR成像的影响很小。因此本文将基于地球局部球体模型对高分宽幅星载SAR的俯仰向DBF处理方法进行阐述。图1为星载SAR与地球表面目标的几何关系示意图。基于地球局部球体模型,地球表面目标的回波时刻
$\tau $
与下视角
$\theta $
之间的对应关系可以根据星载SAR与地球表面目标的几何关系推导得到(图1)
|
$\theta (\tau) = {\rm{acos}}\left({\frac{{4{{\left({{R_{\rm{e}}} + {H_0}} \right)}^2} - 4R_{\rm{e}}^2 + {{({\rm{c}}\tau)}^2}}}{{4{\rm{c}}\tau \left({{R_{\rm{e}}} + {H_0}} \right)}}} \right)$
|
(1) |
式中,
${R_{\rm{e}}}$
表示地球半径,
${H_0}$
表示卫星平台轨道高度,c表示光速。
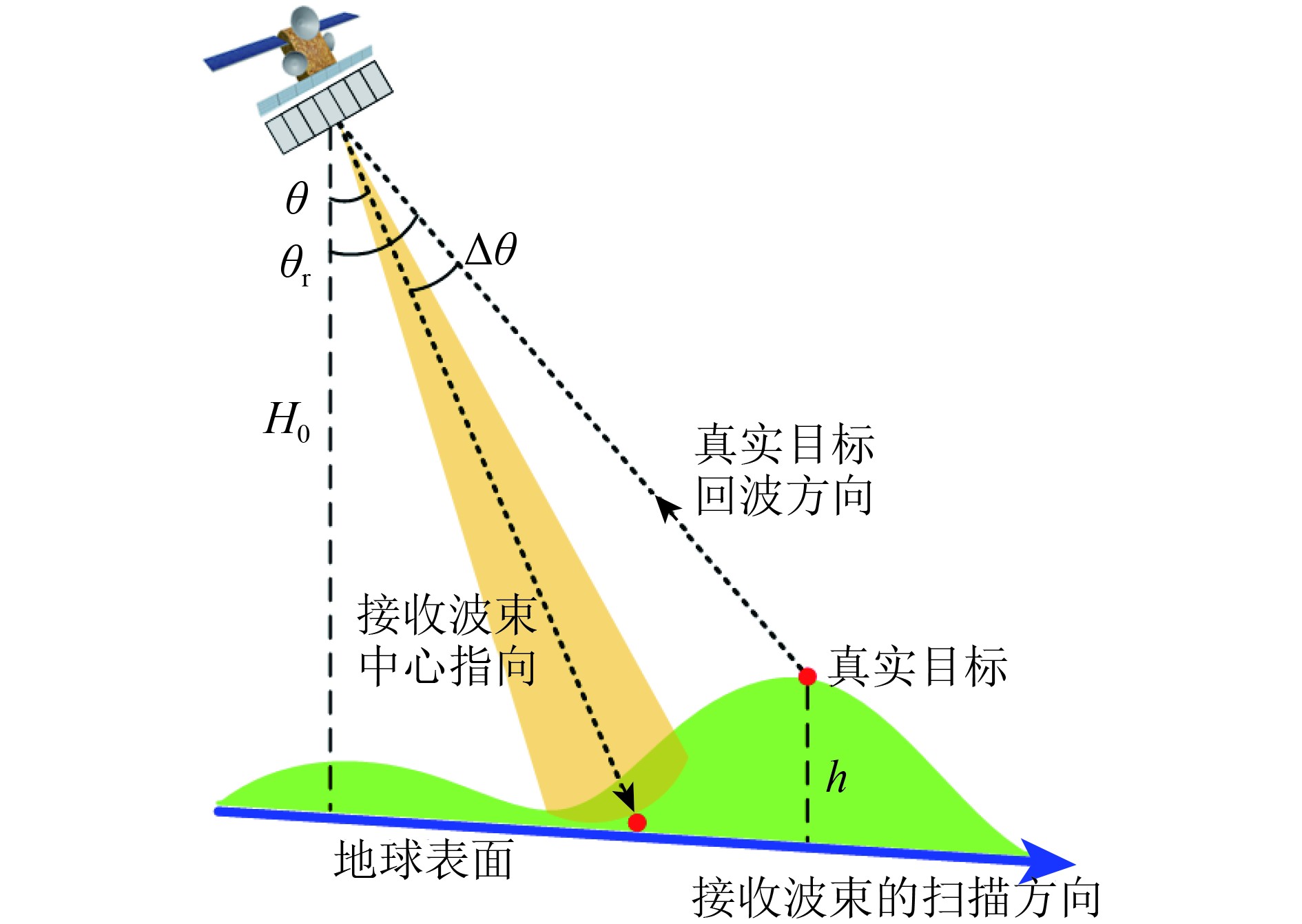
如SCORE方法形成的DBF接收波束指向偏差图中蓝线所示(图2),SCORE方法根据式(1)调整接收波束扫描整个成像场景,在地形起伏较大的区域,这样的波束导向机制将导致接收波束中心指向与真实目标回波方向发生偏移,从而造成真实目标回波的接收增益明显降低,影响星载SAR系统的成像质量。在相同斜距条件下,SCORE方法形成的接收波束中心指向角
$\theta $
与真实目标下视角
${\theta _{\rm{r}}}$
之间相差
$\Delta \theta = {\theta _{\rm{r}}} - \theta $
,由此导致的系统性能损耗可直观地通过方向图损耗PL(Pattern Loss)进行评估
|
${\rm{PL}} = \frac{{{C_{{\rm{DBF}}}}\left({{\theta _{\rm{r}}}} \right)}}{{{C_{{\rm{DBF}}}}\left(\theta \right)}}$
|
(2) |
|
${\theta _{\rm{r}}}(\tau) = {\rm{acos}}\left({\frac{{4{{\left({{R_{\rm{e}}} + {H_0}} \right)}^2} - 4{{\left({{R_{\rm{e}}} + h} \right)}^2} + {{(c\tau)}^2}}}{{4c\tau \left({{R_{\rm{e}}} + {H_0}} \right)}}} \right)$
|
(3) |
式中,
${C_{{\rm{DBF}}}}\left(\theta \right)$
表示DBF接收波束方向图,h表示真实目标的高程值。
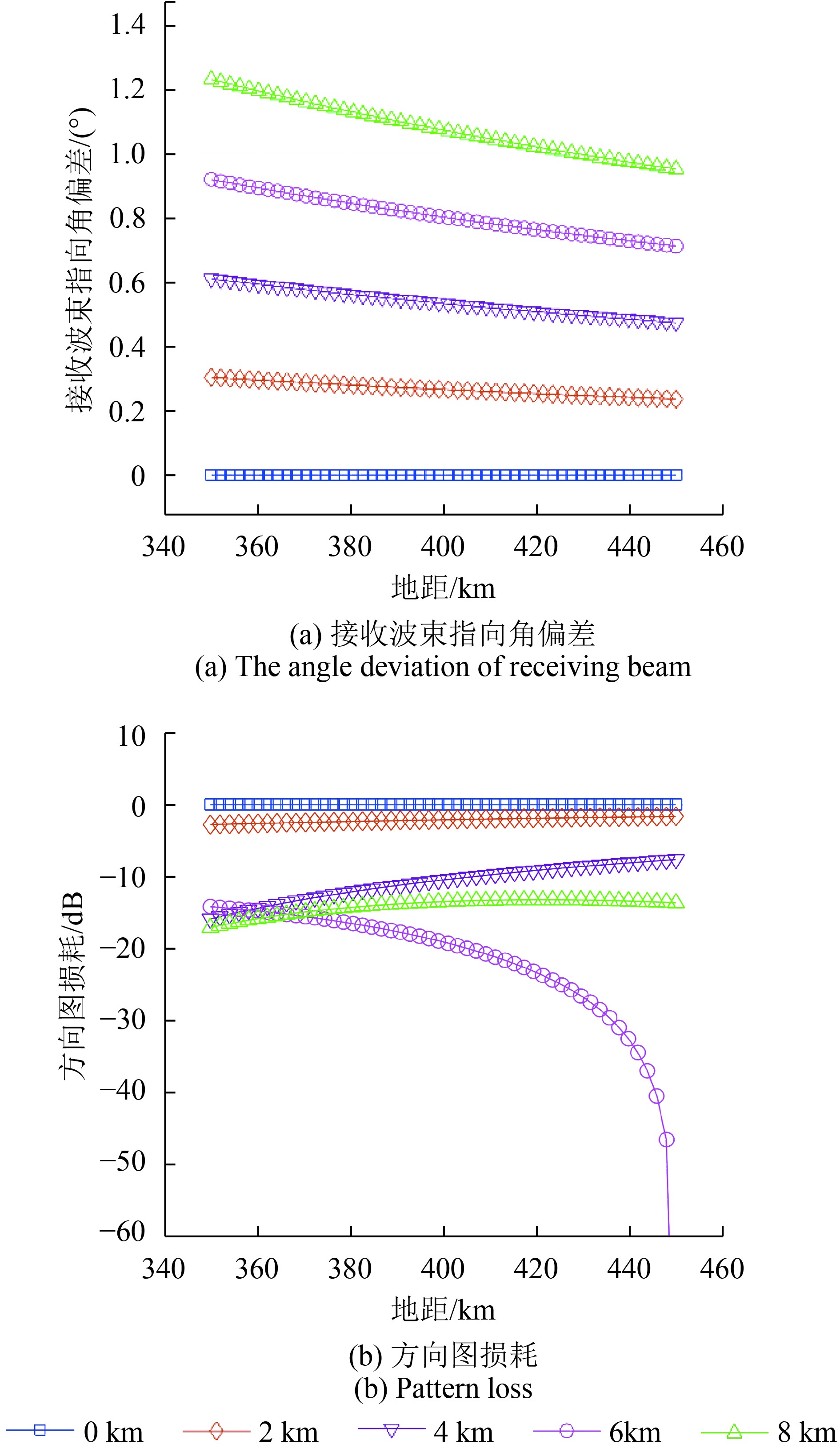
图3(a)为根据仿真参数(表1)计算得到的不同地面高程情况下整个测绘带的接收波束指向角偏差。可见,该角度偏差值随着地面高程值的增加而变大,这将导致回波信号增益出现损耗。图3(b)为不同地面高程情况下整个测绘带的PL值变化曲线。由于方向图损耗是由DBF接收波束方向图和
$\Delta \theta $
共同确定的,不同地面高度对应的PL值曲线的变化趋势都不相同。当地面高度为6 km时,由于
$\Delta \theta $
接近DBF接收波束方向图的零陷位置,因此方向图损耗较大。如图3所示,当地面高度大于4 km时,SCORE方法的接收波束指向偏差引起的方向图损耗在整个测绘带内都降低超过了7.6 dB,这将严重影响SAR系统的成像性能。因此,利用俯仰向DBF技术调整接收波束指向真实目标回波方向是高分宽幅星载SAR系统的关键问题。
SAR系统采用侧视成像的方式,生成的SAR图像为斜距图,即地面目标在图像距离向上的先后顺序是按照这些地面目标与SAR系统之间的斜距大小排列的。在地形起伏较大的区域,叠掩现象将会出现在SAR图像中。在SAR图像平面上的叠掩区域,每个距离门单元都包含了多个具有相同斜距但是下视角和高程值不相同的目标回波。针对这些距离门单元的DBF接收波束指向问题,需要考虑以下两点:(1)由于星载SAR系统的接收天线高度有限,通常难以利用DBF接收波束对这些目标进行分离提取;(2)星载SAR系统在进行高分辨率、宽测绘带成像时,应用俯仰向DBF的目的是保证回波信号的信噪比和接收增益。因此,对于叠掩区域,可以根据实际应用需求调整DBF接收波束指向距离门单元中的某一目标。对于发生透视收缩的区域和地形起伏较小的区域,由于SAR图像中的距离门单元对应单一目标,DBF接收波束指向角可根据SAR图像上距离门对应时刻、数字高程图和卫星轨道参数计算得到。
表 1(Table 1)

表 1 仿真参数
Table 1 Simulation parameters
| 仿真参数 |
参数值 |
| 地球半径/km |
6371 |
| 轨道高度/km |
500 |
| 卫星速度/(m/s) |
7612 |
| 载频/GHz |
9.65 |
| 脉冲宽度/μs |
40 |
| 信号带宽/MHz |
250 |
| 视角范围/(°) |
34.5—41.1 |
| 天线法线视角/(°) |
37.8 |
| 天线高度/m |
2.5 |
| 俯仰向子孔径数目 |
25 |
|
表 1 仿真参数
Table 1 Simulation parameters
|
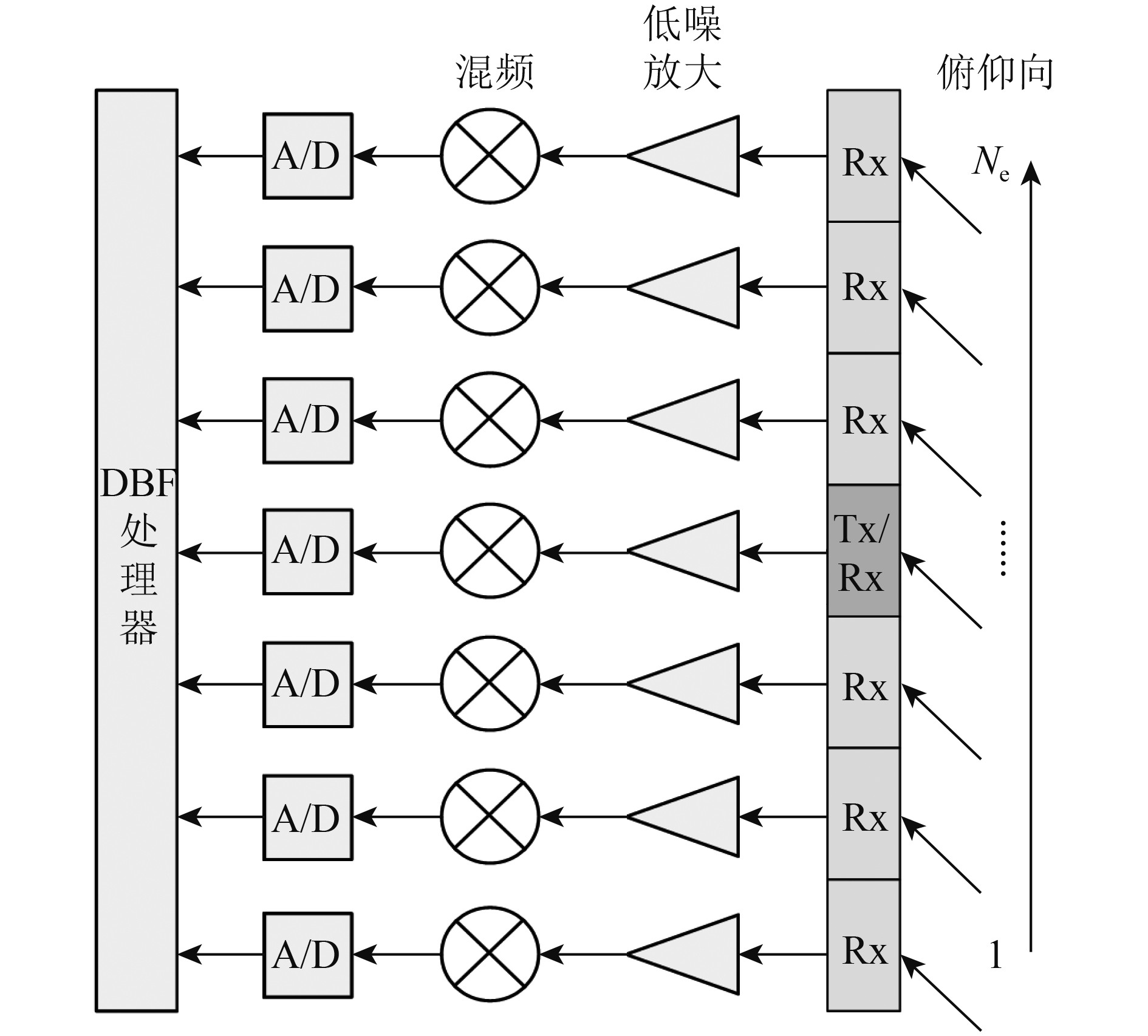
3、处理方法 星载SAR系统的接收天线在俯仰向由
${N_{\rm{e}}}$
个俯仰向子孔径组成(图4),每个俯仰向子孔径的方向图都覆盖整个成像场景。假设
${N_{\rm{e}}}$
为奇数,中间的俯仰向子孔径发射线性调频脉冲信号照射整个测绘带,所有俯仰向子孔径同时接收地面场景回波。以点目标情况进行说明,俯仰向第n个子孔径接收到的目标回波信号
${s_n}\left(t \right)$
可表示为
|
$\begin{split} {s_n}\left(t \right) = & {A_0}{\rm{rect}}\left({\frac{{t - {t_0}}}{{{T_{\rm{p}}}}}} \right)\exp\left({ - j2{\text{π}} {f_{\rm{c}}}{t_0}} \right) \\ & \exp\left({j{\text{π}}{k_{\rm{r}}}{{\left({t - {t_0}} \right)}^2}} \right)\exp\left({\frac{{j2{\text{π}} {f_{\rm{c}}}{d_{\rm{n}}}\sin \left({{\theta _{\rm{r}}} - {\theta _{\rm{c}}}} \right)}}{\rm{c}}} \right) \end{split} $
|
(4) |
式中,
${A_0}$
表示与双程天线方向图增益和目标后向散射系数相关的常数,
${t_0}$
表示目标双程时延,
${T_{\rm{p}}}$
表示发射信号脉冲宽度,
${f_{\rm{c}}}$
表示雷达载频,
${k_{\rm{r}}}$
表示调频率,
${\theta _{\rm{c}}}$
表示天线法线的下视角。
${\rm{rect}}\left(\cdot \right)$
表示范围在[−0.5,0.5]的归一化矩形窗。
${d_n} = \left({n - \dfrac{{{N_{\rm{e}}} - 1}}{2}} \right)d$
,表示第n个俯仰向子孔径相对于中间俯仰向子孔径的距离,d为俯仰向子孔径的高度。为了降低目标回波的脉冲展宽损耗,对每个俯仰向子孔径回波信号进行匹配滤波处理,得到
|
$\begin{aligned} {{\bar s}_n}\left(t \right) = & \sqrt {\left| {{k_{\rm{r}}}} \right|} {T_{\rm{p}}}{A_0}\exp\left({ - j2{\text{π}} {f_{\rm{c}}}{t_0}} \right) \\ & {\rm{sinc}}\left({{k_{\rm{r}}}{T_{\rm{p}}}\left({t - {t_0}} \right)} \right)\exp\left({\frac{{j2{\text{π}} {f_{\rm{c}}}{d_{\rm{n}}}\sin \left({{\theta _{\rm{r}}} - {\theta _{\rm{c}}}} \right)}}{\rm{c}}} \right) \end{aligned} $
|
(5) |
考虑所有俯仰向子孔径接收回波的匹配滤波结果可得
|
${{s}}\left(t \right) = {C_0}\left(t \right){{a}}\left({{\theta _{\rm{r}}}} \right) + {{e}}\left(t \right)$
|
(6) |
|
${C_0}\left(t \right) = \sqrt {\left| {{k_{\rm{r}}}} \right|} {T_{\rm{p}}}{A_0}\exp\left({ - j2{\text{π}} {f_{\rm{c}}}{t_0}} \right){\rm{sinc}}\left({{k_{\rm{r}}}{T_{\rm{p}}}\left({t - {t_0}} \right)} \right)$
|
(7) |
|
$\begin{split} {{a}}\left({{\theta _{\rm{r}}}} \right) = & \begin{array}{*{20}{c}} {\left[ {\exp\left({\dfrac{{j2{\text{π}} {f_{\rm{c}}}{d_{\rm{1}}}\sin \left({{\theta _{\rm{r}}} - {\theta _{\rm{c}}}} \right)}}{\rm{c}}} \right)} \right.}& \cdots \end{array} \\ & {\left. {\exp\left({\frac{{j2{\text{π}} {f_{\rm{c}}}{d_{{N_{\rm{e}}}}}\sin \left({{\theta _{\rm{r}}} - {\theta _{\rm{c}}}} \right)}}{\rm{c}}} \right)} \right]^{\rm{T}}} \end{split} $
|
(8) |
式中,
${{a}}\left({{\theta _{\rm{r}}}} \right)$
表示目标回波的导向矢量,
${{e}}\left(t \right)$
表示
${N_{\rm{e}}} \times 1$
的噪声矢量。这些俯仰向子孔径接收回波的匹配滤波结果在数字波束形成处理器中加权累加,生成等效的高增益DBF波束指向目标,实现高增益接收目标回波信号。根据第2节的分析可知,为了确保DBF接收波束中心指向目标回波方向,每个距离门单元的俯仰向DBF加权矢量ω应根据目标波达角
${\theta _{\rm{r}}}$
进行计算,其计算公式为ω
$\left(t \right) = {{{a}}^ * }\left({{\theta _{\rm{r}}}\left(t \right)} \right)$
。由式(3)可知,计算距离门单元对应的目标下视角需要已知目标的高程值。因此,需要基于星载SAR成像几何模型,根据真实地形的数字高程图和卫星轨道参数计算距离门单元对应的目标高程值。
图5为基于星载SAR成像几何的目标定位模型示意图。根据Curlander(1982)和陈尔学(2004)的文献可知,SAR图像平面上的像元可根据以下3个方程进行定位,分别是
|
$R = \left| {{{{R}}_{\rm{s}}} - {{{R}}_{\rm{t}}}} \right|$
|
(9) |
|
${f_{\rm{d}}} = - \frac{2}{{{\textit{λ}} R}}{{{V}}_{\rm{s}}}\left({{{{R}}_{\rm{s}}} - {{{R}}_{\rm{t}}}} \right)$
|
(10) |
|
$x_{\rm{t}}^2 + y_{\rm{t}}^2 + {\textit{z}}_{\rm{t}}^2 = {\left({{R_{\rm{e}}} + h} \right)^2}$
|
(11) |
式中,
$R$
表示目标到卫星平台的斜距,
${{{R}}_{\rm{s}}}$
表示地固坐标系中的原点到卫星平台的距离矢量,
${{{V}}_{\rm{s}}}$
表示地固坐标系中卫星平台速度矢量,
${{{R}}_{\rm{t}}}$
表示地固坐标系中的原点到目标的距离矢量,
${f_{\rm{d}}}$
表示多普勒频率,
${\textit{λ}} $
表示波长,
$\left({{x_{\rm{t}}},{y_{\rm{t}}},{{\textit{z}}_{\rm{t}}}} \right)$
表示目标在地固坐标系中的坐标。
距离门单元对应的目标高程值可利用上述方程进行计算,具体实现过程为:首先根据星载SAR系统的方位向采样间隔和距离向采样间隔对DEM数据进行插值,以确保在计算过程中每个距离门单元都能对应上地面目标的高程值。由于DEM数据通常以大地经纬度表示位置坐标,需要根据地球模型将其转换为
$\left({{x_{\rm{t}}},{y_{\rm{t}}},{{\textit{z}}_{\rm{t}}}} \right)$
的坐标形式。然后根据成像场景确定相应的卫星轨道参数,包括卫星的位置矢量
${{{R}}_{\rm{s}}}$
和速度矢量
${{{V}}_{\rm{s}}}$
。最后根据距离门单元在SAR图像平面中的位置,联合以上3个方程计算相应的目标高程值。
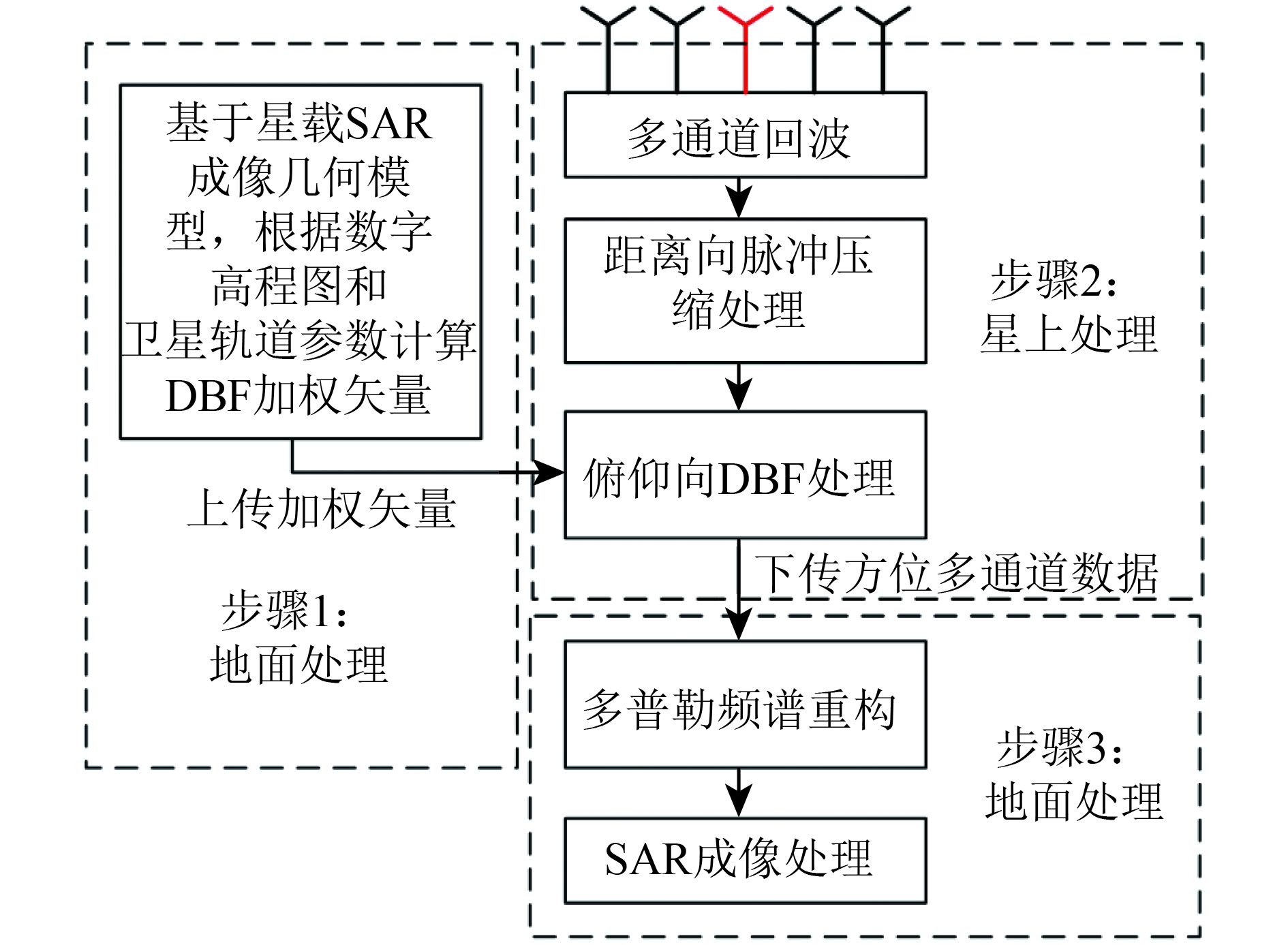
基于DEM的高分宽幅星载SAR处理方法的主要流程包含3个重要步骤(图6):
(1)基于星载SAR成像几何模型,根据数字高程图和卫星轨道参数建立SAR图像平面上的距离门单元与地面高度之间的对应关系,然后计算每个距离门单元的DBF加权矢量,并通过地面雷达站上传DBF加权矢量至卫星平台;
(2)星载SAR系统开机并接收俯仰向多孔径回波数据,经过距离向脉冲压缩处理后,利用DBF加权矢量对每个距离门单元的俯仰向多孔径回波信号进行加权求和得到俯仰向单通道数据,然后将方位向多通道数据下传至地面雷达站;
(3)对地面雷达站接收到方位向多通道数据进行多普勒频谱重构处理,最后利用传统成像算法对方位向多通道重构数据进行成像。
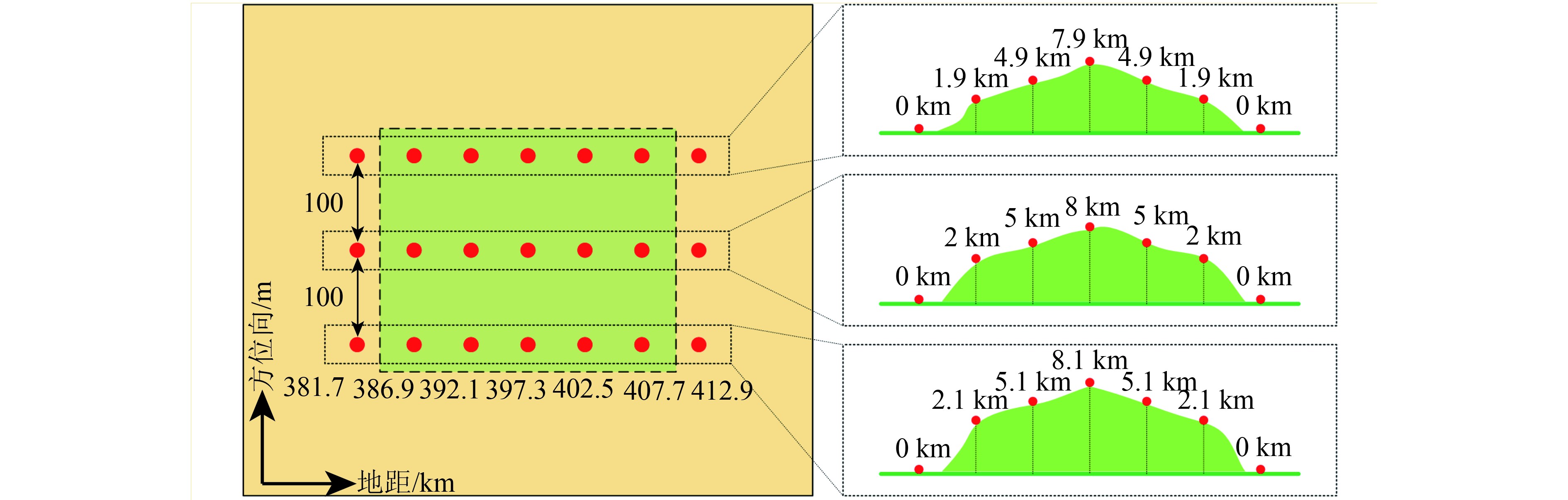
4、仿真实验 本节将通过一个X波段的高分宽幅星载SAR系统来仿真验证本文所提处理方法。该系统的天线高度为2.5 m,由25个俯仰向子孔径组成,每个俯仰向子孔径高度为0.1 m。图7为成像场景示意图。21个点目标在成像场景中等间隔排列,这些点目标在地距向高度起伏较大,在方位向高度起伏较小。在仿真实验中,俯仰向中间子孔径以宽波束照射,所有俯仰向子孔径在每个方位向采样时刻接收成像场景回波。假设所有点目标的回波幅度都被归一化处理,在所有俯仰向子孔径接收的回波信号中加入高斯白噪声,并且已知成像场景的地面高程值数据。
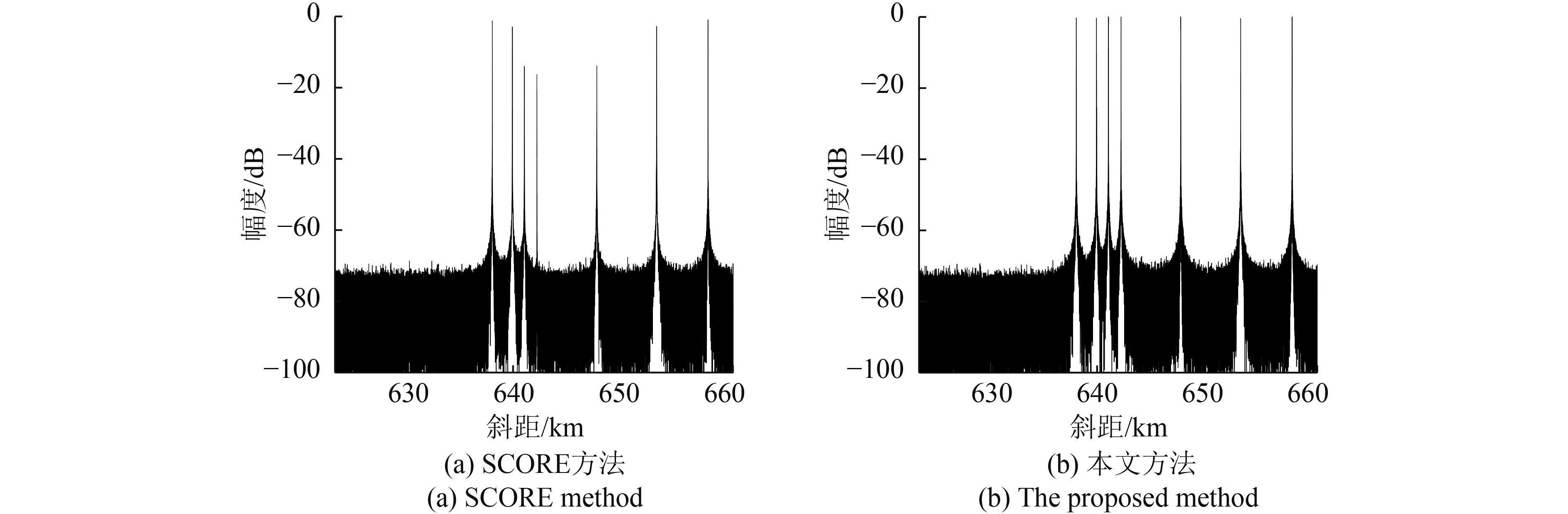
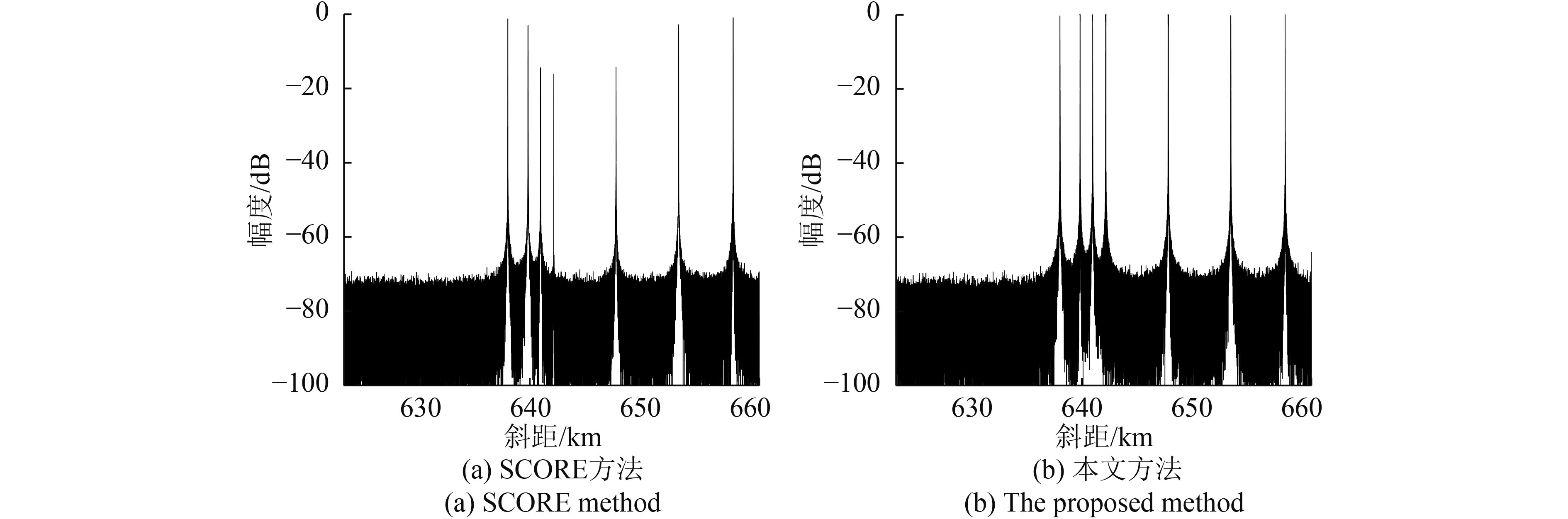
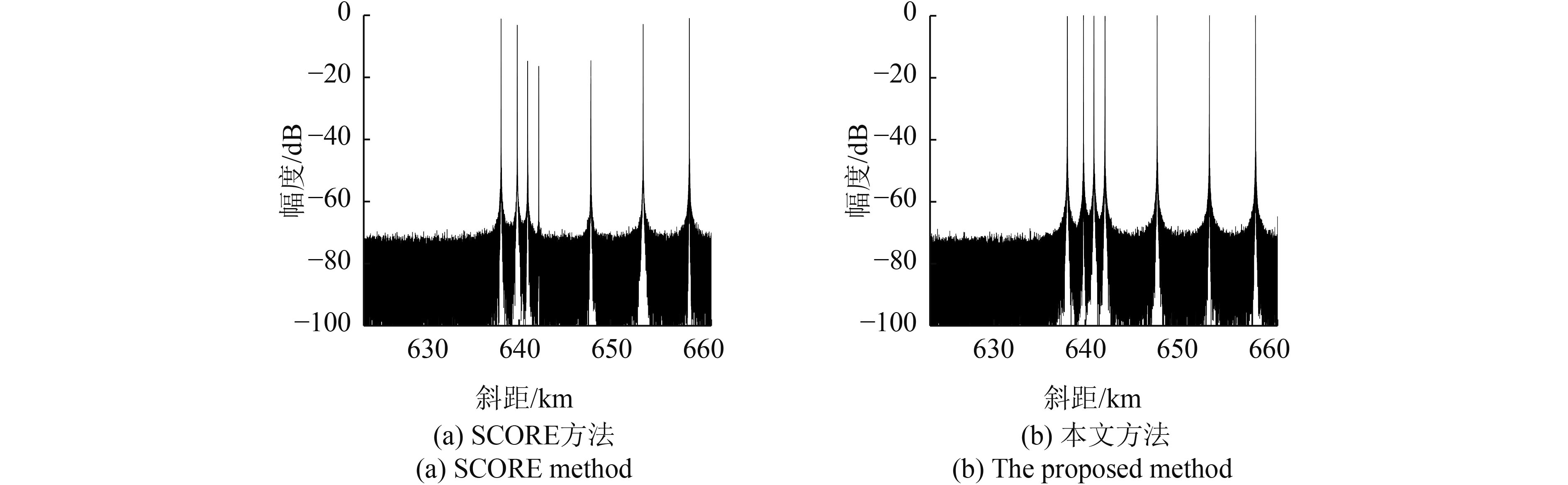
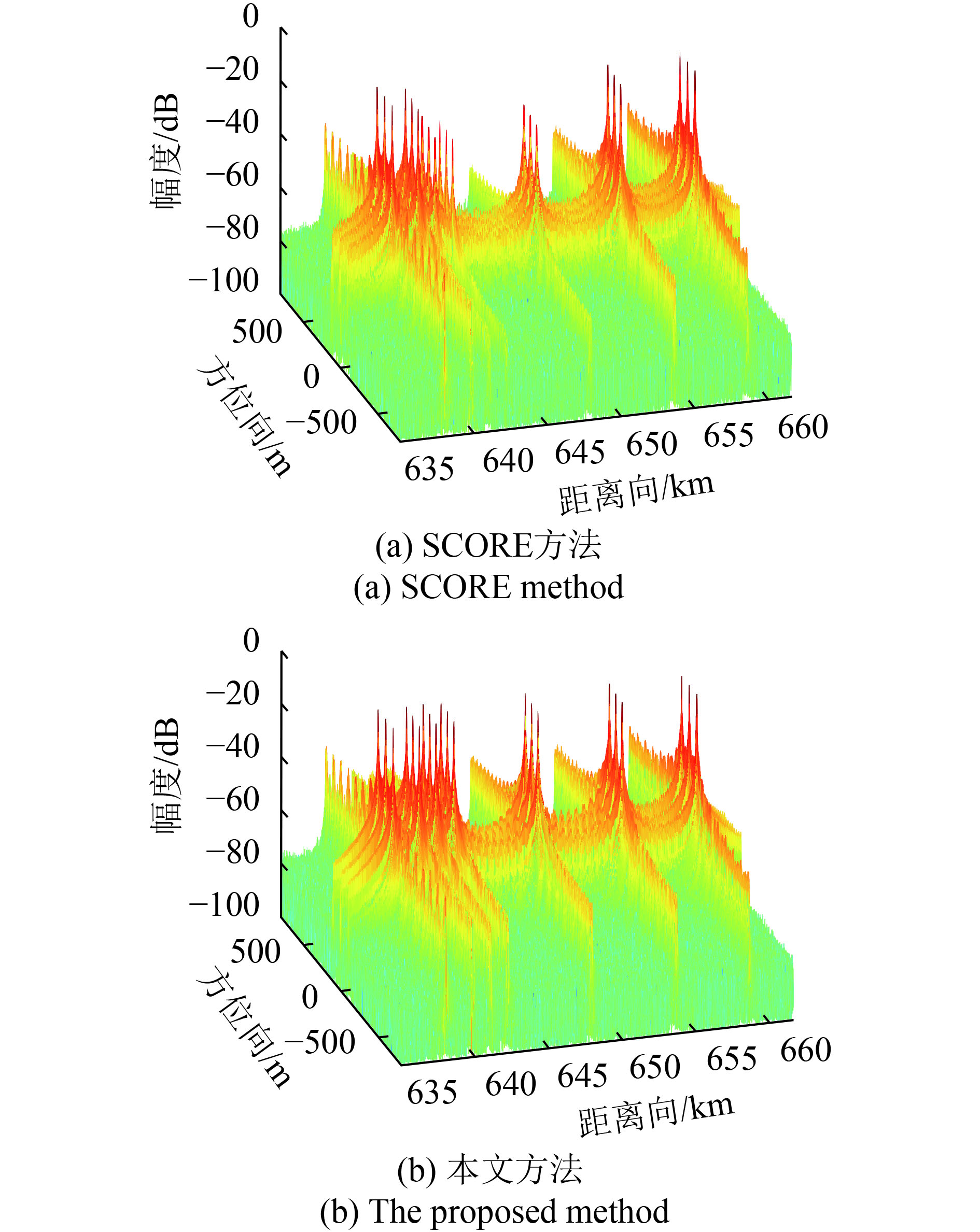
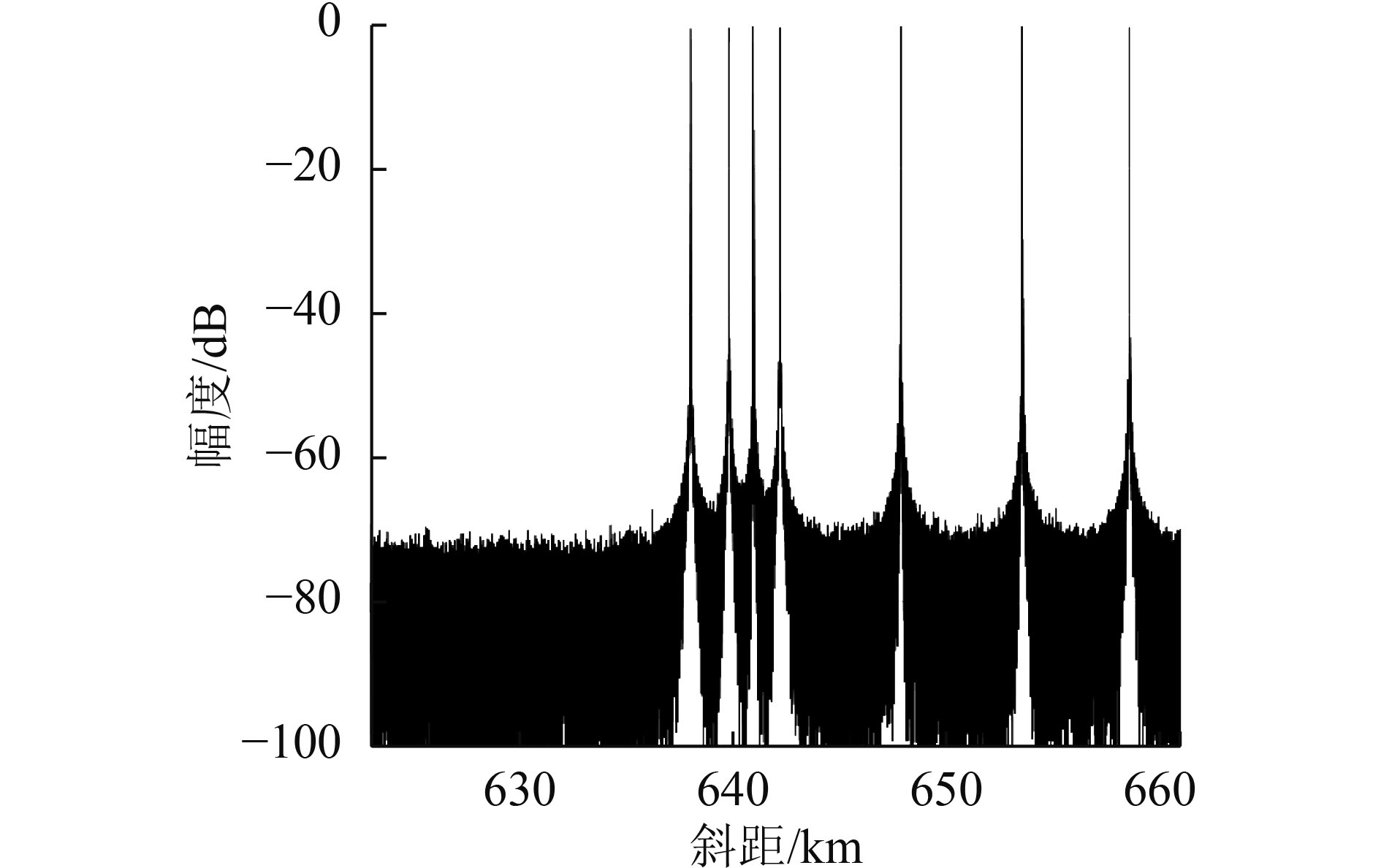
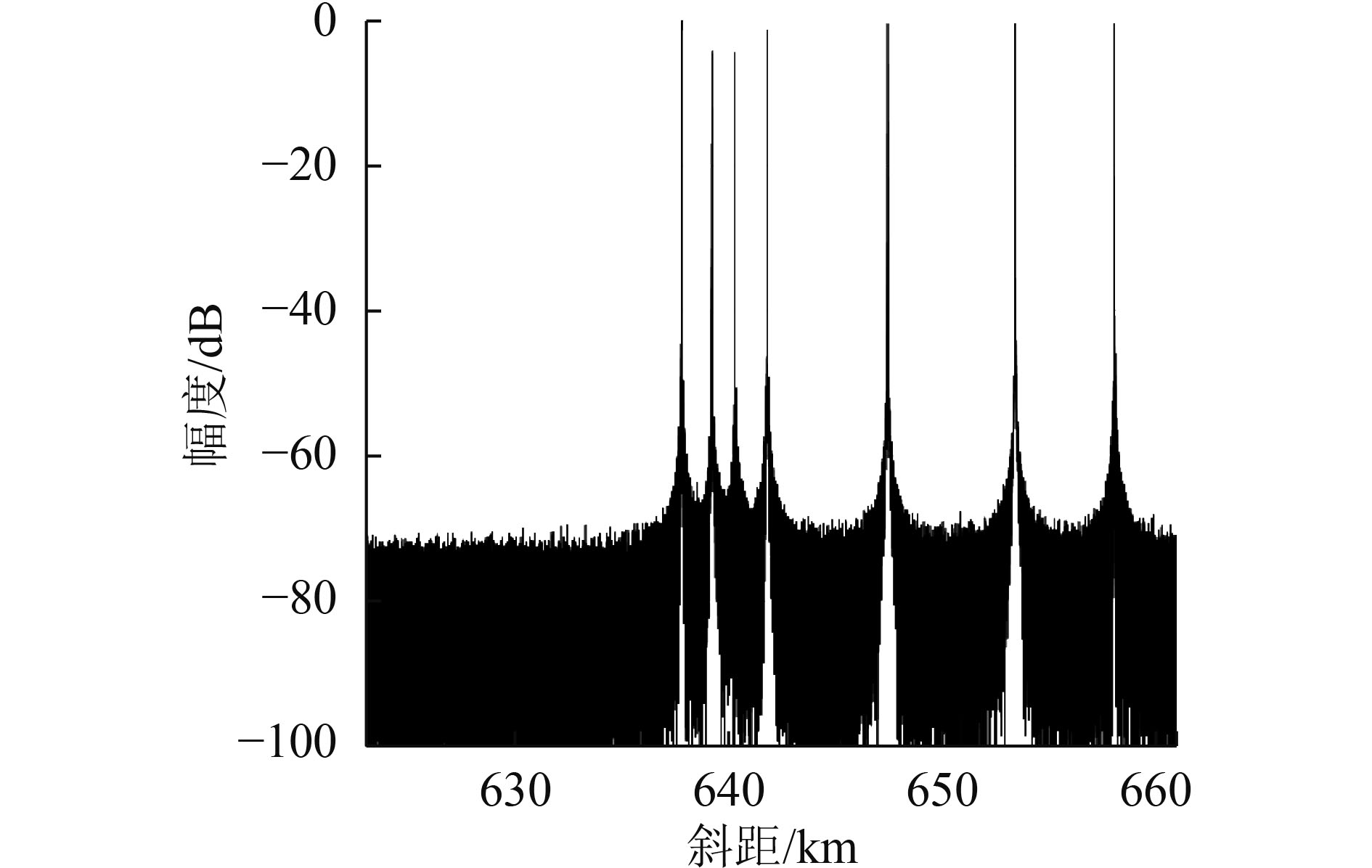
采用本文方法和SCORE方法进行仿真实验。图8(a)、图9(a)和图10(a)分别为采用SCORE方法处理得到的成像场景中第1行、第2行和第3行目标的1维成像结果。在较大地形起伏区域内(图7中的矩形虚线区域),由于SCORE方法形成的接收波束指向出现偏差,目标回波的接收增益出现了不同程度的衰减,这将导致该区域范围的SAR成像质量下降。图8(b)、图9(b)和图10(b)分别为采用本文方法处理得到的成像场景中第1行、第2行和第3行目标的1维成像结果。由于在计算DBF加权矢量时考虑了地面场景的高程数据,本文方法能够确保所有目标对应的接收波束指向偏差较小,因此成像场景中的所有目标信号幅度都保持一致。表2为图8、图9和图10对应的目标信号幅度。可以看出:当地面高程值大于1.9 km时,SCORE方法处理得到的目标信号幅度下降都超过2.8 dB,最大下降超过16 dB,这意味着较大地形起伏区域的目标回波增益都存在较大衰减,而这将严重影响SAR系统的成像性能;相比于SCORE方法,本文方法处理得到的目标信号幅度下降都小于0.4 dB,因此能够确保SAR系统具有较好的成像质量。为了进一步验证所提出的处理方法,对成像场景进行2维仿真。图11(a)和图11(b)分别为采用SCORE方法和本文方法处理得到的2维仿真结果。对比可见,本文方法能够有效改善整个成像场景的回波信号接收增益,确保高分宽幅星载SAR系统的成像性能。
表 2(Table 2)

表 2 目标信号幅度
Table 2 Amplitude of target signals
| SCORE方法 |
|
本文方法 |
| 第1行 |
第2行 |
第3行 |
第1行 |
第2行 |
第3行 |
| −1.21 |
−1.21 |
−1.21 |
|
−0.27 |
−0.27 |
−0.27 |
| −2.95 |
−3.00 |
−3.23 |
−0.27 |
−0.03 |
−0.08 |
| −14.01 |
−14.51 |
−14.81 |
−0.15 |
−0.14 |
−0.24 |
| −16.29 |
−16.22 |
−16.44 |
−0.18 |
0.00 |
−0.26 |
| −13.85 |
−14.22 |
−14.59 |
−0.05 |
−0.15 |
−0.18 |
| −2.89 |
−2.84 |
−2.93 |
−0.39 |
−0.21 |
−0.08 |
| −0.88 |
−0.88 |
−0.88 |
−0.13 |
−0.13 |
−0.13 |
|
表 2 目标信号幅度
Table 2 Amplitude of target signals
|
5、DEM数据误差的影响分析 由于DEM数据都存在分辨率限制和高程误差,这将导致根据DEM数据计算得到的地面目标高程值会出现偏差,并对高分宽幅星载SAR的俯仰向DBF处理产生影响,本节将通过仿真实验对这一影响进行分析。采用表1所示的仿真参数对图7所示成像场景中的第2行目标进行仿真实验。假定由DEM数据误差引起的目标高程偏差服从均匀分布。当目标高程值存在100 m偏差时,采用本文方法对俯仰向多通道回波信号进行处理得到的仿真结果如图12所示。可见,目标信号幅度都保持一致,这意味着:在这种情况下目标高程偏差对本文方法的影响较小。当目标高程值存在1000 m偏差时,采用本文方法进行处理得到的仿真结果(图13)。可见,第2个目标和第3个目标的信号幅度出现较大的衰减,这意味着SAR系统成像性能将会受到影响。由表3可知,只有存在较大的高程值偏差时,本文方法才会受到较大的影响。但是,考虑30 m分辨率的SRTM DEM数据的绝对高程精度为16 m (Rabus 等,2003),12 m分辨率的TerraSAR-X/Tandem-X DEM数据的绝对高程精度为10 m (Krieger 等,2007),这意味着根据DEM数据计算得到的地面目标高程值的偏差通常会小于100 m,因此由DEM数据误差引起的目标高程偏差对本文方法影响较小。
表 3(Table 3)

表 3 不同高程偏差情况下的第2行目标信号幅度
Table 3 Signal amplitude of the second row targets for different elevation deviations
| 目标信号幅度/dB |
| 无高程偏差 |
存在100 m高程偏差 |
存在1000 m高程偏差 |
| −0.27 |
−0.45 |
−0.14 |
| −0.03 |
−0.28 |
−4.15 |
| −0.14 |
−0.05 |
−4.24 |
| 0.00 |
−0.39 |
−1.20 |
| −0.15 |
−0.06 |
−0.33 |
| −0.21 |
−0.16 |
−0.41 |
| −0.13 |
−0.26 |
−0.31 |
|
表 3 不同高程偏差情况下的第2行目标信号幅度
Table 3 Signal amplitude of the second row targets for different elevation deviations
|
6、结 论 在地形起伏较大区域,高分宽幅星载SAR系统采用传统SCORE方法处理回波信号时将面临接收波束指向偏差问题,导致接收回波增益降低。针对这一问题,本文提出了一种DEM数据辅助的俯仰向DBF处理方法。通过仿真实验可看出,本文方法不仅能够确保在俯仰向DBF处理过程中接收波束指向正确,有效改善回波信号的接收增益,并且对DEM数据误差有较强的适应性。
根据对俯仰向DBF接收波束扫描指向问题的分析,本文方法从星载SAR成像几何模型的角度出发,充分利用了地面场景的数字高程图数据,对促进俯仰向DBF处理在高分宽幅星载SAR系统的有效应用具有一定的理论意义。
在实际处理过程中,由于本文解决的是俯仰向DBF接收波束指向问题,因此主要针对方位向地形起伏较小的成像场景。本研究的下一步目标是针对方位向地形起伏较大的区域设计相应的系统处理方案,并探讨该处理方案如何实现工程化的应用。