| 基于葵花-8卫星大气产品的地表下行短波辐射计算 |
收稿日期: 2018-01-24
2. College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China
3. College of Geography Science, Inner Mongolia Normal University, Hohhot 010022, China
4. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
5. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
太阳辐射是地球上一切生命活动的主要能量来源,也是地球气候形成最重要的因子,对地表辐射平衡、能量交换以及天气气候的形成具有决定性的意义(Houborg 等,2007;Wild,2009)。作为地表太阳辐射的重要组成部分,地表下行短波辐射DSSR (Downward Surface Shortwave Radiation)是地表辐射平衡的重要分量,也是陆面模型和气候模式的关键输入参数,因此准确估算DSSR对全球辐射收支平衡和太阳能估算等应用研究具有重要意义(Zhang 等,2014;Huang 等,2016)。
卫星遥感具有快速、大面积观测目标物的优势而成为获取DSSR的重要手段。基于卫星资料的DSSR估算方法主要分为统计法和物理法(Pinker和Ewing,1985;Dedieu 等,1987;Deneke 等,2005)。统计法利用大量地面观测数据与卫星观测信号进行统计分析来建立DSSR的经验模型。统计法具有计算速度快、算法结构简单的特点,然而计算过程中没有充分考虑物理机制,当计算结果出现误差时,很难追溯到误差的来源。物理方法具有计算精度高、物理机制明确的优势,然而计算速度一般低于统计法。关于统计法的研究方面,Cano等(1986)基于晴天指数和阴天指数建立静止卫星可见光波段反照率与DSSR的统计关系,经测试两个不同时间段的数据发现建立的统计模型与实测DSSR值具有较好的一致性。陈金娥和李集明(1997)利用GMS静止卫星获取的云量资料,借助云量与日照百分率之间的非线性关系以及后者与总辐射间的线性关系,确立DSSR估算方法,进而分析了西藏地区太阳能时空分布特征。关于物理法的研究方面,魏合理等(2003)利用GMS-5卫星可见光通道的反照率,结合6S大气辐射传输模式估算DSSR,获得了较高的反演精度(日平均方差约为10%)。余予等(2007)利用地基观测的气溶胶、水汽和臭氧数据作为MODTRAN、6S、SBDART等3种大气辐射传输模式的输入参数,模拟了晴空条件下的太阳直接辐射和散射辐射,发现直接辐射的观测数据和模拟结果具有较好的一致性,然而散射辐射的观测和模拟之间的相差较大。黎微微等(2017)利用MODIS大气产品资料计算了不同云天条件下的DSSR,并进一步探讨了云—气溶胶双层结构对DSSR的估算误差。此外,有些学者融合了统计法和物理法,如Takenaka等(2011)利用大气辐射传输模式来训练神经网络,进而利用训练好的神经网络结合卫星资料来估算DSSR,并利用SKYNET地基站点观测数据验证了算法的可靠性,然而该算法并没有考虑气溶胶对DSSR的影响。Tang等(2016)利用MODIS极轨卫星大气产品和MTSAT静止卫星资料,结合神经网络方法获得了高时空分辨率的DSSR产品。以上的统计物理混合法在一定程度上发挥了两种方法在计算速度和精度上优势,但由于构建的神经网络的仍属于浅层神经网络,与深度学习中的“深度神经网络”有所差别,其DSSR估算精度可有进一步的提升空间。
卫星云、霾的精确检测(Husi 等,2014;Shang 等,2017,2018),及其光学、微物理参数的准确反演(Letu 等,2016)有利于提高不同云、气溶胶背景下的DSSR计算精度。DSSR时空变化较大,传统极轨卫星(如Aqua/MODIS)很难获取其连续变化情况,新一代静止气象卫星葵花-8(Himawari-8)具有高达10 min的圆盘(Full-disk)观测能力(Bessho 等,2016),可近实时获取DSSR。目前日本宇宙航空研究开发机构(JAXA)对外公开的葵花-8的辐射产品,没有将其反演的云、气溶胶产品作为DSSR估算的输入数据,因而没有形成一整套的DSSR估算算法流程,缺乏产品输出的一致性。而该辐射算法是基于(Frouin和Murakami,2007)等的工作,同时该算法在晴空下没有充分考虑气溶胶对太阳辐射的影响,在云天条件下也没有考虑不同云相态对太阳辐射的影响,因此在重气溶胶污染背景或云天条件下估算的DSSR精度受限。本文首先利用大气辐射传输模式RSTAR,对影响DSSR的主要因子做了敏感性分析,基于敏感性分析结果构建了计算DSSR的查找表,开发了地表辐射的快速计算方法,进而利用JAXA葵花-8二级云和气溶胶产品数据作为快速化方法的输入参数,计算了DSSR。最后利用地面观测数据验证了本文计算的DSSR与JAXA同时期的葵花-8二级DSSR产品(以下简称JAXA DSSR)。
2、数据与模式 (2.1) 葵花-8卫星资料与地基验证数据葵花-8卫星搭载了世界上先进的下一代气象观测传感器—可见光/红外辐射计AHI(Advanced Himawari Imager),相比以往静止卫星传感器实现了更高的空间、时间和光谱分辨率。AHI共16个波段:从0.47—13.3 μm,包含了3个可见光波段、3个近红外波段、10个红外线波段。其中0.64 μm波段分辨率为0.5 km,0.46 μm、0.51 μm和0.86 μm波段分辨率为1 km,其余分辨率为2 km。全部通道每10 min可获取一次,针对日本地区和特定目标可实现2.5 min观测一次(Bessho 等,2016)。日本宇宙航空研究开发机构JAXA(Japan Aerospace Exploration Agency)在“P-Tree”FTP系统(ftp.ptree.jaxa.jp[2018-01-24])上对外开放了葵花-8卫星产品的下载。本研究利用2016年4、7、10和12月的一级产品、二级云和气溶胶产品作为计算DSSR的输入数据,具体参数如表1所示。
|
|
表 1 本研究使用的葵花-8卫星产品 Table 1 Himawari-8 satellite products used in this study |
其中云掩码和云相态以二进制编码的形式存储于二级云产品的QA(Quality Assurance)波段中,如表2所示。
|
|
表 2 云掩码和云相态二进制编码bit位 Table 2 Bit information of cloud mask and cloud phase |
本文所使用的DSSR验证数据分别来自太阳辐射观测网SolRad-Net(Solar Radiation Network)和美国国家海洋和大气管理局(NOAA)的浮标观测数据GTMBA(Global Tropical Moored Buoy Array)。SolRad-Net和GTMBA均提供了高观测频率(最高2 min/次)的地表太阳辐射数据集,可用来验证本研究计算的瞬时DSSR结果(SolRad-Net:https://solrad-net.gsfc.nasa.gov/index.html;GTMBA:https://www.pmel.noaa.gov/tao/drupal/disdel/[2018-01-24])。表3列出了本研究所使用的观测站点,其中Yonsei站点位于陆地,0n_165e位于赤道上的海洋表面,可分别用于评估本文DSSR算法在陆地和海洋上的准确度。
|
|
表 3 本研究所使用的DSSR验证数据 Table 3 In-situ measurements data used in this study |
RSTAR是由(Nakajima和Tanaka, 1986,1988;Stamnes 等,1988)等开发的一套适用于平面平行大气的辐射传输数值模式,计算波长可覆盖0.17—1000 μm,假设的平面平行大气从海平面到120 km最高可分50层,有6种大气模式(热带、中纬度夏季、中纬度冬季、高纬度夏季、高纬度冬季、美国标准大气)可供选择,预设由9种基本成分(Water,Ice,Dust-like,Water-soluble,Sea Salt,Soot,Volcanic-ash,75% H2SO4,Yellow sand)组成的11类气溶胶模型。云模型有水云和由球形、椭球形、六角柱形等不同冰晶模型组成的冰云可供选择。具体模拟时,需要输入任一像素点的太阳、卫星几何角度等参数;给定需要计算的各波段中心波长和宽度,以及每一点的风速;还要选择大气部分的相关参数,主要是:大气模式类型、大气的次层数、组成气溶胶模型的粒子类型及其体积混合比、相对湿度等;另外还必须选择一个波段,给定其初始气溶胶光学厚度值用于迭代计算。通过设置以上参数后,可以得到下列输出量:每一波段对应的每个大气层面上总的光学厚度、气溶胶光学厚度、瑞利光学厚度、单次散射反照率、不对称因子、太阳入射辐照度、向下辐射通量、向上辐射通量、大气顶辐亮度等。该模式计算方案灵活,计算精度高,考虑因素多,输出结果丰富。在本文中,主要运用RSTAR模拟不同太阳、大气(云、气溶胶)和地表条件下的地表下行短波辐射,进而构建地表下行短波辐射的快速计算查找表。
3、地表下行短波辐射的估算方法图1为利用葵花−8卫星二级云、气溶胶产品估算DSSR的总体流程(辅助数据为一级产品中的太阳天顶角)。首先利用大气辐射传输模式RSTAR构建晴空和云天条件下的DSSR查找表;然后利用云、气溶胶产品结合查找表计算DSSR;最后利用地基观测数据验证计算结果的可靠性。
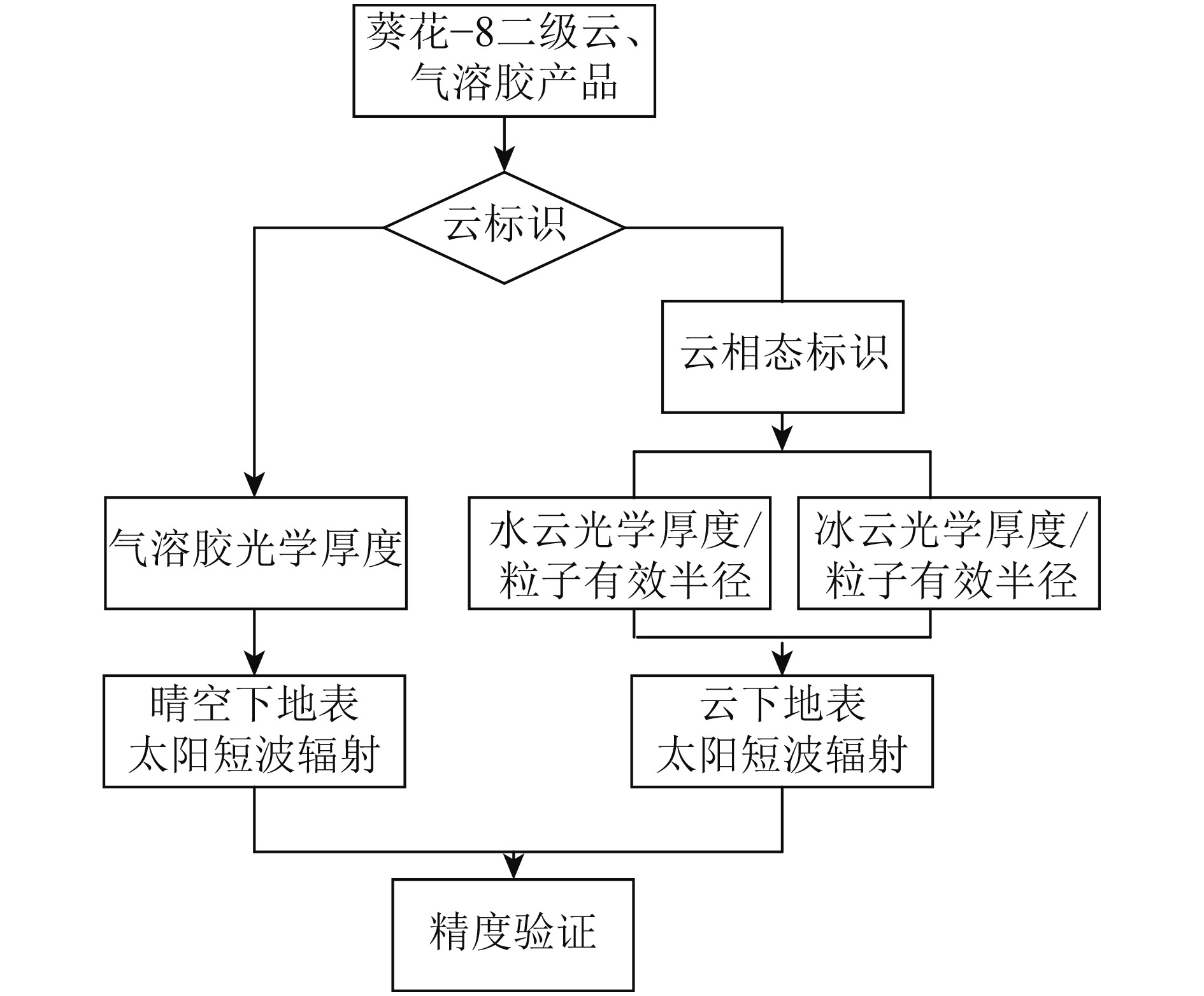
|
| 图 1 地表下行短波辐射估算流程图 Figure 1 Flow chart of DSSR estimation |
在构建查找表之前,需要对影响DSSR的因子做敏感性分析,进而根据敏感性分析结果进一步构建查找表,目的是减少查找表的冗余,提高查找效率。其中敏感性分析结果见4.1节。
基于敏感性分析结果,利用大气辐射传输模式RSTAR分别构建了晴空和有云(水云、冰云)条件下的DSSR查找表。对于晴空:太阳天顶角为0°、5°、10°、15°、20°、25°、30°、35°、40°、45°、50°、55°、60°、70°、80°和90°;气溶胶光学厚度0—3,间隔为0.25。而对于云下的DSSR估算,按云相态(水云、冰云)进一步区分。对于水云:太阳天顶角为0°、5°、10°、15°、20°、25°、30°、35°、40°、45°、50°、55°、60°、70°、80°和90°;水云光学厚度为1、5、10、20、30、50、100、150;水云粒子有效半径为4 μm、8 μm、16 μm、32 μm。对于冰云的设置为:太阳天顶角为0°、5°、10°、15°、20°、25°、30°、35°、40°、45°、50°、55°、60°、70°、80°和90°;冰云光学厚度为1、5、10、20、30、50、100、150;冰云粒子有效半径为16 μm、32 μm、64 μm、128 μm。在以上的模拟过程中,大气模式设定为美国标准大气,地表反照率为0.1。需要说明的是,在冰云的DSSR模拟过程中,不同冰晶粒子的形状对DSSR的影响较大,选择合适的冰晶粒子形状有助于准确模拟到达地表的太阳辐射。1991年实施的ICE国际卷云实验项目证实冰晶的基本形状为近似六角形(胡斯勒图 等,2015)。因此,在模拟冰云的DSSR时,选取六棱柱形冰晶粒子作为冰云粒子。此外,为了能够计算特殊情况(台风)的DSSR,将水云、冰云的光学厚度拓展到了150,同时也能与JAXA葵花-8二级云产品中的云光学厚度范围(0—150)相匹配。
由于模式输出的是在特定太阳几何位置、大气和地表条件下的光谱地表下行辐射,因此需要将光谱地表下行辐射对太阳短波部分(0.3—3.0 μm)进行积分
| $S = \int\limits_{0.3\;{\rm{{\text{μ}} m}}}^{3.0\;{\rm{{\text{μ}} m}}} {S({\textit{λ}})} {\rm{d}}{\textit{λ}} $ | (1) |
式中,
为了分别计算晴空和云下的DSSR,首先需要对晴空和云进行识别。本研究利用葵花-8二级云产品中的QA波段所包含的云相态识别结果来区分晴空和云。在QA波段里的第5、6 bit位置信息,标识了云相态的反演结果:晴空(00)、水云(01)、混合相态(10)和冰云(11),见表2。因此,对于晴空,提取葵花-8一级产品中的太阳天顶角和二级气溶胶产品中的气溶胶光学厚度,结合查找表,查表得到晴空下的DSSR。在查表过程中,对于没有出现在表中的数值,采用线性内插的方式来获得。而对于云天,根据云相态,提取葵花-8一级产品中的太阳天顶角和二级云产品中的水云/冰云光学厚度和水云/冰云粒子有效半径,结合查找表,查表得到云下的DSSR。
(3.2) 精度评价方法为了评价DSSR计算结果的准确性,采用了平均偏差(BIAS)、均方根误差(RMSE)和相关系数(R)来评估(Qin 等,2018)
| ${\rm{BIAS}} = \frac{1}{n}\sum\limits_{i = 1}^n {({S_i} - {O_i})} $ | (2) |
| ${\rm{RMSE}}{\rm{ = }}\sqrt {\frac{{\sum\limits_{i = 1}^n {{{({S_i} - {O_i})}^2}} }}{n}} $ | (3) |
| $R = \frac{{\sum\limits_{i = 1}^n {({S_i} - \overline S })({O_i} - \overline O)}}{{\sqrt {\sum\limits_{i = 1}^n {{{({S_i} - \overline S)}^{\rm{2}}}\sum\limits_{i = 1}^n {{{({O_i} - \overline O)}^{\rm{2}}}} } } }}$ | (4) |
式中,
为了合理构建查找表,需要对DSSR影响因子做敏感性分析,基于敏感性分析结果,构建合理的查找表有助于提高DSSR的计算速度和精度。图2为利用RSTAR大气辐射传输模式对太阳天顶角、云光学厚度、云粒子有效半径、气溶胶光学厚度和地表反照率的敏感性模拟结果。

|
| 图 2 地表下行短波辐射对不同太阳、大气和地表条件的敏感性模拟结果 Figure 2 Sensitivities of DSSR to different solar geometry, atmosphere and surface conditions |
图2(a)模拟了不同水云光学厚度和不同太阳天顶角对到达DSSR的影响(大气模式假设为美国标准大气(US standard),地表反照率假设为0.1),通过模拟可知,在同一太阳天顶角(或云光学厚度)下,随着云光学厚度(或太阳天顶角)的增加,到达地表的太阳辐射在逐渐减少;另一方面,随着太阳天顶角的变大,DSSR随着云光学厚度的变大而提前变得不“敏感”。图2(b)模拟了不同水云/冰云有效粒子半径对DSSR的影响(太阳天顶角假设为0°,地表反照率假设为0.1,冰晶形状假设为六棱柱),从模拟结果可以看出,在同一云光学厚度下,不论水云还是冰云,DSSR随着云粒子有效半径的增大而变大;另一方面,不同水云粒子有效半径模拟得到的下行短波辐射均要高于不同冰云粒子有效半径下的下行短波辐射,因此有时为了简化模型而仅考虑水云时,计算的结果可能会高估真实的DSSR。因此,考虑不同云相态,同时使用非球形冰晶粒子有助于提高DSSR的计算精度。图2(c)模拟了不同大气模式对DSSR的影响(太阳天顶角假设为0°,地表反照率假设为0.1,气溶胶模式假设为大陆型)。从模拟结果可以看出,DSSR随气溶胶光学厚度的变大而变小,同时不同大气模式模拟的结果具有一定的差异。中纬度冬季的DSSR模拟结果最高,美国标准大气模拟的结果在气溶胶光学厚度大于0.5时,小于其他大气模式的模拟结果。图2(d)模拟了不同地表反照率对DSSR的影响。从模拟的结果可以看出,在有气溶胶的背景下,DSSR随地表反照率的变大而变大,这部分能量可能主要来自于地气之间的多次散射。从图2的模拟结果可以看出,太阳天顶角、气溶胶光学厚度、云光学厚度、水云冰云粒子有效半径、地表反照率对DSSR都有影响,其中云光学厚度、太阳天顶角和气溶胶光学厚度影响程度最大,而云粒子有效半径、地表反照率影响相对上述三者较小。因此,本文为了实现快速化计算,在查找表构建过程中考虑了主要的影响因素:太阳天顶角、云光学厚度、气溶胶光学厚度、云粒子有效半径,将地表反照率假设为0.1,大气模式默认为美国标准大气。
(4.2) 地表下行太阳短波辐射计算结果图3为2016-04-01 T 02:00本文计算的DSSR结果与同时刻JAXA DSSR产品的对比,其中第2列的图像是葵花-8卫星整个圆盘区域的观测范围,第1列和第3列分别为圆盘区域(80°E—160°W,60°S—60°N)的局部放大图。图3中每个图像从上往下依次为:真彩图、JAXA DSSR产品、本文计算的DSSR结果。从图3的真彩图可以看出,在整个圆盘区域,有约为一半的地区被云所覆盖,同时在整个圆盘图像的中央部分有明显的太阳耀光。

|
| 图 3 本文计算的DSSR与JAXA葵花-8二级DSSR产品的对比 Figure 3 Comparison of DSSR between this study and Himawari-8 L2 DSSR product |
从图3的DSSR计算结果可以看出,本文计算的DSSR与JAXA DSSR在空间分布上一致性较好,如晴空区域:从图像中心至图像边缘,本文计算的DSSR结果与JAXA DSSR变化区域较为一致;云覆盖区域:澳大利亚以南的云覆盖区域、澳大利亚以西的部分云覆盖区域、中国部分云覆盖区域,均与JAXA DSSR的一致性良好。但部分区域有较大的差异,如图像的中央部分,本文计算的DSSR较JAXA的DSSR偏大(颜色表现为深红);在太阳耀光的区域,JAXA将该部分计算结果进行了全部的剔除,而本文则根据输入的云、气溶胶产品的反演情况,进行了动态的处理,获得了连续的DSSR分布。
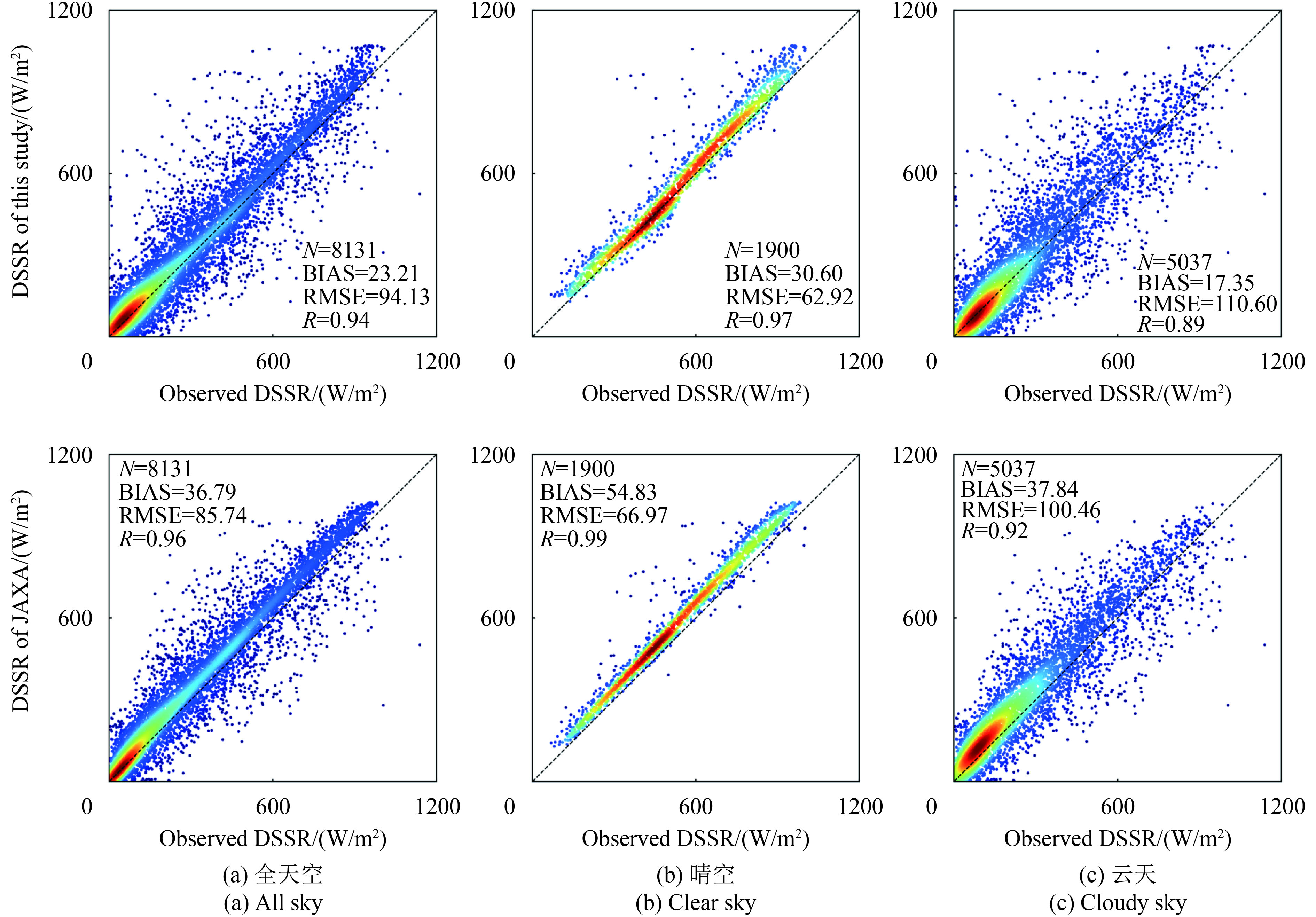
(4.3) 地表下行短波辐射计算精度评价通过以上的定性分析表明,本研究计算得到的DSSR结果与JAXA DSSR在空间上具有良好的一致性。为了定量评价本研究的DSSR计算精度,利用位于韩国首尔延世大学的Yonsei陆地观测站点(以下简称陆地站点)和位于赤道的海洋浮标数据0n_165e(以下简称海洋站点)进行验证。同时,为了方便与JAXA DSSR进行对比,也利用了上述的两个观测数据验证了同时期JAXA DSSR。图4、5分别为2016年4、7、10和12月共4个月在陆地站点和海洋站点DSSR的验证结果。为了更加清晰地看出点的分布与聚集情况,将验证结果绘制成了散点密度图。
|
| 图 4 本文DSSR与JAXA葵花-8二级DSSR产品在Yonsei站点(陆地)的验证结果 Figure 4 DSSR validation results between this study and JAXA L2 DSSR product at Yonsei site |
在图4、5中,颜色由蓝到青、再到深红表示散点密度在逐渐变大。两个观测站点的总体验证结果显示,本文计算的DSSR与观测的DSSR在全天空(All sky)、晴空(Clear sky)和云天(Cloudy sky)下均具有较高的精度,在两个站点的所有验证情况中,相关系数R均大于0.88。在陆地站点,验证结果显示本文计算的DSSR和JAXA DSSR均有较高的精度(晴空和云天条件下的绝大部分验证点聚集在1∶1线附近),但后者在晴空下表现出了高估的现象,大部分验证结果位于1∶1线之上(BIAS=54.83 W/m2),云天条件下也表现出了低值高估的现象(红色部分的散点密度高于1∶1线)。而本文计算的DSSR不论在晴空还是云天,高散点密度值区域均能较好的分布在1∶1线两侧。在海洋站点,两者DSSR验证结果与观测值也均具有较高的相关性(相关系数R均大于0.88),高散点密度的区域位于1∶1线附近,然而BIAS和RMSE相对陆地站点则要差了很多。两者的RMSE在全天空、晴空和云天下均大于了90 W/m2,尤其是在晴空的条件下。此外,JAXA DSSR在云天条件下仍表现出了低值高估的现象。
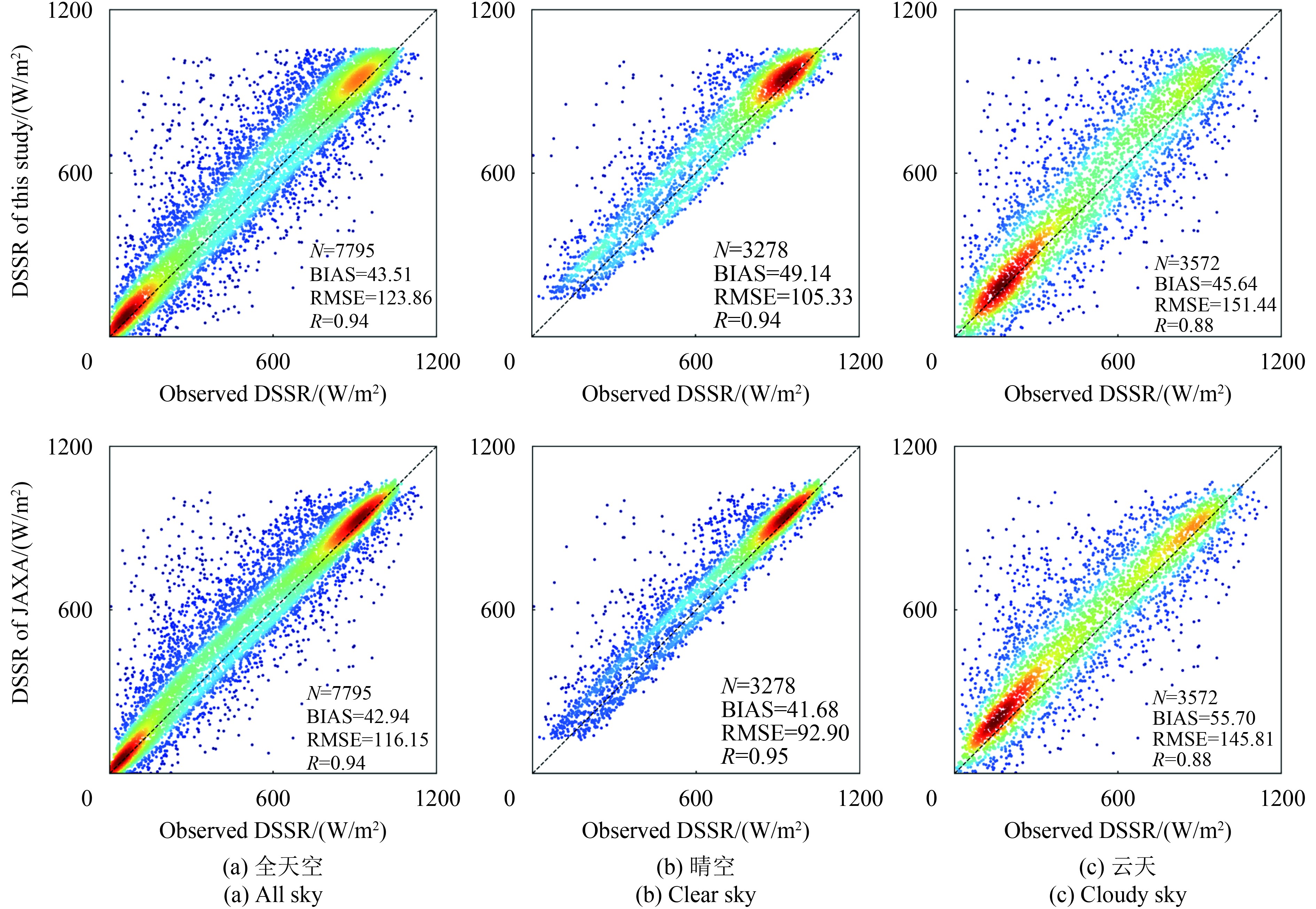
|
| 图 5 本文DSSR与JAXA葵花-8二级DSSR产品在0n_165e站点(海洋)的验证结果 Figure 5 DSSR validation results between this study and JAXA L2 DSSR product at 0n_165e site |
由于本研究在构建查找表的过程中考虑了气溶胶对DSSR的影响,因此在陆地站点晴空下的精度验证结果在RMSE和BIAS方面较JAXA DSSR有优势。此外,在云天下,本研究考虑了非球形冰晶粒子(六棱柱)对DSSR的影响,也显示出了一定的优势(散点密度高值区聚集在1∶1线上)。在海洋站点,验证结果要差于陆地,可能来自以下3个方面:(1)输入计算的云、气溶胶产品精度的问题:在赤道附近,受太阳强烈直射的影响,海表因镜面反射呈现太阳耀光,可能导致卫星云、气溶胶参数的反演结果具有较大的误差,进而误差传递到本研究。(2)没有考虑水汽含量的变化:赤道附近水汽含量较大,且水汽对太阳辐射具有吸收作用。本文为了实现快速计算,构建查找表过程中采用了模式默认的水汽柱总量,因此在水汽变化较大的区域,可能会带来较大的误差。(3)气溶胶模式的假设带来的误差:本文为了实现快速计算,将气溶胶模式假设为大陆型,给海洋上空的DSSR计算带来一定的误差。其他如地表反照率、大气模式的假定,也会带来一定的误差。
5、结 论本文首先利用大气辐射传输模式RSTAR对地表下行短波辐射(DSSR)进行了敏感性分析,基于敏感性分析结果并重点考虑云和气溶胶对DSSR的影响,构建了DSSR的查找表,开发了DSSR的快速计算方法,进而利用JAXA葵花-8二级云和气溶胶参数产品作为快速化方法的输入数据计算了DSSR。最后,利用Yonsei站点(陆地)和0n_165e站点(海洋)观测资料分别验证了2016年4、7、10和12月共4个月本研究获得的DSSR和同期的JAXA葵花-8二级DSSR产品。得到以下结论:
(1)敏感性分析方面:发现太阳天顶角、云光学厚度和气溶胶光学厚度对DSSR的影响较大,而云粒子有效半径和地表反照率的影响相对上述三者较小,在构建查找表的过程中需要重点考虑前三者。
(2)精度验证方面:本文计算得到的DSSR与JAXA DSSR在空间分布上一致性较好。在两个观测站点,两者的DSSR与观测的DSSR在全天空、晴空和云天条件下的相关系数R均大于0.88,具有较高的精度;此外,本文在利用大气辐射传输模式构建冰云DSSR查找表时,考虑了非球形冰晶粒子,获得了比JAXA DSSR在两个站点更小的BIAS的验证结果。在陆地站点,晴空条件下的验证结果(BIAS:30.60 W/m2,RMSE:62.92 W/m2)要优于JAXA DSSR(BIAS:54.83 W/m2,RMSE:66.97 W/m2)。在海洋站点,全天空下的DSSR验证精度(BIAS:43.51 W/m2,RMSE:123.86W/m2)较低于JAXA DSSR (BIAS:42.94 W/m2,RMSE:116.15 W/m2)。
通过考虑地表反照率、大气水汽等的变化可进一步改进模型,有望更进一步提高本文的DSSR在陆地和海洋上的估算精度。
志 谢 感谢日本宇宙航空研究开发机构(JAXA)提供的葵花-8卫星产品数据、SolRad-Net提供的Yonsei站点观测数据、美国国家海洋和大气管理局(NOAA)提供的0n_165e海洋浮标观测数据。
| [1] | Bessho K, Date K, Hayashi M, Ikeda A, Imai T, Inoue H, Kumagai Y, Miyakawa T, Murata H, Ohno T, Okuyama A, Oyama R, Sasaki Y, Shimazu Y, Shimoji K, Sumida Y, Suzuki M, Taniguchi H, Tsuchiyama H, Uesawa D, Yokota H and Yoshida R. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites[J]. Journal of the Meteorological Society of Japan. Series II, 2016, 94 (2) : 151 –183. DOI: 10.2151/jmsj.2016-009 |
| [2] | Cano D, Monget J M, Albuisson M, Guillard H, Regas N and Wald L. A method for the determination of the global solar radiation from meteorological satellite data[J]. Solar Energy, 1986, 37 (1) : 31 –39. DOI: 10.1016/0038-092x(86)90104-0 |
| [3] | 陈金娥, 李集明. 关于利用卫星数据计算西藏地区太阳能资源的研究[J]. 太阳能学报, 1997, 18 (2) : 113 –116. Chen J E and Li J M. Estimation solar energy resource for Tibet region with satellite data[J]. Acta Energiae Solaris Sinica, 1997, 18 (2) : 113 –116. DOI: 10.10071BF02951625 |
| [4] | Dedieu G, Deschamps P Y and Kerr Y H. Satellite estimation of solar irradiance at the surface of the earth and of surface albedo using a physical model applied to Metcosat data[J]. Journal of Climate and Applied Meteorology, 1987, 26 (1) : 79 –87. DOI: 10.1175/1520-0450(1987)026<0079:seosia>2.0.co;2 |
| [5] | Deneke H, Feijt A, van Lammeren A V and Simmer C. Validation of a physical retrieval scheme of solar surface irradiances from narrowband satellite radiances[J]. Journal of Applied Meteorology, 2005, 44 (9) : 1453 –1466. DOI: 10.1175/jam2290.1 |
| [6] | Frouin R and Murakami H. Estimating photosynthetically available radiation at the ocean surface from ADEOS-II global imager data[J]. Journal of Oceanography, 2007, 63 (3) : 493 –503. DOI: 10.1007/s10872-007-0044-3 |
| [7] | Houborg R, Soegaard H, Emmerich W and Moran S. Inferences of all-sky solar irradiance using Terra and Aqua MODIS satellite data[J]. International Journal of Remote Sensing, 2007, 28 (20) : 4509 –4535. DOI: 10.1080/01431160701241902 |
| [8] | Huang J P, Yu H P, Guan X D, Wang G Y and Guo R X. Accelerated dryland expansion under climate change[J]. Nature Climate Change, 2016, 6 (2) : 166 –171. DOI: 10.1038/nclimate2837 |
| [9] | Husi L T, Nagao T M, Nakajima T Y and Matsumae Y. Method for validating cloud mask obtained from satellite measurements using ground-based sky camera[J]. Applied Optics, 2014, 53 (31) : 7523 –7533. DOI: 10.1364/ao.53.007523 |
| [10] | 胡斯勒图, 包玉海, 许健, 青松, 包钢. 基于六角形和球形冰晶模型的卷云辐射特征研究[J]. 光谱学与光谱分析, 2015, 35 (5) : 1165 –1168. Husltu, Bao Y H, Xu J, Qing S and Bao G. Radiative properties of cirrus clouds based on hexagonal and spherical ice crystals models[J]. Spectroscopy and Spectral Analysis, 2015, 35 (5) : 1165 –1168. DOI: 10.3964/j.issn.1000-0593(2015)05-1165-04 |
| [11] | Letu H, Ishimoto H, Riedi J, Nakajima T Y, Labonnote L C, Baran A J, Nagao T M and Skiguchi M. Investigation of ice particle habits to be used for ice cloud remote sensing for the GCOM-C satellite mission[J]. Atmospheric Chemistry and Physics, 2016, 16 (18) : 12287 –12303. DOI: 10.5194/acp-16-12287-2016 |
| [12] | 黎微微, 胡斯勒图, 陈洪滨, 尚华哲. 利用MODIS资料计算不同云天条件下的地表太阳辐射[J]. 遥感技术与应用, 2017, 32 (4) : 643 –650. Li W W, Letu H, Chen H B and Shang H Z. Estimation of surface solar radiation using MODIS satellite data and RSTAR model[J]. Remote Sensing Technology and Application, 2017, 32 (4) : 643 –650. DOI: 10.11873/j.issn.1004-0323.2017.4.0643 |
| [13] | Nakajima T and Tanaka M. Matrix formulations for the transfer of solar radiation in a plane-parallel scattering atmosphere[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 1986, 35 (1) : 13 –21. DOI: 10.1016/0022-4073(86)90088-9 |
| [14] | Nakajima T and Tanaka M. Algorithms for radiative intensity calculations in moderately thick atmospheres using a truncation approximation[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 1988, 40 (1) : 51 –69. DOI: 10.1016/0022-4073(88)90031-3 |
| [15] | Pinker R T and Ewing J A. Modeling surface solar radiation: model formulation and validation[J]. Journal of Climate and Applied Meteorology, 1985, 24 (5) : 389 –401. DOI: 10.1175/1520-0450(1985)024<0389:mssrmf>2.0.co;2 |
| [16] | Qin W M, Wang L C, Lin A W, Zhang M, Xia X G, Hu B and Niu Z G. Comparison of deterministic and data-driven models for solar radiation estimation in China[J]. Renewable and Sustainable Energy Reviews, 2018, 81 : 579 –594. DOI: 10.1016/j.rser.2017.08.037 |
| [17] | Shang H Z, Chen L F, Letu H, Zhao M, Li S S and Bao S H. Development of a daytime cloud and haze detection algorithm for Himawari-8 satellite measurements over central and eastern China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122 (6) : 3528 –3543. DOI: 10.1002/2016JD025659 |
| [18] | Shang H Z, Letu H, Nakajima T Y, Wang Z M, Ma R, Wang T X, Lei Y H, Ji D B, Li S S and Shi J C. Diurnal cycle and seasonal variation of cloud cover over the Tibetan Plateau as determined from Himawari-8 new-generation geostationary satellite data[J]. Scientific Reports, 2018, 8 (1) : 1105 . DOI: 10.1038/s41598-018-19431-w |
| [19] | Stamnes K, Tsay S C, Wiscombe W and Jayaweera K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media[J]. Applied Optics, 1988, 27 (12) : 2502 –2509. DOI: 10.1364/ao.27.002502 |
| [20] | Takenaka H, Nakajima T Y, Higurashi A, Higuchi A, Takamura T, Pinker R T and Nakajima T. Estimation of solar radiation using a neural network based on radiative transfer[J]. Journal of Geophysical Research: Atmospheres, 2011, 116 (D8) : D08215 . DOI: 10.1029/2009jd013337 |
| [21] | Tang W J, Qin J, Yang K, Liu S M, Lu N and Niu X L. Retrieving high-resolution surface solar radiation with cloud parameters derived by combining MODIS and MTSAT data[J]. Atmospheric Chemistry and Physics, 2016, 16 (4) : 2543 –2557. DOI: 10.5194/acp-16-2543-2016 |
| [22] | 魏合理, 徐青山, 张天舒. 用GMS-5气象卫星遥测地面太阳总辐射[J]. 遥感学报, 2003, 7 (6) : 465 –471. Wei H L, Xu Q S and Zhao T S. Observation of solar irradiance at the surface from GMS-5[J]. Journal of Remote Sensing, 2003, 7 (6) : 465 –471. DOI: 10.3321/j.issn:1007-4619.2003.06.006 |
| [23] | Wild M. Global dimming and brightening: a review[J]. Journal of Geophysical Research: Atmospheres, 2009, 114 (D10) : D00D16 . DOI: 10.1029/2008jd011470 |
| [24] | 余予, 夏祥鳌, 陈洪滨, 王振会, 王普才, 李占清. 晴空大气太阳短波辐射观测与模式比较[J]. 太阳能学报, 2007, 28 (3) : 233 –240. Yu Y, Xia X A, Chen H B, Wang Z H, Wang P C and Li Z Q. A comparasion between measured and modeled clear-sky surface solar irradiance[J]. Acta Energiae Solaris Sinica, 2007, 28 (3) : 233 –240. DOI: 10.3321/j.issn:0254-0096.2007.03.002 |
| [25] | Zhang X T, Liang S L, Zhou G Q, Wu H R and Zhao X. Generating Global LAnd Surface Satellite incident shortwave radiation and photosynthetically active radiation products from multiple satellite data[J]. Remote Sensing of Environment, 2014, 152 : 318 –332. DOI: 10.1016/j.rse.2014.07.003 |

