海洋覆盖了地球面积的71%，海水光学参数的测量对研究全球气候变化和物质循环具有重要的意义(Dickey 等，2006)。原位测量利用高光谱吸收或者衰减设备现场测量水体，探测精度高，是目前探测水体光学参数最成熟的方法之一，然而此种方式受限于低探测效率(Behrenfeld和Boss，2006)。卫星被动遥感技术能够提供全球尺度的水色信息，但是该方式无法提供足够的海洋垂直分布情况(Dickey 等，2006)。声学探测系统广泛应用于水体的垂直分布测量，但是其工作平台局限于水面或水下，无法应用于飞机平台和卫星载荷。海洋激光雷达作为一种主动式光学遥感设备，可用于探测水体的光学特性，能够对上层海洋垂直分布结构进行遥感测量，具备高时空分辨率、昼夜连续观测、全球尺度测量等优势(Vasilkov 等，2001)。

目前，海洋激光雷达已能够成功应用于生物探测、浮游植物层分布研究、浅海地形测绘、海洋内波探测等相关研究(Zhou 等，2019)。然而，利用激光雷达探测水体光学参数的研究相对较少。由于海洋激光雷达回波信号同时取决于海水对激光的衰减和后向散射，从回波信号反演出所需的光学参数存在困难。米散射激光雷达无光谱鉴频能力，反演水体光学参数时必须进行水体悬浮物激光雷达比的假设，探测精度有限。高光谱分辨率激光雷达(HSRL)增加带有窄带滤光片的通道，能将水体的后向散射和衰减参数分离开来，提高水体光学参数的反演精度(Zhou 等，2017)。

自主研制了一套船载米散射激光雷达，用于探测海水光学参数垂直廓线。该系统在黄海海域进行了实验测量。在准单次散射模型中纳入原位测量的光学参数，模拟了理想的激光雷达回波信号，并与系统响应卷积后精确复现了实验的激光雷达信号。分析了水体悬浮物激光雷达比对米散射激光雷达和Fernald迭代后向积分法(后文简称Fernald法)的影响，给出了当前水域最合适的水体悬浮物激光雷达比。基于标定的水体悬浮物激光雷达比，采用Fernald法获得了走航时的激光雷达衰减系数。提出了一种基于米散射激光雷达数据和原位测量的后向散射数据的算法(后文简称融合算法)，模拟了高光谱分辨率激光雷达反演激光雷达衰减系数的过程，并比较分析了该算法与Fernald法的反演结果。实验表明海洋激光雷达能够有效探测水体光学参数，水体悬浮物激光雷达比对米散射激光雷达的应用至关重要，发展无需相关假设的HSRL是未来海洋激光雷达的发展方向。

研制的船载海洋激光雷达系统主要由激光发射系统、接收系统以及信号采集和处理系统三大部分组成，系统结构示意图如图1所示。激光发射系统主要为一台倍频调Q的Nd:YAG脉冲激光器，激光波长为532 nm，出射能量约为5 mJ，脉宽约为10 ns，重频为10 Hz，经一系列的偏振分光棱镜、转向棱镜和凹透镜等光学器件组成的激光发射光路后射入海水。接收系统包括光学接收和光电转换两部分，由望远镜、线偏振片、光阑、干涉滤光片、准直透镜、光电探测器等组成，望远镜采用口径为100 mm的折射式望远镜，视场约为200 mrad，用于接收大气及海水产生的后向散射光。信号采集和处理系统由高速采集卡和计算机组成，采集卡用于接收探测器输出的电信号，采样频率为500 MHz，对应的深度分辨率约为0.22 m，计算机负责对采样数据进行实时存储、处理和显示。

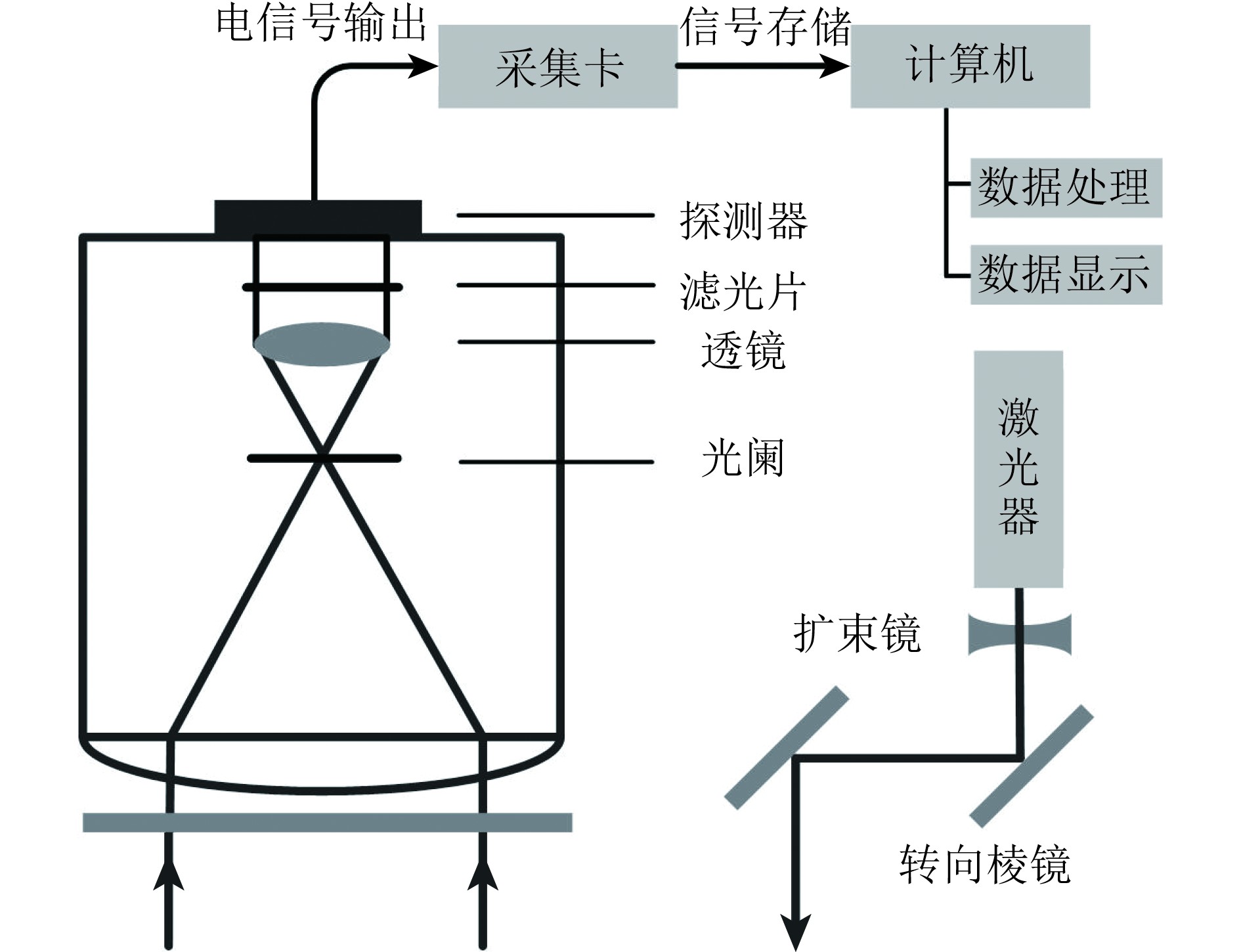
图 1 研制的海洋激光雷达系统结构示意图 Figure 1 Block diagram of the oceanic lidar configuration

通常假设海洋激光雷达的回波信号满足准单次散射近似模型(Xu 等，2018)，即回到接收器的激光经历了前进和返回过程中的多次前向传输和单次后向散射，其幅值可以写为(Zhou 等，2017)

式中， $A$ 为激光雷达常数， ${\textit{z}}$ 为激光雷达的出射距离， $n$ 为水体的折射率， $H$ 为距离水面的高度， $\;{\beta ^{\text{π}} }$ 和 $\alpha $ 分别为180度体散射系数和激光雷达衰减系数，下标w和下标p表示水分子和水体悬浮物。

式(1)表明，激光雷达方程同时依赖于水体的衰减和后向散射光学特性，从海洋激光雷达回波信号中反演出所需的光学参数存在一定困难。Fernald法通过假设水体悬浮物激光雷达比来反演激光雷达衰减系数(Fernald，1984)，即

式中， $D\left({\textit{z}} \right) = P\left({\textit{z}} \right){\left({nH + {\textit{z}}} \right)^2}$ 为距离校正后的回波信号， $\phi \left({\textit{z}} \right) = \exp \left( {2\left({{R_{\rm{s}}} - 1} \right)\int_{\textit{z}}^{{{\textit{z}}_{\rm{c}}}} {{\alpha _{\rm{w}}}\left({\textit{z}} \right){\rm{d}}{\textit{z}}} } \right)$ 。 ${R_{\rm{s}}}$ 为水体悬浮物激光雷达比 ${S_{\rm{p}}}$ 和纯水激光雷达比 ${S_{\rm{w}}}$ 的比值。水体的光学特性为已知量， ${S_{\rm{w}}}$ 近似为216， ${\alpha _{\rm{w}}}$ 近似采用纯海水的漫射衰减系数，即0.0519 m⁻¹。 ${{\textit{z}}_{\rm{c}}}$ 为边界深度，该深度处水体悬浮物的 ${\alpha _{\rm{p}}}$ 通过原位或者斜率法测量得到。

Fernald法反演米散射激光雷达数据的精度严重依赖于假设的水体悬浮物激光雷达比，发展HSRL有望减少其产生的误差。已有研究(Zhou 等，2017)证明HSRL可以通过分离水分子和水体悬浮物的回波信号，无需假设相关参数，即可单独估算水体的180度后向散射和衰减信息。然而，目前中国还未研制出稳定可靠的海洋HSRL。提出一种结合米散射激光雷达和原位数据的融合算法，用于模拟HSRL反演 $\alpha $ 的过程。180度后向散射系数 $\;{\beta ^{\text{π}} }\left({\textit{z}} \right)$ 由原位测量值代替，从而，激光雷达方程中只存在激光雷达衰减系数 $\alpha \left({\textit{z}} \right)$ 这一个未知数。对式(1)进行变形和整理，得到激光雷达衰减系数如下

2017年8月在黄海水域开展了自研的海洋激光雷达探测水体光学参数的实验。实验海域主要包括近岸的平山岛水域( ${\rm{11}}{{\rm{9}}^{\rm{o}}}{\rm{5}}{{\rm{4}}'}{\rm{E}}$ , ${\rm{3}}{{\rm{5}}^{\rm{o}}}{{\rm{8}}'}{\rm{N}}$ )和远岸的冷水团水域( ${\rm{12}}{{\rm{2}}^{\rm{o}}}{{\rm{0}}'}{\rm{ E}}$ , ${\rm{3}}{{\rm{5}}^{\rm{o}}}{\rm{3}}{{\rm{9}}'}{\rm{ N}}$ )，水深分别为27 m和46.4 m，现场采样测量得到的总悬浮物浓度分别约为2.00 mg/L和1.07 mg/L。已有的研究(Gordon，1982)表明，当激光雷达接收视场较大时，激光雷达衰减系数 $\alpha $ 趋向于漫射衰减系数 ${K_{\rm{d}}}$ ，因此可以用原位测量的 ${K_{\rm{d}}}$ 近似代替激光雷达方程中的 $\alpha $ 。采用WET Labs公司的 AC-9和HOBI Labs公司的HS-6两款原位仪器分别测量532 nm时海水中悬浮物的吸收系数和后向散射系数，数据的深度分辨率为1 m，进而计算得到180°后向散射系数 $\;{\beta ^{\text{π}} }$ 和漫射衰减系数 ${K_{\rm{d}}}$ (Churnside，2015)。将原位测量值 $\;{\beta ^{\text{π}} }$ 和 ${K_{\rm{d}}}$ 代入公式，采用最小二乘法计算系统常数 $A$ ，得到了匹配度很好的理想激光雷达廓线。随后，考虑激光雷达系统的影响，将理想信号与激光雷达系统响应卷积，得到建模的激光雷达廓线(Lee等，2013)。

海洋激光雷达系统安装于科考船前甲板处，距离水面约为11 m。每100组激光雷达回波信号平均为1组廓线，从而减少环境噪声的影响。选择原位作业时段的20条(200 s)激光雷达廓线与原位数据进行对比，以得到更加准确的实验对比效果。图2示出了近岸和远岸水域的测量结果，黑色虚线为实测的激光雷达廓线，红点为原位数据代入公式后得到的理想激光雷达廓线，红色实线为红点经过系统响应卷积后的建模激光雷达廓线。图2(a)为水体相对浑浊的近岸水域测量数据，激光雷达信号强度衰减快，在水深12 m处信噪比已经达不到有效测量的要求。在深度范围0—2 m处的激光雷达信号相对较低，可能是由近岸水域表层变动大且存在湍流等原因造成的。图2(b)的测量水域为水体相对清洁的远岸水域，激光雷达的有效探测深度明显增加到20 m水深处。

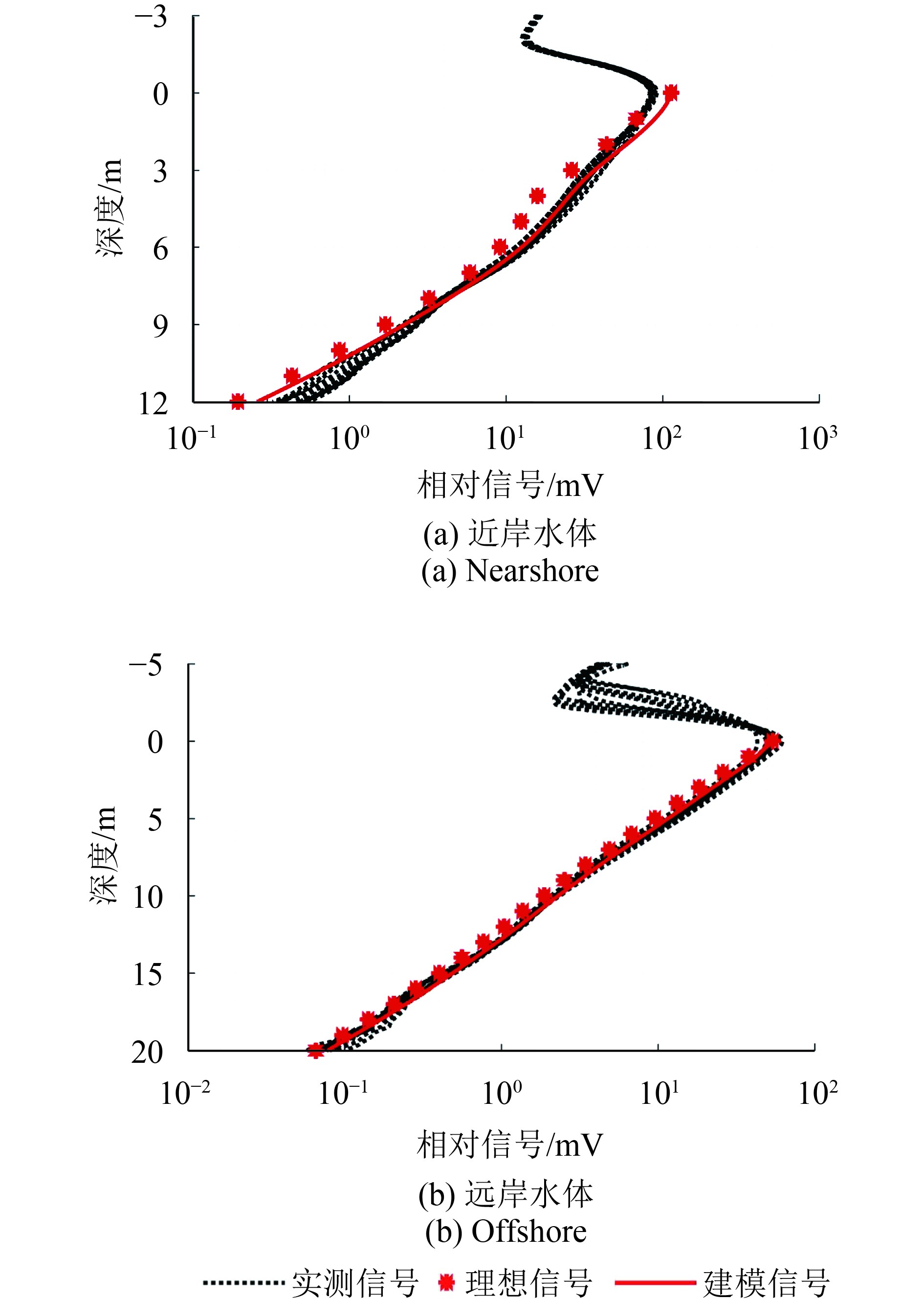
图 2 实测和建模的激光雷达廓线对比图 Figure 2 Examples of measured and modeled lidar profile versus depth

图3定量分析了在两块水域实测和建模的激光雷达廓线的吻合情况，用误差分析图来表示。图中的横坐标为深度，纵坐标为实测的20条激光雷达廓线和包含原位信息的建模激光雷达廓线幅值的平均比值，即 $10\log \left({{{{P_{\rm{lidar}}}} / {{P_{\rm{model}}}}}} \right)$ 。误差线表示实测值和建模值比值的标准差。图3(a)中实测与建模值在0—3 m匹配度区别于其他深度范围，原因可能为实验当天较大的海风导致了近水面悬浮物较大的变化。但0—3 m的匹配度仍然可以接受，实测和建模信号的比值在−1dB以内。图3(a)和(b)表明，在近岸和远岸水域内，建模和实测激光雷达廓线的比值在3—9 m和0—18 m的深度范围内分别小于 $ \pm 0.2{\rm{ dB}}$ 和 $ \pm 0.4{\rm{ dB}}$ ，实测信号的相对误差分别小于5%和10%。该实验结果优于文献(Lee 等，2013)所展示的机载激光雷达探测结果，原因可能是船载激光雷达与原位设备时空匹配度较高。误差线表明两块水域所选的激光雷达廓线比较平稳。总体来说，在近岸和远岸水域中，实测和建模的激光雷达廓线在深度范围分别为3—9 m和0—18 m时匹配度较高，可以进一步开展水体光学参数的反演和分析。

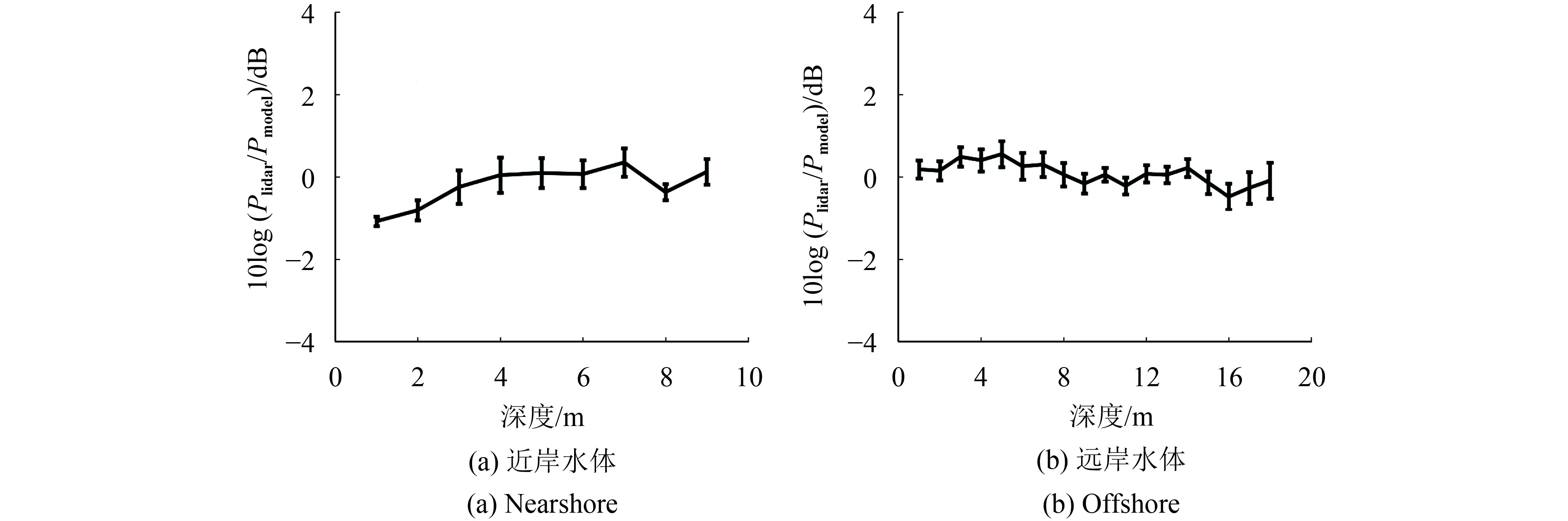
图 3 实测和建模的激光雷达廓线幅值的比值(dB) Figure 3 Average ratio (in decibels) of measured to modeled lidar returns as a function of depth

图4给出了所假设的不同水体悬浮物激光雷达比 ${S_{\rm{p}}}$ 下近岸和远岸水域的Fernald法反演激光雷达衰减系数 $\alpha $ 的情况，图中的红点表示原位测量的漫射衰减系数。反演程序中标定点的激光雷达衰减系数采用原位值 ${K_{\rm{d}}}$ 反演，因此参考点的 $\alpha $ 不随 ${S_{\rm{p}}}$ 变化。考虑到水面浪花等复杂多变的状况，目前激光雷达信号无法准确用于近水面处的数据反演，因而后续分析舍弃了0—3 m深度范围内的数据。图4表明，Fernald法的反演精度高度依赖所选取的 ${S_{\rm{p}}}$ 。随着后向不断迭代过程，较小的 ${S_{\rm{p}}}$ 偏差可能会造成反演的激光雷达衰减系数存在较大误差。如图4所示，采用最小二乘法计算得到，近岸水域和远岸水域的 ${S_{\rm{p}}}$ 分别在120 sr和210 sr附近值的反演效果最佳。

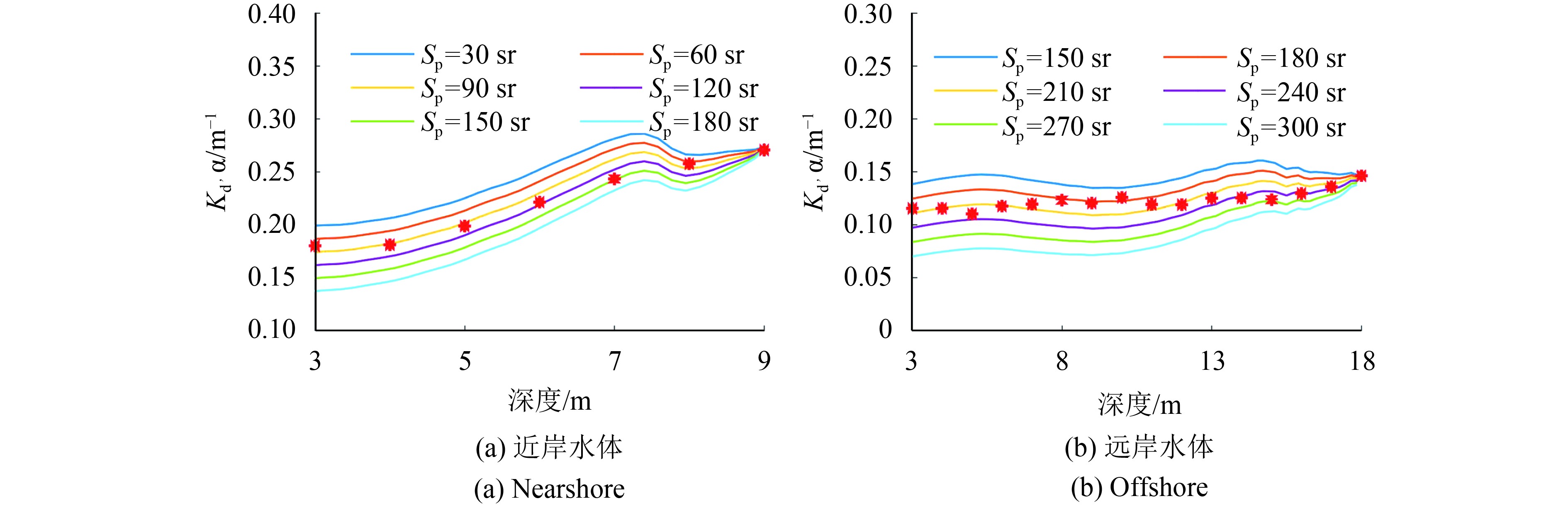
图 4 水体悬浮物激光雷达比对激光雷达衰减系数的影响 Figure 4 The impact of lidar ratio of particulate on the lidar attenuation coefficient

上述结果表明，米散射激光雷达需要辅助方法提供精确的水体悬浮物激光雷达比，否则无法保证激光雷达衰减系数 $\alpha $ 的反演精度。在实际应用中，可以利用原位测量数据和Fernald法反演米散射激光雷达数据进行局部区域的水体悬浮物激光雷达比定标，然后采用Fernald法反演走航时段一定水域范围内的光学参数。图5展示了近岸和远岸作业点附近各一个小时内走航数据的反演结果，主要观察走航水域光学性质变化以及可能的分层情况。如图5(a)所示，激光雷达在11:00—11:50观测到多次水体分层现象，分层深度在5—9 m。该深度范围内的 $\alpha $ 明显高于其他深度层次内的反演结果，可能原因是该深度范围内的水体悬浮物聚集并呈现不规则分布，导致反演的 $\alpha $ 在5—9 m都有较大值并呈现多次分层现象。图5(b)示出了远岸水域的时空分布情况，激光雷达在14:10—14:20观察到深度为6 m以下的水体轻微浑浊现象，推测为浮游植物在垂直方向上的分布不同。整个走航时段内深度范围为13米以下观测到明显分层现象，此深度范围内的 $\alpha $ 明显高于其周围深度。可能是由于该深度范围存在密集的浮游植物层以及水深处水体悬浮物的聚集现象。

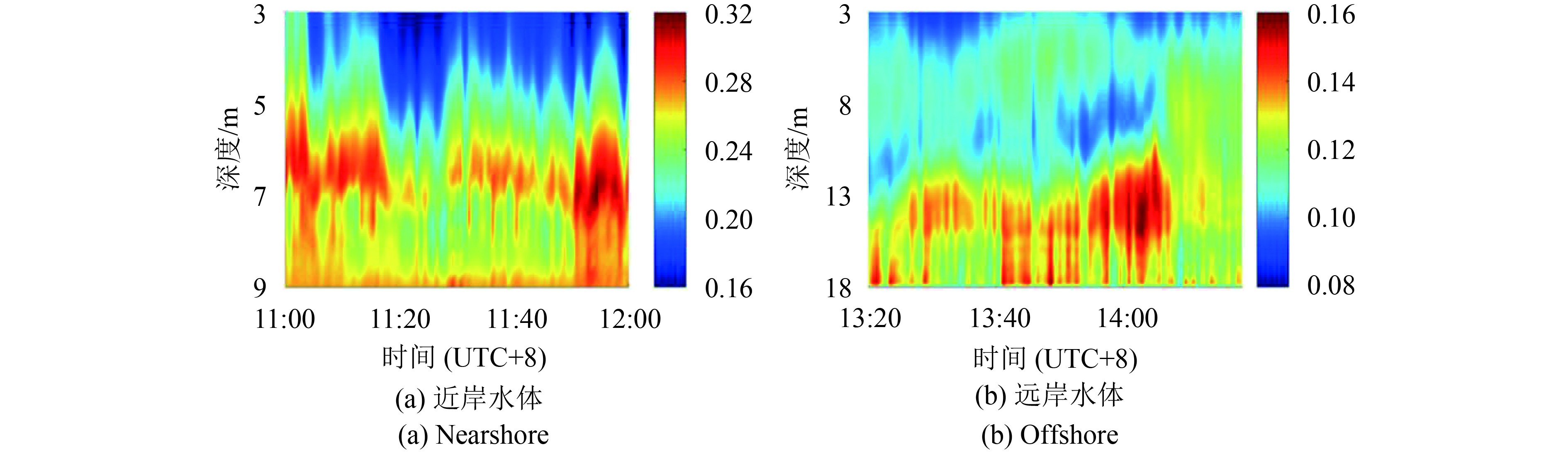
图 5 标定水体悬浮物激光雷达比下的Fernald法反演走航时激光雷达衰减系数 Figure 5 Lidar attenuation coefficient while navigating estimated by Fernald method with calibrated lidar ratio of particulate

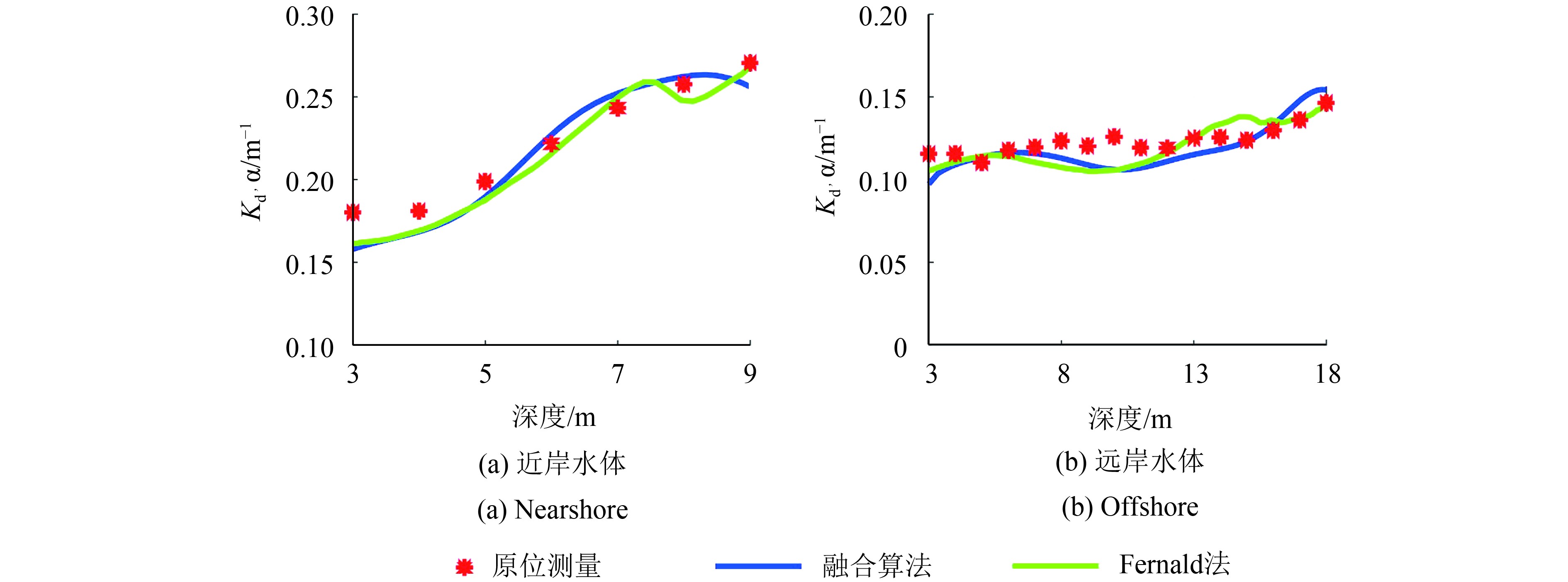
3.2节展示了Fernald法反演米散射激光雷达数据的结果，并采用标定的水体悬浮物激光雷达比反演了走航时段一定水域内的激光雷达数据。本节将引入融合算法反演激光雷达衰减系数，并将两种算法的精度进行一定的比较。图6示出了最佳水体悬浮物激光雷达比时的Fernald法和融合算法反演的激光雷达衰减系数 $\alpha $ 。蓝色实线为融合算法反演的 $\alpha $ 平均值，红点为原位测量的漫射衰减系数 ${K_{\rm{d}}}$ ，绿色实线为Fernald法反演的 $\alpha $ 平均值。从图6(a)和(b)可以看出，近岸水域的漫射衰减系数随水深而逐渐增加，Fernald法反演的激光雷达衰减系数在深度为8 m处有一个拐点，可能是由于近岸水域水浅，泥沙等悬浮颗粒物的再悬浮现象明显，导致该深度附近水体悬浮物激光雷达比变化明显。而远岸水域的漫射衰减系数值随水深变化不明显，稳定在 $0.12{\rm{ }}{{\rm{m}}^{ - 1}}$ 附近。Fernald法反演的 $\alpha $ 在深度范围14—18 m内有些许抖动现象，可能为该深度范围内的激光雷达廓线信噪比稍差或者该深度范围水中悬浮物质轻微分层。总体而言，在近岸和远岸水域，采用融合算法和最佳水体悬浮物激光雷达比下的Fernald法反演的 $\alpha $ 在深度范围分别为3—9 m和3—18 m差别较小，且都与原位测量值匹配较好。

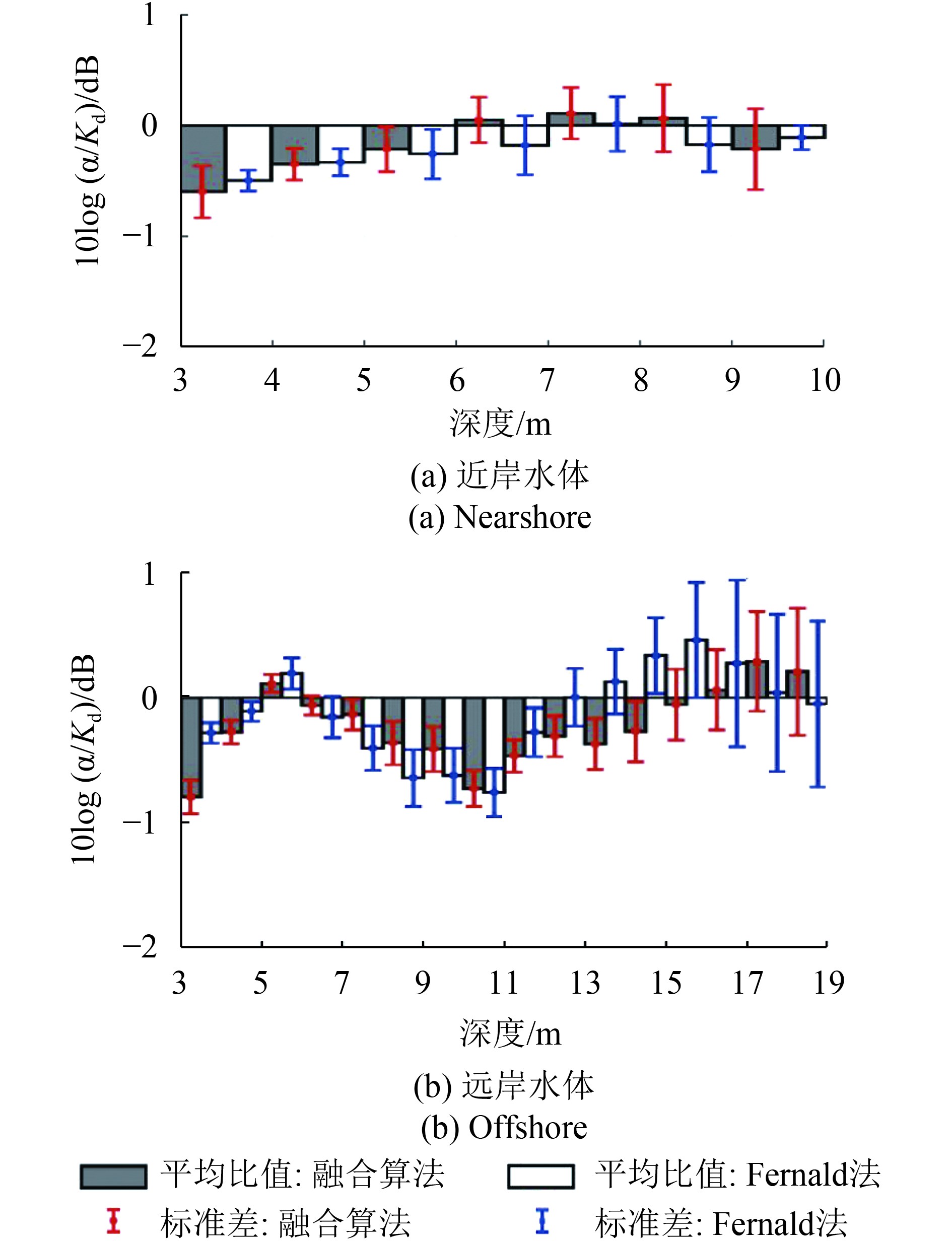
图7进行了整数深度值下的定量误差分析，得到以对数形式 $10\log \left({{\alpha / {{K_{\rm{d}}}}}} \right)$ 表达的反演精度。柱状图表示反演的激光雷达衰减系数和原位测量值之间的平均比值，灰色和白色分别表示融合算法和Fernald法在整数深度下反演的匹配情况。误差线表示反演值和原位数据比值的标准差。图7(a)定量分析了在近岸水域采用融合算法和Fernald法反演的 $\alpha $ 与原位数据的匹配误差，在3—9 m的深度范围内，采用融合算法和Fernald法，二者的平均比值均在 $ \pm 0.5\;{\rm{ dB}}$ 范围内，反演误差均不超过11%。误差线表明在整个深度范围内两种方法反演值相对平稳，没有出现异常大的波动。图7(b)展示了在远岸水域Fernald法和融合算法的反演值与原位测量值的匹配情况，在3—18 m的深度范围内，采用融合算法和Fernald法，二者的比值小于 $ \pm 0.7\;{\rm{ dB}}$ ，反演误差均在17%以内。误差分析结果表明在深度范围14—18 m内误差线有点偏大，这可能是由于此处激光雷达信号信噪比偏小且噪声抖动稍大，也可能是该深度范围内水中物质的快速变化。总体来说，两块水域的反演结果表明融合算法反演精度与标定水体悬浮物激光雷达比下的Fernald法相当。

图 6 融合算法及Fernald法反演的激光雷达衰减系数平均值与原位测量值随深度变化的趋势 Figure 6 Depth profiles of average lidar attenuation coefficient estimated by fusion algorithm and Fernald method, as well as in situ measurement

图 7 整数深度值下的融合算法和Fernald法反演激光雷达衰减系数与原位测量值之间的平均比值(dB表示) Figure 7 Average ratio (in decibels) of modeled to measured lidar attenuation coefficients as a function of integer depth，with fusion algorithm and Fernald method

目前，Fernald法是一种米散射激光雷达数据反演的成熟算法，反演结果依赖于激光雷达比，标定激光雷达比的情况下Fernald法反演精度能有保证。同时，Fernald法为一个迭代的求解过程，需要选择迭代的初始值，即边界深度处的水体光学参数。所以，Fernald法需要获取激光雷达比和光学特性初始值，且其反演结果同这两个参数的准确程度息息相关。然而，激光雷达比和光学特性初始值的准确获取需要通过辅助仪器或方法实现。Fernald 法的不足限制了米散射激光雷达的应用，发展HSRL将有助于消除激光雷达比等参数的干扰。融合算法借助米散射激光雷达回波信号和原位仪器测量的180度后向散射系数，模拟了HSRL反演水体光学参数的过程，表明HSRL具有在数据反演时相对于米散射激光雷达无需相关假设等优势。目前，HSRL正在被国内多家单位研制中。在未来，其将采用具有高光谱分辨能力的光谱鉴频器，用于分离回波信号中的水分子瑞利散射成分和与水体悬浮物米散射成分，不需要假设激光雷达比等参数即可反演出衰减和后向散射等光学参数。

高垂直分辨率激光雷达系统对于探测上层水体的固有光学参数廓线具有重要意义。本文验证了自主研制的米散射激光雷达系统的探测精度，在近海和远海的有效深度范围内探测误差分别在5%和10%左右。进一步，开发了适用于米散射激光雷达的Fernald法，并采用融合算法对无需假设激光雷达比的高光谱分辨率激光雷达(HSRL)进行了评估。开发的Fernald算法通过米散射激光雷达数据，实现了上层水体衰减和后向散射光学产品的反演。提出的融合算法模拟了HSRL反演水体光学参数的过程，展示了HSRL在水体光学参数反演等方面的优势。

Fernald法是一种米散射激光雷达数据反演的成熟算法，但其仍然具有一定的假设，基于合适的水体悬浮物激光雷达比的Fernald法可以有效应用于米散射激光雷达的反演。在未来，无需假设的HSRL在海水光学参数探测领域具有更大的优势，是海洋激光雷达的发展方向，具有巨大的应用前景。

志 谢 此次野外实验得到了国家卫星海洋应用中心的资助，现场实测水体生物光学数据由国家海洋技术中心测量和处理分析，实验船舶得到了青岛海力海洋调查科技服务有限公司等单位的协助与支持，在此表示衷心的感谢！