土壤湿度是水文、气象和农业环境研究中重要的参数，也是某一个位置或区域内水资源循环的重要指标，开展土壤湿度估算对于气候气象预报、洪水灾害以及水资源循环等相关研究具有重要意义(Sabater 等，2008；彭学峰 等，2017；金双根 等，2017)。传统的土壤湿度监测方法主要包括烘干称重法、中子仪法、时域反射仪法、频域反射仪法等，这些方法需要进行实地操作，处理过程往往较为烦杂，仅适用于小范围内的土壤湿度测量，存在时空分辨率低、成本过高、工作效率低等缺点(Le 等，2002；严颂华 等，2011)。近年来，利用GPS反射信号获取土壤表面湿度成为了一种新型的遥感监测手段，具有成本低、高效率、高分辨率等优点。Martin-Neira于1993年首次利用GPS反射信号实现了海洋高度的测量(Martin-Neira，1993)，在此基础上，两种新的GPS遥感技术被提出：一种是GPS-R反射遥感技术；另一种是GPS-IR多径干涉遥感技术。其中，GPS-IR主要是利用直射和反射信号在接收机单天线处叠加所产生的干涉实现地表环境参数的估算，已经在土壤湿度监测中得到了认可(Rodriguez-Alvarez 等，2009)。而且，GPS天线和接收器都比较适用于地面遥感，因为卫星信号主要采用L波段(L1和L2载波)进行传输，该波段的电磁波在大气中衰减少，并能有效穿透植被(Rodriguez-Alvarez 等，2009)。Tsang等(1985)对于地表特性的微波遥感技术研究已超过了30年，证实了该技术获取地表环境参数的有效性。对于微波频率，Hallikainen等(1985)表明地面的介电常数很大程度上取决于其含水量。目前，GPS反射信号已被应用于估算雪深、海平面高度、土壤水分含量和植被指数等测站环境参数及其变化(严颂华 等，2011；Ferrazzoli 等，2011；Cardellach 等，2012；金双根 等，2017)。针对土壤介电常数与土壤湿度之间的关系研究，Dobson等(1985)构建了基于简化的经验或半经验土壤湿度反演模型，并给出了不同环境条件下的土壤湿度估算效果。然而，这些模型涉及到众多的参数，且建模过程较为复杂，存在受人为经验影响、泛化能力不强、适用范围受限等缺陷。敖敏思等(2015)研究表明在一定卫星高度截止角内，采用SNR观测值可实现土壤湿度变化趋势的反演，利用指数函数能够有效描述相对延迟相位与土壤湿度之间的关系。Bilich和Larson(2007)研究开发了利用SNR数据来映射多路径环境的方法，通过利用小波变换实现了反射信号相关信息的分离，并证实了反射信号的幅度和频率与多路径环境有着密切的关系，并以此修正相位观测值，取得较好结果。Zavorotny等(2010)证明了利用相对延迟相位反演土壤湿度比振幅更有优势。基于其他遥感手段对植被散射问题的相关研究成果，众多学者也展开了对采用GPS反射信号进行土壤湿度估算中的植被效应修正、植被含水量估计、植被参数估计等研究工作(Wu 等，2012)。Chew等(2015)针对近地表土壤含水量对GPS多路径的影响，开发了土壤水分检索算法，并研究了近地表植被变化对信噪比SNR(Signal Noise Ratio)的影响。由于测站周边的土壤表面粗糙度、植被覆盖信息、土壤水分含量等多路径因素对GPS信号的影响均不一样，直接建立准确的土壤湿度估算模型较为困难。而且，不同时刻的GPS卫星信号受多路径效应的影响程度也不一样。已有的研究较少考虑到多卫星融合估算土壤湿度的优势，估算过程也难免人为干预影响，不利于估算精度的提高。如果土壤湿度是随着时间和空间尺度变化的事件，那么采用GPS-IR技术进行土壤湿度估算可看成是一个非线性回归问题。

基于上述研究，本文提出了一种基于多卫星融合的土壤湿度最小二乘支持向量机滚动式估算模型。最小二乘支持向量机LS-SVM (Least Squares Support Vector Machine)是Suykens和Vandewalb于1999年提出的机器学习方法，能够较好地解决小样本、非线性和高维模式识别等实际问题(Suykens和Vandewalle，1999)，已在建筑物变形预警、滑坡预测等非线性事件处理中得到广泛应用(Xie 等，2017)。与人工神经网络、最小二乘拟合算法等传统非线性方法相比，LS-SVM模型需要更少的建模数据即可实现样本的测试，具有更强的泛化能力。因此，本文将最小二乘支持向量机引入到土壤湿度估算中，建立基于多卫星融合的土壤湿度最小二乘支持向量机估算模型。同时，考虑到LS-SVM模型的参数优化问题，采用网格搜索法选取LS-SVM的最优参数(Yang 等，2015；Xie 等，2017)。经美国板块边界观测计划PBO提供的监测数据，对比分析利用单颗、多颗GPS卫星进行土壤湿度估算的可行性，研究和验证滚动式估算的有效性。

GPS信噪比是反映接收机天线信号质量的指标，主要受接收机天线增益参数、接收机中相关器的状态和多路径效应等因素的共同影响(敖敏思 等，2015)。多路径效应是指GPS接收机同时接受到来自测站附近不同反射体反射的卫星信号和卫星直射信号，这两种信号经过相互叠加产生干涉，造成接收机观测值与真值之间存在一定的偏差，随之产生多路径误差。GPS卫星高度角与接收机天线增益之间存在正比关系，较高的卫星高度角有利于天线增益的增大，进而提高信噪比SNR；反之，天线增益减小，信噪比SNR受多路径环境影响更为明显(张双成 等，2016)。因此，信噪比SNR与多路径环境存在直接的关系，通过利用信噪比SNR值建立多路径效应评估模型，有利于估算地表环境参数。SNR可描述为(敖敏思 等，2015；Chew 等，2015)

式中， $\mathop {SNR}\limits^ \cdot $ 表示信噪比观测值SNR， ${\dot S_d}(0)$ 表示直射信号，‘0’代表初始相位， ${\dot S_m}(\phi)$ 表示反射信号，‘ $\phi $ ’代表反射信号的相位值。

反射信号的幅度值可采用直角形式表示(敖敏思 等，2015；Chew 等，2015)

式中， $\psi $ 表示与卫星接收机几何位置相关的函数变量，代表直射与反射信号之间的相对相位差(单位：rad)。

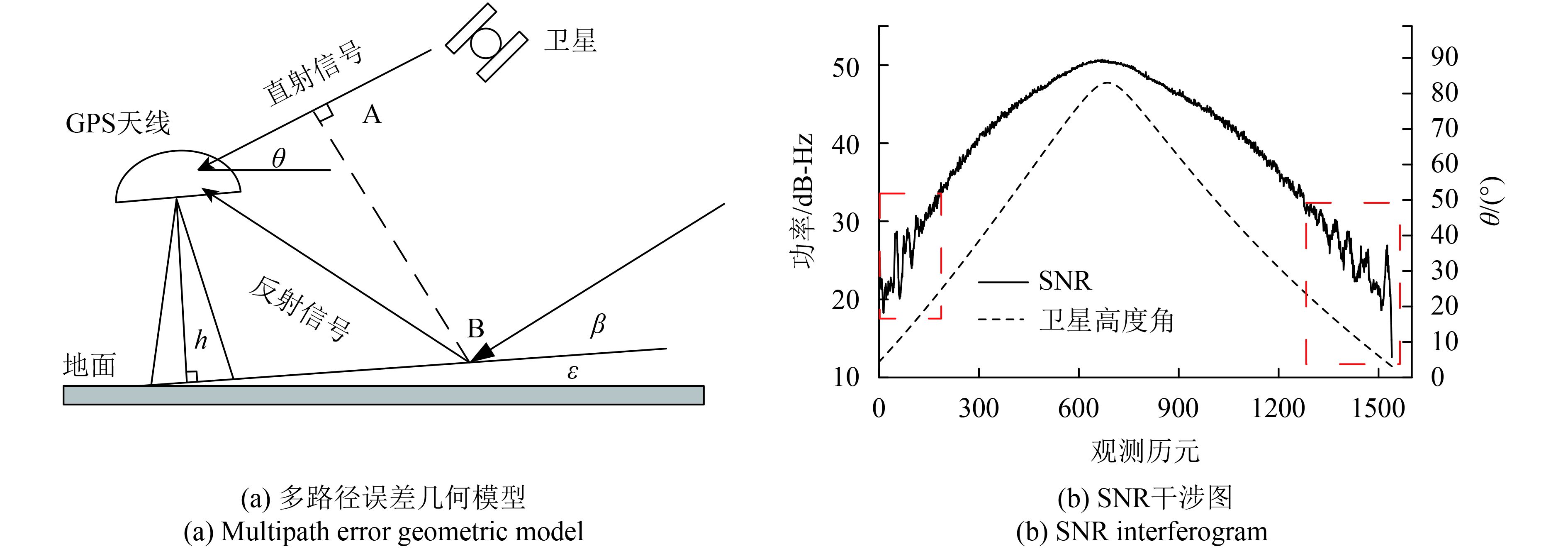
因此，GPS天线接收的信号往往是直接、反射信号叠加混合的信号(图1)。图1(b)代表P041测站2011年第318天，PRN31卫星的SNR干涉图。可见，在低卫星高度角下，GPS信噪比受多路径影响较为突出(图1(b)中的红色框区域)。不同的卫星信号受多路径影响的程度均不一样，土壤湿度信息主要包含在多路径环境影响的成分中(Chew 等，2016)。如何在多路径环境影响的成分中获取与土壤湿度相关的信息是需要探讨的问题。

图 1 地面多路径误差几何模型及SNR Figure 1 Geometric model of ground multi-path error and SNR

图1(a)中， $\theta $ 代表卫星信号入射高度角， $h$ 代表天线距离底面的垂直高度， $\varepsilon $ 代表坡面的倾斜角度， $\beta $ 代表卫星信号与坡面间的夹角。当 $\varepsilon $ 较小时，可表示为

结合图1，可推导出卫星直射信号与反射信号之间的相位差为(叶险峰，2016)

由式(4)可见，相位差 $\psi $ 与入射角 $\theta $ 相关，那么和入射角 $\theta $ 一样，随着时间 $t$ 的变化， $\psi $ 也会随之变化，其变化角频率 ${\omega _t}$ 为(叶险峰，2016)

从式(5)可见， $\psi $ 与 $\sin \theta $ 之间存在线性关系。

Chew等(2015)研究表明：SNR观测值与 $\psi $ 之间存在一种正弦或余弦关系，而且GPS土壤湿度仅与多路径反射信号相关，那么去除GPS卫星直射信号后的多路径反射信号与 $\sin \theta $ 之间仍存在某一固定频率的正弦(或余弦)函数关系，表示为

式中， $\theta $ 表示卫星入射高度角， ${\textit{λ}} $ 表示载波波长、 $H$ 表示GPS天线高； ${A_{MP2}}$ 代表多路径反射信号的相对幅度， ${\phi _{MP2}}$ 代表相对延迟相位。

如果令 ${u_0}{\rm{ = }}\sin \theta $ ， $f{\rm{ = }}\dfrac{{2{\text{π}}H}}{{\textit{λ}} }$ ，式(6)简化为

可见， ${A_{MP2}}$ 和 ${\phi _{MP2}}$ 即为待求的特征参数。Chew等(2016)研究表明：相对延迟相位是估算土壤湿度变化的最佳度量指标，其与地表土壤湿度之间存在较强的相关性。因此，本文主要是基于多卫星的相对延迟相位建立土壤湿度估算模型。

设GPS卫星相对延迟相位集 ${x}$ 为

式中， $N$ 代表年积日， $M$ 代表卫星的个数。

设给定的训练集样本为 $\left\{ {\left. {\left({{{x}_i}, {{y}_i}} \right)\left| {i{\rm{ = }}1, 2, \cdots, l} \right.} \right\}} \right.$ ，对应于相对延迟相位集 ${{x}_i}$ 的土壤湿度集为 ${{y}_i}$ 。那么，在利用相对延迟相位估算土壤湿度的应用中， ${{x}_i} \in {R^q}$ 代表 $q$ 维相对延迟相位输入样本， ${{y}_i} \in R$ 代表土壤湿度输出样本。LS-SVM估计的回归问题可等价为最小化下列泛函(Suykens和Vandewalle, 1999；Huang 等，2014)

式中， $\gamma $ 表示正则化参数， ${{e}_i}$ 表示拟合误差， $\varphi \left(\cdot \right)$ 表示核函数， ${w}$ 表示权系数向量， $b$ 表示阈值。

定义式(9)的拉格朗日函数为

式中， ${{a}_i}$ $(i = 1, 2, \cdots, l)$ 代表拉格朗日乘子。根据KKT(Karush-Kuhn-Tucker)条件，对拉格朗日函数求偏导得到最优解

消去式(11)的变量 ${w}$ 和 ${{e}_i}$ ，设 ${{x}_i}$ 和 ${{x}_j}$ 分别代表训练集第 $i$ 个和第 $j$ 个样本输入值，引入满足Mercer条件的核函数 $K\left({{{x}_i}, {{x}_j}} \right){\rm{ = }}{{{\varphi}} ^{\rm{T}}}\left({{{x}_i}} \right) \times {{\varphi}} \left({{{x}_j}} \right)$ $\left({i, j{\rm{ = }}1, 2, \cdots, l} \right)$ 得到线性方程组

式中， ${A}$ 表示 $1 \times {I}$ 单位列向量， ${{F}_0}$ 表示 ${I} \times {I}$ 单位矩阵， ${y}{\rm{ = }}{\left[ {{y_1}, {y_2}, \cdots, {y_l}} \right]^{\rm{T}}}$ ， ${a}{\rm{ = }}{\left[ {{a_1}, {a_2}, \cdots, {a_l}} \right]^{\rm{T}}}$ 。

由于 ${B}{\rm{ = }}K\left({{{x}_i}, {{x}_j}} \right) + {\gamma ^{ - 1}}{{F}_0}$ 为对称的正定矩阵，采用最小二乘算法求解式(12)可得

那么，在点 ${{x}^*}$ 处的土壤湿度估算表达式为

由于LS-SVM性能的优劣很大程度上取决于核函数 $K$ 、核参数 $\sigma $ 和正则化参数 $\gamma $ 的最优选取。Bishop(2006)对参数和函数的作用、选择和构造进行了详细讨论。考虑到径向基函数RBF(Radial Basis Function)能很好地反应模型的复杂程度，普适性较好。因此，本文选定其为LS-SVM的核函数。同时，采用网格搜索法(Yang 等，2015)进行 $\sigma $ 和 $\gamma $ 参数优选。

本文建模具体过程如下：

(1) 反射信号有效分离。采用TEQC软件解算GPS监测数据得到SNR2值(L2载波)，通过二次多项式拟合分离GPS直射和反射信号；

(2) 反射信号重采样。对随历元变化的反射信号进行重采样，转化为与卫星入射高度角正弦值 ${\rm{sin}}\theta $ 之间的关系；

(3) 参数估计。采用非线性最小二乘算法(Johnson 等，1981)对重采样后的反射信号进行正弦拟合，得到相对延迟相位。同时，考虑到最小二乘算法迭代的步长及其他参数问题，本文利用置信区间算法(Powell和Yuan，1990)进行确定；

(4) 土壤湿度估算模型。通过线性回归方程对相对延迟相位和土壤湿度进行相关性分析，并合理设置相关系数的阈值范围选取有效卫星，进而建立LS-SVM非线性拟合模型；

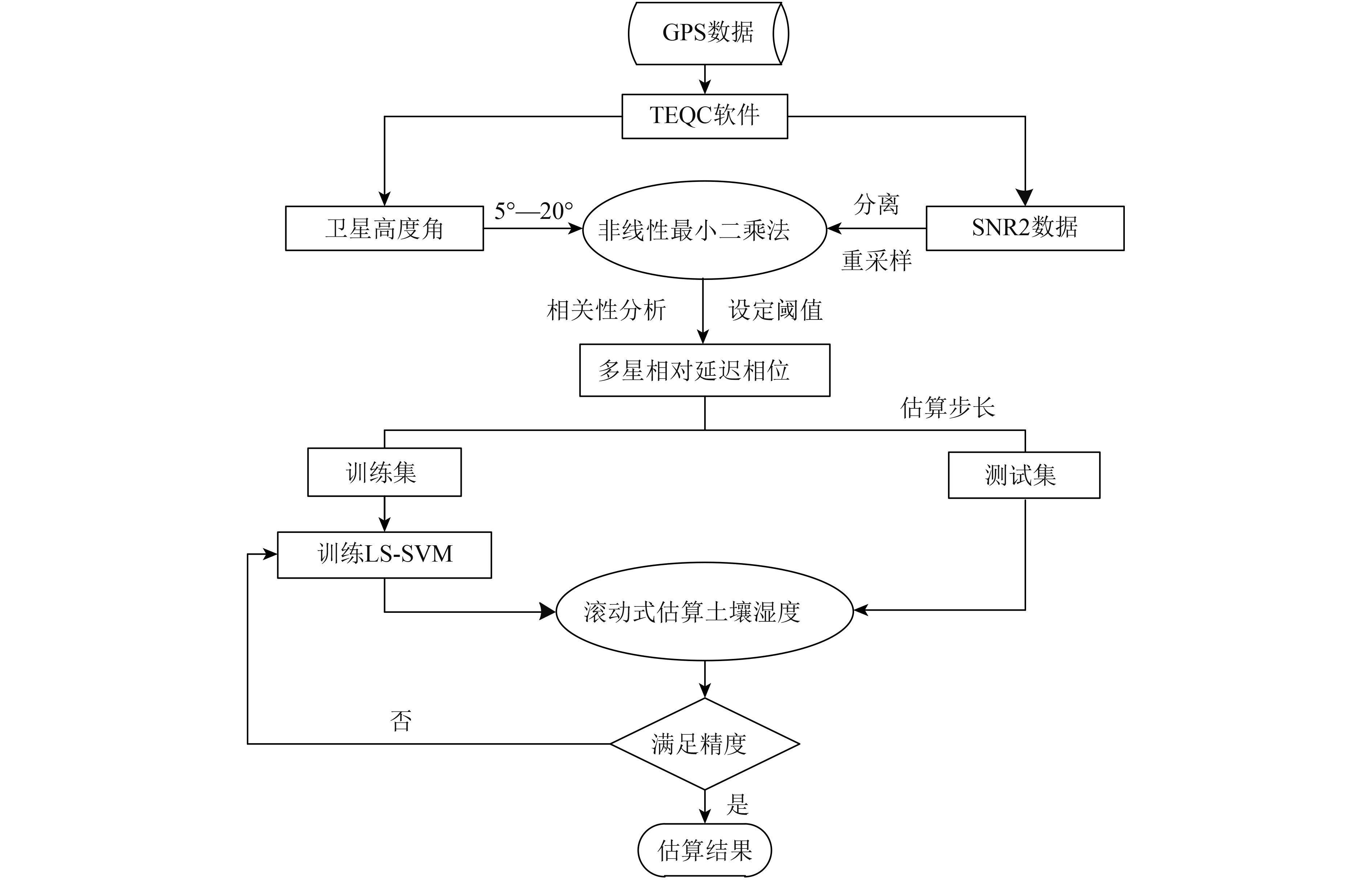
(5) 滚动式估算。设选定 ${x}$ 的前 $n$ 时段作为模型的训练样本，估算步长为 ${b_1}$ ，滚动式估算模式为：设输入训练样本1为 ${E} = \left\{ {{{x}_1}, {{x}_2}, \cdots, {{x}_n}} \right\}$ ，则输入测试样本1为 ${F} = \left\{ {{{x}_{n + 1}}, {{x}_{n + 2}}, \cdots, {{x}_{n + {b_1}}}} \right\}$ ；进而设输入训练样本2为 ${E} = \left\{ {{{x}_{1 + {b_1}}}, {{x}_{2 + {b_1}}}, \cdots, {{x}_{n{\rm{ + }}{b_1}}}} \right\}$ ，则输入测试样本2为 ${F} = \left\{ {{{x}_{n + {b_1} + 1}}, {{x}_{n + {b_1} + 2}}, \cdots, {{x}_{n + 2{b_1}}}} \right\}$ ，依此类推估算。模型流程如图2所示。

图 2 土壤湿度滚动式估算流程 Figure 2 The rolling estimation process of soil moisture

选取美国板块边界观测计划PBO (http://xenon.colorado.edu/portal[2017-10-10])提供的监测数据(P041和P043测站)进行实验。两个测站分别处于西经105.194267°、北纬39.949493°和西经104.185702°、北纬43.881146°，均能够记录L2C观测值，很早就开展土壤湿度分析，具有一定的代表性。已有研究表明，L2C信号的频率对土壤的最大穿透深度为5 cm(Njoku和Entekhabi，1996)，由于GPS-IR仅分析来自于低卫星高度角的反射信息，其实际感测深度可能为2.5 cm或更小(Chew 等，2016)。从图3的美国Landsat TM多光谱影像(空间分辨率30 m)和P041测站图可看出，该测站周边地形较为平坦、开阔且植被稀少，主要以草为覆盖植被，有利于土壤湿度监测。站点均采用钢制三角支架安置，接收机型号为TRIMBLE NERT9，采用SCIT的天线罩，天线型号为TRM59800.80。P041测站2011年第67—290 d(共224 d)和P043测站2015年第73—294 d(共222 d)的土壤湿度SMC(Soil Moisture Content)及降雨量如图4所示。图4中，降雨量主要来自于北美土地资料同化系统(NLDAS)产品；每天的土壤水分产品都是通过L2C观测值反演，基于8个或更多卫星轨道的平均值来实现的；土壤湿度值基于GPS卫星相位(phi)的波动来计算，其中SMC = SMC_min + 0.0148 phi，主要是根据STATSGO监测数据集中的剩余水分含量来确定每个点的最小土壤水分值(SMC_min)(Chew 等，2015, 2016)。Larson等(2010)研究表明：采用菲涅耳原理可确定土壤湿度的有效测量区域，GPS信号的菲涅耳区域是一组与卫星高度角、方位角和接收机天线高相关的椭圆；当卫星高度截止角为5°时，有效距离理论最大值距天线中心约45 m。由于PBO天线高度倾向于1.5—2.1 m，每个卫星轨道的感测区域约为120 m²(Larson和Nievinski，2013)。那么，将多个轨道结合起来总感应面积约为1000 m²。

图 3 测站周边环境 Figure 3 Surround environment of station

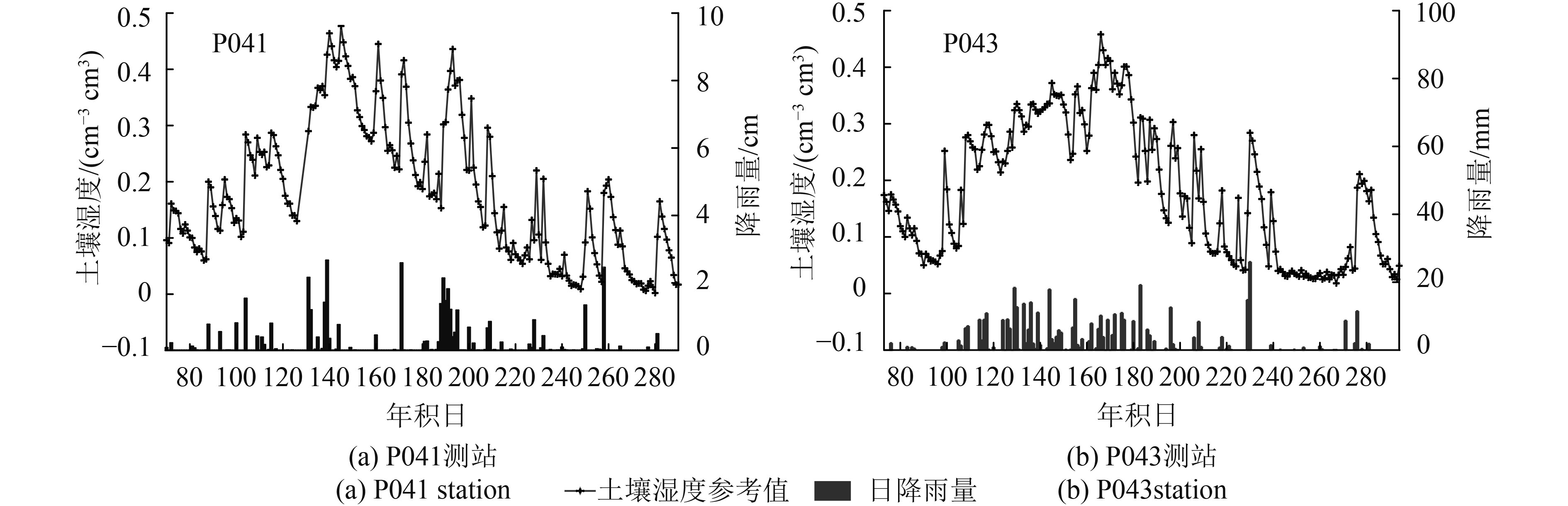
图 4 不同测站的土壤湿度及降雨量 Figure 4 Soil moisture and rainfall of different stations

从图4(a)可看出，该时段内显著降水13次，分别为第88、100、104、115、131—132、137—140、143—144、171、186—195、207—211、231—232、250、255—258 d，其中，最大降雨量达到2.67 cm。对应于降水，土壤湿度均明显上升，特别是131—132、137—140和186—195 d。同样，由于连续性降雨，P043测站周边的土壤湿度变化较为剧烈，呈现出非线性和随机性。当降水停止，土壤湿度逐渐减少和回落。可见，降水是土壤湿度变化的主要原因，P041和P043测站的降雨量较为丰富，适合开展土壤湿度研究。

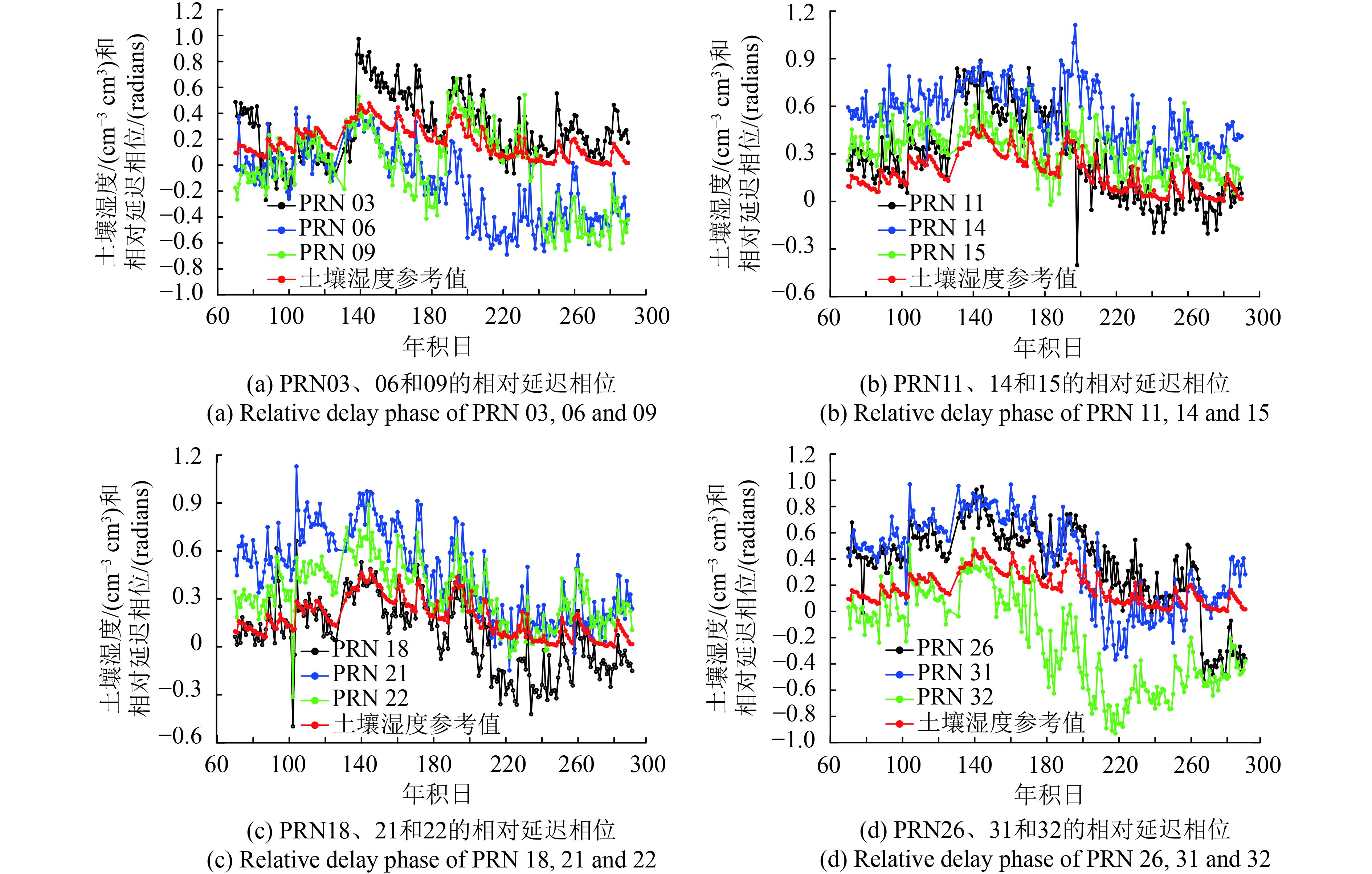
因此，本文分别选取P041测站2011年第67—290 d和P043测站2015年第73—294 d的监测数据，采样率为30 Hz，设置截止卫星高度角为5°—20°。利用TEQC解算GPS接收机监测数据得到SNR2值，经二次多项式拟合分离各卫星的直、反射信号，并采用非线性最小二乘法估算各卫星的相对延迟相位。限于篇幅，试验中仅给出P041测站有效波段的PRN03、06、09、11、14、15、18、21、22、26、31和32号卫星进行分析，各卫星的相对延迟相位与土壤湿度的关系见图5。

图 5 P041测站的相对延迟相位与土壤湿度关系图 Figure 5 Relationship between relative delayed phase and soil moisture of P041 station

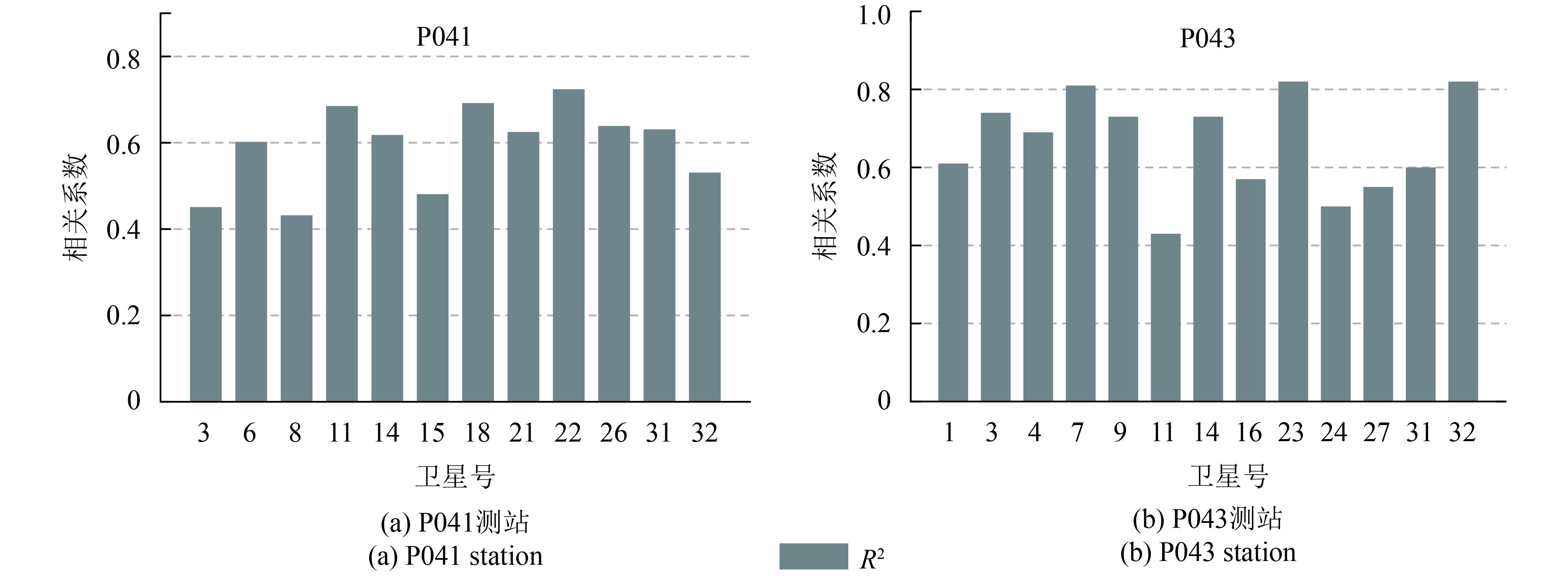
由图5可知，当土壤湿度上升或下降波动时，各卫星的相对延迟相位均能做出响应。对于131—132、137—140和186—195 d，各卫星的相位延迟呈现了较大的浮动，这与持续性降雨造成的土壤湿度急剧上升相关。整个时段内，两个测站部分卫星的相对相位延迟与土壤湿度之间的线性回归方程系数R²(图6)。可见，不同卫星的相对相位延迟与土壤湿度之间的相关性均不一样。进一步对比各卫星发现，不同卫星对于土壤湿度变化的响应模式并不一致，同一卫星的相对延迟相位在不同时段均出现异常跳变现象，这主要是由于在观测过程中卫星相对于GPS天线的几何运动轨迹以及卫星本身的性能不同、地表多路径环境影响所造成的。因此，直接通过某种方法或者手段剔除单颗卫星异常跳变值较为困难，也不利于土壤湿度连续性估算模型的建立。通过多颗卫星融合形成互补，经非线性拟合定权实现土壤湿度估算成为可能。

图 6 相对延迟相位与土壤湿度之间的相关系数分析 Figure 6 The correlation coefficient between delayed phase and soil moisture

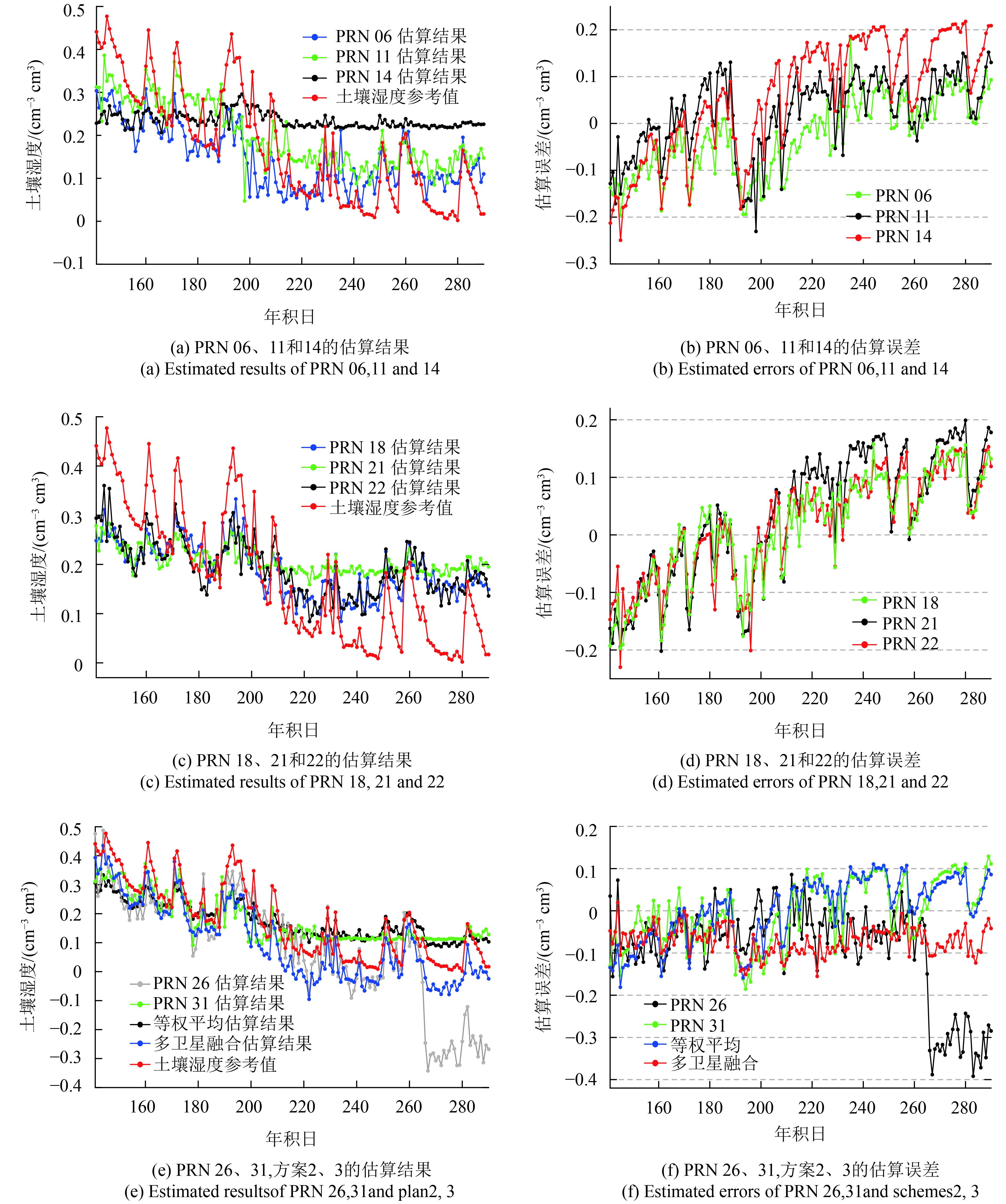
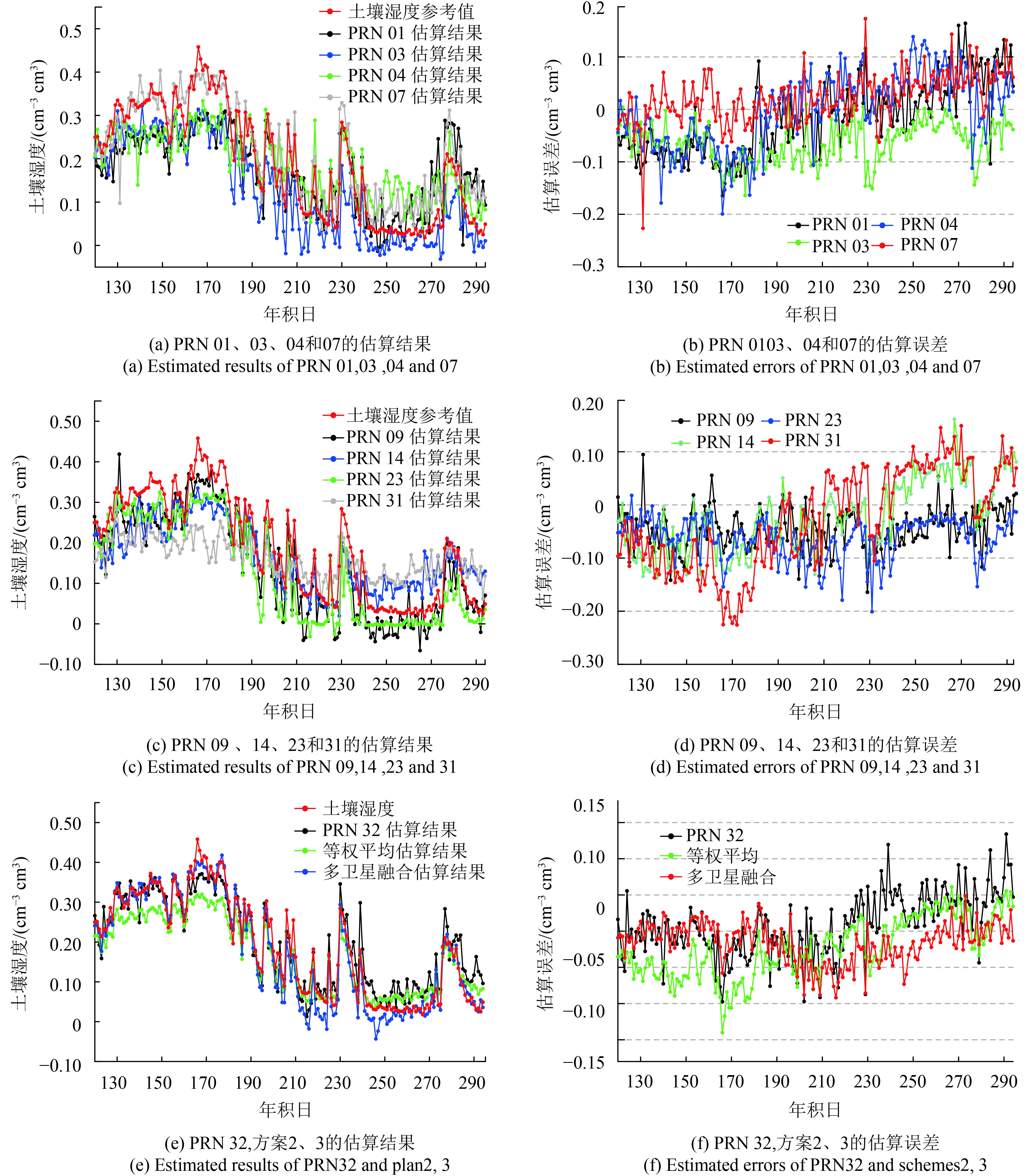
为了验证多卫星融合估算的可行性和有效性，本文设置线性回归方程系数R²大于0.6的阈值范围，分别选取P041测站8颗卫星和P043测站9颗卫星的相对延迟相位建立LS-SVM土壤湿度估算模型，设立3种方案进行对比分析：方案1建立基于单颗卫星的滚动式估算、方案2对方案1各单颗卫星的反演结果取均值(等权平均)、方案3基于多卫星融合的滚动式估算。为了减少建模误差，需要对相对延迟相位进行预处理，将数据统一归化到[−1，1]，经模型估算后再还原到原始区间。对于P041测站，以第67—140 d为训练样本，后第141—290 d为测试样本，选取估算步长为1。比如，当估算步长取1，则通过第67—140 d建模来估算第141 d，然后采用第68—141 d建模估算第142 d，以此类推迭代计算，直到估算到第290 d。同理，P043测站采用73—119 d为训练样本，后第120—294 d为测试样本，估算步长为1。以美国板块边界观测计划PBO提供的土壤水分产品作为参考值，各方案的估算结果如图7和图8所示。限于篇幅，仅给出了P041测站的估算结果与土壤湿度之间的线性回归分析(图9)。

从图7和图8可见，采用单颗卫星进行土壤湿度估算，难以准确掌握土壤湿度的变化规律，估算误差基本呈递增趋势；对于土壤湿度波动较大的时段，估算过程极易出现异常跳变现象。特别是土壤湿度值较小的时段，部分卫星的估算结果出现明显的失真现象，如P041测站的14、26和31号卫星。这些主要是由于单颗卫星信号在某时刻某方向受地表多路径环境影响较大，使得有用的土壤湿度反射信息受到干扰，估算过程极易出现异常跳变现象。通过对各卫星的估算结果进行等权平均，估算误差的波动程度仍较为剧烈，如图7的第180—290 d。进一步对比各单颗卫星和方案2的估算误差发现，采用方案2估算的误差变化趋势易受单颗卫星估算误差的影响，而且没有能够有效地抑制估算过程异常跳变值的出现。方案3能够更好的反应土壤湿度的变化趋势，估算误差更为平稳，有效改善了采用单颗卫星进行土壤湿度估算时，估算结果极易出现异常跳变的现象。可见，不同的卫星反映着不同方向的地表环境信息，采用单颗卫星估算难以准确掌握某个区域内土壤湿度信息；综合各卫星的估算结果，在一定程度上抑制了地表多路径环境对土壤湿度估算的影响，采用非线性定权比直接采用等权平均更有优势。

图 7 P041土壤含水量估算结果及误差分析 Figure 7 Estimation content and error analysis of soil moisture with P041

图 8 P043土壤含水量估算结果及误差分析 Figure 8 Estimation content and error analysis of soil moisture with P043

为了进一步综合评定各方案的性能，本文采用R²、均方根误差(RMSE)、平均绝对误差(MAE)和最大误差(MAX)进行评定。限于篇幅，只给出了P041测站部分卫星估算结果的R²(图9)。结合表1和表2发现，方案2和方案3的各项精度指标较为接近，采用方案3的估算结果与土壤湿度之间的R²分别为：0.942和0.962，前者相对于单一卫星至少提高了18.18%；RMSE、MAE分别为0.079和0.032、0.073和0.024，MAX最小。可见，采用等权平均方法和多星融合估算方法相对于单颗卫星，其估算精度均有所提高。结合图7、图8综合对比分析：采用多星融合估算，不仅保证了估算过程局部误差的稳定性，而且相对于等权平均方法更能有效地抑制采用单颗卫星估算时极易出现异常跳变的现象，反演过程不易受单颗卫星的影响。

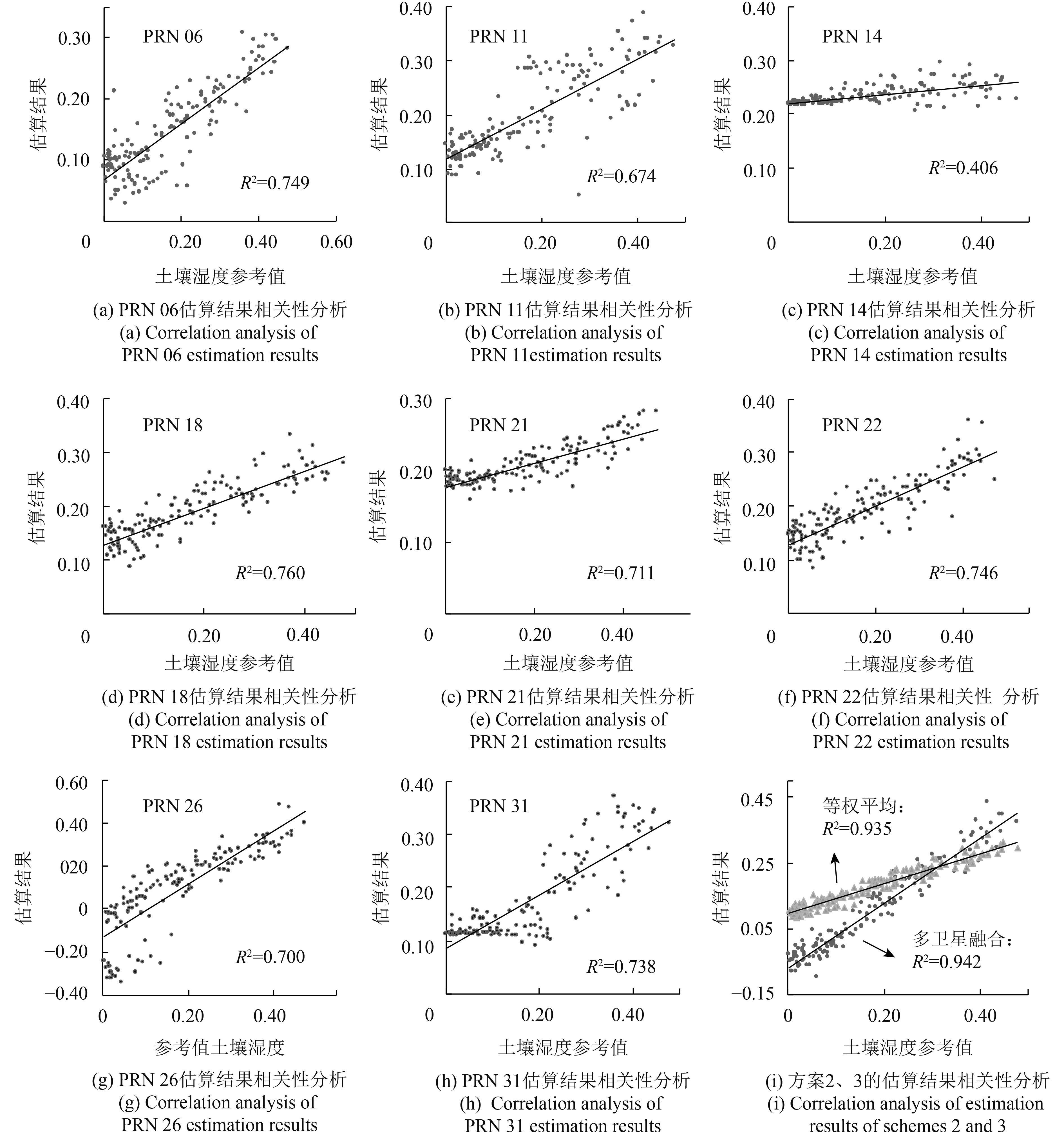
图 9 模型估算结果与土壤湿度参考值的线性回归分析 Figure 9 Linear regression analysis of estimation results and soil moisture reference value

表 1(Table 1)

表 1 P041测站各模型土壤湿度估算精度统计表 Table 1 Estimation accuracy of soil moisture in each model with P041 P041测站 等权平均 多星融合 6 11 14 18 21 22 26 31 R2 0.749 0.674 0.406 0.760 0.711 0.746 0.700 0.738 0.935 0.942 RMSE 0.085 0.086 0.135 0.091 0.115 0.091 0.145 0.077 0.074 0.079 MAE 0.070 0.072 0.119 0.078 0.101 0.078 0.103 0.065 0.063 0.073 MAX 0.196 0.231 0.249 0.197 0.202 0.230 0.392 0.185 −0.181 −0.155

表 1 P041测站各模型土壤湿度估算精度统计表 Table 1 Estimation accuracy of soil moisture in each model with P041

表 2(Table 2)

表 2 P043测站各模型土壤湿度估算精度统计表 Table 2 Estimation accuracy of soil moisture in each model with P043 P043测站 等权平均 多星融合 01 03 04 07 09 14 23 31 32 R2 0.739 0.916 0.784 0.869 0.905 0.800 0.914 0.690 0.890 0.969 0.962 RMSE 0.072 0.074 0.070 0.052 0.060 0.070 0.074 0.097 0.044 0.047 0.032 MAE 0.060 0.064 0.058 0.040 0.050 0.059 0.063 0.084 0.035 0.040 0.024 MAX −0.165 −0.164 −0.199 −0.227 −0.164 0.161 −0.201 −0.226 0.134 −0.140 −0.092 　注：RMSE、MAE、MAX单位为cm−3·cm3。

表 2 P043测站各模型土壤湿度估算精度统计表 Table 2 Estimation accuracy of soil moisture in each model with P043

综上，基于多卫星融合的LS-SVM滚动式估算模型充分融合了各卫星的性能，使得各卫星的相对延迟相位之间形成了互补；不同的卫星在不同时刻反映着不同方向的地表环境信息，通过多星融合在一定程度上有效改善了单颗卫星难以适应地表多路径影响的问题。而且，多卫星融合相对于单一卫星更能适应不同湿度程度的土壤，在估算过程中LS-SVM并未发生过拟合现象，模型的性能也得到了较好的发挥，优于直接对各卫星进行等权平均的结果。

土壤湿度及其变化的准确和长期监测对环境科学研究具有重要意义。针对目前土壤湿度研究更多局限于采用单颗卫星进行估算以及较少涉及机器学习方法，本文从多星融合思路出发，提出了基于多星融合的土壤湿度LS-SVM滚动式估算模型，得出以下结论：

(1) 观测过程中GPS天线受卫星几何运动轨迹和卫星自身性能影响，不同卫星的相对延迟相位对于地表土壤湿度的响应模式均不同，与土壤湿度存在一定的相关性，采用线性回归方程能够较好描述两者之间的关系。通过合理设定相关性的阈值范围实现卫星的有效选取。

(2) 算法充分发挥了LS-SVM在土壤湿度中的优势，能够有效综合了各卫星的性能，通过非线性定权方式实现各卫星相对延迟相位之间的互补，有效改善了采用单颗卫星进行估算时，其结果极易出现异常跳变的现象。而且，相对于等权平均方法，采用多星融合估算模式不易受单颗卫星的相对延迟相位变化趋势的影响。

(3) 算法只需较少的建模数据即可实现较长时间的估算，拟合过程表现较为稳定；采用滚动式能够实现较长时间的估算，估算误差较为平稳。

综上所述，土壤湿度问题可当作一个非线性事件进行处理，多卫星融合模式应用于土壤湿度估算是可行、有效的。下一步工作将对如何确定模型最佳输入变量的长度，并通过在不同环境条件下的多源数据以及融入植被信息、温度、降雨量等变量展开更为深入研究。

志 谢 此次实验的GPS监测数据均可从UNAVCO获得，土壤湿度参考值来自于http://xenon.col-orado.edu/portal[2017-10-10]。在此衷心的感谢PBO H 2 O和UNAVCO。