| 顾及空间非平稳特征的遥感干旱监测 |
收稿日期: 2017-09-14
2. University of Chinese Academy of Sciences, Beijing 100049, China
3. Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350108, China
4. College of Geography and Environment, Jiangxi Normal University, Nanchang 330000, China
干旱是一种极为复杂的自然灾害现象,严重影响社会经济发展、工农业生产及生态环境等各个领域(Zhang 等,2017)。干旱主要分为4种类型:气象干旱(Meteorological Drought)、农业干旱(Agriculture Drought)、水文干旱(Hydrological Drought)、社会经济干旱(Socioeconomic Drought)(Wilhite,2005)。由于近几十年来生态环境问题的恶化,旱灾爆发的频率与所造成的损失逐年递增,引发了国际上的广泛关注(Zhou 等,2012;Keyantash和Dracup,2004;Wilhelmi和Wilhite,2002)。
根据数据源,目前的干旱监测方法分为基于地面数据的干旱监测方法与基于遥感数据的干旱监测方法。前者一般以地面采集的气象、农业信息为基础,如降水、地表蒸散、温度等,并通过特定的数学模型综合为统一的地面旱情监测指数(Kangas和Brown,2007;Zargar 等,2011)。常用的地面监测指数包括帕尔默干旱严重指数PDSI(Palmer Drought Severity Index)(Palmer,1965)、标准降水指数SPI(Standardized Precipitation Index)(Edwards和McKee,1997;Hayes 等,2000)、标准蒸散降水指数SPEI(Standardized Precipitation Evapotranspiration Index,)(Vicente-Serrano 等,2010)等。地面监测方法具有明确的物理机制和较好的监测精度,然而由于干旱属于区域性的灾害过程,站点式的观测值难以在大尺度上实现连续的空间覆盖,而通过内插方法得到的面状结果极大依赖于插值方法和站点分布模式又不具有明确的物理含义(Hao 等,2015)。美国旱情监测协会USDM(U.S. Drought Monitor)以地方研究志愿者和气象观测站提供的当地监测信息为基础,结合专家经验,提供了每两周更新一次的面状旱情监测数据,并获得了广泛的认可。然而其绘制过程复杂,依赖主观知识,使得其难以及时快速的对旱情信息进行反馈。随着遥感应用技术在近年来的飞速发展,其具有空间连续、覆盖范围广、数据成本低的优势,在探测旱情发展过程及强度方面表现出巨大的优势(Hao 等,2015;Kogan,1997),因而国内外(聂娟 等,2018;王丽涛 等,2011;武晓波 等,1998)基于多源遥感数据发展出一系列的遥感旱情监测指数。从单一角度反映地面状态的旱情指数包括归一化植被指数NDVI(Normalized Difference Vegetation Index)、植被条件指数VCI(Vegetation Condition Index)、温度条件指数TCI(Temperature Condition Index)、降水条件指数PCI(Precipitation Condition Index)、土壤水分条件指数SMCI(Soil Moisture Condition Index)等。这些指数从多个角度反映了地面状态,间接表达干旱的发展过程。近年来,研究表明干旱监测过程应该更多关注于多指标综合模型的发展,其能够更加稳健和全面地对旱情进行表达(Aghakouchak 等,2015)。为了加强旱情监测模式的科学性同时提高监测精度,许多研究从地面的植被、温度、水分、降水状态出发,考虑多种地表因素对旱情发展过程的综合影响,提出了遥感综合干旱监测指数(Du 等,2013;Hao 等,2015;Rhee 等,2010;Zhang和Jia,2013)。
然而,目前的遥感多状态综合指数大多属于全局性的监测模型,以经验系数或全局模型对各地表状态进行建模,假定了旱情模式的空间平稳性,不符合干旱过程的实际情况。由于干旱是具有复杂性的区域化地理空间事件,不同的植被类型、土壤条件、生态环境会引起局部干旱模式存在较大差异,具有空间非平稳特征(Spatial Non-stationarity)。因而,全局性的遥感监测模型难以探测旱情空间关系的细微变化,得到的结果是研究区内的宏观平均,掩盖了大尺度范围下旱情的空间局部特征。
地理加权回归技术GWR(Geographically Weighted Regression),将数据的空间位置嵌入到回归系数中,既能够描述变量间的关系,又能够反映数据的空间变化特征。与其他非平稳探测模型相比,GWR建模过程简单,能够直观地刻画空间非平稳关系,且模型参数估计结果随地理空间位置变化,能够反映局域模型的空间差异状态。本文考虑将地理加权回归模型引入遥感干旱监测过程,以挖掘其在旱情监测应用上的潜力,主要关注于气象干旱的监测过程,但由于综合性的遥感旱情检测指数也能够在一定程度上反映其他类型的干旱状况,因此也选用其他类型的旱情指数进行对比分析。以美国大陆(CONUS)为研究区域,构建2002年—2011年共10年基于GWR模型的旱情指数,实现非全域性的遥感旱情监测过程。同时通过与多遥感旱情指数监测效果进行对比分析,评价GWR模型对于干旱监测的能力,为发展局域性的遥感旱情监测指数提供参考。
2、数据与方法 (2.1) 研究区与数据选取美国本土大陆地区作为主要的研究区域。该区域土地覆盖范围辽阔,地形复杂,气候类型与生态类型多样,自然资源丰富,旱灾爆发频率较高,且美国官方提供了大量的旱情权威监测数据,非常适合干旱模型的评价与分析研究。其地表覆被概况图(NLCD地表覆盖图)如图1所示。

|
| 图 1 美国大陆概况图(Jiao 等,2016) Figure 1 A summary map of the Continental United States (Jiao et al.,2016) |
数据类型主要包括地面监测数据集SDS(Station Data Sets)与多源遥感数据集RDS(Remote Sensing Data Sets)。具体的数据处理过程如下:
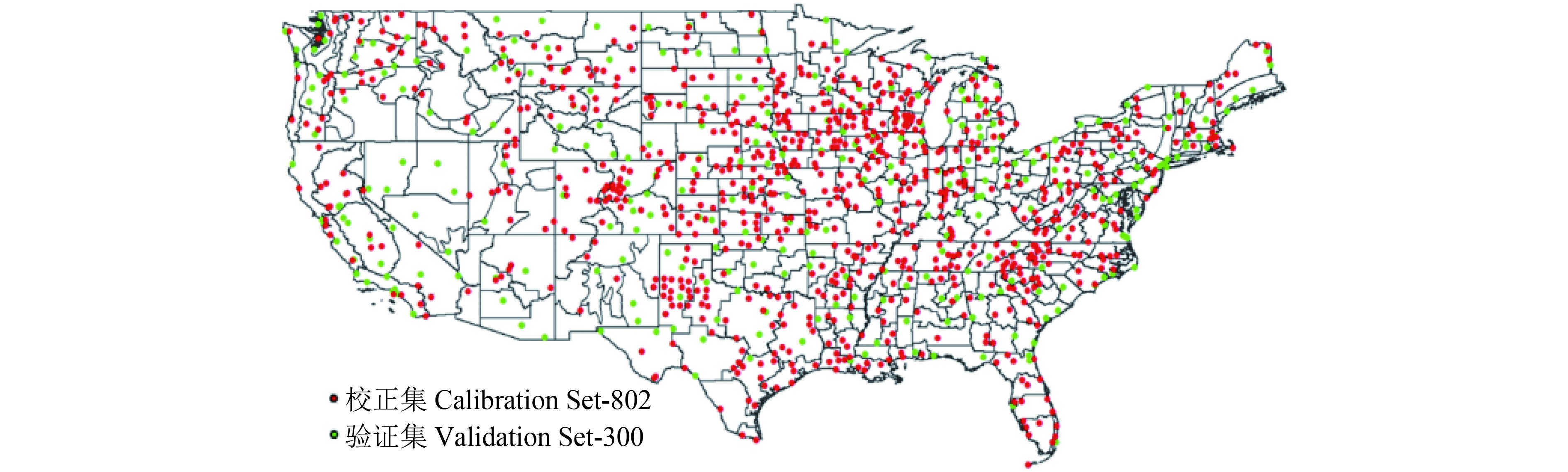
(1)地面监测数据集。地面监测数据集SDS主要以离散式的干旱监测指数为主,包括加强型Palmer指数PMDI(Palmer Modified Drought Index)、帕尔默水资源干旱指数PHDI(Palmer Hydrological Drought Index)、Z指数ZNDX(Z-index,)以及多尺度的SPI指数(SPI-n),这些指数被广泛应用于遥感旱情监测效果的定量评价研究中。SPI-n指数考虑研究区内当期与前期的降水关系,给出当期的旱情指标;PMDI、PHDI、ZNDX指数综合降水、土壤、温度等多种因素,以标准化函数进行整合,给出当前的地面旱情状态。Jiao等(2016)对各站点监测指数进行了详尽的介绍。美国环境信息中心NCEI(National Centers for Environmental Information)及国家气候数据中心NCDC(National Climatic Data Center)等以站点的形式提供了可获取的地面旱情监测数据。本文在全美范围内筛选出2002年—2011年共10年能够连续提供观测数据的站点,共计1102个,并提取各站点的元数据用于数据重组织及矢量文件的制作。由于GWR模型需要地面监测数据作为辅助,选用PMDI指数作为标准地面建模数据,将可用PMDI监测站点大致以3∶1的比例随机分划,分别作为本研究的校正数据集(Nc=802)和验证数据集(Nv=300),同时其他类型的站点监测数据全部作为验证数据集使用。PMDI各站点的空间分布如下图2所示。
(2)USDM面状监测数据集。美国旱情监测协会USDM(U.S. Drought Monitor)提供了每两周更新一次的全美旱情监测图。该数据同样以地面监测数据为基础,同时结合各州、县等相关气象研究学者、专家和志愿者定期提供的当地旱情资料,并由相关领域专家结合当地生态、气候环境进行绘制。USDM将旱情规划为5个等级:D0-轻微干旱、D1-中度干旱、D2-严重干旱、D3-极度干旱、D4-异常干旱,是目前最为权威的面状旱情监测数据,并广泛应用于各遥感监测结果的评价研究中。本文以该数据作为标准面状监测图,用于研究GWR方法用于遥感旱情监测过程的适用效果。
|
| 图 2 地面旱情监测数据分布 Figure 2 Distribution of ground drought data |
(3)多源遥感数据集RSDS(Remote Sensing Data Sets)。本文使用多源遥感数据及产品对研究区内地表状态进行反演,构建遥感单一旱情监测指数。主要数据产品包括MODIS MOD09A1地表反射率8 d合成产品、MODIS MOD11A2地表温度8 d合成产品、TRMM 3B43月尺度降雨数据合成产品、AMSR-AE-LAND3土壤水分数据产品。
NASA陆地过程分布式数据档案中心(LP DAAC)和NASA地球观测数据和信息系统(EOSDIS)分别提供了MODIS MOD09A1与MOD11A2的数据地址。下载2002年—2011年各年的089—297 d,共17个条带(h07v06,h08-h13,v04-v06)的数据用于完整覆盖美国大陆(CONUS)范围,同时用于监测主要的植被生长期。使用QA质量文件掩膜处理云覆盖区域,并根据各景数据所占月天数对8 d产品进行加权处理并合成30 d一景的月数据。根据式(1)应用预处理后的MOD09A1构建植被状态指数(VCI),MOD11A2构建温度状态指数(TCI),并进行空间重采样使其具有0.005°的空间分辨率。
| ${\rm{VCI}} = \frac{{{\rm{NDVI}} - {{\rm{NDVI}}_{\min}}}}{{{{\rm{NDVI}}_{\max}} - {{\rm{NDVI}}_{\min}}}}$ | (1) |
| ${\rm{TCI}} = \frac{{{{{BT}}_{\max}} - {{BT}}}}{{{{{BT}}_{\max}} - {{{BT}}_{\min}}}}$ | (2) |
式中,NDVI值以MOD09A1数据产品的近红与红波段进行构建;BT为MOD11A2产品各像素上的亮温值。VCI可理解为时间序列上归一化的NDVI指数。为保证VCI、TCI指数与地面旱情的正相关特性,TCI的构建在分子上与其他指数有所差异。
NASA数据信息服务中心(DISC)提供了TRMM各传感器监测数据与多传感器产品数据集。TRMM 3B43产品具有0.25°的空间分辨率和30 d的时间分辨率,是全球覆盖范围内的月降水数据产品集。将数据统一在WGS84坐标系统下,并重采样至0.005°,用于计算完整CONUS的降水状态指数(PCI)。
| ${\rm{PCI}} = \frac{{{\rm{TRMM}} -{ {\rm{TRMM}}_{\min}}}}{{{{\rm{TRMM}}_{\max}} - {{\rm{TRMM}}_{\min}}}}$ | (3) |
美国国家冰雪中心(NSIDC)提供了由AMSR-E获取的地表数据以及不同的地表反演产品,本文主要应用AMSR-E提供的AE-LAND3数据,该产品基于地表散射和辐射物理模型,利用地表参数回归模型LPRM(Land Parameter Retrieval Model)对全球覆盖范围内的土壤含水量进行反演,具有25 km的空间分辨率,24 h的时间分辨率,广泛应用于土壤水分的监测中。土壤水分状态指数(SMCI)构建方法如式(4)。
| ${\rm{SMCI}} = \frac{{{\rm{AMSRE}} - {{\rm{AMSRE}}_{\min}}}}{{{{\rm{AMSRE}}_{\max}} - {{\rm{AMSRE}}_{\min}}}}$ | (4) |
各遥感单一旱情监测指数统一在WGS-84坐标系统下,通过重采样与月最大合成法进行时空分辨率的统一,使其具有0.005°的空间分辨率和30 d的时间分辨率,覆盖2002年—2011年各年4—10月整个CONUS,共66景数据,每景数据为11557×4968像素。
(2.2) 地理加权回归模型(GWR)空间非平稳性(Spatial Non-stationarity)指因地理位置的变化而引起的变量间关系或结构的变化。Brunsdon等(1996)基于局部光滑的思想,提出了地理加权回归GWR (Geographically Weighted Regression)方法,其是对传统全局回归方法,如最小二乘法的优化,考虑空间数据的非平稳特征和自相关问题,将数据的空间位置嵌入模型中,允许模型参数在地理空间上存在区域性变化。现阶段GWR方法已经被广泛应用于各学科和领域,如地质学、环境科学、房产特征价格模型、景观生态学、健康卫生研究以及犯罪研究(Brunsdon 等,1996;Ivajnšič 等,2014;Propastin,2012;Song 等,2014;Xu和Lin,2017)。
图3为GWR模型预测过程示意图。P1、P2为待估计点,其余为地面监测点。设随机变量y与x1,x2,
| $\begin{split} y = & {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + \ldots + {\beta _p}{x_p} + \varepsilon = \\ & {\beta _0} + \mathop \sum \limits_1^p {{{\beta}} _{{k}}}{{{x}}_{{k}}} + \varepsilon \end{split}$ | (5) |
式中,独立变量xk (k=1, 2,

|
| 图 3 GWR模型预测过程图示 Figure 3 The principle of GWR model |
| $\left\{ {\begin{array}{*{20}{c}} {E\left(\varepsilon \right) = 0}\\ {Var\left(\varepsilon \right) = {\sigma ^2}} \end{array}} \right.$ | (6) |
当
| $\hat {{\beta}} = {\left({{{X}}'{{X}}} \right)^{ - 1}}{{X}}'{{Y}}$ | (7) |
因变量向量Y的回归值或称为拟合值
| $\hat {{Y}} = {{X}}\hat {{\beta}} = {{X}}{\left({{{X}}'{{X}}} \right)^{ - 1}}{{X}}'{{Y}}$ | (8) |
式中,
| ${{X}} = \left[ {\begin{array}{*{20}{c}} 1 & {{x_{11}}} & \cdots & {{x_{1p}}}\\ 1 & {{x_{21}}} & \cdots & {{x_{2p}}}\\ \vdots & \vdots & \cdots & \vdots \\ 1 & {{x_{n1}}} & \cdots & {{x_{np}}} \end{array}} \right], {{Y}} = \left[ {\begin{array}{*{20}{c}} {{Y_1}}\\ {{Y_2}}\\ \vdots \\ {{Y_n}} \end{array}} \right], \hat {{\beta }} = \left[ {\widehat {\begin{array}{*{20}{c}} {{\beta _0}}\\ {\widehat {\begin{array}{*{20}{c}} {{\beta _1}}\\ \vdots \\ {\widehat {{\beta _{p + 1}}}} \end{array}}} \end{array}}} \right]$ |
P1、P2可根据全部采样点解算的
为了探测参数的空间变化,地理加权回归(GWR)技术对式(5)表示的一般线性模型(OLR)进行扩展,允许回归参数在空间上具有一定的变化,扩展后模型的回归参数是位置i的函数,权重则根据地理空间位置确定,得到了区域性的回归模型,GWR模型可以表示如下
| $\begin{split} {y_i} = & {\beta _0}\left({{u_i}, {v_i}} \right) + \mathop \sum \limits_{k = 1}^p {{{\beta}} _{{k}}}\left({{{{u}}_{{i}}}, {{{v}}_{{i}}}} \right){{{x}}_{{{ik}}}} + {\varepsilon _i}\\ & i = 1, 2, \cdots, n \end{split}$ | (9) |
式中,(ui,vi)是第i个采样点的坐标位置,可以用地理坐标经纬度或投影坐标进行表示;βk(ui,vi)是第i个采样点上的第k个待求回归参数,是采样位置(ui,vi)的函数。为了表述方便,通常将式(9)简记为
| $\begin{split} {y_i} = & {\beta _{i0}} + \mathop \sum \limits_{k = 1}^p {{{\beta}} _{{{ik}}}}{{{x}}_{{{ik}}}} + {\varepsilon _i}\\ & i = 1, 2, \cdots, n \end{split}$ | (10) |
i点上的局部回归参数估计值
| $\widehat {{{{\beta}} _{{i}}}} = {\left({{{X}}'{{{W}}_{{i}}}{{X}}} \right)^{ - 1}}{{X}}'{{{W}}_{{i}}}{{y}}$ | (11) |
式中,
| ${{X}} = \left[ {\begin{array}{*{20}{c}} \!\! 1 & {{x_{11}}} & \cdots & {{x_{1p}}}\!\! \\ \!\! 1 & {{x_{21}}} & \cdots & {{x_{2p}}}\!\! \\ \!\! \vdots & \vdots & \cdots & \vdots\!\! \\ \!\! 1 & {{x_{n1}}} & \cdots & {{x_{np}}}\!\! \end{array}} \right], {{{W}}_{{i}}} = \left[ {\begin{array}{*{20}{c}} \!\! {{W_{i1}}}&0&0&0\!\! \\ \!\! 0 & {{W_{i2}}} & \vdots & \vdots \!\! \\ \!\! \vdots & \vdots & \ddots &0\!\! \\ \!\! 0&0&0 & {{W_{in}}}\!\! \end{array}} \right]$ |
式中,Wi是n×n的加权矩阵,对角元素是观测值位置j与回归位置i之间距离的函数,非对角元素全为0,矩阵Wi可记做Wi=diag(Wi1,Wi2,
本文选用广泛使用的高斯核函数,用于GWR模型的构建,可具体表示为
| ${w_{ij}} = \exp\left({ - {{\left({\frac{{{d_{ij}}}}{b}} \right)}^2}} \right)$ | (12) |
式中,dij为两点间的距离函数,b是描述权重与距离间函数关系的非负衰减参数(Brunsdon 等,1996)。
因此对于i点处的局部因变量拟合值(或回归值)
| $\widehat {{y_i}} = {{{X}}_{{i}}}\widehat {{{{\beta}} _{{i}}}} = {{{X}}_{{i}}}{\left({{{X}}'{{{W}}_{{i}}}{{X}}} \right)^{ - 1}}{{X}}'{{{W}}_{{i}}}y$ | (13) |
对于GWR模型,P1、P2点上各有一组局部最优回归系数,避免了OLR模型在全部回归点上使用同一组回归系数的问题。
选取PMDI指数作为标准旱情监测数据,与大多数的遥感综合监测指数研究过程类似(Hao 等,2015;Du 等,2013),同样考虑影响旱情的4个主要因素:降水、土壤、植被、温度作为回归模型的解释变量,并应用全域OLR方法和局域GWR方法,构建全局的和局部的遥感旱情监测模型,如下式
| $\begin{split} \widehat {{\rm{PMDI}}_{{\rm{OLR}}}} = & {\alpha _0} + {\alpha _1} \times {\rm{PCI}} + {\alpha _2} \times {\rm{SMCI}} + \\ & {\alpha _3} \times {\rm{VCI}} + {\alpha _4} \times {\rm{TCI}} \end{split}$ | (14) |
| $\begin{split} \widehat {{\rm{PMDI}}_{{\rm{GWR}}}\left({u, v} \right) }=& {\beta _0}\left({u, v} \right) + {\beta _1}\left({u, v} \right) \times {\rm{PCI}}\left({u, v} \right) + \\ & {\beta _2}\left({u, v} \right) \times {\rm{SMCI}}\left({u, v} \right){\rm{}} + {\beta _3}\left({u, v} \right) \times \\ & {\rm{VCI}}\left({u, v} \right) + {\beta _4}\left({u, v} \right) \times {\rm{TCI}}\left({u, v} \right) \end{split}$ | (15) |
式中,
ArcGIS 10.3将GWR模型的构建过程集成在空间统计工具箱内,通过地理加权回归分析工具可以快速实现模型的构建。同时对于任意不具有地面监测值的待预测像素点,ArcGIS提供了“附加参数”模块,用于在此类像素上的参数预测过程,其主要通过寻找该预测点邻近的部分数据点实现模型的局部拟合优化。
3、结果与分析 (3.1) GWR模型监测结果由于PMDI指数将旱情发展过程划分为11个等级,覆盖从极度湿润到极度干旱,而USDM监测图将正常与湿润等级全部规划为非旱区,仅对旱情划分为5个等级。因此,参照研究论文重新定义了OLR、GWR监测结果的旱情等级,以便于与USDM对比分析,PMDI旱情等级重定义如表1。
|
|
表 1 PMDI指数旱情等级重定义(Svoboda 等,2002) Table 1 The severity of drought divided by PMDI(Svoboda et al., 2002) |
OLR与GWR方法监测结果如图4。根据图4可知2011年美国德克萨斯州发生了罕见的旱灾事件,USDM表明受灾最为严重的地区覆盖全美约54个气候子带,包括德克萨斯州的大部分地区以及新墨西哥州、俄克拉何马州、密西西比州等附近8个州的局部地区,同时在东南角的弗罗里达州和佐治亚州也在该年发生短期的干旱事件。对比两种监测模型,基于GWR方法的监测模型的旱情空间分布模式能够很好地符合整体的USDM结果,对旱情发生的地区与强度能够较好的表达,但在局部地区和细节监测效果上与USDM结果有所出入,这是由于遥感影像以0.005°为空间分辨率,每个像元地面覆盖范围较大,同时还存在混合像元的问题,难以达到USDM手工绘制精度。相比之下,OLR监测结果在对旱情等级定义上存在误差,如2011年4月结果中,将南部德克萨斯州附近D3级旱情错判为D2和D1级,并且由于OLR模型在全域上应用统一的模型参数,使得局域模型偏离局部最优模型,在监测结果上存在“椒盐”现象,如在2011年8月、9月上的监测结果,在西北区域的华盛顿州附近存在离散的旱情等级(图5),由于旱情往往是大范围内的事件,离散的监测数据往往充当噪声的角色,严重影响旱情监测精度与目视效果。

|
| 图 4 2011年USDM、GWR、OLR监测结果对比 Figure 4 The results of USDM, GWR and OLR model in 2011 |

|
| 图 5 2011年9月监测结果局部对比 Figure 5 The local amplification results of GWR, OLR and standard USDM on September, 2011 |
选取两个典型的子分割区域,统计2011-04—2011-09各月上旱情等级的变化(各等级旱情面积占总区域面积的百分比),结果如表2所示,所选取的分区在图4上以彩色边线勾画(子区1蓝色、子区2紫色)。对于子区1,表现为严重的旱情爆发状态,且随着时间的推移该区域的旱情等级逐渐增强,在9月时达到最大,GWR结果能够表现这一旱情变化过程,且对旱情等级的判别基本符合标准USDM结果;而OLR虽然也能够反映旱情的变化过程但在旱情等级的界定上存在一定的偏差,如在7月上将旱情等级判定为D3级,而真实的地面结果为D4级。对于子区2,在初期表现为非旱区状态,而后期爆发了等级较低的旱情事件,GWR结果与USDM在4—7月完全一致,在8月、9月能够表现低等级的干旱状态;而OLR结果在7月即与标准结果产生较大的偏差,同时在7—9月上的监测结果表现为各个等级的旱情在空间分布上较为离散,且随时间的变化不明显,难以反映旱情的变化过程。
|
|
表 2 USDM与GWR、OLR旱情等级监测结果局部统计分析 Table 2 Local statistical analysis of USDM and GWR, OLR drought monitoring results |
相较于OLR模型,GWR模型能够获取随空间位置变化的局部最优参数,实现了对模型空间变化的探测过程。图6为2002年8月GWR优化的旱情监测模型的局部参数。图中某个因子越红表明该因子对局部旱情监测模型的影响强度越大,反之,越绿表明对模型的影响越小。图6(b)表明,PCI因子在东部的密歇根州、印第安纳州、密苏里州等附近具有较高的影响系数,在宾夕法尼亚州、纽约、弗吉尼亚州附近具有较低影响系数;图6(c)、图6(d)表明TCI、SMCI因子在整个研究范围内对旱情指数PMDI的影响强度较低,保持在0.7以下,TCI仅在中部的爱荷华州附近具有较高的响应强度,而SMCI在阿肯色州附近与西北部的华盛顿州、爱达荷州具有相对较高的影响强度;VCI因子在整体上对旱情模型的影响较大,在整个大平原区域和西北部地区都具有1.5以上的影响参数;截距项在整个研究范围内随位置变化明显,显示出局部相似的特征。综上来看,各因子对旱情模型的影响强度随空间位置的变化而发生改变,导致旱情监测模型的空间非平稳特征,GWR方法相较于其他全域性方法能够探测空间关系的变化,因此与USDM标准图具有较好的吻合度。

|
| 图 6 2002年8月GWR旱情监测模型局部参数 Figure 6 The local drought monitor parameters of GWR on August, 2002 |
为了定量评价GWR模型的旱情监测效果,对2002年—2011年各月上的监测结果进行定量分析,并选用两种拟合优度度量:相关系数R,均方根误差RMSE来定量评估旱情监测结果,RMSE、R的计算如下式
| ${\rm{RMSE}} = \sqrt {{N^{ - 1}}\mathop \sum \limits_{i = 1}^N {{\left({{X_i} - {Y_i}} \right)}^2}} $ | (15) |
| ${{R}} = \frac{{\mathop \sum \limits_{i = 1}^N \left({{X_i} - \bar X} \right)\left({{Y_i} - \bar Y} \right)}}{{\sqrt {\mathop \sum \limits_{i = 1}^N {{\left({{X_i} - \bar X} \right)}^2}} \sqrt {\mathop \sum \limits_{i = 1}^N {{\left({{Y_i} - \bar Y} \right)}^2}} }}$ | (16) |
式中,Xi是第i个基于遥感的干旱指数;
结果如图7所示,图7(a)为2002年—2011年各月(4—10月)上的遥感监测结果与地面监测数据PMDI间的均方根误差,图7(b)为两者的相关系数。图7表明GWR技术的监测结果在各月上的均方根误差均小于OLR,GWR方法的最小RMSE达到约1.07,而OLR方法的RMSE最小约1.69;GWR方法的相关系数均大于OLR,最大R值高达约0.84,而OLR方法的相关系数最大约0.56,显著低于改进的局域优化监测方法。表明了GWR技术较OLR技术在旱情监测方面具有显著的优势性。

|
| 图 7 2002年—2011年逐月(4—10月)遥感旱情监测结果精度分析 Figure 7 Accuracy analysis results about drought monitoring accuracy in month scale from 2002 to 2011 |
进一步,选取PMDI、PHDI、ZNDX、SPI-01、SPI-03、SPI-06、SPI-09、SPI-12、SPI-24分别作为地面验证数据,对研究区内时间序列上的全部监测结果进行一致性的评价,结果如图8。图8(a)、图8(b)分别为GWR、OLR技术的监测结果与各验证数据的散点图。GWR模型监测效果与PMDI监测值相关性最高,R值达到0.8552;GWR模型监测值与多尺度SPI值的相关性呈显著规律性变化,与一个月尺度上的SPI-01值相关性最差,R=0.5611;随着尺度的增加,GWR模型与SPI-n的相关性逐渐增大,当n=9时,与SPI-09的一致性达到最大值R=0.7360。随后随着尺度的增大,相关性逐渐降低,与SPI-24的相关性降低至R=0.5821。OLS模型与PMDI旱情指数一致性最高R=0.6256;与ZNDX相关性仅次于PMDI,R为0.6064;OLS与多尺度SPI相关性也呈现规律变化,在n=3时,一致性R达到最大0.5834,随后呈现明显的下降趋势。对比GWR模型与OLS模型在整个时间序列上的监测效果,除ZNDX外,GWR模型相较于OLS模型均显示出较高的一致性水平,再次证明了其相对于全局OLR模型的优势。

|
| 图 8 2002年—2011年GWR、OLR旱情监测结果一致性分析 Figure 8 Correlation analysis results of GWR and OLR model from 2002 to 2011 |
选取多种广泛应用的遥感旱情监测指数与本文所提出的基于GWR技术的旱情监测结果进行对比分析,评价GWR技术在遥感旱情监测方面的表现能力。选取的遥感旱情监测指数包括OMDI(optimized meteorological drought index)、OVDI(optimized vegetation drought index)(Hao 等,2015)、SDCI(Scaled Drought Condition Index)(Rhee 等,2010)、SDI(synthesized drought index)(Du 等,2013)、MIDI(Microwave Integrated Drought Index)(Zhang和Jia,2013)、VHI(Vegetation Heath Index)(Kogan 等,1995)以及应用GWR模型与OLR模型得到的旱情监测结果。
以气候子区域为最小分割单元,计算各指数与PMDI、PHDI、ZNDX、SPI-n在344个气候子区域4—10月的拟合度量值。
以2011年7月作为参考月份,各遥感旱情监测结果如图9。综合表3、表4,GWR结果在与PMDI、PHDI、SPI-03、SPI-06、SPI-09、SPI-12上均表现出最高的相关性与最低的均方根误差,其中与PMDI的相关系数R=0.855,与SPI-03的均方根误差RMSE=0.972;图9中,GWR监测结果在所有遥感指数中表现总体最优,更加符合USDM标准结果,且目视效果最佳。用于建模的基础因子PCI、SMCI、TCI、VCI指数在单独用于旱情监测时难以准确表达旱情等级和区域:如PCI因子虽然与SPI-01指数在时间序列上具有较好的一致性,但在单景数据,如图9中的监测效果并不突出。VCI因子由于受到植被生长阶段的影响,难以在时间序列上准确监测旱情的变化(Ji和Peters,2003)。相较于单一的地面监测指数,多遥感指数综合的监测模型能够更好的监测旱情的变化。由于综合指数将多地面状态融合,避免了单一状态异常所引起的错误监测结果,因此具有更加稳健的表现效果。如SDI、SDCI、OVDI、OMDI等在时间序列上的R值均达到0.5附近,RMSE保持在2附近,图9中SDI、OVDI在德克萨斯州附近的监测结果也与USDM吻合,但相较与GWR模型,其在东北部纽约、宾夕法尼亚、俄亥俄州附近的监测结果不佳。OVDI、OMDI与GWR监测过程类似,同样需要结合地面监测信息通过限制最优算法解算遥感监测模型,OVDI与GWR所用基础数据相同,但在监测结果上与GWR相差较多,尤其是在东北部地区的表现效果较差。综合对比多种遥感旱情监测方法,GWR模型监测结果更加吻合于标准USDM结果,与实际地面监测值的最高相关系数R达到0.855,均方根误差RMSE达到0.972,具有较好的表现效果。GWR结果通过将多单一旱情指数进行综合,能够从多角度监测旱情状态,同时其对空间非平稳的探测能够有效提高旱情的监测精度。
|
|
表 3 不同遥感干旱指数与站点干旱指数的均方根误差RMSE分布 Table 3 RMSE distribution between different remote sensing drought index and ground index |
|
|
表 4 不同遥感干旱指数与站点干旱指数的相关系数R分布 Table 4 Correlation coefficient distribution between different remote sensing drought index and ground index |

|
| 图 9 2011年7月多种遥感旱情指数监测结果对比 Figure 9 The comparison of different remote sensing drought monitoring results on July, 2011 |
考虑传统遥感干旱监测模型往往假定旱情模式的空间均一特征,忽略旱情事件的空间非平稳特性,因而得到的旱情精度较差。提出使用GWR方法并结合PCI、TCI、VCI、SMCI等4种遥感因子实现了旱情信息的非平稳建模监测过程。通过2002年—2011年间月尺度时间序列上的实验表明,相较于传统全域性的遥感旱情监测方法,本文所提出方法能够在区域上更加精细的刻画旱情信息,显著提升了利用遥感数据进行旱情信息监测的精度。一方面这是由于旱情本身即具有空间非平稳过程的区域化地理事件,其模式随空间位置的变化而有所差异,这一点在本文中也已得到证实;另一方面GWR模型通过将区域变量的位置特征嵌入模型优化过程,能够解算区域化变量与遥感干旱数据间的最优局部关系,实现了对旱情事件非平稳性的精细表达。
然而,虽然GWR模型能够有效探测旱情的局部发展模式,但相较于其他模型,如OLR、MIDI的计算效率显著较低,在实际应用上还有待优化。同时由于GWR仍需站点监测数据的支撑,因此在地面观测缺失的情况下难以展开应用。如何有效利用历史监测数据与多源数据,深入研究旱情模式的局部特征,将有利于发展独立于地面监测数据的非平稳旱情监测方法,利用GWR对长时间局部区域的旱情模式探测还有待深入开展。最后,空间非平稳探测模型种类较多,各具优缺,利用其他非平稳探测模型实现结合遥感数据的旱情建模过程还有待深入研究。
| [1] | Aghakouchak A, Farahmand A, Melton F S, Teixeira J, Anderson M C, Wardlow B D and Hain C R. Remote sensing of drought: progress, challenges and opportunities[J]. Reviews of Geophysics, 2015, 53 (2) : 452 –480. DOI: 10.1002/2014RG000456 |
| [2] | Brunsdon C, Fotheringham A S and Charlton M E. Geographically weighted regression: a method for exploring spatial nonstationarity[J]. Geographical Analysis, 1996, 28 (4) : 281 –298. DOI: 10.1111/j.1538-4632.1996.tb00936.x |
| [3] | Du L T, Tian Q J, Yu T, Meng Q Y, Jancso T, Udvardy P and Huang Y. A comprehensive drought monitoring method integrating MODIS and TRMM data[J]. International Journal of Applied Earth Observation and Geoinformation, 2013, 23 : 245 –253. DOI: 10.1016/j.jag.2012.09.010 |
| [4] | Edwards D C and McKee T B. 1997. Characteristics of 20th century drought in the United States at multiple time scales. Colorado State University |
| [5] | Hao C, Zhang J H and Yao F M. Combination of multi-sensor remote sensing data for drought monitoring over Southwest China[J]. International Journal of Applied Earth Observation and Geoinformation, 2015, 35 : 270 –283. DOI: 10.1016/j.jag.2014.09.011 |
| [6] | Hayes M, Svoboda M D and Wilhite D A. 2000. Monitoring drought using the standardized precipitation index//Wilhite D A, ed. Drought: A Global Assessment. London: Routledge: 168–180 |
| [7] | Ivajnšič D, Kaligarič M and Žiberna I. Geographically weighted regression of the urban heat island of a small city[J]. Applied Geography, 2014, 53 : 341 –353. DOI: 10.1016/j.apgeog.2014.07.001 |
| [8] | Ji L and Peters A J. Assessing vegetation response to drought in the northern great plains using vegetation and drought indices[J]. Remote Sensing of Environment, 2003, 87 (1) : 85 –98. DOI: 10.1016/S0034-4257(03)00174-3 |
| [9] | Jiao W Z, Zhang L F, Chang Q, Fu D J, Cen Y and Tong Q X. Evaluating an enhanced vegetation condition index (VCI) based on VIUPD for drought monitoring in the continental United States[J]. Remote Sensing, 2016, 8 (3) : 224 . DOI: 10.3390/rs8030224 |
| [10] | Kangas R S and Brown T J. Characteristics of US drought and pluvials from a high‐resolution spatial dataset[J]. International Journal of Climatology, 2007, 27 (10) : 1303 –1325. DOI: 10.1002/joc.1473 |
| [11] | Keyantash J A and Dracup J A. An aggregate drought index: assessing drought severity based on fluctuations in the hydrologic cycle and surface water storage[J]. Water Resources Research, 2004, 40 (9) : W09304 . DOI: 10.1029/2003WR002610 |
| [12] | Kogan F N. Application of vegetation index and brightness temperature for drought detection[J]. Advances in Space Research, 1995, 15 (11) : 91 –100. DOI: 10.1016/0273-1177(95)00079-T |
| [13] | Kogan F N. Global drought watch from space[J]. Bulletin of the American Meteorological Society, 1997, 78 (4) : 621 –636. DOI: 10.1175/1520-0477(1997)078<0621:GDWFS>2.0.CO;2 |
| [14] | 聂娟, 邓磊, 郝向磊, 刘明, 贺英. 高分四号卫星在干旱遥感监测中的应用[J]. 遥感学报, 2018, 22 (3) : 400 –407. Nie J, Deng L, Hao X L, Liu M and He Y. Application of GF-4 satellite in drought remote sensing monitoring: A case study of Southeastern Inner Mongolia[J]. Journal of Remote Sensing, 2018, 22 (3) : 400 –407. DOI: 10.11834/jrs.20187067 |
| [15] | Palmer W C. 1965. Meteorological Drought. U.S. Department of Commerce, Weather Bureau. |
| [16] | Propastin P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data[J]. International Journal of Applied Earth Observation and Geoinformation, 2012, 18 : 82 –90. DOI: 10.1016/j.jag.2011.12.013 |
| [17] | Rhee J, Im J and Carbone G J. Monitoring agricultural drought for arid and humid regions using multi-sensor remote sensing data[J]. Remote Sensing of Environment, 2010, 114 (12) : 2875 –2887. DOI: 10.1016/j.rse.2010.07.005 |
| [18] | Song W Z, Jia H F, Huang J F and Zhang Y Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China [J]. Remote Sensing of Environment, 2014, 154 : 1 –7. DOI: 10.1016/j.rse.2014.08.008 |
| [19] | Svoboda M, LeComte D, Hayes M, Heim R, Gleason K, Angel J, Rippey B, Tinker R, Palecki M, Stooksbury D, Miskus D and Stephens S. The drought monitor[J]. Bulletin of the American Meteorological Society, 2002, 83 (8) : 1181 –1190. DOI: 10.1175/1520-0477-83.8.1181 |
| [20] | Vicente-Serrano S M, Beguería S and López-Moreno J I. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index[J]. Journal of Climate, 2010, 23 (7) : 1696 –1718. DOI: 10.1175/2009JCLI2909.1 |
| [21] | 王丽涛, 王世新, 周艺, 王福涛, 刘文亮. 旱情遥感监测研究进展与应用案例分析[J]. 遥感学报, 2011, 15 (6) : 1322 –1330. Wang L T, Wang S X, Zhou Y, Wang F T and Liu W L. Advances and application analysis of drought monitoring using remote sensing[J]. Journal of Remote Sensing, 2011, 15 (6) : 1322 –1330. |
| [22] | Wilhelmi O V and Wilhite D A. Assessing vulnerability to agricultural drought: a Nebraska case study[J]. Natural Hazards, 2002, 25 (1) : 37 –58. DOI: 10.1023/A:1013388814894 |
| [23] | Wilhite D A. 2005. Drought and Water Crises: Science, Technology, and Management Issues. Boca Raton: CRC Press: 327–329 |
| [24] | 武晓波, 阎守邕, 田国良, 王世新, 肖春生. 在GIS支持下用NOAA/AVHRR数据进行旱情监测[J]. 遥感学报, 1998, 4 (2) : 280 –284. Wu X B, Yan S Y, Tian G L, Wang S X and Xiao C S. Using NOAA/AVHRR data to monitor drought with GIS technique[J]. Journal of Remote Sensing, 1998, 4 (2) : 280 –284. |
| [25] | Xu B and Lin B Q. Factors affecting CO2 emissions in China’s agriculture sector: evidence from geographically weighted regression model [J]. Energy Policy, 2017, 104 : 404 –414. DOI: 10.1016/j.enpol.2017.02.011 |
| [26] | Zargar A, Sadiq R, Naser B and Khan F I. A review of drought indices[J]. Environmental Reviews, 2011, 19 (NA) : 333 –349. DOI: 10.1139/a11-013 |
| [27] | Zhang A Z and Jia G S. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data[J]. Remote Sensing of Environment, 2013, 134 : 12 –23. DOI: 10.1016/j.rse.2013.02.023 |
| [28] | Zhang L F, Jiao W Z, Zhang H M, Huang C P and Tong Q X. Studying drought phenomena in the Continental United States in 2011 and 2012 using various drought indices[J]. Remote Sensing of Environment, 2017, 190 : 96 –106. DOI: 10.1016/j.rse.2016.12.010 |
| [29] | Zhou L, Zhang J, Wu J J, Zhao L, Liu M, Lü A F and Wu Z T. Comparison of remotely sensed and meteorological data-derived drought indices in mid-eastern China[J]. International Journal of Remote Sensing, 2012, 33 (6) : 1755 –1779. DOI: 10.1080/01431161.2011.600349 |

