| G0分布下基于白化滤波的极化SAR图像CFAR检测 |
收稿日期: 2018-07-12
2. No.92118 Unit of PLA, Zhoushan 316000, China
由于具有全天时、全天候以及不同目标特性的鉴别能力,极化合成孔径雷达已经成为重要的遥感信息获取源(刘涛 等,2013)。极化SAR图像相比单通道SAR图像而言包含有更丰富的信息,基于极化SAR图像数据,国内外学者在目标检测方面进行了卓有成效的研究,比较著名的检测器有Novak和Burl (1990)提出的极化白化滤波(PWF)检测器,Boerner等(1988)提出的极化匹配滤波(PMF)检测器等。PWF检测器后由Lopes、Sery和刘国庆等人(Lopes和Sery,1997;刘国庆 等,1998)将其推广至多视数据,提出了多视极化白化滤波(MPWF)检测器。在最早由Goldstein(1973)提出的适用于对数正态分布的双参数恒虚警(2P-CFAR)检测器基础上,Novak等(1991)提出了基于MPWF检测量的2P-CFAR检测,2P-CFAR检测器可以较好地抑制相干斑,并且具有自适应求解检测阈值的优势,因此应用较为广泛。
检测量分布模型的准确建立及检测阈值表达式的获得可以有效提高CFAR检测性能。多变量乘积模型是目前常用的杂波统计模型,需要考虑的两个因素分别是相干斑噪声和纹理特性(皮亦鸣 等,2002),在相干斑噪声矢量服从复高斯分布假设下,极化SAR杂波协方差矩阵的分布类型取决于纹理变量。当纹理变量为常数、Gamma分布时MPWF检测量分别服从Gamma、K分布。Gamma、K分布常被用来对海杂波进行建模,二者作为描述海杂波的经典模型,可在很宽的条件范围内与杂波幅度分布很好地匹配,但是在高分辨强海杂波背景下,上述分布不能较好地描述杂波。G0分布是由Frery等(1997)提出的逆Gamma纹理下的一种乘积模型,能很好地对高分辨海杂波区域进行建模,针对G0分布下的杂波建模及CFAR检测已经做了相关研究(贺志国 等,2009;Stinco 等,2011;Wang 等,2011;鲁统臻 等,2011;王娜 等,2011;Weinberg,2013;Zhao 等,2013),但是虚警概率闭合解析表达式的难以获得这个关键问题尚未得到解决。针对此问题,本文提出了一种G0分布下基于MPWF的CFAR检测方法,推导出了G0分布MPWF检测量的概率密度函数,并对该密度函数积分后得到了虚警概率关于检测阈值的闭合解析表达式,通过数值计算方法即可得到检测阈值。本方法得出了虚警概率的解析表达形式,这与直接通过积分计算CFAR检测阈值相比大大缩减了运算时间,提高了算法的实时性。日本玉野附近地区的AIRSAR实测数据实验结果表明G0分布对高分辨不均匀海区的良好拟合性能,本文所提方法具有更优的虚警抑制效果,同时非G0分布海区的CFAR检测结果表明本文方法具有较强的鲁棒性。
2、MPWF检测量统计建模在非均匀场景下,目标和杂波反射情况可以被表征为两个部分:一个是复高斯分布的多径干扰造成的相干斑噪声;另一个是反映场景起伏度的纹理变量(皮亦鸣 等,2002)。在单视情况下,我们假设相干斑噪声和纹理变量是相互独立的,则对于极化散射矢量s,利用乘积模型(Jakeman和Pusey,1976;Jao,1984;Novak 等,1989)可以表示为
| ${s} = \sqrt \tau {y}$ | (1) |
在这个式子中,假设纹理变量等同地影响了各个极化通道。式中,s为极化散射矢量,τ为服从逆Gamma分布的纹理标量,y为服从复高斯分布的相干斑矢量。
对极化散射矢量进行多视处理后的协方差矩阵为(Liu 等,1998)
| ${C} = \frac{1}{L}\sum\limits_{i = 1}^L {{{s}_i}{s}_i^{\rm{H}}} = \frac{1}{L}\sum\limits_{i = 1}^L {{\tau _i}{{y}_i}{y}_i^{\rm{H}}} $ | (2) |
式中,C为多视处理后的协方差矩阵,L为视数,i表示第i个像素点,s为极化散射矢量,上标H表示共轭转置,τ为纹理变量,y为复高斯分布相干斑矢量。假设多视处理的像素点具有相同的纹理变量,即τi独立于i,此时上式可简化为(Liu 等,1998)
| ${C} = \tau {Y}$ | (3) |
式中,
| ${Y} = \frac{1}{L}\sum\limits_{i = 1}^L {{y_i}y_i^{\rm{H}}} $ | (4) |
假设y相互独立,则Y服从归一化复Wishart分布。
极化散射矢量s经MPWF处理后输出为(Liu 等, 1998)
| ${\textit{z}}= \frac{1}{L}\sum\limits_{i = 1}^L {{s}_i^{\rm{H}}{{\Sigma }^{ - 1}}{{s}_i}} = Tr\left({{{\Sigma }^{ - 1}}{C}} \right)$ | (5) |
式中,L为视数,s为极化散射矢量,Σ为散射矢量s统计平均后的协方差矩阵,Tr(·)表示矩阵的迹,C为极化散射矢量s的多视协方差矩阵,Σ可以表示为(Khan和Guida,2014)
| ${\Sigma } = E\left({C} \right) = E\left(\tau \right)E\left({Y} \right) = E\left(\tau \right){P}$ | (6) |
式中,E(·)为统计均值,Y为复高斯相干斑矢量y的多视协方差矩阵,P表示相干斑矢量y统计平均后的协方差矩阵,将式(3)与式(6)代入式(5),得(Khan和Guida,2014)
| ${\textit{z}} = \frac{\tau }{{E\left(\tau \right)}}Tr\left({{{P}^{ - 1}}{Y}} \right) = {\tau _{\rm{1}}}x$ | (7) |
式中,τ1为归一化纹理标量,x= Tr(P–1Y),为相干斑矢量经MPWF后输出。可以看出,极化散射矢量s的MPWF输出可以分解为上述两部分的乘积。已知Y服从归一化复Wishart分布,则x服从尺度参数为d,形状参数为Ld的Gamma分布(Khan和Guida,2014)
| $\gamma \left({d, Ld} \right) = \frac{{{L^{Ld}}{x^{Ld - 1}}}}{{\Gamma \left({Ld} \right)}}{{\rm{e}}^{ - Lx}}$ | (8) |
式中,Γ(·)为Gamma函数。
我们由逆Gamma分布的PDF来推导归一化之后的PDF,逆Gamma分布PDF为(Witkovský,2001)
| $f\left({y;\alpha, \beta } \right) = \frac{{{\beta ^\alpha }}}{{\Gamma \left(\alpha \right)}}{y^{ - \alpha - 1}}\exp \left({ - \frac{\beta }{y}} \right){\rm{ }}\left({\alpha, {\rm{ }}\beta, {\rm{ }}y > 0} \right)$ | (9) |
式中,α为反映区域均匀度的形状参数,β为与区域平均能量有关的尺度参数。归一化处理即是令y在定义域内期望为1,即
| $\int_0^{ + \infty } {yf\left({y;\alpha, \beta } \right){\rm{d}}y} = 1$ | (10) |
由上式可得β=α−1,将该关系式代入式(9),可得到归一化逆Gamma分布纹理标量τ1的PDF为
| $f\left({{\tau _1};{\textit{λ}} } \right) = \frac{{{{\left({{\textit{λ}} - 1} \right)}^{\textit{λ}} }}}{{\Gamma \left({\textit{λ}} \right)}}{\tau _1}^{ - {\textit{λ}} - 1}\exp \left({\frac{{1 - {\textit{λ}}}}{{{\tau _1}}}} \right){\rm{ }}\left({{\textit{λ}}, {\rm{ }}{\tau _1} > 0} \right)$ | (11) |
式中,λ为形状参数。式(7)中MPWF检测量z为两个不同分布的独立变量的乘积,则检测量z的PDF为
| $f\left(z \right) = \int_0^{ + \infty } {\frac{1}{{{\tau _1}}}f\left({x;d, Ld} \right)f\left({{\tau _1};{\textit{λ}} } \right){\rm{d}}{\tau _1}} $ | (12) |
将x=z/τ1代入上式得
| $f\left({\textit{z}} \right) = \frac{{{L^{Ld}}{z^{Ld - 1}}{{\left({{\textit{λ}} - 1} \right)}^{\textit{λ}} }}}{{\Gamma \left({Ld} \right)\Gamma \left({\textit{λ}} \right)}}\int_0^{ + \infty } {\frac{1}{{{\tau _1}^{Ld + {\textit{λ}} + 1}}}\exp \left({\frac{{1 - {\textit{λ}} - Lz}}{{{\tau _1}}}} \right){\rm{d}}{\tau _1}} $ | (13) |
式中,L为视数,d为极化散射矢量s的维数,z为MPWF检测量,λ为逆Gamma分布的形状参数,τ1为归一化纹理标量。根据积分公式(Bateman,1954)
| $\int_0^{ + \infty } {{x^{s - 1}}\exp \left({ - \alpha {x^{ - h}}} \right){\rm{d}}x = } {h^{ - 1}}{\alpha ^{{s/h}}}\Gamma \left({{{ - s}/h}} \right)$ | (14) |
式(13)可以化为
| $f\left({\textit{z}} \right) = \frac{{{L^{Ld}}{{\textit{z}}^{Ld - 1}}{{\left({{\textit{λ}} - 1} \right)}^{\textit{λ}} }\Gamma \left({Ld + {\textit{λ}} } \right)}}{{\Gamma \left({Ld} \right)\Gamma \left({\textit{λ}} \right){{\left({{\textit{λ}} + L{\textit{z}} - 1} \right)}^{Ld +{\textit{λ}}}}}}$ | (15) |
式(15)则为G0分布MPWF检测量z的PDF,L为视数,在CFAR检测中为了降低数据相关性对理论模型的影响,L取为等效视数,d为极化散射矢量s的维数,λ为纹理标量的形状参数,本质上反映了被测区域的均匀度,当λ趋近于无穷大时,G0分布退化为Gamma分布。
3、CFAR检测阈值求解和算法流程检测区域MPWF检测量z的PDF已知为式(15),给定检测阈值T,对式(15)积分可得到MPWF检测量z的累积分布函数(CDF)为
| ${F_{\textit{z}}}\left(T \right) = \int_0^T {\frac{{{L^{Ld}}{{\left({{\textit{λ}} - 1} \right)}^{\textit{λ}} }\Gamma \left({Ld + {\textit{λ}} } \right)}}{{\Gamma \left({Ld} \right)\Gamma \left({\textit{λ}} \right)}}\frac{{{{\textit{z}}^{Ld - 1}}}}{{{{\left({{\textit{λ}} + L{\textit{z}} - 1} \right)}^{Ld +{\textit{λ}}}}}}{\rm{d}}{\textit{z}}} $ | (16) |
根据积分公式(Gradshteyn和Ryzhik,2007)
| $\int_0^u {\frac{{{x^{\mu - 1}}{\rm{d}}x}}{{{{\left({1 + \beta x} \right)}^v}}} = \frac{{{u^\mu }}}{\mu }{}_2{F_1}\left({v, \mu ;1 + \mu ; - \beta u} \right)} $ | (17) |
式(16)可化为
| $\begin{split} {F_{\textit{z}}}\left(T \right) = & \frac{{{L^{Ld}}\Gamma \left({Ld + {\textit{λ}}} \right)}}{{\Gamma \left({Ld} \right)\Gamma \left({\textit{λ}} \right){{\left({{\textit{λ}} - 1} \right)}^{Ld}}}}\int_0^T {\frac{{{{\textit{z}}^{Ld - 1}}}}{{{{\left({1 + \frac{L}{{{\textit{λ}} - 1}}{\textit{z}}} \right)}^{Ld + {\textit{λ}} }}}}{\rm{d}}z}= \\ & \frac{{\Gamma \left({Ld + {\textit{λ}} } \right)}}{{\Gamma \left({Ld} \right)\Gamma \left({\textit{λ}}\right)Ld}}{\left({\frac{{LT}}{{{\textit{λ}} - 1}}} \right)^{Ld}}{}\\ & {_2}{F_1}\left({Ld + {\textit{λ}}, Ld;1 + Ld; - \frac{{LT}}{{{\textit{λ}} - 1}}} \right) \end{split} $ | (18) |
上式即为MPWF检测量z的累积分布函数,可见其虚警概率为闭合解析表达形式
| $\begin{split} {P_{fa}} = & 1 - {F_{\textit{z}}}\left(T \right) = \\ & 1 - \frac{{\Gamma \left({Ld + {\textit{λ}} } \right)}}{{\Gamma \left({Ld} \right)\Gamma \left({\textit{λ}} \right)Ld}}{\left({\frac{{LT}}{{{\textit{λ}} - 1}}} \right)^{Ld}}{} \\ & {_2}{F_1}\left({Ld + {\textit{λ}}, Ld;1 + Ld; - \frac{{LT}}{{{\textit{λ}} - 1}}} \right) \end{split} $ | (19) |
式中,2F1(·)为高斯超几何函数,通过设置合理的CFAR检测恒虚警概率Pfa,可通过数值求解的方法解出具体的检测阈值。
本文中采用基于MPWF混合矩的纹理参数估计方法(崔浩贵,2014)估计纹理变量的形状参数,采用基于子矩阵对数累积量的估计方法(刘涛 等,2012;Liu 等,2016)对等效视数进行估计。基于MPWF检测量的CFAR检测方法流程如图1所示,具体实现过程为
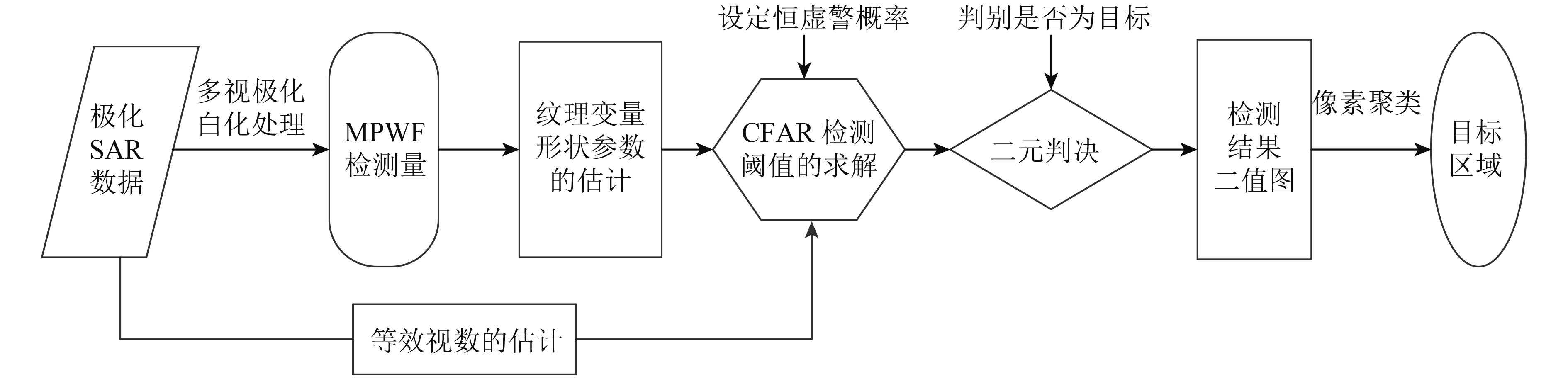
|
| 图 1 CFAR检测方法流程图 Figure 1 The process of CFAR detection method |
步骤 1 对极化SAR协方差矩阵数据进行MPWF处理,得到检测统计量;
步骤 2 利用协方差矩阵数据估计等效视数,同时由步骤1得到的MPWF检测统计量估计逆Gamma分布纹理变量的形状参数;
步骤 3 将估计得到的形状参数、等效视数和设置的恒虚警概率代入式(19)利用数值求解方法求解出检测阈值,数值求解方法借鉴了二分法(贺志国 等,2009)求解阈值的思想;
步骤 4 遍历图像所有像素进行二元判决,检测值高于阈值为目标,低于阈值为杂波,得到整幅图像的二值结果图;
步骤 5 对二值结果图进行像素聚类处理,聚类处理可以使目标点更加突出,同时可以滤除部分孤立的虚警点。
4、实验结果及分析基于本文所提CFAR检测方法,首先采用仿真数据比较了本文方法和贺治国方法(2009)中直接积分法求解阈值的CPU运行时间,然后采用日本玉野附近的AIRSAR实测数据进行了数据拟合分析,最后对实测数据区域进行了CFAR检测,并对检测结果进行了分析。
(4.1) 获取阈值的CPU运行时间分析本节比较了本方法和贺志国等(2009)方法中直接积分获取阈值的CPU运行时间,得到了两种方法在不同等效视数和G0分布形状参数下求解检测阈值的CPU运算时间曲线,验证了本文解析方法在检测阈值求解上可以极大缩减运算时间。
通过蒙特卡洛仿真产生仿真数据,两种典型场景和目标的极化参数(Novak 等,1989, 1991)如表1所示。在杂波σHH一定的情况下,改变目标σHH的值则TCR(单位为dB,下同)也随之改变,因此在实验过程中我们通过改变目标σHH的大小来实现TCR的变化。
|
|
表 1 几种典型杂波场景的极化参数表 Table 1 The polarimetric parameters of several typical clutter backgrounds |
根据表1中树林杂波极化协方差矩阵参数产生杂波仿真数据,数据量为10000,恒虚警概率设置为10–3,设置等效视数变化范围为4—16,G0分布形状参数λ分别设置为2、5、20,分别利用本文解析方法和贺志国等(2009)方法中直接积分法计算检测阈值,实际虚警概率如图2所示,上述两种方法的CPU运行时间对比如图3所示。从图2可以看出,上述两种方法获得的实际虚警概率均在10–3左右,与理论值吻合较好。图3(a)中本文解析方法的CPU运行时间均小于1 s,而贺志国等(2009)方法中直接积分法的运行时间均大于本文解析方法,从图3(b)的运行时间缩短倍数来看,最低的在3倍左右,最高的接近32倍。综合来看,使用本文解析方法求解阈值可以节省大量的时间,极大地提高了算法的实时性。
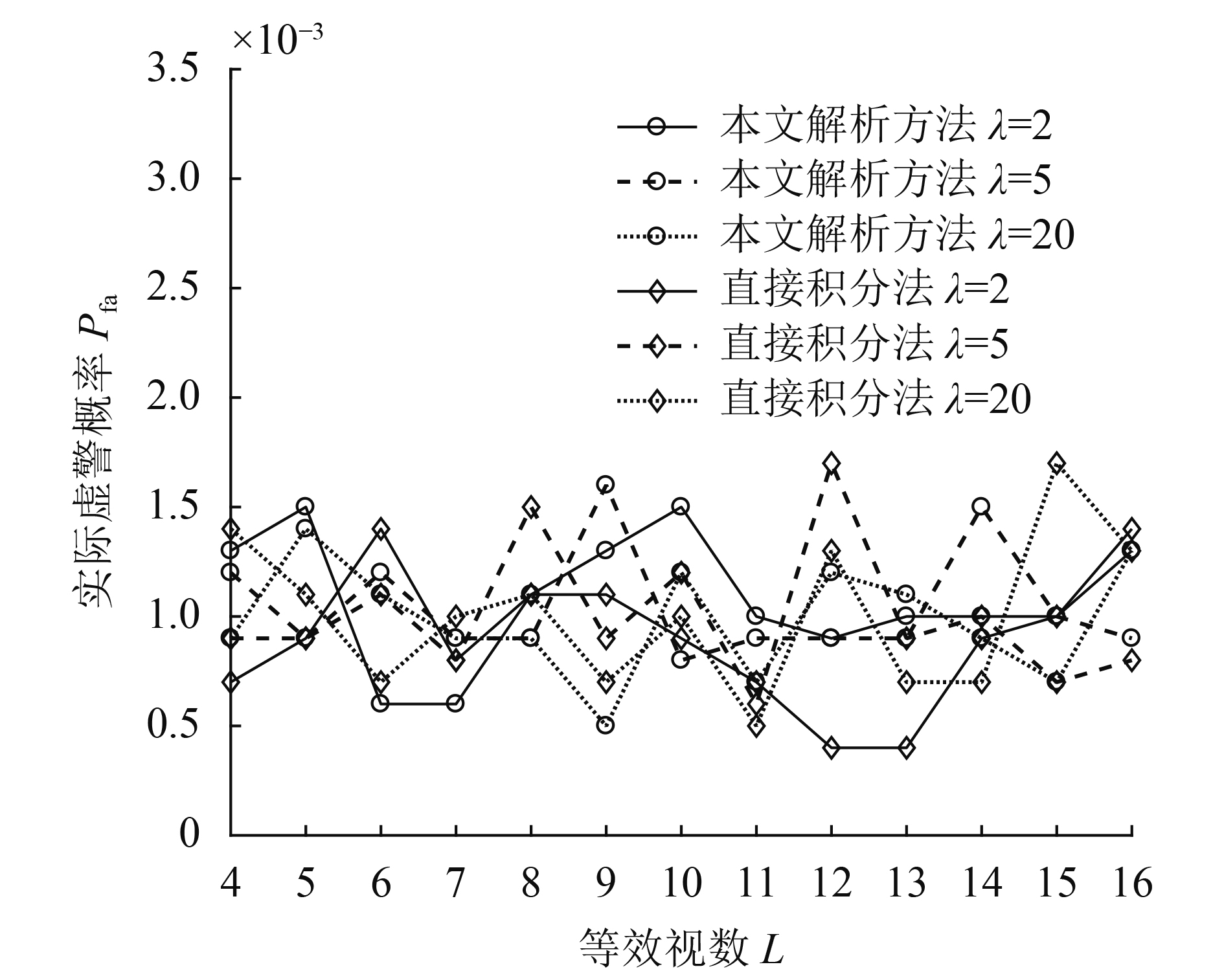
|
| 图 2 两种方法实际虚警概率 Figure 2 The real false alarm probabilities of the two methods |
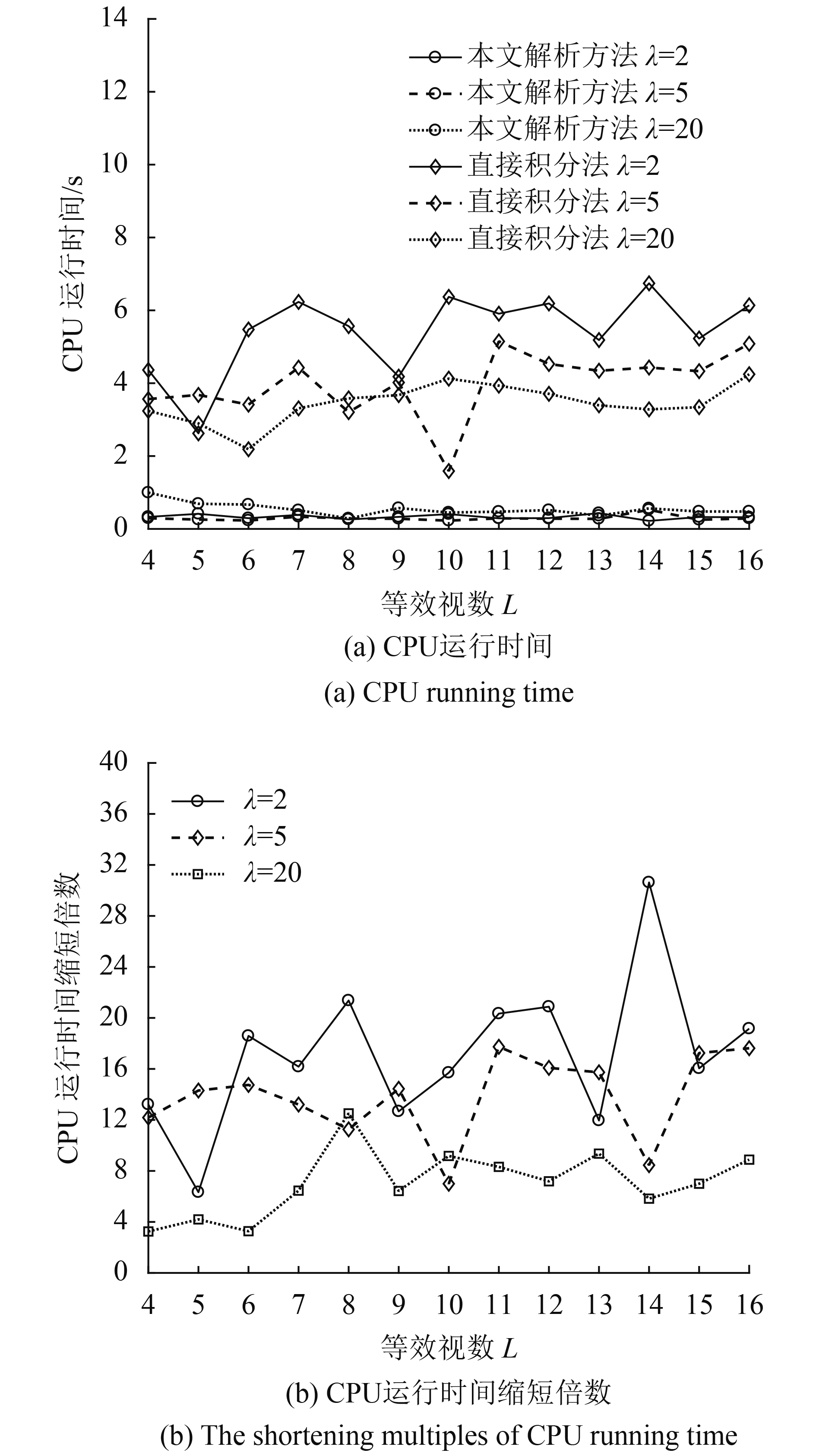
|
| 图 3 不同方法的CPU运行时间对比 Figure 3 The comparison of CPU running time with different methods |
本文方法得到了虚警概率关于检测阈值的解析表达形式,在计算阈值过程中可以直接通过解析表达式求解,因此相比于直接积分方法,利用表达式获取阈值可以节省大量时间,增强实时性。
(4.2) MPWF检测量拟合性能分析通过AIRSAR实测数据比较了本方法、种劲松和朱敏慧(2003)方法和张嘉峰等(2018)方法的数据拟合性能,种劲松和朱敏慧(2003)方法和张嘉峰等(2018)方法分别是基于K分布和Wishart分布下的CFAR检测,与本文G0分布下的CFAR检测方法进行数据拟合分析具有针对性。
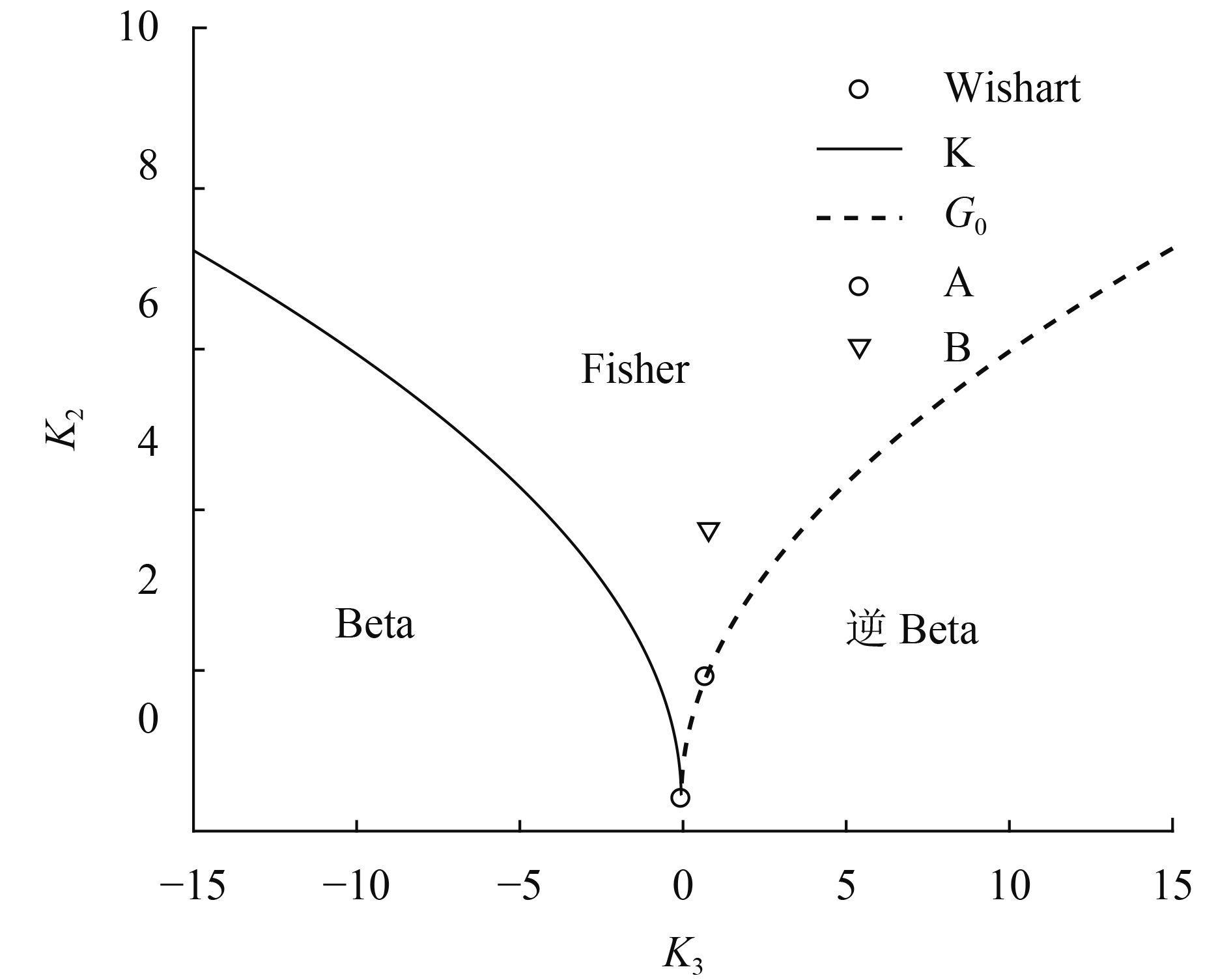
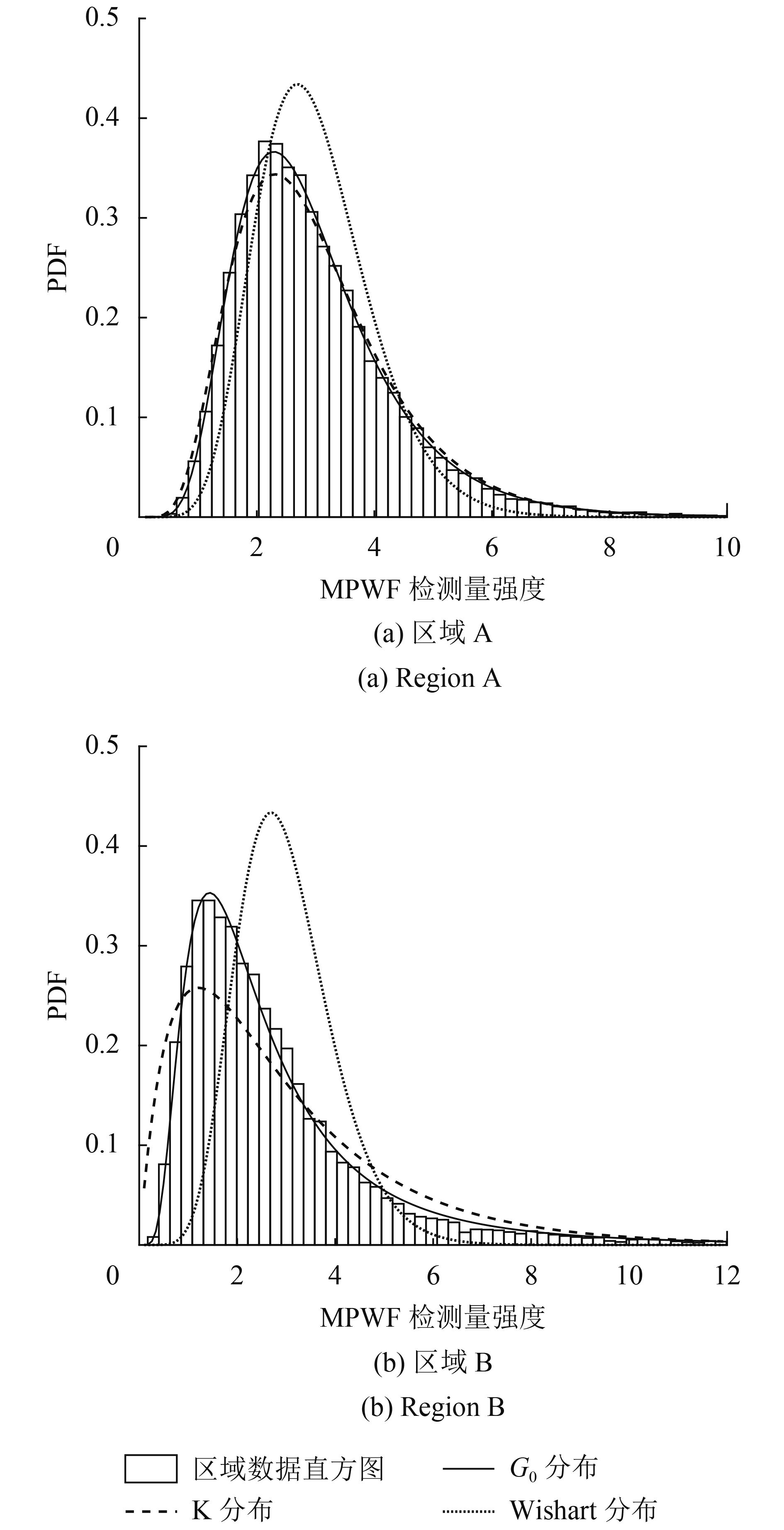
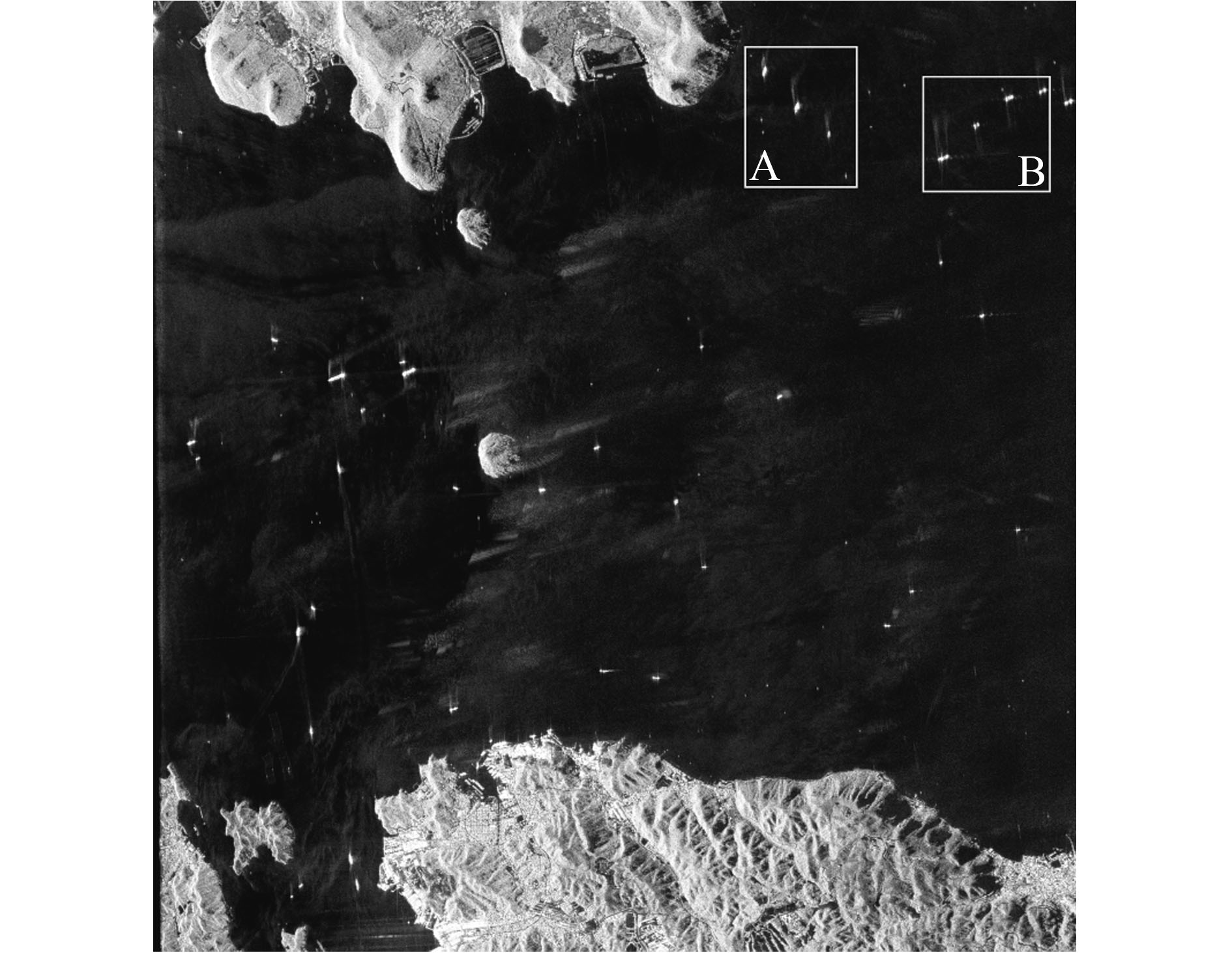
采用美航局对日本玉野Kojimawan附近区域得到的AIRSAR数据(https://vertex.daac.asf.alaska.edu)[2018-07-12]进行数据拟合分析,选择波段为L波段,选取区域如图4中A、B所示,图5为区域A、B基于对数累积量的模型辨识结果。由图5可以看出,区域A散点位于G0分布区域,可认为区域A纹理变量服从G0分布,区域B散点靠近G0分布,可验证G0分布对不完全服从G0分布区域的拟合效果。对A、B分别进行参数估计,等效视数L估计结果分别为3.25和3.24,G0分布参数λ分别为12.40和3.29,区域A、B的协方差矩阵通过求协方差矩阵均值得到,经多视白化处理后得到MPWF检测量。区域A、B的检测量直方图和不同分布类型下的PDF拟合曲线如图6所示。
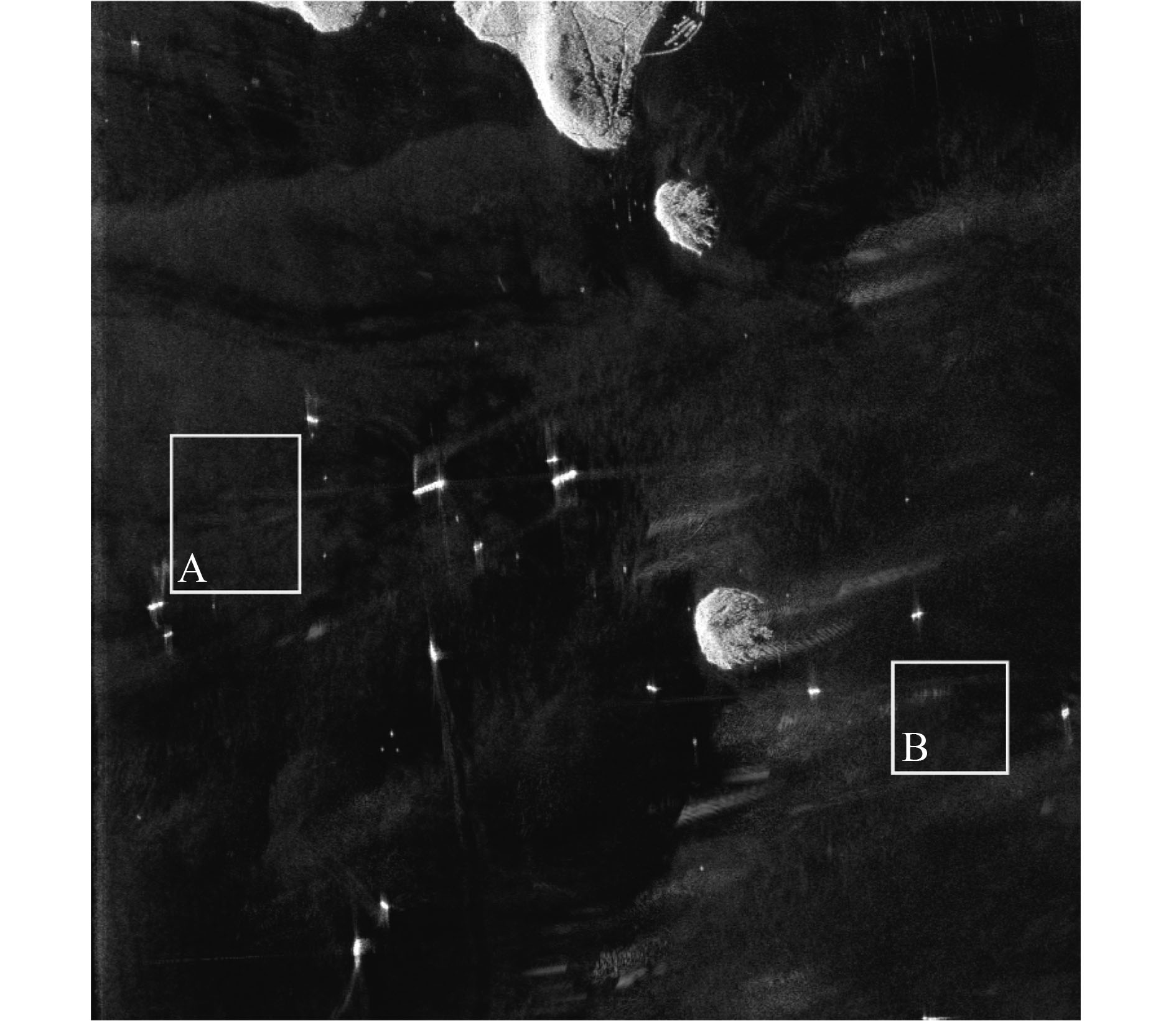
|
| 图 4 数据拟合区域 Figure 4 Data fitting regions |
|
| 图 5 区域AB模型辨识结果 Figure 5 The model recognition results of A and B |
|
| 图 6 各检测方法PDF拟合曲线 Figure 6 The PDF fitting curves of methods |
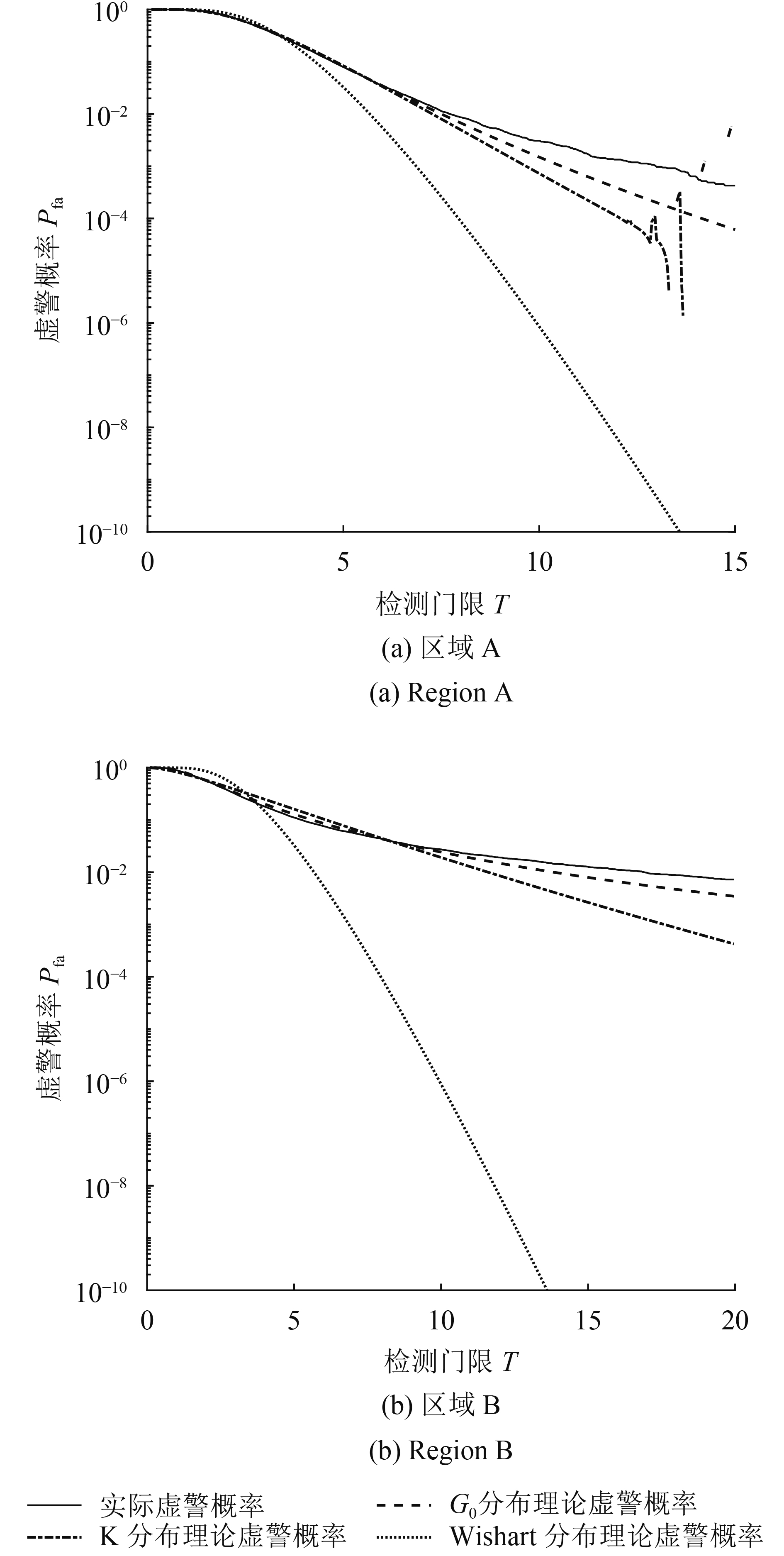
目视来看,对于区域A和B来说,图6中MPWF检测量直方图与G0分布PDF曲线拟合效果都是最好的。进一步,采用理论虚警概率与实际虚警概率的拟合结果来评估各分布对于区域A、B检测量的拟合程度,将估计得到的等效视数和G0分布参数代入式(19),则可求出特定门限下的理论虚警概率值,实际虚警概率为高于该门限检测量个数与检测量总数之比。不同分布类型下理论与实际虚警概率拟合结果如图7所示。可以看出,当虚警概率较低时,本文方法获取的理论虚警概率与实际虚警概率最为接近,而K分布、Wishart分布则偏离较多,这是由于区域A、B的纹理变量最接近G0分布造成的。综上分析,以及本文中MPWF检测量z的PDF为基于G0分布下,在纹理变量近似服从G0分布的区域,采用本文检测方法可以更好地拟合MPWF检测量,也可以更好地保证CFAR检测的恒虚警前提。
|
| 图 7 各检测方法虚警概率拟合曲线 Figure 7 The false alarm probability fitting curves of methods |
本部分对日本玉野Kojimawan附近区域的AIRSAR实测数据进行CFAR检测结果分析,所采用检测方法为本方法、种劲松和朱敏慧(2003)方法、张嘉峰等(2018)方法、王娜等(2011)方法和2P-CFAR算法,检测区域分别为G0分布区域和非G0分布区域,以验证本方法在G0分布和非G0分布杂波特性下的检测性能。
4.3.1. G0分布区域检测结果分析CFAR检测区域A、B如图8所示,滤除舰船目标后基于对数累计量进行模型辨识,结果如图9所示。从图7的辨识结果来看,两个区域的k2/k3散点图均落于G0分布曲线上,因此可以判断A、B区域大致服从G0分布。
|
| 图 8 CFAR检测区域 Figure 8 The CFAR detection regions |
|
| 图 9 区域AB模型辨识结果 Figure 9 The model recognition results of A and B |
对区域A、B的所有杂波和目标的协方差矩阵取平均作为杂波和目标协方差矩阵,分别经过MPWF和MPMF处理得到检测量。对区域A、B的等效视数和纹理变量形状参数λ进行估计(Liu 等,2016),区域A、B的等效视数估计结果分别为3.48和3.73,λ估计结果均为6.30。区域A的CFAR检测结果如图10所示,其中Pfa表示虚警概率。

|
| 图 10 区域A检测结果 Figure 10 The detection results of region A |
由图10可以看出,经MPWF处理后,图10(b)中目标被增强为很亮的像素点,但在目标边缘和其他部分区域,杂波也被增强,设置恒虚警概率为10–5,分别得到本文方法、种劲松和朱敏慧等(2003)方法、张嘉峰等(2018)方法、王娜等(2011)方法和2P-CFAR算法的检测结果图。图10(c)中7个目标被全部检测出来,杂波也得到了很好地抑制,仅在目标边缘存在少量的虚警点。图10(d)中目标全部被检测出来且基本无虚警,检测效果更佳,图10(e)、图10(f)、图10(g)中虽然目标也全部被检测出来,但虚警点数目较多,检测效果较差。降低恒虚警概率至10–7,图10(h)中虚警点得到了有效抑制,同时保留下了所有目标,图10(i)相比图10(d)来看,即将出现漏警,因此对于文献[31]中方法来说,取恒虚警概率为10–5为宜。图10(k)、图10(l)中通过降低虚警率,虚警得到了较好的抑制,且图10(k)比图10(l)抑制效果更好。图10(j)相比图10(e)来看,虚警抑制的改善效果不明显,相比其他方法检测效果较差。
区域B的CFAR检测结果如图11所示,其中Pfa表示虚警概率。

|
| 图 11 区域B检测结果 Figure 11 The detection results of region B |
当恒虚警概率为10–4时,本文方法和其他4种算法的检测结果分别为图图11(c)和图图11(d)、图11(e)、图11(f)、图11(g)。可以看出,所有方法均可以检测出全部5个目标,且图11(c)、图11(d)、图11(g)中虚警得到了很好地抑制,而图11(e)、图11(f)中虚警较严重,影响了对目标的判断。降低恒虚警概率为10–6,图11(i)中出现了漏警,仅能检测出4个目标,且部分目标由于恒虚警概率过低出现了分裂,因此对于文献[31]检测方法,恒虚警概率不宜取得过低,图11(j)、图11(k)中虚警点数量大大减少,同时未出现漏警情况,检测效果改善明显。
表2给出了区域A、B检测结果的主要参数,其中,Ngt为目标的总个数,Ntd为实际检测到的目标个数,Nfa为虚警区域个数,Nom为漏警数,Pd为检测概率,FoM为品质因数(Wei 等,2014),品质因数定义如下
|
|
表 2 舰船检测结果各项参数 Table 2 The parameters of ships detection results |
| ${\rm{FoM}} = \frac{{{N_{\rm{td}}}}}{{\left({{N_{\rm{fa}}} + {N_{\rm{gt}}}} \right)}}$ | (20) |
从表2中可以看出,对于区域A,5种方法均能检测出全部目标,检测性能主要体现在对虚警的抑制效果上。恒虚警概率为10–5时,本文方法和种劲松和朱敏慧(2003)方法的虚警点数量分别为1个和0个,虚警抑制效果较好,而张嘉峰等(2018)方法、王娜等(2011)方法和2P-CFAR算法虚警数较多,与图10结合来看,也可看出虚警区域对真实目标检测的影响。当虚警概率降至10–7时,所有检测方法的虚警区域数量均有所下降,且未出现漏警。同时从品质因数来看,本文方法虽略低于种劲松和朱敏慧(2003)方法,但高于其他检测方法。对于区域B,当恒虚警概率为10–4时,本文方法和种劲松和朱敏慧(2003)方法均无虚警,虚警抑制效果优于其他方法。降低恒虚警概率至10–6,种劲松和朱敏慧(2003)方法出现漏警,从图11中也可看出部分目标已分裂为两个目标,这影响了对单个目标的判断,张嘉峰等(2018)方法、王娜等(2011)方法和2P-CFAR算法虚警均得到抑制,但张嘉峰等(2018)方法中虚警数量仍存在。从品质因数来看,本文方法均高于或等于其他检测方法,具有更优的检测性能。综合来看,在绝大多数情况下,本文方法的检测效能优于其他检测方法,品质因数平均高出其他检测方法15.78%,种劲松和朱敏慧(2003)方法的主要问题在于易出现漏警,而其他方法对虚警的抑制效果均较差。
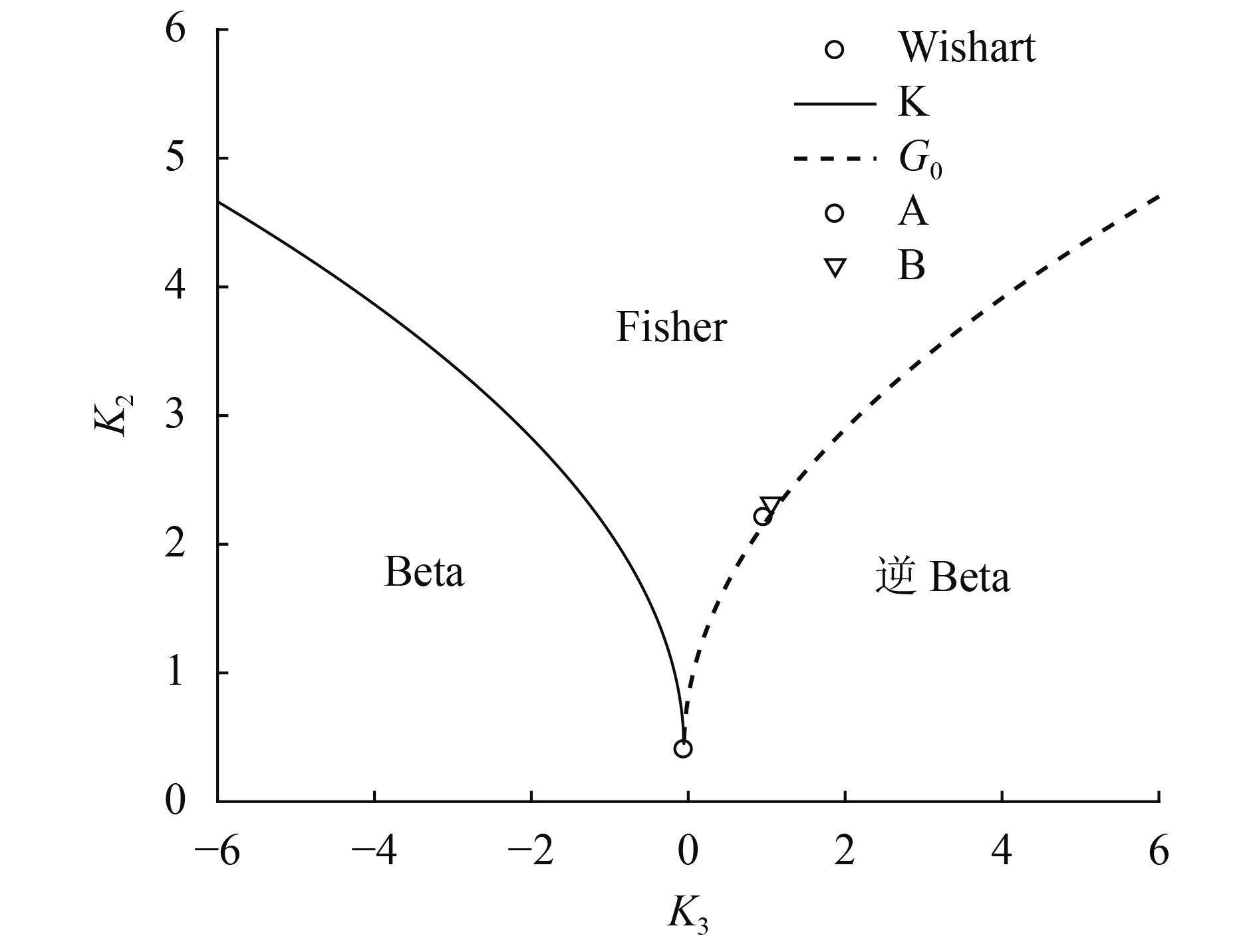
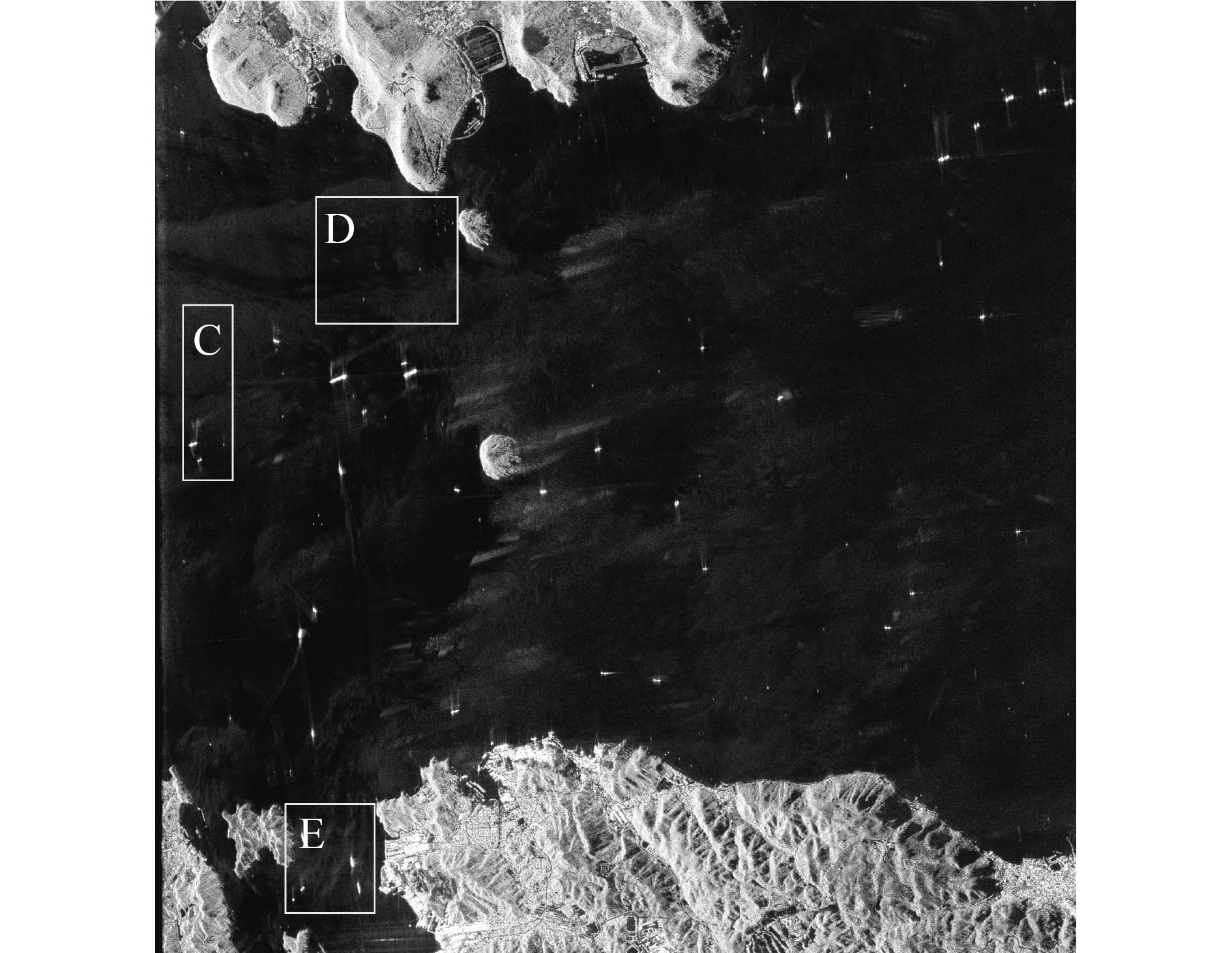
4.3.2. 非G0分布区域检测结果分析本文方法在G0分布区域具有良好的检测性能,为验证鲁棒性,选取图12中非G0分布区域进行CFAR检测。C、D、E分别为K分布、Fisher分布、逆Beta分布,这3块检测区域的模型辨识结果(不含目标)如图13所示。区域C、D、E散点分别位于K、Fisher、逆Beta分布区域,因此认为杂波分别服从K、Fisher、逆Beta分布。
|
| 图 12 CFAR检测区域 Figure 12 The CFAR detection regions |
|
| 图 13 区域CDE模型辨识结果 Figure 13 The model recognition results of C, D and E |
分别对区域C、D、E内所有杂波和目标的协方差矩阵取平均作为杂波和目标协方差矩阵,分别经过MPWF和MPMF处理得到检测量。对区域A、B的等效视数和纹理变量形状参数λ进行估计(Liu 等,2016),区域C、D、E的等效视数估计结果分别为2.88、3.57和3.38,λ估计结果分别为2.39、3.37和1.59。区域C、D、E的CFAR检测结果如图14所示,其中Pfa表示虚警概率。

|
| 图 14 区域C、D、E检测结果 Figure 14 The detection results of region C, D and E |
由图14可看出,区域C所有方法中目标均可被检测出,但只有本文方法和种劲松和朱敏慧(2003)方法检测结果中无虚警,张嘉峰等(2018)方法和2P-CFAR算法中出现了大量虚警,王娜等(2011)方法中出现了少量虚警,影响了目标判断。对于区域D来说,本文方法和王娜等(2011)方法检测出了9个目标中的8个,但未出现虚警,种劲松和朱敏慧(2003)方法、张嘉峰等(2018)方法和2P-CFAR算法未出现漏警,但均出现了不同程度的虚警,张嘉峰等(2018)方法结果中虚警尤其较多,极易被误判为小目标。区域E中,所有方法均可检测出全部4个目标,从虚警抑制效果来看,本文方法和王娜等(2011)方法的抑制效果最好,仅出现了少量虚警,而明显不是目标的陆地区域杂波在种劲松和朱敏慧(2003)方法、张嘉峰等(2018)方法和2P-CFAR算法检测结果中并未被有效滤除。综上分析,本文方法在K分布、Fisher分布和逆Beta分布区域均具有最优的虚警抑制效果和较高的检测概率,鲁棒性较强,但也存在小目标被漏检的风险。
4.3.3. 恒虚警保持性能分析本文方法基于杂波统计模型,由4.2节可得当杂波统计模型越“接近”所提G0分布时,本文CFAR检测的恒虚警保持效果越好,CFAR检测结果越良好,这体现在本文方法具有较强的鲁棒性。为更精确量化评估本文方法对于某一杂波模型的虚警保持性能,定义虚警损失率(CFAR Loss,CL)如下
| ${C_L} = \left| {20\log \left({{{\bar P}_{\rm{fa}}}/{P_{\rm{fa}}}} \right)} \right|$ | (21) |
式中,CL表征了某区域杂波给定检测阈值下的实际虚警概率
为分析本方法的鲁棒性,通过表1中树林极化协方差矩阵参数分别生成A、B、C、D、E、F 6块极化SAR协方差矩阵数据,6块数据分别服从Fisher、K、G0、Wishart、Beta、逆Beta分布,采用上述CL定义分析鲁棒性。各仿真数据纹理变量参数如表3所示。表3中α、λ分别为K分布、G0分布形状参数,u、v分别为Fisher、Beta、逆Beta分布的自由度参数,为各数据假定为G0分布的形状参数估计结果。
|
|
表 3 各仿真数据纹理变量参数 Table 3 Textures of simulation data |
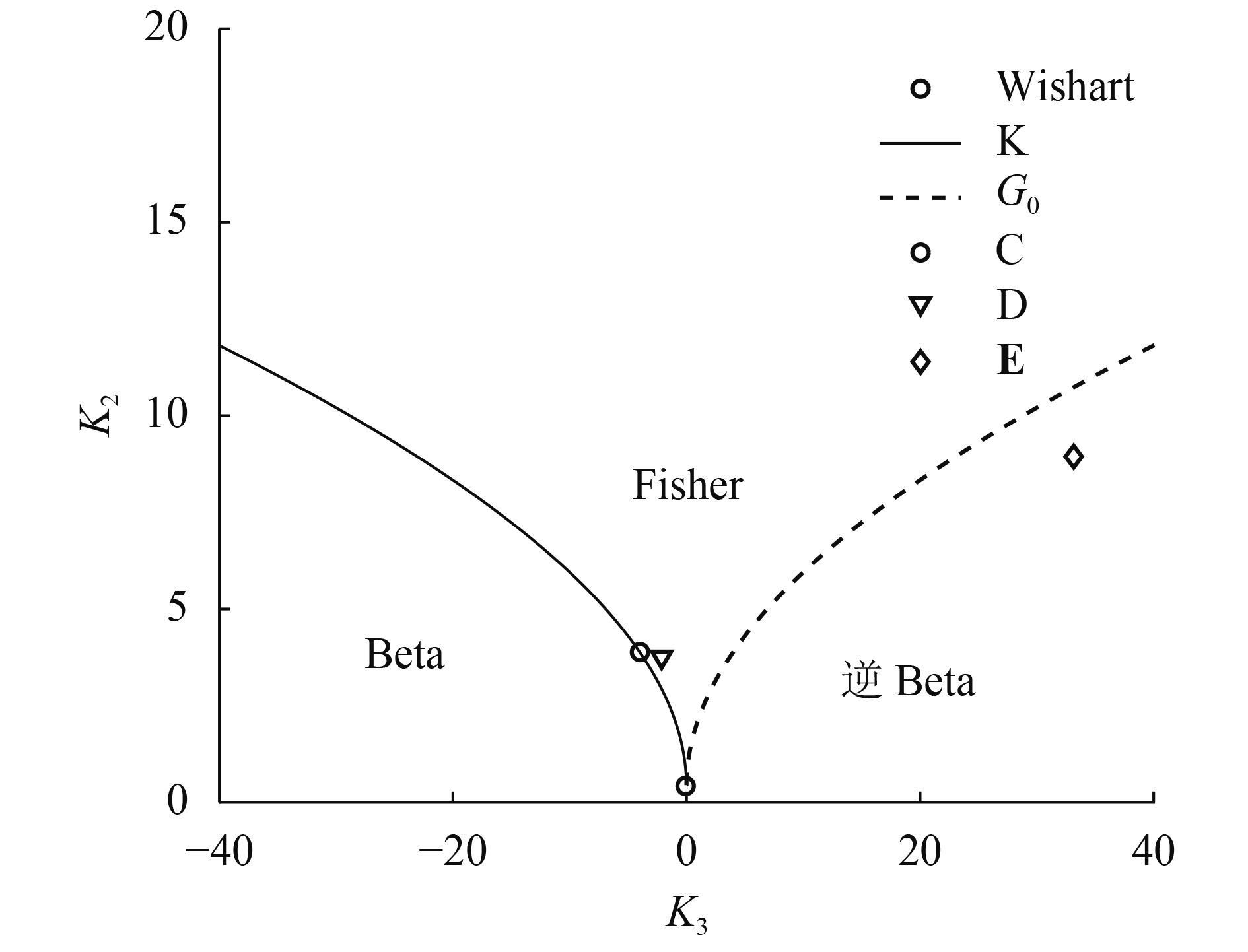
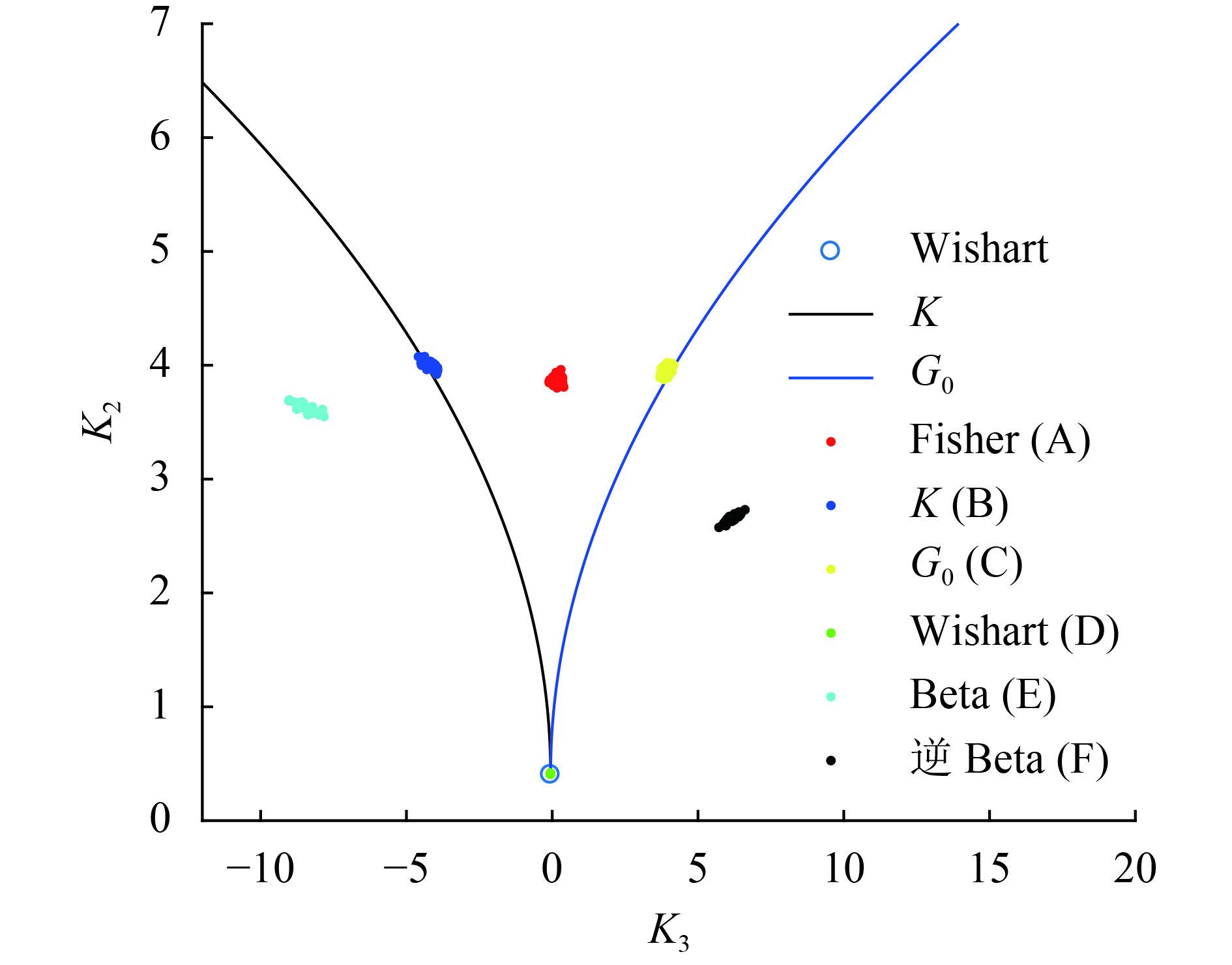
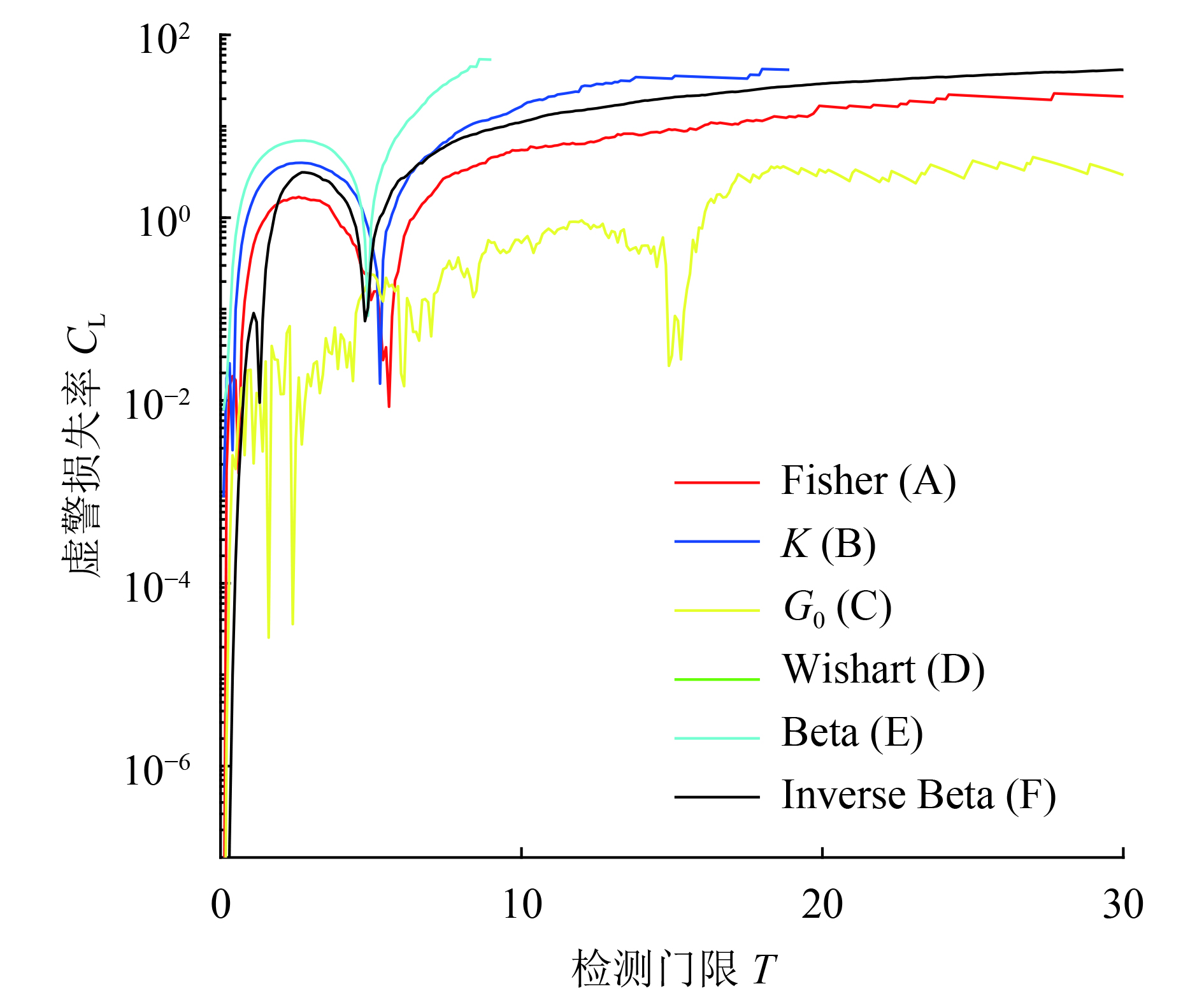
A、B、C、D、E、F 6块区域数据的模型辨识结果如图15所示,虚警损失率CL随检测门限T变化如图16所示。由于Wishart分布数据参数估计结果为1.5223×103,数值较大,导致其CL为无穷大,故在图16中无显示。
|
| 图 15 各区域模型辨识结果 Figure 15 The model recognition results of regions |
|
| 图 16 虚警损失率CL随检测门限T变化图 Figure 16 The relationship between CLand T |
从图16中可以看出,G0分布数据CL在大范围检测门限下均为最小,表明本文方法在G0分布区域具有最好的虚警保持性能,CFAR检测效果最好。其他分布数据方面,Fisher、逆Beta和K分布数据CL在大范围检测门限下依次增大,反映在图15中为散点区域距离G0分布曲线距离逐渐增大,而Beta分布数据散点距离G0分布曲线最远,因此图16中CL在大范围检测门限下为最大。在这6块极化SAR协方差数据中,Wishart分布数据CL为无穷大,因此采用本文方法对Wishart分布区域进行CFAR检测理论上是失效的,此外,其他分布数据的CFAR检测效果取决于与G0分布曲线的“距离”,“距离”越近则CFAR检测效果越好,因此本文方法具有较强鲁棒性的原因在于检测区域的模型辨识散点区域与G0分布曲线距离较近。需要说明的是,上述“距离”并不是图15中k2/k3平面中某散点区域与G0分布曲线的平面距离(否则Wishart分布数据的CFAR检测将会是有效的)。
5、结 论针对基于MPWF的G0分布下CFAR检测虚警概率解析表达式难以求解的难题,本文提出了一种具有解析虚警概率表达式的极化SAR图像CFAR检测方法。仿真数据实验结果表明,本方法在求解CFAR阈值时可节省大量时间,实时性更佳;AIRSAR实测数据实验结果表明,G0分布对不均匀海区拟合性能良好,本方法在CFAR检测中虚警抑制效果良好,同时在非G0分布海区的CFAR目标检测中表现出较强的鲁棒性,定义虚警损失率量化分析虚警保持性能,以说明本方法鲁棒性较强的原因。本文所提方法并未以滑窗为基本单元进行参数估计以及CFAR检测,同时在更普遍的广义逆高斯分布(GIG)分布假设下的基于MPWF的虚警概率解析形式也尚未得出,因此采取滑窗方式进行自动目标检测以及在GIG分布下推导出虚警概率的解析形式是我们今后研究的主要内容。
| [1] | Bateman H. 1954. Tables of Integral Transforms. New York: McGraw-Hill Book Company, Inc.: 313 |
| [2] | Boerner W M, Kostinski A and James B. 1988. On the concept of the polarimetric matched filter in high resolution radar imagery: an alternative for speckle reduction//Proceedings of 1988 International Geoscience and Remote Sensing Symposium. Edinburg: [s.n.]: 69–72 |
| [3] | 种劲松, 朱敏慧. SAR图像局部窗口K-分布目标检测算法[J]. 电子与信息学报, 2003, 25 (9) : 1276 –1280. Chong J S and Zhu M H. Target detection algorithm of SAR image based on local window K-distribution[J]. Journal of Electronics and Information Technology, 2003, 25 (9) : 1276 –1280. |
| [4] | 崔浩贵. 2014. 极化SAR图像统计建模及其参数估计方法研究. 武汉: 海军工程大学: 123–125 Cui H G. 2014. Research on Statistical Modelling and Parameters Estimation of PolSAR Imagery. Wuhan: Naval University of Engineering: 123–125 |
| [5] | Frery A C, Muller H J, Yanasse C C F and Sant’Anna S J S. A model for extremely heterogeneous clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35 (3) : 648 –659. DOI: 10.1109/36.581981 |
| [6] | Goldstein G B. False-alarm regulation in log-normal and weibull clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9 (1) : 84 –92. DOI: 10.1109/TAES.1973.309705 |
| [7] | Gradshteyn I S and Ryzhik I M. 2007. Table of Integrals, Series, and Products. 7th ed. San Diego, CA: Academic Press: 316 |
| [8] | 贺志国, 周晓光, 陆军, 匡纲要. 一种基于G0分布的SAR图像快速CFAR检测方法 [J]. 国防科技大学学报, 2009, 31 (1) : 47 –51. He Z G, Zhou X G, Lu J and Kuang G Y. A fast CFAR detection algorithm based on the G0 distribution for SAR images [J]. Journal of National University of Defense Technology, 2009, 31 (1) : 47 –51. DOI: 10.3969/j.issn.1001-2486.2009.01.010 |
| [9] | Jakeman E and Pusey P. A model for non-Rayleigh sea echo[J]. IEEE Transactions on Antennas and Propagation, 1976, 24 (6) : 806 –814. DOI: 10.1109/TAP.1976.1141451 |
| [10] | Jao J. Amplitude distribution of composite terrain radar clutter and the κ-distribution[J]. IEEE Transactions on Antennas and Propagation, 1984, 32 (10) : 1049 –1062. DOI: 10.1109/TAP.1984.1143200 |
| [11] | Khan S and Guida R. On fractional moments of multilook polarimetric whitening filter for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52 (6) : 3502 –3512. DOI: 10.1109/TGRS.2013.2273128 |
| [12] | 刘国庆, 黄顺吉, Torre A, Rubertone F. 一种新的多视全极化SAR目标检测器及其性能分析[J]. 信号处理, 1998, 14 (2) : 110 –116. Liu G Q, Huang S J, Torre A and Rubertone F. A new multi-look polarimetric SAR target detector and its performance analysis[J]. Signal Processing, 1998, 14 (2) : 110 –116. |
| [13] | Liu G Q, Huang S J, Torre A and Rubertone F. The multilook polarimetric whitening filter (MPWF) for intensity speckle reduction in polarimetric SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36 (3) : 1016 –1020. DOI: 10.1109/36.673694 |
| [14] | 刘涛, 崔浩贵, 高俊. Wishart分布矩阵行列式值的统计特性及其在参数估计中的应用[J]. 电子学报, 2013, 41 (6) : 1231 –1237. Liu T, Cui H G and Gao J. Statistics of the determinant of the Wishart distributed matrix and its application to parameter estimation[J]. Acta Electronica Sinica, 2013, 41 (6) : 1231 –1237. DOI: 10.3969/j.issn.0372-2112.2013.06.030 |
| [15] | 刘涛, 崔浩贵, 毛滔, 席泽敏, 高俊. 基于子矩阵对数累积量的极化合成孔径雷达图像等效视图数估计新方法[J]. 中国科学: 信息科学, 2012, 42 (11) : 1459 –1470. Liu T, Cui H G, Mao T, Xi Z M and Gao J. Novel estimation of the equivalent number of looks in polari-metric SAR imagery based on log-cumulants of sub-covariance- matrix[J]. Scientia Sinica (Informationis), 2012, 42 (11) : 1459 –1470. DOI: 10.1360/112011-1189 |
| [16] | Liu T, Cui H G, Xi Z M and Gao J. Novel estimators of equivalent number of looks in polarimetric SAR imagery based on sub-matrices[J]. Science China Information Sciences, 2016, 59 (6) : 062309 . DOI: 10.1007/s11432-015-5480-x |
| [17] | Lopes A and Sery F. Optimal speckle reduction for the product model in multilook polarimetric SAR imagery and the wishart distribution[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35 (3) : 632 –647. DOI: 10.1109/36.581979 |
| [18] | 鲁统臻, 张杰, 纪永刚, 张晰, 孟俊敏. 基于G0分布的高海况SAR船只目标检测方法 [J]. 海洋科学进展, 2011, 29 (2) : 186 –195. Lu T Z, Zhang J, Ji Y G, Zhang X and Meng J M. Ship target detection algorithm based on G0 distribution for SAR images under rough sea conditions [J]. Advances in Marine Science, 2011, 29 (2) : 186 –195. DOI: 10.3969/j.issn.1671-6647.2011.02.008 |
| [19] | Novak L M and Burl M C. Optimal speckle reduction in polarimetric SAR imagery[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26 (2) : 293 –305. DOI: 10.1109/7.53442 |
| [20] | Novak L M, Burl M C and Irving W W. 1991. Optimal polrimetric procesing for enhanced target detetion//Proceedings of 1991 National Telesystems Conference. Atlanta: 69–75 |
| [21] | Novak L M, Sechtin M B, Cardullo M J. Studies of target detection algorithms that use polarimetric radar data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25 (2) : 150 –165. DOI: 10.1109/7.18677 |
| [22] | 皮亦鸣, 邹琪, 黄顺吉. 极化SAR相干斑抑制——极化白化滤波器[J]. 电子与信息学报, 2002, 24 (5) : 597 –603. Pi Y M, Zou Q and Huang S J. Speckle reduction of polarimetric SAR—polarimetric whitening filter[J]. Journal of Electronics and Information Technology, 2002, 24 (5) : 597 –603. |
| [23] | Stinco P, Greco M and Gini F. 2011. Adaptive detection in compound-Gaussian clutter with inverse-gamma texture//Proceedings of 2011 IEEE CIE International Conference on Radar. Chengdu: IEEE: 434–437 [DOI: 10.1109/CIE-Radar.2011.6159570] |
| [24] | 王娜, 时公涛, 陆军, 匡纲要. 一种新的极化SAR图像目标CFAR检测方法[J]. 电子与信息学报, 2011, 33 (2) : 395 –400. Wang N, Shi G T, Lu J and Kuang G Y. A new polarimetric SAR image CFAR target detecting method[J]. Journal of Electronics and Information Technology, 2011, 33 (2) : 395 –400. DOI: 10.3724/SP.J.1146.2010.00023 |
| [25] | Wang N, Liu L, Hu C B, Kuang G Y and Jiang Y M. 2011. A novel polarimetric CFAR target detection method//Proceedings of 2011 International Workshop on Multi-Platform/multi-Sensor Remote Sensing and Mapping. Xiamen: IEEE: 1–6 [DOI: 10.1109/M2RSM.2011.5697368] |
| [26] | Wei J J, Li P X, Yang J, Zhang J X and Lang F K. A new automatic ship detection method using L-band polarimetric SAR imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7 (4) : 1383 –1393. DOI: 10.1109/JSTARS.2013.2269996 |
| [27] | Weinberg G V. Coherent CFAR detection in compound Gaussian clutter with inverse gamma texture[J]. EURASIP Journal on Advances in Signal Processing, 2013, 2013 : 105 . DOI: 10.1186/1687-6180-2013-105 |
| [28] | Witkovský V. Computing the distribution of a linear combination of inverted gamma variables[J]. Kybernetika, 2001, 37 (1) : 79 –90. |
| [29] | 张嘉峰, 朱博, 张鹏, 王明春, 刘涛. Wishart分布情形下极化SAR图像目标CFAR检测解析方法[J]. 电子学报, 2018, 46 (2) : 433 –439. Zhang J F, Zhu B, Zhang P, Wang M C and Liu T. Polarimetric SAR imagery target CFAR detection analytical algorithm with Wishart distribution[J]. Acta Electronica Sinica, 2018, 46 (2) : 433 –439. DOI: 10.3969/j.issn.0372-2112.2018.02.024 |
| [30] | Zhao Y N, Pang X Y and Yin B. 2013. Adaptive radar detection for targets in compound-Gaussian clutter with inverse-gamma texture//Proceedings of IET International Radar Conference 2013. Xi’an: IEEE: 1–4 [DOI: 10.1049/cp.2013.0249] |

