遥感影像变化检测是全球变化研究的重要内容(Chen 等，2015)，已应用于诸多领域，如灾后应急与评估(Samadzadegan和Rastiveisi，2008)、环境变化检测(Varma 等，2014；Chen 等，2013)和地理数据更新(Chen 等，2012)。近30年来，国内外许多学者对变化检测方法从不同角度进行了研究(张晓东 等，2006；李德仁，2003)，总体来讲可以分为两大类:一类是基于两期遥感影像的变化检测方法，主要有直接比较法(Chen 等，2011；Bruzzone和Prieto，2000；Johnson和Kasischke，1998)、分类后比较法(Post-Classification Comparison)(Barnhart和Crosby，2013；Ahmad，2012；Serra 等，2003)及其他组合方法(hybrid)(Ghofrani，2014)等；另一类是使用矢量数据和遥感影像相结合的变化检测方法(Sofina和Ehlers，2016；Adesina和Mavomi，2014)。由于影响地物光谱特性变化的因素比较复杂，除了地物本身的物理特性之外，成像时间、地域差异、环境和传感器等外在因素都会不同程度地影响地物的光谱特性，基于两期遥感影像的变化检测方法要么存在工作量大、分类误差累积传递到变化信息中，要么存在数据条件要求苛刻、难以充分利用快速发展的多源遥感影像数据等诸多不足(魏东升和周晓光，2017)。近年来，许多应用需求的参考数据中包含了一期分类矢量数据，这些矢量数据包含有位置、形状、大小和类别属性等先验信息，一些学者使用这些先验信息分割遥感影像，通过影像对象纹理特征在空间上的差异性进行变化检测，有效地提高了变化检测结果的精度和效率(魏东升和周晓光，2017；Sofina和Ehlers，2016；Adesina和Mavomi，2014)。但是，在变化检测中，需要从分割后的影像对象中抽取一定数量、具有相同类别属性的样本，其中不可避免地抽到类别属性不一致的样本，如何剔除这些样本是抽样过程中必须解决的重点问题，在目前已有的方法中，一般是通过人工目视判别完成的(魏东升和周晓光，2017；李亮 等，2013)。样本的自动提取是实现自动变化检测的关键环节，因此，解决变化检测样本自动抽样问题具有一定的理论意义和实用价值。

用矢量数据分割遥感影像，获得的影像对象具有清晰完整的边界、空间位置、先验类别和光谱信息。对于具有相同先验类别属性的影像对象而言，它们的光谱特征既具有相似性，也具有差异性，这些差异性有可能是由于地域环境的差异引起的，也有可能是因为影像对象验后类别的变化造成的。判断影像对象是否变化的标准是通过待检测影像对象与样本影像对象由光谱信息表示的特征差异来实现的。因此，用于变化检测的样本，一方面要求在空间分布上必须能够体现出因地域环境差异引起的光谱特征差异，这属于样本布设方法问题；另一方面样本对象无论是空间位置、形状大小，还是验后类别属性都必须是正确的，然而，样本是从含有先验类别属性的影像对象中抽取的，其中可能包含验后类别属性已经变化了的影像对象，由于类别属性的变化，这些影像对象的光谱特征在空间上具有明显的差异，必须从样本中剔除。在抽样过程中，只要选择合适的抽样区域，就可以确保样本布设结果中包含验后类别属性已经变化的影像对象的个数较少，而且变化为同类别的影像对象的个数更少，这类验后类别属性已经变化的影像对象属于异常数据集。由此可知，样本自动提取主要包括样本的空间布设和异常样本的自动检测两个环节，样本空间分布的合理性是提高变化检测精度的前提条件，异常样本的自动检测是实现自动变化检测的关键环节。

样本的空间布设需要考虑两个方面的因素：(1)地域环境差异引起的地物光谱特征差异，这主要体现在影像对象的空间分布和地形差异方面；(2)样本布设结果中变化的影像对象应是少量的，这主要体现在抽样区域的选择方面。因此，可以根据影像对象的空间分布、地形特征和抽样区域范围进行优化样本空间布设。选择合适的抽样区域，能够满足绝大部分样本的验后类别属性没有发生变化，而且变化为同一类别的样本会更少，即未变化的样本属于典型正常区域数据集，而变化的样本属于低密度区域异常数据集。局部可达密度LRD(Local Reachability Density)定量描述了影像对象在特征空间内与其邻域内点的密集程度(Radovanović 等，2015；Aggarwal和Yu，2001；Breunig 等，2000)，一个对象的局部可达密度越大，表示该对象与邻域内对象划分为同一类别的概率就越大。本文运用局部可达密度算法，构建一个衡量样本在特征空间内的异常度指标，进行异常样本检测，自动提取变化检测样本。

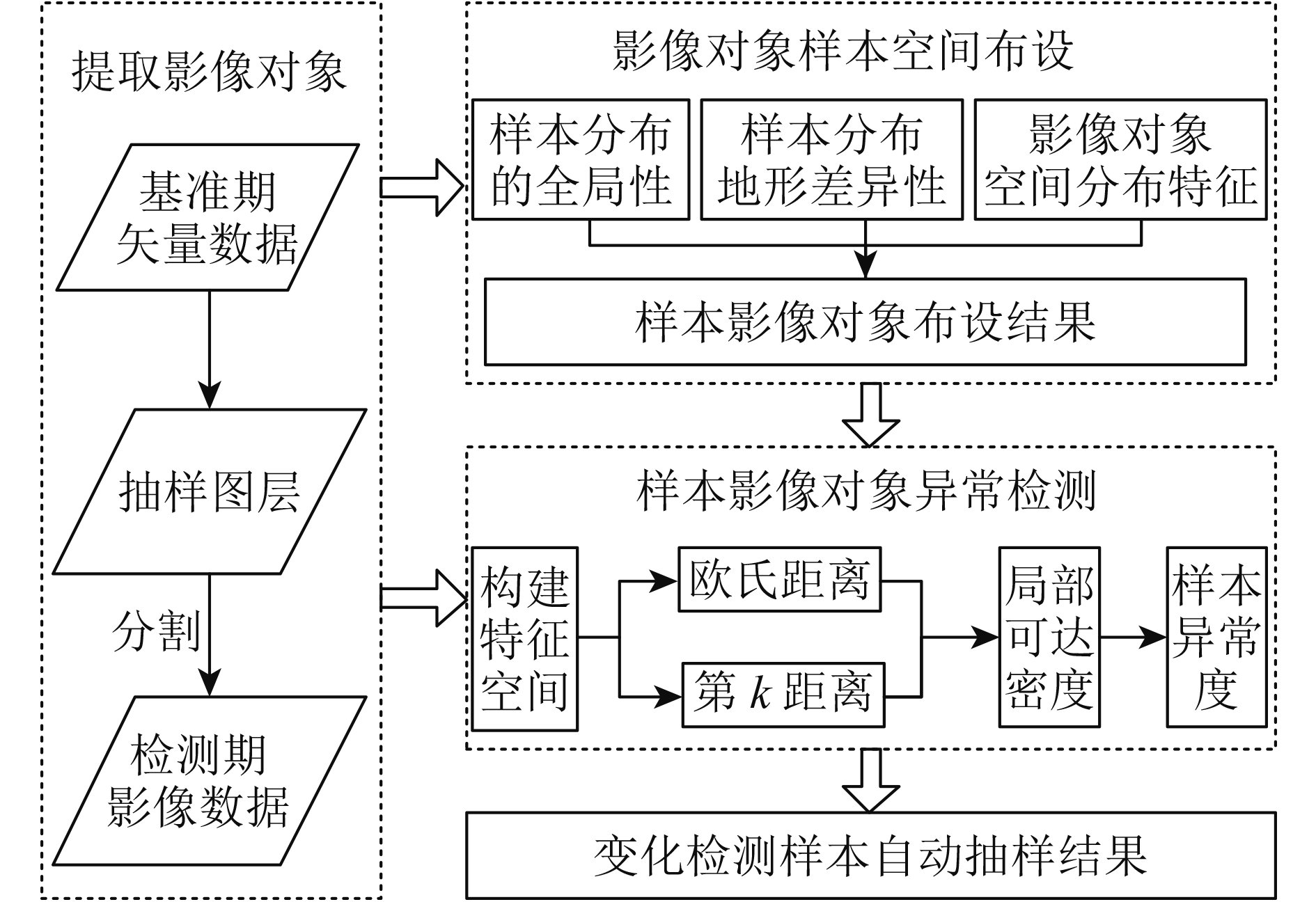
在遥感影像结合矢量数据先验信息的变化检测中，变化检测样本的自动提取就是根据影像对象的先验特征信息布设样本，然后根据样本光谱特征描述的纹理特征空间差异性，检测出与先验类别不一致的样本，提取出变化检测样本，主要包括从矢量数据中获取抽样图层、用抽样图层分割遥感影像、从分割后的影像对象中布设变化检测样本和异常样本检测等步骤，变化检测样本提取流程如图1所示。

图 1 变化检测样本自动提取流程图 Figure 1 Flowchart of the change detection sampling method

首先从基准期矢量数据中提取抽样图层，用抽样图层分割遥感影像，获取影像对象。抽样图层中地理要素的先验信息可作为影像对象样本空间布设的参考信息，而且分割后的影像对象包含有相同的先验类别属性和具有差异性的光谱信息，这些光谱信息表示的特征空间可用于异常样本检测。

其次是从分割后的影像对象中布设样本。为了提高变化检测结果精度，样本必须能够体现影像对象总体的基本特征，所以样本的选取要具有随机性，样本的空间分布要具有合理性。由于影像对象的光谱信息因地域环境变化而有所差异，因此，样本布设应考虑影像对象的空间分布和地形差异。此外，在布设的样本中，验后类别属性变化的样本必须满足异常数据的特征，即在抽样过程中，验后类别属性变化的影像对象被抽中的概率必须是低的，因此，抽样区域必须从局部变化区域扩展到全局区域，以确保异常检测中的典型正常区域数据集就是未变化影像对象，异常数据集就是变化了的影像对象。由此可知，可以根据影像对象的空间分布、地形差异和抽样区域的全局特征来布设变化检测样本。

最后检测异常样本，提取出变化检测样本。由于异常样本与典型正常区域样本有显著的光谱特征差异，因此可以根据异常检测原理对异常样本进行异常检测。其方法是依据样本的光谱信息构建特征空间向量，分别计算各样本间的欧氏距离和各样本的第k距离及其k距离邻域(k为邻域参数，表示一个对象邻域内应包含最少对象的个数，第k距离为包含k个对象邻域内的最远距离)，然后计算样本的局部可达密度，由局部可达密度计算样本的异常度指数，并根据异常度指数值大小判断样本的验后类别是否变化，完成变化检测样本自动提取。

样本的空间分布是否合理直接影响到样本异常检测结果的准确性，进而影响变化检测结果精度。样本空间布设的合理性一方面应体现出典型正常区域数据集表示的正确性和唯一性。因为异常检测方法就是要检测出样本中低密度区域的数据集，如果典型正常区域数据集不能表示样本的先验类别特征、或者具有多类别特征，那么样本数据异常检测结果就不能体现样本的先验类别。由于同一抽样图层中的影像对象具有相同的先验类别属性，样本空间布设只需要考虑样本对象的验后类别与先验类别属性是否一致，而且具有这种一致性的影像对象出现的概率会随着抽样区域的扩大而增加，因此样本布设必须考虑抽样区域的全局特性。另一方面，为了提高变化检测结果精度，样本必须能够体现出总体的数字特征。因此，样本布设必须具有随机性、样本分布要满足均匀性和样本要具有代表性，也就是说，在样本布设中，影像对象密集区域应布设较多样本，相反，稀疏区域应布设较少的样本，而且不同地形范围内样本布设的比利应具有合理性，但是特殊地形区域(如坡度较大区域、唯一影像对象区域)应保证具有一定的样本。

根据上述讨论可知，抽样区域范围、抽样区域内影像对象的分布特征和抽样区域地形特征都对样本空间合理分布产生直接影响，因此，本文采用规则格网进行样本的空间分配和布设。首先将抽样区域划分为 $r \times c$ 个规则的抽样格网，抽样格网大小可以根据抽样区域范围、影像对象总数和样本需求个数进行适当确定；其次将抽样区域按地形差异划分为t个层级，然后根据抽样格网内影像对象个数和地形起伏情况计算抽样格网内布设的样本个数，设 $S{N_{r \times c}}$ 表示抽样格网中位于第 $r$ 行、 $c$ 列格网样本布设的个数，则有

式中，Ion和STN分别为抽样区域内影像对象总数和样本布设总数， $Ion_{r \times c}^j$ 表示第r行、c列格网内地形特征为第j层级的影像对象个数。从式(1)可知，抽样格网内地形特征为第j层级的影像对象越密集，样本布设个数就越多，反之则越少。如果抽样格网内存在影像对象，但是按式(1)计算的抽样格网内的样本布设个数为0，则抽样格网内应随机布设唯一样本，以确保影像对象稀疏区域内样本的代表性。

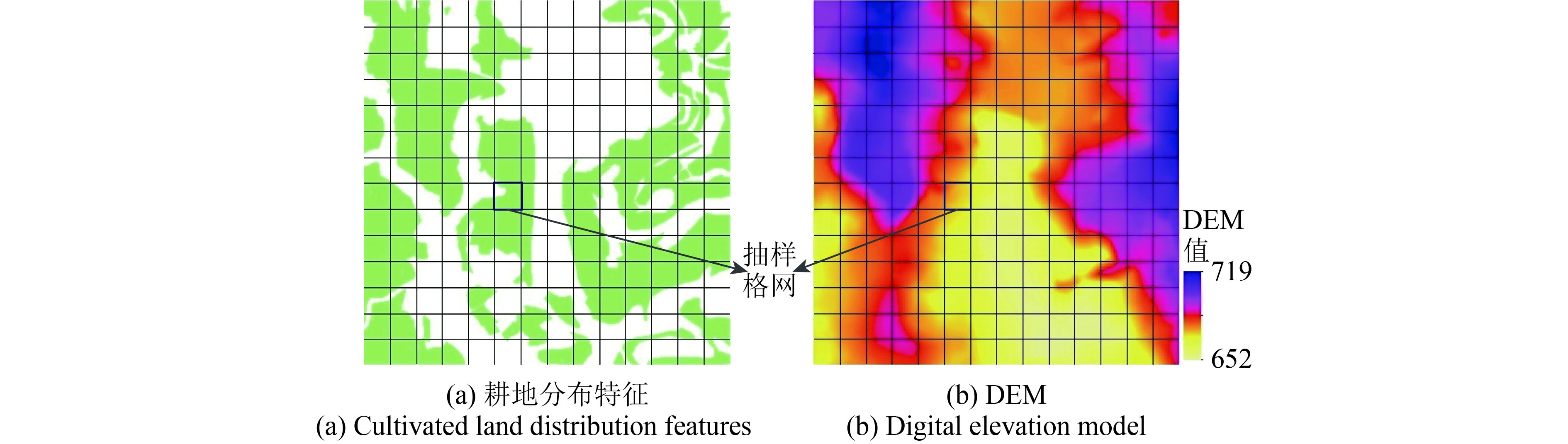
图2表示了一抽样格网内耕地样本布设原理，图2(a)为抽样区域内的耕地图层，图2(b)为对应抽样区域内用DEM表示的地形。由图2(b)可知，抽样区域最低海拔高程为652 m，最高海拔高程为719 m，按10 m等高距可将抽样区域划分为7个抽样层级，示例中的抽样格网共包含2个抽样层级，分别为第3、4层级。抽样区域共有耕地类对象1028个，计划布设样本224个，抽样格网中位于第3层级的耕地类对象有21个，第4层级的有15个，则抽样格网中应布设耕地样本总数为6个，其中第3层级样本数为4个，第4层级样本数为2个。

图 2 样本空间布设原理 Figure 2 The principle of space layout of samples

根据矢量数据抽样图层先验信息布设的样本中，存在变化了的样本，但相对于未变化的样本来说，这些变化了的样本的个数是极少的，属于异常数据集。由矢量数据分割遥感影像，获得的影像对象既含有先验类别属性，又包含影像对象的光谱特征信息，如何利用这些特征信息实现对异常样本的自动检测，影像对象特征空间构建是其重要环节。纹理特征作为重要的视觉表达方式已广泛应用于各类高分辨率遥感图像处理中(金晶 等，2014；沈小乐 等，2014；虞欣，2009)，基于像元及其邻域灰度属性的灰度共生矩阵理论已经广泛应用于各种纹理分析中，被理论和实践证明是最有效的纹理分析方法之一，有较强的自适应性和鲁棒性(Zhuang 等，2016；Eichkitz 等，2013；Ulaby 等，1986)。因此，可以用灰度共生矩阵描述的纹理特征参数来构建影像对象的特征空间，但是这些纹理特征参数多达14种(Haralic 等，1973)，而且由于不同纹理特征参数描述同类别影像对象，以及同一纹理特征参数描述不同类别影像对象的纹理都具有差异性，所以在构建影像对象的特征空间时，必须根据影像对象先验类别属性选择最优的纹理特征参数。魏东升和周晓光(2017)依据贡献度指数对纹理特征参数进行加权，设影像对象j的特征空间 ${{F}}sp(o{b_j})$ (Feature Space，Fsp)，可以表示为

式中， ${f_i}(i = 1, 2, \cdots, 14)$ 为14种纹理特征参数， $p_i^j(i = 1, 2, \cdots, 14)$ 为影像对象j的第i个纹理特征参数对应先验类别的纹理特征贡献度指数，GainRat $({C_j}, {f_i})$ 为第i个纹理特征参数 ${f_i}$ 对影像对象j对应先验类别 ${C_j}$ 的信息增益率。式中，当贡献度指数低于40%时，就不选择这种纹理特征参数，对应的 $p_i^j = 0$ ，此外，由于各种纹理特征参数值取值区间的差异性， ${f_i}$ 均是经过归一化处理。

在遥感影像上，引起地物光谱信息变化的原因很多，既有成像时间、地域环境和传感器等因素，也包括人为因素和突发性地质灾害引起的变化。与前者相比，人为因素和突发性地质灾害造成的变化是变化检测研究的目的和重点，而且在顾及抽样图层先验信息的样本布设中，这些因素引起影像对象特征空间的变化是局部的、具有典型的空间异常特征。Hawkins(1980)、Atkinson(1986)先后从不同角度提出了异常(Outlier)的概念，一般来讲，异常是指在数据集中偏离大部分数据的数据，使人怀疑这些数据的偏离并非由随机因素产生，而是产生于不同的机制。在本文中，异常可以定义为特征空间内低密度区域的数据集，这些异常数据与典型正常区域数据不同，但具有相对性。Ramaswamy等(2000)从数据的空间分布特征提出了密度异常概念，首先计算每个数据邻域内点的可达距离，再用可达距离计算每个数据的局部异常因子LOF(Local Outlier Factor)，最后根据LOF检测出异常数据集，这对单个的、孤立的异常点数据检验有很好的效果。但是，在需要检测的样本数据中，可能有大量的在特征空间内具有相同特征的异常数据集，如典型正常区域样本数据集是耕地，而样本数据集中包含了大部分的林地，这些林地应属于异常数据集，利用LOF进行异常检测可能会把林地当作典型正常区域数据集，误判为耕地，因此会使自动样本提取失败。为了能更准确地检测出样本数据集中的异常数据，依据局部可达密度原理，考虑样本数据集的全局特征，提出特征空间异常度计算方法，具体算法为

(1)计算样本影像对象在特征空间的可达距离(Reachability Distance)。设 $Rdi{s_k}(o{b_j}, o{b_i})$ 表示对象 $o{b_i}$ 到 $o{b_j}$ 的第k可达距离，则有

式中，k为邻域参数，表示一个样本对象邻域内应包含最少的样本对象个数，设对象 $o{b_i}$ 的第k邻域为 ${N_k}(o{b_i})$ ，则 $k \leqslant {N_k}(o{b_i})$ 。 $d(o{b_j}, o{b_i})$ 表示在特征空间内对象 $o{b_i}$ 到 $o{b_j}$ 的欧氏距离， $k - dis(o{b_i})$ 表示对象 $o{b_i}$ 的第k距离，表示包含k个对象邻域内的最远距离。

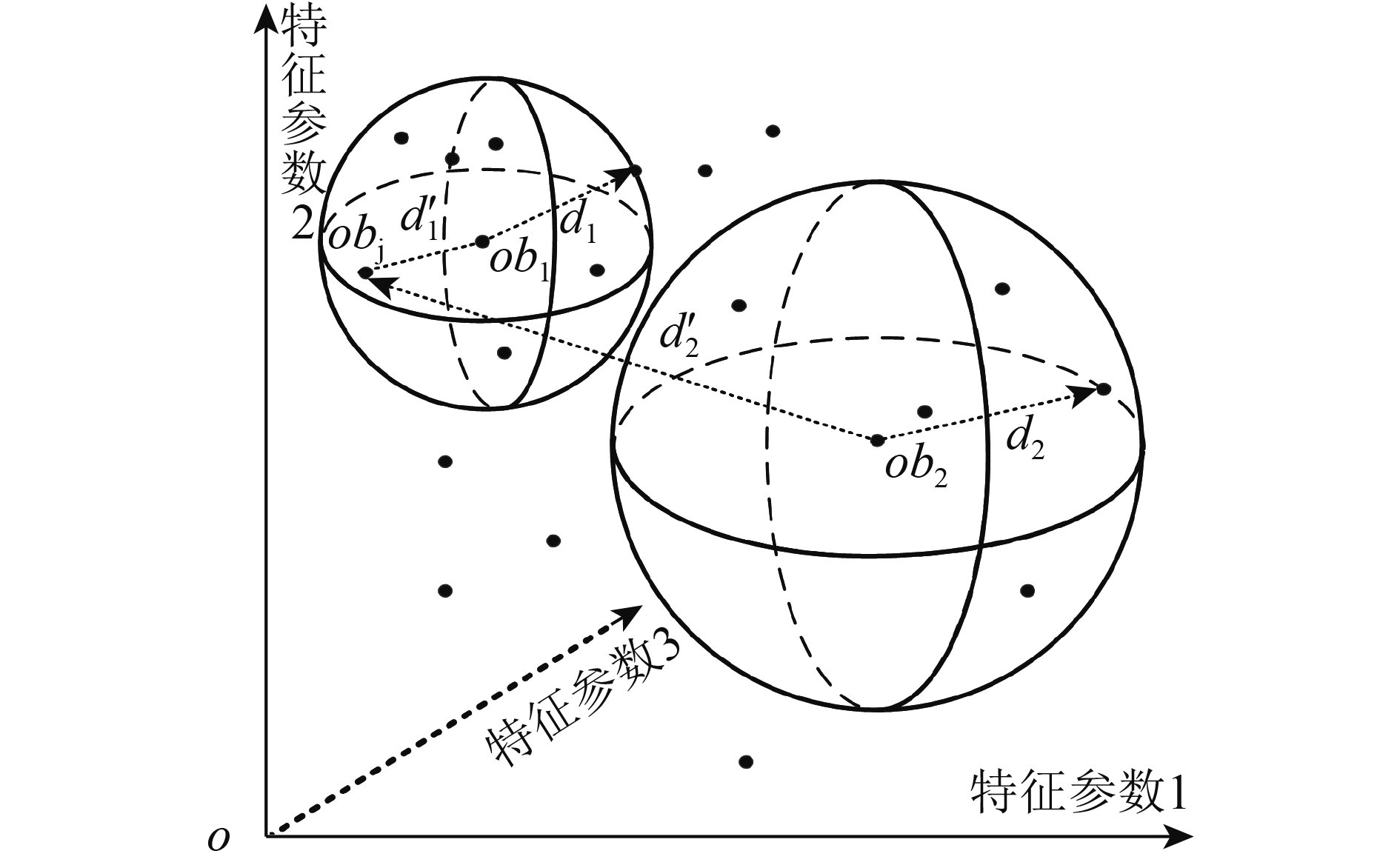
图3表示了在三维特征空间内对象 ${{o}}{{{b}}_1}\text{、}{{o}}{{{b}}_2}$ 到对象 $o{b_j}$ 的第5可达距离计算原理。在图3中，对象 ${{o}}{{{b}}_1}$ 的第5距离为 ${{{d}}_1}$ ，对象 ${{o}}{{{b}}_1}$ 到对象 $o{b_j}$ 的欧氏距离为 ${{{d'}}_1}$ ，因为 ${{{d}}_1} > {{{d'}}_1}$ ，所以对象 ${{o}}{{{b}}_1}$ 到对象 $o{b_j}$ 的第5可达距离为 ${{{d}}_1}$ ，而对象 ${{o}}{{{b}}_2}$ 的第5距离为 ${{{d}}_2}$ ，对象 ${{o}}{{{b}}_2}$ 到对象 $o{b_j}$ 的欧氏距离为 ${{{d'}}_2}$ ，且 ${{{d}}_2} < {{{d'}}_2}$ ，所以对象 ${{o}}{{{b}}_2}$ 到对象 $o{b_j}$ 的第5可达距离为 ${d'_2}$ 。

图 3 影像对象在三维特征空间的可达距离 Figure 3 Reachability distance of image objects in the three-dimensional feature space

(2)计算样本影像对象的局部可达密度。设 $LRD(o{b_j})$ 表示对象 $o{b_j}$ 的局部可达密度，则有

局部可达密度 $LRD(o{b_j})$ 表示了对象j的第k邻域内的对象到对象j的平均可达距离的倒数，局部可达密度值越大，表示在特征空间内对象j和邻域内的对象属于同一类别的概率就越大，反之则越小。

(3)由局部可达密度计算影像对象特征空间异常度Fsoi(Feature Space Outlier Index)。设样本对象 $o{b_j}$ 的异常度指数为 ${Fsoi}(o{b_j})$ ，则有

式中，D表示样本对象集合。 $Fsoi(o{b_j})$ 的值介于0到100%之间，其值的相对大小刻画了样本对象的异常程度，值越大表示样本对象的特征空间偏离典型正常样本群体的概率就越大，在给定先验类别属性的样本自动识别中就排除该类对象作为抽样对象。

研究区域位于四川省平昌县某镇，试验数据为一幅矢量地形图和一幅高分辨率的遥感影像图。矢量地形图由GPS-RTK数字化测图获得，测图比例尺为1∶1000，成图时间为2014年04月(图4(a))，包含1954个地理对象和7种地物要素类别，包括耕地、林地、水体、道路、草地、荒地和居民地。影像数据为Google Earth卫星影像，影像获取时间为2016年08月(图4(b))，影像的空间分辨率为0.6 m，包含红、绿、蓝3个波段，影像大小包含2334×2334个像元。由矢量地形图获取高程数据，建立DEM表示研究区域的地形特征，如图4(c)，研究区域属于山地地形，地形起伏变化较大，最低海拔高程为652 m，最高海拔高程为719 m。研究区域耕地、林地类要素较多，居民地要素相对较少，都具有明显的变化特征，因此，我们的抽样试验以耕地、林地和居民地为例，来验证本文变化检测样本自动提取方法的有效性。

图 4 变化检测样本抽样数据 Figure 4 Test data set of sampling

首先从2014年的矢量地图中分别提取耕地、林地和居民地抽样图层，并将抽样区域按实地水平距离100 m×100 m划分为规则的抽样格网。然后用抽样图层分割2016年影像数据，获取影像对象。根据DEM数据(图4(c))表示的地形特征，按10 m等高距将抽样区域划分为7个抽样层级，耕地、林地和居民地影像对象在不同抽样层级中的分布特征如图5所示。

图 5 耕地、林地和居民地空间分布特征 Figure 5 Spatial distribution features of cultivated land, woodland and building

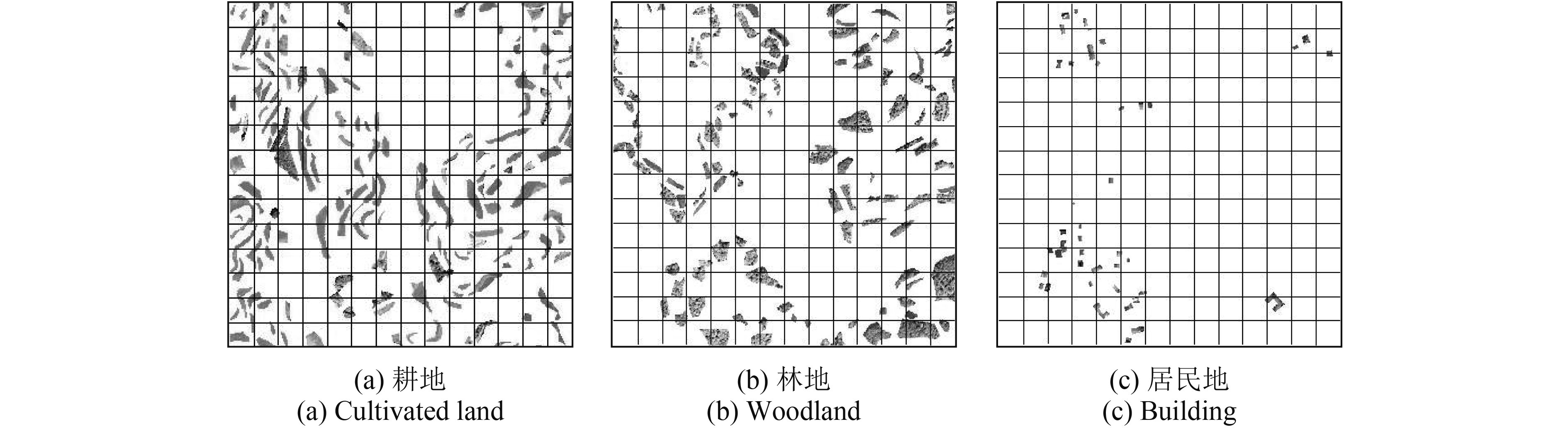
抽样区域内包含耕地影像对象总数1028个、林地625个、居民地159个，本试验中，在抽样区域内计划布设耕地样本224个、林地样本167个、居民地样本122个。由于抽样区域内居民地影像对象相对较少，所以样本布设比例较高，样本绝对个数还是少于耕地和林地的样本数，但这并不会影响试验结果的有效性。根据耕地、林地和居民地影像对象在各层级的分布特征，首先计算出各抽样格网内每一层级布设的样本个数，然后采用随机抽样方法，对每个格网进行样本布设(图6)。

图 6 耕地、林地和居民地样本布设结果 Figure 6 The result of space layout of cultivated land, woodland and building samples

图6中的样本布设结果是根据影像对象的先验信息获得的，由于人为的或者突发性灾害因素，这些先验信息在检测期遥感影像上可能已经发生变化，这就导致样本布设结果中包含有发生了变化的影像对象类别。根据抽样区域的全局特性，这些变化的影像对象抽到的概率较小，相对于未变化的样本影像对象而言，变化为同类别样本对象的个数是少量的，属于局部异常数据集。例如在随机布设的224个耕地样本中未变化的有188个，变化的样本仅有36个，而且变化的36个样本中属于同类别的就更少了，耕地变化为居民地的样本仅6个，耕地变化为林地的相对较多一些，有15个。因此，可以根据异常数据检测原理，检测出样本布设中与先验类别不一致的影像对象。

在影像对象异常检测中，首先构建影像对象的特征空间向量，根据影像对象先验类别属性，耕地由角二阶矩ASM(Angular Second Moment)、对比度CON(Contrast)、逆差矩IDM(Inverse Difference Moment)、熵ENT(Entropy)、平方和SSQ(Sum of Squares)、差熵DENT(Difference Entropy)和差方差DVA(Difference Variance)7个特征参数构成特征空间向量，林地由角二阶矩、逆差矩、熵、均值(Mean)、总方差(Sum Variance)和总平均(Sum Average)6个特征参数构成特征空间向量，居民地由逆差矩、熵、对比度、差熵和角二阶矩5个特征参数构成特征空间向量。其次是计算影像对象的第K距离和可达距离，然后计算局部可达密度，并由局部可达密度计算异常度指数。k值的大小体现了一个样本邻域内应包含的最少样本个数，由于邻域内样本个数越多，其隶属于同一类的概率就越小，因此k值的大小，会影响第K距离的大小，进而会影响影像对象的异常度指数。图7表示了在不同k值下样本异常度大小的频率分布直方图，横轴表示异常度指数大小，纵轴表示在给定异常度指数区间内样本出现的频率。

图 7 异常检测频率分布 Figure 7 Frequency distribution of outlier detection

从图7中可以直观看出，随着k值的增大，低异常度样本的个数逐渐增多，高异常度样本的个数逐渐减少。而且当k值达到一定取值区间时(图7(a)中k取值在35−90)，高异常度样本个数趋于稳定，而当k取值过大时(接近样本总数)，样本中几乎全是低异常度样本(图7(c)中k取120)，则会导致异常检测结果失败。影像对象异常检测就是要去除样本中高异常度的影像对象，因此，由图7中试验数据可知，k值按样本总数的1/5左右选择时，不会影响异常检测结果的准确性。

为了定量分析影像对象异常检测的总体效果，在不同k值和不同异常度阈值下，对异常检测中的误检、漏检和总体精度进行了分析，其中误检指原本为与先验类别一致的样本被误判为异常样本，漏检指原本为异常样本而没有被检测出来。耕地、林地和居民地异常检测结果精度分析见表1。

表 1(Table 1)

表 1 耕地、林地和居民地异常检测精度分析 Table 1 Accuracy analysis of outlier detection for cultivated land, woodland and building k 异常度阈值/% 耕地 林地 居民地 误检率/% 漏检率/% 总精度/% 误检率/% 漏检率/% 总精度/% 误检率/% 漏检率/% 总精度/% 10 90 0 66.7 89.28 0 68.2 86.27 0 71.1 85.29 80 7.4 0 93.75 3.5 0 95.43 0 0 100 70 9.6 0 91.96 9.8 0 92.16 0 0 100 20 90 0 47.2 92.41 0 65.4 88.43 0 69.2 84.88 80 4.9 0 95.98 0 0 100 0 0 100 70 12.2 0 89.73 2.4 0 98.03 0 0 100 35 90 0 11.1 98.20 0 65.8 87.54 0 70.2 83.18 80 2.6 0 97.76 0 0 100 0 0 100 70 11.7 0 90.17 0 0 100 0 0 100 50 90 0 27.7 95.53 0 85.4 82.35 0 80.2 81.35 80 0 0 100 0 0 100 0 0 100 70 6.9 0 94.20 0 0 100 0 0 100 65 90 0 47.2 92.41 0 91.2 82.35 0 81.3 80.24 80 0 0 100 0 0 100 0 14.3 100 70 4.2 0 96.42 0 0 100 0 0 100 90 90 0 58.3 90.62 0 89.8 82.12 0 85.7 79.43 80 0 0 100 0 21.3 94.12 0 32.8 91.23 70 2.6 0 97.76 0 0 100 0 0 100 105 90 0 88.9 85.71 0 94.2 80.11 0 100 76.41 80 0 11.1 98.2 0 23.1 91.32 0 57.2 87.54 70 0 0 100 0 0 100 0 0 100

表 1 耕地、林地和居民地异常检测精度分析 Table 1 Accuracy analysis of outlier detection for cultivated land, woodland and building

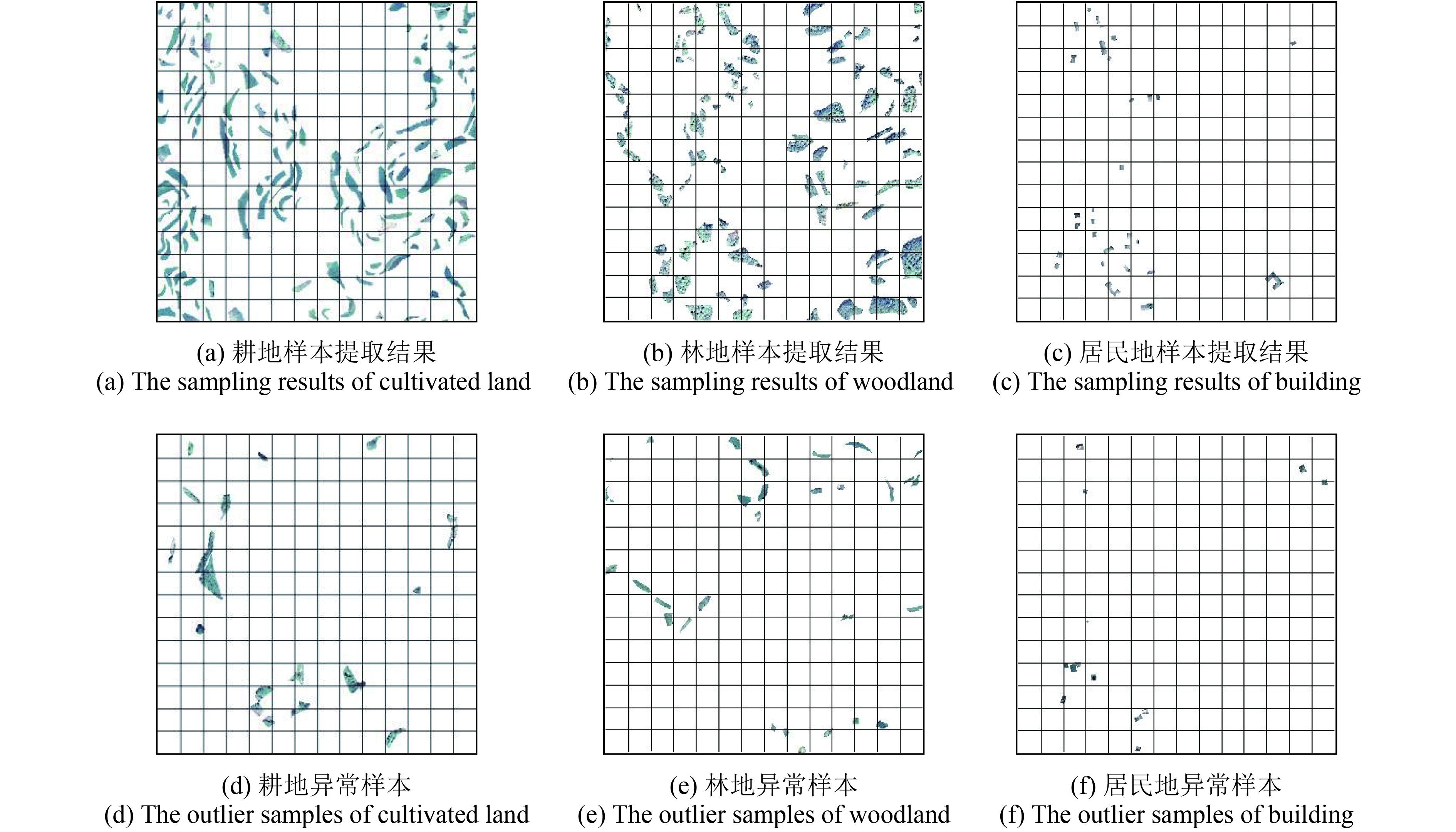
从表1可知，在异常度阈值取80%，k值低于90时，耕地的漏检率为0，林地的漏检率为21.3%，居民地的漏检率为32.8%。在异常度阈值取80%，k值低于65时，林地的漏检率为0, 而居民地只有当k值低于50时，漏检率才为0，其原因是林地的样本总数比耕地少，而居民地的样本总数最少，所以k值相对于样本总数的比例对异常检测结果精度有直接影响。而且，当耕地k在区间50−90取值，林地k在区间20−65取值，居民地k在区间10−50取值，异常度阈值取80%时，误检率和漏检率均为零，总体检测精度为100%。在设定异常度阈值为70%的条件下，无论k取何值时，耕地、林地和居民地的漏检率均为0。在样本影像对象异常检测中，只要能满足所抽取样本的验后类别与先验类别属性一致，则抽样就是成功的。也即是说，在异常检测中我们可以以牺牲一定的误检率来换取0漏检率。因此，为了获得0漏检率和较高的检测精度，一般情况下，k可以按布设样本总数的1/5−1/3取值，异常度阈值可设定为80%。本试验中，耕地取k=50、林地取k=35、居民地取k=20，异常度阈值设定为80%，异常检测结果如图8。

图 8 异常检测结果 Figure 8 The result of outlier detection

在充分利用矢量数据先验信息的基础上，为了实现遥感影像的自动变化检测，对变化检测样本的自动提取方法进行了研究，主要包括样本的空间布设和异常样本探测。样本布设采用分图层、根据地形分层级、按规则格网和影像对象空间分布特征进行随机抽样，从而确保了样本布设结果既具有随机性，也具有代表性和均质性，即既体现了抽样图层中影像对象的总体数字特征，也体现了典型正常区域样本数据集表示的正确性和唯一性。

在异常样本探测中，k的取值会影响样本对象的异常度指数，但是按样本总数的1/5—1/3取值时，异常度指数相对趋于稳定。异常度指数阈值的设定不同也会影响异常样本探测结果精度出现差异，较低的阈值可以获得异常样本较低的漏检率和较高的误检率，而较高的阈值会获得相反的结果。在样本提取结果中，更关心的是漏检率，可以以牺牲一定的误检率来换取0漏检率，一般情况下，将异常度阈值设定在80%或70%时可以获得0漏检率和较高的检测精度。该抽样方法对自动变化检测技术的实现具有一定的理论和实用价值，在灾后应急、地表环境监测等领域有较实用的价值。

然而，样本空间分布的差异性如何影响变化检测结果精度、样本布设结果中异常样本相对个数的多少对异常探测精度有多大影响以及如何选取合适的异常度阈值实现0误检率，这些都需要进一步的研究。