| 瑞利光学厚度模型的适用性讨论与条件性构建 |
收稿日期: 2018-09-14
2. Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China
3. Institute of Desert Meteorology, China Meteorological Administration, Urumqi 830002, China
大气中有各种气体成份以及水滴、尘埃等气溶胶颗粒,太阳辐射在大气中传输时受到大气的影响,其强度、传输方向以及偏振状态均会发生变化(Liou,2002;Bohren和Huffman,1983)。大气对电磁波的作用归纳为吸收、散射和折射,由于折射过程一般与能量收支问题关系较小而常被忽略(吴北婴 等,1998;Liou,2002;Bohren和Huffman,1983; 梁继,2010)。大气对光的散射重要而又普遍,因此,对散射现象的研究将能更好地了解散射过程对太阳辐射传输的影响。以尺度参数α(
瑞利散射是降低遥感影像“清晰度”或“对比度”造成影像辐射畸变、图像模糊的主要原因(赵英时,2003)。同时瑞利散射在影像邻近效应中将贡献出仅次于米氏散射的作用(Reinersman和Carder,1995;Miesch 等,1999;Liang 等,2001, 2002;Liang,2004)。瑞利光学厚度的参数反演随着高光谱遥感和高空间分辨率遥感的发展而越来越重要,在大气辐射传输模型的散射模块中也将迎来新的改进。比如ATCOR-2/3在2015年Ver 9.0版本中及时更新了CO2浓度默认值为400 ppm (Richter和Schläpfer,2018)。可见瑞利散射的大气校正和瑞利光学厚度的模拟对清洁大气的紫外—蓝绿红等较短波段的太阳辐射通量的精确模拟尤其重要。
大气中计算瑞利光学厚度ROD(Rayleigh Optical Depth)有很多不同的技术(Bodhaine 等,1999;Teillet,1990),概括讲包括数值模拟模型和利用瑞利散射理论构建的理论离散模型等。这两类模型都是以特定大气温度、大气压强和干空气大气分子体积比尤其以特定CO2浓度为大气背景条件而构建的函数(Möller,1957;Marggraf和Griggs,1969;Stephens,1994;Hansen和Travis,1974;Leckner,1978;Fröhlich和Shaw,1980;Dutton 等,1994)。然而自工业革命以来,全球CO2浓度持续增长,2015年已超过400 ppm,近3年更是以2.25 ppm/a的速度在增加(NOAA Research News,2015;Vaughan,2015)。虽然影响ROD的计算精度主要取决于大气气压、温度与湿度廓线的精度,CO2分子因其体积浓度相对较小被认为对总散射系数的影响极小,但随着全球CO2浓度的变化,气体分子体积比的微小改变,散射强度比如瑞利散射的强度会不会随之而变化、如何变化以及变化多少,都有待进一步的定量化研究。
鉴于这些问题,本文首先从大气散射理论和瑞利光学厚度理论出发,探讨文献或辐射传输模型中常见的近似数值模型与理论离散模型在CO2浓度变化下的优缺点及其适应性;然后以理论离散模型为基础,初步拟合构建适应当前CO2浓度下的瑞利光学厚度近似数值模型。
2、大气散射大气对辐射散射削弱作用的强弱取决于大气分子与气溶胶散射粒子的数密度(Ns, 量纲L–3, L为长度, 单位常用cm–3),以及每个大气分子m(瑞利散射)与散射粒子p(米氏散射)的散射截面σsc(scattering cross section, 单位常用cm2)与消光截面σex(extinction cross section)。散射理论就是研究如何计算不同大气分子与颗粒物的散射截面σsc与消光截面σex。
(2.1) 瑞利散射强度瑞利散射(Rayleigh scattering)也称分子散射(Molecular scattering),散射光强度可用式(1)表达。自然光的粒子近似散射光辐照度I与入射光辐照度I0的关系为(吴北婴 等,1998)
| ${{I}} = \frac{{{{{I}}_0}}}{{{r^2}}}{\gamma ^2}{\left({\frac{{2{{\text{π}}}}}{{\textit{λ}}}} \right)^4}\frac{{1 + {\rm{co}}{{\rm{s}}^2}\varTheta }}{2} = {{{I}}_0}{\rm{exp}}\left[ { - {{\tau }}\left({\textit{λ}} \right){{x}}} \right]$ |
式中,粒子对非偏振太阳光的散射强度I(λ)与入射光强I0成正比,与大气分子和观测点之间距离平方(r2)成反比。散射强度I还取决于极化率γ、入射波波长λ、散射角Θ(θ, φ),这3个参数为太阳光大气分子散射与粒子散射引入了许多重要的物理特征(Liou,2002)。大气质量x在数值上近似为secθ,θ为太阳天顶角。τ(λ)为总的消光光学厚度(Optical Depth)。
(2.2) 瑞利散射截面一般地,散射效率因子Qsc是指粒子的散射截面σsc与粒子的几何截面(S, S=2πr2)之比,即
| ${{{Q}}_{{\rm{sc}}}} = {{{\sigma }}_{{\rm{sc}}}}/{\rm{S}}$ | (2) |
式中,散射截面作为等效截面是指散射函数σ(θ, φ)在整个空间(即4π立体角上)的积分,即
若单位体积的干洁空气中有Ns个独立散射的粒子,引用“独立散射条件下总散射是各粒子散射之和”的原理,令单位体积中各分子散射截面之和为分子体散射系数
| ${{\kappa }}_{{\rm{sc}}}^{{m}} = {{{N}}_{\rm{s}}}{{\sigma }}_{{\rm{sc}}}^{{m}}$ | (3) |
式中,分子体散射系数
定义标准大气STP(standard air)干空气的条件为 1013.25 hPa(即1 atm)、288.15 K(15 ℃)、CO2含量300 ppm。瑞利散射截面解析表达式式(4) (Bucholtz,1995;Bodhaine 等,1999)
| ${{\sigma }}_{{\rm{sc}}}^{{m}}\left({\textit{λ}} \right) = \frac{{24{{\text{π}}^3}}}{{{{\textit{λ}} ^4}{{N}}_{\rm{s}}^2}}{\left({\frac{{{{n}}_{{s}}^2 - 1}}{{{{n}}_{{s}}^2 + 2}}} \right)^2}\left({\frac{{6 + 3{{\delta }}}}{{6 - 7{{\delta }}}}} \right)$ | (4) |
| $f\left( \varDelta \right) = \left( {6 + 3\delta } \right)/\left( {6 - 7\delta } \right)$ | (5) |
式中,f(Δ)为去极化项(depolarization term);δ为去极化因子(depolarization factor),也称各向异性因子(anisotropic factor),表征大气分子的折射指数ns沿着x、y和z方向的变化(吴北婴 等,1998)。Ns不受混合气体的影响,但随温度和压强而变化;f(Δ)独立于温度和压强,仅受混合气体的影响(Bodhaine 等,1999),Δ泛指大气成分,如N2、O2、Ar、CO2等。显然,ns和
空气看作干空气和水汽的混合物。大气折射指数的计算,与大气分子在外电场作用下的极化情况有关,极化率γ(polarizability)由电磁波的频散原理导出(Liou,2002),表达式就是著名的洛伦兹—洛伦茨公式(Lorentz-Lorenz formula),即
| ${{\gamma }} = \frac{3}{{4{\text{π}}{{{N}}_{{s}}}}}\left({\frac{{n_s^2 - 1}}{{n_s^2 + 2}}} \right)$ | (6) |
式中,ns是大气分子的无量纲折射指数。由于指数虚部太小,在太阳可见光谱的散射讨论中常忽略大气分子对太阳辐射的吸收作用。ns特指大气折射指数的实部。由于ns与1之差只有万分之几,在电波传播中常用大气折射指数差s用式(7)表示。
| ${{s}} = \left({{n_{{s}} } - 1} \right) \times {10^6}$ | (7) |
已知空气的极化率γ与相对介电常数ε的关系
| ${{\gamma }} = {{\varepsilon }} - 1$ | (8) |
已知介电常数ε和折射指数ns之间的关系
| ${{\varepsilon }} - 1 = n_{{s}} ^2 - 1 \approx 2\left({{n_{{s}} } - 1} \right)$ | (9) |
根据式(6)—式(9)导出大气折射指数ns的表达式。标准状态下干空气含有不同CO2浓度的大气折射指数及指数差常用模型总结如表1。
|
|
表 1 干空气大气折射指数常用模型 Table 1 Common models for air refraction index |
从表1中可以看出,Edlén (1966)更新了Edlén (1953)标准大气下干空气的大气折射指数的三项式公式,并成为新的标准公式。需要说明的是,Peck和Reeder (1972)在对比工作中认定Edlén (1966)公式中CO2浓度为330 ppm,与Edlén (1966)文献中实际提到的CO2浓度300 ppm并不一致。
本文利用Edlén (1966)文献中式(17)计算任意CO2浓度下(xCO2)的大气折射指数,则标准大气(1atm, 15 ℃)下的大气折射指数计算如下
| $\normalsize{\frac{{{{\left( {n - 1} \right)}_{x{\rm{C}}{{\rm{O}}_2}}}}}{{{{\left( {n - 1} \right)}_{300}}}} = 1 + 0.540\left( {x{\rm{C}}{{\rm{O}}_2} - 300 \cdot {{10}^{ - 6}}} \right)}$ | (10) |
同时,利用Edlén (1966)文献中式(15)来进一步修正该CO2浓度(xCO2)在不同温度T和压强P下的大气折射指数
| $\normalsize{{\left( {n - 1} \right)_{x{\rm{C}}{{\rm{O}}_2},{\rm{TP}}}} = {\left( {n - 1} \right)_{x{\rm{C}}{{\rm{O}}_2}}} \times \frac{{0.00138823P}}{{1 + 0.003671T}}}$ | (11) |
式中,T为摄氏温度(℃),P为毫米汞柱压强(mmHg)。Bodhaine等(1999)也有提到式(10),并将Peck和Reeder (1972)中330 ppm的折射指数代替了Edlén (1966)中300 ppm的折射指数作为标准公式。
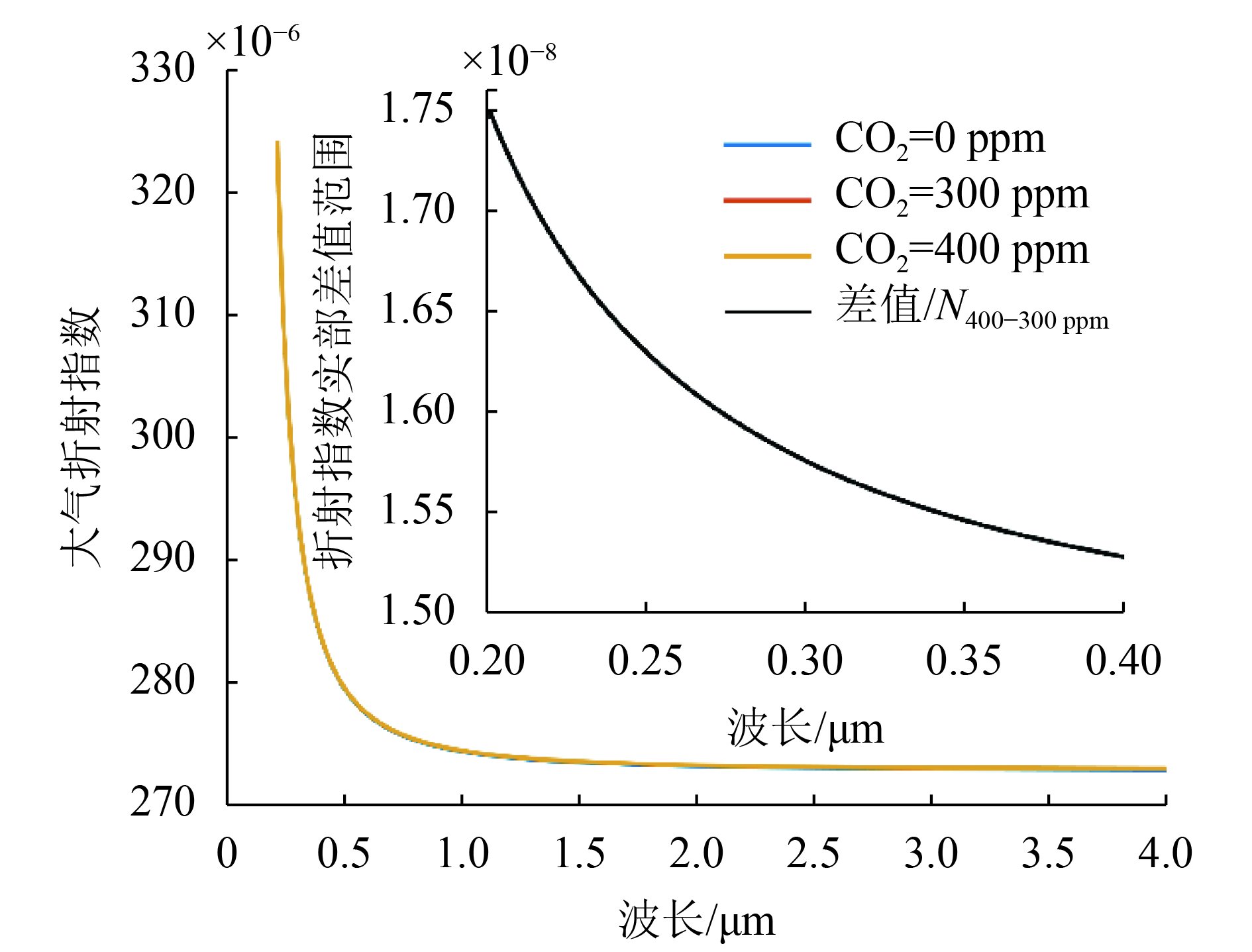
采用Edlén (1966)的标准公式(表1)以保证CO2浓度的一致性,Zhang等(2006, 2008)的研究也证明了Edlén (1966)标准公式的精度可靠。利用Edlén (1966)公式和式(10),分别作CO2浓度为0、300 ppm、400 ppm共3条大气折射指数差(ns−1)·106(图1),黑色线代表400 ppm与300 ppm的折射指数差值,波长越短,差值越大,最大差值在0.2 μm处的1.75%(×10–6)附近,即0.2 μm处的n400 ppm与n300 ppm比值为1.000054,说明了CO2浓度的变化对干空气折射指数存在影响且不可忽略。
|
| 图 1 大气折射指数的模拟 Figure 1 Simulation of refraction index of dry air |
根据太阳辐射衰减的消光原理,大气总的消光光学厚度τex(λ)可分解为
| $\normalsize{{\tau _{{\rm{ex}}}}\left({\textit{λ}} \right) = {\tau _{\rm{m}}}\left({\textit{λ}} \right) + {\tau _{\rm{p}}}\left({\textit{λ}} \right) + {\tau _{\rm{g}}}\left({\textit{λ}} \right)}$ | (12) |
式中,τm(λ)为瑞利光学厚度,τp(λ)为气溶胶光学厚度,τg(λ)为混合气体分子的吸收光学厚度(如O3、NO2、均匀混合气体等)。瑞利光学厚度代表了大气分子相对于给定波长入射光的衰减率,整个分子大气在给定波长上的光学厚度可由散射截面来计算,形如
| $\normalsize{{\tau _{\rm{m}}}\left( {\textit{λ}} \right) = \int_0^{{Z_\infty }} {\sigma _{{\rm{sc}}}^{\rm{m}}} \left({\textit{λ}} \right){N_s}\left( Z \right){\rm{d}}Z}$ | (13) |
式中,Ns(Z)是随着高度变化的分子数密度,
| ${{\tau _{\rm{m}}}\left({\textit{λ}} \right) = \frac{{24{{\text{π}} ^3}{N_c}}}{{{{\textit{λ}} ^4}N_s^2}}{\left( {\frac{{n_s^2 - 1}}{{n_s^2 + 2}}} \right)^2}\left( {\frac{{6 + 3\delta }}{{6 - 7\delta }}} \right)\left( {\frac{P}{{{P_0}}}} \right)\left( {\frac{{{T_0}}}{T}} \right)}$ | (14) |
在文献和大气辐射传输模型中,典型的常见的瑞利光学厚度近似数值模拟方法总结如表2。
|
|
表 2 瑞利光学厚度代表性数值模型 Table 2 ROD Numerical models for dry air |
从表2中可以看出,所有模型都是波长的函数,并且近似与波长的4次方成反比(λ–4);只有Marggraf和Griggs (1969)和Dutton等(1994)与地理位置的高程相关,并且只有Dutton等(1994)的CO2浓度是330 ppm,其余4个模型看作在全球上是一个“稳定”的定值(Liang,2004)。
Bodhaine等(1999)认为,假定瑞利光学厚度在0.3 μm处的数值为1,那么该处0.1%的瑞利光学厚度误差将等价于0.55 μm处10%的气溶胶光学厚度误差。换句话说,瑞利光学厚度在数值上虽然变化量非常小,其影响实际与气溶胶光学厚度同等重要。
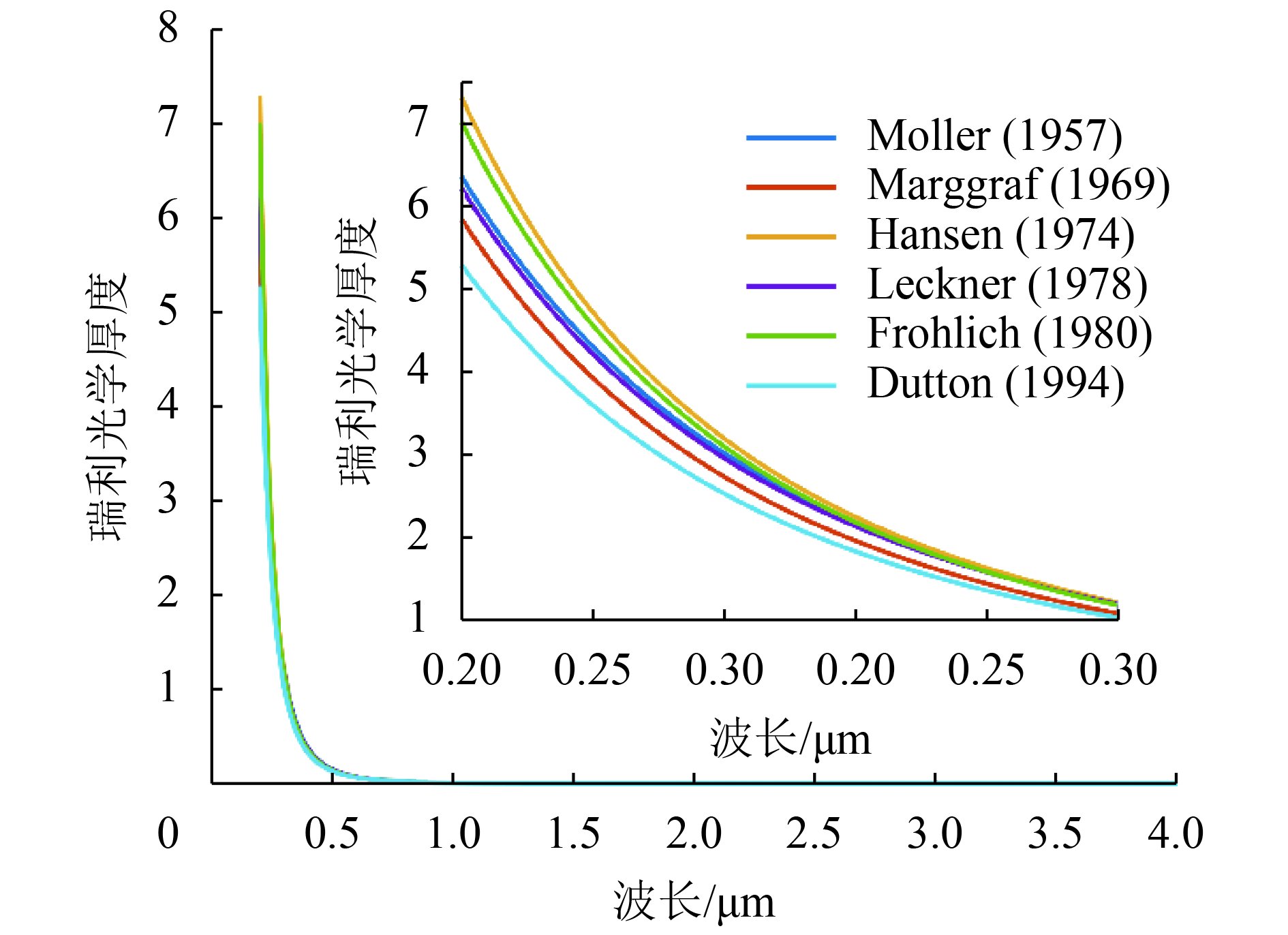
以内蒙古自治区阿尔山火车站为例(简称“6.阿尔山”, Arxan, 982 m),分别计算0.2—4.0 μm波段的瑞利光学厚度(图2)。ROD模拟值的大小排序为:Hansen和Travis (1974)>Fröhlich和Shaw (1980)>Möller (1957)>Leckner (1978)>Marggraf和Griggs (1969)>Dutton等(1994),且最大差值在0.2 μm处的2.0152附近。
|
| 图 2 阿尔山地区瑞利光学厚度的模拟 Figure 2 Simulation of Rayleigh optical depth in Arxan |
在“6.阿尔山”实例中,0.3 μm处6大代表模型的对比差值可达18.40%。可见,(1)近似数值模型模拟瑞利光学厚度时在没有验证数据的基础上很难判断哪个模型的模拟精度会更好,因此大气辐射传输模型中ROD模块的选择如SMART模型选用的Leckner (1978)公式在精度方面应有客观的评价;(2)所有数值模型针对的CO2浓度及其模型的适应性均有待提高;(3)高程和大气压强的影响不可忽略。
需要说明的是,Marggraf和Griggs (1969)原文和Teillet (1990)引文中均对Marggraf公式有书写错误。通过作图对比(图2),验证并确认了Stephens (1994)和Bodhaine等(1999)对Marggraf公式的书写和引用才是正确的公式表达(表2)。
(3.2) 理论离散模型瑞利光学厚度模拟中,近似数值模型简单方便,但适用性和精度有待提高。鉴于这点,本文使用散射理论构建的离散模型,该模型的精确计算所需物理常数和观测值均取自国际CODATA最新推荐(Mohr,2016),根据式(14)简化得到
| $\normalsize{{\tau _{\rm{m}}}\left( {\textit{λ}} \right) = \sigma _{{\rm{sc}}}^{\rm{m}}\left( {\textit{λ}} \right)\frac{{P\cdot{{\rm{N}}_{\rm{A}}}}}{{{M_{{\rm{air}}}}\cdot{\rm{g}}}}}$ | (15) |
式中,NA为阿佛加德罗常数(Avogadro constant, 1atm NA=6.022140857×1023 mol–1);Mair为大气平均分子数(molecular weight, gmol–1);g为重力加速度(acceleration of gravity, m/s2);P为压强(pressure,
大气成分及其体积百分比相对比较稳定,最新的干空气大气成分及其体积比见表3 (Picard 等,2008)。
|
|
表 3 干空气大气成分及其体积比(Picard 等,2008) Table 3 Composition and volume weight of dry airfrom CIPM-2007 (Picard et al., 2008) |
一般地,干空气大气平均分子摩尔质量数(
| ${{M_{{\rm{air}}}} = \sum\limits_i {\left( {{C_{{\Delta _i}}}{M_{{\Delta _i}}}} \right)}\large/\sum\limits_i {\left( {{C_{{\Delta _i}}}} \right)} }$ | (16) |
则大气平均分子摩尔质量数Mair随CO2浓度(xCO2)变化的计算如下
| ${{M_{{\rm{air}}}} = 28.95943578 + 15.0556 \times \left({x{\rm{C}}{{\rm{O}}_2}} \right)}$ | (17) |
利用式(17),分别模拟CO2浓度为300 ppm和400 ppm的大气平均分子摩尔质量为28.963952和28.965458,二者相差0.1506%。
3.2.2. 去极化项与散射截面Young(1980, 1981)建议将f(Δ)赋值1.0480代替Penndorf (1957)给定值1.0608,这将使得瑞利散射强度降低1.2%;而且因为f(Δ)也取决于波长,该值不能应用于整个光谱。根据Alms等(1975)和Bates(1984)的研究成果,忽略其他大气成分,可以获得
| ${F\left({{{\rm{N}}_2}} \right) = 1.034 + 3.170 \cdot {10^{ - 4}}/{{\textit{λ}}^2}}$ | (18) |
| ${F\left({{{\rm{O}}_2}} \right) = 1.096 + 1.385\frac{{{{10}^{ - 3}}}}{{{{\textit{λ}}^2}}} + 1.448\frac{{{{10}^{ - 4}}}}{{{{\textit{λ}}^4}}}}$ | (19) |
| ${F\left({{\rm{Ar}}} \right) = 1.00}$ | (20) |
| ${F\left({{\rm{C}}{{\rm{O}}_2}} \right) = 1.15}$ | (21) |
由式(18)—(21)生成混合大气去极化项f(Δ)为
| ${f\left( \varDelta ,{\textit{λ}} \right) = \sum\limits_i {\left[ {{C_{{\Delta _i}}}f\left( {{\Delta _i}} \right)} \right]} /\sum\limits_i {\left( {{C_{{\Delta _i}}}} \right)}} $ | (22) |
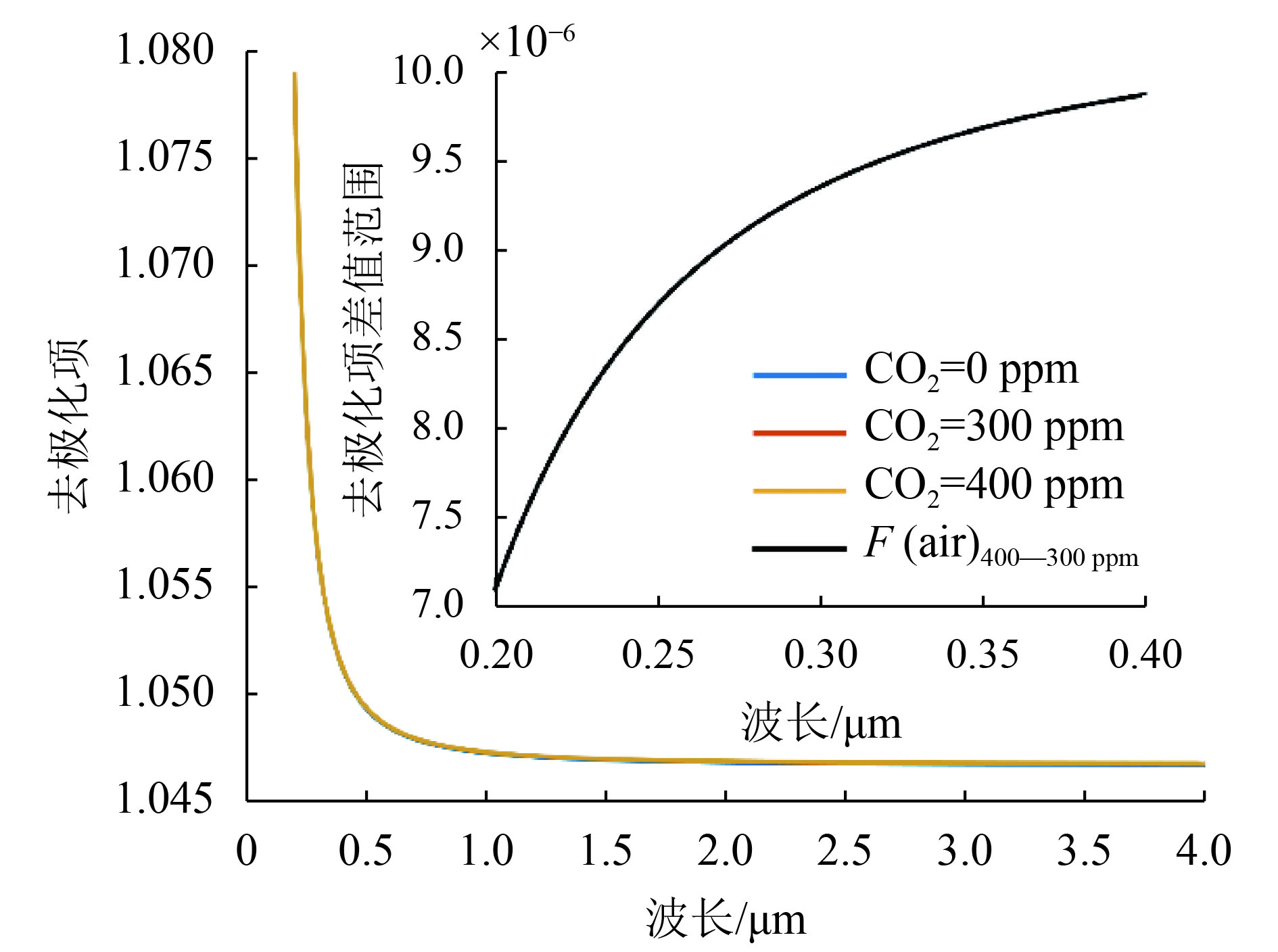
从图3中可见,去极化项随波长而逐渐变小;以CO2浓度400 ppm和300 ppm的去极化项对比,以波长0.2—4.0 μm为例,最小差值发生在0.2 μm处的7.089386×10–6附近,最大差值在4.0 μm处的10.325763×10–6附近;以CO2浓度400 ppm和0 ppm的去极化项对比,最小差值在0.2 μm处的2.836605×10–5附近,最大差值在4.0 μm处的4.131545×10–5附近。整体来看CO2浓度的变化对去极化项的影响比较小,紫外和蓝光波段的差值比近红和短波红外的差值更小。
|
| 图 3 不同CO2浓度的去极化项模拟 Figure 3 Calculation of depolarization terms for various CO2 concentrations |
由式(4)、(9)和(22),进一步简化合并大气分子的瑞利散射截面如下
| ${\sigma _{{\rm{sc}}}^m\left({\textit{λ}} \right) = \frac{{32{{\text{π}}^3}}}{{3{{\textit{λ}} ^4}N_s^2}}{\left( {{n_s} - 1} \right)^2}f\left( {\varDelta ,{\textit{λ}}} \right)}$ | (23) |

|
| 图 4 瑞利散射截面模拟 Figure 4 Rayleigh scattering cross section simulation |
分子数密度Ns与温度和气压相关,而散射截面又与分子数密度相关。忽略散射截面随高程的变化,根据式(23)作大气条件P0=1 atm、T=15 ℃、CO2浓度分别为0、300 ppm和400 ppm共3条瑞利散射截面图,数量级10−25 cm2 (如图4),其中,1 atm Ns(T=15 ℃)=2.546 9174×1019 cm−3,也称洛施密特常量(Losch-midt constant)。瑞利散射截面随波长而变化,近似与波长的4次方成反比;以CO2浓度400 ppm和300 ppm的瑞利散射截面对比,最大差值在0.2 μm处的0.41377‰(×10−25) cm2附近;以CO2浓度400 ppm和0 ppm的瑞利散射截面对比,最大差值在0.2 μm处的1.654986‰(×10−25) cm2附近。整体来看CO2浓度的变化对瑞利散射截面有一定的影响,且在紫外、蓝波段更显著。
3.2.3. 重力加速度据国际CODATA组织和史密森尼学会(Smith-sonian Institution)推荐(Forsythe,2003),标准重力加速度为9.80665 m/s2,该值是国际度量衡委员会(International Committee on Weights and Measures)于1901年在纬度45°地区最初采用的标准值,比该地区实际测量高了大约万分之五,即g(45°)=9.80616 m/s2。该标准值实际测量于45°32′33″纬度地区,即g(45°32′33″)=9.80665 m/s2。
假设某地理位置所在纬度ϕ(°)海平面处重力加速度为gϕ,t=cos2ϕ,则gϕ的表达式为(Letestu,1966;Bodhaine 等,1999)
| ${{g_\phi } = 980.616\left({1 - 0.0026373t + 0.0000059{t^2}} \right)}$ | (24) |
若该点海拔高程为Z(m),则该处随高程变化的重力加速度gϕz计算(Letestu,1966;Bodhaine 等,1999)
| $\left\{ \begin{aligned} & a1 = \left( {3.085462 \times {{10}^{ - 4}} + 2.27 \times {{10}^{ - 7}}t} \right) \times Z\\ & a2 = \left( {7.25400 \times {{10}^{ - 11}} + 1.0 \times {{10}^{ - 13}}t} \right) \times {Z^2}\\ & a3 = \left( {1.51700 \times {{10}^{ - 17}} + 6.0 \times {{10}^{ - 20}}t} \right) \times {Z^3}\\ & \;\;{g_{\phi z}} = \left( {{g_\phi } - a1 + a2 - a3} \right)/100 \end{aligned} \right.$ | (25) |
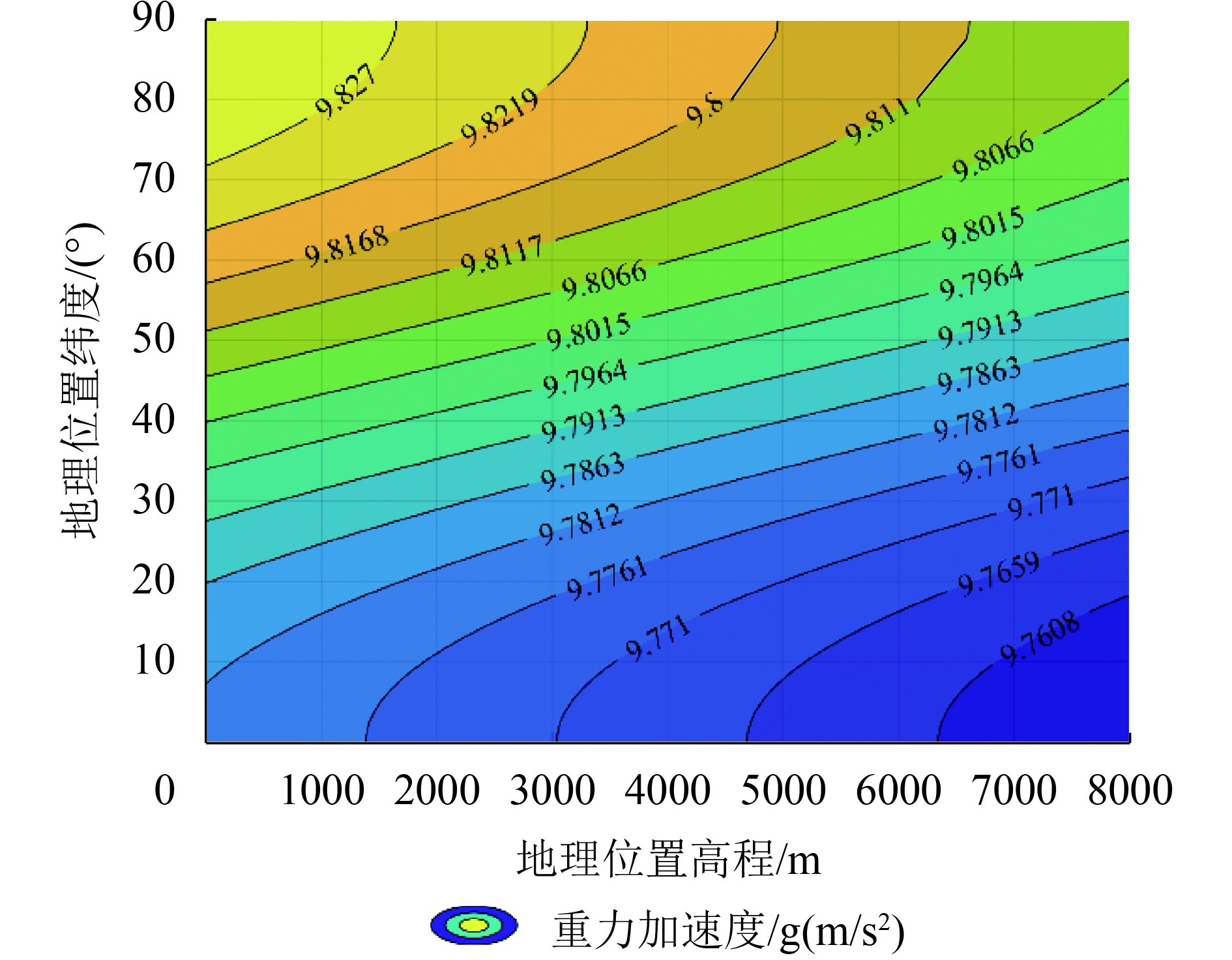
依式(25)作图(图5),重力加速度gϕz随纬度ϕ和高程Z而变化,且随着纬度越高,或海拔越低,重力加速度会增大;反之亦然。
|
| 图 5 重力加速度的模拟 Figure 5 Simulation of gravitational acceleration |
为保持与表1中的干空气折射指数和表2中ROD模拟公式的大气温度的条件一致,本文以地理位置1. 唐古拉山,2. 八一冰川,3. 珠峰站,4. 玉龙雪山,5. 玛纳斯河,6. 阿尔山,7. 奈曼站,8. 科技大学,9. 珠海分校为例(表4),假定大气条件T=15 ℃、CO2=400 ppm,模拟:随高程变化的大气压强(P)、混合大气平均摩尔质量数(Mair)、各地理位置的重力加速度(gϕz)、大气折射指数(ns)、去极化项( f(Δ))、瑞利散射截面(σscm)等参数,再通过理论离散模型来模拟波长在0.2—4.0 μm的ROD (τm(λ)),模拟结果见图6 (λ=0.2—0.55 μm)。
|
|
表 4 瑞利光学厚度模拟试验地理位置分布 Table 4 Geographical distribution of ROD simulation |
|
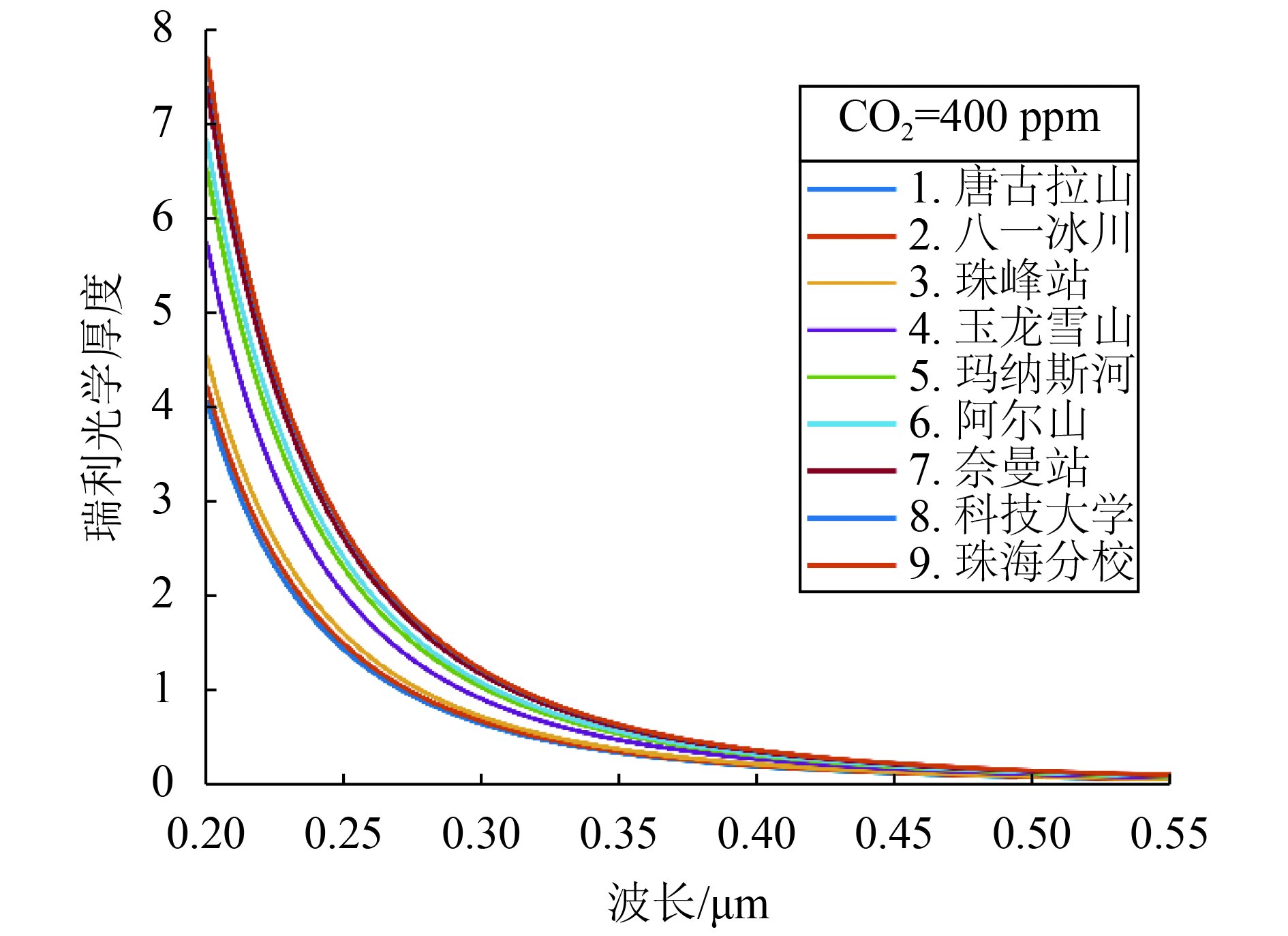
| 图 6 各地理位置的瑞利光学厚度模拟 Figure 6 ROD simulation of various geographic locations |
从图6和表5可以发现,ROD随波长变化,且在红绿蓝光—紫外波段方向的变化更显著;ROD随高程(或者压强)变化而变化,且高程越高,ROD相比越小;高程越低,ROD越大。对比“1. 唐古拉山”和“9. 珠海分校”的ROD,在0.20 μm、0.30 μm、0.40 μm、0.50 μm共4个中心波长的对比差值分别是3.6847、0.5767、0.1708、0.0680。可见瑞利光学厚度主要由波长λ和高程Z共同作用,且高程影响很大。
(4.2) 近似数值模拟模型的构建由理论离散模型模拟的ROD数据进一步拟合构建波长在0.2—4.0 μm的9个不同海拔高度的数值模型。从表6中可以发现,构建的f(x)=aλb数值模拟模型中,b=−4.529;同时根据高程Z和系数a的关系,继续模拟系数得到a=0.005179·e–0.0001249Z,R2-adjusted为0.9999,RMSE为3.779E−06。
|
|
表 5 瑞利光学厚度对比分析 Table 5 Comparison and analysis of ROD |
|
|
表 6 瑞利光学厚度的数值模拟方程 Table 6 Numerical simulation equations of ROD |
此时模拟该大气状况(15℃, CO2=400 ppm)下ROD数值模拟的完整结构式如下
| ${{\tau _m}\left({\textit{λ}} \right) = 0.005179{{\textit{λ}} ^{ - 4.529}} \cdot {{\rm{e}}^{ - 0.0001249Z}}}$ | (26) |
式(26)简称本文模型,R2-adjusted为0.9997,RMSEROD在0.005824—0.011090,模拟表7中RMSEROD与高程Z的关系如:RMSEROD= 0.01111·e−0.0001248Z,R2-adjusted为0.9999,RMSE为6.419E−06。也就是说,随着高程Z的变化,本文模型的RMSEROD也随之变化,且高程越高,RMSEROD越小;当高程为0时,RMSEROD有最大值0.01111。
|
|
表 7 CO2对瑞利光学厚度贡献对比 Table 7 Comparison of CO2 contribution to ROD (×10−3) |
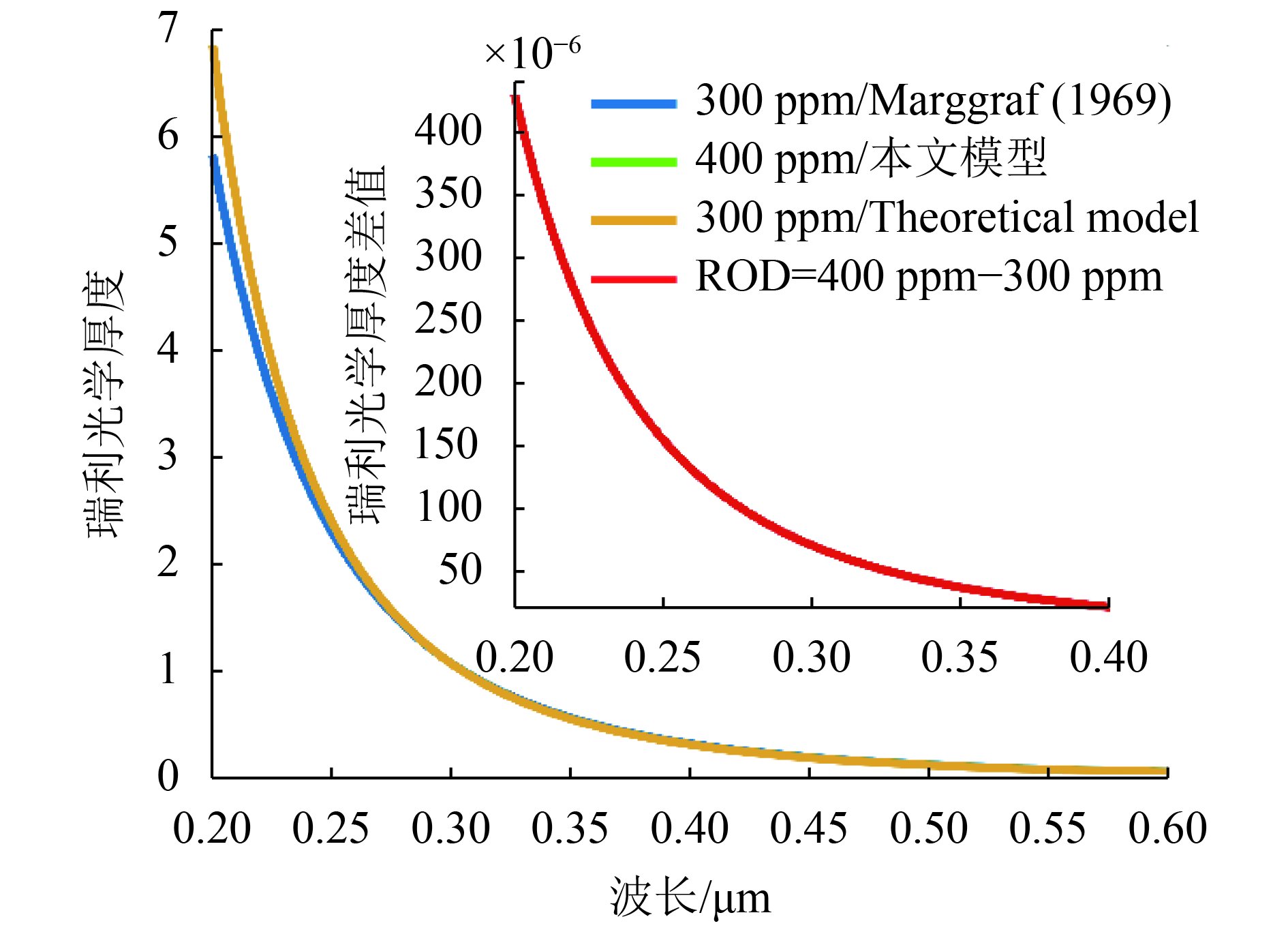
取CO2浓度300 ppm 的Marggraf和Griggs (1969)公式、400 ppm的本文模型,和300 ppm的式(15),以“6. 阿尔山”为例,分别模拟该地区瑞利光学厚度(图7)。
|
| 图 7 阿尔山地区瑞利光学厚度的数值模拟对比 Figure 7 Comparison of numerical simulation of ROD in Arxan |
从图7结合表2中可以看出,阿尔山地区ROD的排序:Hansen和Travis (1974)>Fröhlich和Shaw (1980)>本文模型>理论离散式(15)>Möller (1957)>Leckner (1978)>Marggraf和Griggs (1969)>Dutton等(1994),这说明表2中大部分典型的近似数值模型存在ROD低估的现象;在大气温度、大气压强和高程相同且CO2浓度相差100 ppm的情况下,本文模型和式(15)模拟的ROD在0.2 μm处明显高于Marggraf和Griggs (1969),且二者差值分别为1.02675755、1.02632806;本文模型与式(15)模拟的ROD差值在0.20 μm、0.30 μm、0.40 μm、0.50 μm共4个波长分别是:4.295×10–4、6.968×10–5、2.08×10–5、8.30×10–6,这说明CO2浓度的变化在紫外—蓝绿波段对ROD的影响虽然很小(10–6—10–4),但确实存在且ROD随着CO2浓度的增大而增大。
(4.4) CO2浓度的贡献以理论离散公式(15)为背景,模拟1 atm和15℃大气状况下CO2浓度为400 ppm和300 ppm分别对ROD的贡献(表6)。从表6中可以看出,CO2浓度对ROD的贡献随着高程的增加而减少;随CO2浓度的增加,对ROD的贡献随之也增加。在紫外—蓝波段CO2浓度对ROD的贡献在10–4—10–3数量级,CO2浓度的贡献不可忽略,尤其目前全球CO2浓度仍在以2.25 ppm/a的速度增长。
5、结 论(1)瑞利散射强度是波长的函数,波长越短,散射强度越大。与理论离散公式(15)相比,表2中大部分典型近似模型存在低估ROD的现象;通过式(15),导出400 ppm的近似数值模型(本文模型),即瑞利散射强度I与波长λ的4.529次方成反比,即:I∝λ–4.529,指数上的差别主要原因是理论离散公式(15)修正了大气折射指数和分子数密度在温度和气压上的变化;紫外—蓝波段CO2浓度对ROD的贡献在10−4—10−3数量级。
(2) 瑞利光学厚度理论离散模型涉及物理参数众多,使用最新发布的物理常数有利于减少模型误差。常见物理常数发布组织有:国际CODATA和NIST网站;Smithsonian Institution (史密森尼学会)、International Meteorological Tables、CIPM,等等。
(3) 瑞利光学厚度理论离散模型,物理意义明确,但各相关输入的物理参数求解复杂;近似数值模拟模型主要是波长λ和高程Z的函数,计算简单,速度快,但模型对大气条件和CO2浓度的适应性较差。数值模型可由理论离散模型拟合构建,在相同大气条件下理论离散模型的模拟结果相对更优。
(4) 瑞利散射截面
(5) 瑞利散射对紫外—蓝绿红波段影响最大。蓝绿波段位于水体衰减系数最小、散射最弱的波段,对水体的穿透力最大;而积雪表面尤其是新雪表面在蓝绿波段有强的反射作用。也就是说,瑞利散射会对定量估计水体和积雪表面的辐射通量的影响较大,如水体在蓝绿波段水深的反演、积雪在蓝绿波段黑碳浓度的反演等。
鉴于理论离散模型和近似数值模型的优缺点,以及每个近似数值模型均有特定大气条件的限制。因此,后续的研究工作主要分为下述几点展开:
(1) 进一步探讨数值模型系数在不同大气条件下(如温度、压强、CO2浓度)的变化规律,以提高近似数值模拟模型的自适应性;
(2) 借助全球碳卫星观测系统,反演全球CO2浓度分布状况,耦合全球DEM数据和温度场数据,进一步解析全球瑞利光学厚度的分布,以科学严谨的态度评估“全球是定值”的问题;
(3) 改进如WW模型、DISORT模型、ART模型等积雪辐射传输模型中瑞利光学厚度的模拟算法,以提高雪冰遥感中对蓝绿波段敏感的黑碳浓度的反演精度及其误差估计;
(4) 随着高空间分辨率遥感和高光谱遥感的发展,影像像元的邻边效应辐射的贡献越来越明显,分解气溶胶光学厚度的影响后,评估瑞利散射对山区雪面高分影像邻边效应的影响将是提高雪面反照率精度的新视角之一。
志 谢 感谢兰州大学草地农业科技学院黄晓东副教授、中国科学院寒区旱区环境与工程研究所何晓波副研究员和冯克庭工程师分享模拟试验中所需要的部分信息!
| [1] | Alms G R, Burnham A K and Flygare W H. Measurement of the dispersion in polarizabilities anisotropies[J]. Journal of Chemical Physics, 1975, 63 (8) : 3321 –3326. DOI: 10.1063/1.431821 |
| [2] | Bates D R. Rayleigh scattering by air[J]. Planetary and Space Science, 1984, 32 (6) : 785 –790. DOI: 10.1016/0032-0633(84)90102-8 |
| [3] | Bodhaine B A, Wood N B, Dutton E G and Slusser J R. On Rayleigh optical depth calculations[J]. Journal of Atmospheric and Oceanic Technology, 1999, 16 (11) : 1854 –1861. DOI: 10.1175/1520-0426(1999)016<1854:ORODC>2.0.CO;2 |
| [4] | Bohren C F and Huffman D R. 1983. Absorption and Scattering of Light by Small Particles. New York: Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim: 530 |
| [5] | Bucholtz A. Rayleigh-scattering calculations for the terrestrial atmosphere[J]. Applied Optics, 1995, 34 (15) : 2765 –2773. DOI: 10.1364/AO.34.002765 |
| [6] | Dutton E G, Reddy P, Ryan S and DeLuisi J J. Features and effects of aerosol optical depth observed at Mauna Loa, Hawaii: 1982-1992[J]. Journal of Geophysical Research: Atmospheres, 1994, 99 (D4) : 8295 –8306. DOI: 10.1029/93JD03520 |
| [7] | Edlén B. The dispersion of standard air[J]. Journal of the Optical Society of America, 1953, 43 (5) : 339 –344. DOI: 10.1364/JOSA.43.000339 |
| [8] | Edlén B. The refractive index of air[J]. Metrologia, 1966, 2 (2) : 71 –80. DOI: 10.1088/0026-1394/2/2/002 |
| [9] | Forsythe W E. 2003. Smithsonian Physical Tables. 9th ed. Washington: the Smithsonian Institution: 898. |
| [10] | Fröhlich C and Shaw G E. New determination of Rayleigh scattering in the terrestrial atmosphere[J]. Applied Optics, 1980, 19 (11) : 1773 –1775. DOI: 10.1364/AO.19.001773 |
| [11] | Hansen J E and Travis L D. Light scattering in planetary atmospheres[J]. Space Science Reviews, 1974, 16 (4) : 527 –610. DOI: 10.1007/BF00168069 |
| [12] | Leckner B. The spectral distribution of solar radiation at the earth’s surface-Elements of a Model[J]. Solar Energy, 1978, 20 (2) : 143 –150. DOI: 10.1016/0038-092X(78)90187-1 |
| [13] | Letestu S. 1966. International Meteorological Tables. Geneva: Secretariat of the World Meteorological Organization: 327 |
| [14] | 梁继. 2010. 雪面反照率反演与多尺度效应研究. 北京: 中国科学院研究生院: 131 Liang J. 2010. Snow Albedo Retrieval and Multiscale Analysis of Remote Sensing, Dissertation submitted to Cold and Arid Regions Environmental and Engineering Research Institute (CAREERI). Beijing: University of Chinese Academy of Sciences: 131 |
| [15] | Liang S, Fang H and Chen M. Atmospheric correction of landsat ETM+ land surface imagery. I. Methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39 (11) : 2490 –2498. DOI: 10.1109/36.964986 |
| [16] | Liang S L. 2004. Quantitative Remote Sensing of Land Surfaces. New York, NY: John Wiley and Sons, Inc. |
| [17] | Liang S L, Fang H L, Morisette J T, Chen M Z, Shuey C J, Walthall C L and Daughtry C S T. Atmospheric correction of Landsat ETM+ land surface imagery. II. Validation and applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40 (12) : 2736 –2746. DOI: 10.1109/TGRS.2002.807579 |
| [18] | Liou K N. 2002. An Introduction to Atmospheric Radiation. 2nd ed. Amsterdam: Elsevier |
| [19] | Marggraf W A and Griggs M. Aircraft measurements and calculations of the total downward flux of solar radiation as a function of altitude[J]. Journal of the Atmospheric Sciences, 1969, 26 (3) : 468 –477. DOI: 10.1175/1520-0469(1969)026<0469:AMACOT>2.0.CO;2 |
| [20] | Miesch C, Briottet X, Kerr Y H and Cabot F. Monte Carlo approach for solving the radiative transfer equation over mountainous and heterogeneous areas[J]. Applied Optics, 1999, 38 (36) : 7419 –7430. DOI: 10.1364/AO.38.007419 |
| [21] | Mohr P J, Newell D B and Taylor B N. CODATA recommended values of the fundamental physical constants: 2014[J]. Journal of Physical and Chemical Reference, 2016, 45 (4) : 043102 . DOI: 10.1063/1.4954402 |
| [22] | Möller F. 1957. Strahlung in der unteren Atmosphäre//Bartels J, ed. Geophysik II/Geophysics II. Berlin, Heidelberg: Springer [DOI: 10.1007/978-3-642-45881-1_2] |
| [23] | NOAA Research News. 2015. Greenhouse gas benchmark reached, global carbon dioxide concentrations surpass 400 parts per million for the first month since measurements began[EB/OL]. https://www.democraticunderground.com/112785204[2018-07-27] |
| [24] | Peck E R and Reeder K. Dispersion of air[J]. Journal of the Optical Society of America, 1972, 62 (8) : 958 –962. DOI: 10.1364/JOSA.62.000958 |
| [25] | Penndorf R. Tables of the refractive index for standard air and the Rayleigh scattering coefficient for the Spectral Region Between 0.2 and 20.0 μ and their Application to Atmospheric Optics[J]. Journal of the Optical Society of America, 1957, 47 (2) : 176 –182. DOI: 10.1364/JOSA.47.000176 |
| [26] | Picard A, Davis R S, Gläser M and Fujii K. Revised formula for the density of moist air (CIPM-2007)[J]. Metrologia, 2008, 45 (2) : 149 –155. DOI: 10.1088/0026-1394/45/2/004 |
| [27] | Reinersman P N and Carder K L. Monte Carlo simulation of the atmospheric point-spread function with an application to correction for the adjacency effect[J]. Applied Optics, 1995, 34 (21) : 4453 –4471. DOI: 10.1364/AO.34.004453 |
| [28] | Richter R and Schläpfer D. 2018. Atmospheric/Topographic Correction for Satellite Imagery[EB/OL]. [2018-07-26]. https://www.rese-apps.com/pdf/atcor3_manual.pdf |
| [29] | 盛裴轩, 毛节泰, 李建国, 张霭琛, 桑建国, 潘乃先. 2003. 大气物理学. 北京: 北京大学出版社: 522 Sheng P X, Mao J T, Li J G, Zhang A C, Sang J G and Pan N X. 2003. Atmospheric Physics. Beijing: Peking University Press: 522 |
| [30] | Stephens G L. 1994. Remote Sensing of the Lower Atmosphere. Oxford: Oxford University Press: 523 |
| [31] | Teillet P M. Rayleigh optical depth comparisons from various sources[J]. Applied Optics, 1990, 29 (13) : 1897 –1900. DOI: 10.1364/AO.29.001897 |
| [32] | Vaughan A. 2015. Global Carbon Dioxide Levels Break 400ppm Milestone. The Guardian. https://www.theguardian.com.environment/2015/may/06/global_carbon_dioxide_levels_break_400ppm_milestone[2018-09-14] |
| [33] | 吴北婴, 李卫, 陈洪滨. 1998. 大气辐射传输实用算法. 北京: 气象出版社: 138 Wu B Y, Li W and Chen H B. 1998. Practical Method of Atmospheric Radiative Transfer. Beijing: Meteorological Press, 138 |
| [34] | Young A T. Revised depolarization corrections for atmospheric extinction[J]. Applied Optics, 1980, 19 (20) : 3427 –3428. DOI: 10.1364/AO.19.003427 |
| [35] | Young A T. On the Rayleigh-scattering optical depth of the atmosphere[J]. Journal of Applied Meteorology, 1981, 20 (3) : 328 –330. DOI: 10.1175/1520-0450(1981)020<0328:OTRSOD>2.0.CO;2 |
| [36] | Zhang J, Lu Z H, Menegozzi B and Wang L J. Application of frequency combs in the measurement of the refractive index of air[J]. Review of Scientific Instruments, 2006, 77 (8) : 083104 . DOI: 10.1063/1.2239036 |
| [37] | Zhang J, Lu Z H and Wang L J. Precision refractive index measurements of air, N2, O2, Ar, and CO2 with a frequency comb [J]. Applied Optics, 2008, 47 (17) : 3143 –3151. DOI: 10.1364/AO.47.003143 |
| [38] | 赵英时. 2003. 遥感应用分析原理与方法. 北京: 科学出版社: 478 Zhao Y S. 2003. Principle and Method of Remote Sensing Application Analysis. Beijing: Science Press: 478 |

